Early Detection of Crop Injury from Glyphosate on Soybean and Cotton Using Plant Leaf Hyperspectral Data
Abstract
:1. Introduction
2. Methodology
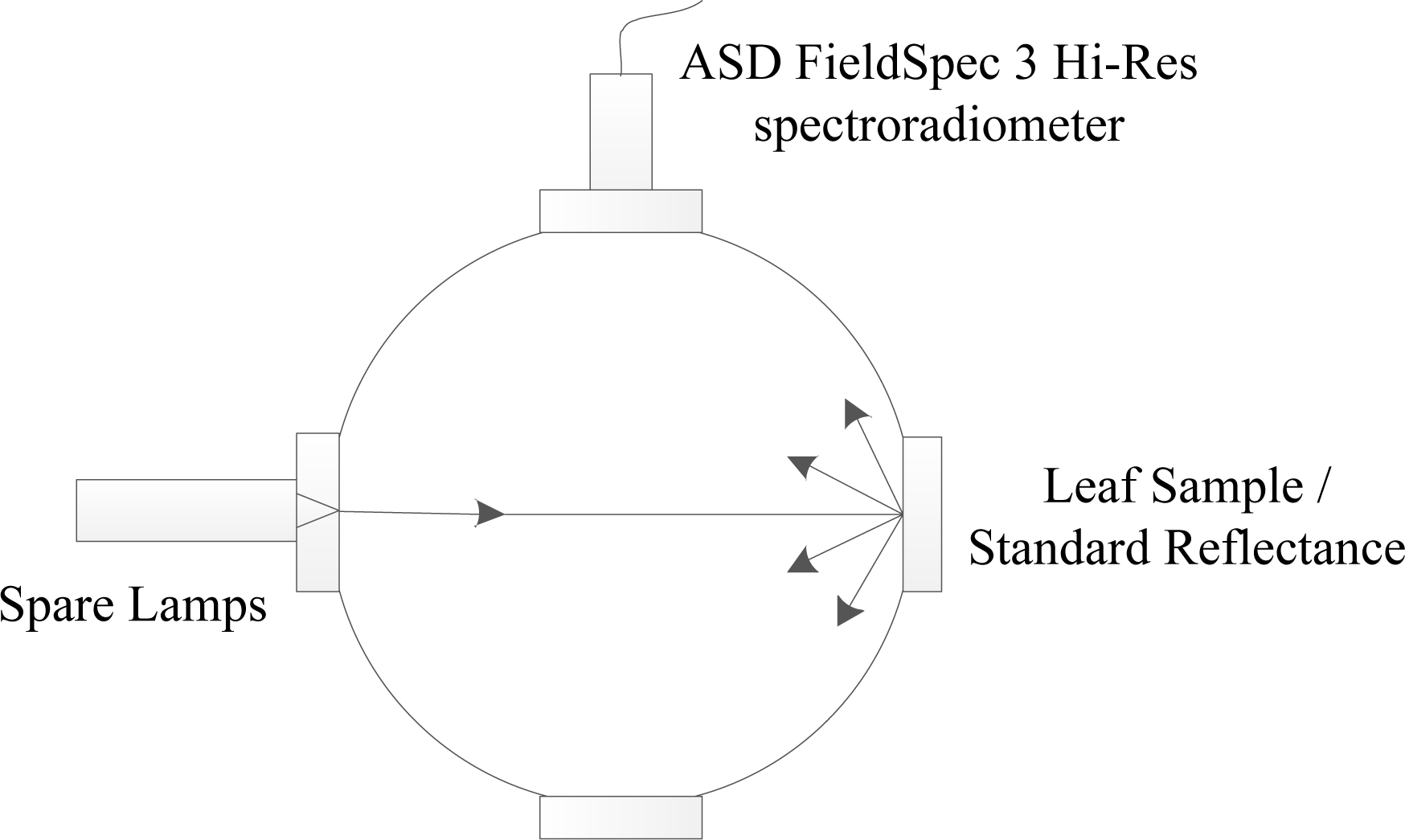
2.1. Experiment Design and Data Measurement
2.2. Spectral Indices for Glyphosate Injury Detection
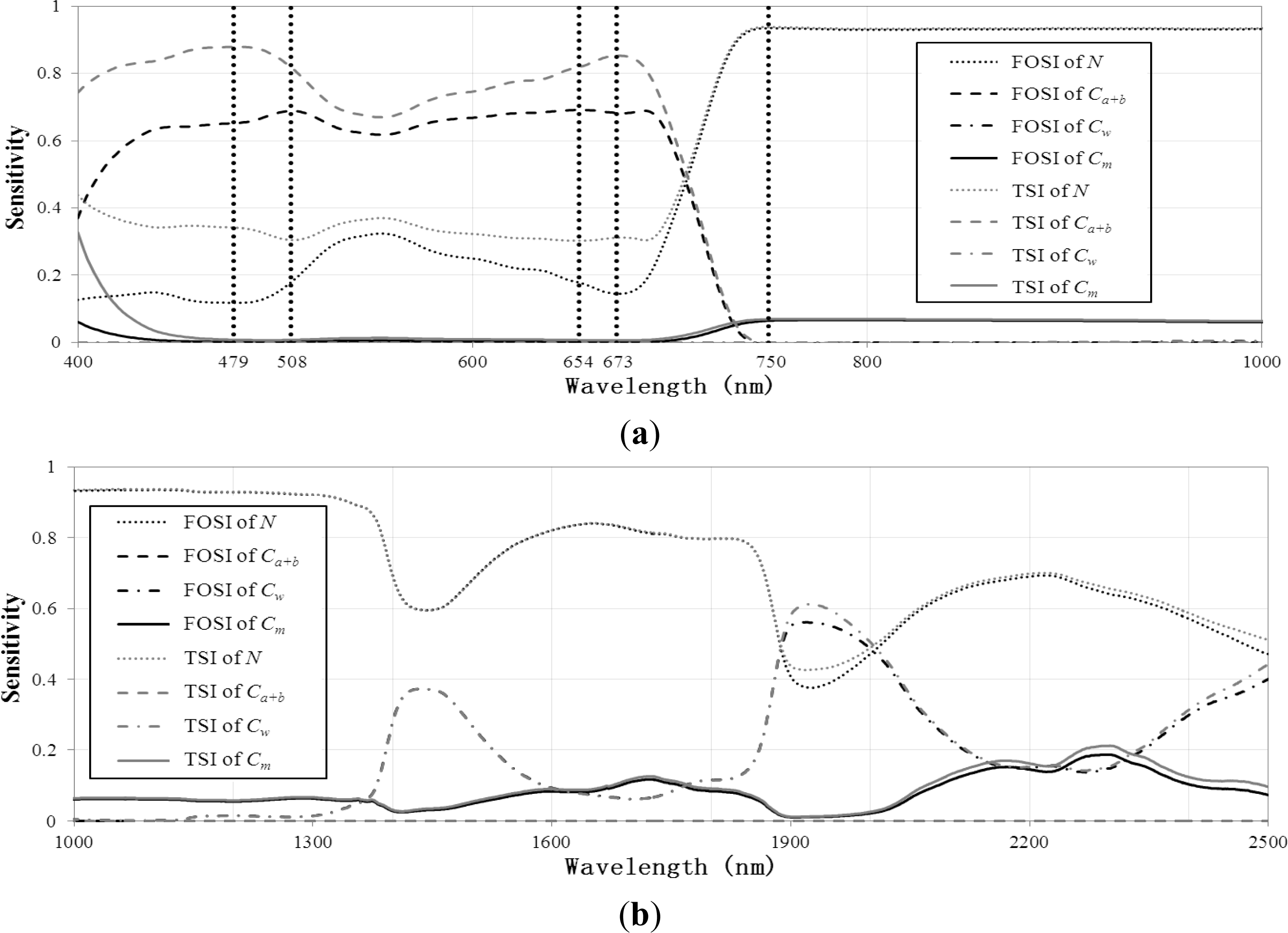
2.3. Spectral Band Selection Based on Sensitivity Analysis of PROSPECT Model
2.4. Feature Extraction Procedure
2.5. Statistical Analysis
3. Results and Discussion
3.1. Variations in Leaf Biochemical Contents after Treatment
3.2. Variations in Spectral Indices after Treatment
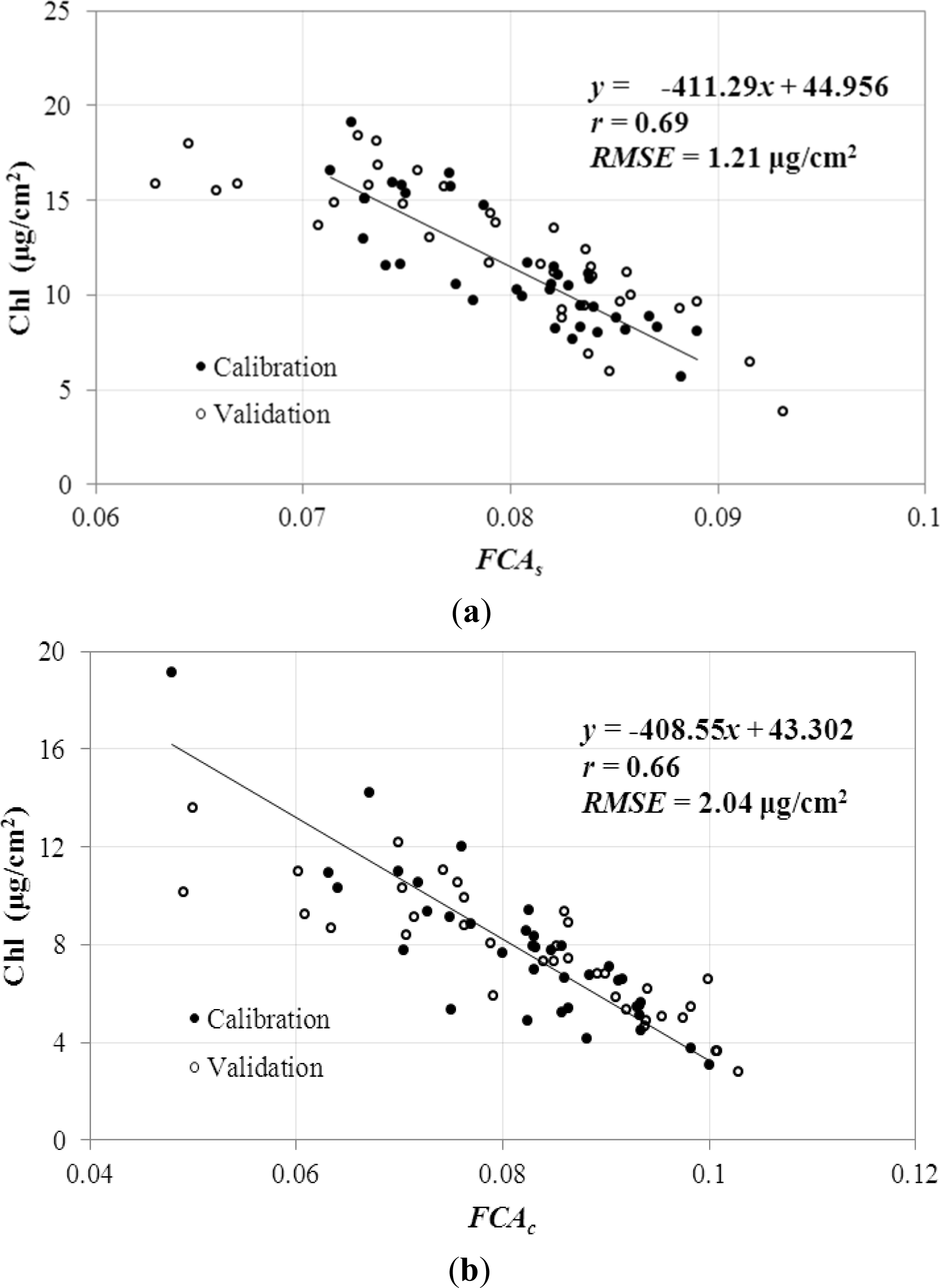
3.3. FCA Feature Extraction
3.4. Leaf Stress Detection by FCA Feature
3.5. Cross Validation for FCA Feature
3.6. Injury Detection Success by FCA Features
3.7. Advantages and Potential of the FCA Features
4. Conclusions
Acknowledgments
Author Contributions
Disclaimer
Conflicts of Interest
References
- Bellaloui, N.; Reddy, K.N.; Zablotowicz, R.M.; Mengistu, A. Simulated glyphosate drift influences nitrate assimilation and nitrogen fixation in non-glyphosate-resistant soybean. J. Agric. Food Chem 2006, 54, 3357–3364. [Google Scholar]
- Huang, Y.; Thomson, S.J.; Molin, W.T.; Reddy, K.N.; Yao, H. Early detection of soybean plant injury from glyphosate by measuring chlorophyll reflectance and fluorescence. J. Agric. Sci 2012, 4, 117–124. [Google Scholar]
- Ding, W.; Reddy, K.N.; Krutz, L.J.; Thomson, S.J.; Huang, Y.; Zablotowicz, R.M. Biological response of soybean and cotton to aerial glyphosate drift. J. Crop Improv 2011, 25, 291–302. [Google Scholar]
- Reddy, K.N.; Hoagland, R.E.; Zablotowicz, R.M. Effect of glyphosate on growth, chlorophyll, and nodulation in glyphosate-resistant and susceptible soybean (Glycine max) varieties. J. New Seeds 2000, 2, 37–52. [Google Scholar]
- Koger, C.H.; Shaner, D.L.; Krutz, L.J.; Walker, T.W.; Buehring, N.; Henry, W.B.; Thomas, W.E.; Wilcut, J.W. Rice (Oryza sativa) response to drift rates of glyphosate. Pest Manag. Sci 2005, 61, 1161–1167. [Google Scholar]
- Reddy, K.N.; Ding, W.; Zablotowicz, R.M.; Thomson, S.J.; Huang, Y.; Krutz, L.J. Biological responses to glyphosate drift from aerial application in non-glyphosate-resistant corn. Pest Manag. Sci 2010, 66, 1148–1154. [Google Scholar]
- Ding, W.; Reddy, K.N.; Zablotowicz, R.M.; Bellaloui, N.; Arnold Bruns, H. Physiological responses of glyphosate-resistant and glyphosate-sensitive soybean to aminomethylphosphonic acid, a metabolite of glyphosate. Chemosphere 2011, 83, 593–598. [Google Scholar]
- Sammons, D.R.; Tran, M. Examining yellow flash in Roundup ready soybean. North Cent. Weed Sci. Soc. Proc 2008, 63, 120. [Google Scholar]
- Mamy, L.; Barriuso, E.; Gabrielle, B. Environmental fate of herbicides trifluralin, metazachlor, metamitron and sulcotrione compared with that of glyphosate, a substitute broad spectrum herbicide for different glyphosate-resistant crops. Pest Manag. Sci 2005, 61, 905–916. [Google Scholar]
- Krezhova, D.D.; Yanev, T.K.; Ivanov, S.V.; Alexieva, V.S. Remote Sensing of the Effect of the Herbicide Glyphosate on the Leaf Spectral Reflectance of Pea Plants (Pisum Sativum l.). In New Developments and Challenges in Remote Sensing; Millpress: Rotterdam, The Netherlands, 2007; pp. 45–52. [Google Scholar]
- Moshou, D.; Bravo, C.; West, J.; Wahlen, S.; McCartney, A.; Ramon, H. Automatic detection of “yellow rust” in wheat using reflectance measurements and neural networks. Comput. Electron. Agric 2004, 44, 173–188. [Google Scholar]
- Oppelt, N.; Mauser, W. Hyperspectral monitoring of physiological parameters of wheat during a vegetation period using AVIS data. Int. J. Remote Sens 2004, 25, 145–159. [Google Scholar]
- Duveiller, G.; Weiss, M.; Baret, F.; Defourny, P. Retrieving wheat green area index during the growing season from optical time series measurements based on neural network radiative transfer inversion. Remote Sens. Environ 2011, 115, 887–896. [Google Scholar]
- Carter, G.A. Ratios of leaf reflectances in narrow wavebands as indicators of plant stress. Int. J. Remote Sens 1994, 15, 697–703. [Google Scholar]
- Riaño, D.; Vaughan, P.; Chuvieco, E.; Zarco-Tejada, P.J.; Ustin, S.L. Estimation of fuel moisture content by inversion of radiative transfer models to simulate equivalent water thickness and dry matter content: Analysis at leaf and canopy level. IEEE Trans. Geosci. Remote Sens 2005, 43, 819–826. [Google Scholar]
- Blackburn, G.A. Wavelet decomposition of hyperspectral data: A novel approach to quantifying pigment concentrations in vegetation. Int. J. Remote Sens 2007, 28, 2831–2855. [Google Scholar]
- Colombo, R.; Meroni, M.; Marchesi, A.; Busetto, L.; Rossini, M.; Giardino, C.; Panigada, C. Estimation of leaf and canopy water content in poplar plantations by means of hyperspectral indices and inverse modeling. Remote Sens. Environ 2008, 112, 1820–1834. [Google Scholar]
- Gamon, J.A.; Peñuelas, J.; Field, C.B. A narrow-waveband spectral index that tracks diurnal changes in photosynthetic efficiency. Remote Sens. Environ 1992, 41, 35–44. [Google Scholar]
- Peñuelas, J.; Gamon, J.A.; Fredeen, A.L.; Merino, J.; Field, C.B. Reflectance indices associated with physiological changes in nitrogen- and water-limited sunflower leaves. Remote Sens. Environ 1994, 48, 135–146. [Google Scholar]
- Blackburn, G.A.; Ferwerda, J.G. Retrieval of chlorophyll concentration from leaf reflectance spectra using wavelet analysis. Remote Sens. Environ 2008, 112, 1614–1632. [Google Scholar]
- Cheng, T.; Rivard, B.; Sanchez-Azofeifa, A. Spectroscopic determination of leaf water content using continuous wavelet analysis. Remote Sens. Environ 2011, 115, 659–670. [Google Scholar]
- Huang, Y.; Thomson, S.J.; Ortiz, B.V.; Reddy, K.N.; Ding, W.; Zablotowicz, R.M.; Bright, J.R. Airborne remote sensing assessment of the damage to cotton caused by spray drift from aerially applied glyphosate through spray deposition measurements. Biosyst. Eng 2010, 107, 212–220. [Google Scholar]
- Yao, H.; Huang, Y.; Hruska, Z.; Tomson, S.J.; Reddy, K.N. Using vegetation index and modified derivative for early detection of soybean plant injury from glyphosate. Comput. Electron. Agric 2012, 89, 145–157. [Google Scholar]
- Jacquemoud, S.; Baret, F. PROSPECT: A model of leaf optical properties spectra. Remote Sens. Environ 1990, 34, 75–91. [Google Scholar]
- Integrating Sphere User Manual ASD; Document 600660 Rev. B; ASD Inc: Boulder, CO, USA, 2008.
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the Great Plains with ERTS. NASA Spec. Publ 1974, 351, 309–317. [Google Scholar]
- Barnes, J.D.; Balaguer, L.; Manrique, E.; Elvira, S.; Davison, A.W. A reappraisal of the use of DMSO for the extraction and determination of chlorophylls a and b in lichens and higher plants. Environ. Exp. Bot 1992, 32, 85–100. [Google Scholar]
- Filella, I.; Peñuelas, J. The red edge position and shape as indicators of plant chlorophyll content, biomass and hydric status. Int. J. Remote Sens 1994, 15, 1459–1470. [Google Scholar]
- Le Maire, G.; François, C.; Dufrene, E. Towards universal broad leaf chlorophyll indices using PROSPECT simulated database and hyperspectral reflectance measurements. Remote Sens. Environ 2004, 89, 1–28. [Google Scholar]
- Fourty, T.; Baret, F.; Jacquemoud, S.; Schmuck, G.; Verdebout, J. Leaf optical properties with explicit description of its biochemical composition: Direct and inverse problems. Remote Sens. Environ 1996, 56, 104–117. [Google Scholar]
- Baret, F.; Fourty, T. Estimation of leaf water content and specific leaf weight from reflectance and transmittance measurements. Agronomie 1997, 17, 455–464. [Google Scholar]
- Jacquemoud, S.; Ustin, S.L.; Verdebout, J.; Schmuck, G.; Andreoli, G.; Hosgood, B. Estimating leaf biochemistry using the PROSPECT leaf optical properties model. Remote Sens. Environ 1996, 56, 194–202. [Google Scholar]
- Jacquemoud, S.; Bacour, C.; Poilve, H.; Frangi, J.P. Comparison of four radiative transfer models to simulate plant canopies reflectance: Direct and inverse mode. Remote Sens. Environ 2000, 74, 471–481. [Google Scholar]
- Feret, J.B.; François, C.; Asner, G.P.; Gitelson, A.A.; Martin, R.E.; Bidel, L.P.; Ustin, S.L.; le Maire, G.; Jacquemoud, S. PROSPECT-4 and 5: Advances in the leaf optical properties model separating photosynthetic pigments. Remote Sens. Environ 2008, 112, 3030–3043. [Google Scholar]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. PROSPECT + SAIL models: A review of use for vegetation characterization. Remote Sens. Environ 2009, 113, S56–S66. [Google Scholar]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Saisana, M.; Tarantola, S. Global Sensitivity Analysis, The Primer; John Wiley & Sons Ltd: West Sussex, UK, 2008. [Google Scholar]
- Cukier, R.I.; Fortuin, C.M.; Schuler, K.E.; Petschek, A.G.; Schaibly, J.H. Study of the sensitivity of coupled reaction systems to uncertainties in rate coefficients. I Theory. J. Chem. Phys 1973, 59, 3873–3878. [Google Scholar]
- Cukier, R.I.; Levine, H.B.; Shuler, K.E. Nonlinear sensitivity analysis of multiparameter model systems. J. Comput. Phys 1978, 26, 1–42. [Google Scholar]
- Koda, M.; Mcrae, G.J.; Seinfeld, J.H. Automatic sensitivity analysis of kinetic mechanisms. Int. J. Chem. Kinet 1979, 11, 427–444. [Google Scholar]
- Saltelli, A.; Tarantola, S.; Chan, K. A quantitative, model independent method for global sensitivity analysis of model output. Technometrics 1999, 41, 39–56. [Google Scholar]
- Lejeune, M.; Caliński, T. Canonical analysis applied to multivariate analysis of variance. J. Multivar. Anal 2000, 72, 100–119. [Google Scholar]
- Li, P.; Wang, Q. Retrieval of leaf biochemical parameters using PROSPECT inversion: A new approach for alleviating ill-posed problems. IEEE Trans. Geosci. Remote Sens 2011, 49, 2499–2506. [Google Scholar]
- Knipling, E.B. Physical and physiological basis for the reflectance of visible and near-infrared radiation from vegetation. Remote Sens. Environ 1970, 1, 155–159. [Google Scholar]
- Zhao, F.; Gu, X.; Verhoef, W.; Wang, Q.; Yu, T.; Liu, Q.; Huang, H.; Qin, W.; Chen, L.; Zhao, H. A spectral directional reflectance model of row crops. Remote Sens. Environ 2010, 114, 265–285. [Google Scholar]

| Crop | Soybean | Cotton | |||||
|---|---|---|---|---|---|---|---|
| Group | CTRL | 0.25X | 0.5X | CTRL | 0.25X | 0.5X | |
| Chl (μg/cm2) Mean/Standard deviation of 3 leaves in the same group | 6 HAT | 12.2172 a/0.6027 | 13.1233 a/0.5775 | 14.1676 a/0.3419 | 10.3935 a/0.6027 | 10.0439 a/0.5775 | 9.9327 a/0.3419 |
| 24 HAT | 13.2172 a/0.3601 | 13.0325 a/0.5403 | 12.7367 b/0.6982 | 9.9763 a/0.3601 | 9.1208 ab/0.5403 | 8.5738 b/0.6982 | |
| 48 HAT | 13.4515 a/0.3874 | 10.0867 b/0.3066 | 9.1455 c/0.7285 | 10.3043 a/0.3874 | 9.0895 b/0.3066 | 7.9085 c/0.7285 | |
| 72 HAT | 13.8702 a/0.4047 | 9.5917 b/0.3931 | 7.8026 c/0.4269 | 10.1291 a/0.4047 | 8.2778 b/0.3931 | 6.3582 c/0.4270 | |
| EWT (g/cm2) Mean/Standard deviation of 3 leaves in the same group | 6 HAT | 0.0121 a/0.0002 | 0.0121 a/0.0005 | 0.0120 a/0.0008 | 0.0167 a/0.0003 | 0.0169 a/0.0005 | 0.0167 a/0.0008 |
| 24 HAT | 0.0119 a/0.0007 | 0.0122 a/0.0007 | 0.0123 a/0.0003 | 0.0174 a/0.0007 | 0.0169 a/0.0007 | 0.0174 a/0.0003 | |
| 48 HAT | 0.0119 a/0.0004 | 0.0120 a/0.0005 | 0.0123 a/0.0006 | 0.0179 a/0.0005 | 0.0182 a/0.0005 | 0.0182 a/0.0006 | |
| 72 HAT | 0.0120 a/0.0006 | 0.0123 a/0.0008 | 0.0124 a/0.0004 | 0.0180 a/0.0006 | 0.0178 a/0.0008 | 0.0184 a/0.0004 | |
| LMA (g/cm2) Mean/Standard deviation of 3 leaves in the same group | 6 HAT | 0.0024 a/0.0001 | 0.0024 a/0.0001 | 0.0024 a/0.0001 | 0.0029 a/0.0001 | 0.0028 a/0.0002 | 0.0027 a/0.0001 |
| 24 HAT | 0.0023 a/0.0001 | 0.0024 a/0.0001 | 0.0024 a/0.0001 | 0.0029 a/0.0001 | 0.0030 a/0.0002 | 0.0028 a/0.0001 | |
| 48 HAT | 0.0023 a/0.0001 | 0.0023 a/0.0001 | 0.0024 a/0.0001 | 0.0030 a/0.0001 | 0.0031 a/0.0001 | 0.0033 a/0.0001 | |
| 72 HAT | 0.0022 a/0.0001 | 0.0023 a/0.0001 | 0.0024 a/0.0001 | 0.0030 a/0.0001 | 0.0031 a/0.0001 | 0.0032 a/0.0001 | |
| Crop | Soybean | Cotton | |||||
|---|---|---|---|---|---|---|---|
| Group | CTRL | 0.25X | 0.5X | CTRL | 0.25X | 0.5X | |
| Chl (μg/cm2) Mean/Standard deviation of 3 leaves in the same group | 6 HAT | 13.3673 a/0.4227 | 13.2032 a/0.7414 | 13.1985 a/0.2118 | 9.8102 a/0.4227 | 9.9867 a/0.7414 | 9.9867 a/0.2118 |
| 24 HAT | 12.2172 b/0.3440 | 13.2699 a/0.3515 | 11.5416 b/0.4833 | 9.5656 a/0.3439 | 9.6951 a/0.3515 | 9.5951 a/0.4833 | |
| 48 HAT | 13.9737 a/0.5056 | 10.5587 b/0.6570 | 9.3648 c/0.6506 | 10.5367 a/0.5056 | 9.0423 b/0.6570 | 7.8207 c/0.6506 | |
| 72 HAT | 14.3165 a/0.3541 | 9.9559 b/0.3172 | 7.8462 c/0.4954 | 10.3765 a/0.3541 | 7.8915 b/0.3172 | 6.5954 c/0.4954 | |
| EWT (g/cm2) Mean/Standard deviation of 3 leaves in the same group | 6 HAT | 0.0118 a/0.0003 | 0.0120 a/0.0008 | 0.0120 a/0.0003 | 0.0166 a/0.0003 | 0.0165 a/0.0008 | 0.0166 a/0.0003 |
| 24 HAT | 0.0120 a/0.0007 | 0.0123 a/0.0003 | 0.0124 a/0.0003 | 0.0172 a/0.0006 | 0.0168 a/0.0003 | 0.0175 a/0.0003 | |
| 48 HAT | 0.0119 a/0.0004 | 0.0125 a/0.0007 | 0.0126 a/0.0005 | 0.0177 a/0.0003 | 0.0177 a/0.0006 | 0.0184 a/0.0005 | |
| 72 HAT | 0.0118 a/0.0007 | 0.0122 a/0.0007 | 0.0125 a/0.0004 | 0.0182 a/0.0004 | 0.0175 a/0.0007 | 0.0183 a/0.0004 | |
| LMA (g/cm2) Mean/Standard deviation of 3 leaves in the same group | 6 HAT | 0.0023 a/0.0001 | 0.0023 a/0.0001 | 0.0023 a/0.0001 | 0.0029 a/0.0001 | 0.0028 a/0.0001 | 0.0026 a/0.0001 |
| 24 HAT | 0.0023 a/0.0002 | 0.0024 a/0.0001 | 0.0024 a/0.0002 | 0.0030 a/0.0002 | 0.0031 a/0.0001 | 0.0028 a/0.0002 | |
| 48 HAT | 0.0022 a/0.0001 | 0.0023 a/0.0002 | 0.0024 a/0.0001 | 0.0030 a/0.0001 | 0.0032 a/0.0002 | 0.0032 a/0.0001 | |
| 72 HAT | 0.0023 a/0.0001 | 0.0023 a/0.0001 | 0.0023 a/0.0001 | 0.0029 a/0.0001 | 0.0031 a/0.0001 | 0.0031 a/0.0001 | |
| Index | Definition |
|---|---|
| NDVI * | , Normalized Difference Vegetation Index |
| RVI * | , Ratio Vegetation Index |
| SAVI * | , where L = 0.5, Soil Adjusted Vegetation Index |
| DVI * | R800 − R680, Difference Vegetation Index |
| dg ** | minimum amplitude of the first derivative reflectance in the green region, at approx. 570 nm |
| dG ** | maximum amplitude of the first derivative reflectance in the green region, at approx. 525 nm |
| dRE ** | maximum amplitude of the first derivative reflectance in the red-edge region, at approx. 700–710 nm |
| CGFN ** | , normalized difference between dG and dg |
| EGFN ** | , normalized difference between dRE and dG |
| WRE ** | Wavelength position of the Red Edge (i.e., the maximum amplitude wavelength position of the first derivative reflectance in the red-edge region) |
| PRI ** | , Physiological Reflectance Index |
| NPCI ** | , Normalized Pigments Chlorophyll ratio Index |
| NPQI *** | , Normalized Phaeophytinization Quotient Index |
| SFDR **** | Sum of the First Derivative Reflectance between 680 nm and 780 nm |
| HAT (h) | Index | CTRL Group | 0.25X Group | 0.5X Group |
|---|---|---|---|---|
| 6 | NDVI | 0.8187 a | 0.8205 a | 0.8167 a |
| RVI | 10.0944 a | 10.1608 a | 9.9265 a | |
| SAVI | 0.5963 a | 0.5910 a | 0.5881 a | |
| DVI | 0.3862 a | 0.3789 a | 0.3781 a | |
| dg | −0.0024 a | −0.0024 a | −0.0025 a | |
| dG | 0.0033 a | 0.0033 a | 0.0034 a | |
| dRE | 0.0104 a | 0.0101 a | 0.0102 a | |
| CGFN | 6.5295 a | 6.328 a | 6.4118 a | |
| EGFN | 0.5173 a | 0.5079 a | 0.5027 a | |
| WRE ** | 709 a | 707 a | 705 a | |
| PRI | 0.0198 a | 0.0198 a | 0.0204 a | |
| NPCI | 0.0016 a | 0.0016 a | −0.0012 a | |
| NPQI | −0.0358 a | −0.0368 a | −0.0376 a | |
| SFDR | 0.3876 a | 0.3805 a | 0.3733 a | |
| 24 | NDVI | 0.8229 a | 0.8157 a | 0.8187 a |
| RVI | 10.3650 a | 10.2972 a | 10.4699 a | |
| SAVI | 0.5839 a | 0.5805 a | 0.5875 a | |
| DVI | 0.3694 a | 0.3723 a | 0.3794 a | |
| dg | −0.0024 a | −0.0025 a | −0.0025 a | |
| dG | 0.0033 a | 0.0035 a | 0.0036 a | |
| dRE | 0.0099 a | 0.0102 a | 0.0106 a | |
| CGFN | 6.1602 a | 6.0017 a | 5.9571 a | |
| EGFN | 0.5025 a | 0.4888 a | 0.4975 a | |
| WRE ** | 706 a | 706 a | 706 a | |
| PRI | 0.0195 a | 0.0201 a | 0.0211 a | |
| NPCI | 0.0402 a | 0.0452 a | 0.0493 a | |
| NPQI | −0.0337 a | −0.0291 a | −0.0343 a | |
| SFDR | 0.3688 a | 0.3728 a | 0.3779 a | |
| 48 | NDVI | 0.8357 a | 0.8137 b | 0.8057 b |
| RVI | 10.7239 a | 9.3939 b | 9.2385 b | |
| SAVI | 0.5887 a | 0.5860 ab | 0.5825 b | |
| DVI | 0.3741 a | 0.3732 b | 0.3727 b | |
| dg | −0.0022 a | −0.0026 a | −0.0026 a | |
| dG | 0.0030 a | 0.0037 a | 0.0040 a | |
| dRE | 0.0099 a | 0.0105 a | 0.0108 a | |
| CGFN | 5.3727 a | 5.5219 a | 5.0925 a | |
| EGFN | 0.5199 a | 0.4743 a | 0.4624 a | |
| WRE ** | 704 a | 702 a | 702 a | |
| PRI | 0.0069 b | 0.0155 ba | 0.0205 a | |
| NPCI | 0.0045 b | 0.0328 a | 0.0364 a | |
| NPQI | −0.0314 a | −0.0305 a | −0.0403 a | |
| SFDR | 0.3747 a | 0.3736 a | 0.3749 a | |
| 72 | NDVI | 0.8210 a | 0.8111 b | 0.7834 c |
| RVI | 10.1770 a | 9.6108 b | 8.4101 c | |
| SAVI | 0.5943 a | 0.5696 b | 0.5675 b | |
| DVI | 0.3828 a | 0.3703 b | 0.3677 b | |
| dg | −0.0023 a | −0.0026 a | −0.0027 a | |
| dG | 0.0031 a | 0.0037 a | 0.0045 a | |
| dRE | 0.0101 a | 0.0104 a | 0.0118 a | |
| CGFN | 6.4162 a | 5.8877 a | 4.4841 a | |
| EGFN | 0.5426 a | 0.4797 a | 0.4489 a | |
| WRE ** | 711 a | 703 b | 701 b | |
| PRI | 0.0013 c | 0.0117 b | 0.0212 a | |
| NPCI | 0.0153 c | 0.0328 b | 0.0876 a | |
| NPQI | −0.0329 a | −0.0357 a | −0.0361 a | |
| SFDR | 0.3839 a | 0.3799 a | 0.3709 a | |
| HAT (h) | Index | CTRL Group | 0.25X Group | 0.5X Group |
|---|---|---|---|---|
| 6 | NDVI | 0.7908 a | 0.7886 a | 0.7853 a |
| RVI | 8.5872 a | 8.5408 a | 8.5376 a | |
| SAVI | 0.5888 a | 0.5860 a | 0.5799 a | |
| DVI | 0.3903 a | 0.3921 a | 0.3854 a | |
| dg | −0.0025 a | −0.0028 a | −0.0027 a | |
| dG | 0.0034 a | 0.0040 a | 0.0039 a | |
| dRE | 0.0108 a | 0.0114 a | 0.0112 a | |
| CGFN | 5.4463 a | 5.3628 a | 5.3454 a | |
| EGFN | 0.5007 a | 0.4777 a | 0.4810 a | |
| WRE ** | 703 a | 700 a | 701 a | |
| PRI | 0.0206 a | 0.0212 a | 0.0208 a | |
| NPCI | 0.0957 a | 0.0976 a | 0.1025 a | |
| NPQI | 0.0023 a | 0.0020 a | 0.0028 a | |
| SFDR | 0.3899 a | 0.3921 a | 0.3816 a | |
| 24 | NDVI | 0.7936 a | 0.7917 a | 0.7880 a |
| RVI | 8.7672 a | 8.6153 a | 8.4444 a | |
| SAVI | 0.5857 a | 0.5876 a | 0.5769 a | |
| DVI | 0.3849 a | 0.3878 a | 0.3760 a | |
| dg | −0.0025 a | −0.0026 a | −0.0024 a | |
| dG | 0.0037 a | 0.0036 a | 0.0034 a | |
| dRE | 0.0107 a | 0.0106 a | 0.0106 a | |
| CGFN | 5.9509 a | 6.1741 a | 6.2811 a | |
| EGFN | 0.4877 a | 0.4920 a | 0.5157 a | |
| WRE ** | 702 a | 704 a | 704 a | |
| PRI | 0.0175 a | 0.0165 a | 0.0168 a | |
| NPCI | 0.0673 a | 0.0640 a | 0.0659 a | |
| NPQI | 0.0112 a | 0.0103 a | 0.0093 a | |
| SFDR | 0.3855 a | 0.3884 a | 0.3764 a | |
| 48 | NDVI | 0.7890 a | 0.7828 a | 0.7865 a |
| RVI | 8.4550 a | 8.4173 a | 8.4373 a | |
| SAVI | 0.5786 a | 0.5813 a | 0.5843 a | |
| DVI | 0.3832 a | 0.3839 a | 0.3857 a | |
| dg | −0.0026 a | −0.0025 a | −0.0026 a | |
| dG | 0.0037 a | 0.0036 a | 0.0036 a | |
| dRE | 0.0109 a | 0.0105 a | 0.0108 a | |
| CGFN | 6.0213 a | 5.9717 a | 6.1377 a | |
| EGFN | 0.4933 a | 0.4937 a | 0.5035 a | |
| WRE ** | 703 a | 703 a | 703 a | |
| PRI | 0.0155 b | 0.0201 ba | 0.0219 a | |
| NPCI | 0.0898 a | 0.0843 a | 0.0783 a | |
| NPQI | 0.0013 a | 0.0018 a | 0.0015 a | |
| SFDR | 0.3841a | 0.3835 a | 0.3843 a | |
| 72 | NDVI | 0.8015 a | 0.7874 b | 0.7841 b |
| RVI | 9.1241 a | 8.4317 b | 8.4278 b | |
| SAVI | 0.5827 a | 0.5433 b | 0.5364 b | |
| DVI | 0.3670 a | 0.3517 b | 0.3482 b | |
| dg | −0.0023 a | −0.0024 a | −0.0024 a | |
| dG | 0.0031 a | 0.0033 a | 0.0033 a | |
| dRE | 0.0101 a | 0.0106 a | 0.0104 a | |
| CGFN | 7.0570 a | 7.0137 a | 6.8710 a | |
| EGFN | 0.5340 a | 0.5269 a | 0.5211 a | |
| WRE ** | 707 a | 706 a | 706 a | |
| PRI | 0.0136 a | 0.0149 a | 0.0196 a | |
| NPCI | 0.0772 a | 0.0827 a | 0.0784 a | |
| NPQI | 0.040 a | −0.0038 a | 0.0045 a | |
| SFDR | 0.3798 a | 0.3958 a | 0.3894 a | |
| HAT (h) | CTRL Group | 0.25X Group | 0.5X Group |
|---|---|---|---|
| 6 | 0.07304 a | 0.07288 a | 0.07173 a |
| 24 | 0.07123 b | 0.07433 ba | 0.07700 a |
| 48 | 0.07157 c | 0.07880 b | 0.08265 a |
| 72 | 0.07485 c | 0.08182 b | 0.08899 a |
| HAT (h) | CTRL Group | 0.25X Group | 0.5X Group |
|---|---|---|---|
| 6 | 0.07004 a | 0.07452 a | 0.07315 a |
| 24 | 0.07178 b | 0.08347 a | 0.08570 a |
| 48 | 0.06748 c | 0.07873 b | 0.08613 a |
| 72 | 0.07177 c | 0.08287 b | 0.09011 a |
| HAT (h) | CTRL Group | 0.25X Group | 0.5X Group |
|---|---|---|---|
| Round I | |||
| 6 | 0.07190 a | 0.07241 a | 0.07047 a |
| 24 | 0.07001 b | 0.07525 ab | 0.07763 a |
| 48 | 0.07154 c | 0.07737 b | 0.08391 a |
| 72 | 0.07349 c | 0.08061 b | 0.08962 a |
| Round II | |||
| 6 | 0.07400 a | 0.07393 a | 0.07317 a |
| 24 | 0.06983 b | 0.07394 b | 0.07602 a |
| 48 | 0.07182 c | 0.07753 b | 0.08387 a |
| 72 | 0.07514 c | 0.08090 b | 0.08802 a |
| HAT (h) | CTRL Group | 0.25X Group | 0.5X Group |
|---|---|---|---|
| Round I | |||
| 6 | 0.06876 b | 0.07297 a | 0.07435 a |
| 24 | 0.07012 b | 0.08467 a | 0.08367 a |
| 48 | 0.06606 c | 0.07719 b | 0.08365 a |
| 72 | 0.07158 c | 0.08060 b | 0.09010 a |
| Round II | |||
| 6 | 0.07181 a | 0.07642 a | 0.07428 a |
| 24 | 0.07210 b | 0.08293 a | 0.08791 a |
| 48 | 0.06826 c | 0.07807 b | 0.08540 a |
| 72 | 0.07358 c | 0.08110 b | 0.09058 a |
| From Group | Number of FCAs Values (Round I + Round II) Classified into Group | Accuracy (%) | ||
|---|---|---|---|---|
| CTRL | 0.25X | 0.5X | ||
| 6 HAT | ||||
| CTRL | 2 (2 + 0) | 2 (0 + 2) | 2 (1 + 1) | 33 |
| 0.25X | 3 (1 + 2) | 1 (1 + 0) | 2 (1 + 1) | 17 |
| 0.5X | 1 (0 + 1) | 3 (1 + 2) | 2 (2 + 0) | 33 |
| 24 HAT | ||||
| CTRL | 2 (1 + 1) | 3 (2 + 1) | 1 (0 + 1) | 50 |
| 0.25X | 1 (1 + 0) | 4 (1 + 3) | 1 (1 + 0) | 67 |
| 0.5X | 0 (0 + 0) | 1 (1 + 0) | 5 (2 + 3) | 83 |
| 48 HAT | ||||
| CTRL | 6 (3 + 3) | 0 (0 + 0) | 0 (0 + 0) | 100 |
| 0.25X | 0 (0 + 0) | 6 (3 + 3) | 0 (0 + 0) | 100 |
| 0.5X | 0 (0 + 0) | 0 (0 + 0) | 6 (3 + 3) | 100 |
| 72 HAT | ||||
| CTRL | 6 (3 + 3) | 0 (0 + 0) | 0 (0 + 0) | 100 |
| 0.25X | 0 (0 + 0) | 6 (3 + 3) | 0 (0 + 0) | 100 |
| 0.5X | 0 (0 + 0) | 0 (0 + 0) | 6 (3 + 3) | 100 |
| From Group | Number of FCAc Values (Round I + Round II) Classified into Group | Accuracy (%) | ||
|---|---|---|---|---|
| CTRL | 0.25X | 0.5X | ||
| 6 HAT | ||||
| CTRL | 1 (0 + 1) | 3 (2 + 1) | 2 (1 + 1) | 17 |
| 0.25X | 3 (1 + 2) | 1 (1 + 0) | 2 (1 + 1) | 17 |
| 0.5X | 1 (1 + 0) | 3 (2 + 1) | 2 (0 + 2) | 33 |
| 24 HAT | ||||
| CTRL | 5 (2 + 3) | 1 (1 + 0) | 0 (0 + 0) | 83 |
| 0.25X | 0 (0 + 0) | 4 (2 + 2) | 2 (1 + 1) | 67 |
| 0.5X | 1 (0 + 1) | 1 (1 + 0) | 4 (2 + 2) | 67 |
| 48 HAT | ||||
| CTRL | 6 (3 + 3) | 0 (0 + 0) | 0 (0 + 0) | 100 |
| 0.25X | 0 (0 + 0) | 6 (3 + 3) | 0 (0 + 0) | 100 |
| 0.5X | 0 (0 + 0) | 0 (0 + 0) | 6 (3 + 3) | 100 |
| 72 HAT | ||||
| CTRL | 6 (3 + 3) | 0 (0 + 0) | 0 (0 + 0) | 100 |
| 0.25X | 0 (0 + 0) | 6 (3 + 3) | 0 (0 + 0) | 100 |
| 0.5X | 0 (0 + 0) | 0 (0 + 0) | 6 (3 + 3) | 100 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhao, F.; Huang, Y.; Guo, Y.; Reddy, K.N.; Lee, M.A.; Fletcher, R.S.; Thomson, S.J. Early Detection of Crop Injury from Glyphosate on Soybean and Cotton Using Plant Leaf Hyperspectral Data. Remote Sens. 2014, 6, 1538-1563. https://doi.org/10.3390/rs6021538
Zhao F, Huang Y, Guo Y, Reddy KN, Lee MA, Fletcher RS, Thomson SJ. Early Detection of Crop Injury from Glyphosate on Soybean and Cotton Using Plant Leaf Hyperspectral Data. Remote Sensing. 2014; 6(2):1538-1563. https://doi.org/10.3390/rs6021538
Chicago/Turabian StyleZhao, Feng, Yanbo Huang, Yiqing Guo, Krishna N. Reddy, Matthew A. Lee, Reginald S. Fletcher, and Steven J. Thomson. 2014. "Early Detection of Crop Injury from Glyphosate on Soybean and Cotton Using Plant Leaf Hyperspectral Data" Remote Sensing 6, no. 2: 1538-1563. https://doi.org/10.3390/rs6021538
APA StyleZhao, F., Huang, Y., Guo, Y., Reddy, K. N., Lee, M. A., Fletcher, R. S., & Thomson, S. J. (2014). Early Detection of Crop Injury from Glyphosate on Soybean and Cotton Using Plant Leaf Hyperspectral Data. Remote Sensing, 6(2), 1538-1563. https://doi.org/10.3390/rs6021538





