3.1. Scaling the Hyperion to Terra MODIS
Helder
et al. have described an approach to derive the absolute calibration model using a well-calibrated sensor in 2012 [
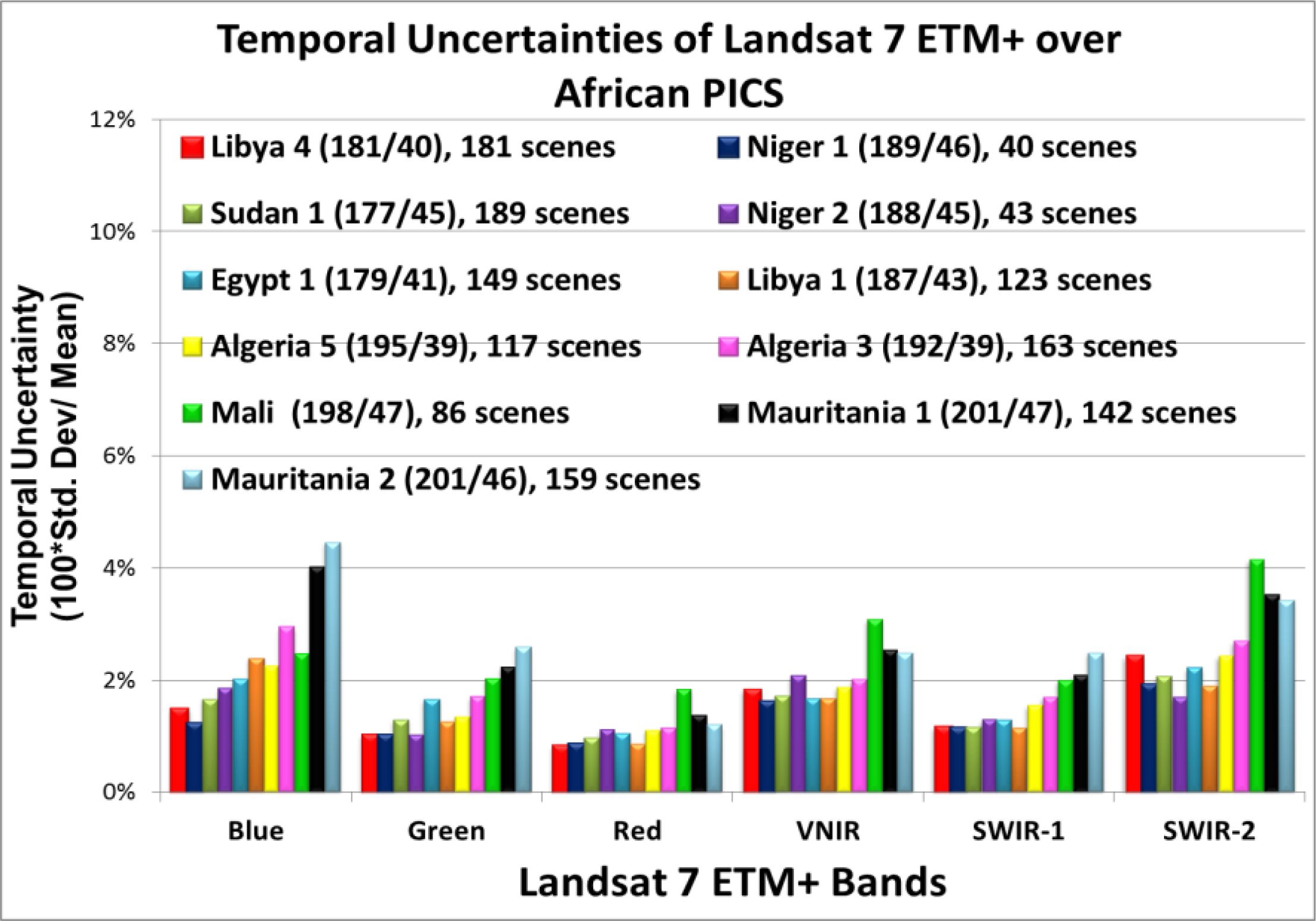
5]. The method used Terra MODIS as the reference, and the Hyperion hyperspectral sensor as the source for the spectral profile. By using MODIS as a source for absolute calibration, a normalization factor can be calculated to scale the Hyperion spectrum so that, when integrated over the MODIS spectral bandpass, it will produce the comparable TOA reflectance of Terra MODIS. The scale factor was calculated using five available pairs of MODIS/Hyperion scenes that were collected essentially simultaneously (within 30 min) with nadir-viewing angles (±5°) and an essentially constant solar zenith angle of 30 ± 5°. The gain factors that were obtained on each date and for each MODIS band (listed in order of increasing wavelength) are shown in
Table 2. All average gain values agree to within ±3%, indicating good consistency between the two sensors at all wavelengths with uncertainties (standard deviation/mean) in each measurement of 2% or less. Statistical analysis indicated that the mean values could be clustered into three groups: band 7, bands 2, 3 and 6 in one cluster, with bands 1 and 4 in another cluster (significance level, α = 0.05). The final step for calculating the scale factor was to linearly interpolate the values in
Table 1 in those spectral ranges covered by the MODIS bands.
3.2. BRDF Model
Various models from the literature have classified BRDF as physical (based on first principle), semi-empirical or empirical models. A physics-based BRDF model—taking, for instance, sand—is based on the complete characterization of physical characteristics of the sand such as its composition, irregular particle shape, refractive index, surface roughness, spectral reflectance,
etc. Widely used semi-empirical models such as the Ross-Li model [
19], Roujean model [
20], and Snyder model [
21] are kernel driven, whereas BRDF is modeled as a weighted sum of volume scattering, geometric scattering and isotropic terms. These kernels are derived from approximations to physical BRDF models, so that they retain physical meaning. A study done over bright desert targets with the use of the Snyder model on Polarization and Anisotropy of Reflectance for Atmospheric Sciences Couples with Observations from a Lidar (PARASOL) data has suggested that bidirectional effects are limited to reflectance variations of about 15% [
22].
In this approach, the empirical BRDF model is derived using the apparent trends between TOA reflectance versus solar zenith angle and viewing zenith angle. While the obvious disadvantage of using the empirical model is the need for the large number of data samples to build the statistical model, it will be shown in the coming sections that the model works reasonably well for the sensors if the sensor viewing angles are restricted to within ±20 degrees of nadir.
3.2.1. BRDF Model for Solar Zenith Angle
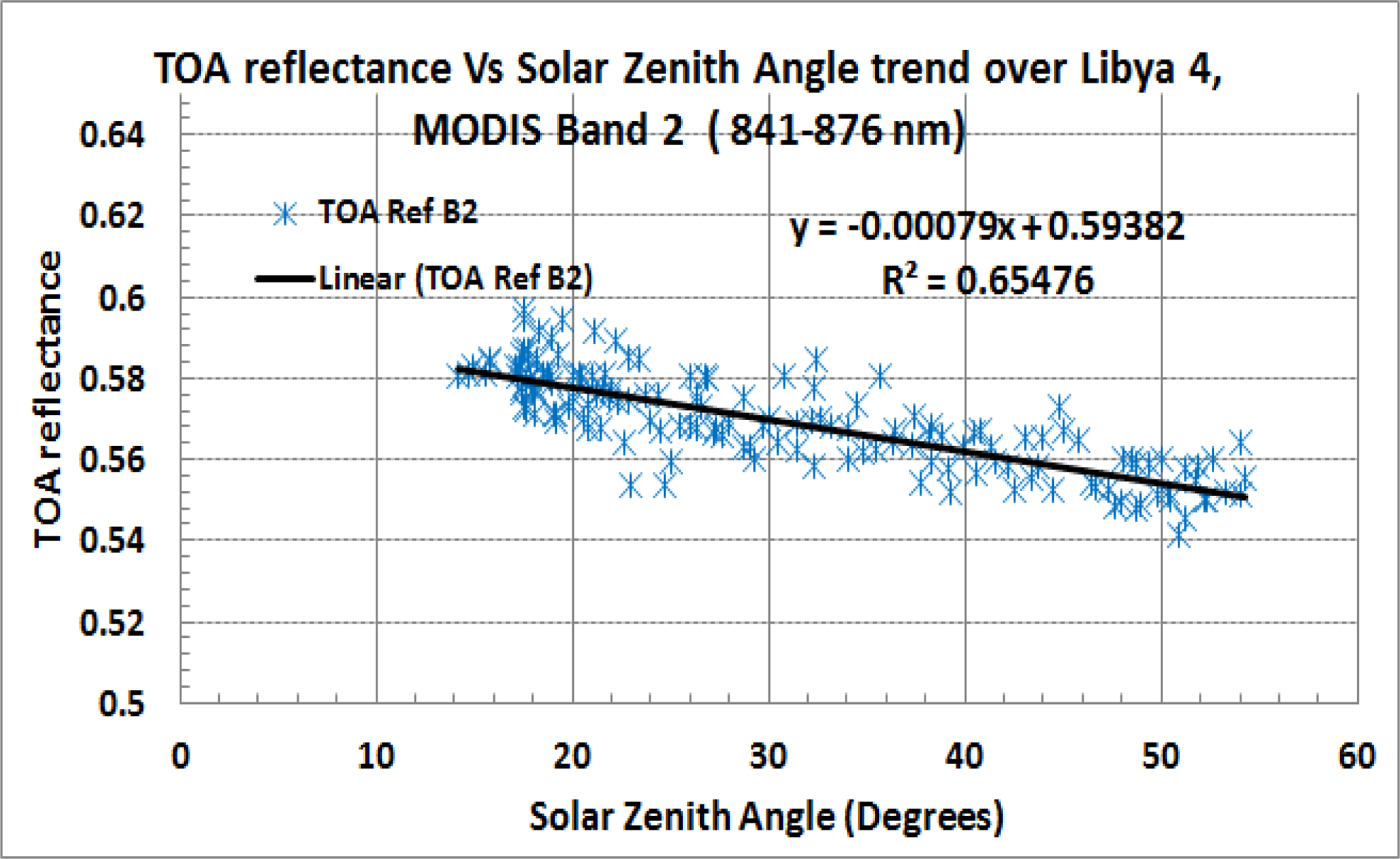
An empirical BRDF model to account for the varying solar zenith angle was derived using nadir-looking Terra MODIS observations. Approximately 160 observations of Libya 4 at scene center (nadir ±7.5°) acquired over 3,000 days were plotted as a function of solar zenith angle (SZA), as shown in
Figure 3. The plot shows good coverage of solar zenith angles ranging from 16 degrees to 56 degrees. Although the surface reflectance model such as the Ross-Li or Snyder model, is more complicated and rigorous than a linear fit, it was found that a model like the Ross-Li [
16], which has a cubic term, did not provide a statistically significant improvement over a linear model. Thus, a simple linear model was fitted to the data to provide a first-order BRDF correction factor based upon solar zenith angle.
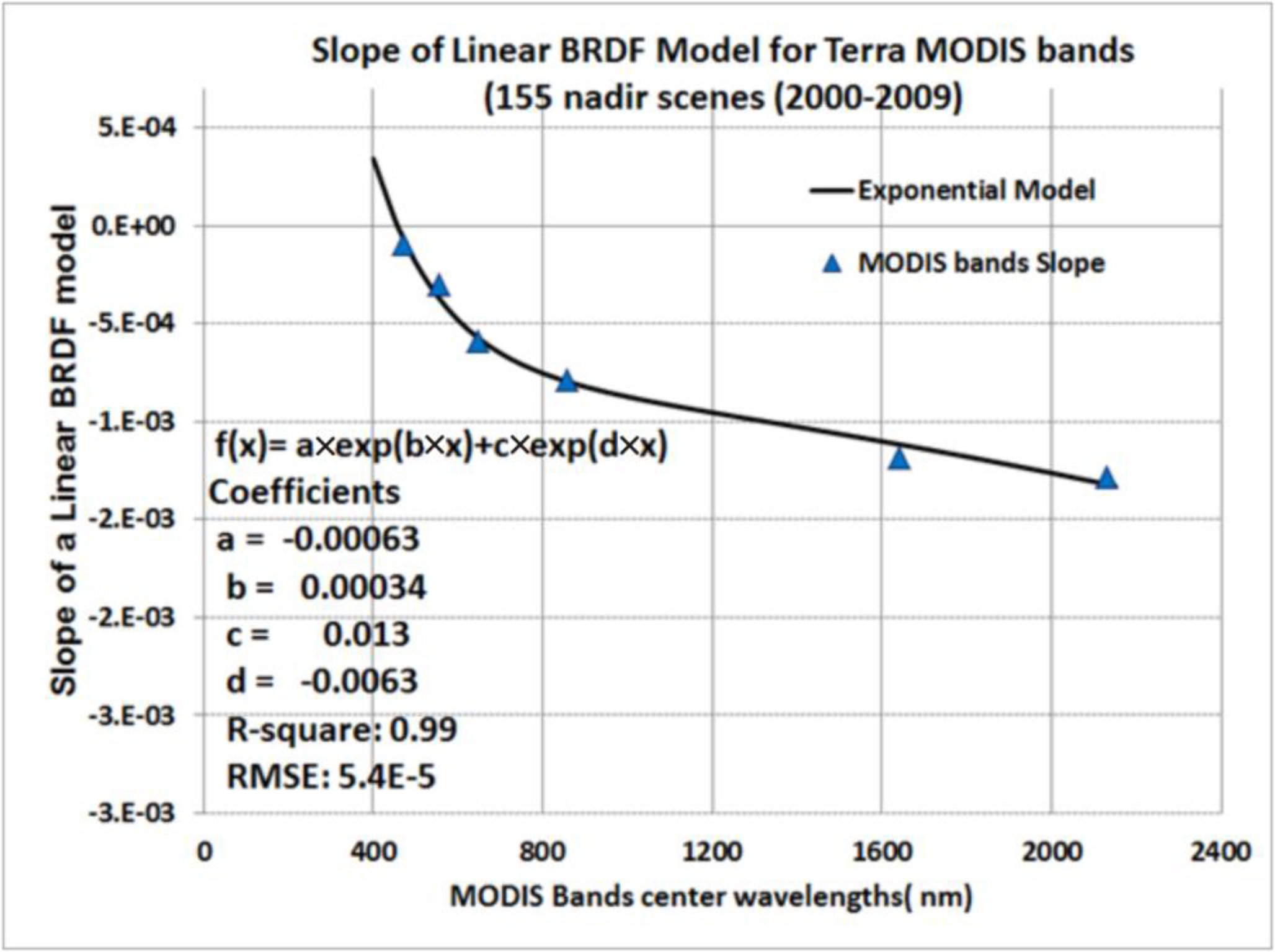
Figure 2 shows an example of the linear fit for MODIS Band 2 (NIR). A similar model was generated for the six solar reflective bands of Terra MODIS. The slope of the linear term of these six bands was then plotted
versus center wavelength, as shown in the
Figure 4. The plot shows that the BRDF changes as a function of wavelength, with the SWIR channel exhibiting a greater impact on BRDF.
Figure 4 also shows that these coefficients, derived using linear fit, could be further modeled using a two-piece exponential fit with very low value of residual error, supporting the use of this model.
3.2.2. BRDF Model for Viewing Zenith Angle
BRDF, due to varying viewing zenith angle (VZA), was modeled in a similar way. In this case, spectrally cleaner (high transmittance and reflectance), each bandwidth of approximately 10 nm, they were used to build the model.
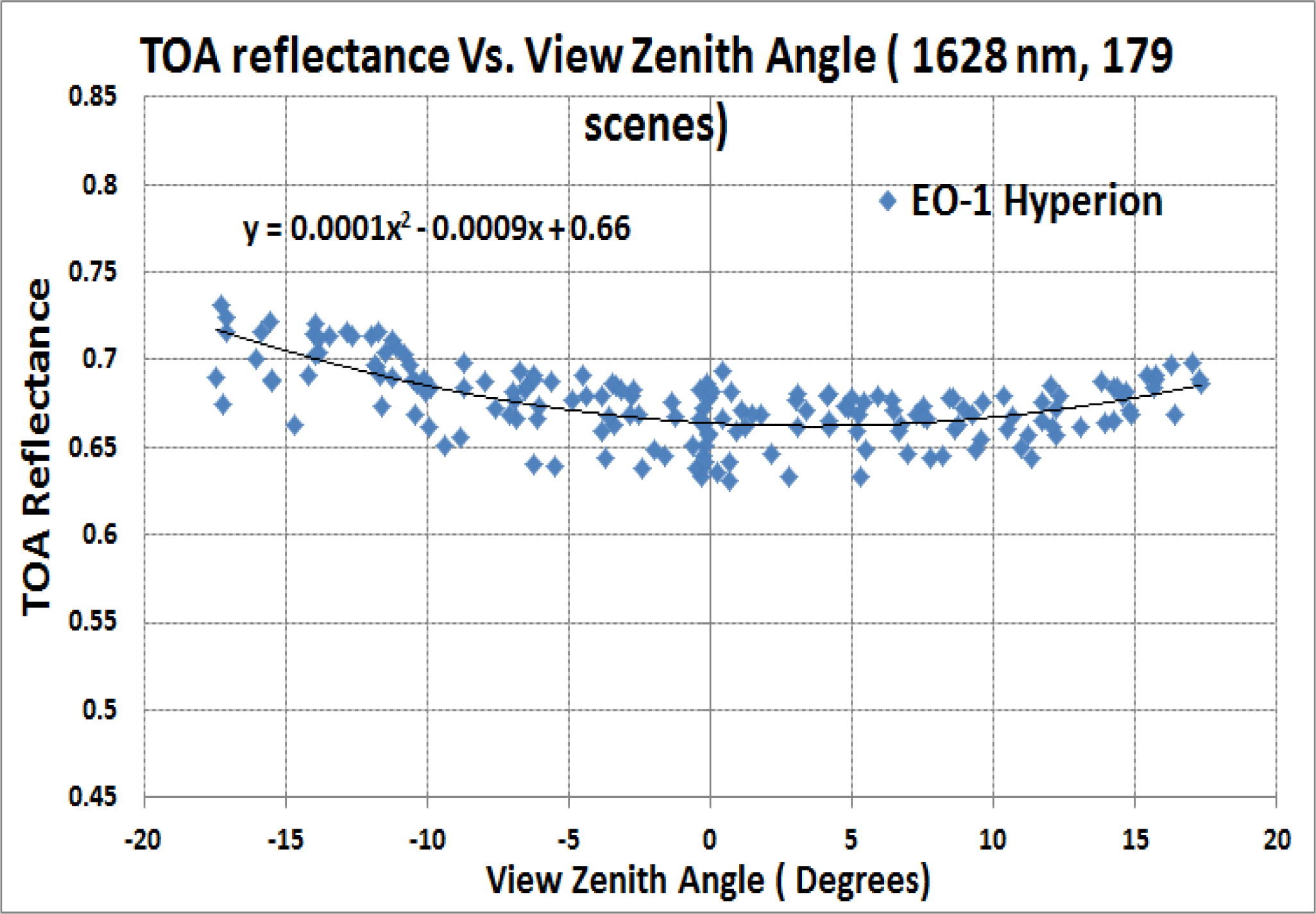
Figure 5 shows TOA reflectance plotted as a function of viewing zenith angle for the 1,628 nm Hyperion channel, where the atmosphere is nearly transparent. It can be also seen from the plot that the VZA for Hyperion is confined to ±18 degrees. As stated previously, the equations for surface BRDF models can be complex, such as the Ross-Li model [
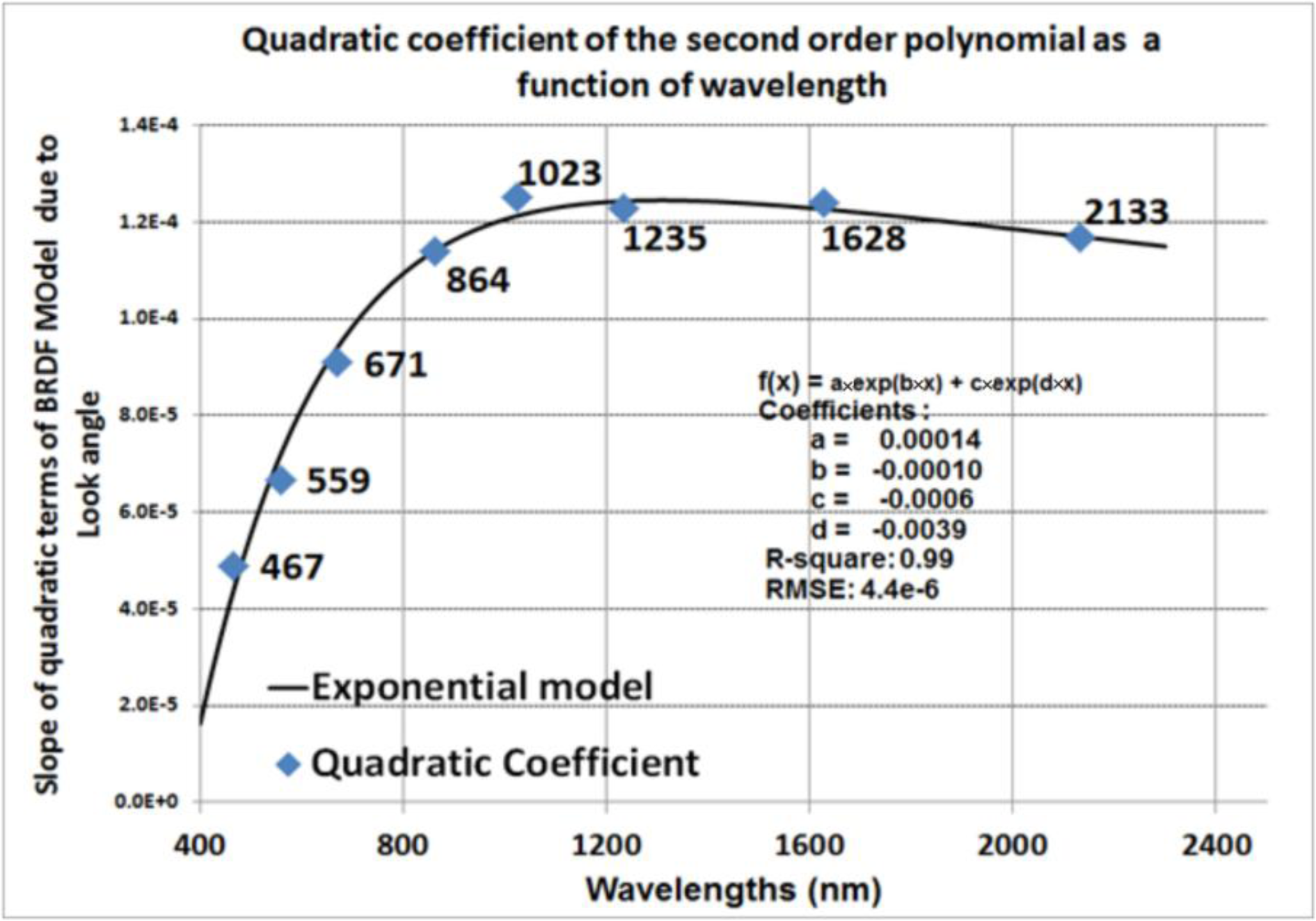
19], but a simple second order polynomial was found to be an adequate estimate for BRDF correction for this desert site (a higher order fit was not statistically justifiable). The procedure was repeated for eight different Hyperion channels centered on a spectral region where there is minimal atmospheric effect. When the slope of the first order and second order term was plotted as a function of wavelength, it was noticed that the slope of the first order terms was essentially constant. However it turned out that the coefficient of the second order term could be modeled as a two-exponential function of wavelength with very low residual error as shown in
Figure 6.
The net result is an empirical BRDF model for solar zenith and viewing zenith angle that parameterizes changes in angular reflectance as an exponential function of wavelength. It was also observed that the solar azimuth and the solar zenith angles were highly correlated because of the limited samples of the satellite data with respect to these angles as the orbital conditions were fairly fixed. Thus, only the BRDF changes due to solar zenith angle need to be addressed.
3.3. Development of Atmospheric Model
At this point in the development of the model, all major surface parameters have been accounted for. However, it must be emphasized that in this semi-empirical approach, these have been derived as observed from top-of-atmosphere. The next step is to extend the model to include atmospheric correction. In general, a typical atmospheric model is achieved using a full up radiative transfer model using tools such as MODTRAN [
23], 6S [
24],
etc., where parameters such as aerosol optical depth, columnar water vapor, different gaseous composition are provided to the model to provide an estimate of the upward radiance scattered from the atmosphere, diffuse radiances, upwelling and downwelling transmittances,
etc. In the empirical approach presented here, the model is based on sensor data observed from the top-of-atmosphere.
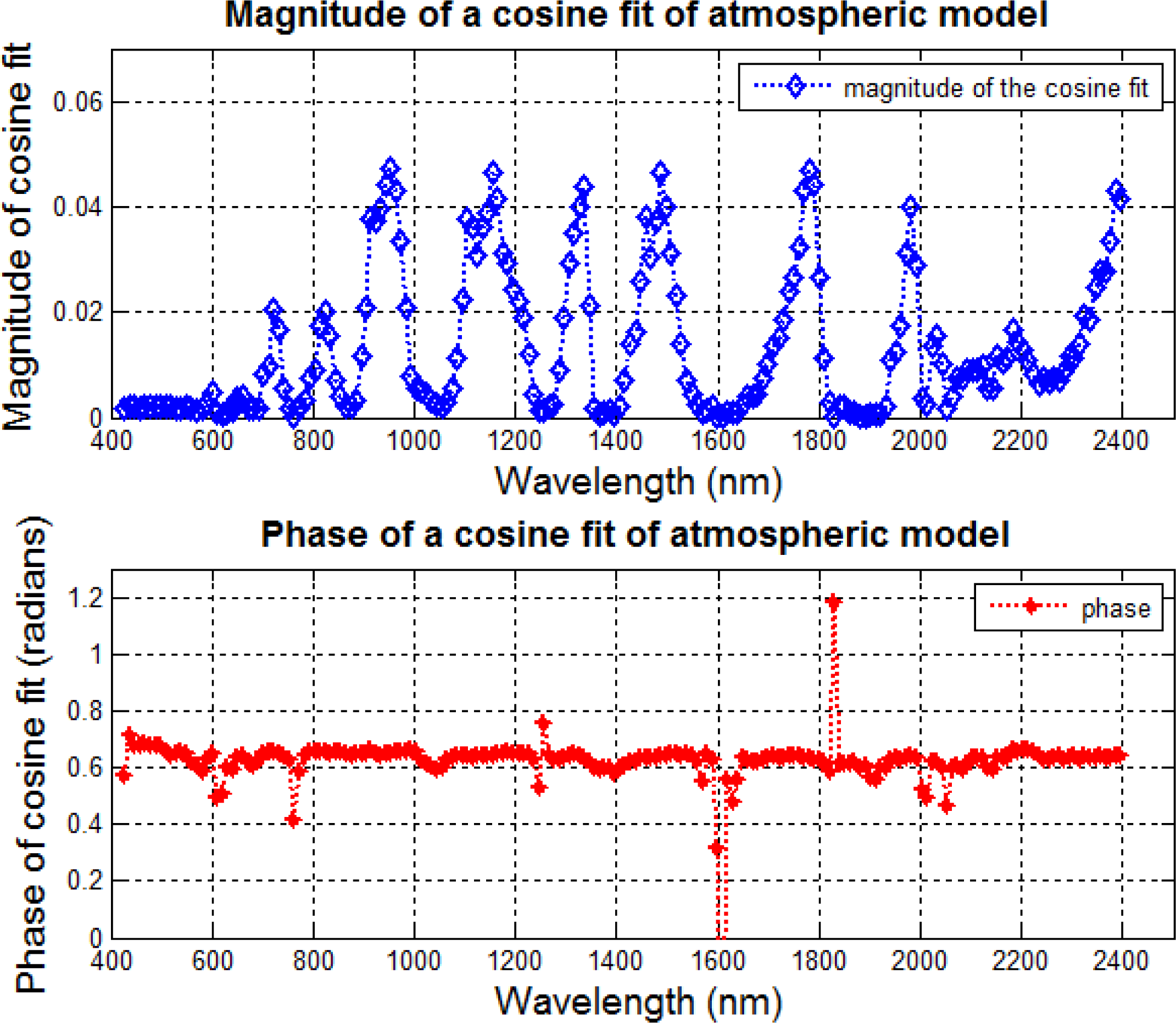
After applying the model to long time series of Landsat data, it was observed that residual seasonal variations exist. For example, TOA reflectance was still slightly higher in the summer months than in the winter months even after surface effects had been removed. This suggests small changes in the atmosphere likely due to seasonal changes in aerosol patterns and molecular absorption. Even though quite small in magnitude, they could be identified through Fourier analysis of the residuals and a simple cosine function was derived and added to the model to account for these seasonal patterns. The value of the magnitude and phase of this function is shown in
Figure 7 as calculated for each Hyperion wavelength. Not surprisingly, the phase was essentially constant and the period was 365.2 days.
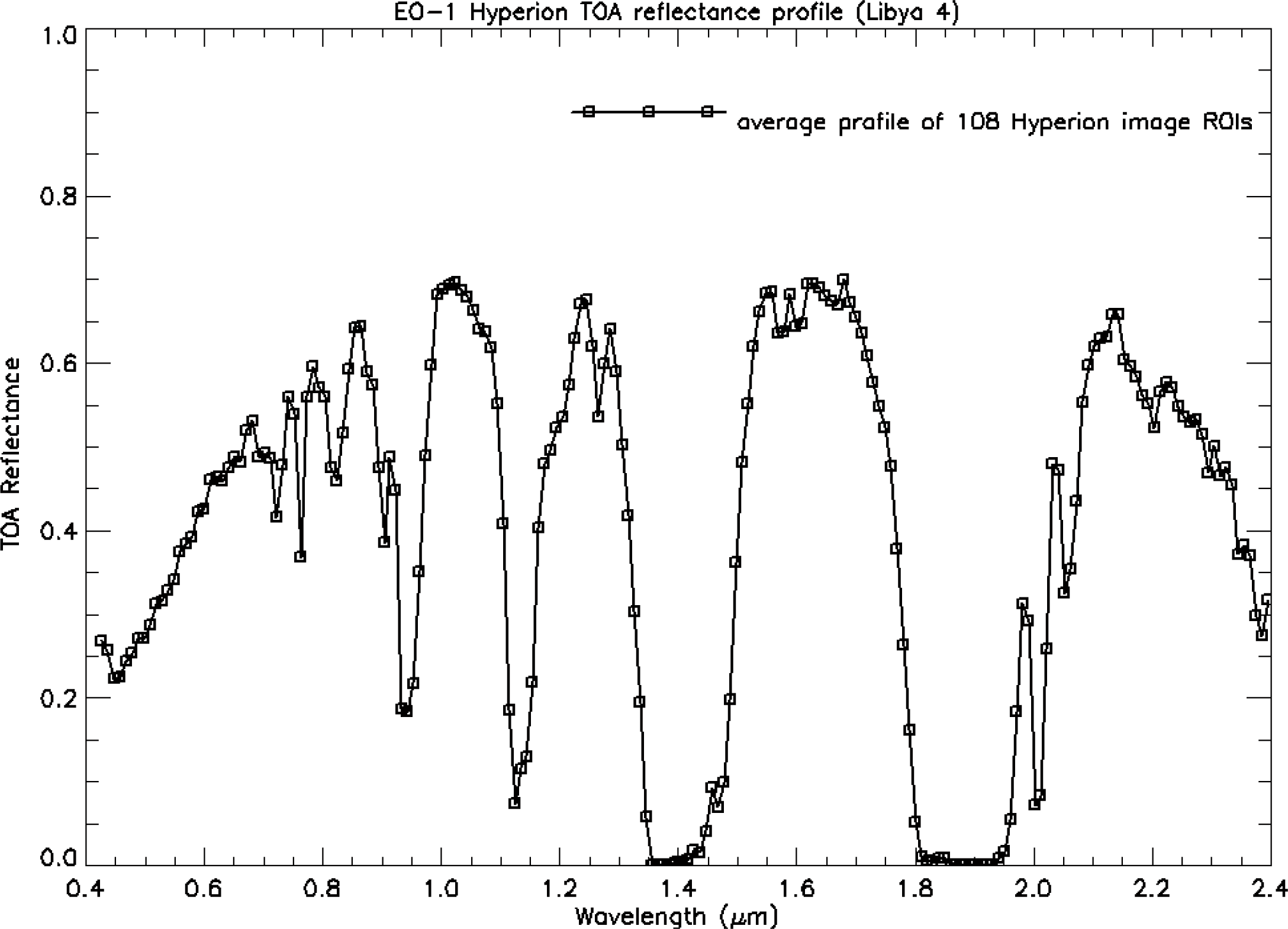
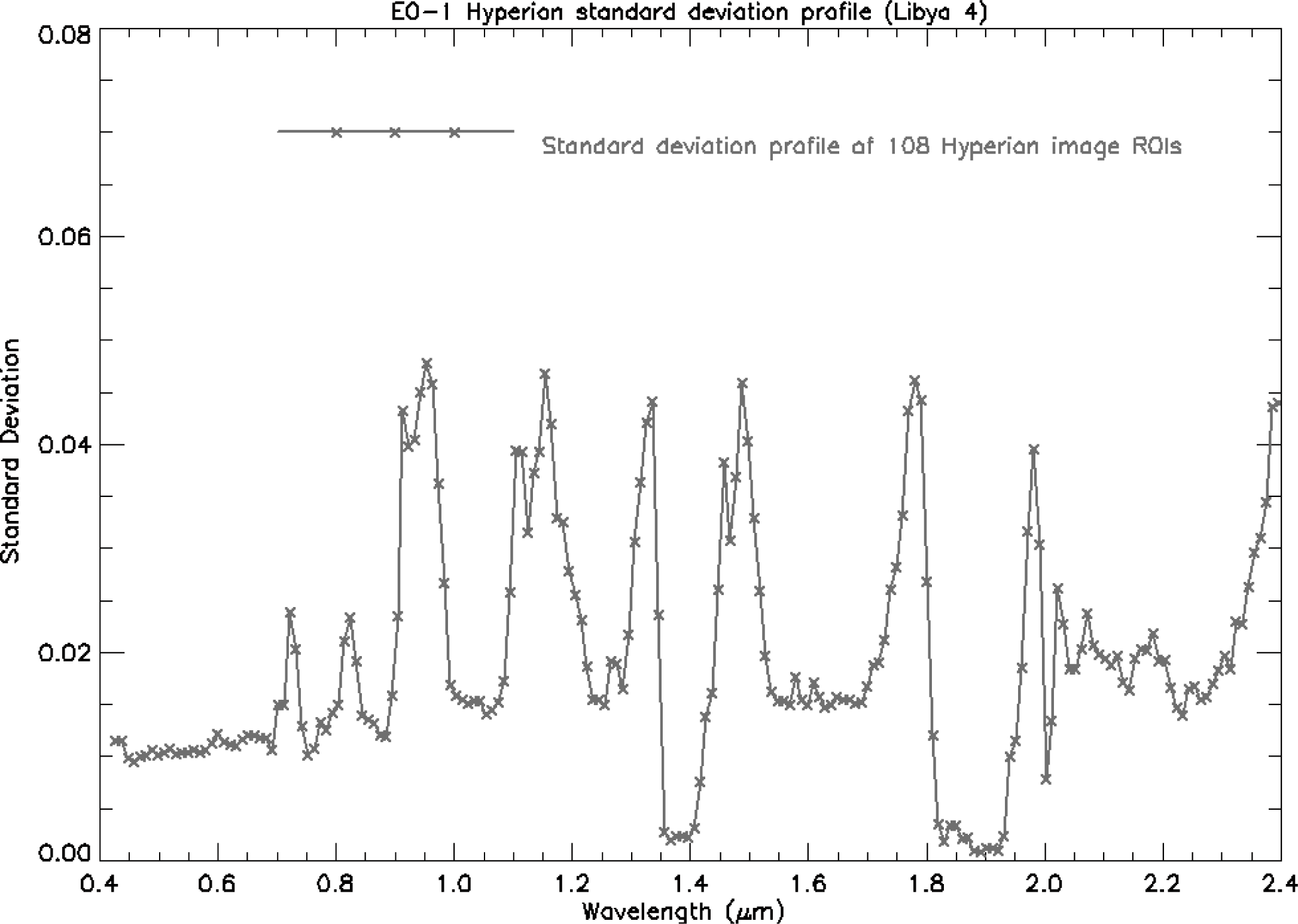
Figures 8 and
9 show the Hyperion TOA reflectance profile derived using 108 cloud-free images over Libya 4 and standard deviation in TOA reflectance from 2004 to 2010 plotted as a function of center wavelength, respectively. It can be seen from these plot that the apparent TOA reflectance is very low or close to zero at wavelengths where atmospheric absorption occurs and the variability is also high at these wavelengths. On comparing these plots with the magnitude plot in
Figure 7, it can be seen that the magnitude as calculated by the atmospheric model is higher around the major atmospheric absorption wavelengths; the higher the magnitude of the absorption, the higher is the amplitude of the atmospheric model. On the other hand, when statistical tests indicated that the slope of the phase response is zero,
i.e., the phase of the model is fairly constant and, for simplicity, an average phase of 0.63 was used for calculation purposes.
Thus the resulting simple model is
where
ρ represents the TOA spectral reflectance for the Libya 4 PICS using Hyperion,
K(
λ) is the scaling factor to place the Hyperion spectra
ρh(
λ), on the MODIS-calibrated scale described in Section 3.1,
fA(
t) represents the atmospheric model which is a function of time of year as described in Section 3.3,
m1(
λ),
m2(
λ) and
m3(
λ) represent the coefficients needed for SZA and VZA correction as described in Section 3.1. The BDRF model has been scaled to a 30-degree solar zenith angle. This model is a modification differing from that presented by Helder
et al. [
5] as it has a functional form of the BRDF model to include off-nadir-viewing angles in the range of ±20° and a simple atmospheric model.
Since the model is based on Terra MODIS, the first step test of the efficacy of the model was to implement it on the Terra MODIS measurements themselves. For convenience, blue asterisks have been used for satellite observation and black circles for the Libya 4 model. The output of the model has been presented in two ways: as systematic offset (bias) calculated as root mean squared error (RMSE) between model predictions and satellite measurements, and as random uncertainties calculated as the standard deviation of the offset between model predictions and satellite measurements. It should also be noted that the percentage difference is calculated as model-predicted values minus the satellite values divided by the model.
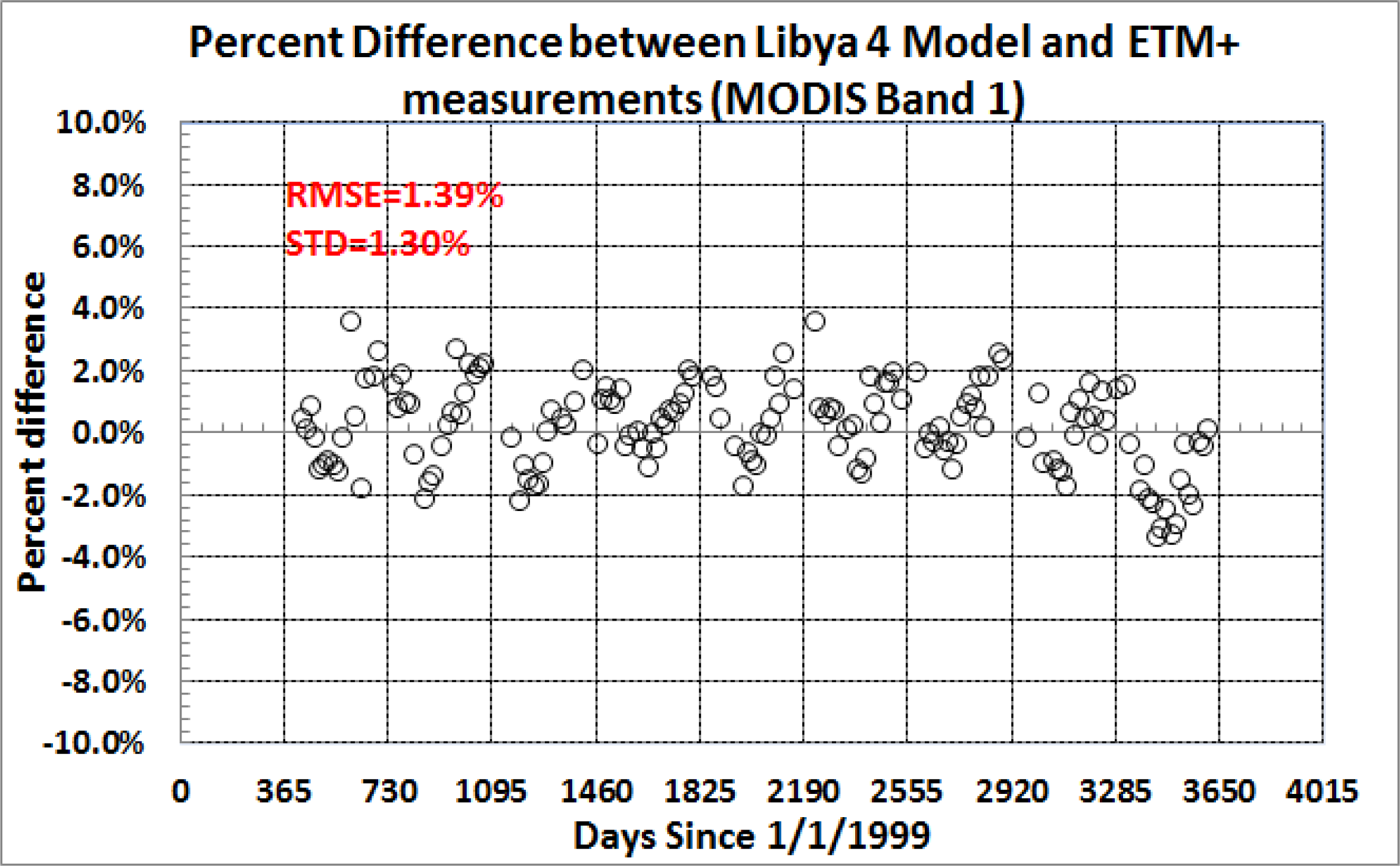
Figure 10 illustrates the application of this model to Terra MODIS red band (band 1 for MODIS and band 3 for Landsat) data collected over Libya 4, while
Figure 11 shows the percentage difference between the model predictions and the MODIS measurements. The bias between the model and the measurements is 1.39% with a standard deviation of 1.3%.
Table 3 shows the summarized results for different solar reflective MODIS bands obtained using the same approach. The RMSE, or bias between the model and MODIS, is under 2% in all bands and is well within the combined uncertainties of MODIS and Hyperion upon which the model was based. The inclusion of the atmospheric model improves the standard deviation presented in the article by Helder
et al. [
11], especially at the longer wavelengths, by about 0.4%. The scatter in the residues (labeled “STD of residues” in
Table 3) is an indication of how much of the model is yet to be explained. Atmospheric, higher order BRDF effects and also small random deviations in instrument response could all be contributing factors. In this case, the level of instability of the atmosphere over the Libya 4 site, at least with respect to the MODIS spectral bandpasses, is evident with differences between model prediction and satellite measurements is essentially between 1% and 2%.
3.4. Validation of the Model Using Satellite Measurements
As mentioned earlier, the measurements from different sets of well-calibrated satellite sensors were used to validate the model. These instruments include Terra and Aqua MODIS, L7 ETM+ and L8 OLI, ENVISAT MERIS and UK-2 DMC and it is important to note that these sensors were calibrated independently of Terra MODIS. Results for the red band of several of these sensors will be shown and the results for all the bands will be summarized in this section. For MERIS, the red band located at 0.657–0.672 μm has been chosen to show as a representative.
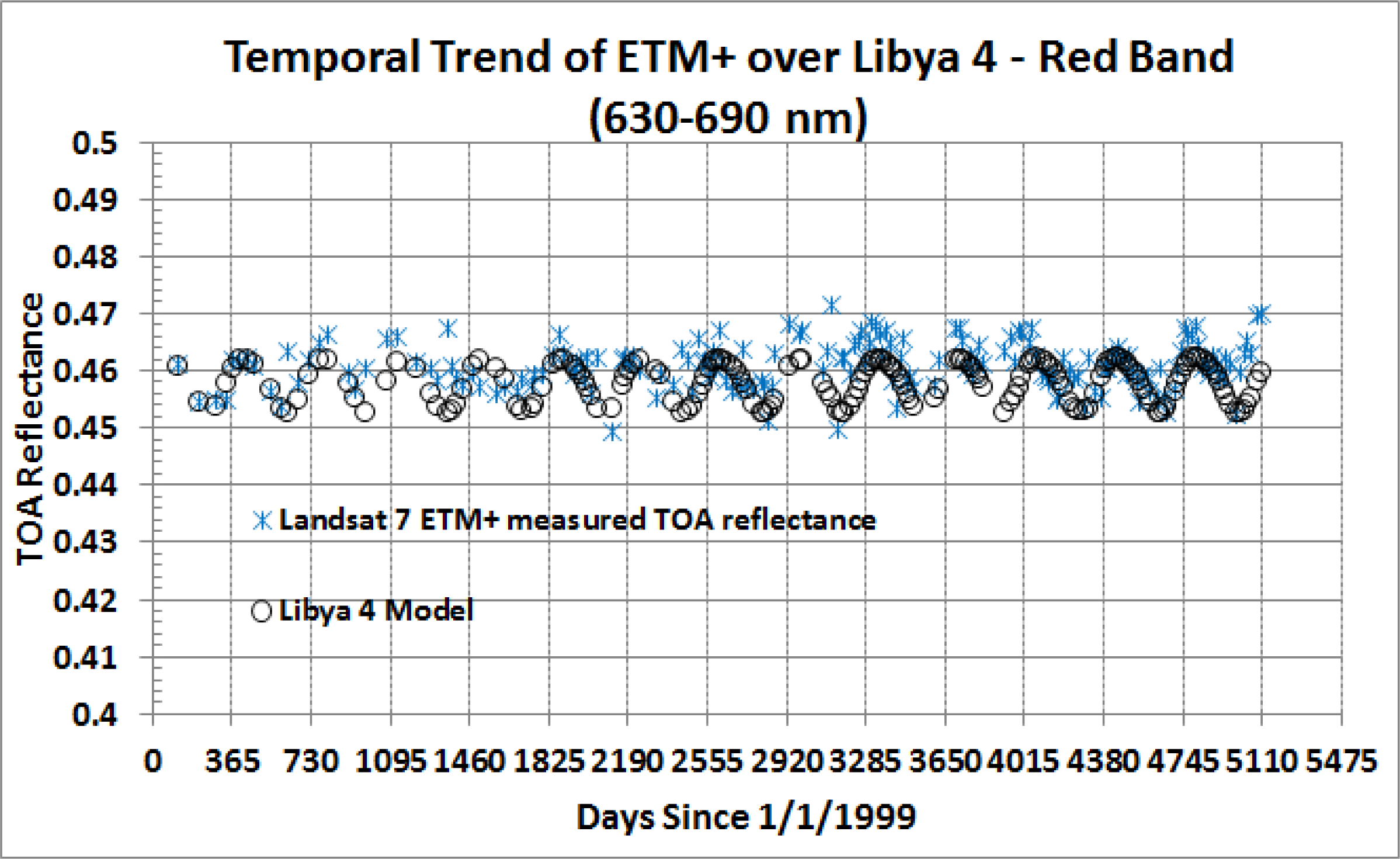
A comparison can be made between the Libya 4 model prediction and at-sensor reflectance derived from ETM+ measurements as shown in
Figure 12 where the circles show the absolute calibration prediction and the asterisks show ETM+ measurements for band 3 (“red” band). It should be noted that the radiometric calibration of the L7 ETM+ was updated in March 2013 and a detailed description of the process has been presented by Barsi
et al. [
14]. The results presented in this section are based on the updated calibration.
Figure 13 shows the percentage difference between the model predictions and satellite measurements, which is on the order of 1.1% RMSE. Thus, these results are well within the specified calibration uncertainties associated with these sensors (5% for Landsat, 2% for MODIS). It is interesting to compare the results shown in
Figures 7 and
10. The amount of bias between the model and the measurements is similar for both instruments. Also, in both cases, there is a random variability (standard deviation of differences between model prediction and satellite measurements) of about 1% attributable primarily to atmospheric differences and site spectral behavior.
Figure 14 illustrates the application of this model to UK2 DMC data that was collected over Libya 4 from 2009 to 2012. The viewing angle for these datasets ranged from nadir to 18 degrees.
Figure 15 shows the percent difference between the model predictions and the UK2 DMC measurements. The bias between the model and the measurements is 1.54% with a standard deviation of 1.54%. Note that while spectral bandpasses for ETM+ and DMC are similar, atmospheric scattering caused by non-nadir-viewing geometries may have not have been adequately explained by the model. This may have caused the standard deviation to be slightly higher than ETM+.
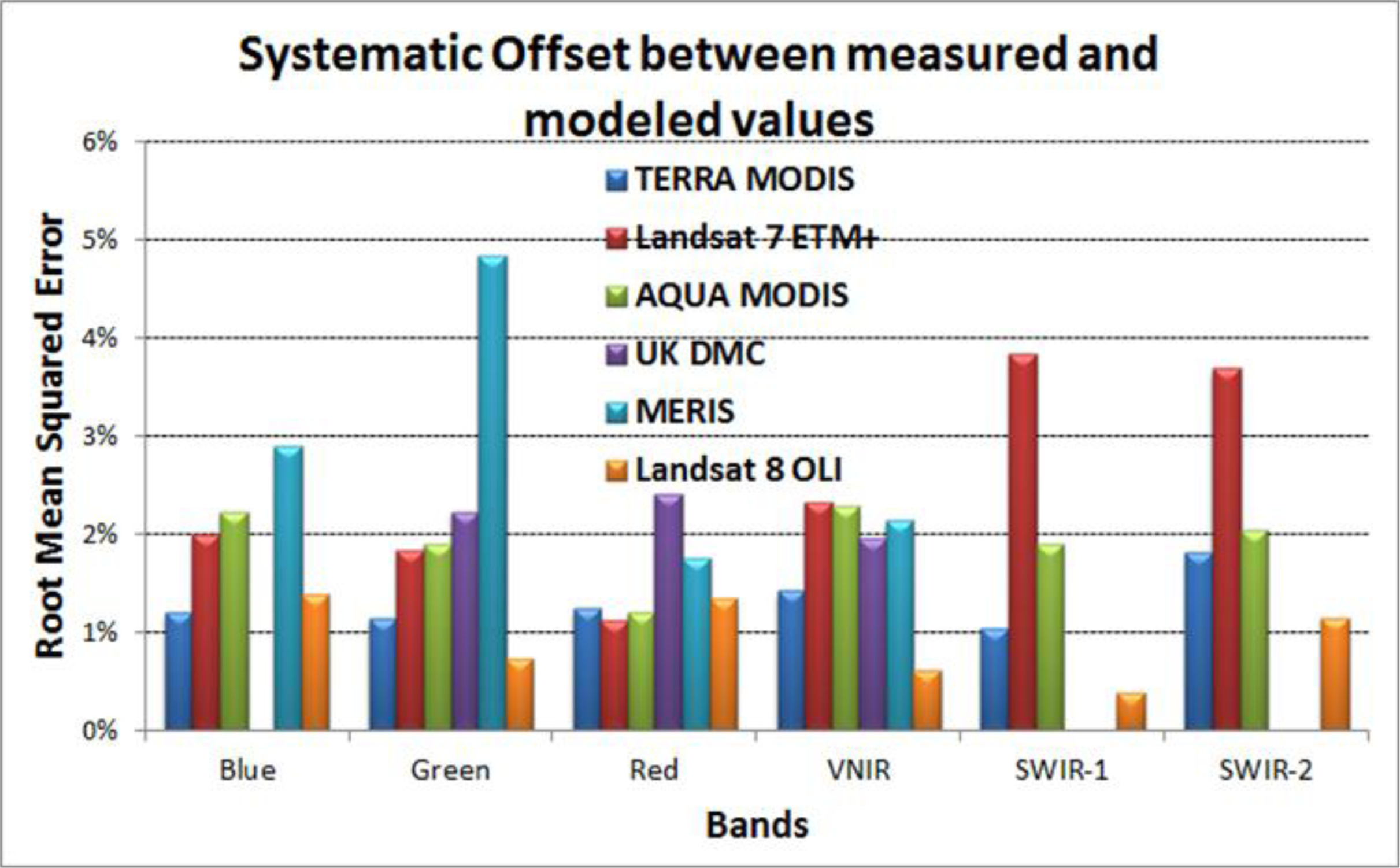
A similar approach is applied to all the sensors introduced earlier through the visible to SWIR bands and the results are summarized in
Figures 16 and
17. The RMSE or bias between the model and satellite-measured values, which are illustrated in
Figure 16, shows that in general, the systematic, as well as random uncertainty, is within 3%. The offset between model predictions and L7 ETM+ SWIR and MERIS green channels approaches 4%. This offset between the model and satellite-measured values are likely based on real differences in the calibration of not only ETM+, MERIS and Terra MODIS but also Hyperion calibration uncertainties.
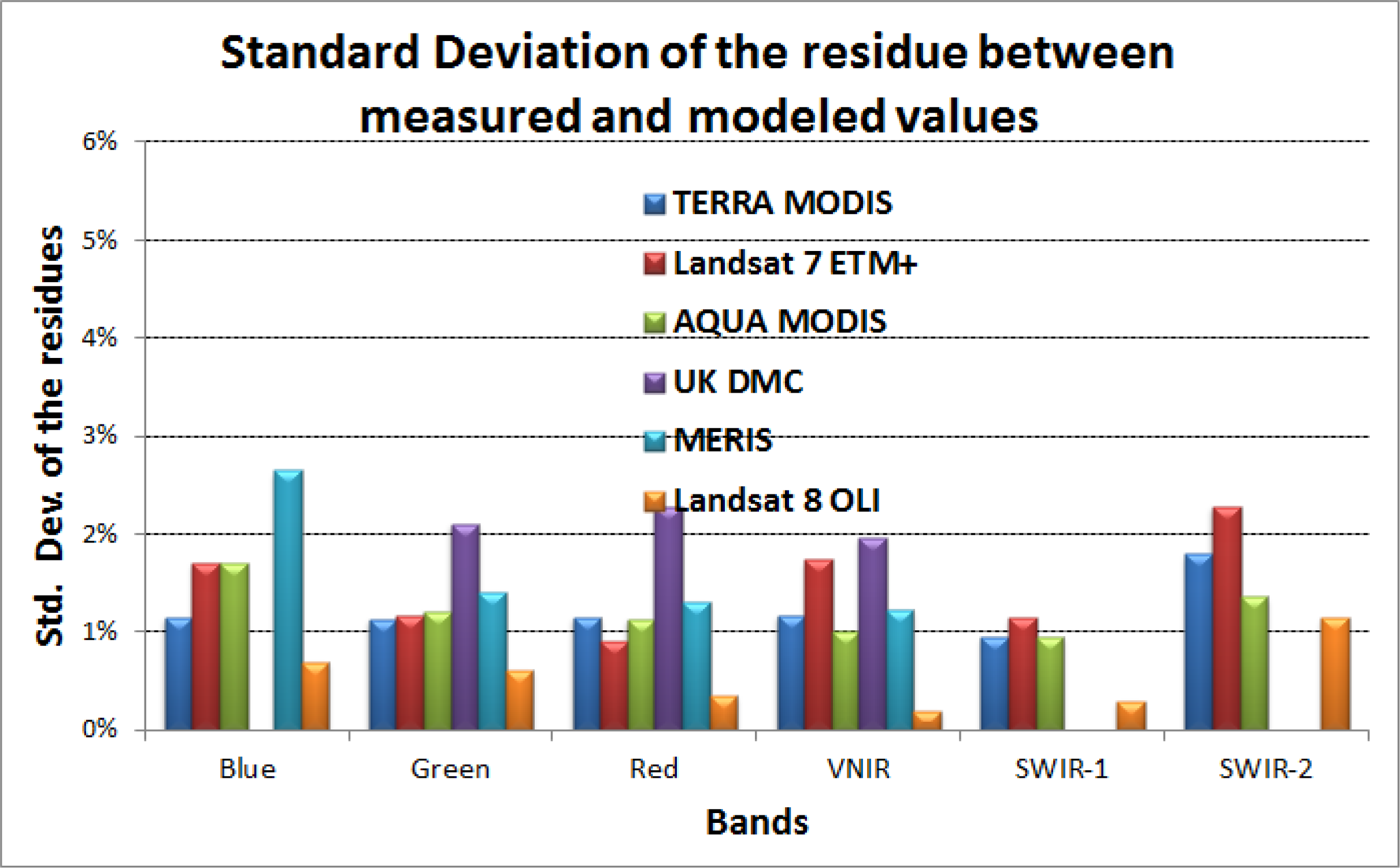
Figure 17 shows the estimates of random variability in the model. In general, these uncertainties are within 2%. The Terra MODIS and MERIS spectral bandpasses are narrower and avoid the molecular features more than Landsat and DMC instruments, and are therefore less affected by changes in the atmosphere. In the case of MERIS and DMC, these uncertainties are probably increased due to the increased path length scattering due to non-nadir acquisitions which is not adequately explained by the empirical model.
It should also be noted that the stated absolute calibration accuracy of Terra MODIS is about 2% and that of Hyperion is about 4%. The combined uncertainty (assumed uncorrelated) of these instruments is 4.5%. Thus, in all the cases, differences predicted by the model are well within the combined uncertainties of the two sensors used to develop the model. The systematic difference (or the accuracy) between the model and satellite measurements is within 3%. Part of the remaining difference is primarily attributed to the real calibration differences between Terra MODIS, EO-1 Hyperion and various sensors under study. It can be seen that the random uncertainties (or precision), shown in
Figure 17 are generally better than 2%. Similar work performed by Govaerts
et al. over Libya 4 showed mean accuracy of 3% when his model was validated with different satellite sensors using three-year observations from 2006 to 2009 [
9]. However their approach was based on using solar irradiance as forcing function coupled with a BRDF model and a radiative transfer atmospheric model. Thus the comparison between these two approaches shows that it is possible to develop a PICS-based calibration model with a mean accuracy of 3%. However, his model only extended to SWIR-1 band, whereas the work presented in this article extends up to SWIR-2 band (2,395 nm).
It is interesting to note that both systematic and random does not vary smoothly as a function of wavelength. A portion of this is primarily driven by atmospheric changes as the spectral bandpass differences between Terra MODIS and other sensors are large enough to respond differently to atmospheric conditions at the time of overpass. The empirical atmospheric model did account for the residual seasonal variations in the satellite datasets, but this model is too simple to account for the complex atmospheric phenomenon. Similarly, the empirical BRDF model provided a limiting BRDF samples as the solar zenith angles and the view zenith angle ranges were limited since the orbital conditions of the satellite were fixed. Both the precision and accuracy of the model shown in
Figures 16 and
17 can be improved by using the first principles approach, which would use the sun as a solar forcing function rather than using a single sensor as a calibrated radiometer, a surface BRDF model based on the physical properties of the surface and a full up atmospheric transfer model using climatological data. Data from climatological databases such as Aerosol Robotic Network (AERONET) and metrological observation from various National Oceanic and Atmospheric Administration (NOAA) can be used to develop atmospheric model.