Remotely Sensed Monitoring of Small Reservoir Dynamics: A Bayesian Approach
Abstract
:1. Introduction
2. Datasets
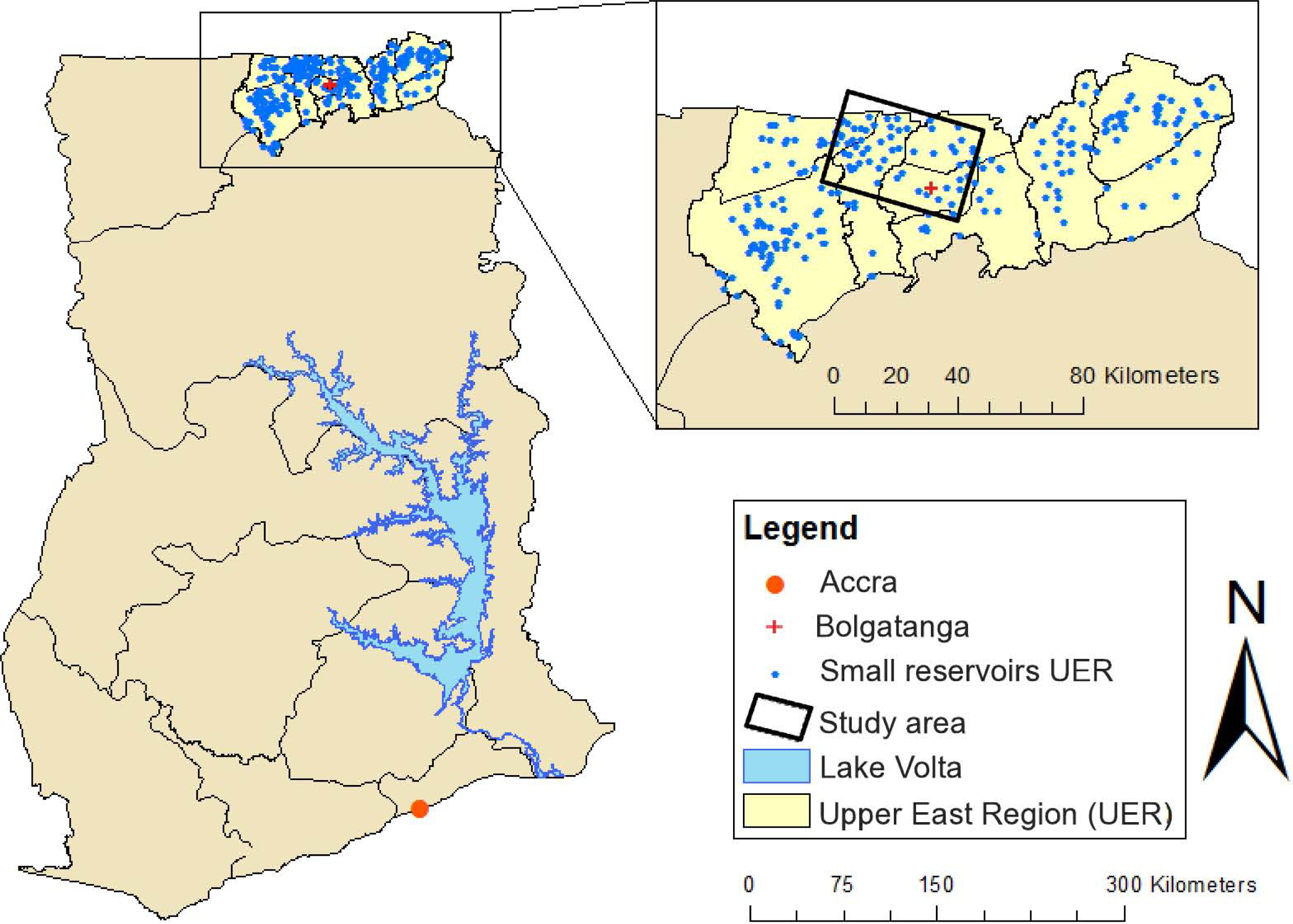
2.1. Ground Truth
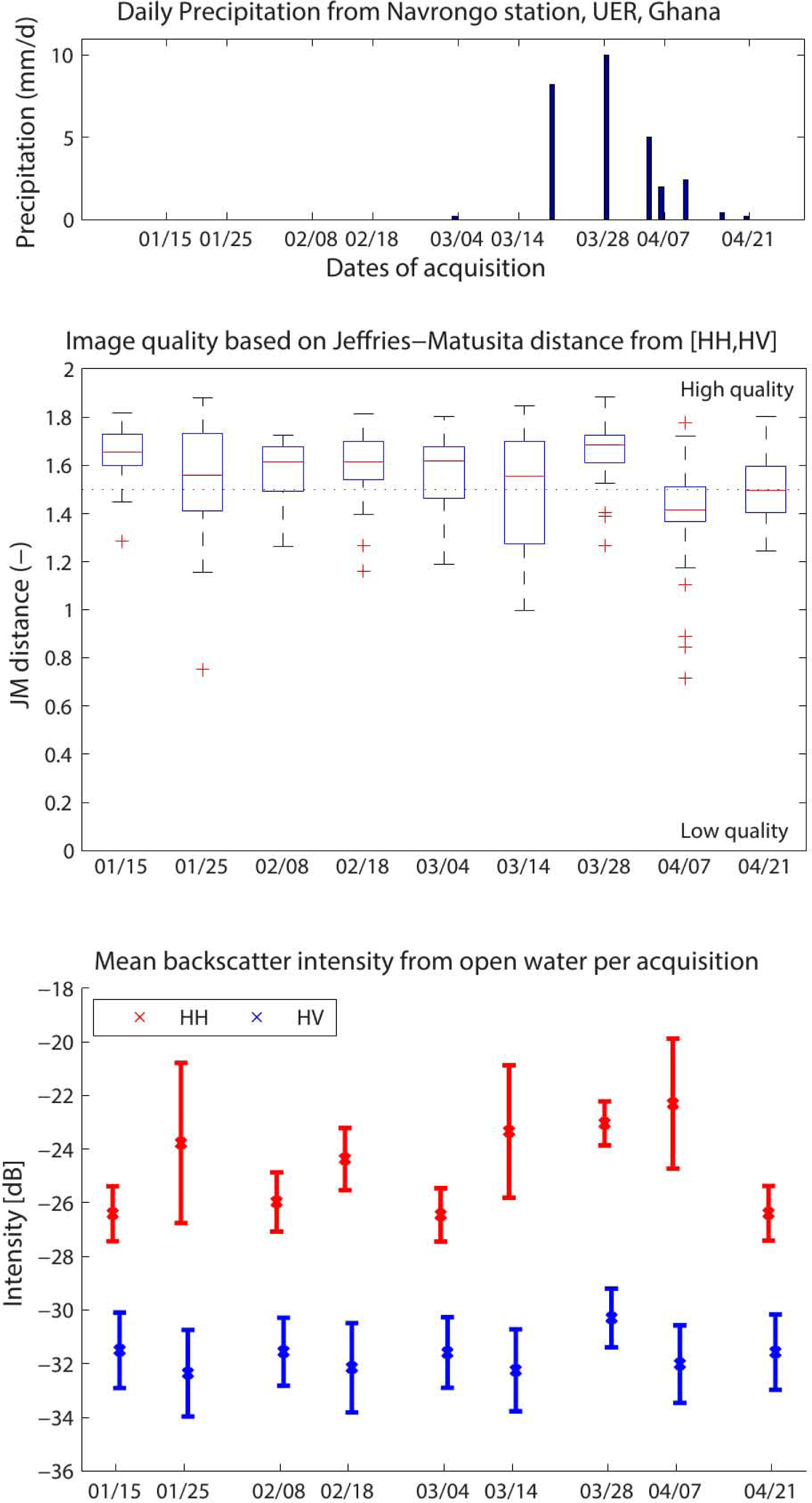
2.2. Precipitation Data
2.3. Radarsat-2 SAR Data
3. Methods
3.1. Pre-Processing SAR Imagery
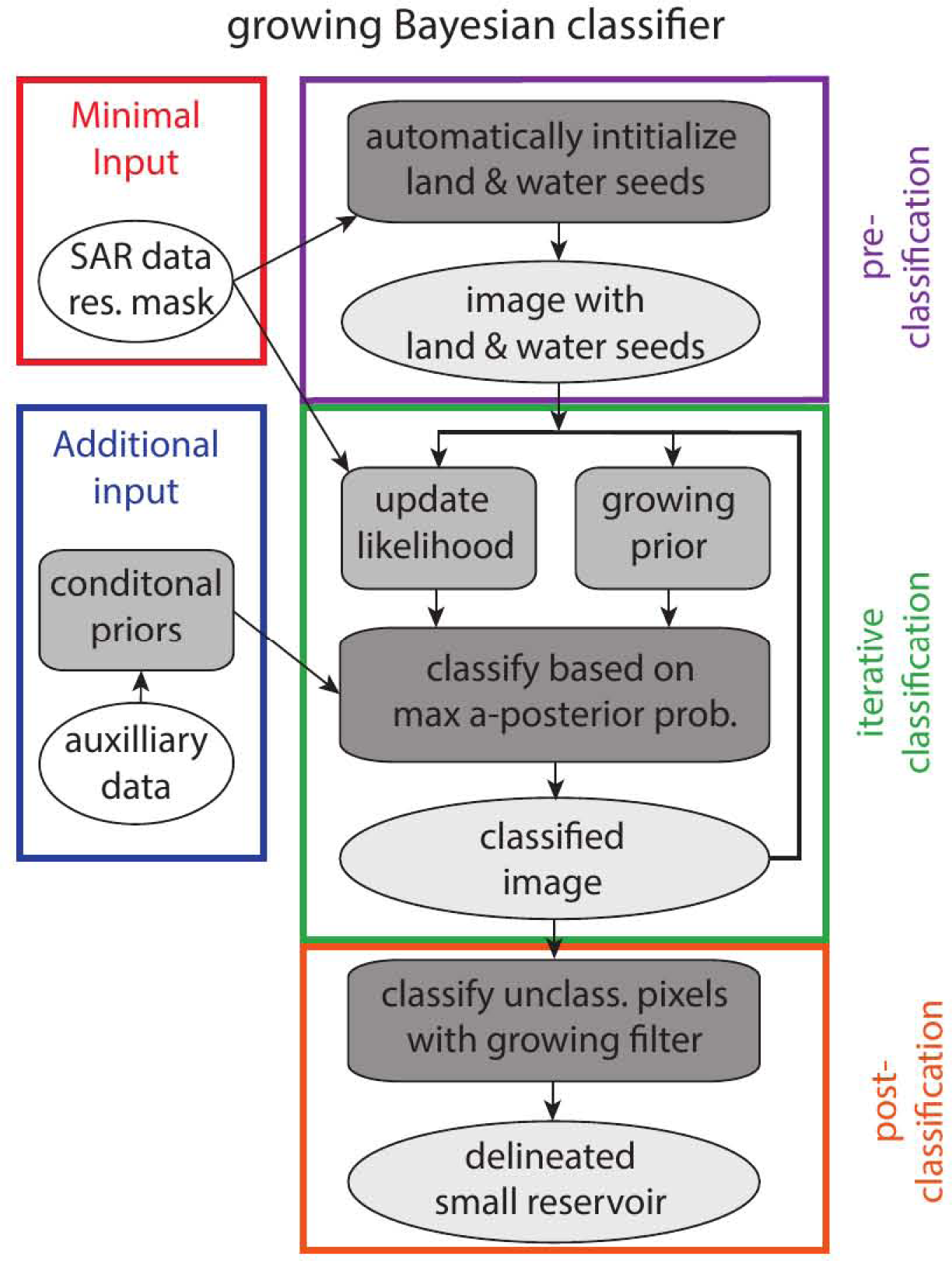
3.2. Growing Bayesian Classifier
3.2.1. Basic Growing Bayesian Classifier
3.2.2. Extended Growing Bayesian Classifier
4. Results and Discussion
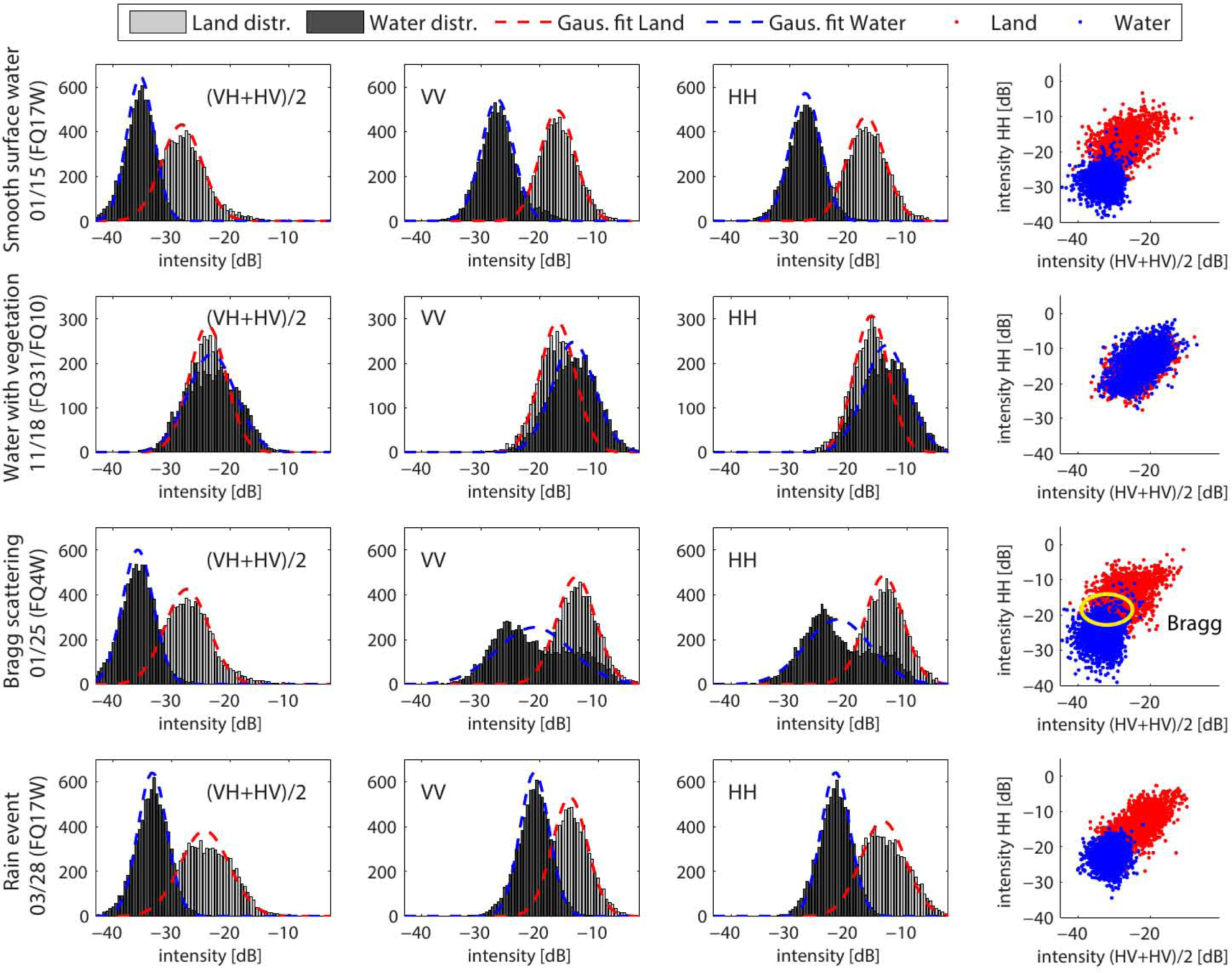
4.1. Polarimetric SAR Remote Sensing of Small Reservoirs for Different Backscatter Scenarios
4.1.1. Smooth Open Water
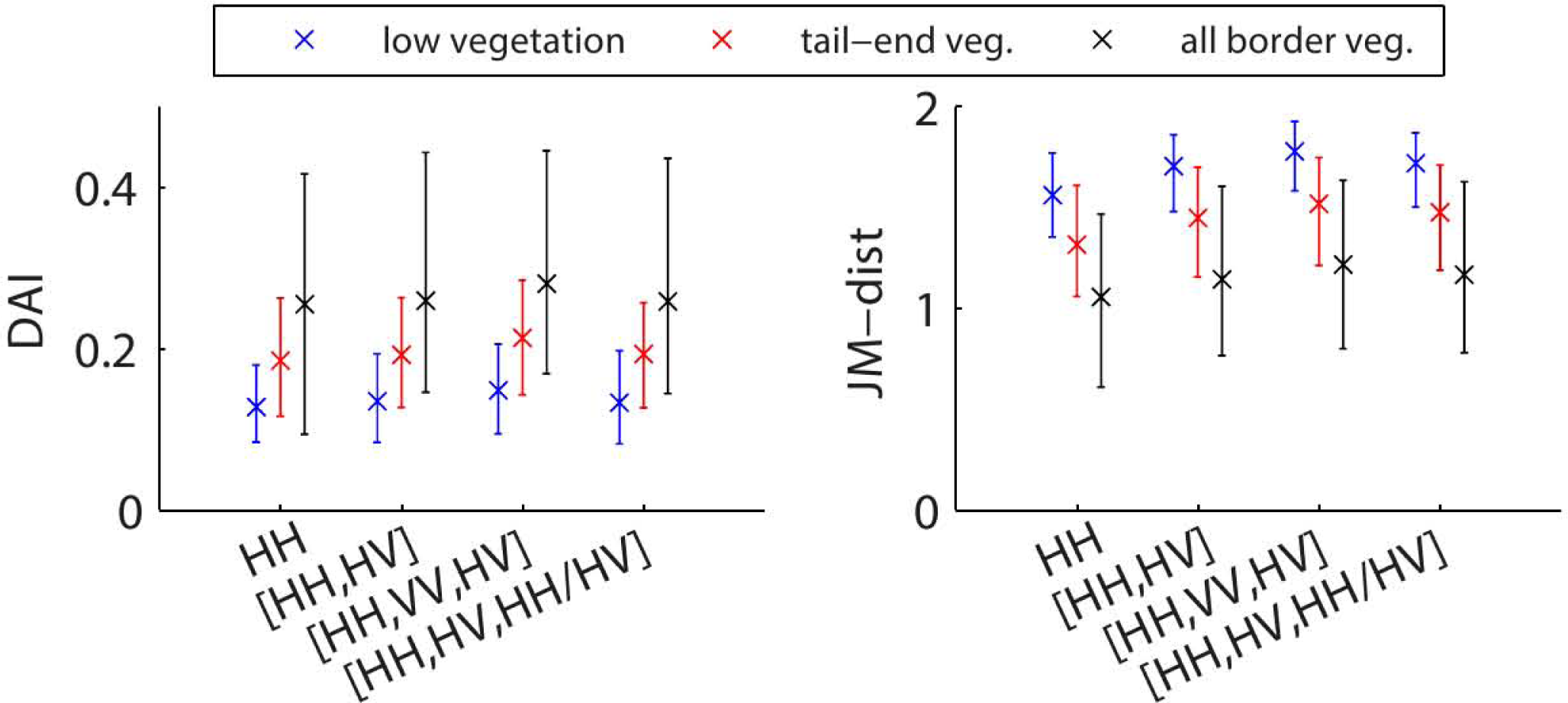
4.1.2. Water With Vegetation
4.1.3. Wind-Induced Bragg Scatter
4.1.4. Rain Event
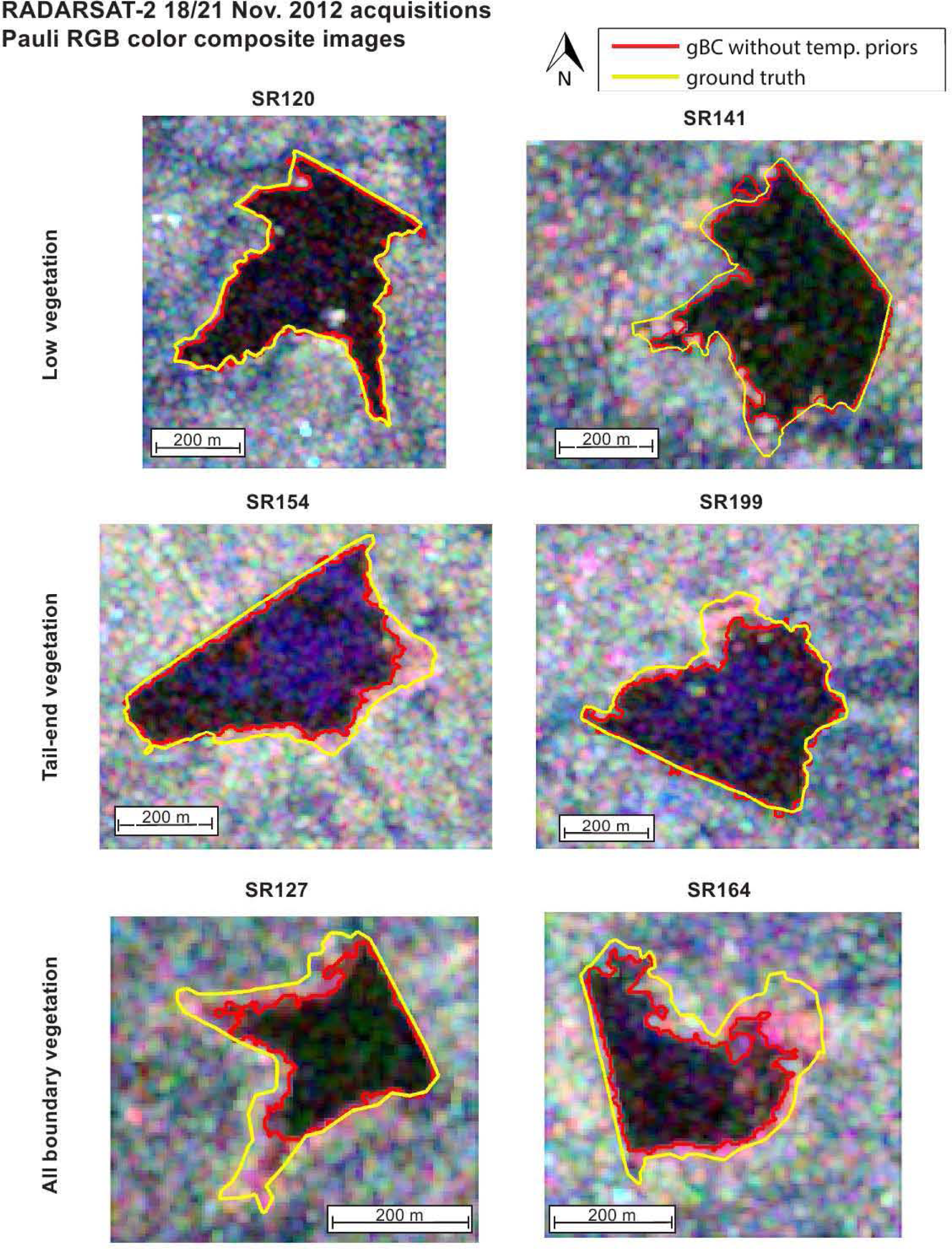
4.2. Comparison with Ground Truth
4.3. Image Quality
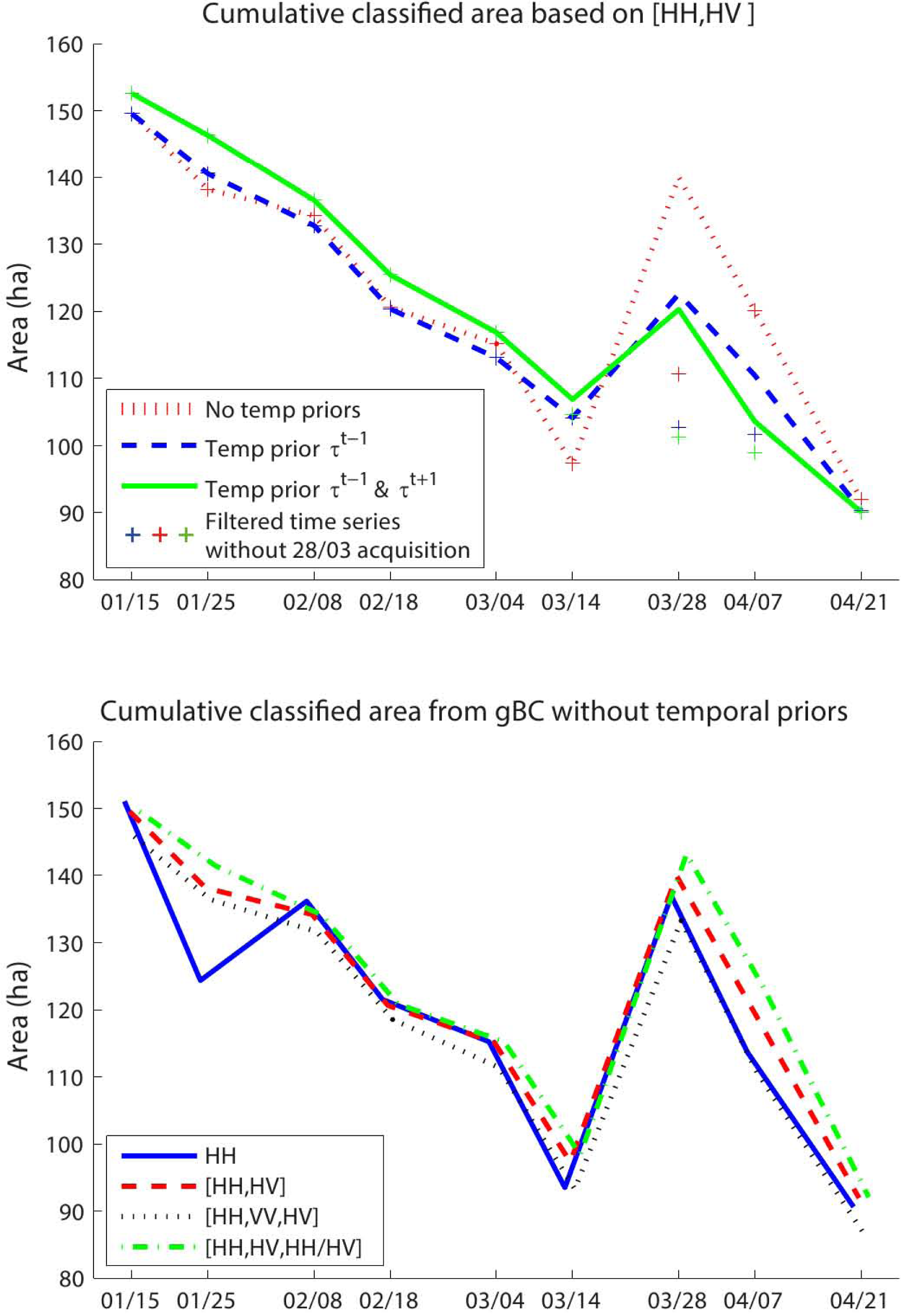
4.4. Time Series Analysis
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Venot, J.P.; Fraiture, C.D.; Nti Acheampong, E. Revisiting Dominant Notions: A Review of Costs, Performance and Institutions of Small Reservoirs in Sub-Saharan Africa; IWMI Research Report 144; International Water Management Institute: Colombo, Sri Lanka, 2012; p. 39. [Google Scholar]
- Leemhuis, C.; Jung, G.; Kasei, R.; Liebe, J. The Volta Basin Water Allocation System: Assessing the impact of small-scale reservoir development on the water resources of the Volta basin, West Africa. Adv. Geosci 2009, 21, 57–62. [Google Scholar]
- Krol, M.S.; de Vries, M.J; van Oel, P.R.; de Araújo, J.C. Sustainability of small reservoirs and large scale water availability under current conditions and climate change. Water Resour. Manag 2011, 25, 3017–3026. [Google Scholar]
- Annor, F.; van de Giesen, N.; Liebe, J; van de Zaag, P.; Tilmant, A.; Odai, S. Delineation of small reservoirs using radar imagery in a semi-arid environment: A case study in the Upper East Region of Ghana. Phys. Chem. Earth, Parts A/B/C 2009, 34, 309–315. [Google Scholar]
- Liebe, J; van de Giesen, N.; Andreini, M. Estimation of small reservoir storage capacities in a semi-arid environment: A case study in the Upper East Region of Ghana. Phys. Chem. Earth 2005, 30, 448–454. [Google Scholar]
- Sawunyama, T.; Senzanje, A.; Mhizha, A. Estimation of small reservoir storage capacities in Limpopo River Basin using geographical information systems (GIS) and remotely sensed surface areas: Case of Mzingwane catchment. Phys. Chem. Earth 2006, 31, 935–943. [Google Scholar]
- Crétaux, J.F.; Birkett, C. Lake studies from satellite radar altimetry. Comptes Rendus Geosci 2006, 338, 1098–1112. [Google Scholar]
- Gao, H.; Birkett, C.; Lettenmaier, D. Global monitoring of large reservoir storage from satellite remote sensing. Water Resour. Res 2012, 48, W09504. [Google Scholar]
- Islam, A.; Bala, S.; Haque, M. Flood inundation map of Bangladesh using MODIS time-series images. J. Flood Risk Manag 2010, 3, 210–222. [Google Scholar]
- McFeeters, S. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. Int. J. Remote Sens 1996, 17, 1425–1432. [Google Scholar]
- Xu, H. Modification of Normalised Difference Water Index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens 2006, 27, 3025–3033. [Google Scholar]
- Mialhe, F.; Gunnell, Y; Mering, C. Synoptic assessment of water resource variability in reservoirs by remote sensing: General approach and application to the runoff harvesting systems of south India. Water Resour. Res 2008, 44, W05411. [Google Scholar]
- Rodrigues, L.; Sano, E.; Steenhuis, T.; Passo, D. Estimation of small reservoir storage capacities with remote sensing in the Brazilian Savannah Region. Water Resour. Manag 2012, 26, 1–10. [Google Scholar]
- Liebe, J.; van de Giesen, N.; Andreini, M.; Steenhuis, T.; Walter, M. Suitability and limitations of ENVISAT ASAR for monitoring small reservoirs in a semiarid area. Geosci. Remote Sens 2009a, 47, 1536–1547. [Google Scholar]
- Bamler, R.; Eineder, M. Accuracy of differential shift estimation by correlation and split-bandwidth interferometry for wideband and delta-k SAR systems. IEEE Geosci. Remote Sens. Lett 2005, 2, 151–155. [Google Scholar]
- Van de Giesen, N. Characterization of West African Shallow Flood Plains with L-and C-Band Radar; Owe, M., Brubaker, K., Ritchie, J., Rango, A., Eds.; IAHS Publication: Wallingford, UK, 2001. [Google Scholar]
- Eilander, D.M. Remotely Sensed Small Reservoir Monitoring: A Bayesian Approach. Delft University of Technology, Delft, The Netherlands, 2013. [Google Scholar]
- Hoekman, D.H.; Vissers, M.A. A new polarimetric classification approach evaluated for agricultural crops. IEEE Trans. Geosci. Remote Sens 2003, 41, 2881–2889. [Google Scholar]
- Besag, J.; York, J.; Mollié, A. Bayesian image restoration, with two applications in spatial statistics. Ann. Inst. Stat. Math 1991, 43, 1–20. [Google Scholar]
- Strahler, A.H. The use of prior probabilities in maximum likelihood classification of remotely sensed data. Remote Sens. Environ 1980, 10, 135–163. [Google Scholar]
- Kailath, T. The divergence and Bhattacharyya distance measures in signal selection. IEEE Trans. Commun. Technol 1967, 15, 52–60. [Google Scholar]
- Cloude, S.; Pottier, E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans. Geosci. Remote Sens 1997, 35, 68–78. [Google Scholar]
- Yang, J.; Yamaguchi, Y.; Yamada, H.; Sengoku, M.; Lin, S. Optimal problem for contrast enhancement in polarimetric radar remote sensing. IEICE Trans. Commun 1999, 82, 174–183. [Google Scholar]
- Yang, J.; Yamaguchi, Y.; Boerner, W.M.; Lin, S. Numerical methods for solving the optimal problem of contrast enhancement. IEEE Trans. Geosci. Remote Sens 2000, 38, 965–971. [Google Scholar]
- Yang, J.; Dong, G.; Peng, Y.; Yamaguchi, Y.; Yamada, H. Generalized optimization of polarimetric contrast enhancement. IEEE Geosci. Remote Sens. Lett 2004, 1, 171–174. [Google Scholar]
- Henderson, F. Environmental factors and the detection of open surface water areas with X-band radar imagery. Int. J. Remote Sens 1995, 16, 2423–2437. [Google Scholar]
- Henderson, F.; Lewis, A. Principles and Applications of Imaging Radar. Manual of Remote Sensing; John Wiley and Sons: New York, USA, 1998; Volume 2. [Google Scholar]
- Valenzuela, G.R. Theories for the interaction of electromagnetic and oceanic waves—A review. Bound.-Layer Meteorol 1978, 13, 61–85. [Google Scholar]
- Brisco, B.; Short, N.; van der Sanden, J.; Landry, R.; Raymond, D. A semi-automated tool for surface water mapping with RADARSAT-1. Can. J. Remote Sens 2009, 35, 336–344. [Google Scholar]
- Dubois, P.C.; van Zyl, J.; Engman, T. Measuring soil moisture with imaging radars. IEEE Trans. Geosci. Remote Sens 1995, 33, 915–926. [Google Scholar]
- Liebe, J.; van de Giesen, N.; Andreini, M.; Walter, M.; Steenhuis, T. Determining watershed response in data poor environments with remotely sensed small reservoirs as runoff gauges. Water Resour. Res 2009, 45, W07410. [Google Scholar]

| Date | Year | Time/Pass | Beam Mode | Incidence Angle (degree) | Pixel Spacing (rg× ax) (m) |
|---|---|---|---|---|---|
| 18 November | 2012 | 05:44:13/desc | FQ31 | 48.3–49.4 | 5.14 × 6.28 |
| 21 November | 2012 | 05:56:37/desc | FQ10 | 29.1–30.9 | 5.19 × 9.26 |
| 15 January | 2013 | 05:52:27/desc | FQ17W | 35.7–8.6 | 5.6 × 7.83 |
| 25 January | 2013 | 06:00:44/desc | FQ4W | 21.3–24.8 | 4.6 × 11.94 |
| 8 February | 2013 | 05:52:27/desc | FQ17W | 35.7–38.6 | 5.6 × 7.83 |
| 18 February | 2013 | 06:00:43/desc | FQ4W | 21.3–24.8 | 4.6 × 11.94 |
| 4 March | 2013 | 05:52:27/desc | FQ17W | 35.7–38.6 | 5.6 × 7.83 |
| 14 March | 2013 | 06:00:43/desc | FQ4W | 21.3–24.8 | 4.6 × 11.94 |
| 28 March | 2013 | 05:52:27/desc | FQ17W | 35.7–38.6 | 5.6 × 7.83 |
| 7 April | 2013 | 06:00:44/desc | FQ4W | 21.3–24.8 | 4.6 × 11.94 |
| 21 April | 2013 | 05:52:27/desc | FQ17W | 35.7–38.6 | 5.6 × 7.83 |
| Growing Prior | v1 | v2 | v3 | v4 |
|---|---|---|---|---|
| land pixels | >=1 | >=1 | 0 | 0 |
| water pixels | 0 | >=1 | >=1 | 0 |
| P(ωland) | 0.5 | 0.5 | 0 | 0 |
| P(ωwater) | 0 | 0.5 | 0.5 | 0 |
| P(ωunclassified) | 0.5 | 0 | 0.5 | l.0 |
| Prior τt−1 | |||
|---|---|---|---|
| Classification in Time Step t-l | Land | Water | Unclassified |
| P(ωland) | 0.6 | 0.25 | 1/3 |
| P(ωwater) | 0.2 | 0.5 | 1/3 |
| P(ωunclassified) | 0.2 | 0.25 | 1/3 |
| Prior τt+1 | |||
|---|---|---|---|
| Classification in time step t + 1 | Land | Water | Unclassified |
| prior τt+1 dry season | |||
| P(ωland) | 0.5 | 0 | 1/3 |
| P(ωwater) | 0.25 | 1 | 1/3 |
| P(ωunclassified) | 0.25 | 0 | 1/3 |
| prior τt+1 rainy season/after rain | |||
| P(ωland) | 0.5 | 0.25 | 1/3 |
| P(ωwater) | 0.25 | 0.5 | 1/3 |
| P(ωunclassified) | 0.25 | 0.25 | 1/3 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Eilander, D.; Annor, F.O.; Iannini, L.; Van de Giesen, N. Remotely Sensed Monitoring of Small Reservoir Dynamics: A Bayesian Approach. Remote Sens. 2014, 6, 1191-1210. https://doi.org/10.3390/rs6021191
Eilander D, Annor FO, Iannini L, Van de Giesen N. Remotely Sensed Monitoring of Small Reservoir Dynamics: A Bayesian Approach. Remote Sensing. 2014; 6(2):1191-1210. https://doi.org/10.3390/rs6021191
Chicago/Turabian StyleEilander, Dirk, Frank O. Annor, Lorenzo Iannini, and Nick Van de Giesen. 2014. "Remotely Sensed Monitoring of Small Reservoir Dynamics: A Bayesian Approach" Remote Sensing 6, no. 2: 1191-1210. https://doi.org/10.3390/rs6021191





