An Extended Fourier Approach to Improve the Retrieved Leaf Area Index (LAI) in a Time Series from an Alpine Wetland
Abstract
:1. Introduction
2. Method
2.1. The Schemes of LAI Retrieval
2.1.1. Radiative Transfer Model
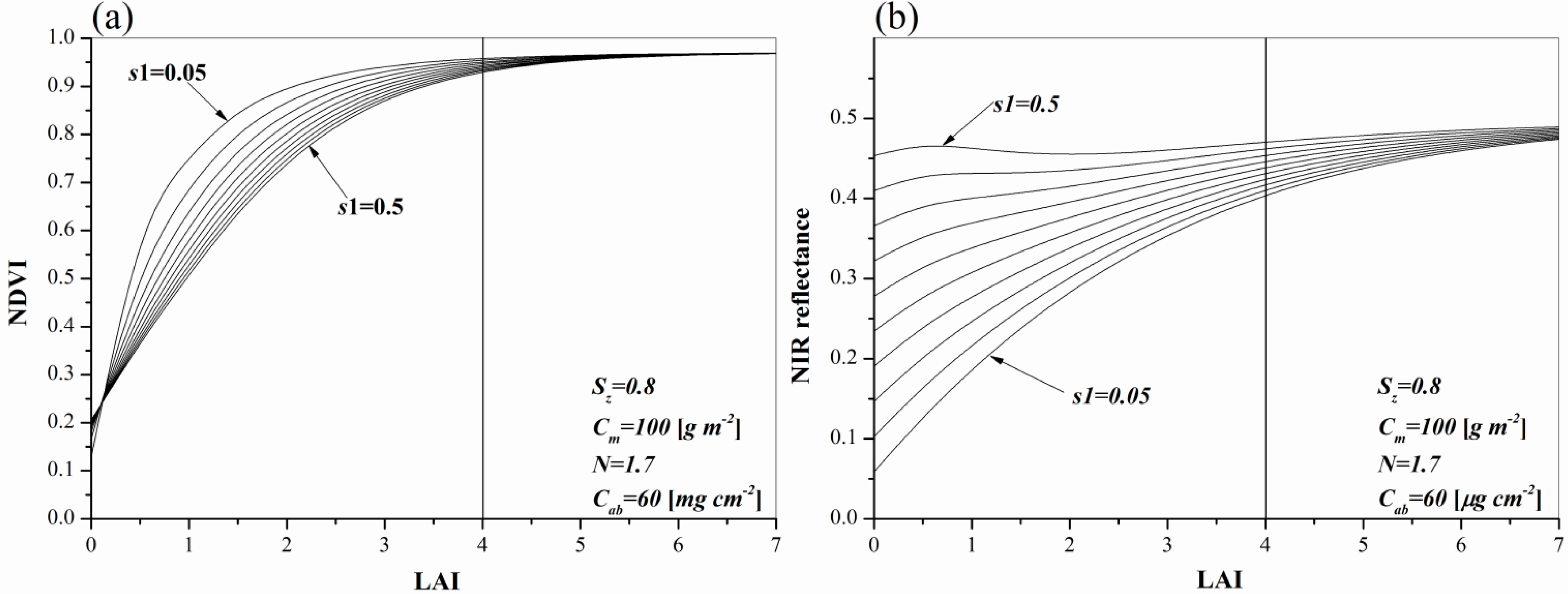
2.1.2. Sensitivity of NDVI and NIR Reflectance to LAI
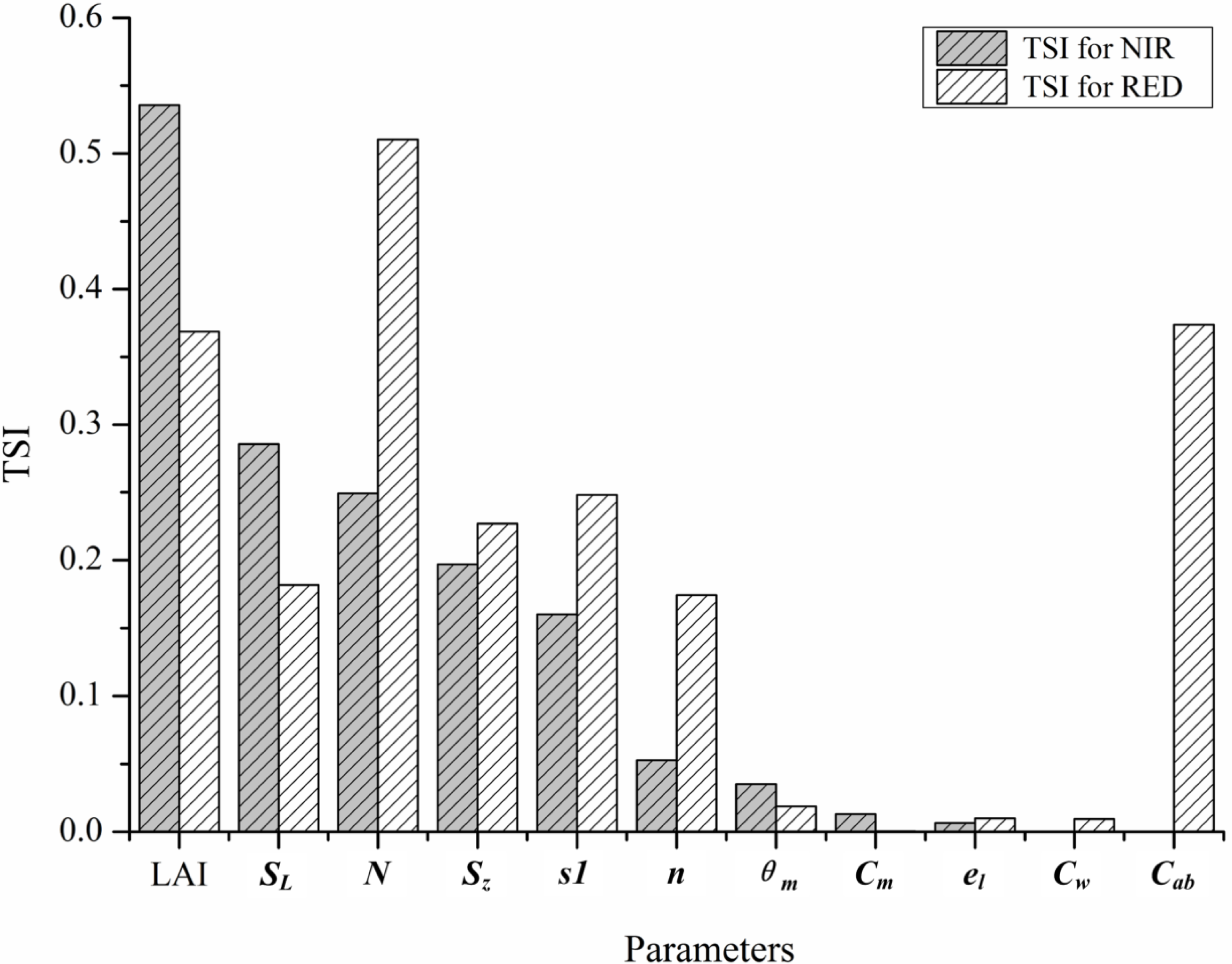
2.1.3. Sensitivity Analysis of ACRM
2.1.4. LAI Retrieval Using the LUT Algorithm
2.2. The Extended Fourier Approach
3. Study Area and Data
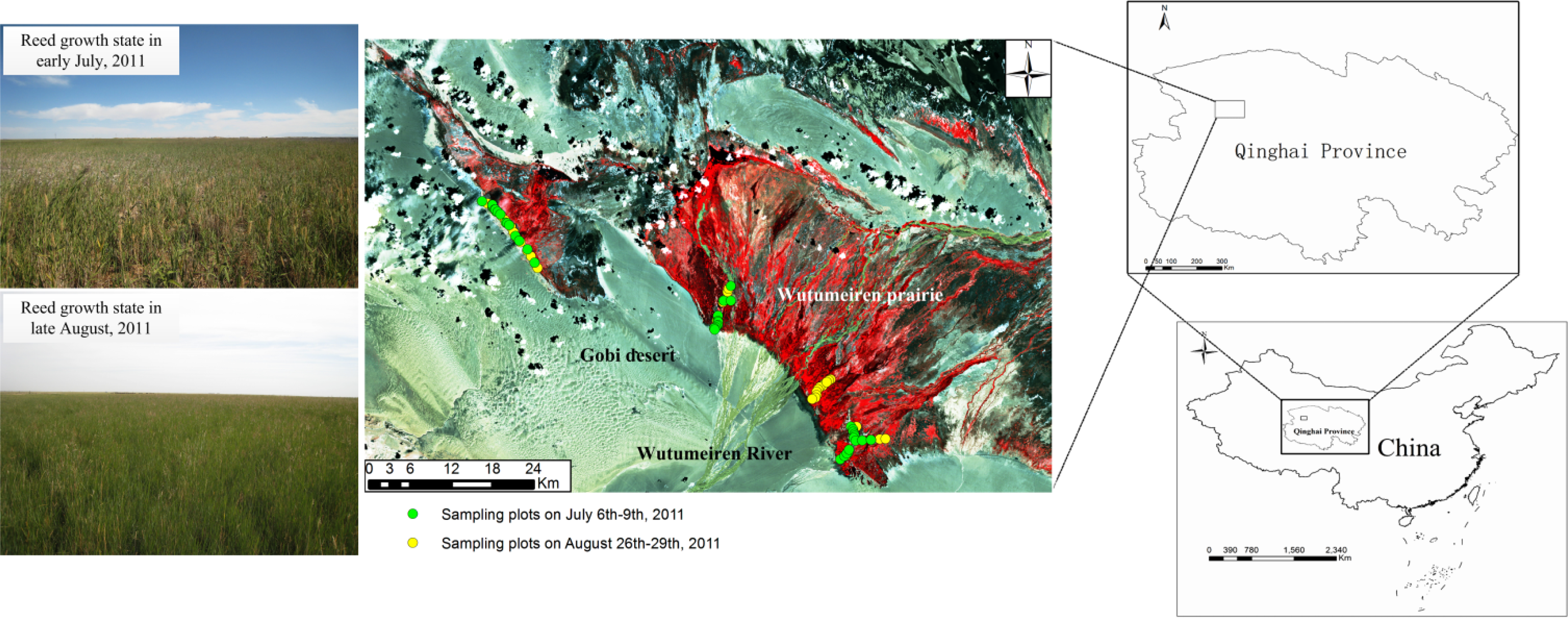
3.1. Study Area
3.2. Satellite Images and Field Measurements
4. Results and Analysis
4.1. Sensitivity of ACRM Inputs to RED and NIR Reflectance and Parameterization of the Inputs
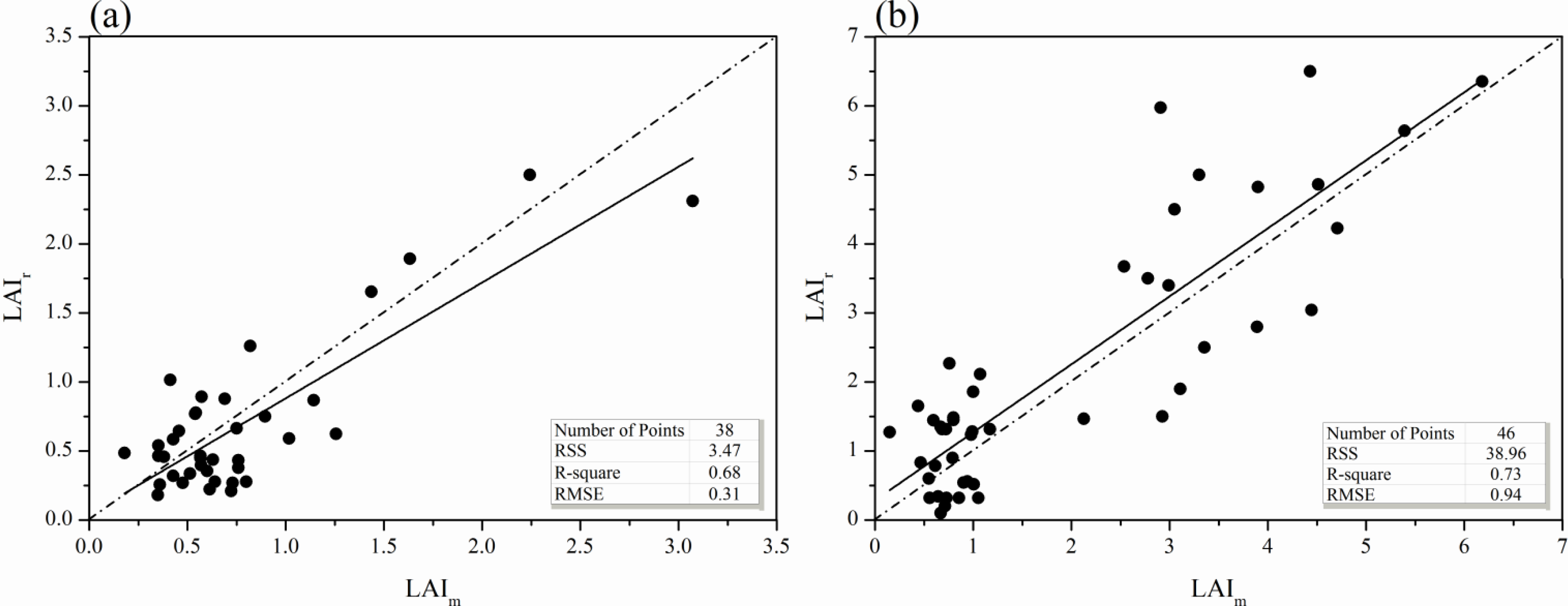
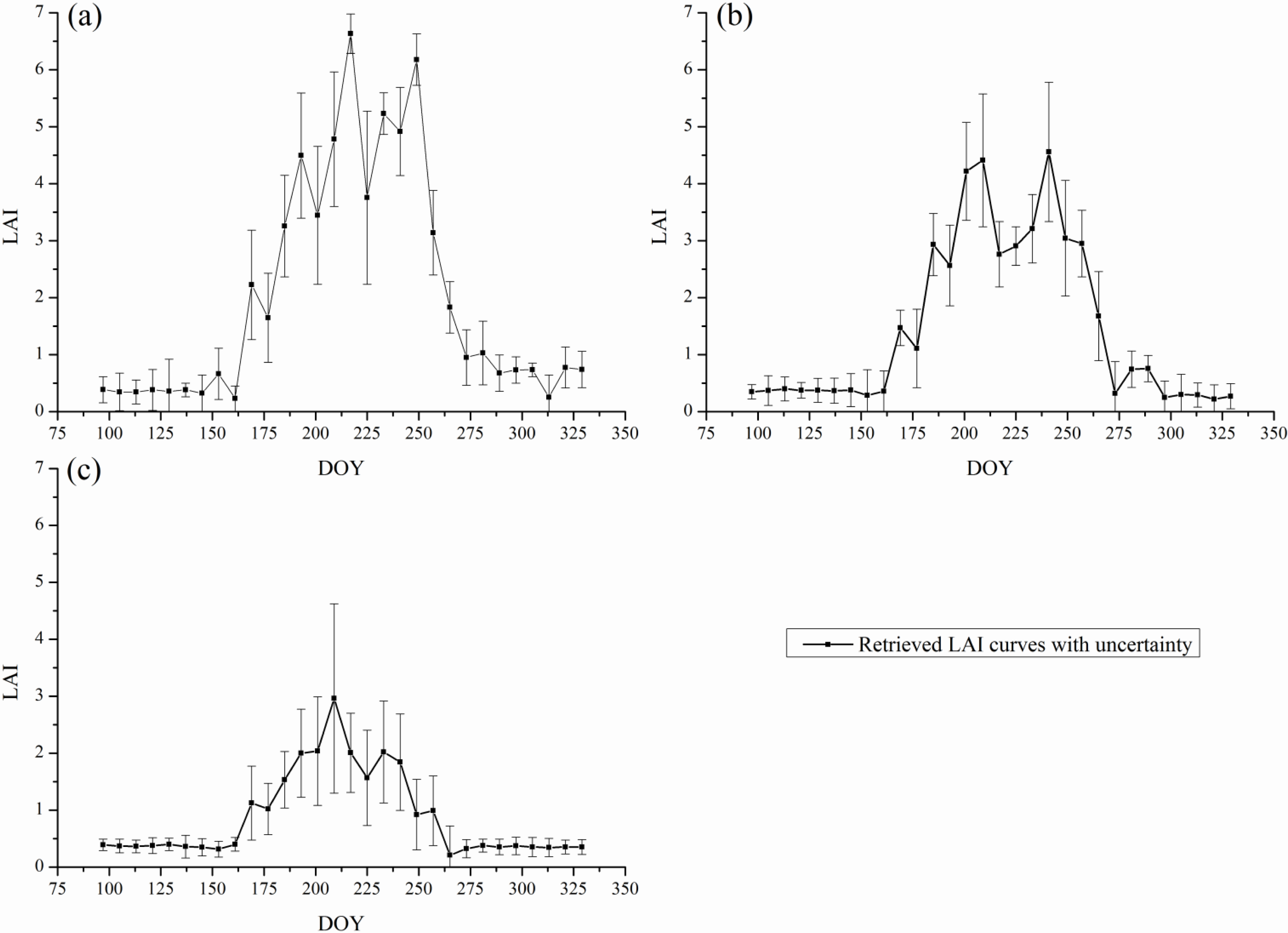
4.2. Retrieved LAI on Each DOY
4.3. Smoothing the LAI Curves Using the Fourier Model
4.4. Improving the LAI Curves Using the Extended Fourier Approach
5. Discussion
6. Concluding Remarks
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Houborg, R.; Soegaard, H.; Boegh, E. Combining vegetation index and model inversion methods for the extraction of key vegetation biophysical parameters using Terra and Aqua MODIS reflectance data. Remote Sens. Environ 2007, 106, 39–58. [Google Scholar]
- Fensholt, R.; Sandholt, I.; Rasmussen, M.S. Evaluation of MODIS LAI, FAPAR and the relation between FAPAR and NDVI in a semi-arid environment using in situ measurements. Remote Sens. Environ 2004, 91, 490–507. [Google Scholar]
- Xiao, Z.; Liang, S.; Wang, J.; Jiang, B.; Li, X. Real-time retrieval of leaf area index from MODIS time series data. Remote Sens. Environ 2011, 115, 97–106. [Google Scholar]
- Darvishzadeh, R.; Skidmore, A.; Schlerf, M.; Atzberger, C. Inversion of a radiative transfer model for estimating vegetation LAI and chlorophyll in a heterogeneous grassland. Remote Sens. Environ 2008, 112, 2592–2604. [Google Scholar]
- Doraiswamy, P.; Hatfield, J.; Jackson, T.; Akhmedov, B.; Prueger, J.; Stern, A. Crop condition and yield simulations using Landsat and MODIS. Remote Sens. Environ 2004, 92, 548–559. [Google Scholar]
- Houborg, R.; Anderson, M.; Daughtry, C. Utility of an image-based canopy reflectance modeling tool for remote estimation of LAI and leaf chlorophyll content at the field scale. Remote Sens. Environ 2009, 113, 259–274. [Google Scholar]
- Meroni, M.; Colombo, R.; Panigada, C. Inversion of a radiative transfer model with hyperspectral observations for LAI mapping in poplar plantations. Remote Sens. Environ 2004, 92, 195–206. [Google Scholar]
- Colombo, R.; Bellingeri, D.; Fasolini, D.; Marino, C.M. Retrieval of leaf area index in different vegetation types using high resolution satellite data. Remote Sens. Environ 2003, 86, 120–131. [Google Scholar]
- Combal, B.; Baret, F.; Weiss, M.; Trubuil, A.; Mace, D.; Pragnere, A.; Myneni, R.; Knyazikhin, Y.; Wang, L. Retrieval of canopy biophysical variables from bidirectional reflectance: Using priori information to solve the ill-posed inverse problem. Remote Sens. Environ 2003, 84, 1–15. [Google Scholar]
- Combal, B.; Baret, F.; Weiss, M. Improving canopy variables estimation from remote sensing data by exploiting ancillary information. Case study on sugar beet canopies. Agronomie 2002, 22, 205–215. [Google Scholar]
- Hermance, J.F.; Jacob, R.W.; Bradley, B.A.; Mustard, J.F. Extracting phenological signals from multiyear AVHRR NDVI time series: Framework for applying high-order annual splines with roughness damping. IEEE Trans. Geosci. Remote Sens 2007, 45, 3264–3276. [Google Scholar]
- Moody, A.; Johnson, D.M. Land-surface phenologies from AVHRR using the discrete fourier transform. Remote Sens. Environ. 2001, 75, 305–323. [Google Scholar]
- Carrão, H.; Gonalves, P.; Caetano, M. A nonlinear harmonic model for fitting satellite image time series: Analysis and prediction of land cover dynamics. IEEE Trans. Geosci. Remote Sens 2010, 48, 1919–1930. [Google Scholar]
- Roerink, G.; Menenti, M.; Verhoef, W. Reconstructing cloudfree NDVI composites using Fourier analysis of time series. Int. J. Remote Sens. 2000, 21, 1911–1917. [Google Scholar]
- Geerken, R.; Zaitchik, B.; Evans, J. Classifying rangeland vegetation type and coverage from NDVI time series using Fourier filtered cycle similarity. Int. J. Remote Sens. 2005, 26, 5535–5554. [Google Scholar]
- Brooks, E.B.; Thomas, V.A.; Wynne, R.H.; Coulston, J.W. Fitting the multitemporal curve: A fourier series approach to the missing data problem in remote sensing analysis. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3340–3353. [Google Scholar]
- Bach, H.; Mauser, W. Methods and examples for remote sensing data assimilation in land surface process modeling. IEEE Trans. Geosci. Remote Sens. 2003, 41, 1629–1637. [Google Scholar]
- Seo, D.-J.; Cajina, L.; Corby, R.; Howieson, T. Automatic state updating for operational streamflow forecasting via variational data assimilation. J. Hydrol. 2009, 367, 255–275. [Google Scholar]
- Naud, C.; Makowski, D.; Jeuffroy, M.-H. Application of an interacting particle filter to improve nitrogen nutrition index predictions for winter wheat. Ecol. Model. 2007, 207, 251–263. [Google Scholar]
- Van Leeuwen, P.J. A variance-minimizing filter for large-scale applications. Mon. Wea. Rev. 2003, 131, 2071–2084. [Google Scholar]
- Smith, P.J.; Dance, S.L.; Nichols, N.K. A hybrid data assimilation scheme for model parameter estimation: Application to morphodynamic modelling. Comput. Fluids 2011, 46, 436–441. [Google Scholar]
- Van Velzen, N.; Segers, A. A problem-solving environment for data assimilation in air quality modelling. Environ. Model. Softw. 2010, 25, 277–288. [Google Scholar]
- Rudd, A.; Roulstone, I.; Eyre, J. A simple column model to explore anticipated problems in variational assimilation of satellite observations. Environ. Model. Softw. 2012, 27, 23–39. [Google Scholar] [Green Version]
- Tripathy, R.; Chaudhari, K.N.; Mukherjee, J.; Ray, S.S.; Patel, N.; Panigrahy, S.; Parihar, J.S. Forecasting wheat yield in Punjab state of India by combining crop simulation model WOFOST and remotely sensed inputs. Remote Sens. Lett. 2012, 4, 19–28. [Google Scholar]
- Confalonieri, R.; Acutis, M.; Bellocchi, G.; Donatelli, M. Multi-metric evaluation of the models WARM, CropSyst, and WOFOST for rice. Ecol. Model. 2009, 220, 1395–1410. [Google Scholar]
- Marin, F.R.; Jones, J.W.; Royce, F.; Suguitani, C.; Donzeli, J.L.; Wander Filho, J.P.; Nassif, D.S.P. Parameterization and evaluation of predictions of DSSAT/CANEGRO for brazilian sugarcane. Agron. J. 2011, 103, 304–315. [Google Scholar]
- Van Dam, J.C.; Groenendijk, P.; Hendriks, R.F.A.; Kroes, J.G. Advances of modeling water flow in variably saturated soils with swap. Vadose Zone J. 2008, 7, 640–653. [Google Scholar]
- Kalnay, E.; Li, H.; Miyoshi, T.; Yang, S.C.; Ballabrera-poy, J. 4-D-Var or ensemble kalman filter? Tellus A 2007, 59, 758–773. [Google Scholar]
- Jakubauskas, M.E.; Legates, D.R.; Kastens, J.H. Harmonic analysis of time-series AVHRR NDVI data. Photogramm. Eng. Remote Sens. 2001, 67, 461–470. [Google Scholar]
- Hermance, J.F. Stabilizing high-order, non-classical harmonic analysis of NDVI data for average annual models by damping model roughness. Int. J. Remote Sens. 2007, 28, 2801–2819. [Google Scholar]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar]
- Sobol, I.M. Sensitivity estimates for nonlinear mathematical models. Math. Model. Comput. Exp. 1993, 1, 407–414. [Google Scholar]
- Kuusk, A. A two-layer canopy reflectance model. J. Quant. Spectrosc. Radiat. Transf. 2001, 71, 1–9. [Google Scholar]
- Iqbal, M. An Introduction to Solar Radiation; Academic Press: Toronto, ON, Canada, 1983. [Google Scholar]
- Price, J.C. On the information content of soil reflectance spectra. Remote Sens. Environ. 1990, 33, 113–121. [Google Scholar]
- Kuusk, A. A multispectral canopy reflectance model. Remote Sens. Environ. 1994, 50, 75–82. [Google Scholar]
- Campbell, G. Derivation of an angle density function for canopies with ellipsoidal leaf angle distributions. Agric. For. Meteorol. 1990, 49, 173–176. [Google Scholar]
- Liang, S. Quantitative Remote Sensing of Land Surfaces; John Wiley and Sons, Inc: New York, NY, USA, 2004. [Google Scholar]
- Kuusk, A. A Markov chain model of canopy reflectance. Agric. For. Meteorol. 1995, 76, 221–236. [Google Scholar]
- Jacquemoud, S.; Baret, F. Prospect: A model of leaf optical properties spectra. Remote Sens. Environ 1990, 34, 75–91. [Google Scholar]
- Nossent, J.; Elsen, P.; Bauwens, W. Sobol’sensitivity analysis of a complex environmental model. Environ. Model. Softw 2011, 26, 1515–1525. [Google Scholar]
- Glen, G.; Isaacs, K. Estimating sobol sensitivity indices using correlations. Environ. Model. Softw 2012, 37, 157–166. [Google Scholar]
- Homma, T.; Saltelli, A. Importance measures in global sensitivity analysis of nonlinear models. Reliab. Eng. Syst. Saf 1996, 52, 1–17. [Google Scholar]
- He, B.; Quan, X.; Xing, M. Retrieval of leaf area index in alpine wetlands using a two-layer canopy reflectance model. Int. J. Appl. Earth Obs. Geoinf 2013, 21, 78–91. [Google Scholar]
- Verhoef, W.; Bach, H. Simulation of hyperspectral and directional radiance images using coupled biophysical and atmospheric radiative transfer models. Remote Sens. Environ 2003, 87, 23–41. [Google Scholar]






| Parameters | Units | Symbol | Value |
|---|---|---|---|
| Sun zenith angle | (°) | θs | - |
| View zenith angle | (°) | θv | - |
| Relative azimuth angle | (°) | θraz | - |
| Ǻngström turbidity coefficient | β | 0.12 | |
| Leaf area index | m2/m2 | LAI | / |
| LAI of ground level | m2/m2 | LAIg | 0.05 |
| Mean leaf angle of Elliptical LAD | (°) | θl | 60.0 |
| Hot spot parameter | SL | 0.5/LAI | |
| Markov clumping parameter | Sz | / | |
| Refractive index | n | 0.9 | |
| Weight of the first basis function | s1 | / | |
| Leaf mesophyll structure | N | / | |
| Chlorophyll a and b content | μg·cm−2 | Cab | / |
| Leaf equivalent water thickness | cm | CW | 0.015 |
| Dry matter content | g·m−2 | Cm | 90 |
| Brown pigment | Cbp | 0.4 |
| Symbol | Range for NDVI-Based Retrieval Scheme | dx | Range for NIR-Based Retrieval Scheme | dx |
|---|---|---|---|---|
| LAI | 0–4 | 0.2 | 2–7 | 0.2 |
| Sz | 0.4–1.0 | 0.2 | 0.4–1.0 | 0.2 |
| s1 | 0.25–0.5 | 0.03 | 0.05–0.25 | 0.03 |
| N | 1.0–2.0 | 0.2 | 1.5–2.5 | 0.1 |
| Cab | 30–90 | 20 | 60 | 0 |
| RSS | R-Square | RMSE | ||
|---|---|---|---|---|
| DOY 177 | LAIr | 3.47 | 0.68 | 0.31 |
| LAIF | 3.42 | 0.67 | 0.30 | |
| LAIeF | 3.15 | 0.72 | 0.29 | |
| DOY 233 | LAIr | 38.96 | 0.73 | 0.94 |
| LAIF | 29.25 | 0.77 | 0.81 | |
| LAIeF | 27.48 | 0.79 | 0.78 | |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Quan, X.; He, B.; Wang, Y.; Tang, Z.; Li, X. An Extended Fourier Approach to Improve the Retrieved Leaf Area Index (LAI) in a Time Series from an Alpine Wetland. Remote Sens. 2014, 6, 1171-1190. https://doi.org/10.3390/rs6021171
Quan X, He B, Wang Y, Tang Z, Li X. An Extended Fourier Approach to Improve the Retrieved Leaf Area Index (LAI) in a Time Series from an Alpine Wetland. Remote Sensing. 2014; 6(2):1171-1190. https://doi.org/10.3390/rs6021171
Chicago/Turabian StyleQuan, Xingwen, Binbin He, Yong Wang, Zhi Tang, and Xing Li. 2014. "An Extended Fourier Approach to Improve the Retrieved Leaf Area Index (LAI) in a Time Series from an Alpine Wetland" Remote Sensing 6, no. 2: 1171-1190. https://doi.org/10.3390/rs6021171





