Illumination and Contrast Balancing for Remote Sensing Images
Abstract
:1. Introduction
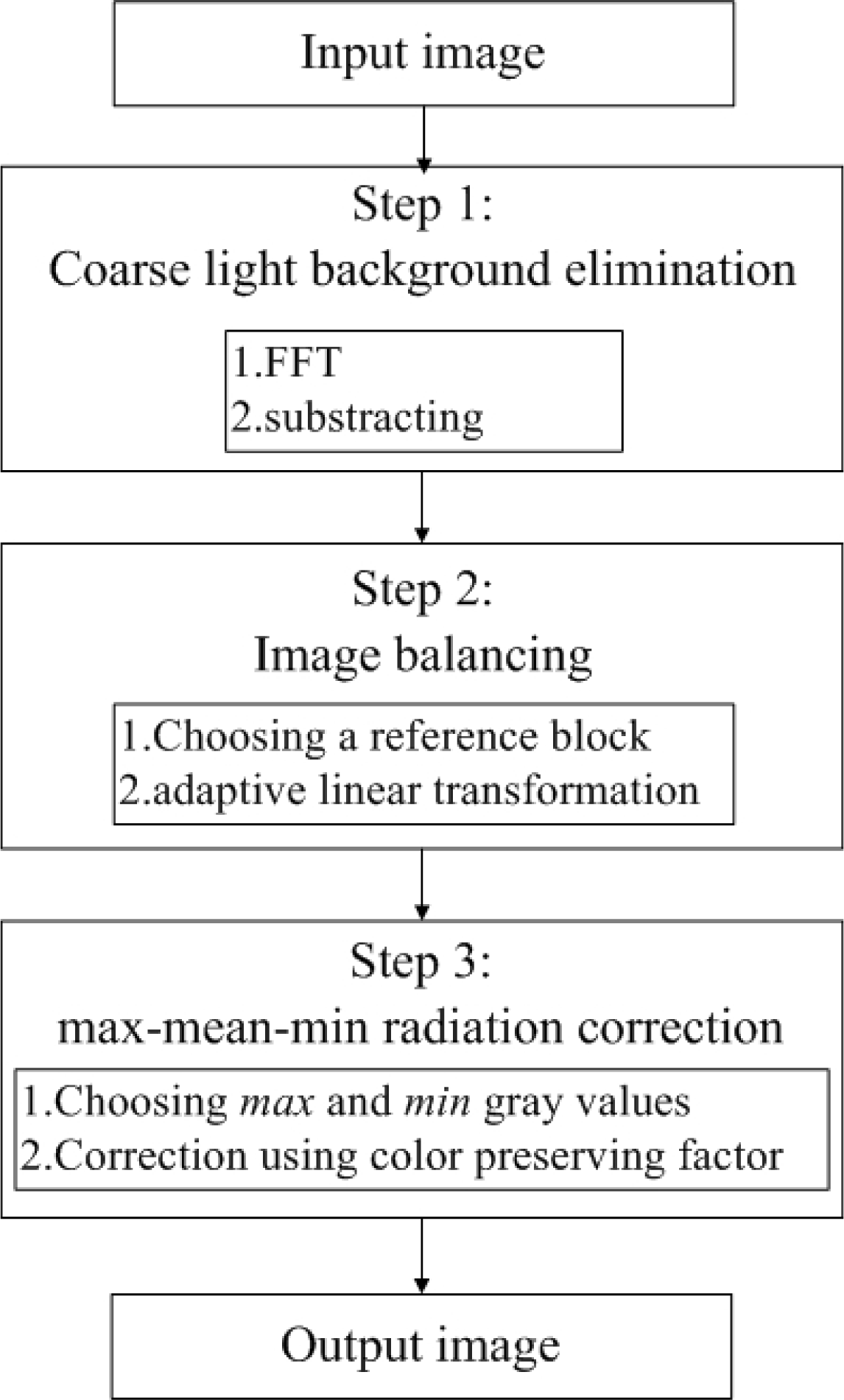
2. Proposed Image Balancing Method
2.1. Coarse Light Background Elimination
2.2. Image Balancing
2.3. Max-Mean-Min Radiation Correction
3. Experiments and Results
3.1. Experiments on Synthetic Image
| Ideal | Horizontal | Vertical | Central | |||||
|---|---|---|---|---|---|---|---|---|
| RMSHE | Proposed | RMSHE | Proposed | RMSHE | Proposed | |||
| MSE | R | 0 | 7,219.97 | 278.38 | 7,787.54 | 284.68 | 7,399.96 | 251.34 |
| G | 0 | 7,086.93 | 271.63 | 7,654.24 | 263.97 | 7,203.09 | 221.47 | |
| B | 0 | 5,992.50 | 209.88 | 6,369.60 | 249.00 | 6,042.68 | 176.41 | |
| Ave | 0 | 6,766.47 | 253.30 | 7,270.46 | 265.88 | 6,881.91 | 216.41 | |
| PSNR | R | +∞ | 9.5454 | 23.6844 | 9.2168 | 23.5872 | 9.4385 | 24.1281 |
| G | +∞ | 9.6262 | 23.7909 | 9.2918 | 23.9152 | 9.5556 | 24.6776 | |
| B | +∞ | 10.3547 | 24.9110 | 10.0897 | 24.1687 | 10.3185 | 25.6654 | |
| Ave | +∞ | 9.8421 | 24.1288 | 9.5328 | 23.8904 | 9.7709 | 24.8237 | |
| HFM | R | 0 | 1.5153 | 1.2680 | 1.3924 | 1.1760 | 1.4167 | 1.1303 |
| G | 0 | 1.4109 | 1.2037 | 1.4628 | 0.8991 | 1.4249 | 1.2390 | |
| B | 0 | 1.5417 | 1.3497 | 1.4743 | 1.3437 | 1.4738 | 1.3733 | |
| Ave | 0 | 1.4893 | 1.2738 | 1.4432 | 1.1396 | 1.4385 | 1.2476 | |
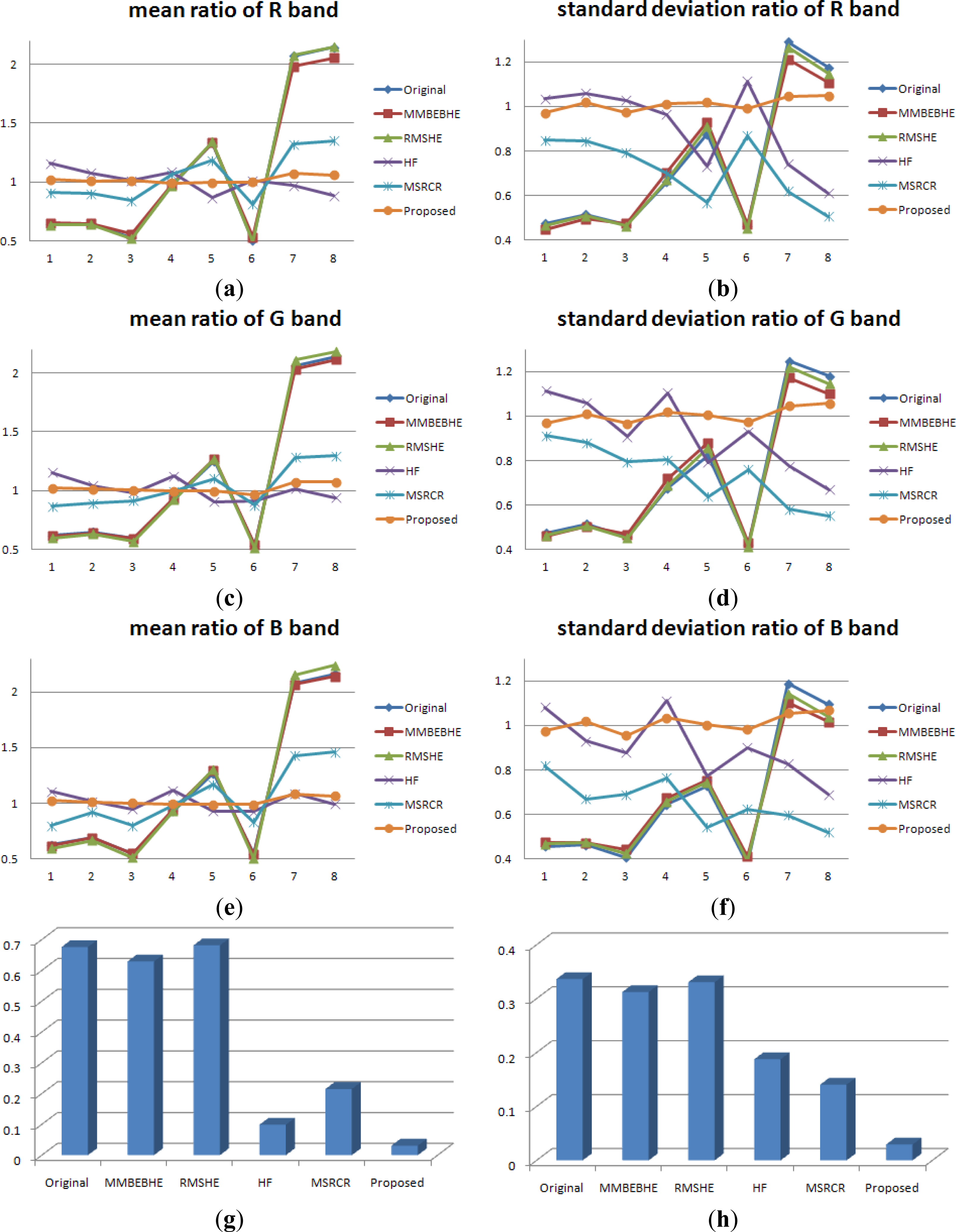
3.2. Experiments on Real Aerial Remote Sensing Images
3.3. Efficiency Comparison
3.4. Experiments on More Aerial Remote Sensing Images
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Du, Y.; Cihlar, J.; Beaubien, J.; Latifovic, R. Radiometric normalization, compositing, and quality control for satellite high resolution image mosaics over large areas. IEEE Trans. Geosci. Remote Sens 2001, 39, 623–634. [Google Scholar]
- Zhu, S.L.; Zhang, Z.; Zhu, B.S.; Cao, W. Experimental comparison among five algorithms of brightness and contrast homogenization (In Chinese). J. Remote Sens 2011, 15, 111–116. [Google Scholar]
- Kim, M.; Chung, M.G. Recursively separated and weighted histogram equalization for brightness preservation and contrast enhancement. IEEE Trans. Consum. Elect 2008, 54, 1389–1397. [Google Scholar]
- Chen, S.D.; Ramli, A.R. Contrast enhancement using recursive mean-separate histogram equalization for scalable brightness preservation. IEEE Trans. Consum. Elect 2003, 49, 1301–1309. [Google Scholar]
- Menotti, D.; Najman, L.; Facon, J.; Araujo, A.A. Multi-histogram equalization methods for contrast enhancement and brightness preserving. IEEE Trans. Consum. Elect 2007, 53, 1186–1194. [Google Scholar]
- Hsia, S.C.; Chen, M.H.; Chen, Y.M. A cost-effective line-based light-balancing technique using adaptive processing. IEEE Trans. Image Process 2006, 15, 2719–2729. [Google Scholar]
- Hsia, S.C.; Tsai, P.S. Efficient light balancing techniques for text images in video presentation systems. IEEE Trans. Circuits Syst. Video Technol 2005, 15, 1026–1031. [Google Scholar]
- Jang, J.H.; Bae, Y.; Ra, J.B. Contrast-enhanced fusion of multisensor images using subband-decomposed multiscale retinex. IEEE Trans. Image Process 2012, 21, 3479–3490. [Google Scholar]
- Jang, J.H.; Kim, S.D.; Ra, J.B. Enhancement of optical remote sensing images by subband-decomposed multiscale retinex with hybrid intensity transfer function. IEEE Geosci. Remote Sens. Lett 2011, 8, 983–987. [Google Scholar]
- Jang, I.S.; Lee, T.H.; Kyung, W.J. Local contrast enhancement based on adaptive multiscale retinex using intensity distribution of input image. J. Imaging Sci. Technol 2011, 55, 040502. [Google Scholar]
- Rahman, Z.; Jobson, D.J.; Woodell, G.A. Investigating the relationship between image enhancement and image compression in the context of the multi-scale retinex. J. Vis. Commun. Image Represent 2011, 22, 237–250. [Google Scholar]
- Lee, S. An efficient content-based image enhancement in the compressed domain using retinex theory. IEEE. Trans. Circuits Syst. Video Technol 2007, 17, 199–213. [Google Scholar]
- Provenzi, E.; Carli, L.D.; Rizzi, A. Mathematical definition and analysis of the Retinex algorithm. J. Opt. Soc. Am. A 2005, 22, 2613–2621. [Google Scholar]
- Rahman, Z.; Jobson, D.D.; Woodell, G.A. Retinex processing for automatic image engancement. J. Electron. Imaging 2004, 13, 100–110. [Google Scholar]
- Liu, J.; Shao, Z.F.; Cheng, Q.M. Color constancy enhancement under poor illumination. Opt. Lett 2011, 36, 4821–4823. [Google Scholar]
- Li, D.R.; Wang, M.; Pan, J. Auto-dodging processing and its application for optical RS images. Geomat. Inf. Sci. Wuhan Univ 2006, 31, 753–756. [Google Scholar]
- Li, H.F.; Zhang, L.P.; Shen, H.F. A perceptually inspired variational method for the uneven intensity correction of remote sensing images. IEEE Trans. Geosci. Remote Sens 2012, 50, 3053–3065. [Google Scholar]
- Christophe, E.; Michel, J.; Inglada, J. Remote sensing processing: From multicore to GPU. IEEE J.-STARS 2011, 4, 643–652. [Google Scholar]
- Lee, C.A; Gasster, S.D.; Plaza, A. Chein-I chang, recent developments in high performance computing for remote sensing: A review. IEEE J.-STARS 2011, 4, 508–527. [Google Scholar]



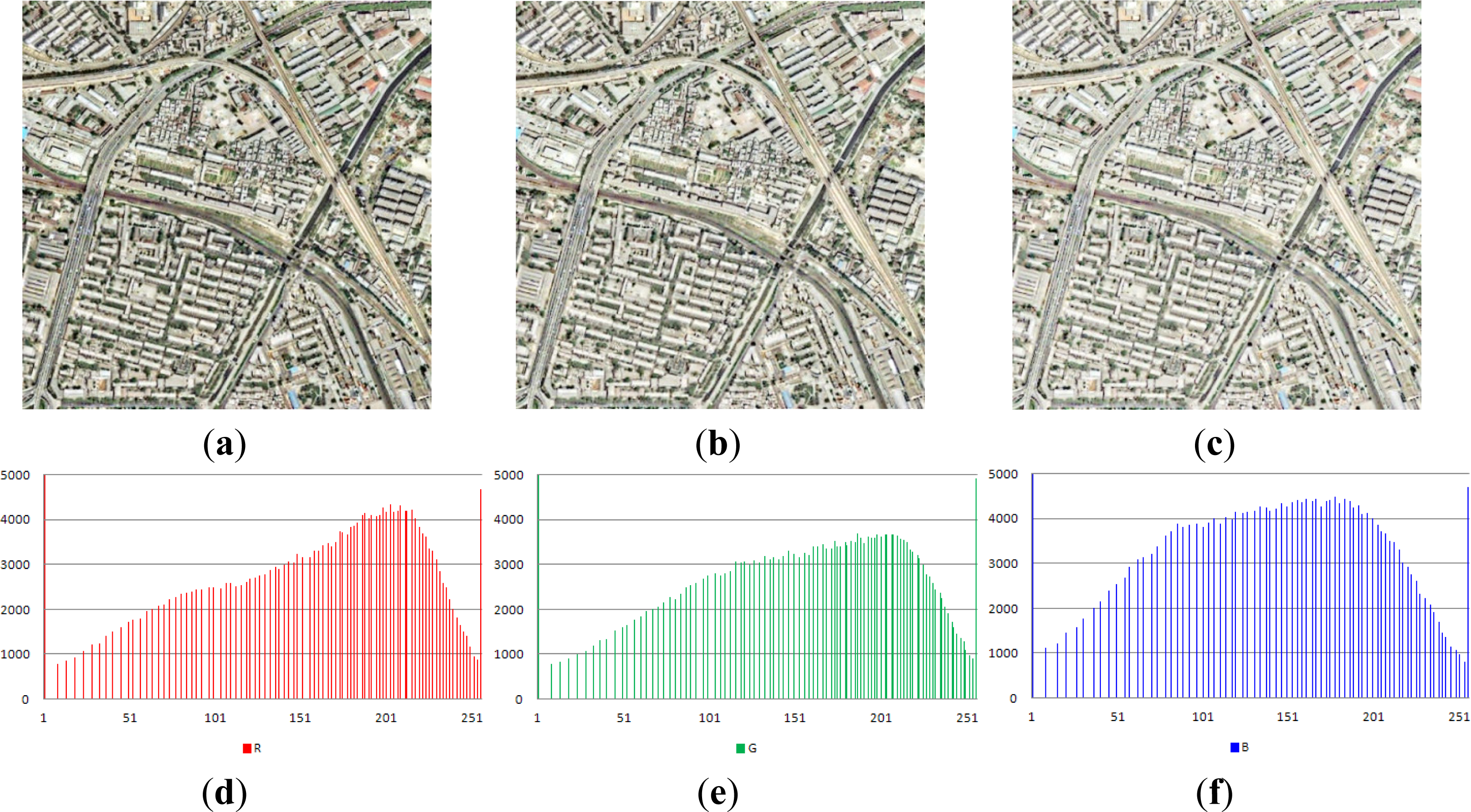









| R | G | B | |
|---|---|---|---|
| blk = 11 | 14.2318 | 15.0589 | 11.8794 |
| blk = 21 | 12.8169 | 13.6315 | 10.7306 |
| blk = 61 | 11.7526 | 12.5331 | 9.8586 |
| R | G | B | ||||
|---|---|---|---|---|---|---|
| 0 | 255 | 0 | 255 | 0 | 255 | |
| Number of pixels in the original image | 1 | 223 | 1 | 1129 | 0 | 40 |
| Number of pixels in Figure 5a | 5,914 | 6,127 | 6,309 | 4,676 | 4,930 | 4,702 |
| Ratio | 2.26% | 2.25% | 2.41% | 1.35% | 1.88% | 1.78% |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Liu, J.; Wang, X.; Chen, M.; Liu, S.; Shao, Z.; Zhou, X.; Liu, P. Illumination and Contrast Balancing for Remote Sensing Images. Remote Sens. 2014, 6, 1102-1123. https://doi.org/10.3390/rs6021102
Liu J, Wang X, Chen M, Liu S, Shao Z, Zhou X, Liu P. Illumination and Contrast Balancing for Remote Sensing Images. Remote Sensing. 2014; 6(2):1102-1123. https://doi.org/10.3390/rs6021102
Chicago/Turabian StyleLiu, Jun, Xing Wang, Min Chen, Shuguang Liu, Zhenfeng Shao, Xiran Zhou, and Ping Liu. 2014. "Illumination and Contrast Balancing for Remote Sensing Images" Remote Sensing 6, no. 2: 1102-1123. https://doi.org/10.3390/rs6021102




