Historical Single Image-Based Modeling: The Case of Gobierna Tower, Zamora (Spain)
Abstract
:1. Introduction
2. Historical Background
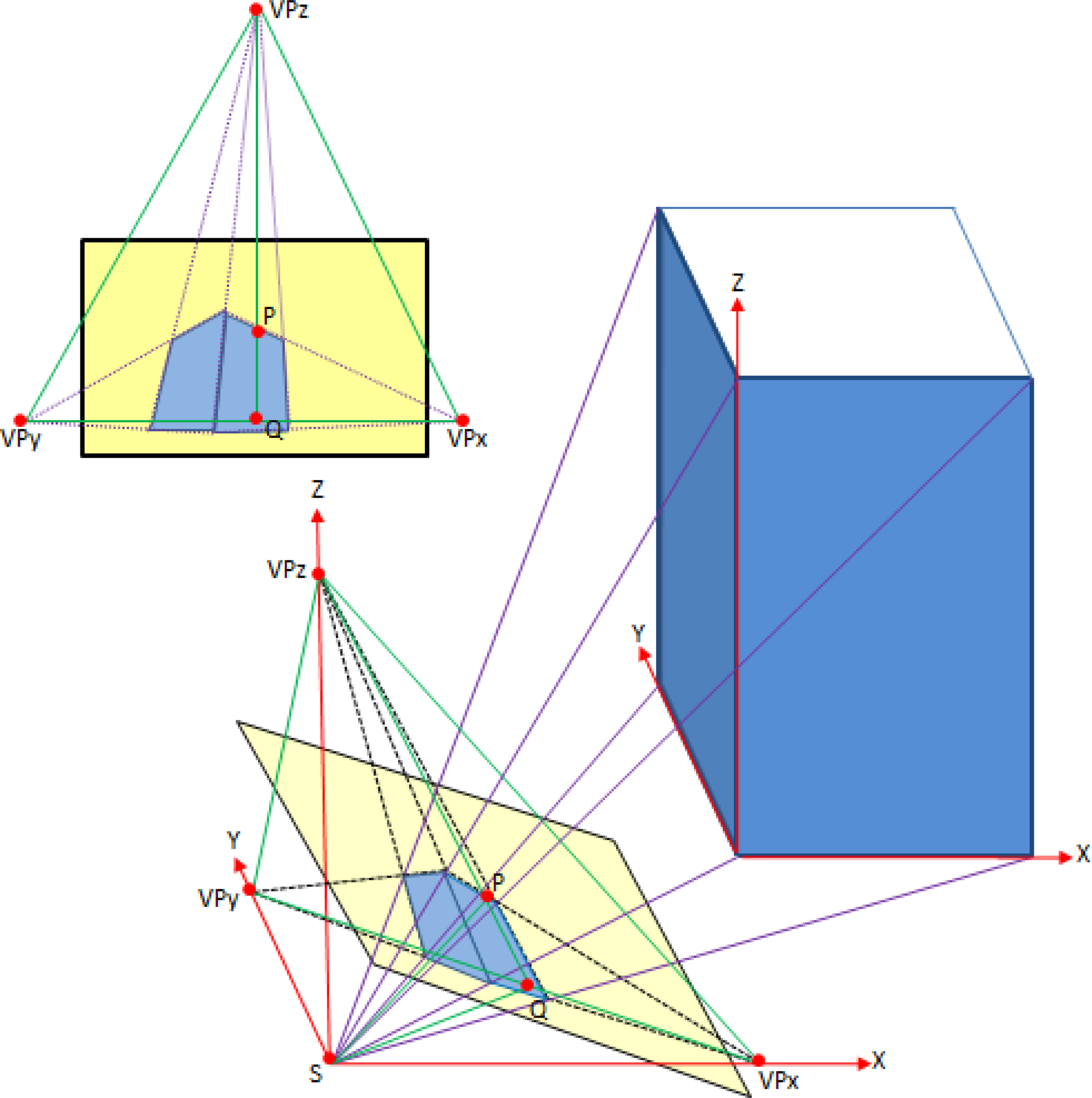
3. Theoretical Basis: Single View Photogrammetry
4. A Case Study: The Historical and Demolished “Gobierna Tower”
4.1. Data Processing
- (a)
- Extracting edge pixels by means of the Canny filter [20].
- (b)
- Clustering pixels into raster segments according to neighboring criteria and with length restrictions in a fashion very similar to the Burns Method [21].
- (c)
- Determining vector lines (first and last points) from raster segments according to a plane collinearity condition.
- (a)
- For every start and end point of every line segment rendered by the automatic or manual extraction, the correspondent line in the parameter space is computed and represented. Every cell that lies on the line receives one vote.
- (b)
- A voting procedure is undertaken so that the most visited cells give the lines that form families of lines that pass through each of the vanishing points.
- (c)
- For all these lines the correspondent parameters (a,b)i are computed.
- (d)
- The best coordinates of each of the vanishing points are computed by applying a least squares criteria to the equation: y0 = aix0 + bi in which (x0,y0) are the coordinates of a vanishing point.
- (e)
- In order to avoid residual outliers, a weighting procedure is applied to the above task, so that a robust M-estimator, modified Danish estimator [24] can be implemented and, thus, the blunders may be expelled from the computation and the reliability can be improved.
- (c)
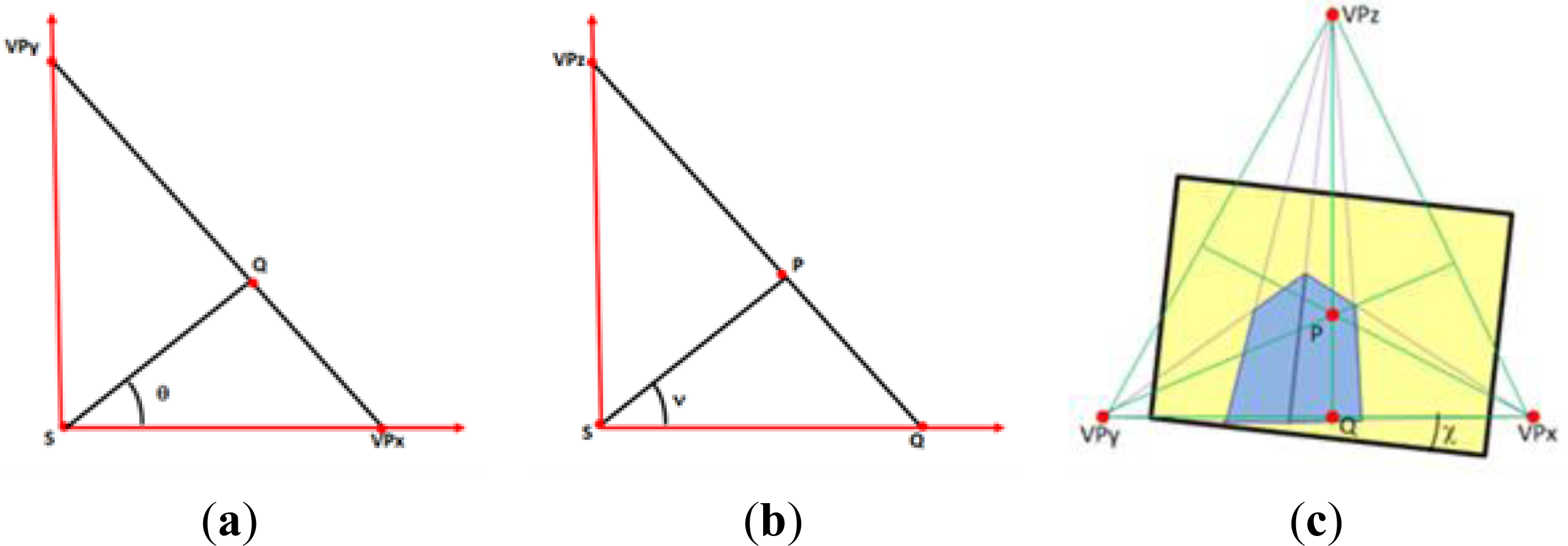
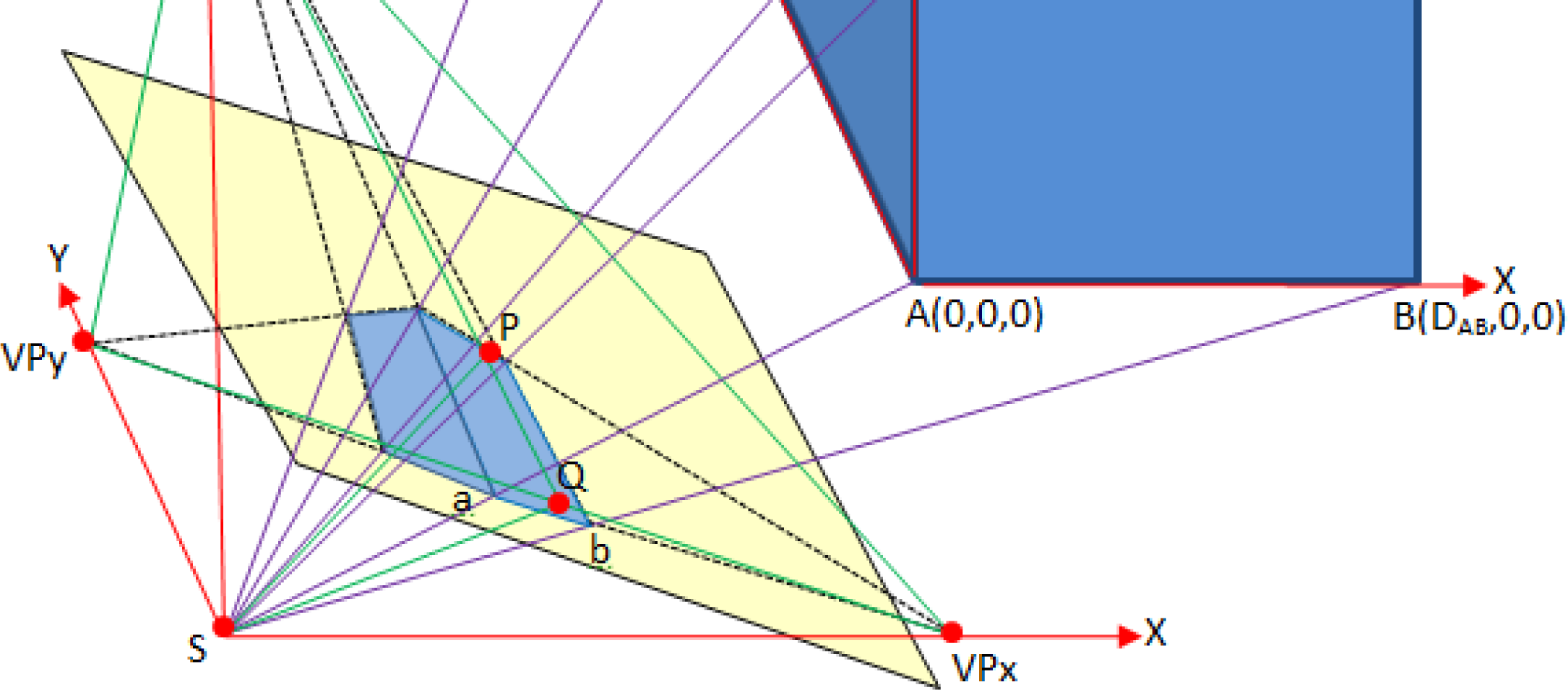
- Once these parameters are known, the coordinates of the point of view, S, can be easily derived by applying a certain restriction to the object (in addition to the point of view itself) and then solving from the collinearity equations (Figure 7). An example case is measuring a horizontal distance in the object and setting the origin of the Datum at one of these points. We can, thus, write six equations for five unknowns: (XYZ)S and the two scale factors for each collinearity condition [25] Equation (4).where xa, ya, xb, yb are the image coordinates of the ground points A and B, respectively, which define the Datum and the known horizontal distance DAB; xp, yp are the principal point, P, coordinates; R is the rotation matrix and Xs, Ys, Zs and λaA, λbB are the unknowns corresponding to the point of view, S, and the two scale factors, respectively.
4.2. Results
5. Conclusions
- (a)
- Manual processing permits achieve better results than automatic processing. This is due to the weakness related to low number of vanishing lines, poor quality image, high number of blunders and poor perspective geometry.
- (b)
- Although robust estimators (especially RANSAC) have proven largely its efficiency in filtering gross errors, this is not the case. As just stated, when the image is poor both in geometry and radiometry, the automatic approach leads to an excessive number of blunders and so, the manual identification of vanishing lines is better.
- (c)
- An original vanishing point method based on the Hough Transform, which guarantees efficiency and quality in the results, even with unfavorable cases (a three-point perspective getting close to two-point perspective), has been successfully applied. Other methods to compute the vanishing points, such as the triangle area minimization or the Gaussian sphere, have not provided good results.
- (d)
- A relative error of 1% has been obtained for the accuracy assessment of the results. This value can be considered very good since the single image-based modeling approach developed involves many steps and thus the corresponding error propagation.
- (e)
- Finally, it should be remarked that the method is only applicable in scenes with strong geometric contents (i.e., presence of structural planes and lines). In addition, the image must have perspective along the three main directions (X,Y,Z) in order to compute the corresponding three vanishing points (VPx,VPy,VPz). Obviously, if these vanishing points are well defined more precision and reliability can be reached for the single image-based modeling approach.
Author Contributions
Conflicts of Interest
References
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2000; Volume 2. [Google Scholar]
- Faugeras, O. Three Dimensional Computer Vision: A Geometric Viewpoint; The MIT Press: Cambridge, UK, 1993. [Google Scholar]
- Zucchelli, M.; Santos-Victor, J.; Christensen, H.I. Pattern Recognition. Proceedings of the IEEE 16th International Conference on Constrained Structure and Motion Estimation from Optical Flow, Québec City, QC, Canada, 11–15 August 2002; pp. 339–342.
- Gonzalez-Aguilera, D.; Gomez-Lahoz, J. From 2D to 3D through modelling based on a single image. Photogram. Record 2008, 23, 208–227. [Google Scholar]
- Debevec, P.E.; Taylor, C.J.; Malik, J. In Modeling and Rendering Architecture from Photographs: A Hybrid Geometry- and Image-Based Approach. Proceedings of the SIGGRAPH, New Orleans, LA, USA, 4–9 August 1996; ACM: New Orleans, LA, USA; pp. 11–20.
- Van den Heuvel, F.A. Automation in Architectural Photogrammetry: Line-Photogrammetry for the Reconstruction from Single and Multiple Images. Delft University of Technology, Delft, The Netherlands, 2003. [Google Scholar]
- Grammatikopoulos, L.; Karras, G.; Petsa, E. Camera Calibration Approaches Using Single Images of Man-Made Objects. Proceedings of the XIX CIPA International Symposium, Antalya, Turkey, 30 September–4 October 2003; pp. 328–332.
- Wilczkowiak, M.; Boyer, E.; Sturm, P. 3D Modeling Using Geometric Constraints: A Parallelepiped Based Approach. Proceedings of the European Conference on Computer Vision, Copenhagen, Denmark, 28–31 May 2002; IV, pp. 221–236.
- Kalisperakis, I.; Rova, M.; Petsa, E.; Karras, G. On Multi-Image Reconstruction from Historic Photographs. Proceedings of the XIX CIPA International Symposium, Antalya, Turkey, 30 September–4 October 2003; pp. 216–219.
- Styliadis, A.D.; Sechidis, L.A. Photography-based façade recovery & 3-D modeling: A cad application in cultural heritage. J. Cult. Herit 2011, 12, 243–252. [Google Scholar]
- Georgoula, O.; Stamnas, A.; Patias, P.; Georgiadis, C.; Fragkoulidou, V. Historical coastal urban landscapes digital documentation and temporal study with 2d/3d modeling functionality: The case of Thessaloniki, Greece. J. Cult. Herit 2012, 14, 396–402. [Google Scholar]
- Gonzalez-Aguilera, D.; Gomez-Lahoz, J.; Rodriguez-Gonzalvez, P. An automatic approach for radial lens distortion correction from a single image. IEEE Sens. J 2011, 11, 956–965. [Google Scholar]
- Caprile, B.; Torre, V. Using vanishing points for camera calibration. Int. J. Comput. Vis 1990, 4, 127–139. [Google Scholar]
- Styliadis, A.D. Historical photography-based computer-aided architectural design: Demolished buildings information modeling with reverse engineering functionality. Autom. Constr 2008, 18, 51–69. [Google Scholar]
- Gonzalez-Aguilera, D. Reconstrucción 3D a Partir de una Sola Vista. University of Salamanca, Salamanca, Spain, 2005. [Google Scholar]
- Piñuela Ximenez, A. Descripción Histórica de la Ciudad de Zamora, su Provincia y Obispado; Diputación de Zamora, Instituto de Estudios Zamoranos “Florián de Ocampo”: Zamora, España, 1987. [Google Scholar]
- Chías Navarro, P.; Abad Balboa, T. Los Caminos y la Construcción del Territorio en Zamora: Catálogo de Puentes; Ministerio de Fomento, Diputación de Zamora, Instituto de Estudios Zamoranos “Florián de Ocampo”: Zamora, España, 2004. [Google Scholar]
- Rodríguez Méndez, F.J.; Andrés Rodrigo, H.; Rubio Cavero, M.P.; García Gago, J.M. El Puente Medieval de Zamora a Comienzos del Siglo XX. Un Estudio del Alcance de la Intervención del Ingeniero Luis de Justo. Anuario 2009 Instituto de Estudios Zamoranos Florián de Ocampo: Zamora, España, 2012; 26, pp. 227–268. Available online: http://www.iezfloriandeocampo.com/?id=17&idn=54&titulo=Colecci%F3n%20Anuarios (accessed on 21 January 2014). (In Spanish).
- Kagan, R.L. Ciudades del Siglo de oro: Las Vistas Españolas de Anton. van den Wyngaerde; Ediciones El Viso: Madrid, España, 1986. [Google Scholar]
- Canny, J. A computational approach to edge detection. IEEE Trans. Pattern Anal. Mach. Intell 1986, 8, 679–698. [Google Scholar]
- Burns, J.B.; Hanson, A.R.; Riseman, E.M. Extracting straight lines. IEEE Trans. Pattern Anal. Mach. Intell 1986, 8, 425–455. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar]
- Hough, P.V.C. Method and Means for Recognizing Complex Patterns. US Patent No. 3,069,654. 18 December 1962.
- Domingo-Preciado, A. Investigación Sobre los Métodos de Estimación Robusta Aplicados a la Resolución de los Problemas Fundamentales de la Fotogrametría. University of Cantabria, Santander, Spain, 2000. [Google Scholar]
- Kraus, K. Photogrammetry (Volume 1); Dümmler Verlag: Bonn, Germany, 1993. [Google Scholar]



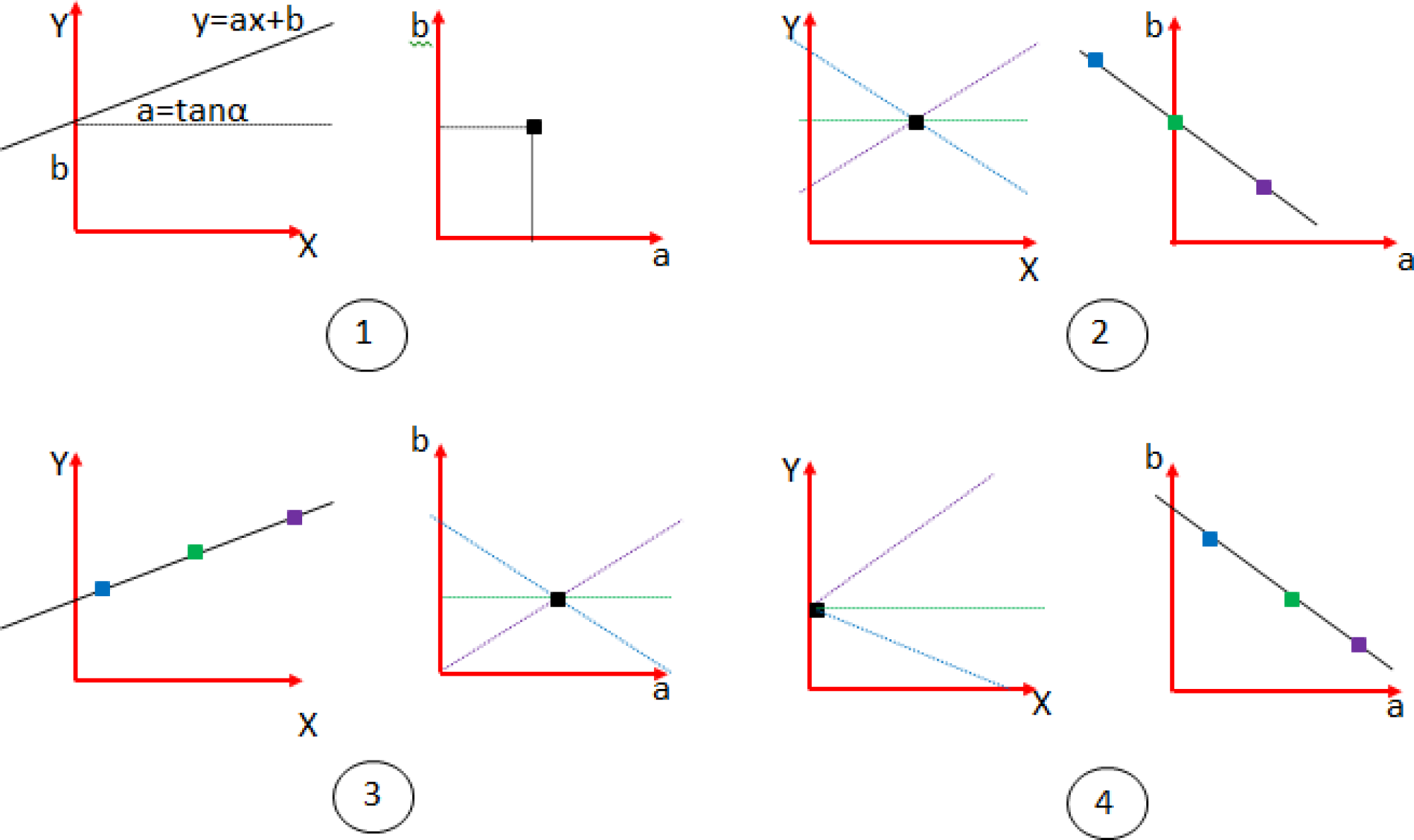




| Case | Image Space | Parameter Space |
|---|---|---|
| 1 | A straight line | A point |
| 2 | A point (family of straight lines that intersect on a point) | A straight line (family of points that belong to a line) |
| 3 | A set of collinear points (that belong to the same line) | A set of lines that intersect on the same point |
| 4 | A vanishing point (set of lines that intersect on a point) | A set of collinear points (the straight line to which they belong represents the vanishing point) |
| Hough Transform + Danish Estimator: (units: pixels) | VPx | VPy | VPz |
|---|---|---|---|
| x | 2,253.8 | −587.42 | 283.55 |
| y | 504.79 | 582.40 | −7,425.58 |
| RMSE | 0.057 | 0.046 | 0.318 |
| Internal Parameters (units: millimetres) | External Parameters (units: degrees, meters) | ||
|---|---|---|---|
| P [x] (mm) | 25.29 | θ: 38.114° | XS: −29.71 |
| P [y] (mm) | 65.40 | ν: 105.5167° | YS: −60.18 |
| f (mm) | 44.86 | χ: 177.5282° | ZS: −13.66 |
| Code | Distances (m) | Discrepancies (m) | Code | Distances (m) | Discrepancies (m) |
|---|---|---|---|---|---|
| L1 | 1.84 | δL1 = 0.01 | L6 | 4.66 | δL6 = 0.04 |
| L2 | 4.08 | δL2 = 0.02 | L7 | 10.05 | δL7 = 0.04 |
| L3 | 4.40 | δL3 = 0.05 | L8 | 5.18 | δL8 = 0.02 |
| L4 | 4.45 | δL4 = 0.05 | L9 | 0.87 | δL9 = 0.03 |
| L5 | 14.38 | δL5 = 0.07 | Known Distance | 8.70 | δKD = 0.00 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Garcia-Gago, J.; Gomez-Lahoz, J.; Rodríguez-Méndez, J.; González-Aguilera, D. Historical Single Image-Based Modeling: The Case of Gobierna Tower, Zamora (Spain). Remote Sens. 2014, 6, 1085-1101. https://doi.org/10.3390/rs6021085
Garcia-Gago J, Gomez-Lahoz J, Rodríguez-Méndez J, González-Aguilera D. Historical Single Image-Based Modeling: The Case of Gobierna Tower, Zamora (Spain). Remote Sensing. 2014; 6(2):1085-1101. https://doi.org/10.3390/rs6021085
Chicago/Turabian StyleGarcia-Gago, Jesús, Javier Gomez-Lahoz, Javier Rodríguez-Méndez, and Diego González-Aguilera. 2014. "Historical Single Image-Based Modeling: The Case of Gobierna Tower, Zamora (Spain)" Remote Sensing 6, no. 2: 1085-1101. https://doi.org/10.3390/rs6021085






