Validation and Application of the Modified Satellite-Based Priestley-Taylor Algorithm for Mapping Terrestrial Evapotranspiration
Abstract
:1. Introduction
2. Methods and Data Sources
2.1. Methods
2.1.1. MS-PT Algorithm
2.1.2. PT-JPL Algorithm
2.1.3. Drought Index and Potential LE Calculations
2.1.4. Trend Analysis
2.2. Data
2.2.1. Eddy Covariance Flux Towers
2.2.2. Meteorological and Satellite Inputs
3. Results and Discussion
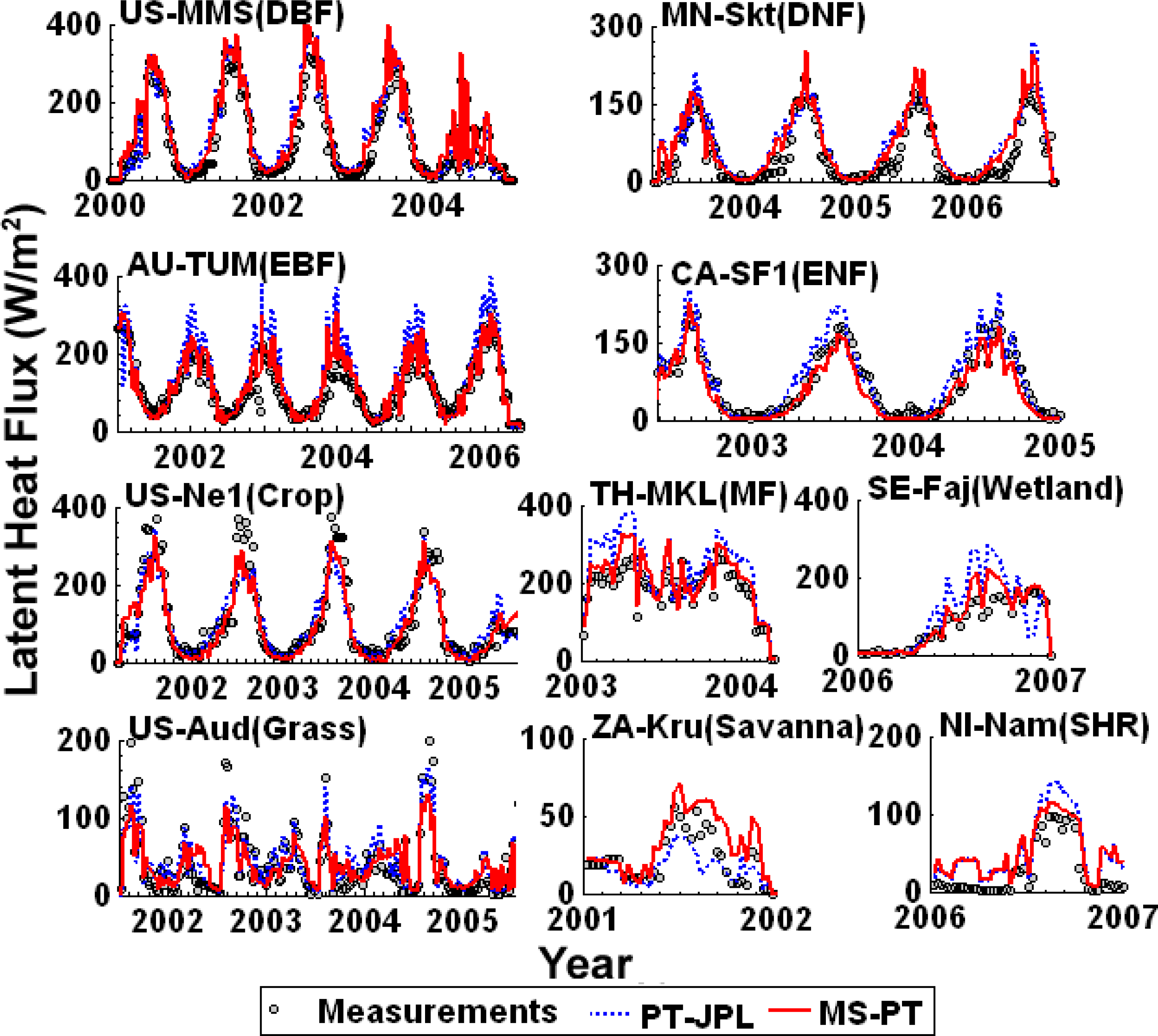
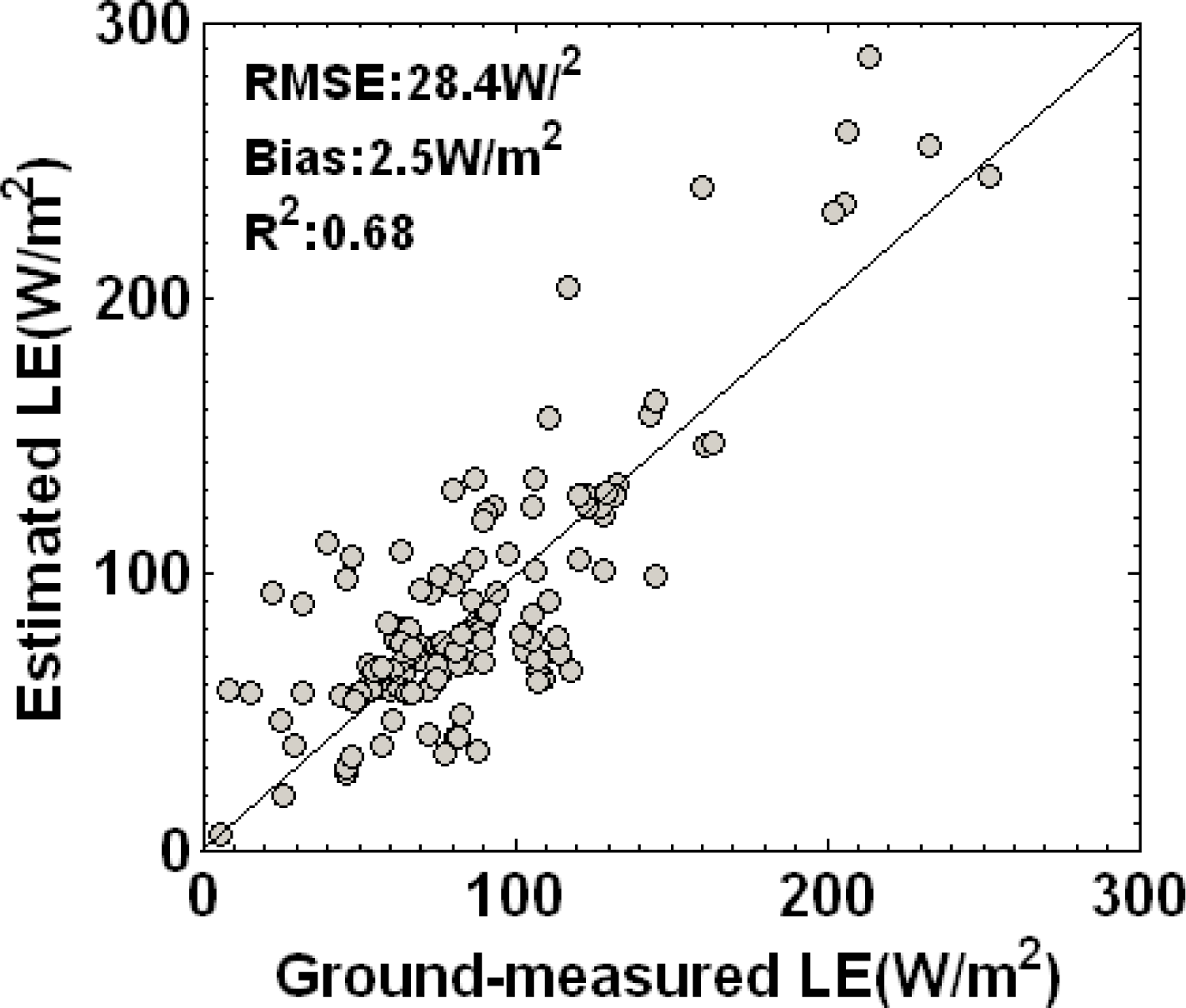
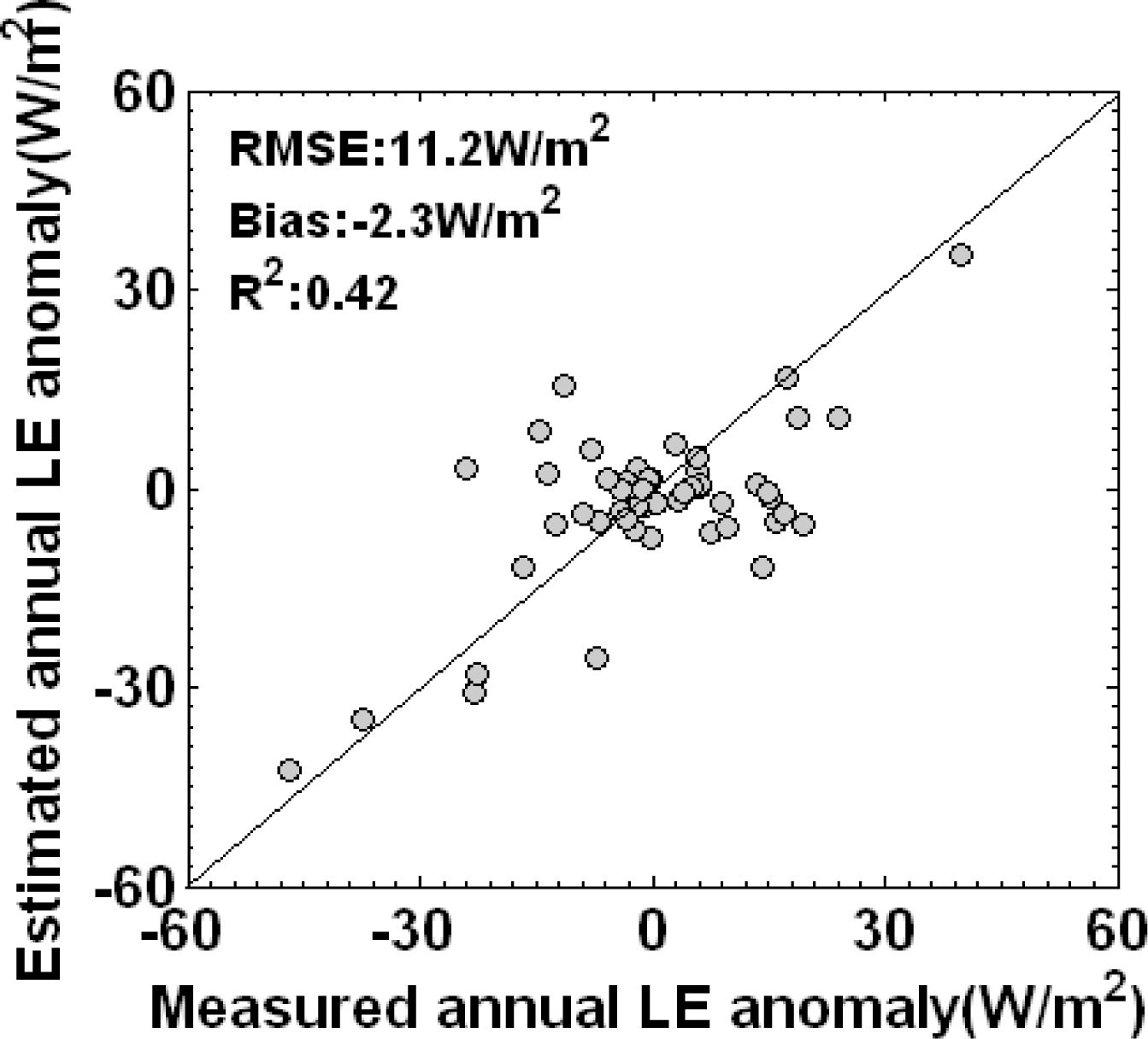
3.1. Validation and Comparison
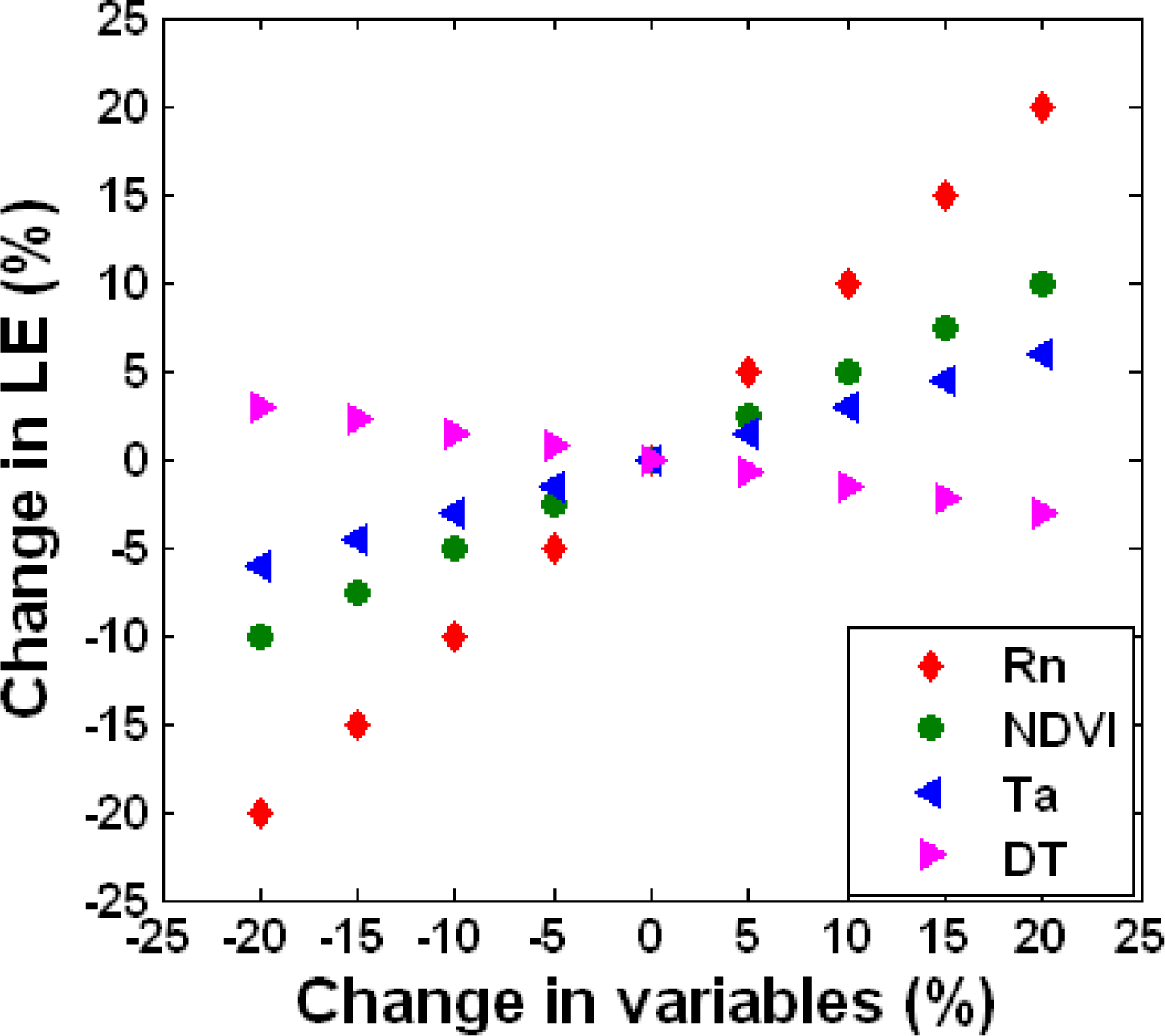
3.2. Sensitivity Analysis
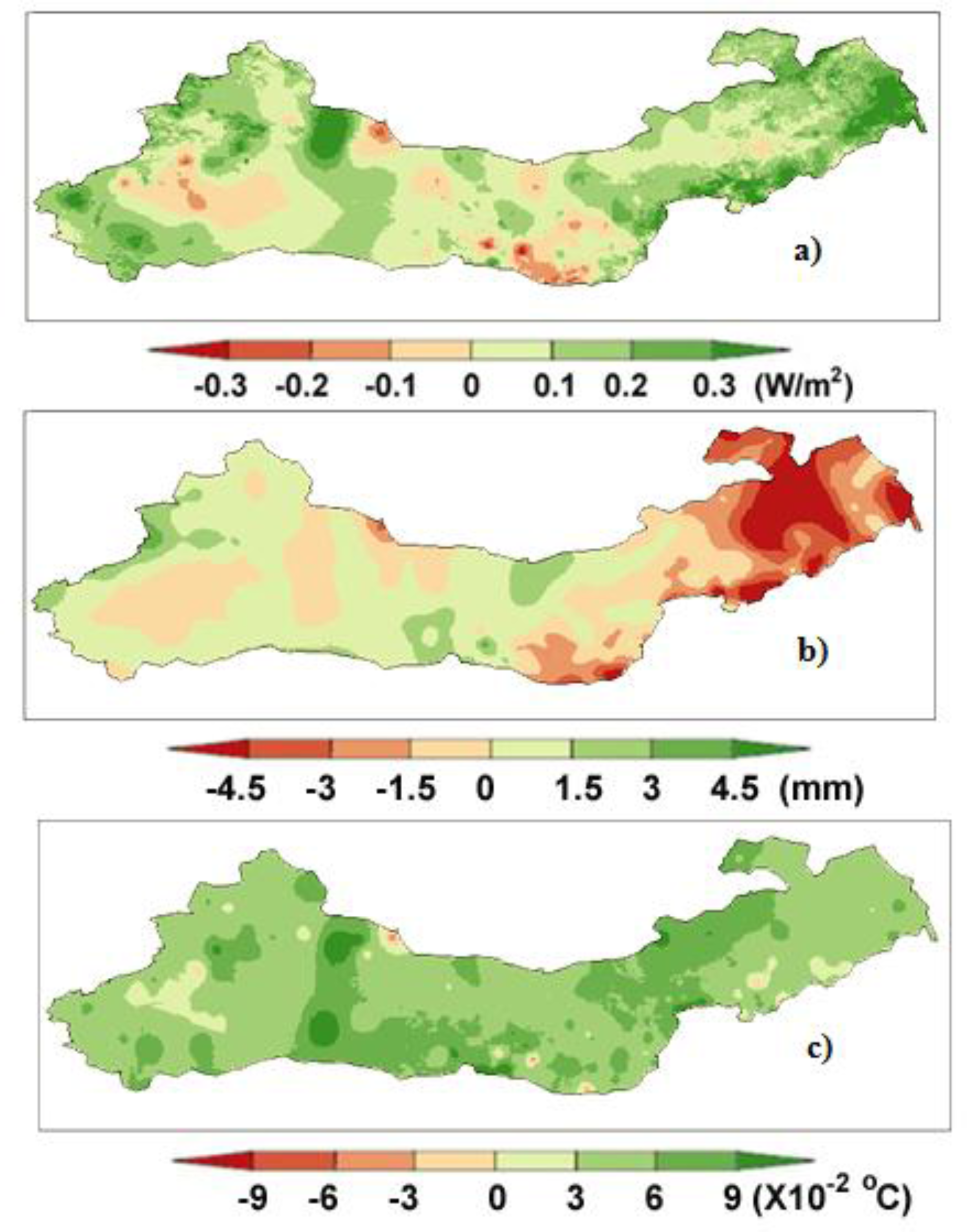
3.3. Application I: Mapping Terrestrial Evapotranspiration of the Three-North Shelter Forest Region of China
3.4. Application II: Monitoring Global Land Surface Drought
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Trenberth, K.E.; Smith, L.; Qian, T.; Dai, A.; Fasullo, J. Estimates of the global water budget and its annual cycle using observational and model data. J. Hydrometeorol 2007, 8, 758–769. [Google Scholar]
- Wang, K.; Wang, P.; Li, Z.Q.; Cribb, M.; Sparrow, M. A simple method to estimate actual evapotranspiration from a combination of net radiation, vegetation index, and temperature. J. Geophys. Res 2007. [Google Scholar] [CrossRef]
- Li, Z.L.; Tang, R.L.; Wan, Z.M.; Bi, Y.Y.; Zhou, C.H.; Tang, B.H.; Yan, G.J.; Zhang, X.Y. A review of current methodologies for regional evapotranspiration estimation from remotely sensed data. Sensors 2009, 9, 3801–3853. [Google Scholar]
- Liang, S.; Wang, K.; Zhang, X.; Wild, M. Review on estimation of land surface radiation and energy budgets from ground measurements, remote sensing and model simulations. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens 2010, 3, 225–240. [Google Scholar]
- Wang, K.; Dickinson, R. A review of global terrestrial evapotranspiration: Observation, modeling, climatology and climatic variability. Rev. Geophys 2012. [Google Scholar] [CrossRef]
- Stisen, S.; Sandholt, I.; Nørgaard, A.; Fensholt, R.; Jensen, K.H. Combining the triangle method with thermal inertia to estimate regional evapotranspiration—Applied to MSGSEVIRI data in the Senegal River basin. Remote Sens. Environ 2008, 112, 1242–1255. [Google Scholar]
- Zhang, K.; Kimball, J.S.; Mu, Q.; Jones, L.A.; Goetz, S.J.; Running, S.W. Satellite based analysis of northern ET trends and associated changes in the regional water balance from 1983 to 2005. J. Hydrol 2009, 379, 92–110. [Google Scholar]
- Zhang, K.; Kimball, J.S.; Nemani, R.R.; Running, S.W. A continuous satellite-derived global record of land surface evapotranspiration from 1983 to 2006. Water Resour. Res 2010. [Google Scholar] [CrossRef]
- Yuan, W.; Liu, S.; Yu, G.; Bonnefond, J.M.; Chen, J.; Davis, K.; Desai, A.R.; Goldstein, A.H.; Gianelle, D.; Rossi, F.; et al. Global estimates of evapotranspiration and gross primary production based on MODIS and global meteorology data. Remote Sens. Environ 2010, 114, 1416–1431. [Google Scholar]
- Yao, Y.; Qin, Q.; Ghulam, A.; Liu, S.; Zhao, S.; Xu, Z.; Dong, H. Simple method to determine the Priestley-Taylor parameter for evapotranspiration estimation using Albedo-VI triangular space from MODIS data. J. Appl. Remote Sens 2011. [Google Scholar] [CrossRef]
- Norman, J.M.; Kustas, W.P.; Humes, K.S. A two-source approach for estimating soil and vegetation energy fluxes in observations of directional radiometric surface temperature. Agric. For. Meteorol 1995, 77, 263–293. [Google Scholar]
- Kustas, W.P.; Norman, J.M. Use of remote sensing for evapotranspiration monitoring over land surfaces. Hydrol. Sci. J 1996, 41, 495–516. [Google Scholar]
- Anderson, M.C.; Norman, J.M.; Diak, G.R.; Kustas, W.P.; Mecikalski, J.R. A two-source time-integrated model for estimating surface fluxes using thermal infrared remote sensing. Remote Sens. Environ 1997, 60, 195–116. [Google Scholar]
- Cleugh, H.A.; Leuning, R.; Mu, Q.; Running, S.W. Regional evaporation estimates from flux tower and MODIS satellite data. Remote Sens. Environ 2007, 106, 285–304. [Google Scholar]
- Mu, Q.; Heinsch, F.A.; Zhao, M.; Running, S.W. Development of a global evapotranspiration algorithm based on MODIS and global meteorology data. Remote Sens. Environ 2007, 111, 519–536. [Google Scholar]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotrans piration algorithm. Remote Sens. Environ 2011, 115, 1781–1800. [Google Scholar]
- Fisher, J.; Tu, K.; Baldocchi, D. Global estimates of the land atmosphere water flux based on monthly AVHRR and ISLSCP-II data, validated at 16 FLUXNET sites. Remote Sens. Environ 2008, 112, 901–919. [Google Scholar]
- Wang, K.; Liang, S. An improved method for estimating global evapotranspiration based on satellite determination of surface net radiation, vegetation index, temperature, and soil moisture. J. Hydrometeorol 2008, 9, 712–727. [Google Scholar]
- Wang, K.; Dickinson, R.; Wild, M.; Liang, S. Evidence for decadal variation in global terrestrial evapotranspiration between 1982 and 2002. Part 1: Model development. J. Geophys. Res 2010. [Google Scholar] [CrossRef]
- Wang, K.; Dickinson, R.; Wild, M.; Liang, S. Evidence for decadal variation in global terrestrial evapotranspiration between 1982 and 2002. Part 2: Results. J. Geophys. Res 2010. [Google Scholar] [CrossRef]
- Yao, Y.; Liang, S.; Cheng, J.; Liu, S.; Fisher, J.; Zhang, X.; Jia, K.; Zhao, X.; Qin, Q.; Zhao, B.; et al. MODIS-driven estimation of terrestrial latent heat flux in China based on a modified Priestley-Taylor algorithm. Agric. For. Meteorol 2013, (171–172), 187–202. [Google Scholar]
- Kalma, J.; McVicar, T.; McCabe, M. Estimating land surface evaporation: A review of methods using remotely sensed surface temperature data accomplished. Surv. Geophys 2008, 29, 421–469. [Google Scholar]
- Jackson, R.; Reginato, R.; Idso, S. Wheat canopy temperature: A practical tool for evaluating water requirements. Water Resour. Res 1977, 13, 651–656. [Google Scholar]
- Jung, M.; Reichstein, M.; Ciais, P.; Seneviratne, S.; Sheffield, J.; Goulden, M.; Bonan, G.; Cescatti, A.; Chen, J.; Richard, D.; et al. Recent decline in the global land evapotranspiration trend due to limited moisture supply. Nature 2010, 467, 951–954. [Google Scholar]
- Boegh, E.; Soegaard, H.; Hanan, N.; Kabat, P.; Lesch, L. A remote sensing study of the NDVI–Ts relationship and the transpiration from sparse vegetation in the Sahel based on high-resolution satellite data. Remote Sens. Environ 1999, 69, 224–240. [Google Scholar]
- Shuttleworth, W.J.; Wallace, J.S. Evaporation from sparse crops an energy combination theory. Quart. J. R. Meteorol. Soc 1985, 111, 839–855. [Google Scholar]
- Monteith, J. Evaporation and environment. Symp. Soc. Exp. Biol 1965, 19, 205–224. [Google Scholar]
- Boni, G.; Entekhabi, D.; Castelli, F. Land data assimilation with satellite measurements for the estimation of surface energy balance components and surface control on evaporation. Water Resour. Res 2001, 37, 1713–1722. [Google Scholar]
- Qin, J.; Liang, S.; Liu, R.; Zhang, H.; Hu, B. A weak-constraint based data assimilation scheme for estimating surface turbulent fluxes. IEEE Geosci. Remote Sens 2007, 4, 649–653. [Google Scholar]
- Pipunic, R.; Walker, J.; Western, A. Assimilation of remotely sensed data for improved latent and sensible heat flux prediction: A comparative synthetic study. Remote Sens. Environ 2008, 112, 1295–1305. [Google Scholar]
- Jiang, L.; Islam, S. Estimation of surface evaporation map over Southern Great Plains using remote sensing data. Water Resour. Res 2001, 37, 329–340. [Google Scholar]
- Yao, Y.; Liang, S.; Qin, Q.; Wang, K.; Zhao, S. Monitoring global land surface drought based on a hybrid evapotranspiration model. Int. J. Appl. Earth Observ 2011, 13, 447–457. [Google Scholar]
- Priestley, C.H.B.; Taylor, R.J. On the assessment of surface heat flux and evaporation using large-scale parameters. Mon. Weath. Rev 1972, 100, 81–92. [Google Scholar]
- Jin, Y.; Randerson, J.; Goulden, M. Continental-scale net radiation and evapotranspiration estimated using MODIS satellite observations. Remote Sens. Environ 2011, 115, 2302–2319. [Google Scholar]
- Miralles, D.G.; Holmes, T.R.H.; de Jeu1, R.A.M.; Gash, G.H.; Meesters, A.G.C.A.; Dolman, A.J. Global land-surface evaporation estimated from satellite-based observations. Hydrol. Earth Syst. Sci 2011, 15, 453–469. [Google Scholar]
- Mueller, B.; Seneviratne, S.I.; Jimenez, C.; Corti, T.; Hirschi, M.; Balsamo, G.; Ciais, P.; Dirmeyer, P.; Fisher, J.; Guo, Z.; et al. Evaluation of global observations-based evapotranspiration datasets and IPCC AR4 simulations. Geophys. Res. Lett 2011. [Google Scholar] [CrossRef]
- Jiang, L.; Islam, S.; Guo, W.; Jutla, A.S.; Senarath, S.U.S.; Ramsay, B.H.; Eltahir, E. A satellite-based daily actual evapotranspiration estimation algorithm over South Florida. Glob. Planet. Chang 2009, 67, 62–77. [Google Scholar]
- Nemani, R.R.; Keeling, C.D.; Hashimoto, H.; Jolly, W.M.; Piper, S.C.; Tucker, C.J.; Myneni, R.B.; Running, S.W. Climate-driven increases in global terrestrial net primary production from 1982 to 1999. Science 2003, 300, 1560–1563. [Google Scholar]
- Jiang, L.; Islam, S. A methodology for estimation of surface evapotranspiration over large areas using remote sensing observations. Geophys. Res. Lett 1999, 26, 2773–2776. [Google Scholar]
- Wang, K.; Li, Z.; Cribb, M. Estimation of evaporative fraction from a combination of day and night land surface temperatures and NDVI: A new method to determine the Priestley-Taylor parameter. Remote Sens. Environ 2006, 102, 293–305. [Google Scholar]
- Carlson, T. An overview of the “Triangle Method” for estimating surface evapotranspiration and soil moisture from satellite imagery. Sensors 2007, 7, 1612–1629. [Google Scholar]
- Tang, R.; Li, Z.; Tang, B. An application of the Ts-VI triangle method with enhanced edges determination for evapotranspiration estimation from MODIS data in arid and semi-arid regions: Implementation and validation. Remote Sens. Environ 2010, 114, 540–551. [Google Scholar]
- Anderson, M.C.; Kustas, W.P.; Norman, J.M.; Hain, C.R.; Mecikalski, J.R.; Schultz, Z.; González-Dugo, M.P.; Cammalleri, C.; D’Urso, G.; Pimstein, A.; et al. Mapping daily evapotranspiration at field to continental scales using geostationary and polar orbiting satellite imagery. Hydrol. Earth Syst. Sci 2011, 15, 223–239. [Google Scholar] [Green Version]
- Yebra, M.; Dijk, A.V.; Leuning, R.; Huete, A.; Guerschman, J.P. Evaluation of optical remote sensing to estimate actual evapotranspiration and canopy conductance. Remote Sens. Environ 2013, 129, 250–261. [Google Scholar]
- Anderson, M.C.; Norman, J.M.; Mecikalski, J.R.; Otkin, J.A.; Kustas, W.P. A climatological study of evapotranspiration and moisture stress across the continental United States based on thermal remote sensing: 1. Model formulation. J. Geophys. Res 2007. [Google Scholar] [CrossRef]
- Anderson, M.C.; Norman, J.M.; Mecikalski, J.R.; Otkin, J.A.; Kustas, W.P. A climatological study of evapotranspiration and moisture stress across the continental United States based on thermal remote sensing: 2. Surface moisture climatology. J. Geophys. Res 2007. [Google Scholar] [CrossRef]
- Yao, Y.; Liang, S.; Qin, Q.; Wang, K. Monitoring drought over the conterminous united states using MODIS and NCEP reanalysis-2 data. J. Meteor. Appl. Climatol 2010, 49, 1665–1680. [Google Scholar]
- Hargreaves, G.H. Defining and using reference evapotranspiration. J. Irrig. Drain. Eng 1994, 120, 1132–1139. [Google Scholar]
- Pinker, R.T.; Zhang, B.; Dutton, E.G. Do satellites detect trends in surface solar radiation? Science 2005, 308, 850–854. [Google Scholar]
- Twine, T.E.; Kustas, W.P.; Norman, J.M.; Cook, D.R.; Houser, P.R.; Meyers, T.P.; Prueger, J.H.; Starks, P.J.; Wesely, M.L. Correcting eddy-covariance flux underestimates over a grassland. Agric. For. Meteorol 2000, 103, 279–300. [Google Scholar]
- Tucker, C.J.; Pinzon, J.E.; Brown, M.E.; Slayback, D.A.; Pak, E.W.; Mahoney, R.; Vermote, E.F.; Saleous, N. An extended AVHRR 8-km NDVI dataset compatible with MODIS and SPOT vegetation NDVI data. Int. J. Remote Sens 2005, 26, 4485–4498. [Google Scholar]
- Wu, J.B.; Xiao, X.M.; Guan, D.X.; Shi, T.T.; Jin, C.J.; Han, S.J. Estimation of the gross primary production of an old-growth temperate mixed forest using eddy covariance and remote sensing. Int. J. Remote Sens 2009, 30, 463–479. [Google Scholar]
- Wang, H.S.; Jia, G.S.; Fu, C.B.; Feng, J.M.; Zhao, T.B.; Ma, Z.G. Deriving maximal light use efficiency from coordinated flux measurements and satellite data for regional gross primary production modeling. Remote Sens. Environ 2010, 114, 2248–2258. [Google Scholar]
- Glenn, E.P.; Huete, A.R.; Nagler, P.L.; Nelson, S.G. Relationship between remotely-sensed vegetation indices, canopy attributes and plant physiological processes: What vegetation indices can and cannot tell us about the landscape. Sensors 2008, 8, 2136–2160. [Google Scholar]
- Zeng, X.B.; Dickinson, R.E.; Walker, A.; Shaikh, M.; DeFries, R.S.; Qi, J.G. Derivation and evaluation of global 1-km fractional vegetation cover data for land modeling. J. Appl. Meteorol 2000, 39, 826–839. [Google Scholar]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring. Remote Sens. Environ 1979, 8, 127–150. [Google Scholar]
- Li, R.; Min, Q.L.; Lin, B. Estimation of evapotranspiration in a mid-latitude forest using the microwave emissivity difference vegetation index (EDVI). Remote Sens. Environ 2009, 113, 2011–2018. [Google Scholar]
- Jang, K.; Kang, S.; Kim, J.; Lee, C.B.; Kim, T.; Kim, J.; Hirata, R.; Saigusa, N. Mapping evapotranspiration using MODIS and MM5 four-dimensional data assimilation. Remote Sens. Environ 2010, 114, 657–673. [Google Scholar]
- Hwang, K.; Choi, M. Seasonal trends of satellite-based evapotranspiration algorithms over a complex ecosystem in East Asia. Remote Sens. Environ 2013, 137, 244–263. [Google Scholar]
- Salvucci, G.D. Soil and moisture independent estimation of stage-two evaporation from potential evaporation and albedo or surface temperature. Water Resour. Res 1997, 33, 111–122. [Google Scholar]
- Gu, L.; Meyers, T.; Pallardy, S.G.; Hanson, P.J.; Yang, B.; Heuer, M.; Hosman, K.P.; Riggs, J.S.; Sluss, D.; Wullschleger, S.D. Direct and indirect effects of atmospheric conditions and soil moisture on surface energy partitioning revealed by a prolonged drought at a temperate forest site. J. Geophys. Res 2006. [Google Scholar] [CrossRef]
- Wu, Y.; Zeng, Y.; Wu, B. Retrieval and analysis of vegetation cover in the Three-North Regions of China based on MODIS data. Chin. J. Ecol 2009, 28, 1712–1718. [Google Scholar]
- Duan, H.; Yan, C.; Tsunekawa, A.; Song, X.; Li, S.; Xie, J. Assessing vegetation dynamics in the Three-North Shelter Forest region of China using AVHRR NDVI data. Environ. Earth Sci 2011, 64, 1011–1020. [Google Scholar]
- Li, S.; Zhai, H. The comparison study on forestry ecological projects in the world (In Chinese). Acta. Ecol. Sin 2002, 22, 1976–1982. [Google Scholar]
- Yao, Y.; Liang, S.; Qin, Q.; Wang, K.; Liu, S.; Zhao, S. Satellite detection of increases in global land surface evapotranspiration during 1984–2007. Int. J. Digit. Earth 2012, 5, 299–318. [Google Scholar]
- Lu, E.; Luo, Y.L.; Zhang, R.H.; Wu, Q.X.; Liu, L.P. Regional atmospheric anomalies responsible for the 2009–2010 severe drought in China. J. Geophys. Res 2011. [Google Scholar] [CrossRef]
- Myneni, R.B.; Yang, W.; Nemani, R.R.; Huete, A.R.; Dickinson, R.E.; Knyazikhin, Y.; Didan, K.; Fu, R.; Negron Juarez, R.I.; Saatchi, S.S.; et al. Large seasonal swings in leaf area of Amazon rainforests. Proc. Natl. Acad. Sci. USA 2007, 104, 4820–4823. [Google Scholar]
- Sasai, T.; Saigusa, N.; Nasahara, K.N.; Ito, A.; Hashimoto, H.; Nemani, R.; Hirata, R.; Ichii, K.; Takagi, K.; Saitoh, T.M.; et al. Satellite-driven estimation of terrestrial carbon flux over Far East Asia with 1-km grid resolution. Remote Sens. Environ 2011, 115, 1758–1771. [Google Scholar]
- Zhao, M.; Running, S.W. Drought-induced reduction in global terrestrial net primary production from 2000 through 2009. Science 2010, 329, 940–943. [Google Scholar]
- Dai, A.G.; Trenberth, K.E.; Qian, T. A global data set of Palmer Drought Severity Index for 1870–2002: Relationship with soil moisture and effects of surface warming. J. Hydrometeorol 2004, 5, 1117–1130. [Google Scholar]
- Robeson, S.M. Applied climatology: Drought. Progr. Phys. Geogr 2008, 32, 303–309. [Google Scholar]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A simple interpretation of the surface temperature-vegetation index space for assessment of surface moisture status. Remote Sens. Environ 2002, 79, 213–224. [Google Scholar]
- Mu, Q.; Zhao, M.; Kimball, J.S.; McDowell, N.G.; Running, S.W. A remotely sensed global terrestrial drought severity index. Bull. Am. Meteor. Soc 2013, 94, 83–97. [Google Scholar]




| Site Name | Country | Land Cover Types | Lat | Lon | Elev | Time Period | Network |
|---|---|---|---|---|---|---|---|
| Sask-Fire 1977 (CA-SF1) | Canada | Evergreen needleleaf forest | 54.49 | −105.82 | 536 | 2003–2005 | FLUXNET |
| UCI-1850 burn site (CA-NS1) | Canada | Evergreen needleleaf forest | 55.88 | −98.48 | 260 | 2002–2005 | AmeriFlux |
| Quebec Mature Boreal Forest Site (CA-Qfo) | Canada | Evergreen needleleaf forest | 49.69 | −74.34 | 382 | 2003–2006 | FLUXNET |
| Ivotuk (US-Ivo) | USA | Open shrubland | 68.49 | −155.75 | 568 | 2003–2006 | AmeriFlux |
| Metolius-old aged ponderosa pine (US-Me4) | USA | Evergreen needleleaf forest | 44.50 | −121.62 | 922 | 2000 | AmeriFlux |
| ARM Southern Great Plains site-Lamont (US-ARM) | USA | Central facility tower crop field | 36.61 | −97.49 | 314 | 2003–2006 | AmeriFlux |
| Audubon Research Ranch (US-Aud) | USA | Grassland | 31.59 | −110.51 | 1,469 | 2002–2006 | AmeriFlux |
| Mead--irrigated continuous maize site (US-Ne1) | USA | Cropland | 41.17 | −96.48 | 361 | 2001–2005 | AmeriFlux |
| Morgan Monroe State Forest (US-MMS) | USA | Deciduous broadleaf forest | 39.32 | −86.41 | 275 | 2000–2005 | AmeriFlux |
| Slashpine-Austin Cary-65y nat regen (US-Sp1) | USA | Evergreen needleleaf forest | 29.74 | −82.22 | 50 | 2000–2005 | AmeriFlux |
| Howland Forest (US-Ho1) | USA | Closed conifer forest | 45.20 | −68.74 | 60 | 2000–2004 | AmeriFlux |
| Santarem-Km83-Logged Forest (BR-Sa3) | Brazil | Cleared forest | −3.02 | −54.97 | 100 | 2000–2003 | AmeriFlux |
| Maun-Mopane Woodland (BW-Ma1) | Botswana | Savanna woodland | −19.92 | 23.56 | 950 | 2000–2001 | FLUXNET |
| Ghanzi Mixed Site (BW-Ghm) | Botswana | Woody savanna | −21.2 | 21.75 | 1,135 | 2003 | FLUXNET |
| Skukuza-Kruger National Park (ZA-Kru) | South Africa | Savanna | −25.02 | 31.50 | 365 | 2001–2003 | FLUXNET |
| Niamey (NI-Nam) | Niger | Open shrubland | 13.48 | 2.18 | 223 | 2006 | ARM |
| Yatir (IL-Yat) | Israel | Evergreen needleleaf forest | 31.35 | 35.05 | 650 | 2001–2006 | FLUXNET |
| Palangkaraya (ID-Pag) | Indonesia | Evergreen broadleaf forest | 2.35 | 114.04 | 30 | 2002–2003 | AsiaFlux |
| CocoFlux (VU-Coc) | Vanuatu | Evergreen broadleaf forest | −15.44 | 167.19 | 80 | 2001–2004 | FLUXNET |
| Mae Klong (TH-Mkl) | Thailand | Mixed deciduous forest | 14.58 | 98.84 | 231 | 2003–2004 | AsiaFlux |
| Howard Springs (AU-How) | Australia | Woody savanna | −12.49 | 131.15 | 5 | 2001–2006 | FLUXNET |
| Tumbarumba (AU-Tum) | Australia | Evergreen broadleaf forest | −35.66 | 148.15 | 1,200 | 2001–2006 | FLUXNET |
| Wallaby Creek (AU-Wac) | Australia | Evergreen broadleaf forest | −37.43 | 145.19 | 545 | 2005–2007 | FLUXNET |
| Tomakomai Flux Research Site (JP-Tmk) | Japan | Japanese larch forest | 42.74 | 141.52 | 140 | 2001–2003 | AsiaFlux |
| Arvaikheer (MN-Arv) | Mongolia | Grassland | 46.23 | 102.83 | 1,728 | 2000–2003 | GAME AAN |
| Southern Khentei Taiga (MN-Skt) | Mongolia | Larch forest | 48.35 | 108.65 | 1,630 | 2003–2006 | AsiaFlux |
| Fukang (CN-Fuk) | China | Grassland | 44.28 | 87.92 | 476 | 2006–2007 | CERN |
| Zotino (RU-Zot) | Russia | Evergreen needleleaf forest | 60.80 | 89.35 | 90 | 2002–2004 | FLUXNET |
| Siberia Yakutsk Larch Forest Site (RU-Ylf) | Russia | Larch forest | 62.26 | 129.24 | 220 | 2003–2004 | AsiaFlux |
| Chokurdakh (RU-Cok) | Russia | Open shrubland | 70.62 | 147.88 | 23 | 2003–2005 | FLUXNET |
| Fyodorovskoye wet spruce stand (RU-Fyo) | Russia | Spruce forest | 56.46 | 32.92 | 265 | 2000–2006 | FLUXNET |
| Kaamanen wetland (FI-Kaa) | Finland | Wetlands | 69.14 | 27.30 | 155 | 2000–2006 | FLUXNET |
| Fajemyr (SE-Faj) | Sweden | Wetlands | 56.27 | 13.55 | 140 | 2005–2006 | FLUXNET |
| Polwet (PL-Wet) | Poland | Wetlands | 52.76 | 16.31 | 54 | 2004–2005 | FLUXNET |
| Neustift/Stubai Valley (AT-Neu) | Austria | Grassland | 47.12 | 11.32 | 970 | 2002–2006 | FLUXNET |
| Amplero (IT-Amp) | Italy | Grassland | 41.90 | 13.61 | 884 | 2002–2006 | FLUXNET |
| Las Majadas del Tietar (ES-Lma) | Spain | Savanna | 39.94 | −5.77 | 260 | 2004–2006 | FLUXNET |
| Griffin-Aberfeldy-Scotland (UK-Gri) | UK | Evergreen needleleaf forest | 56.61 | −3.80 | 340 | 2000–2006 | FLUXNET |
| Tatra (SK-Tat) | Slovak Republic | Evergreen needleleaf forest | 49.12 | 20.16 | 1,050 | 2005 | FLUXNET |
| Foulum (DK-Fou) | Denmark | Cropland | 56.48 | 9.59 | 51 | 2005 | FLUXNET |
| Tharandt (DE-Tha) | Germany | Norway Spruce | 50.97 | 13.57 | 380 | 2000–2006 | FLUXNET |
| Site Name | Bias (W/m2) | RMSE (W/m2) | R2 | |||
|---|---|---|---|---|---|---|
| MS-PT | PT-JPL | MS-PT | PT-JPL | MS-PT | PT-JPL | |
| CA-SF1 | −13.5 | 12.7 | 26.8 | 35.3 | 0.89 | 0.87 |
| CA-NS1 | 22.7 | 36.8 | 50.3 | 68.6 | 0.74 | 0.66 |
| CA-Qfo | 6.8 | −4.7 | 36.1 | 40.1 | 0.71 | 0.51 |
| US-Ivo | −7.7 | 3.9 | 29.3 | 36.1 | 0.53 | 0.54 |
| US-Me4 | 4.6 | 12.3 | 41.1 | 62.2 | 0.75 | 0.78 |
| US-ARM | −13.1 | −3.6 | 43.1 | 39.8 | 0.60 | 0.62 |
| US-Aud | −0.4 | 3.5 | 34.1 | 28.8 | 0.64 | 0.73 |
| US-Ne1 | −13.6 | −5.7 | 45.6 | 54.1 | 0.87 | 0.78 |
| US-MMS | 25.3 | 21.8 | 42.4 | 49.6 | 0.89 | 0.87 |
| US-Sp1 | 46.3 | 56.2 | 60.2 | 81.3 | 0.85 | 0.81 |
| US-Ho1 | 32.2 | 35.8 | 56.3 | 63.5 | 0.83 | 0.78 |
| BR-Sa3 | 10.4 | 17.8 | 29.6 | 39.1 | 0.88 | 0.87 |
| BW-Ma1 | 12.8 | 20.5 | 37.9 | 46.7 | 0.62 | 0.58 |
| BW-Ghm | −9.1 | 18.4 | 38.7 | 41.6 | 0.77 | 0.73 |
| ZA-Kru | −14.8 | −1.1 | 36.8 | 17.8 | 0.45 | 0.50 |
| NI-Nam | 26.4 | 31.3 | 46.2 | 50.1 | 0.54 | 0.61 |
| IL-Yat | 48.6 | 43.7 | 87.6 | 89.1 | 0.41 | 0.40 |
| ID-Pag | 14.3 | 21.2 | 42.7 | 50.4 | 0.70 | 0.68 |
| VU-Coc | 34.3 | 32.1 | 57.6 | 62.5 | 0.89 | 0.85 |
| TH-Mkl | 21.6 | 28.9 | 47.7 | 67.8 | 0.67 | 0.61 |
| AU-How | 13.5 | 23.9 | 44.3 | 61.8 | 0.70 | 0.64 |
| AU-Tum | 10.9 | 26.2 | 34.1 | 56.6 | 0.88 | 0.84 |
| AU-Wac | 22.5 | 28.8 | 47.4 | 61.1 | 0.85 | 0.80 |
| JP-Tmk | 2.6 | 10.2 | 44.7 | 51.4 | 0.71 | 0.66 |
| MN-Arv | −20.4 | −12.5 | 58.7 | 41.6 | 0.44 | 0.54 |
| MN-Skt | 20.1 | 26.1 | 41.6 | 46.5 | 0.72 | 0.69 |
| CN-Fuk | 10.1 | 15.1 | 39.9 | 43.1 | 0.53 | 0.51 |
| RU-Zot | 9.3 | 18.2 | 28.2 | 44.3 | 0.78 | 0.73 |
| RU-Ylf | −0.3 | 4.3 | 10.7 | 11.3 | 0.56 | 0.60 |
| RU-Cok | −12.3 | −1.3 | 28.5 | 49.1 | 0.72 | 0.62 |
| RU-Fyo | 19.1 | 20.8 | 53.3 | 53.8 | 0.80 | 0.75 |
| FI-Kaa | −18.2 | −12.4 | 32.5 | 29.8 | 0.77 | 0.76 |
| SE-Faj | 15.2 | 22.2 | 44.4 | 66.4 | 0.83 | 0.67 |
| PL-Wet | −23.7 | −11.3 | 37.5 | 29.4 | 0.89 | 0.85 |
| AT-Neu | −20.2 | −10.2 | 39.5 | 31.8 | 0.88 | 0.88 |
| IT-Amp | −23.1 | −11.5 | 48.3 | 42.5 | 0.71 | 0.72 |
| ES-Lma | −9.9 | 6.9 | 32.8 | 34.2 | 0.61 | 0.61 |
| UK-Gri | −21.7 | −21.3 | 42.3 | 43.2 | 0.76 | 0.74 |
| SK-Tat | −0.5 | −13.5 | 12.5 | 30.2 | 0.81 | 0.72 |
| DK-Fou | 14.6 | 18.7 | 53.5 | 66.9 | 0.41 | 0.40 |
| DE-Tha | 22.7 | 20.4 | 59.2 | 58.8 | 0.76 | 0.71 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Yao, Y.; Liang, S.; Zhao, S.; Zhang, Y.; Qin, Q.; Cheng, J.; Jia, K.; Xie, X.; Zhang, N.; Liu, M. Validation and Application of the Modified Satellite-Based Priestley-Taylor Algorithm for Mapping Terrestrial Evapotranspiration. Remote Sens. 2014, 6, 880-904. https://doi.org/10.3390/rs6010880
Yao Y, Liang S, Zhao S, Zhang Y, Qin Q, Cheng J, Jia K, Xie X, Zhang N, Liu M. Validation and Application of the Modified Satellite-Based Priestley-Taylor Algorithm for Mapping Terrestrial Evapotranspiration. Remote Sensing. 2014; 6(1):880-904. https://doi.org/10.3390/rs6010880
Chicago/Turabian StyleYao, Yunjun, Shunlin Liang, Shaohua Zhao, Yuhu Zhang, Qiming Qin, Jie Cheng, Kun Jia, Xianhong Xie, Nannan Zhang, and Meng Liu. 2014. "Validation and Application of the Modified Satellite-Based Priestley-Taylor Algorithm for Mapping Terrestrial Evapotranspiration" Remote Sensing 6, no. 1: 880-904. https://doi.org/10.3390/rs6010880





