Continuous Extraction of Subway Tunnel Cross Sections Based on Terrestrial Point Clouds
Abstract
:1. Introduction
2. Extraction of the Central Axis of a Tunnel
2.1. Determination of the Central Axis of a Tunnel Based on 2D Projection
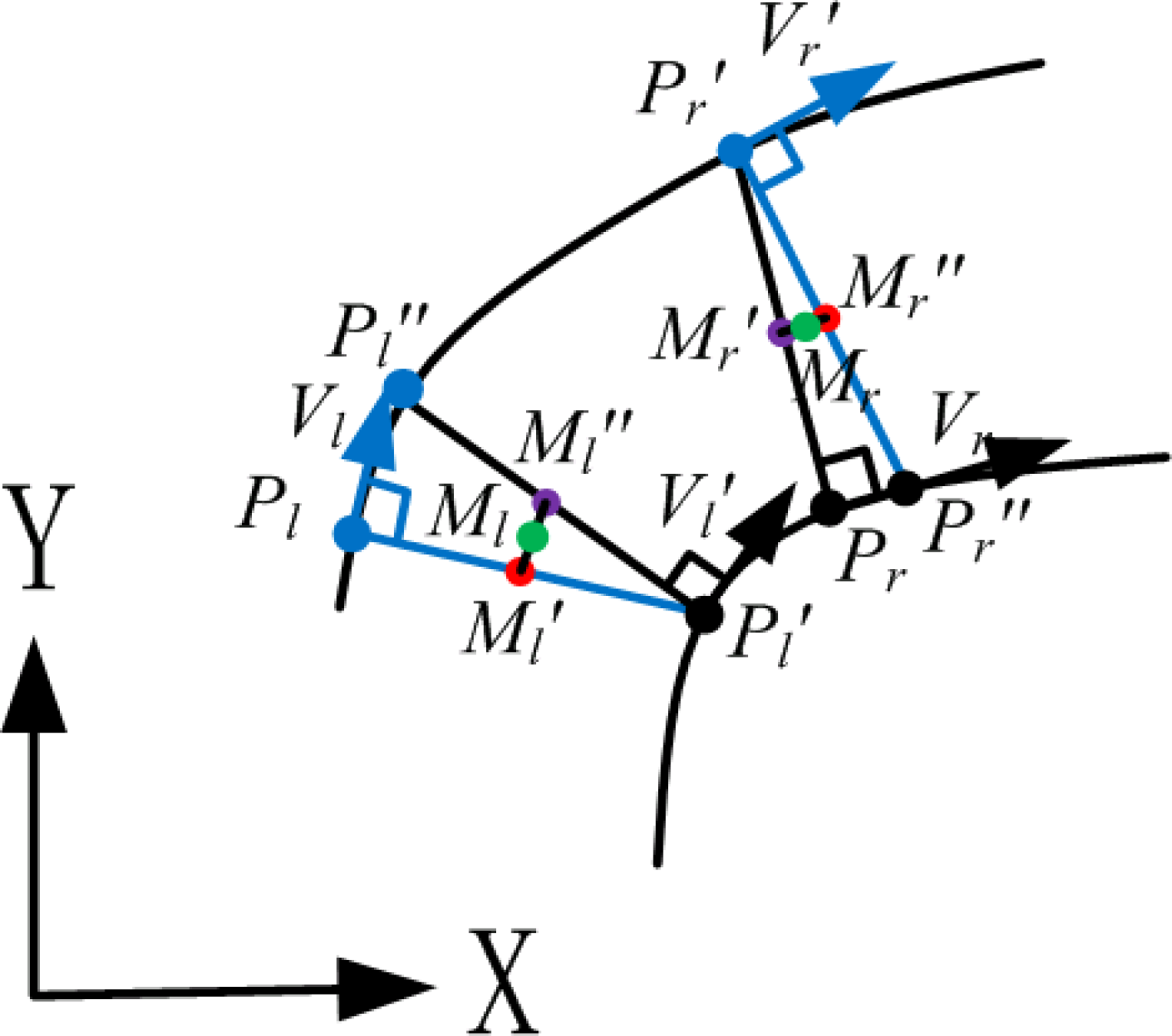
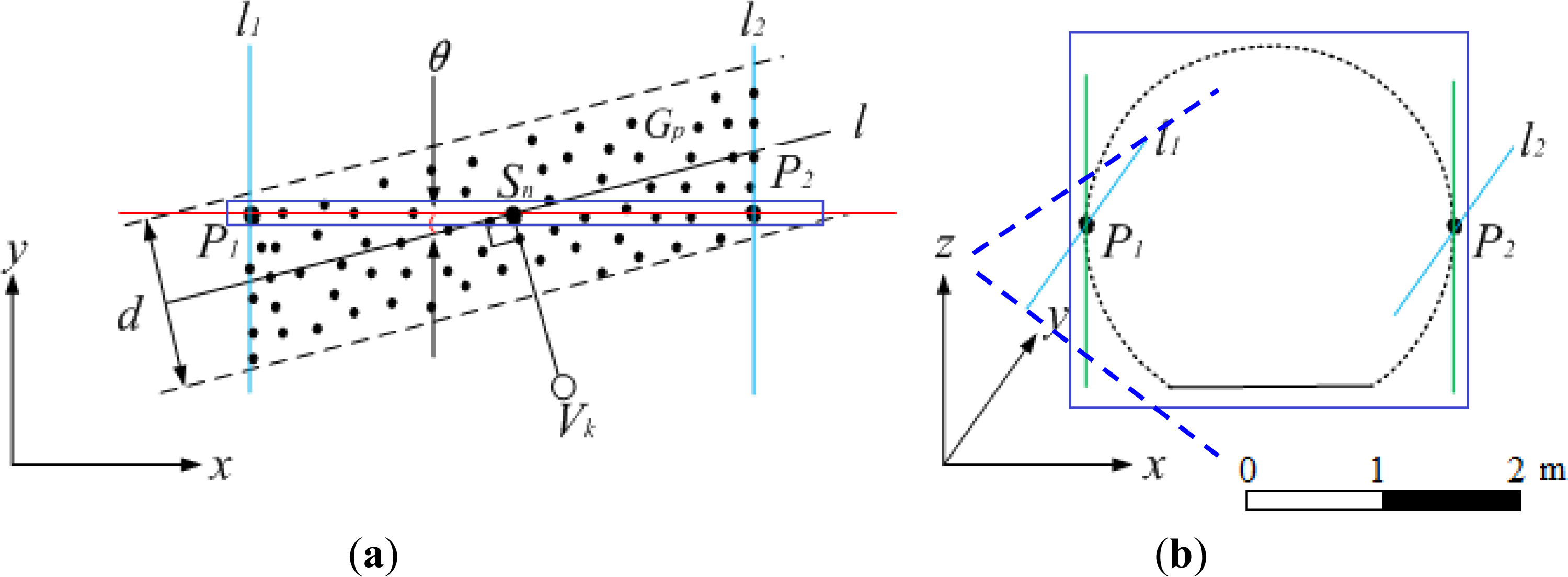
2.1.1. Estimation of the Boundary Points
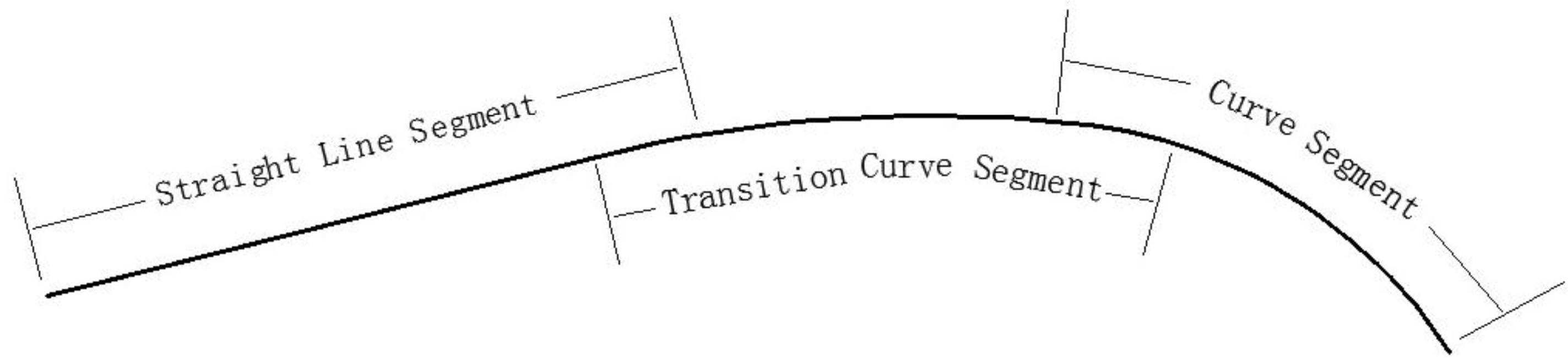
2.1.2. Fitting of the Bounding Lines
- Straight line model:
- Transition curve model:
- Curve model:
2.1.3. Fitting of the Central Axis
2.2. Global Adjustment of the Central Axis Using Segment-Wise Fitting
3. Cross Section Extraction Based on Quadric Parametric Surface Fitting
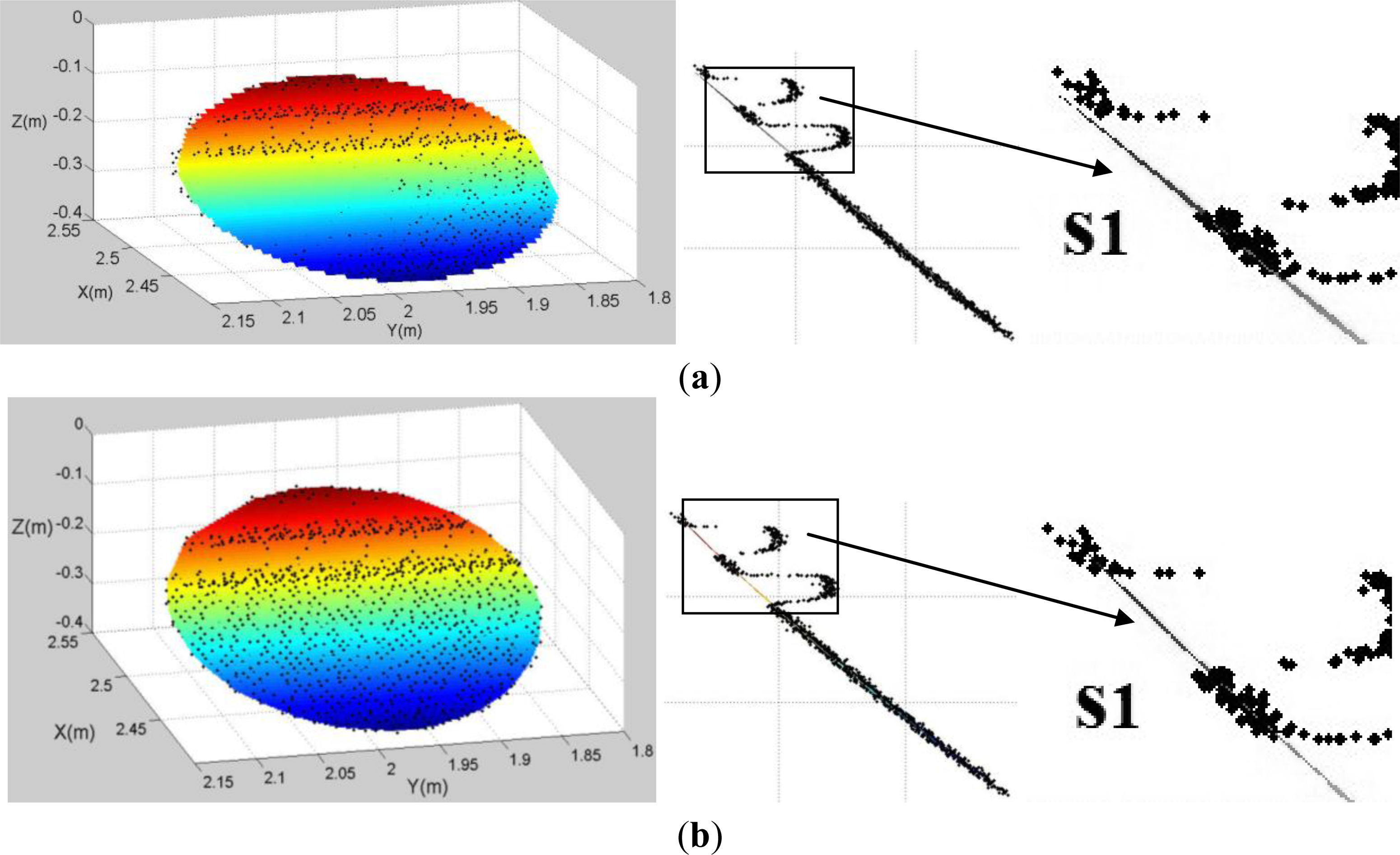
3.1. Adjustment of the Pseudo Cross-Sectional Plane
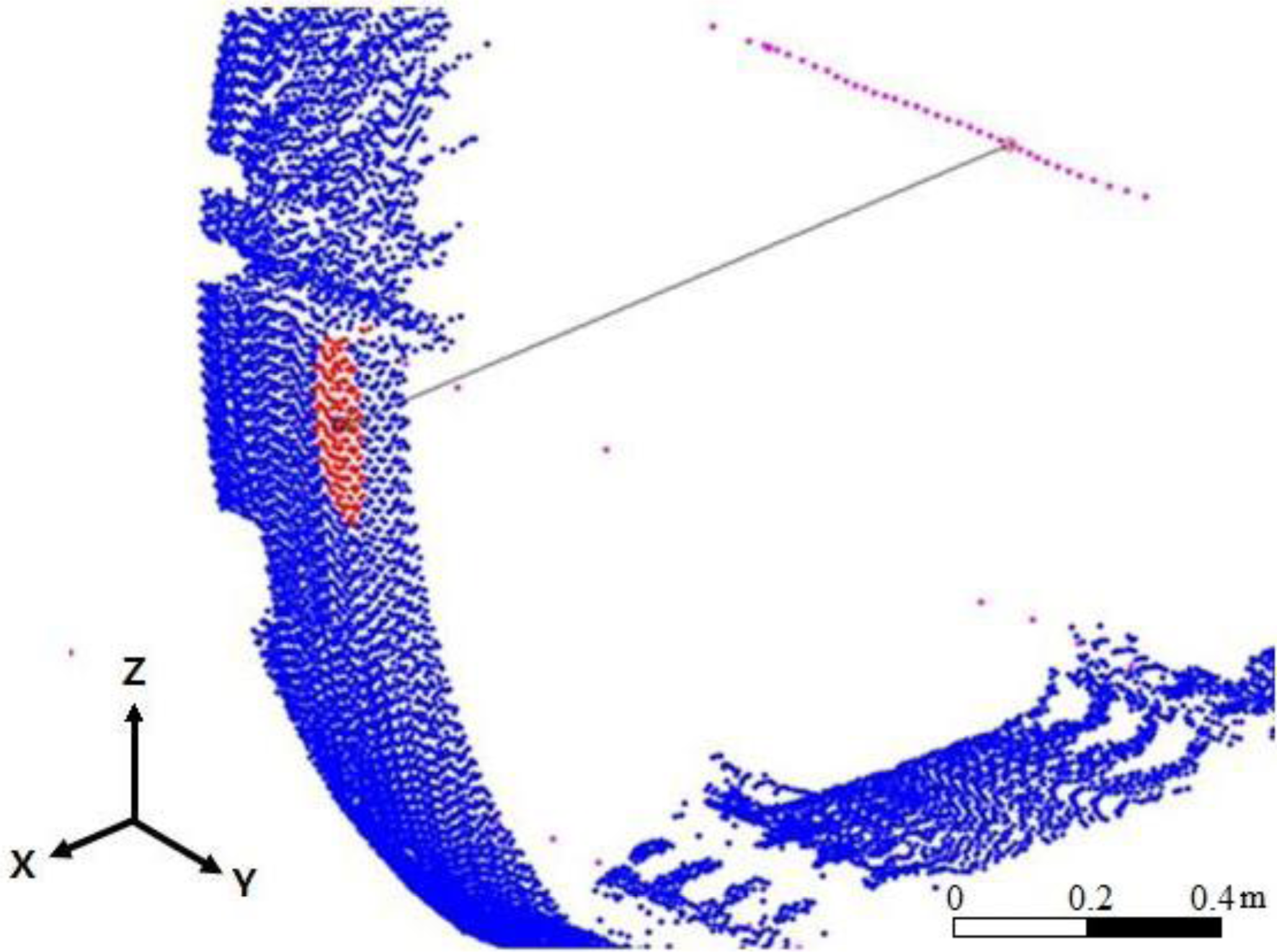
3.2. Continuous Estimation of the Cross-Sectional Point
3.2.1. Quadric Parametric Surface Model
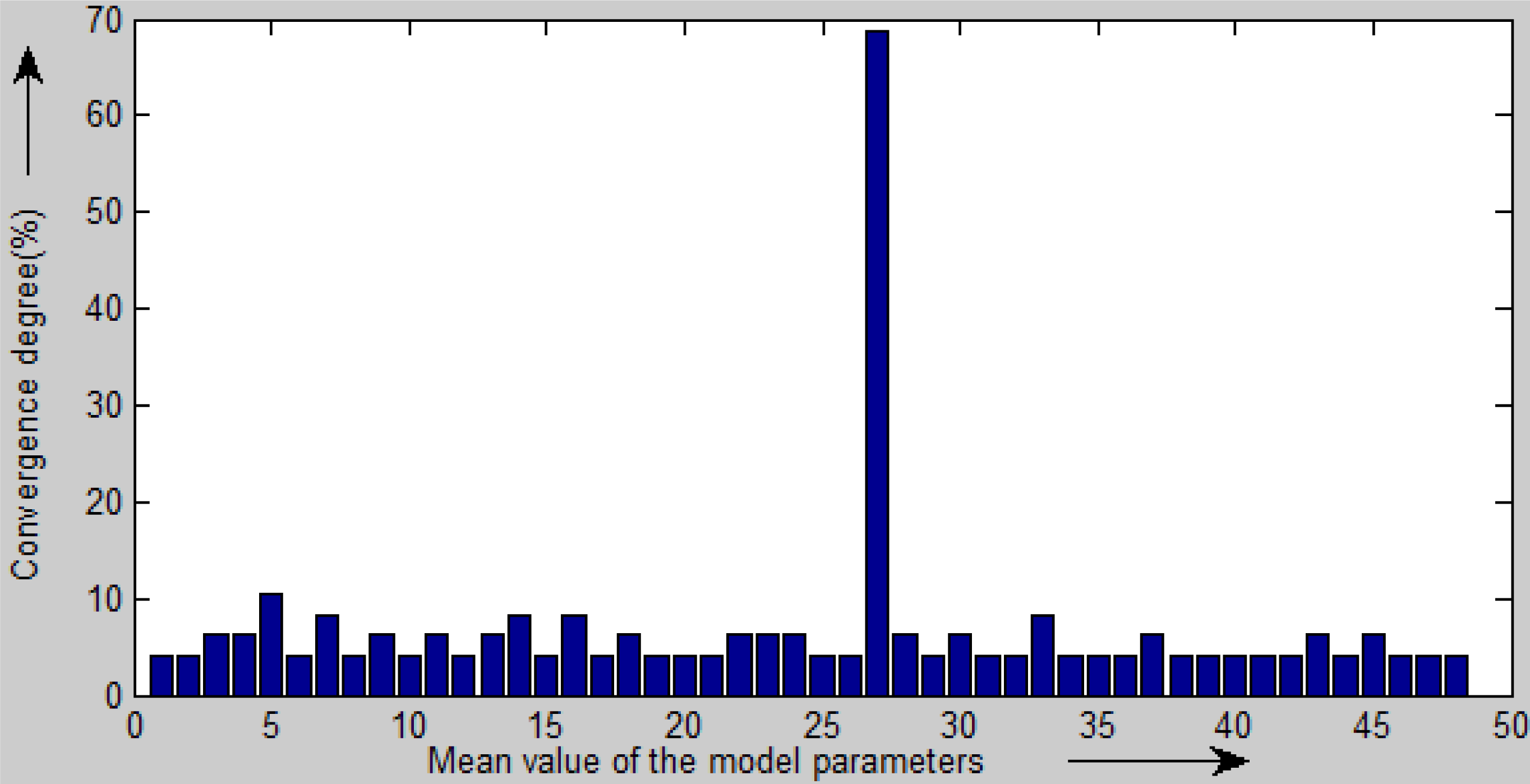
3.2.2. Fitting Process Based on the Improved BaySAC Algorithm
4. Experimental Section
4.1. Central Axis Fitting
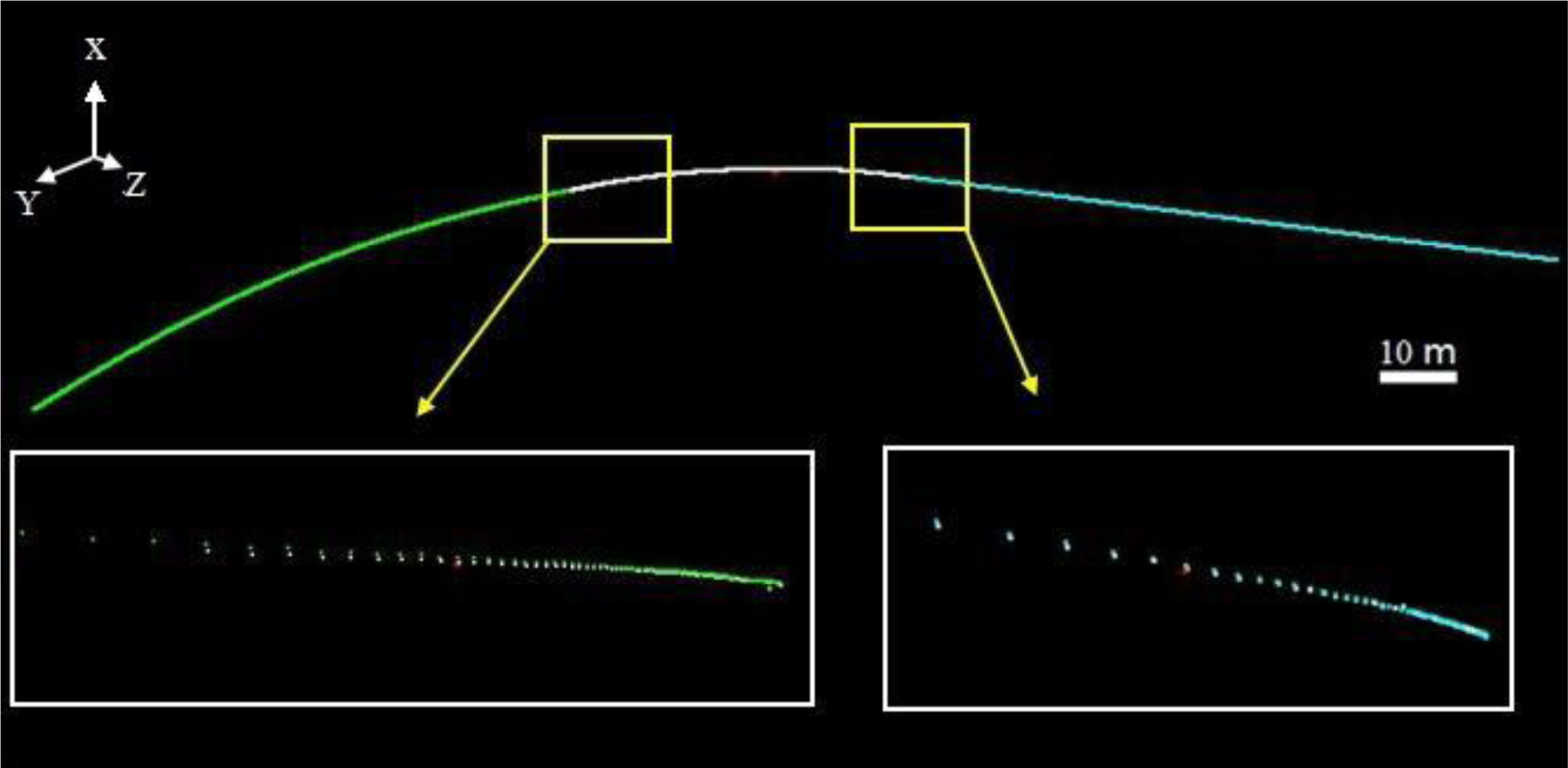
4.1.1. Fitting of the Central Axis Based on the 2D Projection
4.1.2. Global Extraction of the Central Axis Using Segment-Wise Fitting
4.2. Cross Section Extraction Based on Quadric Parametric Surface Fitting
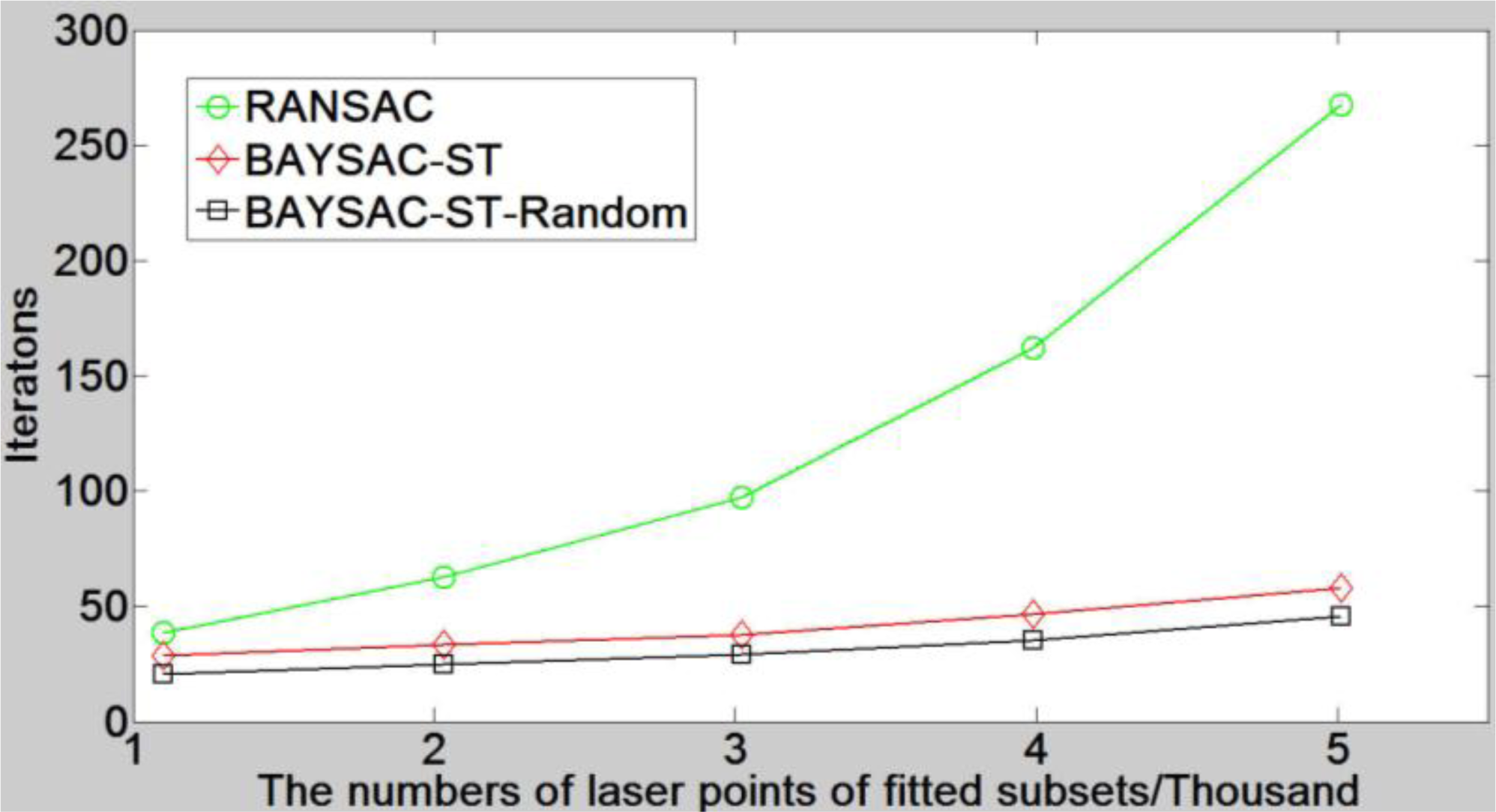
4.2.1. Computational Efficiency
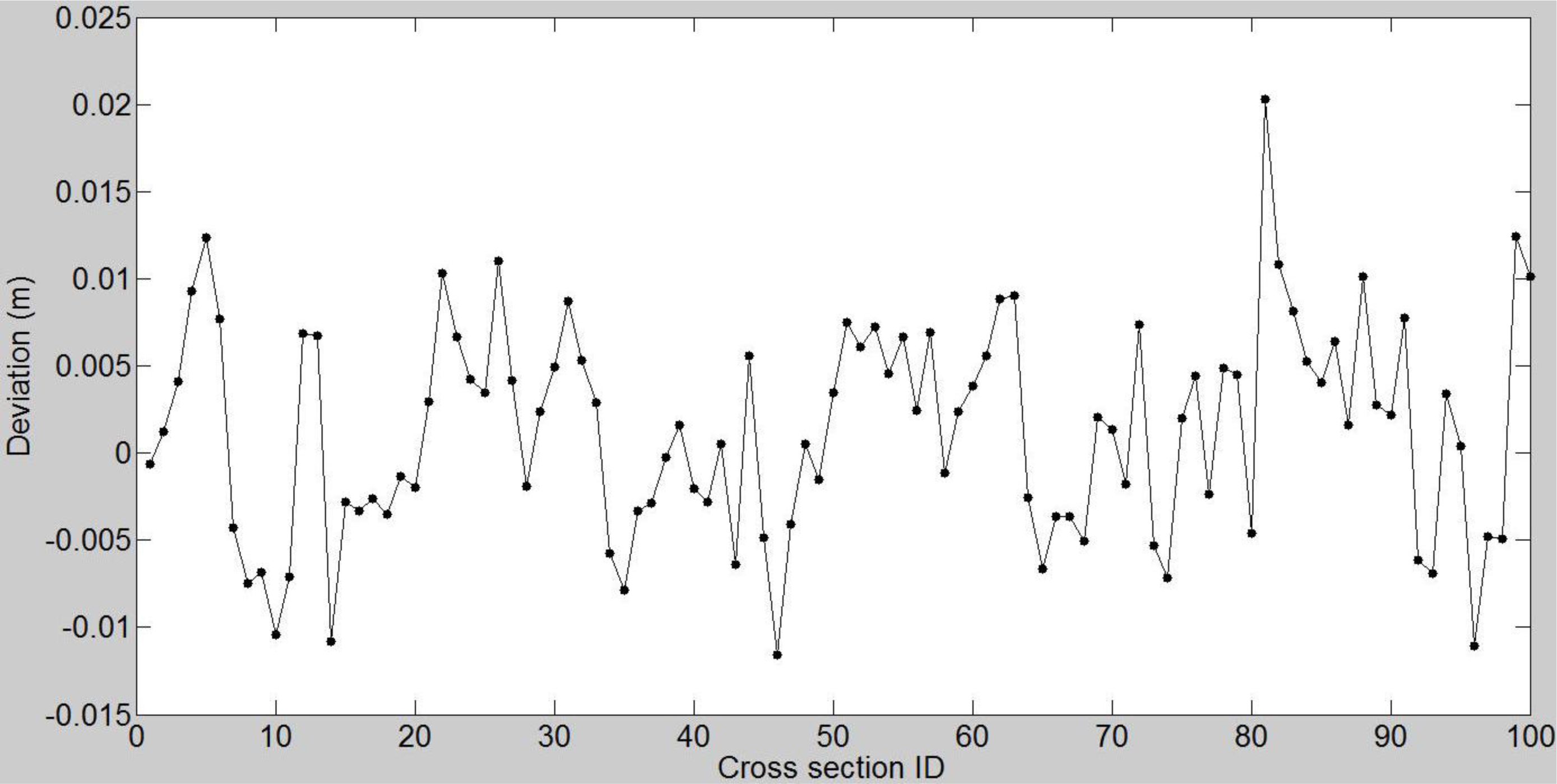
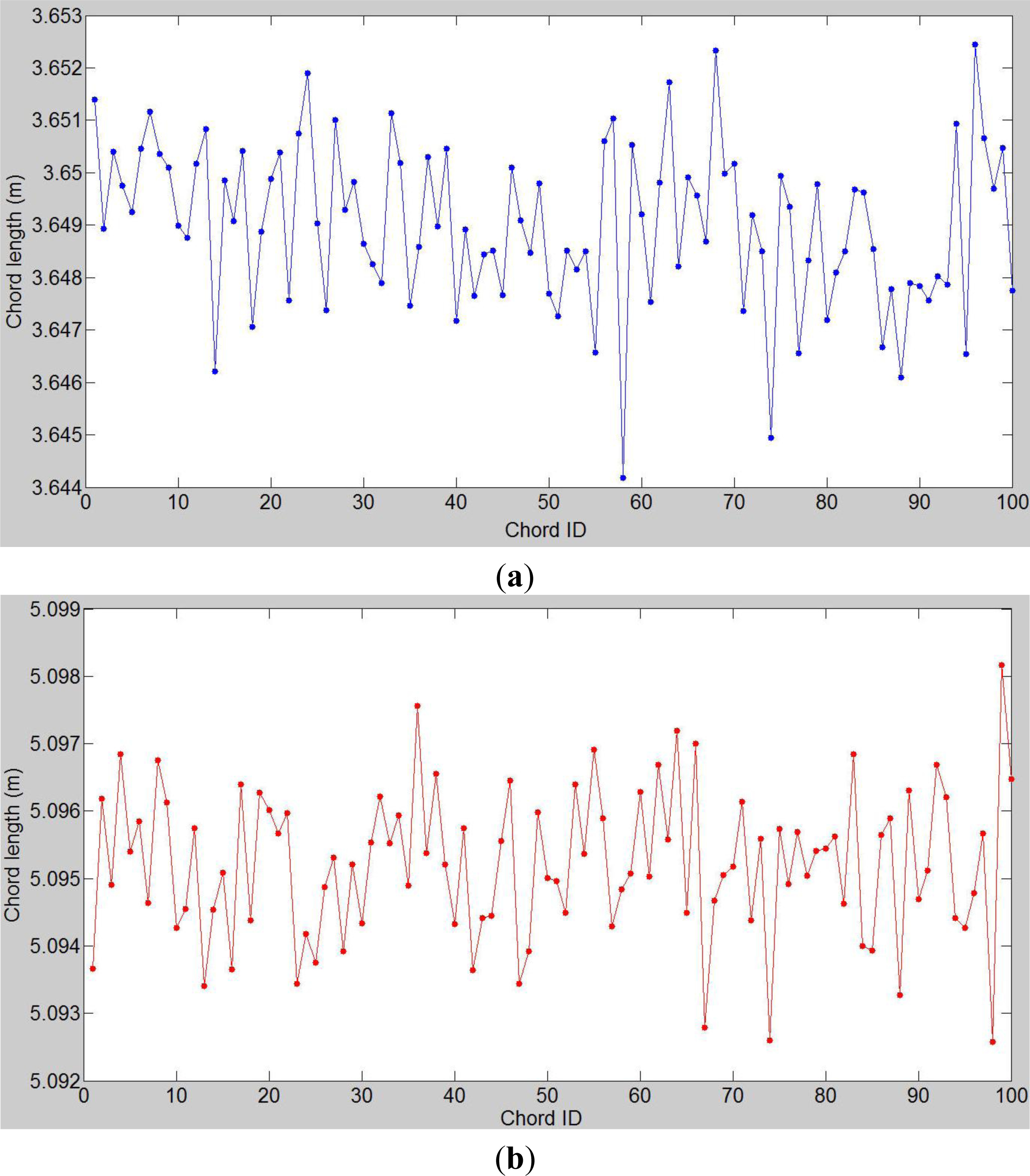
4.2.2. Fitting Accuracy
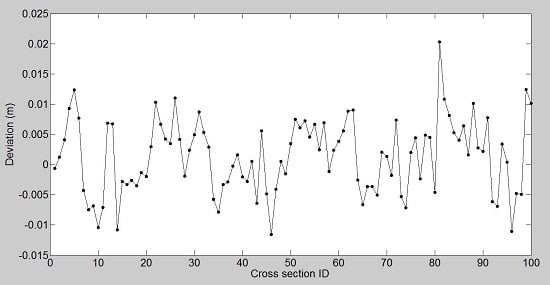
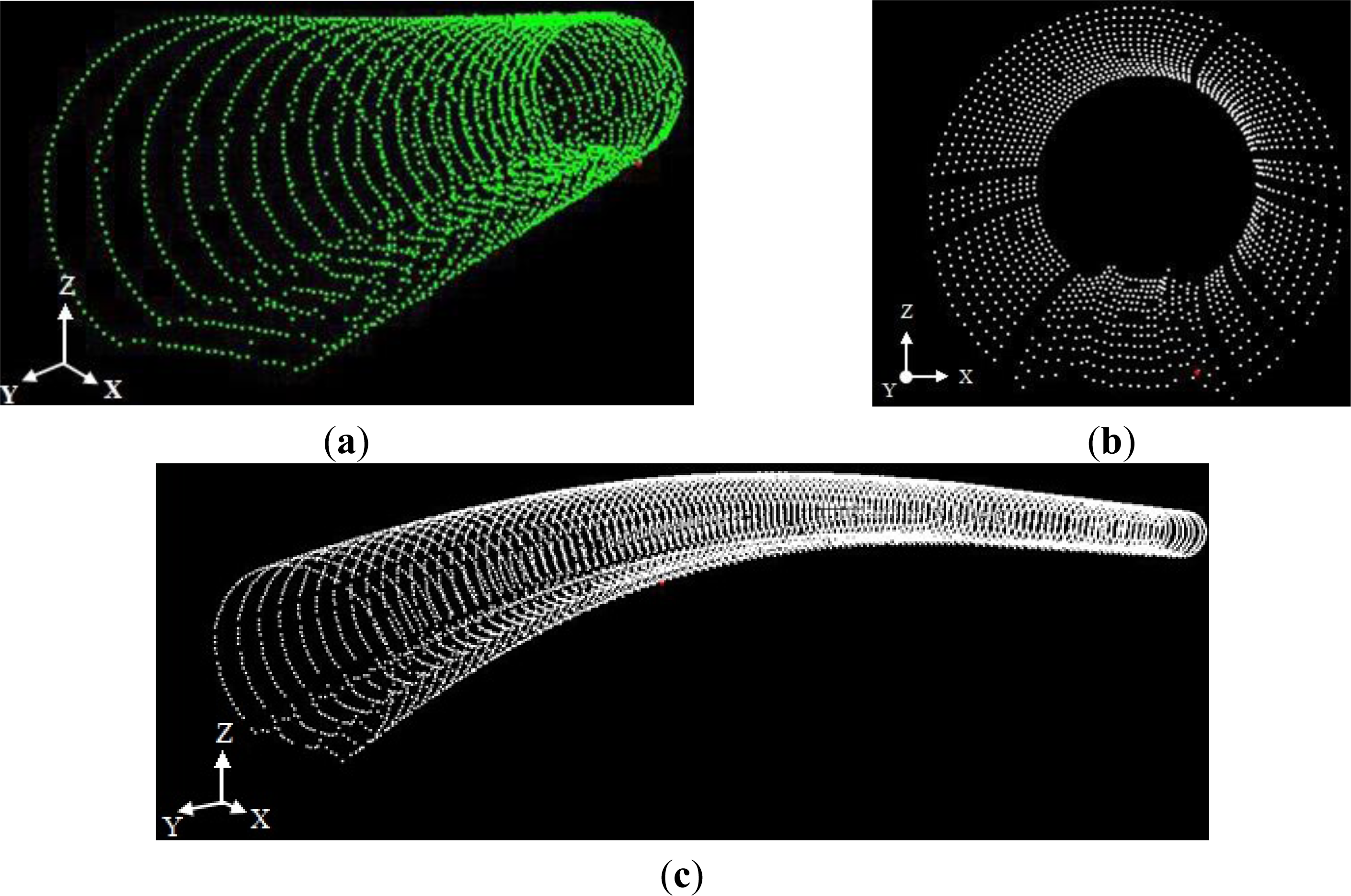
4.2.3. Continuous Extraction of the Cross Sections
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Wang, T.-T.; Jaw, J.-J.; Chang, Y.-H.; Jeng, F.-S. Application and validation of profile-image method for measuring deformation of tunnel wall. Tunn. Undergr. Space Technol. 2009, 24, 136–147. [Google Scholar]
- Paar, G.; Kontrus, H. Three-Dimensional Tunnel Reconstruction Using Photogrammetry and Lasers Scanning. Proceedings of the 3rd Nordost, 9. Anwendungsbezogener Workshop zur Erfassung, Modellierung, Verarbeitung und Auswertung von 3D-Daten, Berlin, Germany, 1 December 2006.
- Tsakiri, M.; Lichti, D.; Pfeifer, N. Terrestrial Laser Scanning for Deformation Monitoring. Proceedings of the 3rd IAG/12th FIG Symposium, Baden, Austria, 22–24 May 2006.
- Gordon, S.J.; Lichti, D.D. Modeling terrestrial laser scanner data for precise structural deformation measurement. ASCE J. Surv. Eng 2007, 133, 72–80. [Google Scholar]
- Van Gosliga, R.; Lindenbergh, R.; Pfeifer, N. Deformation analysis of a bored tunnel by means of terrestrial laser scanning, international archives of photogrammetry. Remote Sens. Spat. Inf. Sci 2006, 36, 167–172. [Google Scholar]
- Lindenbergh, R.; Uchanski, L.; Bucksch, A.; Gosliga, R. Structural monitoring of tunnels using terrestrial laser scanning. Rep. Geod 2009, 87, 231–239. [Google Scholar]
- Schneider, D. Terrestrial Laser Scanner for Area Based Deformation Analysis of Towers and Water Damns. Proceedings of the 3rd IAG Symposium of Geodesy for Geotechnical and Structural Engineering and 12th FIG Symposium on Deformation Measurements, Baden, Austria, 22–24 May 2006; p. 6.
- Monserrat, O.; Crosetto, M. Deformation measurement using terrestrial laser scanning data and least squares 3D surface matching. ISPRS J. Photogramm. Remote Sens 2008, 63, 142–154. [Google Scholar]
- Gruen, A.; Akca, D. Least squares 3D surface and curve matching. ISPRS J. Photogramm. Remote Sens 2005, 59, 151–174. [Google Scholar]
- Pejic', M. Design and optimisation of laser scanning for tunnels geometry inspection. Tunn. Undergr. Space Technol 2013, 37, 199–206. [Google Scholar]
- Yoon, J.; Sagong, M.; Lee, J.S.; Lee, K. Feature extraction of a concrete tunnel liner from 3D laser scanning data. NDT E Int 2009, 42, 97–105. [Google Scholar]
- Gikas, V. Three-dimensional laser scanning for geometry documentation and construction management of highway tunnels during excavation. Sensors 2012, 12, 11249–11270. [Google Scholar]
- Seo, D.-J.; Lee, J.C.; Lee, Y.-D.; Lee, Y.-H.; Mun, D.-Y. Development of cross section management system in tunnel using terrestrial laser scanning technique. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2008, 37, 573–581. [Google Scholar]
- Slob, S.; Hack, H.R.G.K. 3D Terrestrial Laser Scanning as a New Field Measurement and Monitoring Technique. In Engineering Geology for Infrastructure Planning in Europe: A European Perspective; Robert, H., Rafig, A., Robert, C., Eds.; Springer Verlag: Berlin, Germany, 2004; pp. 179–190. [Google Scholar]
- Han, S.; Cho, H.; Kim, S.; Jung, J.; Heo, J. Automated and efficient method for extraction of tunnel cross sections using terrestrial laser scanned data. J. Comput. Civ. Eng 2013, 27, 274–281. [Google Scholar]
- Kang, Z.; Tuo, L.; Zlatanova, S. Continuously deformation monitoring of subway tunnel based on terrestrial point clouds. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2012, XXXIX-B5, 199–203. [Google Scholar]
- Oude Elberink, S.; Khoshelham, K.; Arastounia, M.; Díaz Benito, D. Rail track detection and modelling in mobile laser scanner data. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci 2013, II-5/W2, 223–228. [Google Scholar]
- Telea, A.; van Wijk, J. An Augmented Fast Marching Method for Computing Skeletons and Centrelines. Proceedings of the Symposium on Data Visualisation, Barcelona, Spain, 27–29 May 2002; pp. 251–259.
- Pock, T.; Beichel, R.; Bischof, H. A novel robust tube detection filter for 3D centerline extraction. Lect. Notes Comput. Sci 2005, 3540, 55–94. [Google Scholar]
- Hassouna, M.S. Robust Centerline Extraction Framework Using Level Sets. Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR 2005), New York, NY, USA, 20–25 June 2005; pp. 458–465.
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. ACM Commun 1981, 24, 381–395. [Google Scholar]
- Yang, M.; Lee, E. Segmentation of measured data using a parametric quadric surface approximation. Comput. Aided Des 1999, 31, 449–457. [Google Scholar]
- Kang, Z.; Zhang, L.; Wang, B.; Li, Z.; Jia, F. An optimized BaySAC algorithm for efficient fitting of primitives in point clouds. IEEE. Geosci. Remote Sens. Lett. 2013. [Google Scholar] [CrossRef]








| Laser Scanner | Scan Angular Resolution | n | Range Accuracy |
|---|---|---|---|
| RIEGL VZ-400 | 0.046° | 2,686,866 | ±5 mm |
| ID | Deviations after Global Extraction (m) | Deviations before Global Extraction (m) | ID | Deviations after Global Extraction (m) | Deviations before Global Extraction (m) |
|---|---|---|---|---|---|
| 1 | 0.005 | 0.035 | 13 | 0.001 | 0.056 |
| 2 | −0.003 | −0.026 | 14 | 0.004 | 0.039 |
| 3 | 0.002 | 0.019 | 15 | −0.005 | 0.022 |
| 4 | 0.003 | 0.016 | 16 | 0.003 | 0.047 |
| 5 | −0.005 | 0.002 | 17 | 0.001 | −0.032 |
| 6 | 0.001 | 0.001 | 18 | 0.004 | 0.03 |
| 7 | −0.003 | −0.007 | 19 | 0.001 | 0.038 |
| 8 | 0.002 | 0.003 | 20 | −0.007 | −0.015 |
| 9 | −0.001 | 0.008 | 21 | −0.001 | 0.035 |
| 10 | −0.003 | 0.004 | 22 | 0.003 | 0.002 |
| 11 | 0.0013 | 0.01 | 23 | 0.001 | −0.025 |
| 12 | −0.002 | −0.035 | 24 | 0.002 | 0.015 |
| RMSE | 0.002 | 0.026 | |||
| Point | Point-to-Surface Distance (m) | |
|---|---|---|
| RANSAC | Optimized BaySAC | |
| 1 | 0.0021 | 0.0009 |
| 2 | 0.0020 | 0.0009 |
| 3 | 0.0008 | 0.0002 |
| 4 | 0.0012 | 0.0005 |
| 5 | 0.0016 | 0.0007 |
| 6 | 0.0025 | 0.0015 |
| 7 | 0.0019 | 0.0010 |
| 8 | 0.0010 | 0.0007 |
| 9 | 0.0020 | 0.0015 |
| 10 | 0.0014 | 0.0009 |
| ID | Measured Coordinates (m) | Interpolated Coordinates (m) | Deviation (m) | ||||
|---|---|---|---|---|---|---|---|
| X | Y | Z | X | Y | Z | ||
| 1 | −3.171 | 15.578 | 0.051 | −3.1705 | 15.578 | 0.0510 | 0.0005 |
| 2 | −3.182 | 15.544 | 0.013 | −3.1821 | 15.544 | 0.1330 | 0.0001 |
| 3 | −2.842 | 15.680 | 1.918 | −2.8409 | 15.680 | 1.9173 | 0.0013 |
| 4 | −2.864 | 15.759 | 1.875 | −2.8646 | 15.759 | 1.8754 | 0.0007 |
| 5 | −0.596 | 15.576 | −1.573 | 0.5965 | 15.576 | −1.5744 | 0.0015 |
| Mean deviation (m) | 0.0008 | ||||||
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kang, Z.; Zhang, L.; Tuo, L.; Wang, B.; Chen, J. Continuous Extraction of Subway Tunnel Cross Sections Based on Terrestrial Point Clouds. Remote Sens. 2014, 6, 857-879. https://doi.org/10.3390/rs6010857
Kang Z, Zhang L, Tuo L, Wang B, Chen J. Continuous Extraction of Subway Tunnel Cross Sections Based on Terrestrial Point Clouds. Remote Sensing. 2014; 6(1):857-879. https://doi.org/10.3390/rs6010857
Chicago/Turabian StyleKang, Zhizhong, Liqiang Zhang, Lei Tuo, Baoqian Wang, and Jinlei Chen. 2014. "Continuous Extraction of Subway Tunnel Cross Sections Based on Terrestrial Point Clouds" Remote Sensing 6, no. 1: 857-879. https://doi.org/10.3390/rs6010857