Remote Sensing-Derived Bathymetry of Lake Poopó
Abstract
:1. Introduction
2. Data
3. Methodology
3.1. General Introduction
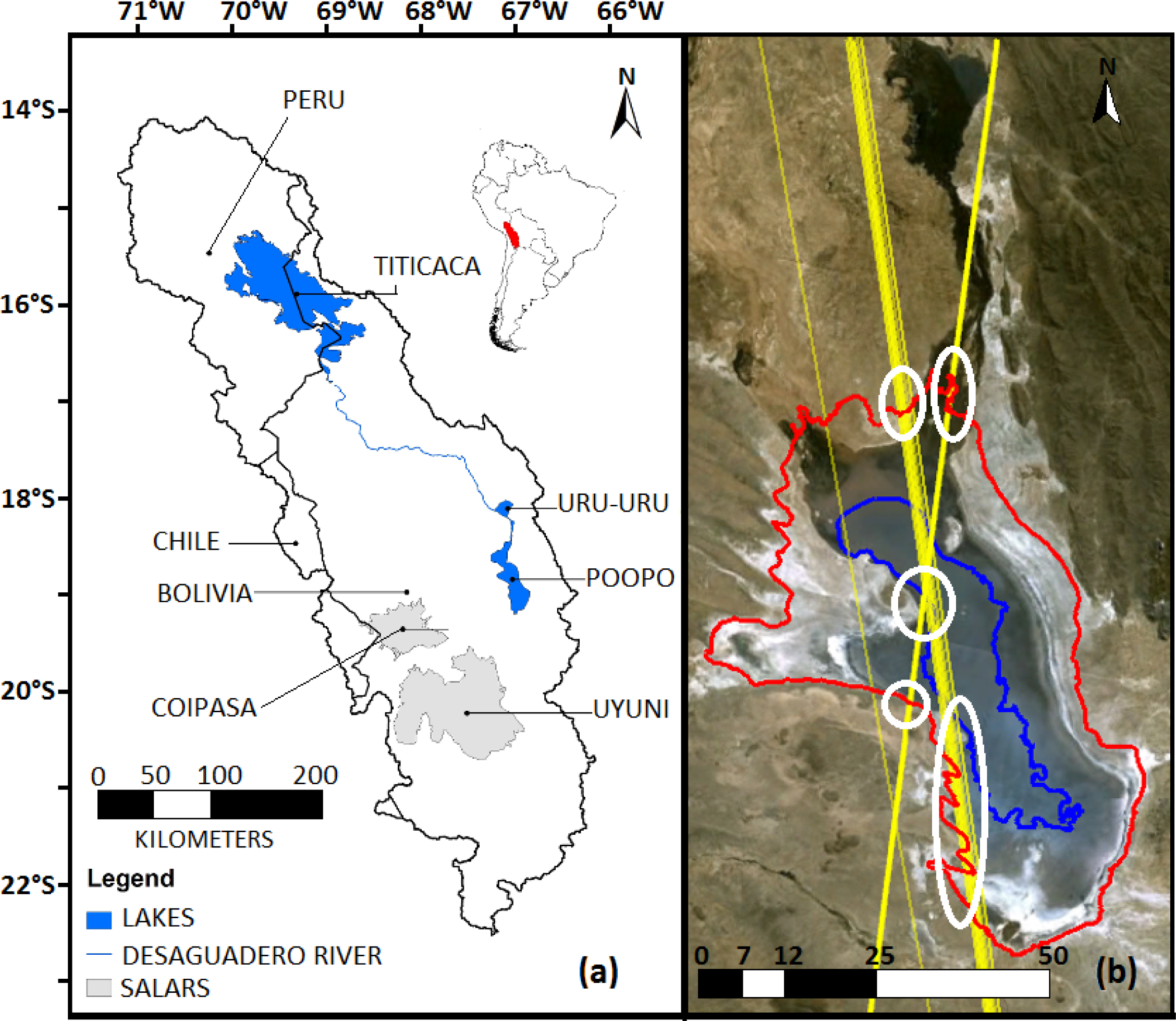
3.2. Water Surface Masks for Bathimetry and Water Surface Area Variations
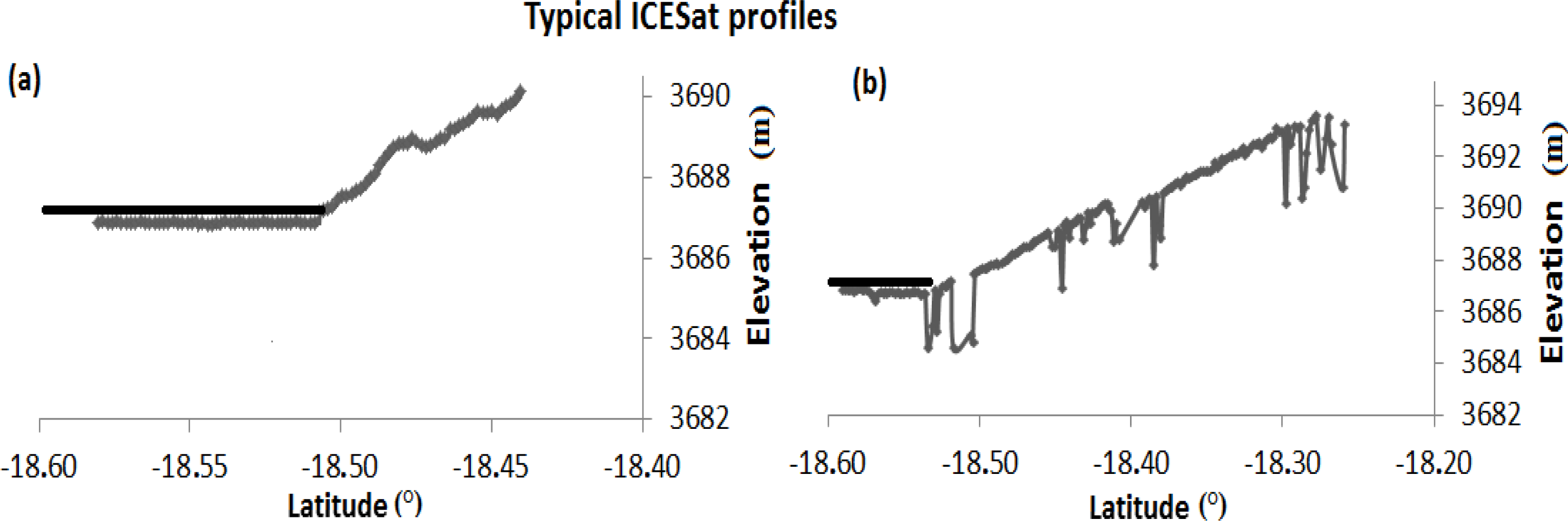
3.3. ICESat Profiles Selection
3.4. Creating Isolines (Isobaths)
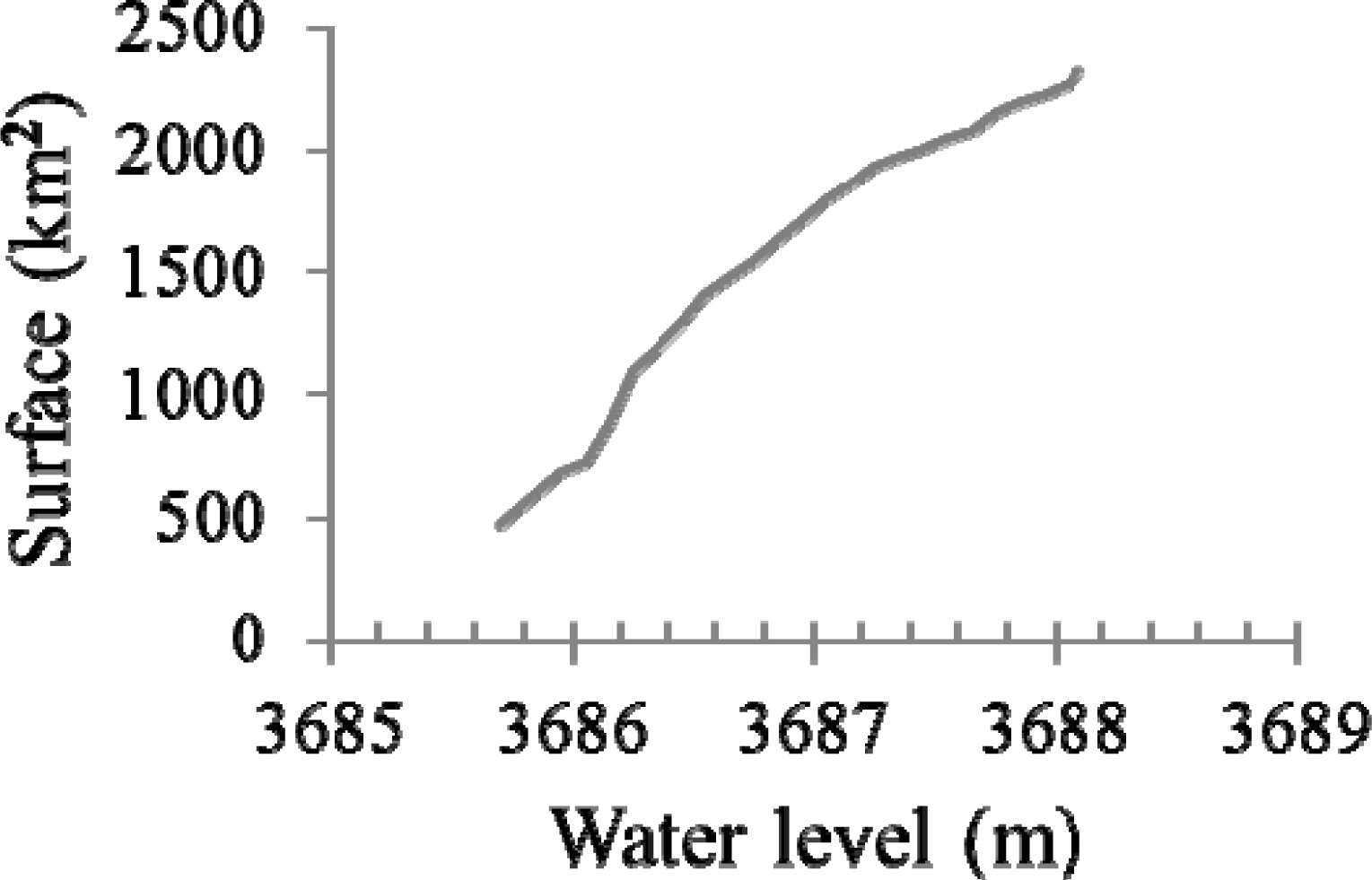
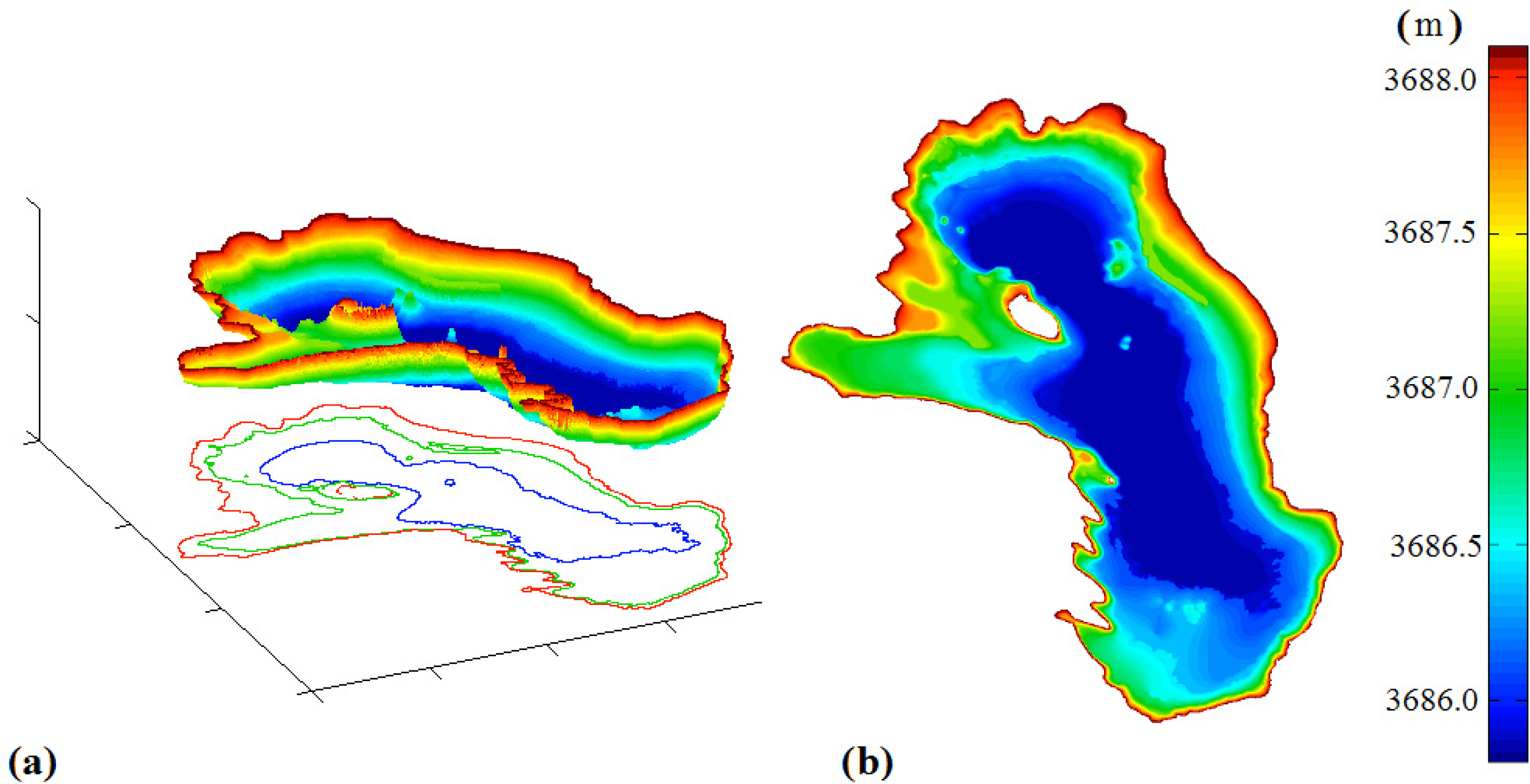
3.5. Bathymetry
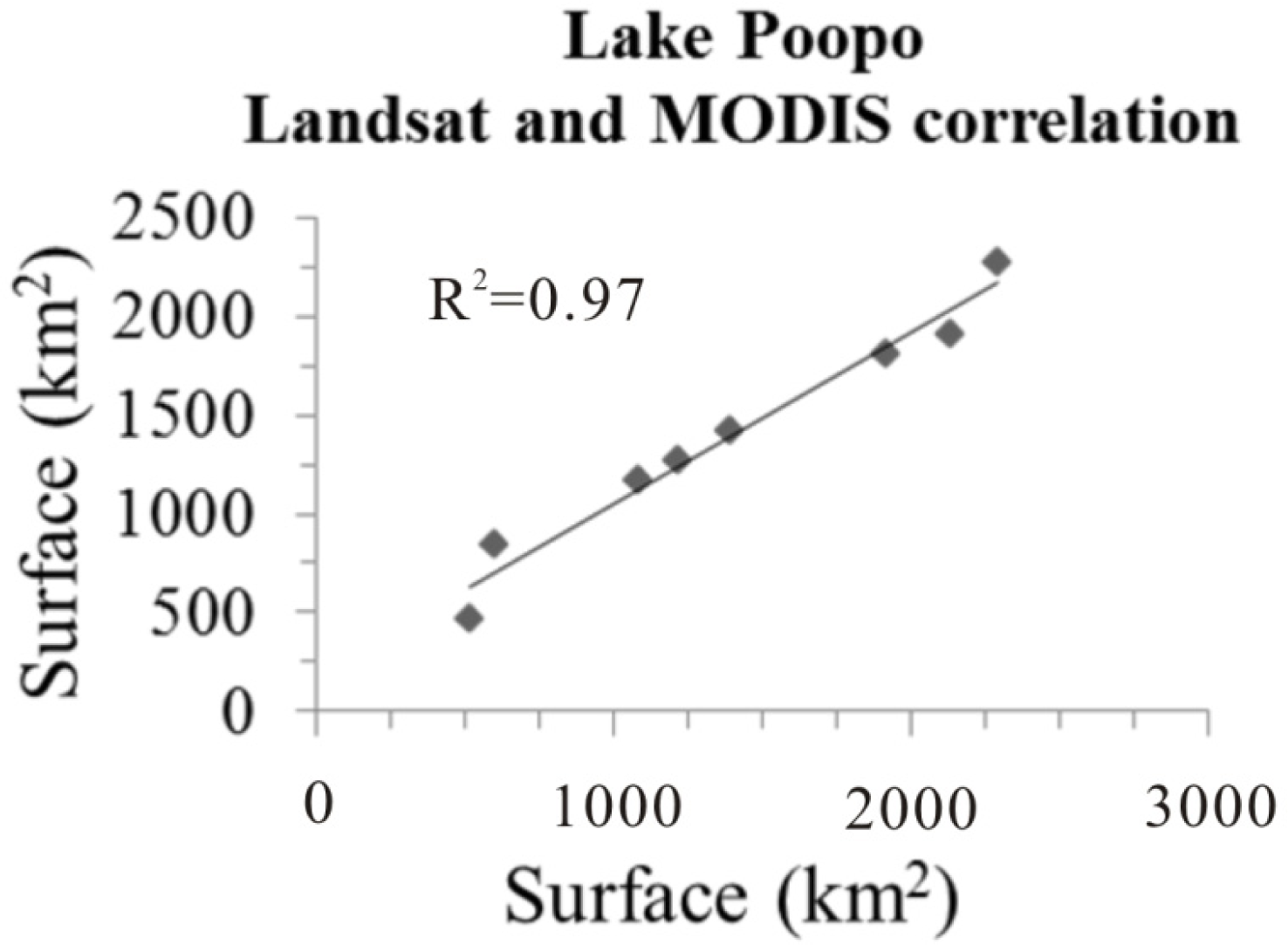
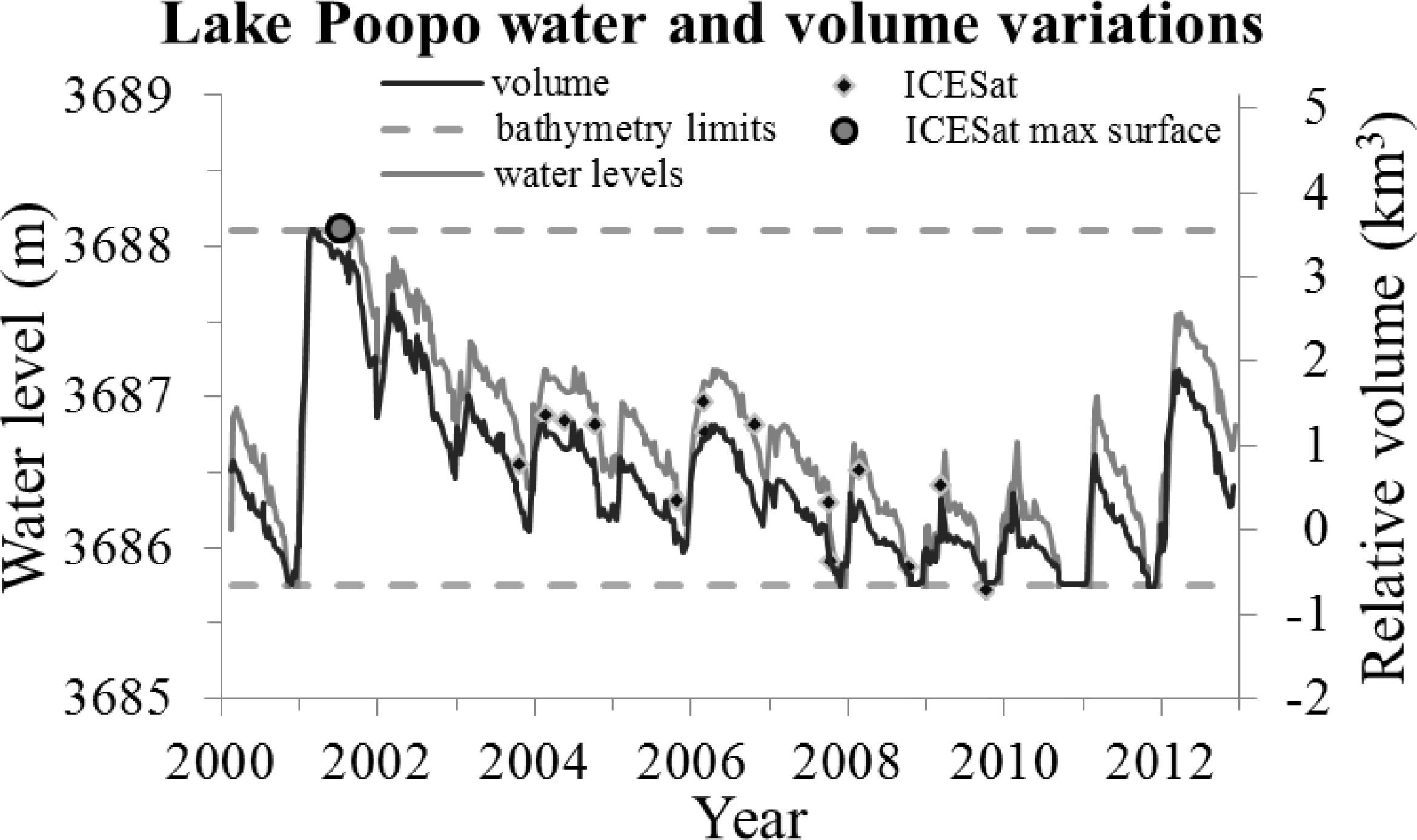
4. Results
5. Discussion and Perspectives
Conflicts of Interest
References
- Abarca Del Rio, R.; Crétaux, J.-F.; Berge-Nguyen, M.; Maisongrande, P. Does Lake Titicaca still control the Lake Poopó system water levels? An investigation using satellite altimetry and MODIS data (2000–2009). Remote Sens. Lett 2012, 3, 707–714. [Google Scholar]
- Pillco Zolá, R.; Bengtsson, L. Long-term and extreme water level variations of the shallow Lake Poopó, Bolivia. Hydrol. Sci. J 2006, 51, 98–114. [Google Scholar]
- Pillco Zolá, R.; Bengtsson, L. Three methods for determining the area-depth relationship of Lake Poopó, a large shallow lake in Bolivia. Lakes Reserv 2007, 12, 275–284. [Google Scholar]
- Condom, T.; Coudrain, A.; Dezetter, A.; Brunstein, D.; Delclaux, F.; Jean-Emmanuel, S. Transient modelling of lacustrine regressions: Two case studies from the Andean Altiplano. Hydrol. Process 2004, 18, 2395–2408. [Google Scholar]
- Crétaux, J.-F.; Calmant, S.; Abarca Del Rio, R.; Kouraev, A.; Bergé-Nguyen, M.; Maisongrande, P.; Rio, R.A. Lakes Studies from Satellite Altimetry. In Coastal Altimetry; Vignudelli, S., Kostianoy, A.G., Cipollini, P., Benveniste, J., Eds.; Springer: Berlin, German, 2011; pp. 509–533. [Google Scholar]
- Cretaux, J.F.; Jelinski, W.; Calmant, S.; Kouraev, A.; Vuglinski, V.; Berge-Nguyen, M.; Gennero, M.C.; Nino, F.; Abarca Del Rio, R.; Cazenave, A.; et al. SOLS: A lake database to monitor in the Near Real Time water level and storage variations from remote sensing data. Adv. Space. Res 2011, 47, 1497–1507. [Google Scholar]
- Cretaux, J.-F.; Berge-Nguyen, M.; Leblanc, M.; Abarca Del Rio, R.; Delclaux, F.; Mognard, N.; Lion, C.; Pandey, R.-K.; Tweed, S.; Calmant, S.; et al. Flood mapping inferred from remote sensing data. Int. Water Technol. J 2011, 1, 48–62. [Google Scholar]
- Abileah, R.; Vignudelli, S.; Scozzari, A. A completely remote sensing approach to monitoring reservoirs water volume. Int. Water Technol. J 2011, 1, 63–77. [Google Scholar]
- Sima, S.; Tajrishy, M. Using satellite data to extract volume-area-elevation relationships for Urmia Lake, Iran. J. Great Lakes Res 2013, 39, 90–99. [Google Scholar]
- Hobi, M.L.; Ginzler, C. Accuracy assessment of digital surface models based on WorldView-2 and ADS80 stereo remote sensing data. Sensors 2012, 12, 6347–6368. [Google Scholar]
- Huguenin, R.L.; Wang, M.H.; Biehl, R.; Stoodley, S.; Rogers, J.N. Automated subpixel photobathymetry and water quality mapping. Photogramm. Eng. Remote Sens 2004, 70, 111–123. [Google Scholar]
- Dekker, A.G; Phinn, S.R.; Anstee, J.; Bissett, P.; Brando, V.E.; Casey, B.; Fearns, P.; Hedley, J.; Klonowski, W.; Lee, Z.P.; et al. Intercomparison of shallow water bathymetry, hydro-optics, and benthos mapping techniques in Australian and Caribbean coastal environments. Limnol. Oceanogr. Methods 2011, 9, 396–425. [Google Scholar]
- Lee, I.; Chang, H.; Ge, L. GPS campaigns for validation of InSAR derived DEMs. Positioning 2005, 1–2, 82–87. [Google Scholar]
- Zwally, H.J.; Schutz, B.; Abdalati, W.; Abshire, J.; Bentley, C.; Brenner, A.; Bufton, J.; Dezio, J.; Hancock, D.; Harding, D.; et al. ICESat’s laser measurements of polar ice, atmosphere, ocean, and land. J. Geodyn 2002, 34, 405–445. [Google Scholar]
- Hien Phan, V.; Lindenbergh, R.; Menenti, M. ICESat derived elevation changes of Tibetan lakes between 2003 and 2009. Int. J. Appl. Earth Obs. Geoinf 2012, 17, 12–22. [Google Scholar]
- Fricker, H.A.; Borsa, A.; Minster, B.; Carabajal, C.; Quinn, K.; Bills, B. Assessment of ICESat performance at the Salar de Uyuni, Bolivia. Geophys. Res. Lett 2005, 32. [Google Scholar] [CrossRef]
- Zwally, H.J.R.; Schutz, C.; Bentley, J.; Bufton, T.; Herring, J.; Minster, J.; Spinhirne, R.T. GLAS/ICESat L1B Global Elevation Data, Version 33; National Snow & Ice Data Center: Boulder, CO, USA, 2003. [Google Scholar]
- Bills, B.G.; Borsa, A.A.; Comstock, R.L. MISR-based passive optical bathymetry from orbit with few-cm level of accuracy on the Salar de Uyuni, Bolivia. Remote Sens. Environ 2007, 107, 240–255. [Google Scholar]
- Zhang, G.; Xie, H.; Kang, S.; Yi, D.; Ackley, S.F. Monitoring lake level changes on the Tibetan Plateau using ICESat altimetry data (2003–2009). Remote Sens. Environ 2011, 115, 1733–1742. [Google Scholar]
- Abileah, R.; Vignudelli, S. Bathymetry from Fusion of Multi-Temporal Landsat and Radar Altimetery. Proceedings of the 6th International Workshop on the Analysis of Multi-temporal Remote Sensing Images (Multi-Temp), Trento, Italy, 12–14 July 2011; pp. 189–192.
- USGS Global Visualization Viewer. Available online: http://glovisusgs.gov/ (accessed on 31 July 2013).
- MODIS Land. Available online: http://modis-land.gsfc.nasa.gov/ (accessed on 31 July 2013).
- NASA. ICESat & ICESat-2. http://icesat.gsfc.nasa.gov/ (accessed on 31 July 2013).
- ICESat/GLAS Data Summaries. Available online: http://nsidc.org/data/icesat/correction-to-product-surface-elevations.html (accessed on 31 July 2013).
- Brenner, A.C.; Bentley, C.R.; Csatho, B.M.; Harding, D.J.; Hofton, M.A.; Minster, J.; Roberts, L.; Saba, J.L. Derivation of Range and Range Distributions from Laser Pulse Waveform Analysis for Surface Elevations, Roughness, Slope, and Vegetation Heights. Available online: http://www.csr.utexas.edu/glas/pdf/Atbd_20031224.pdf (accessed on 31 July 2013).
- McFeeters, S.K. The use of the Normalized Difference Water Index (NDWI) in the delineation of open water features. Int. J. Remote Sens 1996, 17, 1425–1432. [Google Scholar]
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens 2006, 27, 3025–3033. [Google Scholar]
- Polidorio, A.M.; Flores, F.C.; Franco, C.; Imai, N.N.; Tommaselli, A.M.G. Detecção Automática de Sombras e Nuvens em Imagens CBERS e Landsat 7 ETM; Anais XII Simpósio Brasileiro de Sensoriamento Remoto: Goiânia, Brazil, 2005. [Google Scholar]
- Polidorio, A.; Imai, N.; Tommaselli, A. Índice Indicador de Corpos d’ água Para Imagens Multispectrais 2004. Available online: http://www.ufpe.br/cgtg/ISIMGEO/CD/html/Fotogrametria%20e%20Sensoriamento%20Remoto/Artigos/f027.pdf (accessed on 31 July 2013).
- Jain, S.; Saraf, A.; Goswami, A.; Ahmad, T. Flood inundation mapping using NOAA AVHRR data. Water Resour. Manag 2006, 20, 949–959. [Google Scholar]
- Sethre, P.R.; Rundquist, B.C.; Todhunter, P.E. Remote detection of prairie pothole ponds in the Devils Lake Basin, North Dakota. GISci. Remote Sens 2005, 42, 277–296. [Google Scholar]
- Liu, Y.; Song, P.; Peng, J.; Ye, C. A physical explanation of the variation in threshold for delineating terrestrial water surfaces from multi-temporal images: Effects of radiometric correction. Int. J. Remote Sens 2012, 33, 5862–5875. [Google Scholar]
- Clemens, R.S.; Phinn, S.R.; Murray, N.J.; Roelfsema, C.M.; Fuller, R.A. Continental scale mapping of Tidal Flats across East Asia using the Landsat archive. Remote Sens 2012, 4, 3417–3426. [Google Scholar]
- Ji, L.; Zhang, L.; Wylie, B. Analysis of dynamic thresholds for the normalized difference water index. Photogramm. Eng. Remote Sens 2009, 75, 1307–1317. [Google Scholar]
- Justice, C.O.; Townshend, J.R.G.; Vermote, E.F.; Masuoka, E.; Wolfe, R.E.; El Saleous, N.; Roy, D.P.; Morisette, J.T. An overview of MODIS Land data processing and product status. Remote Sens. Environ 2002, 83, 3–15. [Google Scholar]
- Engman, E.T.; Gurney, R.J. Remote Sensing in Hydrology; Chapman and Hall: London, UK, 1991. [Google Scholar]
- Li, R.R.; Kaufman, Y.J.; Gao, B.-C.; Davis, C.O. Remote sensing of suspended sediments and shallow coastal waters. IEEE Trans. Geosci. Remote Sens 2003, 41, 559–566. [Google Scholar]
- Pedinotti, V.; Boone, A.; Decharme, B.; Crétaux, J.F.; Mognard, N.; Panthou, G.; Papa, F.; Tanimoun, B.A. Evaluation of the ISBA-TRIP continental hydrologic system over the Niger basin using in situ and satellite derived datasets. Hydrol. Earth Syst. Sci 2012, 16, 1745–1773. [Google Scholar] [Green Version]
- Pandey, R.K.; Cretaux, J.-F.; Berge-Nguyen, M.; Tiwari, V.M.; Drolon, V.; Calmant, S. Water level estimation by remote sensing for 2008 flood of Kosi. Int. J. Remote Sens 2013, in press. [Google Scholar]
- Crétaux, J.-F.; Létolle, R.; Calmant, S. Investigations on Aral Sea regressions from mirabilite deposits and remote sensing. Aquat. Geochem 2009, 15, 277–291. [Google Scholar]
- Yésou, H.; Huber, C.; Lai, X.; Averty, S.; Li, J.; Daillet, S.; Bergé-Nguyen, M.; Chen, X.; Huang, S.; James, B.; et al. Nine years of water resources monitoring over the middle reaches of the Yangtze River, with ENVISAT, MODIS, Beijing-1 time series, Altimetric data and field measurements. Lakes Reserv 2011, 16, 231–247. [Google Scholar]
- Aires, F.; Papa, F.; Prigent, C.; Crétaux, J.-F.; Berge-Nguyen, M. Characterization and space/time downscaling of the inundation extent over the Inner Niger Delta using GIEMS and MODIS data. J. Hydrometeorol 2013. [Google Scholar] [CrossRef]
- Baghdadi, N.; Lemarquand, N.; Abdallah, H.; Bailly, J.S. The relevance of GLAS/ICESat elevation data for the monitoring of river networks. Remote Sens 2011, 3, 708–720. [Google Scholar]
- GLAS Altimetry Data Dictionary. Available online: http://nsidc.org/data/docs/daac/glas_altimetry/data_dictionary.html (accessed on 31 July 2013).
- Antonio, F. Faster Line Segment Intersection. In Graphics Gems III; Kirk, D., Glassner, A., Eds.; Academic Press: San Diego, CA, USA, 1992; pp. 199–202. [Google Scholar]
- Cormen, T.; Leiserson, C.; Rivest, R.; Stein, C. Determining Whether any Pair of Segments Intersects: Section 33.2. In Introduction to Algorithms; Cormen, T., Leiserson, C., Rivest, R., Stein, C., Eds.; MIT Press: Cambridge, MA, USA, 2001; pp. 934–947. [Google Scholar]
- TriScatteredInterp in MathWorks MATLAB online Documentation Center. Available online: http://www.mathworks.fr/fr/help/matlab/ref/triscatteredinterp.html (accessed on 31 July 2013).
- Meshgrid in MathWorks MATLAB online Documentation Center. Available online: http://www.mathworks.fr/fr/help/matlab/ref/meshgrid.html (accessed on 31 July 2013).
- LEGOS HYDROWEB. Available online: http://www.legos.obs-mip.fr/soa/hydrologie/hydroweb/ (accessed on 31 July 2013).


| No. | Profile Filename Reference |
|---|---|
| 1 | GLA06_633_2103_001_1342_4_01_0001 |
| 2 | GLA06_633_2107_002_0085_2_01_0001 |
| 3 | GLA06_633_2107_002_1342_4_01_0001 |
| 4 | GLA06_633_2109_001_1342_4_02_0001 |
| 5 | GLA06_633_2113_001_1342_4_01_0001 |
| 6 | GLA06_633_2115_001_1342_4_01_0001 |
| 7 | GLA06_633_2115_002_0085_2_01_0001 |
| 8 | GLA06_633_2117_001_1342_4_01_0001 |
| 9 | GLA06_633_2121_001_1342_4_01_0001 |
| 10 | GLA06_633_2121_002_0085_2_01_0001 |
| 11 | GLA06_633_2123_001_1342_4_01_0001 |
| 12 | GLA06_633_2125_002_0085_2_01_0001 |
| 13 | GLA06_633_2129_001_1342_4_01_0001 |
| 14 | GLA06_633_2131_001_1342_4_01_0001 |
| Image | Elevation (m) | SD (m) | N-Profiles |
|---|---|---|---|
| L7_2001_07_08 | 3,688.10 | 0.11 | 12 |
| L7_2001_11_13 | 3,687.71 | 0.09 | 10 |
| L7_2002_10_15 | 3,687.21 | 0.04 | 9 |
| L5_1999_05_24 | 3,687.11 | 0.07 | 12 |
| L5_1999_07_11 | 3,687.00 | 0.05 | 11 |
| L7_1999_08_20 | 3,686.89 | 0.07 | 8 |
| L5_1999_09_13(a1) | 3,686.78 | 0.04 | 7 |
| L5_2004_10_12(a2) | 3,686.78 | 0.05 | 6 |
| L5_2000_05_26(b1) | 3,686.54 | 0.04 | 7 |
| L5_2005_07_11(b2) | 3,686.55 | 0.06 | 6 |
| L7_1999_11_24 | 3,686.46 | 0.06 | 6 |
| L5_2000_07_29 | 3,686.37 | 0.02 | 4 |
| L5_2000_08_30 | 3,686.23 | 0.03 | 3 |
| L5_1998_05_05 | 3,686.10 | 0.08 | 3 |
| L5_2000_10_17 | 3,685.88 | 0.05 | 2 |
| L7_2008_10_15 | 3,685.85 | 0.02 | 1 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Arsen, A.; Crétaux, J.-F.; Berge-Nguyen, M.; Del Rio, R.A. Remote Sensing-Derived Bathymetry of Lake Poopó. Remote Sens. 2014, 6, 407-420. https://doi.org/10.3390/rs6010407
Arsen A, Crétaux J-F, Berge-Nguyen M, Del Rio RA. Remote Sensing-Derived Bathymetry of Lake Poopó. Remote Sensing. 2014; 6(1):407-420. https://doi.org/10.3390/rs6010407
Chicago/Turabian StyleArsen, Adalbert, Jean-François Crétaux, Muriel Berge-Nguyen, and Rodrigo Abarca Del Rio. 2014. "Remote Sensing-Derived Bathymetry of Lake Poopó" Remote Sensing 6, no. 1: 407-420. https://doi.org/10.3390/rs6010407




