1. Introduction
Karst depressions cause damage both in rural areas through the loss of arable land and in urban areas due to damage to buildings, roads, and water supply systems [
1,
2]. Problems caused by karst depressions have motivated many studies on their identification and spatial distribution using remote sensing data [
3,
4]. Historical changes and variations in the number and shape of karst depressions can be obtained from comparative studies of multitemporal images [
5,
6].
Remote sensing also allows inferences about subsurface karst structures (endokarst). The regularity of the patterns and surface alignments of karst features often are associated with joint patterns, faulting and folding. Conduits in karst groundwater are formed from rock dissolution along planes or discontinuities where the flow has characteristics similar to the water surface [
7,
8]. Endokarst environments are typically characterized by open conduits with low capacity for storage and rapid groundwater flow. This intimate relationship between surface water and groundwater defines a system of interconnected caves and superficial features. Due to such relationships, the locations of karst aquifers or preferential flowpaths for groundwater have been inferred by the positions of fracture sets or doline alignments apparent on aerial photographs and satellite images [
9–
11]. In addition, remote-sensing data are used as inputs in GIS models for detecting and monitoring areas vulnerable to groundwater pollution in karst terrain [
12,
13].
Digital terrain data are widely used to describe surface features and quantify topographic characteristics [
14–
17] and morphometric attributes derived from Digital Elevation Models (DEMs) have been used for automatic detection of elemental forms associated with landforms [
18–
20]. Several studies employ terrain attributes to characterize and describe karst processes [
21–
23]. In karst-depression detection studies a promising terrain attribute is the sink depth derived from the depression-filling algorithm [
24–
27]. Such algorithms are an integral component of spatially distributed hydrological models that delineate watersheds, drainage networks and overland flowpaths [
28–
32]. Other methods to automate karst depression recognition include convolution or filtering with kernel windows using focal functions [
33] and the “active-contour” method [
34,
35], an algorithm that delineates sinkhole boundaries with a compactness test and by fitting a local bi-quadratic surface to the points surrounding the potential sinkhole locations. However, tests made with ASTER (Advanced Spaceborne Thermal Emission and Reflection Radiometer) and SRTM (Shuttle Radar Topography Mission) [
25,
26] DEM data have shown that these data are not sufficient for karst depression detection, making it necessary to combine the above approach with other methods to automate and improve the process of depression mapping. For example, Guimarães
et al. [
25] combined this approach with digital classification of spectral images and Siart
et al. [
26] used an iron-oxide ratio and the vegetation infrared/red ratio from Quickbird imagery. The increasing availability of high-resolution DEMs and satellite images promises improved detection of karst depressions through the combination of DEM analysis and remote sensing.
The present paper aims to develop a semi-automatic method for doline identification in central Brazil using three different DEMs: (a) the ASTER Global Digital Elevation Model (ASTER-GDEM) Version 1 from the USA’s National Aeronautics and Space Administration (NASA) and Japan’s Ministry of Economy, Trade and Industry (METI); (b) the SRTM Version 4.1 DEM compiled by the Consultative Group on International Agricultural Research Consortium for Spatial Information (CGIAR-CSI); and (c) the DEM made from the high-resolution satellite sensor Advanced Land Observing Satellite/Panchromatic Remote-sensing Instrument for Stereo Mapping (ALOS/PRISM).
The approach combines a threshold sink depth and morphometric analysis in order to refine the identification of karst depressions. Here, our focus is limited to automated DEM-based classification and we do not address the strong potential for improved identification of dolines by combining DEM analysis with image classification [
22,
23]. We compare performance among sensors to evaluate the efficiency of each data type for use in automated sinkhole mapping and use traditional geomorphological methods of field surveys and visual image interpretation to assess the advantages and limitations of the automated technique.
2. Study Area
Brazil has 425,000–600,000 km
2 of limestone rocks in different biomes [
35] and knowledge of karst areas has been reinforced by speleological studies and investigations of biological, paleoenvironmental, paleontological, and archaeological attributes. Karmann & Sánchez’s [
36] classified speleological provinces in Brazil based on common geological history, stratigraphic associations with carbonate and pelitic sequences, and thickness and extension of carbonate rocks.
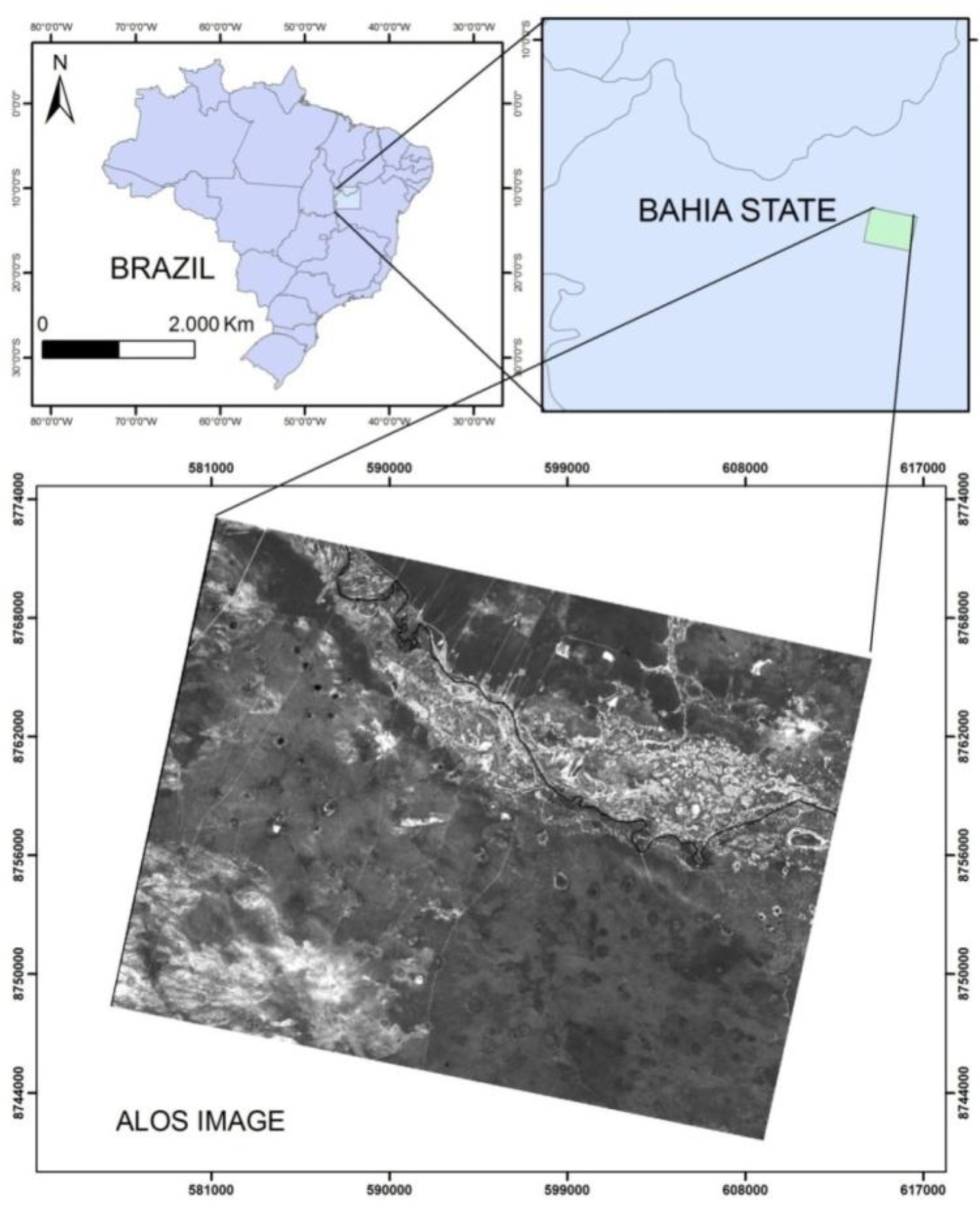
We analyzed a small area of the Bambuí Speleological Province in Central Brazil. This province is underlain by rocks of the Bambuí Group [
37], a Neoproterozoic sedimentary sequence that records at least two transgressive-regressive cycles in the epicontinental basin and possibly deposition in a foreland basin along the west side of the São Francisco Craton during the Brasiliano orogeny [
38–
41]. The study area is located in Bahia State, northeastern Brazil (
Figure 1) where the tropical environment favors karst formation due to the growth of vegetation and biochemical activity increasing water acidity and promoting the development of vertical flow and sinkhole (doline) development. The study area has a high density of dolines associated with the exposure of karstified limestone. The stagnant surface water and shallow groundwater mostly reside in the sinks, forming lakes. Herbaceous vegetation dominates in topographic depressions because trees have low tolerance to shallow groundwater. Thus, dolines commonly are floored by open water or herbaceous vegetation (
Figure 2). The vegetation cover in the study area therefore has little potential influence on the results from different sensor types, unlike other areas with forest.
3. Material and Methods
We compared three different DEMs—ASTER-GDEM, ALOS/PRISM-DEM and SRTM-DEM—all processed in four steps, the first of which was DEM acquisition and evaluation of the best DEM for our purposes. We next identified closed depressions or sinks in the DEMs and digitally “filled” them by interpolation from neighboring elevations outside the depression polygons. We calculated sink depths as the difference between the original and processed DEMs. The final step was the elimination of false detections using morphometric attributes and visual interpretation overlaying the depression vectors on the high-resolution remotely sensed image.
3.1. Digital Elevation Model
We analyzed the potential of DEMs for mapping closed depressions using data from different sensors with various data-acquisition methods and spatial resolution: ASTER-GDEM (30 m), ALOS/PRISM-DEM (5 m) and SRTM-DEM (90 m).
The ASTER-GDEM was generated using ASTER Level-1A bands 3N (nadir-viewing) and 3B (backward-viewing) images from the Visible/Near-Infrared (VNIR) sensor. The VNIR subsystem consists of nadir- and rear-viewing telescopes looking 0° and 27.7° backwards that allow the generation of stereoscopic data with a time lag around one minute [
42]. The Band-3 stereo pair is acquired in the spectral range of 0.78–0.86 μm with a base-to-height ratio of 0.6. In 2006, LP DAAC implemented software based on an automated stereo-correlation method that utilizes the ephemeris and attitude data derived from both the ASTER instrument and the Terra spacecraft platform. This method generates a relative DEM without any ground control points (GCPs). The ASTER-GDEM is an image product with a horizontal resolution of 1 arc-second (30 m) referenced to the UTM coordinate system, and referenced to Earth’s geoid using the EGM96 geopotential model. This product is generated from a stereo-pair of images using the SilcAST software and covers the earth’s surface between 83°N and 83°S, encompassing 99 percent of Earth’s landmass.
The SRTM flown on Space Shuttle Endeavour in February 2,000 carried in the cargo bay two synthetic aperture radars, a C-band system (5.6 cm; C-RADAR) and an X-band system (3.1 cm; X-RADAR) [
43]. Radar data are less sensitive to cloud cover than optical data. Topographic data were acquired from a single flight covering 80% of Earth's land surface in just 11 days, between the latitudes 60°N and 57°S. The flyover produced three-dimensional models with spatial resolutions of 1 arc sec (30 m) and 3 arc sec (90 m) using WGS84 horizontal datum and vertical datum WGS84/EGM96. Vertical accuracy was on the order of 5 m [
44]. The continuous data acquisition (
i.e., day and night regardless of clouds, which are transparent to the RADAR) ensured homogeneous data throughout the globe, making the SRTM-DEM an important tool for studies of the land surface [
44–
46]. SRTM-DEM data have been widely used for geomorphological studies [
47,
48].
The ALOS was launched on 24 January 2006 by the Japan Aerospace Exploration Agency (JAXA) with PRISM on board, which acquires images with spatial resolution of 2.5 m. PRISM produces triplet images that achieve along-track stereoscopy by three independent cameras for viewing nadir, forward and backward where the images are acquired in the same orbit at almost the same time [
41,
49]. The nadir-looking radiometer can provide coverage 70 km wide, and the forward-looking and backward-looking radiometers each provide coverage 35 km wide [
50]. Several studies assess the absolute vertical accuracy (relationship between DEM elevation and true elevation relative to an established vertical datum) of the ALOS/PRISM-DEM. Gruen
et al. [
51] compared the DEM accuracy of ALOS/PRISM data with other satellite or ground control points and found that its accuracy is similar to that obtained by SPOT 5, IKONOS and QuickBird data. Kocaman and Gruen [
52] also found similar results for IKONOS, but reported a lower accuracy compared to SPOT-5 results. Maruya and Ohyama [
49] used ground control points derived from the 1:25,000 mapping to analyze elevation accuracy and found a 6.2 m mean error and a 4.8 m RMSE. Saunier
et al. [
53] verified that the accuracy in height for the ALOS/PRISM-DEM is about 1 m using either five or nine ground control points. In Brazil ALOS/PRISM-DEM was tested in an area with steep slopes and comparison of the results to ground control points (GCP), indicated an accuracy comparable to 1:25,000 scale mapping [
54]. Although the studies described above address the absolute vertical accuracy, for this study the relative vertical accuracy is most important and is obtained from a vertical difference between two points,
i.e., a measure of the point-to-point vertical accuracy within a specific dataset. The absolute vertical error is greater than the relative vertical error, establishing an upper limit for empirical evaluation of relative vertical accuracy.
The stereo DEM extraction from ALOS/PRISM data was done using the commercial software, PCI Geomatica orthoengine. Artifacts in the data were assessed by visual inspection and specific algorithms [
55,
56] that reveal errors on the image border and in areas with cloud cover. Image-border errors were eliminated from the image during resizing by simply removing the noisy strip. The cloud cover is a limitation of this type of data and anomalous values are easily identified by digital processing from a threshold value and thus can be identified and discarded. The scenes used in this study have few and isolated clouds.
3.2. Sink-Depth Image
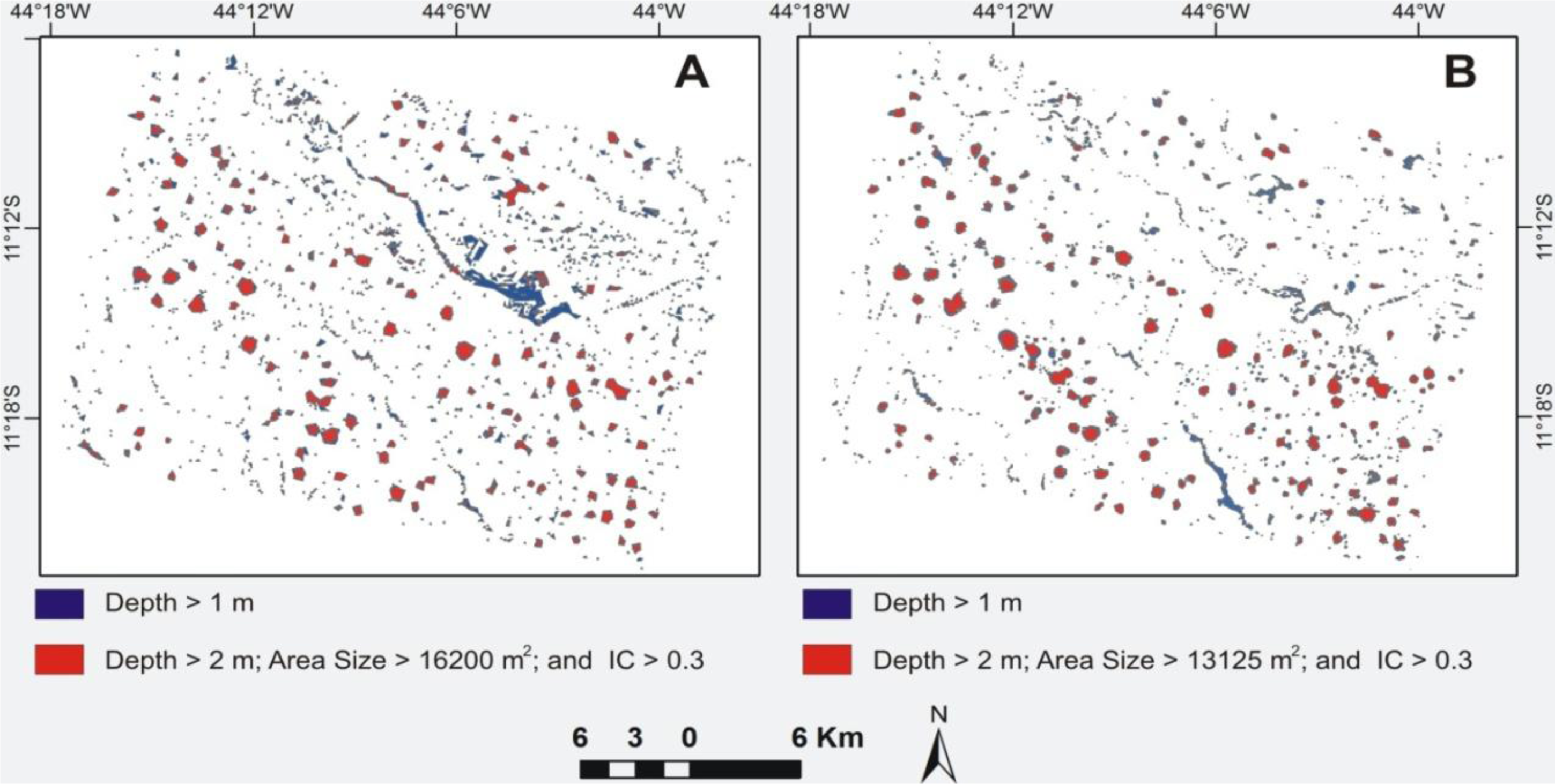
The methodology we used to determine the “sink depth” of closed depressions involved two DEM operations. The first step used the “Fillsink” algorithm from the ArcMap software package [
25] that identifies the point or set of adjacent points surrounded by neighbors with higher elevation and rises to the lowest value on the depressions boundary. This procedure then fills all depressions in the DEM, including both those generated from data errors (spurious artifacts) and those that record real topographic features, such as karst depressions (dolines). The second step was to extract the sink depths in these areas by differencing the maps between the sink-filled (“depressionless” DEM) and original DEM (
Figure 3).
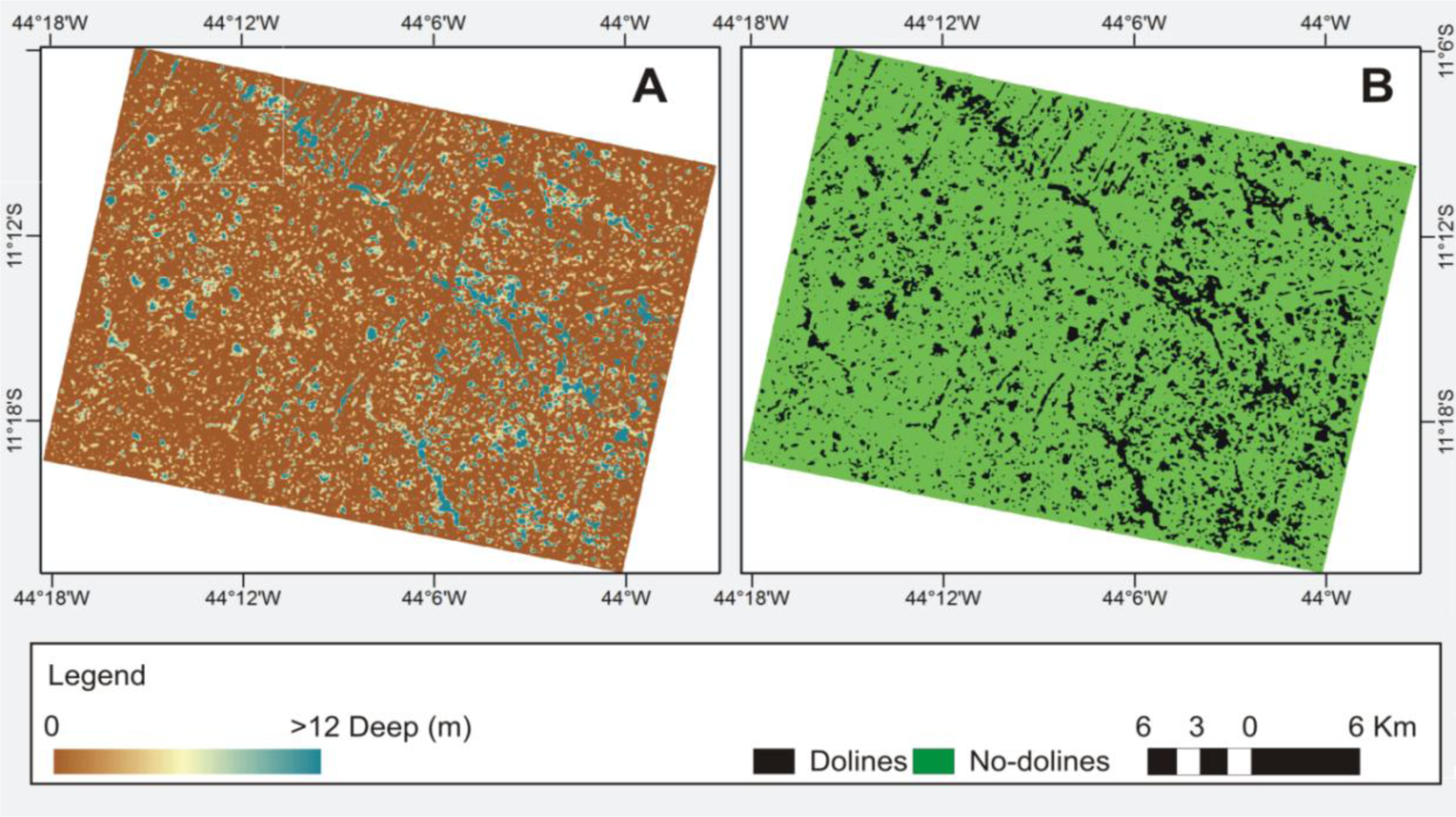
The difference image (
Figure 3C) highlights the different depressions, including the karst enclosed depressions. A binary image is generated from the sink depth image where the depressed areas have value 1, while all other areas have value 0. This binary image is then converted to vector format. The minimum area of depressions corresponds to the spatial resolution of the sensor. However, the polygons show both natural features as well as pits from surface imperfections. Thus, the vectors need to be checked in order to eliminate the errors.
Thus, the key issue is to establish criteria to separate the dolines from the spurious artifacts and other types of depression (e.g., reservoirs or quarries). In this paper, the delimitation of the spurious depressions is derived from threshold values of morphometric attributes, specifically depth, size, and shape.
Evaluation of appropriate threshold values to represent the boundary between dolines and the surrounding landscape (“no-dolines”) was obtained by comparing maps of identified dolines with previous mapping of dolines from field validation and interpretation of higher-spatial-resolution imagery (ALOS-PRISM and Google Earth images). The karst features investigated in the study area are easily identified by visual interpretation, as they are characterized by natural moist grassy vegetation where the water table approaches the surface for part of the year, leading to a striking difference in visual appearance from the surrounding vegetation.
We used a range of different empirical threshold values for the minimum sink depth to identify the best threshold value from the maximum accuracy index between manual and automated classification. In assessing classification and change-detection techniques using remotely sensed images, the threshold values for the delimitation of classes are commonly identified from overall accuracy and a Kappa index [
57–
59]. In this paper we applied the overall accuracy (OA). Performance in identifying true sinkholes is assessed through the intersection of reference and classified polygons. Usually, the polygons obtained by the two methods show distinctions in the dimensions and shapes; but conventional accuracy analysis typically considers only the number of the overlapping polygons. Overall accuracy is calculated by summing the number of polygons classified correctly (True Positive–TP) and dividing by the total number of polygons:
where the number of polygons misclassified is determined by summing the number of False Negatives (FN) (
i.e., no doline identified where one is actually present) and False Positives (FP) (
i.e., doline indicated where none exists). This accuracy analysis does not directly assess true negative.
Inevitably, using the proposed method a mapped doline will be represented by more than one polygon. Redundant data (R) must be considered in computing the accuracy index in order to avoid the overestimation. We used the following equation:
Therefore comparison between doline classifications with previous maps allows the determination of threshold values for delimiting karst depressions in similar regions and reveals the uncertainties of the method.
3.3. Morphometric Analysis
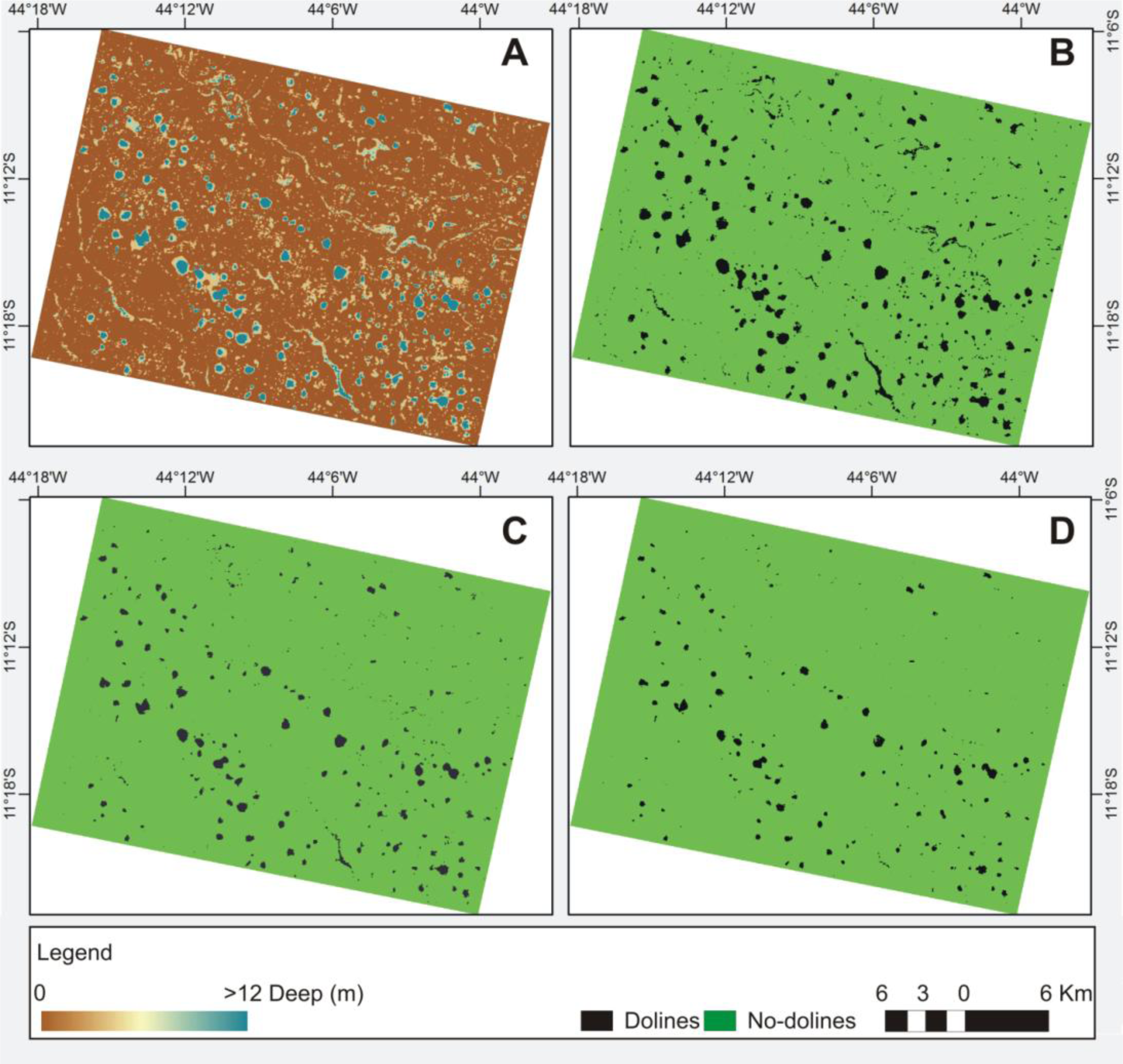
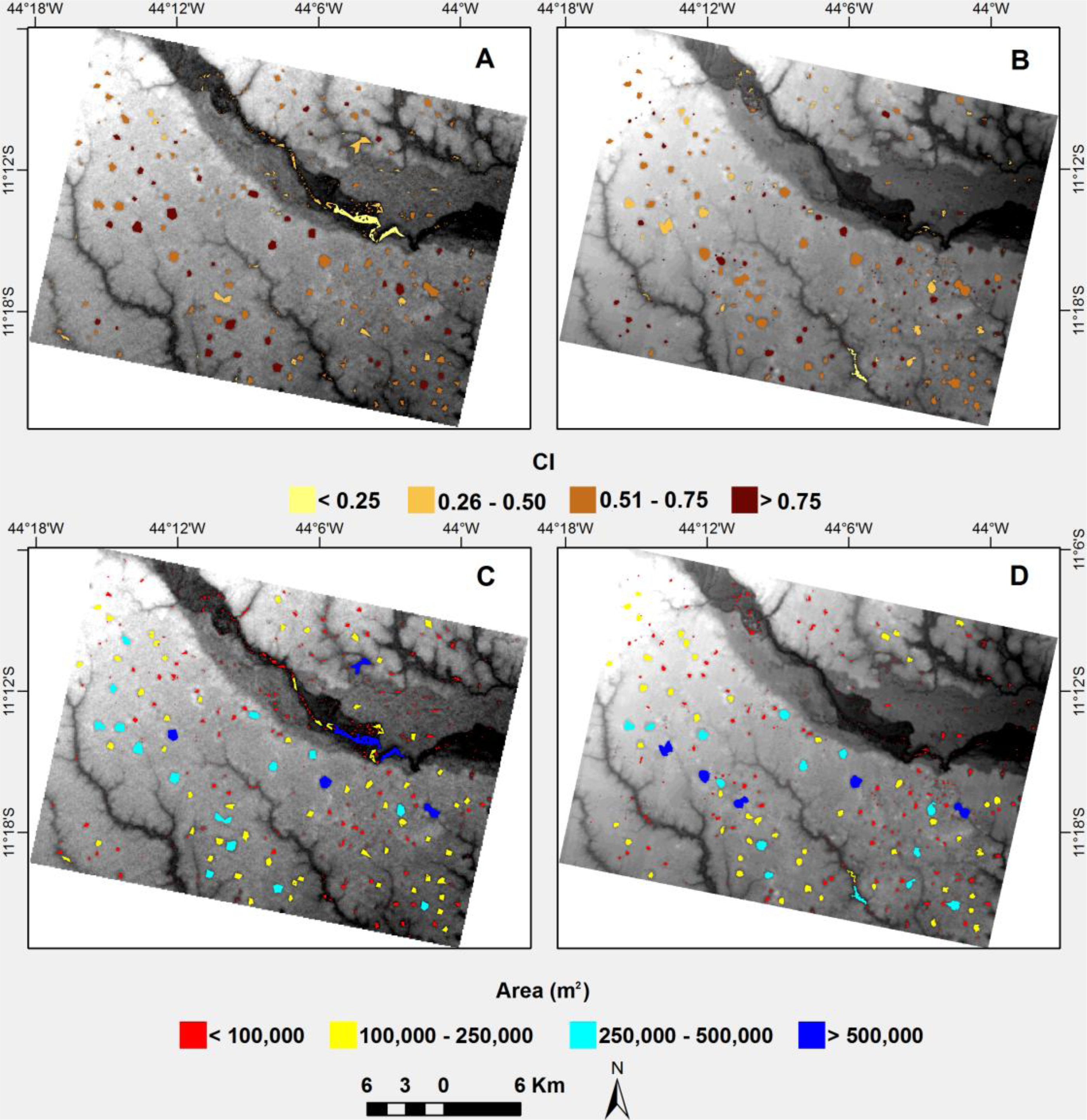
Morphometric analysis may be used to improve the accuracy of predicting doline occurrence and eliminate false dolines. Many of the false dolines can be easily eliminated as being incompatible with known characteristics of karst depressions in the study area (
Figure 4). We used the following morphometric attributes to automate delineation of doline polygons: area, perimeter and circularity index (CI). The area and perimeter of the polygons are automatically added to topological vector data structure. We defined a CI based on area and perimeter values using the following equation:
where A is the area of a polygon and P is its perimeter. A circular shape is represented by value of 1.0,
i.e., the maximum value. In contrast, elongated shapes are represented by lower values. The more circular polygons indicate locations of karstic negative relief elements. In addition to the CI values, average and maximum depth were extracted from the DEM for each polygon.
Visual inspection revealed that erroneous polygons generally had a small area, low circularity and were shallow, suggesting that undesirable polygons can be eliminated using threshold value criteria for these morphometric attributes. We superimposed vectors on Google Earth images to identify polygons that represent correctly karst depressions and thereby evaluate the range of morphometric values suitable for use as threshold criteria.
The dolines obtained by morphometric attributes were compared with a reference map using traditional geomorphological procedures such as field surveys and visual interpretation of high-resolution remote sensing image from ALOS/PRISM and Google Earth. In this comparison are evaluated quantities of correct predictions (TP), Type I errors (FP) and Type II errors (FN).
3.4. Enlargement of Doline Polygons
A greater average depth threshold decreases the number of false dolines. However these deeper thresholds do not give the real plan-view area of the dolines. In order to correct for this error, a new mask with a threshold value > 0 m was built and applied to the true dolines previously selected, eliminating the noisy polygons. In doing this, the polygons generated from the depth data are replaced by polygons generated using the shallow depth threshold. This procedure allows having a real area of the doline to be compared with the areas calculated in visual interpretation. However the exact polygon representation is inherently imprecise because the landform itself is hard to define precisely,
i.e., the closer you look, the less well-defined the edge becomes.
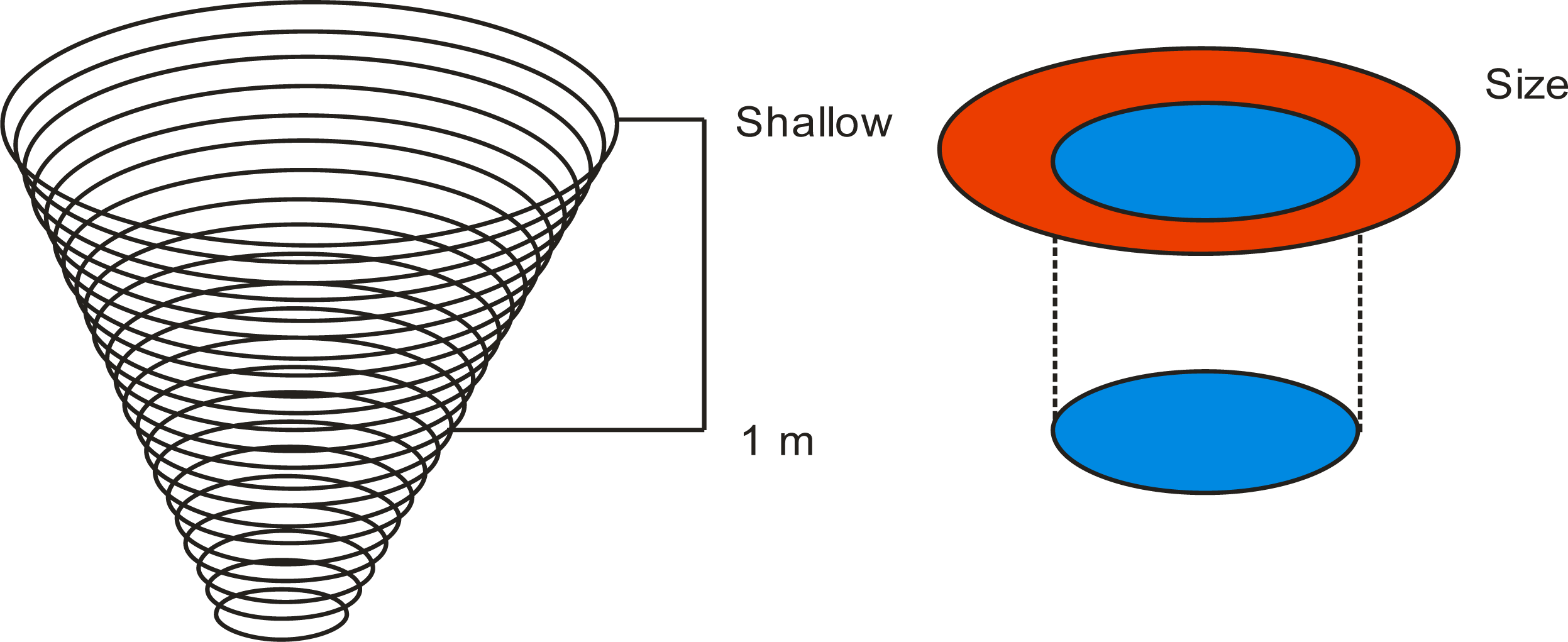
Figure 4 illustrates the hypothetical area of an idealized doline using different thresholds, and how the area decreases with doline depth.
5. Conclusions
Semi-automated landform classification using DEMs provides several advantages: fast acquisition of data over large areas at low cost, analysis of inaccessible zones, reduction of human errors by eliminating manual classification steps, ready comparison of results derived from different datasets, and the reduction in processing time. Our methodology for mapping karst depressions combines morphometric analysis with a minimum threshold value for the sink depth to identify karst depressions. However, some depressions selected by sink depth are actually data errors introduced in generating the surface and should be interpreted with prudence. We suggest a method for the separation of real from incorrectly identified topographic features. The identification of the optimal threshold values for assessing morphometric attributes was made from the highest overall accuracy, considering a reference map built from visual interpretation. These threshold values are limited to areas with similar environmental conditions. Thus studies in new locations must first define the best thresholds using a test area.
In this work, the ASTER-GDEM had severe limitations in the detection of karst features. However, this is not a general criticism of the ASTER-GDEM, which may perform better in other areas or other problems. The GDEM data generation process consists of scene selection, scene division, same-path mosaic generation, stacking, sticking, and filtering for both elevation data and water-body data [
63]. Despite this processing some images may contain imperfections, which are being fixed in another version of the ASTER-GDEM product. Therefore, the doline detection considering other areas or new products may get better results.
SRTM-DEM and ALOS/PRISM-DEM identify more than half of the true dolines with an overall accuracy of approximately 0.5. The ALOS/PRISM-DEM has potentially serious limitations in the presence of clouds, whereas the SRTM-DEM is insensitive to cloud cover. However, the coarser resolution of the SRTM-DEM limits its utility in delineating fine-scale karst features. Practically all the larger sinkholes detected by ALOS were also identified by the SRTM. Therefore SRTM and ALOS data are reasonably well suited for use in large-scale mapping of karst features in Central Brazil.
The algorithm results could be improved by considering three distinct aspects: (a) the addition of other DEM attributes or polygon geometry; (b) the use of DEM with higher spatial resolution (e.g., airborne laser scanning); and (c) the application of other complementary data to the DEM, such as multi-spectral images.
In detecting sinkholes other morphometric information can be used, providing an additional component for spatial analysis. Siart et al. [
26] used the following DEM attributes to assist doline detection: slope, aspect and curvature. However the results were difficult to interpret, due to the visual complexity of the image, and did not contribute significantly to doline detection. With respect to the polygon geometry the eccentricity of an ellipse remains to be tested [
64], although for the present study area this should help little, because the dolines are circular. Thus, tests with other morphometric attributes may provide a little improvement in accuracy of the algorithm in the general application. The main improvements probably lie in the other two mentioned alternatives.
The use of images with higher spatial resolution undoubtedly enables better detection of sinkholes. A particularly promising area for future study is the acquisition of the morphometric attributes from LiDAR (Light Detecting and Ranging) data, which has impressive accuracy for detecting sinkholes and estimating subsidence rates [
65–
68]. Another major advantage of utilizing laser scanning technology is its canopy penetration ability. However, many areas do not have this type of data.
Although beyond the scope of this paper, the use of classification of multi-spectral images can significantly increase the detection accuracy of dolines. Remote-sensing data, whether airborne or satellite-based, offer an alternative way for the doline detection considering karst-dependent features (e.g., sedimentary infills and vegetation). Thus the depressions can locally modify environmental variables: soil moisture, water stagnation, soil erosion and sedimentation, and spatial distributions of the vegetation with relative presence of dominant species. In this approach, some works [
25,
26] demonstrates that the combination of DEMs and high-resolution satellite imagery produce the best results in karst geomorphological research.