A New Approach for the Analysis of Hyperspectral Data: Theory and Sensitivity Analysis of the Moment Distance Method
Abstract
:1. Introduction
2. Materials and Methods
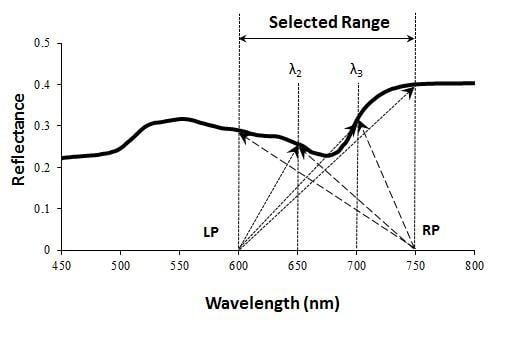
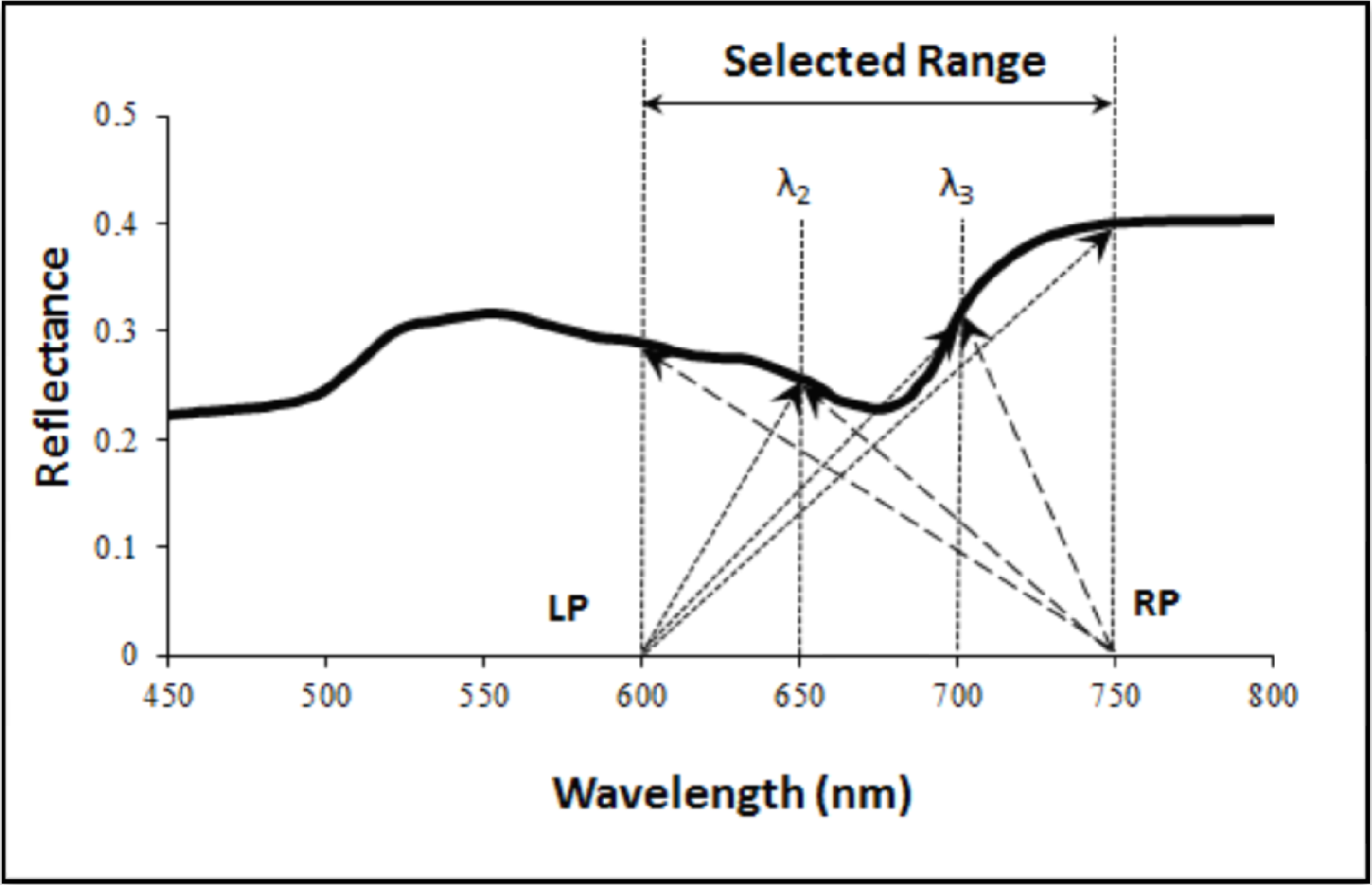
2.1. MD Applied to the Visible and NIR Range for Vegetation Research
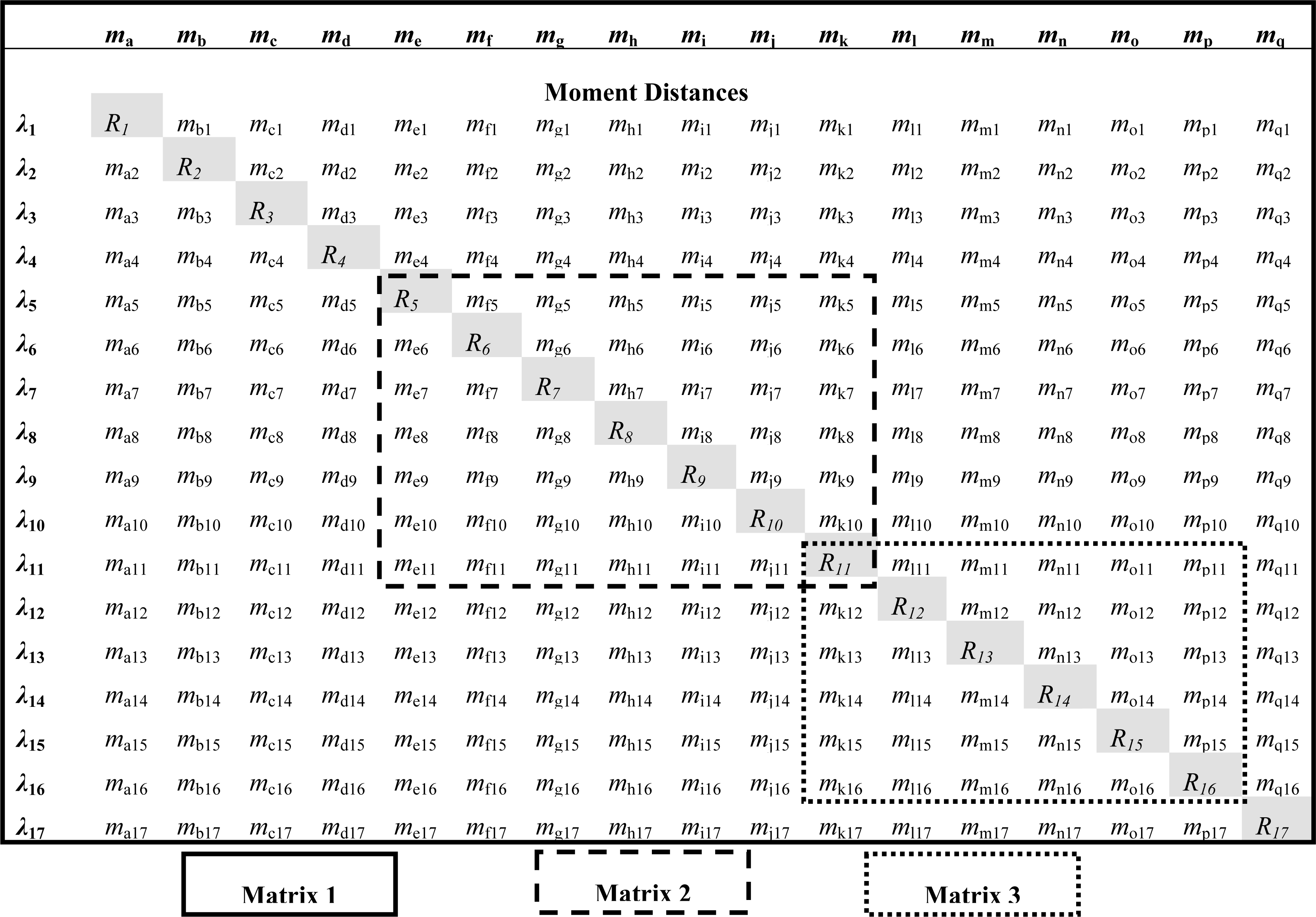
2.2. Definition and Formulation of the Moment Distance (MD)
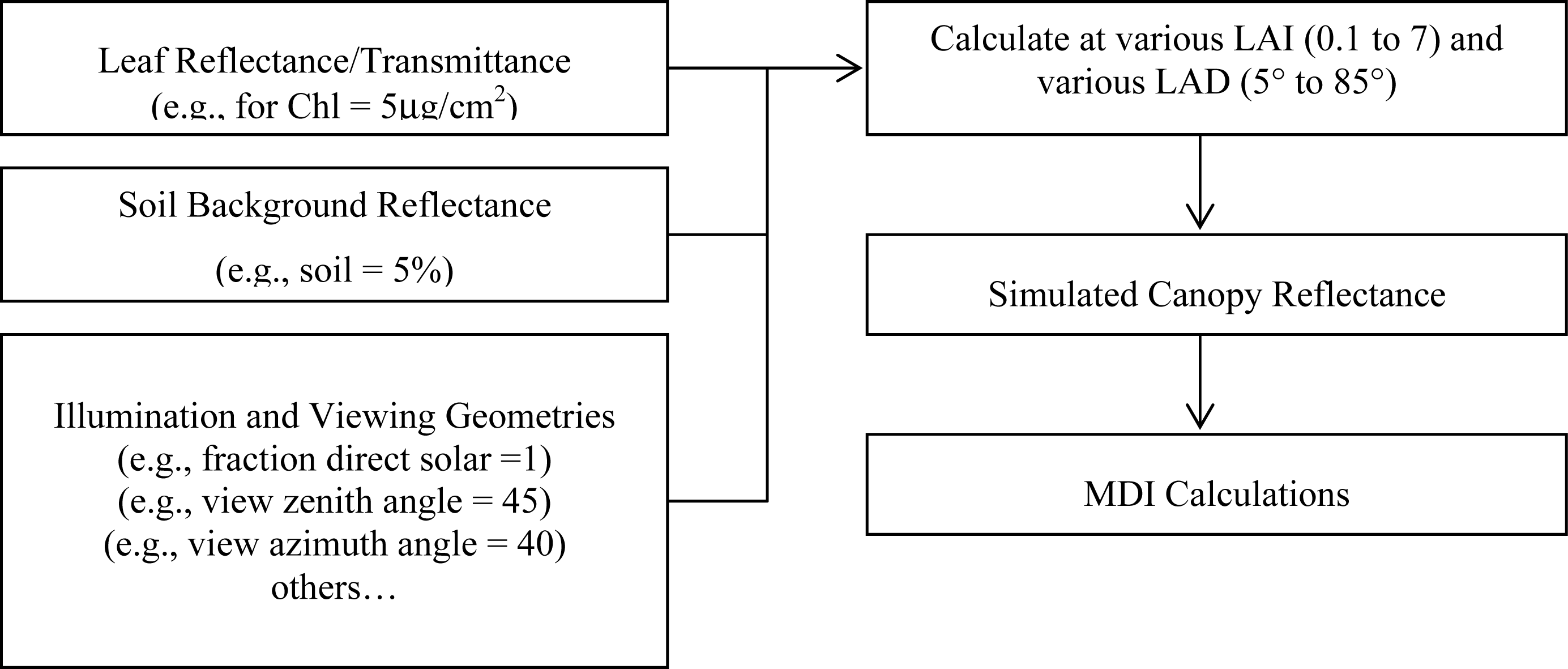
2.3. PROSPECT and SAIL Models
3. Results
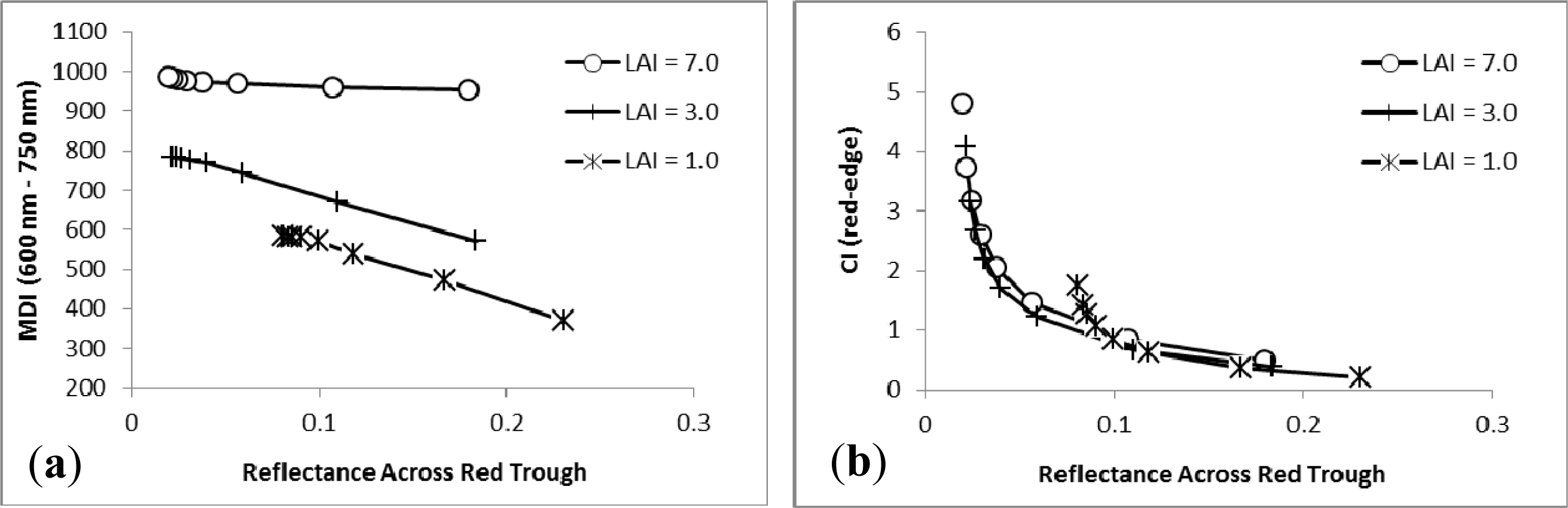
3.1. MDI on Simulated PROSECT/SAIL Reflectance Curves
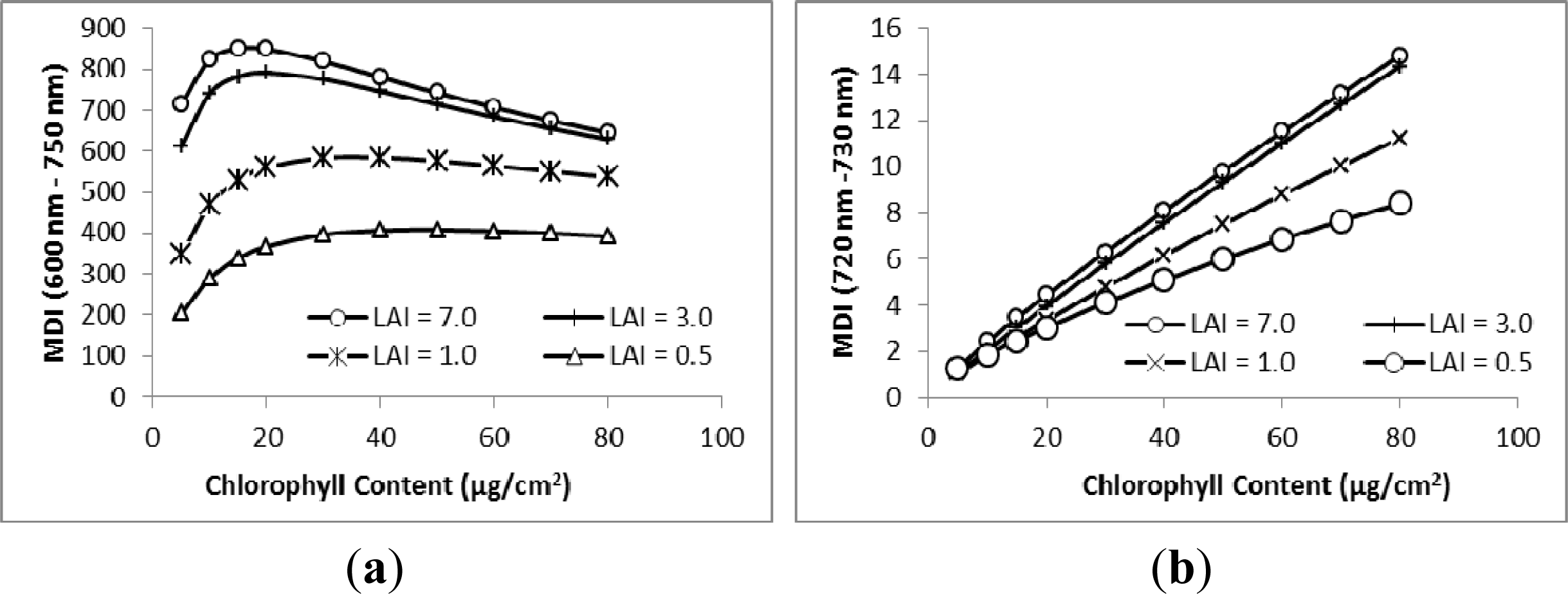
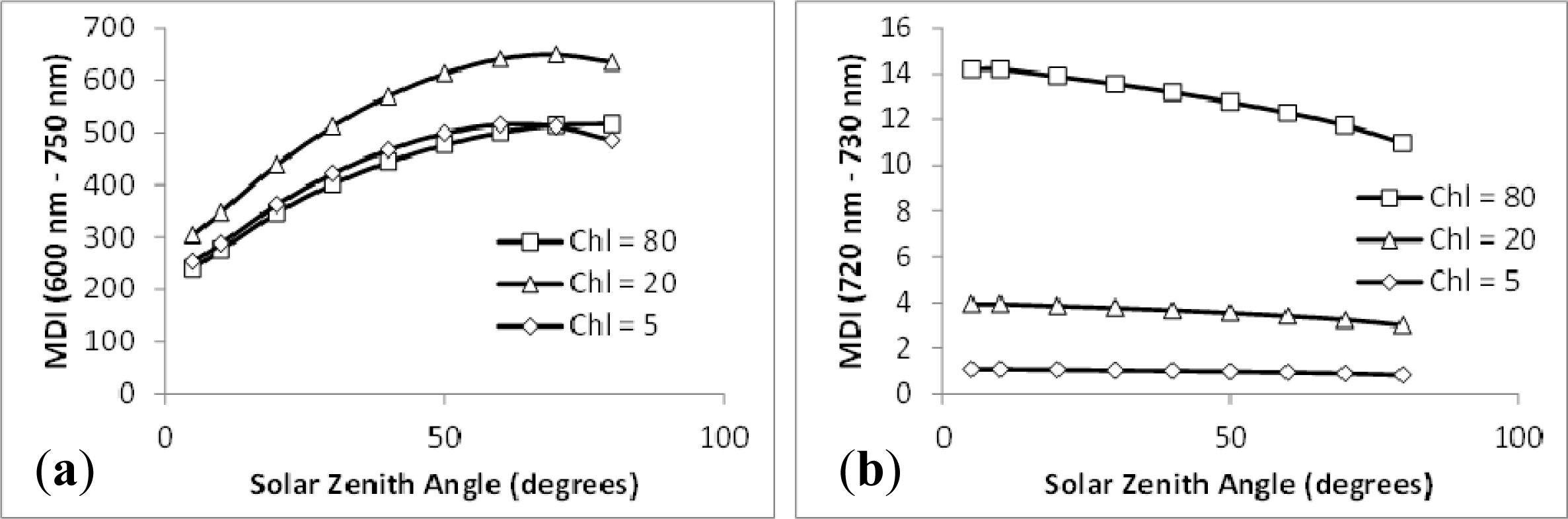
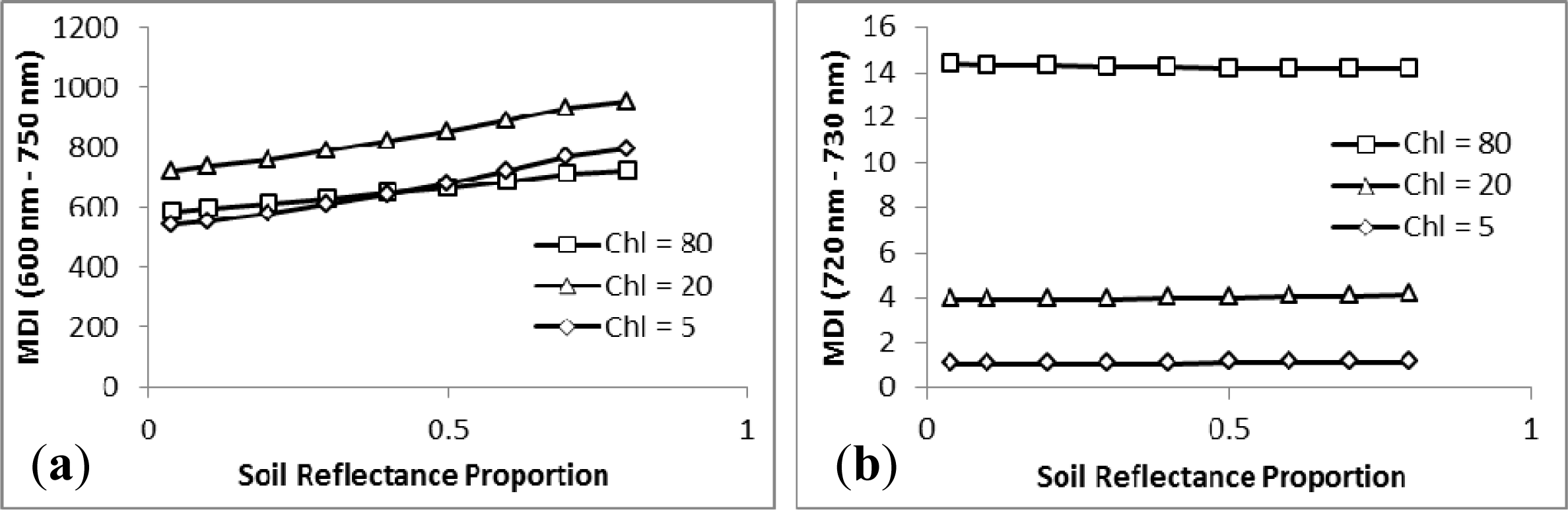
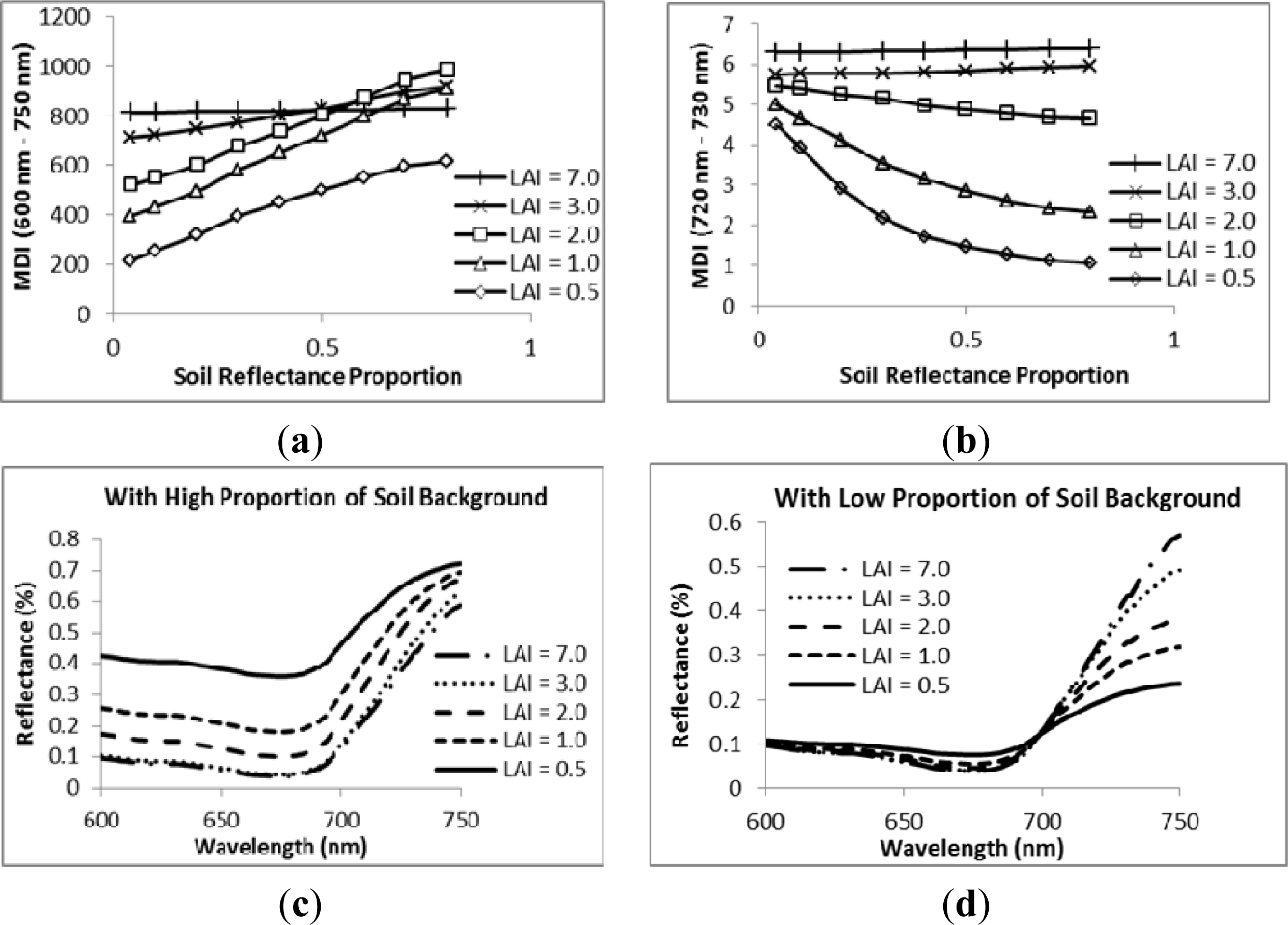
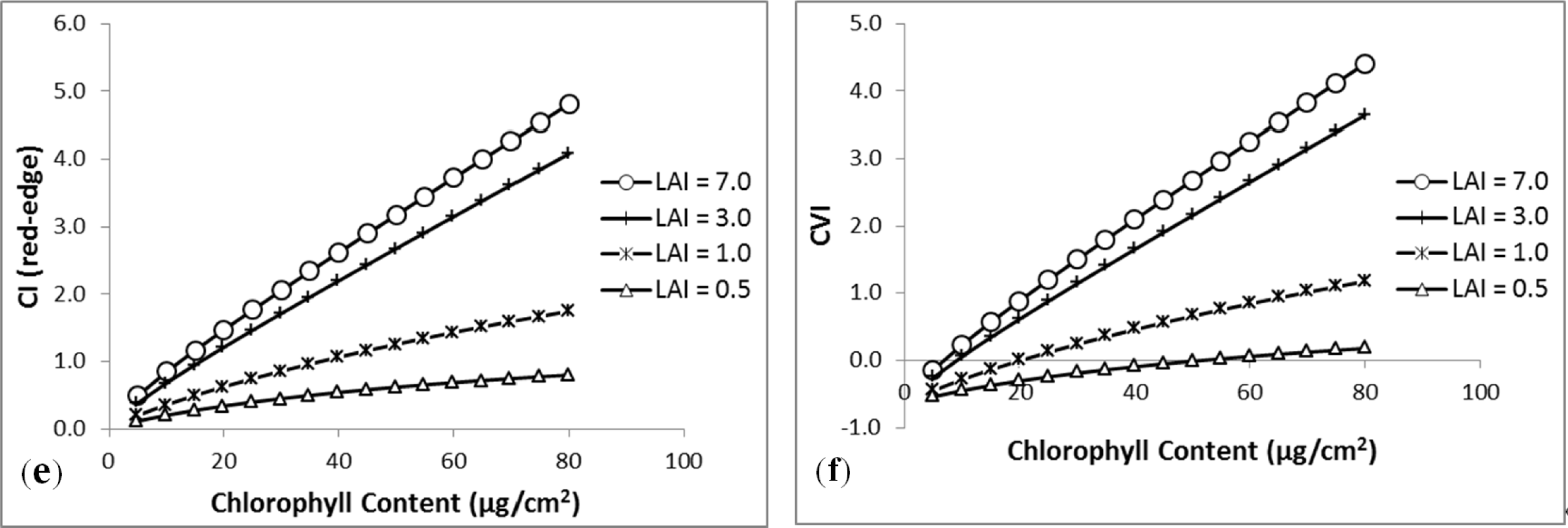
3.2. Sensitivity Analysis
4. Discussion
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Chen, J.M.; Cihlar, J. Retrieving leaf area index of boreal conifer forests using Landsat TM images. Remote Sens. Environ 1996, 55, 153–162. [Google Scholar]
- Gitelson, A.A.; Merzlyak, M.N. Quantitative estimation of chlorophyll-a using reflectance spectra: Experiments with autumn chestnut and maple leaves. J. Photochem. Photobiol. B: Biol 1994, 22, 247–252. [Google Scholar]
- Skianis, G.; Vaiopoulos, D.; Nikolakopoulos, K. A Comparative Study of the Performance of the NDVI, the TVI and the SAVI Vegetation Indices over Burnt Areas, Using Probability Theory and Spatial Analysis Techniques. Proceedings of the 6th International Workshop of the EARSeL Special Interest Group on Forest Fires, Thessaloniki, Greece, 27–29 September 2007.
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ 1979, 8, 127–150. [Google Scholar]
- Clevers, J.G.P.W. Application of a vegetation index in correcting the infrared reflectance for soil background. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 1988, 16, 221–226. [Google Scholar]
- Gitelson, A.A. Wide Dynamic range vegetation index for remote quantification of biophysical characteristics of vegetation. J. Plant Physiol 2004, 161, 165–173. [Google Scholar]
- Steele, M.R.; Gitelson, A.A.; Rundquist, D.C. Nondestructive estimation of anthocyanin content in Grapevine leaves. Am. J. Enol. Vitic 2009, 60, 87–92. [Google Scholar]
- Salas, E.A.L.; Henebry, G.M. Area between peaks feature in the derivative reflectance curve as a sensitive indicator of change in chlorophyll concentration. GISci. Remote Sens 2009, 46, 315–328. [Google Scholar]
- Broge, N.H.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ 2001, 76, 156–172. [Google Scholar]
- Okin, G.S. The contribution of brown vegetation to vegetation dynamics. Ecology 2010, 91, 743–755. [Google Scholar]
- Pettorelli, N.; Vik, J.O.; Mysterud, A.; Gaillard, J.-M.; Tucker, C.J.; Stenseth, N.C. Using the satellite-derived NDVI to assess ecological responses to environmental change. Trends Ecol. Evol 2005, 20, 503–510. [Google Scholar]
- Townshend, J.R.G.; Justice, C.O. Analysis of the dynamics of African vegetation using the normalized difference vegetation index. Int. J. Remote Sens 1986, 7, 1435–1445. [Google Scholar]
- Viña, A.; Henebry, G.M.; Gitelson, A.A. Satellite monitoring of vegetation dynamics: Sensitivity enhancement by the Wide Dynamic Range Vegetation Index. Geophys. Res. Lett 2004. [Google Scholar] [CrossRef]
- Hurcom, S.J.; Harrison, A.R. The NDVI and spectral decomposition for semi-arid vegetation abundance estimation. Int. J. Remote Sens 1998, 19, 3109–3125. [Google Scholar]
- Simms, E.L.; Ward, H. Multisensor NDVI-based monitoring of the Tundra-Taiga interface (Mealy Mountains, Labrador, Canada). Remote Sens 2013, 5, 1066–1090. [Google Scholar]
- Rouse, J.W., Jr.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring Vegetation System in the Great Plains with ERTS. Proceedings of the Third Earth Resources Technology Satellite-1 Symposium, Greenbelt, MD, USA, 10–14 December 1974; pp. 309–317.
- Haboudane, D.; Miller, J.R.; Pattey, E.; Zarco-Tejada, P.J.; Strachan, I.B. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ 2004, 90, 337–352. [Google Scholar]
- Myneni, R.B.; Hall, F.G.; Sellers, P.J.; Marshak, A.L. The interpretation of spectral vegetation indexes. IEEE Trans. Geosci. Remote Sens 1995, 33, 481–486. [Google Scholar]
- Zhao, X.; Tan, K.; Zhao, S.; Fang, J. Changing climate affects vegetation growth in the arid region of the northwestern China. J. Arid Environ 2011, 75, 946–952. [Google Scholar]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ 1996, 55, 95–107. [Google Scholar]
- Elvidge, C.D.; Chen, Z. Comparison of broad-band and narrow-band red and near-infrared vegetation indices. Remote Sens. Environ 1995, 54, 38–48. [Google Scholar]
- Jordan, C.F. Derivation of leaf area index from quality of light on the forest floor. Ecology 1969, 50, 663–666. [Google Scholar]
- Pearson, R.L.; Miller, L.D. Remote Mapping of Standing Crop Biomass for Estimation of the Productivity of the Short-Grass Prairie. Proceedings of the Eighth International Symposium on Remote Sensing of Environment, Pawnee National Grasslands, Colorado, Ann Arbor, MI, USA, 2–6 October 1972; pp. 357–1381.
- Baret, F.; Guyot, G. Potentials and limits of vegetation indices for LAI and APAR assessment. Remote Sens. Environ 1991, 35, 161–173. [Google Scholar]
- Gitelson, A.A.; Viña, A.; Arkebauer, T.J.; Rundquist, D.C.; Keydan, G.; Leavitt, B. Remote estimation of leaf area index and green leaf biomass in maize canopies. Geophys. Res. Lett 2003. [Google Scholar] [CrossRef]
- Brantley, S.T.; Zinnert, J.C.; Young, D.R. Application of hyperspectral vegetation indices to detect variations in high leaf area index temperate shrub thicket canopies. Remote Sens. Environ 2011, 115, 514–523. [Google Scholar]
- Viña, A. Evaluating vegetation indices for assessing productivity along a tropical rain forest chronosequence in Western Amazonia. Isr. J. Plant Sci 2012, 60, 123–133. [Google Scholar]
- Viña, A.; Gitelson, A.A. New developments in the remote estimation of the fraction of absorbed photosynthetically active radiation in crops. Geophys. Res. Lett 2005. [Google Scholar] [CrossRef]
- Aguilar-Amuchastegui, N.; Henebry, G.M. Characterizing tropical forest spatio-temporal heterogeneity using the Wide Dynamic Range Vegetation Index (WDRVI). Int. J. Remote Sens 2008, 29, 7285–7291. [Google Scholar]
- Aguilar-Amuchastegui, N.; Henebry, G.M. Monitoring sustainability in tropical forests: How changes in canopy spatial pattern can indicate forest stands for biodiversity surveys. IEEE Geosci. Remote Sens. Lett 2006, 3, 329–333. [Google Scholar]
- Gitelson, A.A. Remote estimation of crop fractional vegetation cover: The use of noise equivalent as an indicator of performance of vegetation indices. Int. J. Remote Sens 2013, 34, 6054–6066. [Google Scholar]
- Deering, D.W.; Rouse, J.W.; Haas, R.H.; Schell, J.A. Measuring Forage Production of Grazing Units from Landsat MSS Data. Processings of the 10th International Symposium on Remote Sensing of Environment, Ann Arbor, MI, USA, October 1975; pp. 1169–1178.
- Gilabert, M.A.; González-Piqueras, J.; Garcýìa-Haro, F.J.; Meliá, J. A generalized soil-adjusted vegetation index. Remote Sens. Environ 2002, 82, 303–310. [Google Scholar]
- Baret, F.; Jacquemoud, S.; Hanocq, J.F. About the soil line concept in remote sensing. Adv. Sp. Res 1993, 13, 281–284. [Google Scholar]
- Richardson, A.J.; Wiegand, C.L. Distinguishing vegetation from soil background information. Photogramm. Eng. Remote Sens 1977, 43, 1541–1552. [Google Scholar]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A modified soil adjusted vegetation index. Remote Sens. Environ 1994, 48, 119–126. [Google Scholar]
- Perry, J.C.R.; Lautenschlager, L.F. Functional equivalence of spectral vegetation indices. Remote Sens. Environ 1984, 14, 169–182. [Google Scholar]
- Kauth, R.J.; Thomas, G.S. The Tasseled Cap—A Graphic Description of the Spectral-Temporal Development of Agricultural Crops as Seen in Landsat. Proceedings of the Symposium on Machine Processing of Remotely Sensed Data, West Lafayette, IN, USA, 29 June–1 July 1976; pp. 41–51.
- Crist, E.P.; Cicone, R.C. A physically-based transformation of thematic mapper data: The TM Tassed Cap. IEEE. Trans. Geosci. Remote Sens 1984, 22, 256–263. [Google Scholar]
- Gitelson, A.A.; Stark, R.; Grits, U.; Rundquist, D.; Kaufman, Y.; Derry, D. Vegetation and soil lines in visible spectral space: A concept and technique for remote estimation of vegetation fraction. Int. J. Remote Sens 2002, 23, 2537–2562. [Google Scholar]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ 1988, 25, 295–309. [Google Scholar]
- Baret, F.; Guyot, G.; Major, D.J. TSAVI: A Vegetation Index which Minimizes Soil Brightness Effects on LAI and APAR Estimation. Proceedings of the 12th Canadian Symposium on Remote Sensing, Vancouver, BC, Canada, 10–14 July 1989; pp. 1355–1358.
- Major, D.J.; Baret, F.; Guyot, G. A ratio vegetation index adjusted for soil brightness. Int. J. Remote Sens 1990, 11, 727–740. [Google Scholar]
- Bannari, A.; Huete, A.R.; Morin, D.; Zagolski, F. Effects of soil colour and brightness on vegetation index. Int. J. Remote Sens 1996, 17, 1885–1906. [Google Scholar]
- Liu, H.Q.; Huete, A.R. A feedback based modification of the NDVI to minimize canopy background and atmospheric noise. IEEE Trans. Geosci. Remote Sens 1995, 33, 457–465. [Google Scholar]
- Gitelson, A.A.; Keydan, G.P.; Merzlyak, M.N. Three-band model for noninvasive estimation of chlorophyll, carotenoids, and anthocyanin contents in higher plant leaves. Geophys. Res. Lett 2006. [Google Scholar] [CrossRef]
- Nguy-Robertson, A.; Gitelson, A.; Peng, Y.; Vina, A.; Arkebauer, T.; Rundquist, D. Green leaf area index estimation in maize and soybean: Combining vegetation indices to achieve maximal sensitivity. Agron. J 2012, 104, 1336–1347. [Google Scholar]
- Yoshioka, H.; Miura, T.; Demattê, J.A.M.; Batchily, K.; Huete, A.R. Derivation of soil line influence on two-band vegetation indices and vegetation isolines. Remote Sens 2009, 1, 842–857. [Google Scholar]
- Pearlman, J.S.; Barry, P.S.; Segal, C.C.; Shepanski, J.; Beiso, D.; Carman, S.L. Hyperion, a space-based imaging spectrometer. IEEE Trans. Geosci. Remote Sens 2003, 41, 1160–1173. [Google Scholar]
- Kruse, F.A.; Taranik, J.V.; Coolbaugh, M.; Michaels, J.; Littlefield, E.F.; Calvin, W.M.; Martini, B.A. Effect of reduced spatial resolution on mineral mapping using imaging spectrometry—Examples using Hyperspectral Infrared Imager (HyspIRI)-simulated data. Remote Sens 2011, 3, 1584–1602. [Google Scholar]
- Mariotto, I.; Thenkabail, P.S.; Huete, A. R.; Slonecker, E.T.; Platonov, A. Hyperspectral vs. multispectral crop-productivity modeling and type discrimination for the HyspIRI mission. Remote Sens. Environ 2013, 139, 291–305. [Google Scholar]
- Wang, L.; Hunt, E.R.; Qu, J.J.; Hao, X.; Daughtry, C.S.T. Towards estimation of canopy foliar biomass with spectral reflectance measurements. Remote Sens. Environ 2011, 115, 836–840. [Google Scholar]
- Roberts, D.A.; Roth, K.L.; Perroy, R.L. Hyperspectral Vegetation Indices. In Hyperspectral Remote Sensing of Vegetation; Thenkabail, P.S., Lyon, J.G., Huete, A.R., Eds.; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Cho, M.A.; Skidmore, A.K.; Atzberger, C. Towards red-edge positions less sensitive to canopy biophysical parameters for leaf chlorophyll estimation using properties optique spectrales des feuilles (PROSPECT) and scattering by arbitrarily inclined leaves (SAILH) simulated data. Int. J. Remote Sens 2008, 29, 2241–2255. [Google Scholar]
- Filella, I.; Peñuelas, J. The red edge position and shape as indicators of plant chlorophyll content, biomass and hydric status. Int. J. Remote Sens 1994, 15, 1459–1470. [Google Scholar]
- Banskota, A.; Wynne, R.H.; Thomas, V.A.; Serbin, S.P.; Kayastha, N.; Gastellu-Etchegorry, J.P.; Townsend, P.A. Investigating the utility of wavelet transforms for inverting a 3-D radiative transfer model using hyperspectral data to retrieve forest LAI. Remote Sens 2013, 5, 2639–2659. [Google Scholar]
- Gitelson, A.A.; Merzlyak, M.N. Signature analysis of leaf reflectance spectra: Algorithm development for remote sensing of chlorophyll. J. Plant Physiol 1996, 148, 494–500. [Google Scholar]
- Salas, E.A.L.; Henebry, G.M. Separability of maize and soybean in the spectral regions of chlorophyll and carotenoids using the Moment Distance Index. Isr. J. Plant Sci 2012, 60, 65–76. [Google Scholar]
- Horler, D.N.H.; Dockray, M.; Barber, J. The red-edge of plant leaf reflectance. Int. J. Remote Sens 1983, 4, 273–288. [Google Scholar]
- Liao, Q.; Wang, J.; Yang, G.; Zhang, D.; Li, H.; Fu, Y.; Li, Z. Comparison of spectral indices and wavelet transform for estimating chlorophyll content of maize from hyperspectral reflectance. J. App. Remote Sens 2013, 7. [Google Scholar] [CrossRef]
- Gitelson, A.A. Nondestructive Estimation of Foliar Pigment (Chlorophylls, Carotenoids, and Anthocyanins) Contents: Evaluating a Semianalytical Three-Band Model. In Hyperspectral Remote Sensing of Vegetation; Thenkabail, P.S., Lyon, J.G., Huete, A.R., Eds.; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Jacquemoud, S.; Baret, F. PROSPECT: A model of leaf optical properties spectra. Remote Sens. Environ 1990, 34, 75–91. [Google Scholar]
- Verhoef, W. Light scattering by leaf layers with application to canopy reflectance modeling: The SAIL model. Remote Sens. Environ 1984, 16, 125–141. [Google Scholar]
- Atzberger, C.; Darvishzadeh, R.; Schlerf, M.; Le Maire, G. Suitability and adaptation of PROSAIL radiative transfer model for hyperspectral grassland studies. Remote Sens. Lett 2013, 4, 55–64. [Google Scholar]
- Uto, K.; Kosugi, Y. Leaf parameter estimation based on leaf scale hyperspectral imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens 2013, 6, 699–707. [Google Scholar]
- Croft, H.; Chen, J.M.; Zhang, Y.; Simic, A. Modelling Leaf Chlorophyll Content in Broadleaf and Needle Leaf Canopies from Ground, CASI, Landsat TM 5 and MERIS Reflectance Data. Remote Sens. Environ 2013, 133, 128–140. [Google Scholar]
- Navarro-Cerrillo, R.M.; Trujillo, J.; Sanchez de la Orden, M.; Hernandez-Clemente, R. Hyperspectral and multispectral satellite sensors for mapping chlorophyll content in a Mediterranean pinus sylvestris L. plantation. Int. J. Appl. Earth Obs. Geoinf 2014, 26, 88–96. [Google Scholar]
- Feret, J.-B.; François, C.; Asner, G.P.; Gitelson, A.A.; Martin, R.E.; Bidel, L.P.R.; Ustin, S.L.; le Maire, G.; Jacquemoud, S. PROSPECT-4 and 5: Advances in the leaf optical properties model separating photosynthetic pigments. Remote Sens. Environ 2008, 112, 3030–3043. [Google Scholar]
- Clark, R.N.; Swayze, G.A.; Wise, R.; Livo, E.; Hoefen, T.; Kokaly, R.; Sutley, S.J. USGS Digital Spectral Library Splib06a. Available online: http://speclab.cr.usgs.gov/spectral.lib06 (accessed on 10 March 2010).
- Carlson, T.N.; Ripley, D.A. On the relation between NDVI, fractional vegetation cover, and leaf area index. Remote Sens. Environ 1997, 62, 241–252. [Google Scholar]
- Ahern, F.J. The effects of bark beetle stress on the foliar spectral reflectance of Lodgepole Pine. Int. J. Remote Sens 1988, 9, 1451–1468. [Google Scholar]
- Curran, P.J.; Dungan, J.L.; Gholz, H.L. Exploring the relationship between reflectance red edge and chlorophyll content in slash pine. Tree Physiol 1991, 7, 33–48. [Google Scholar]
- Baret, F.; Vanderbilt, V.C.; Steven, M.D.; Jacquemoud, S. Use of spectral analogy to evaluate canopy reflectance sensitivity to leaf optical properties. Remote Sens. Environ 1994, 48, 253–260. [Google Scholar]
- Daughtry, C.S.T.; Gallo, K.P.; Bauer, M.E. Spectral estimates of solar radiation intercepted by corn canopies. Agron. J 1983, 75, 527–531. [Google Scholar]
- Clevers, J.G.P.W.; Kooistra, L.; Salas, E.A.L. Study of heavy metal contamination in river floodplains using the red-edge position in spectroscopic data. Int. J. Remote Sens 2004, 25, 3883–3895. [Google Scholar]
- Gitelson, A.A.; Vina, A.; Rundquist, D.C.; Ciganda, V.; Arkebauer, T.J. Remote estimation of canopy chlorophyll content in crops. Geophys. Res. Lett 2005. [Google Scholar] [CrossRef]
- Wang, F.-M.; Huang, J.-F; Tang, Y.-L; Wang, X.-Z. New vegetation index and its application in estimating leaf area index of rice. Rice Sci 2007, 14, 195–203. [Google Scholar]
- Demetriades-Shah, T.H.; Steven, M.D.; Clark, J.A. High resolution derivative spectra in remote sensing. Remote Sens. Environ 1990, 33, 55–64. [Google Scholar]
- Baret, F.; Jacquemoud, S.; Guyot, G.; Leprieur, C. Modeled analysis of the biophysical nature of spectral shifts and comparison with information content of broad bands. Remote Sens. Environ 1992, 41, 133–142. [Google Scholar]
- Wu, C.; Niu, Z.; Tang, Q.; Huang, W. Estimating chlorophyll content from hyperspectral vegetation indices: Modeling and validation. Agric. For. Meteorol 2008, 148, 1230–1241. [Google Scholar]
- Irons, J.R.; Dwyer, J.L.; Barsi, J.A. The next Landsat satellite: The Landsat Data Continuity Mission. Remote Sens. Environ 2012, 122, 11–21. [Google Scholar]
- Mishra, D.R.; Narumalani, S.; Rundquist, D.; Lawson, M.; Perk, R. Enhancing the detection and classification of coral reef and associated benthic habitats: A hyperspectral remote sensing approach. J. Geophys. Res 2007, 112. [Google Scholar] [CrossRef]
- Hook, S.J.; Myers, J.E.J.; Thome, K.J.; Fitzgerald, M.; Kahle, A.B. The MODIS/ASTER airborne simulator (MASTER)—A new instrument for earth science studies. Remote Sens. Environ 2001, 76, 93–102. [Google Scholar]
- Miller, J.R.; Freemantle, J.R.; Belanger, M.J.; Elvidge, C.D.; Boyer, M.G. Potential for Determination of Leaf Chlorophyll Content Using AVIRIS. Proceedings of the Second Airborne Visible/Infrared Imaging Spectrometer (AVIRIS) Workshop, Pasadena, CA, USA, 4–5 June 1990; pp. 72–77.
- Green, R.O.; Eastwood, M.L.; Sarture, C.M.; Chrien, T.G.; Aronsson, M.; Chippendale, B.J.; Faust, J.A.; Pavri, B.E.; Chovit, C.J.; Solis, M.; et al. Imaging spectroscopy and the Airborne Visible/Infrared Imaging Spectrometer (AVIRIS). Remote Sens. Environ 1998, 65, 227–248. [Google Scholar]
- Liao, L.; Jarecke, P.; Gleichauf, D.; Hedman, T. Performance characterization of the Hyperion imaging spectrometer instrument. Proc. SPIE 2000, 4135. [Google Scholar] [CrossRef]
- Chen, W.; Henebry, G.M. Spatio-spectral heterogeneity analysis using EO-1 Hyperion imagery. Comput. Geosci 2010, 36, 167–170. [Google Scholar]





| Vegetation Index | Equation | Reference | Remarks |
|---|---|---|---|
| Difference Vegetation Index (DVI) | NIR – red | Jordan (1969) [22] | Sensitive to soil background |
| Ratio Vegetation Index (RVI) | NIR/red | Pearson and Miller (1972) [23] | Sensitive to soil background |
| Normalized Difference Vegetation Index (NDVI) | Rouse et al. (1974) [16] | Enhances contrast between soil and vegetation | |
| Modified Simple Ratio (MSR) | Chen and Cihlar (1996) [1] | Improves vegetation sensitivity | |
| Transformed Vegetation Index (TVI) | Deering et al. (1975) [32] | Modifies NDVI with only positive values; <0.71 as non-vegetation and >0.71 as vegetation | |
| Modified Transformed Vegetation Index (MTVI) | where c is a weighing factor | Skianis et al. (2007) [3] | Used with poor vegetation |
| Perpendicular Vegetation Index (PVI) | sin (a)*NIR – cos (a)*red where a is a weighing factor | Richardson and Wiegand (1977) [35] | Utilizes soil line in red-NIR space |
| Green Vegetation Index (GVI) | −0.29*MSS4 −0.56*MSS5 +0.60*MSS6 +0.49*MSS7 | Kauth and Thomas (1976) [38] | 4-band version for MSS |
| −0.2848*TM1−0.2435*TM2−0.5436*TM3 +0.7243*TM4+ 0.0840*TM5−0.1800*TM7 | Crist and Cicone (1984) [39] | 6-band version for TM | |
| Weighted Difference Vegetation Index (WDVI) | Clevers (1988) [5] | Specifically for soil moisture influences | |
| Soil Adjusted Vegetation Index (SAVI) | where L is a correction factor | Huete (1988) [41] | Combines NDVI and soil factor |
| Transformed Soil Adjusted Vegetation Index (TSAVI) | where a is the soil line intercept, s is the soil line slope, and x is an adjustment factor | Baret et al. (1989) [42] | Assumes soil line has arbitrary slope and intercept |
| Soil Adjusted Vegetation Index2 (SAVI2) | Major et al. (1990) [43] | Ratio b/a as the soil-adjustment factor | |
| Enhanced Vegetation Index (EVI) | Liu and Huete (1995) [45] | Modified NDVI with improved sensitivity to high biomass | |
| Wide Dynamic Range Vegetation Index (WDRVI) | where a is a weighing coefficient | Gitelson et al. (2004) [6] | Enhances dynamic range of NDVI |
| Chlorophyll Index Red-edge (CIred-edge) | where red-edge covers 690 to 725 nm and NIR spans the 760 to 800 nm | Gitelson et al. (2006) [46] | Uses a range of bands |
| Combined Vegetation Index (CVI) | Nguy-Robertson et al. (2012) [47] | For moderate to high LAI |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Salas, E.A.L.; Henebry, G.M. A New Approach for the Analysis of Hyperspectral Data: Theory and Sensitivity Analysis of the Moment Distance Method. Remote Sens. 2014, 6, 20-41. https://doi.org/10.3390/rs6010020
Salas EAL, Henebry GM. A New Approach for the Analysis of Hyperspectral Data: Theory and Sensitivity Analysis of the Moment Distance Method. Remote Sensing. 2014; 6(1):20-41. https://doi.org/10.3390/rs6010020
Chicago/Turabian StyleSalas, Eric Ariel L., and Geoffrey M. Henebry. 2014. "A New Approach for the Analysis of Hyperspectral Data: Theory and Sensitivity Analysis of the Moment Distance Method" Remote Sensing 6, no. 1: 20-41. https://doi.org/10.3390/rs6010020