Evaluation of Land Surface Temperature Operationally Retrieved from Korean Geostationary Satellite (COMS) Data
Abstract
:1. Introduction
2. Development of LST Retrieval Algorithm
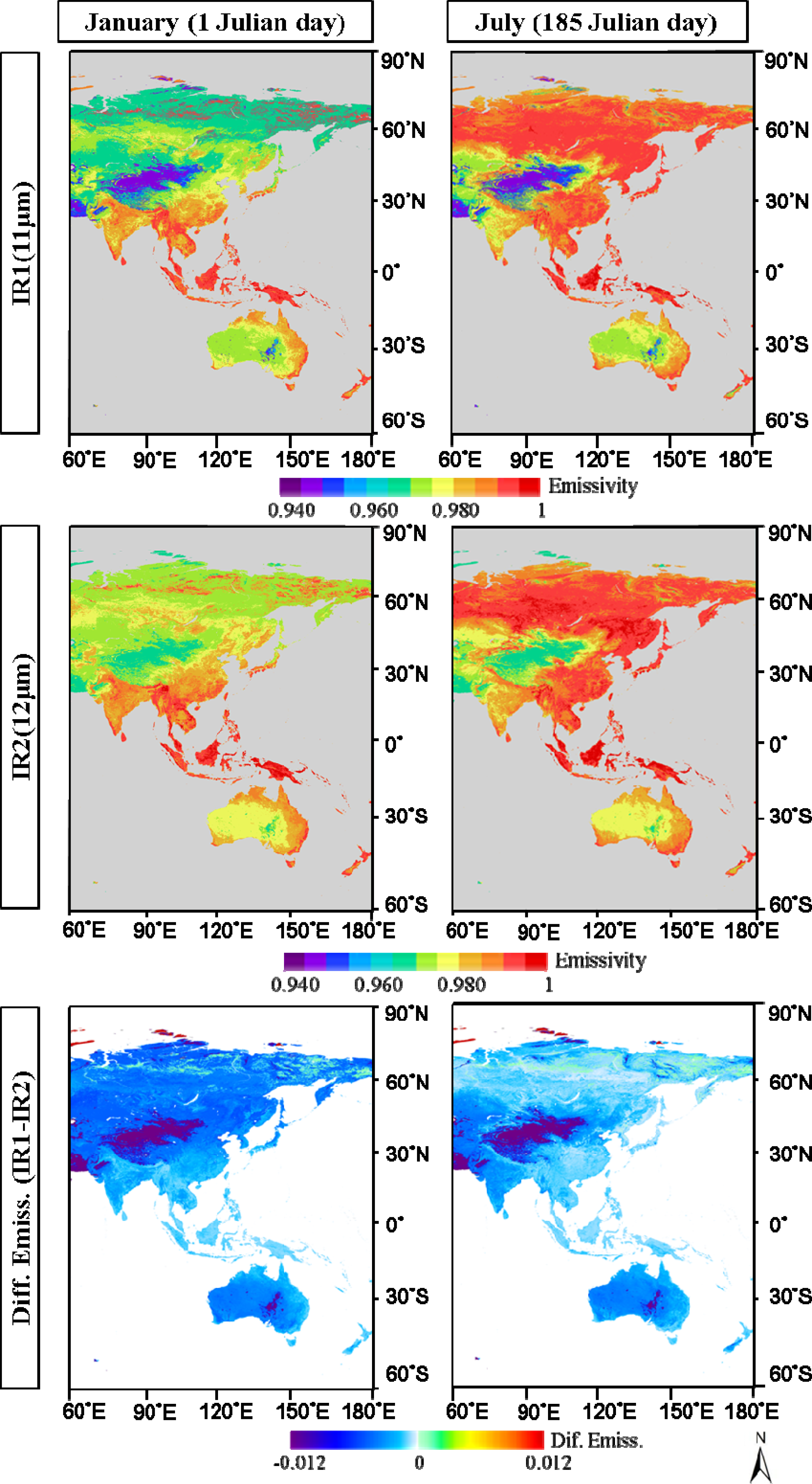
3. Estimation of Surface Emissivity
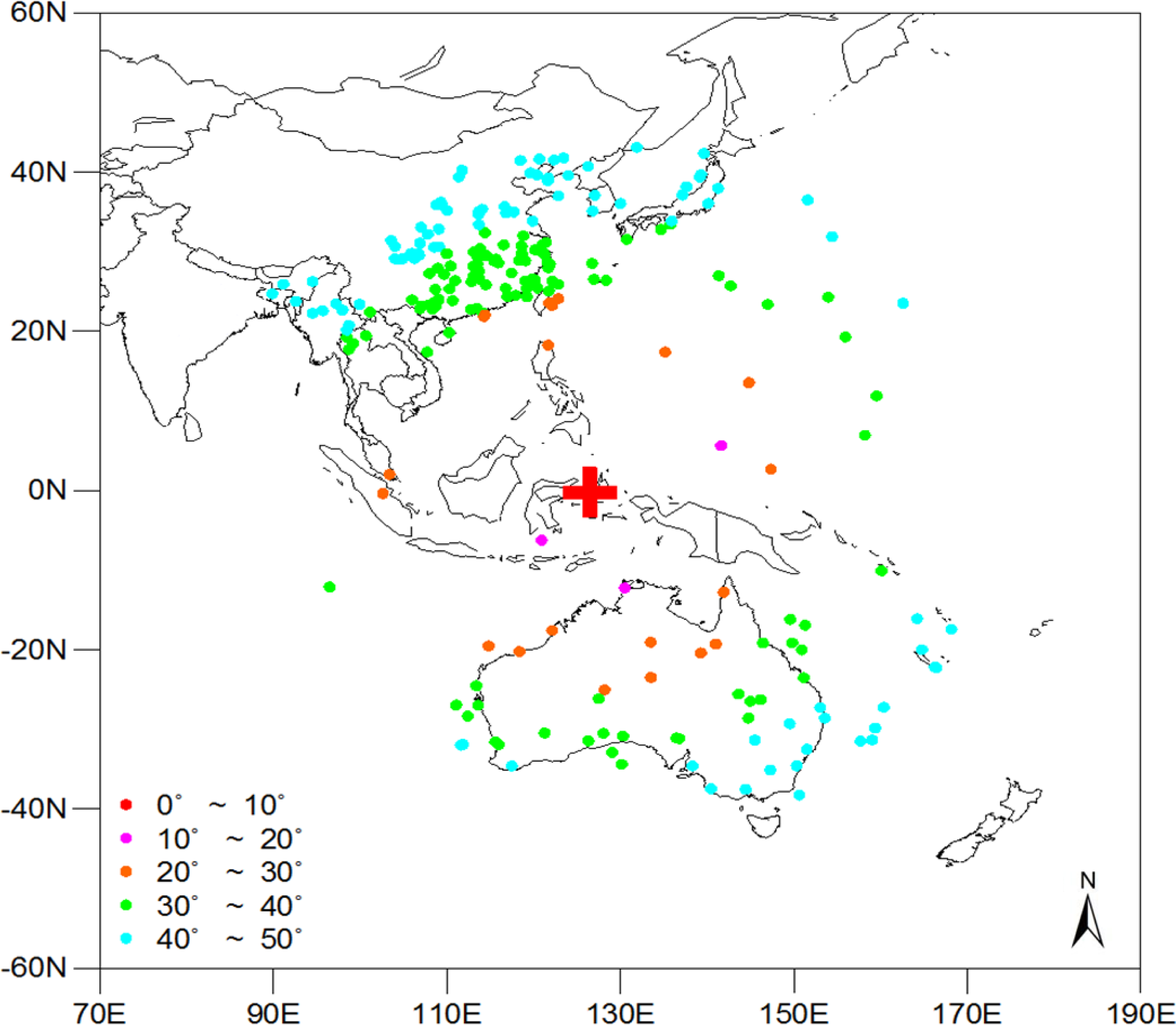
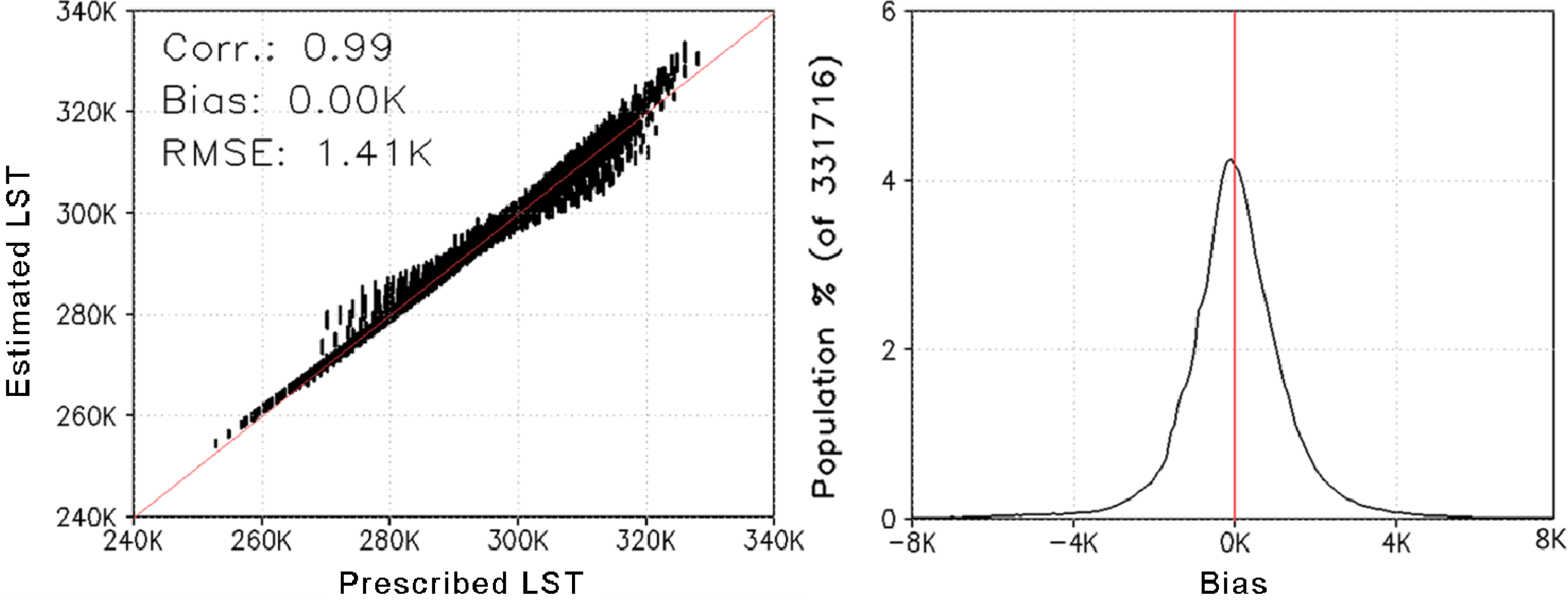
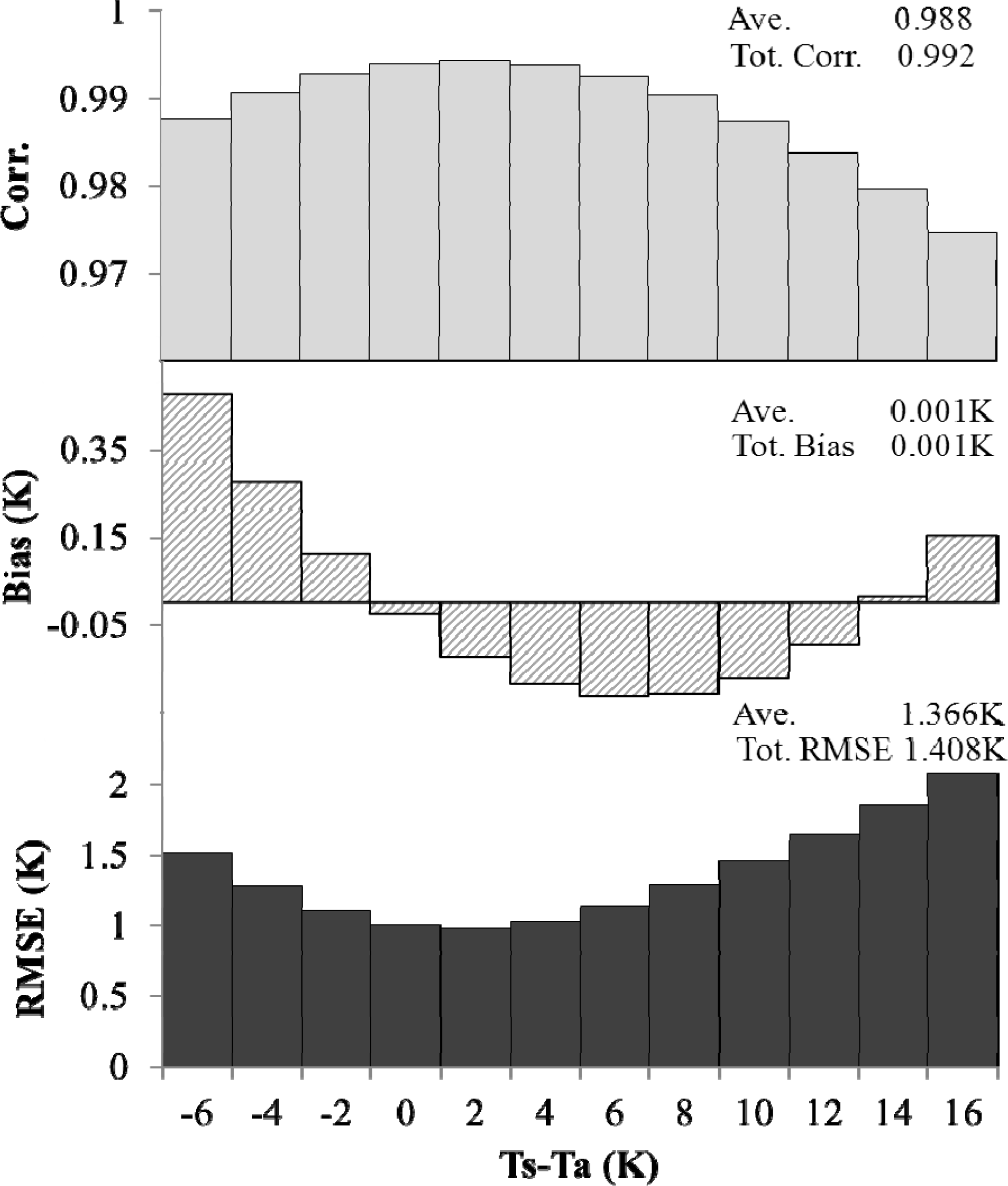
4. Retrieval of LST Data and Evaluation of the Results
5. Summary
Acknowledgments
Conflict of Interest
References and Notes
- Price, J.C. Land surface temperature measurements from the split-window channels of the NOAA 7 AVHRR. J. Geophys. Res 1984, 89, 7231–7237. [Google Scholar]
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature measurement from space. IEEE Trans. Geosci. Remote Sens 1996, 34, 892–905. [Google Scholar]
- Prata, A.J.; Cechet, R.P. An assessment of the accuracy of land surface temperature determination from the GMS-5 VISSR. Remote Sens. Environ 1999, 67, 1–14. [Google Scholar]
- Bodas-Salcedo, A.; Ringer, M.; Jones, A. Evaluation of the surface radiation budget in the atmospheric component of the Hadley Centre Global Environmental Model (HadGEM1). J. Clim 2008, 17, 4723–4748. [Google Scholar]
- Becker, F.; Li, Z.-L. Surface temperature and emissivity at various scales: Definition, measurement and related problems. Remote Sens. Rev 1995, 12, 225–253. [Google Scholar]
- Peres, L.; DaCamara, C.C. Land surface temperature and emissivity estimation based on the two-temperature method: Sensitivity analysis using simulated MSG/SEVIRI data. Remote Sens. Environ 2004, 91, 377–389. [Google Scholar]
- Neteler, M. Estimating daily land surface temperature in mountainous environments by reconstructed MODIS LST data. Remote Sens 2010, 2, 333–351. [Google Scholar]
- Bechtel, B.; Zakšek, K.; Hoshyaripour, G. Downscaling land surface temperature in an Urban area: A case study for Hamburg, Germany. Remote Sens 2012, 4, 3184–3200. [Google Scholar]
- Soliman, A.; Duguay, C.; Saunders, W.; Hachem, S. Pan-arctic land surface temperature from MODIS and AATSR: Product development and intercomparison. Remote Sens 2012, 4, 3833–3856. [Google Scholar]
- Kerr, Y.H.; Lagouarde, J.P.; Imbernon, J. Accurate land surface temperature retrieval from AVHRR data with use of an improved split window. Remote Sens. Environ 1992, 41, 197–209. [Google Scholar]
- Han, K.S.; Viau, A.A.; Anctil, F. An analysis of GOES and NOAA derived land surface temperatures estimated over a boreal forest. Int. J. Remote Sens 2004, 25, 4761–4780. [Google Scholar]
- Suh, M.S.; Kim, S.H.; Kang, J.H. A comparative study of algorithms for estimating land surface temperature from MODIS data. Kor. J. Remote Sens 2008, 24, 65–78. [Google Scholar]
- Trigo, I.; Peres, L.; DaCamara, C.C.; Freitas, S. Thermal land surface emissivity retrieved from SEVIRI/Meteosat. IEEE Trans. Geosci. Remote Sens 2008, 46, 307–315. [Google Scholar]
- Valor, E.; Caselles, V. Mapping land surface emissivity from NDVI: Application to European, African, and South American areas. Remote Sens. Environ 1996, 57, 164–184. [Google Scholar]
- Seemann, S.W.; Borbas, E.E.; Knuteson, R.O.; Stephenson, R.; Huang, H.-L. Development of a global infrared land surface emissivity database for application to clear sky sounding retrievals from multispectral satellite radiance measurements. J. Appl. Meteorol. Climatol 2008, 47, 108–123. [Google Scholar]
- Wan, Z. New refinements and validation of the MODIS land-surface temperature/emissivity products. Remote Sens. Environ 2008, 112, 59–74. [Google Scholar]
- Hulley, G.C.; Hook, S.J.; Baldridge, A.M. Validation of the North American ASTER land surface emissivity database (NAALSED) version 2.0 using pseudo-invariant sand dune sites. Remote Sens. Envrion 2009, 113, 2224–2233. [Google Scholar]
- Inamdar, A.K.; French, A. Disaggregation of GOES land surface temperatures using surface emissivity. J. Geophys. Res 2009, 36, L02408. [Google Scholar] [CrossRef]
- Li, Z.; Li, J.; Jin, X.; Schmit, T.J.; Borbas, E.E.; Goldberg, M.D. An objective methodology for infrared land surface emissivity evaluation. J. Geophys. Res 2010, 115, D22308. [Google Scholar] [CrossRef]
- MODIS UCSB Emissivity Library. Available online: http://www.icess.ucsb.edu/modis/EMIS/html/em.html (accessed on 13 May 2013).
- Jet Propulsion Laboratory: ASTER Spectral Library. Available online: http://speclib.jpl.nasa.gov/ (accessed on 13 May 2013).
- Loveland, T.R.; Reed, B.C.; Brown, J.F.; Ohlen, D.O.; Zhu, Z.; Yang, L.; Merchant, J.W. Development of a global land cover characteristics data base and IGBP DISCover from 1 km AVHRR data. Int. J. Remote Sens 2000, 21, 1251–1277. [Google Scholar]
- Wang, K.C.; Liang, S.L. Evaluation of ASTER and MODIS land surface temperature and emissivity products using long-term surface longwave radiation observations at SURFRAD sites. Remote Sens. Environ 2009, 113, 1556–1565. [Google Scholar]
- Kang, J.H.; Suh, M.S.; Kwak, C.H. Land cover classification over East Asia using Recent MODIS NDVI data (2006–2008). Kor. J. Atmos. Sci 2010, 20, 415–426. [Google Scholar]
- Terra/MODIS. Available online: https://lpdaac.usgs.gov/products/modis_products_table (accessed on 13 May 2013).
- MSG/SEVIRI. Available online: http://www.eumetsat.int/Home/Main/DataProducts/Land/index.htm?l=en (accessed on 13 May 2013).
- Wan, Z.; Zhang, Y.; Zhang, Q.; Li, Z. Validation of the land-surface temperature products retrieved from Terra Moderate Resolution Imaging Spectroradiometer data. Remote Sens. Environ 2002, 83, 163–180. [Google Scholar]
- Wan, Z.; Zhang, Y.; Zhang, Q.; Li, Z.-L. Quality assessment and validation of the MODIS global land surface temperature. Int. J. Remote Sens 2004, 25, 59–74. [Google Scholar]
- Sohrabinia, M.; Rack, W.; Zawar-Reza, P. Analysis of MODIS LST compared with WRF Model and in situ Data over the Waimakariri River Basin, Canterbury, New Zealand. Remote Sens 2012, 4, 3501–3527. [Google Scholar]
- Pinker, R.T.; Sun, D.; Hung, M.-P.; Li, C.; Basara, J.B. Evaluation of satellite estimates of land surface temperature from GOES over the United States. J. Appl. Meteorol. Climatol 2009, 48, 167–180. [Google Scholar]
- Hong, K.O.; Suh, M.S.; Kang, J.H. Development of a land surface temperature-retrieval Algorithm from MTSAT–1R data. Asia Pac. J. Atmos. Sci 2009, 45, 411–422. [Google Scholar]
- Tang, B.; Bi, Y.; Li, Z.L.; Xia, J. Generalized split-window algorithm for estimate of land surface temperature from Chinese geostationary FengYun meteorological satellite (FY–2C) data. Sensors 2008, 8, 933–951. [Google Scholar]
- Korea Meteorological Administration. Development of Meteorological Data Processing Systems of Communication, Ocean and Meteorological Satellite (V); KMA: Seoul, Korea, 2008. [Google Scholar]
- Hong, K.O.; Suh, M.S.; Kang, J.H. Improvement of COMS land surface temperature retrieval algorithm. Korean J. Remote Sens 2009, 25, 507–515. [Google Scholar]
- Korea Meteorological Administration. Retrieval of Land Surface Information from Satellite Data and Their Application; KMA: Seoul, Korea, 2012. [Google Scholar]
- Berk, A.; Anderson, G.P.; Acharya, P.K.; Chetwynd, J.H.; Bernstein, L.S.; Shettle, E.P.; Matthew, M.W.; Adler-Golden, S.M. MODTRAN4 Users’s Mannual; Air Force Research Laboratory: Hanscom AFB, MA, USA, 1999. [Google Scholar]
- Verhoef, W.; Bach, H. Simulation of hyperspectral and directional radiance images using biophysical and atmospheric radiative transfer models. Remote Sens. Environ 2003, 87, 23–41. [Google Scholar]
- Guanter, L.; Richter, R.; Kaufmann, H. On the application of the MODTRAN4 atmospheric radiative transfer code to optical remote sensing. Int. J. Remote Sens 2009, 30, 1407–1424. [Google Scholar]
- Jiménez-Muñoz, J.C.; Sobrino, J.A.; Mattar, C.; Franch, B. Atmospheric correction of optical imagery from MODIS and Reanalysis atmospheric products. Remote Sens. Environ 2010, 114, 2195–2210. [Google Scholar]
- Sobrino, J.A.; Romaguera, M. Land surface temperature retrieval from MSG1–SEVIRI data. Remote Sens. Environ 2004, 92, 247–254. [Google Scholar]
- Laboratoire de Météorologie Dynamique. Available online: http://ara.lmd.polytechnique.fr/htdocs-public/products/TIGR/TIGR.html (accessed on 13 May 2013).
- Coll, C.; Caselles, V. A split-window algorithm for land surface temperature from advanced very high resolution radiometer data: Validation and algorithm comparison. J. Geophys. Res 1997, 102, 16697–16713. [Google Scholar]
- Sobrino, J.A.; Raissouni, N. Toward remote sensing methods for land cover dynamic monitoring: Application to Morocco. Int. J. Remote Sens 2000, 21, 21353–21366. [Google Scholar]
- Sun, D.; Pinker, R.T. Retrieval of surface temperature from the MSG-SEVIRI observations: Part I. Methodology. Int. J. Remote Sens 2007, 28, 5255–5272. [Google Scholar]
- Gu, Y.; Rose, W.I.; Bluth, G.J.S. Retrieval of mass and sizes of particles in sandstorms using two MODIS IR bands: A case study of April 7, 2001 sandstorm in China. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Peres, L.F.; DaCamara, C.C. Emissivity maps to retrieve land-surface temperature from MSG/SEVIRI. IEEE Trans. Geosci. Remote 2005, 43, 1834–1844. [Google Scholar]
- Sobrino, J.A.; Jiménez-Muñoz, J.C.; Sòria, G.; Romaguera, M.; Guanter, L.; Moreno, J.; Plaza, A.; Martínez, P. Land surface emissivity retrieval from different VNIR and TIR sensors. IEEE Trans. Geosci. Remote 2008, 46, 316–327. [Google Scholar]
- Trigo, I.F.; Monteiro, I.T.; Olesen, F.; Kabsch, E. An assessment of remotely sensed land surface temperature. J. Geophys. Res 2008, 113, D17108. [Google Scholar] [CrossRef]
- Momeni, M.; Saradjian, M.R. Evaluating NDVI-based emissivities of MODIS bands 31 and 32 emissivities derived by Day/Night LST algorithm. Remote Sens. Environ 2007, 106, 190–198. [Google Scholar]
- Park, K.H.; Suh, M.S. Inter-comparison of three land surface emissivity data sets (MODIS, CIMSS, KNU) in the Asian-Oceanian regions. Kor. J. Remote Sens 2013, 29, 219–233. [Google Scholar]
- Choi, Y.-S.; Ho, C.-H.; Ahn, M.-H.; Kim, Y.-M. An exploratory study of cloud remote sensing capabilities of the Communication, Ocean and Meteorological Satellite (COMS) imagery. Int. J. Remote Sens 2007, 28, 4715–4732. [Google Scholar]
- Choi, Y.-S. Personal Communication. 27 November 2012.
- Frey, C.M.; Kuenzer, C.; Dech, S. Quantitative comparison of the operational NOAA AVHRR LST product of DLR and the MODIS LST product V005. Int. J. Remote Sens 2012, 33, 7165–7183. [Google Scholar]
- Deneke, H.M.; Roebeling, R.A. Downscaling of METEOSAT SEVIRI 0.6 and 0.8 μm channel radiances utilizing the highresolution visible channel. Atmos. Chem. Phys 2010, 10, 9761–9772. [Google Scholar]
- Wang, W.; Liang, S.; Meyers, T. Validating MODIS land surface temperature products using long-term nighttime ground measurements. Remote Sens. Environ 2008, 112, 623–635. [Google Scholar]
 .
.
 .
.


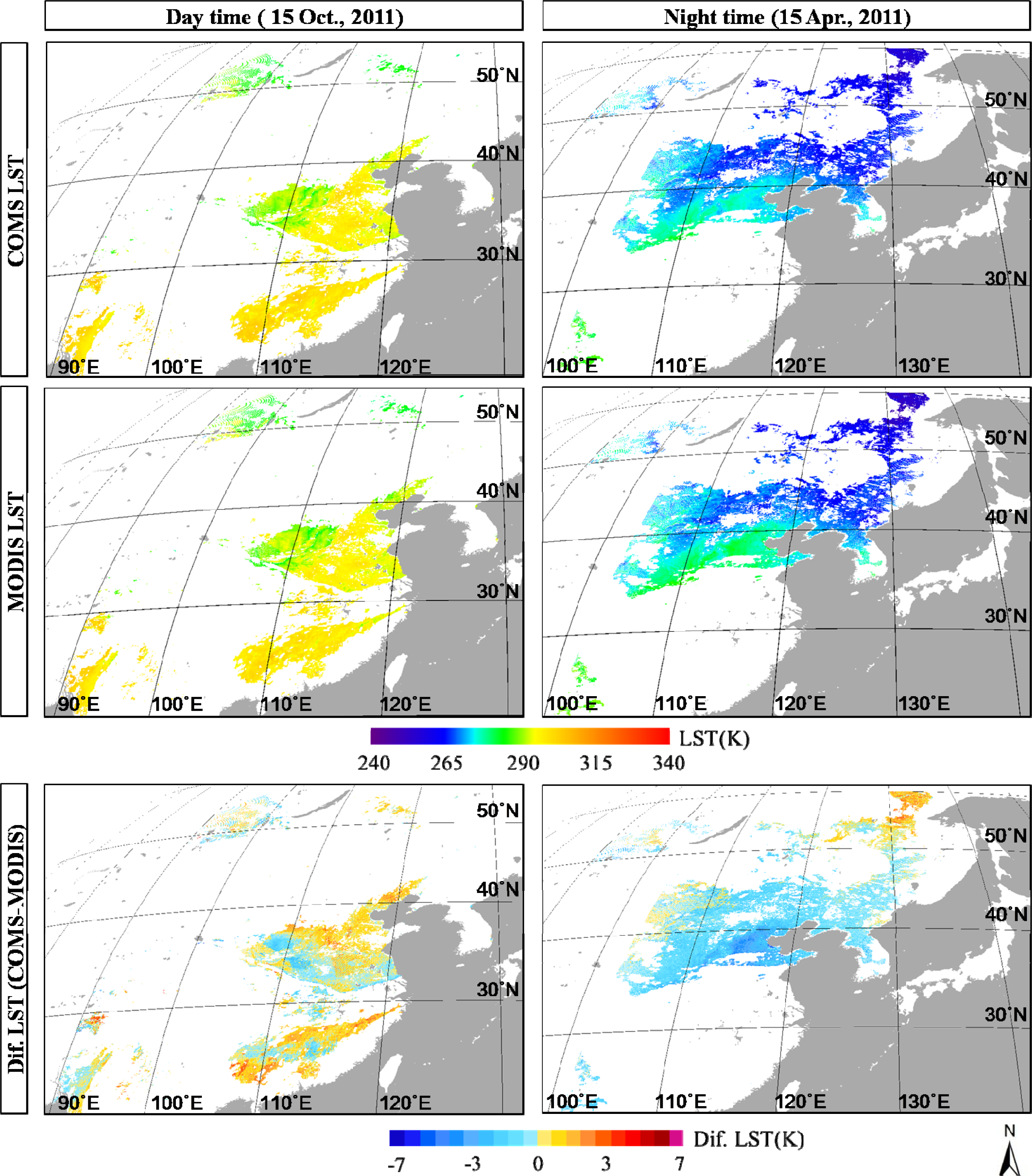

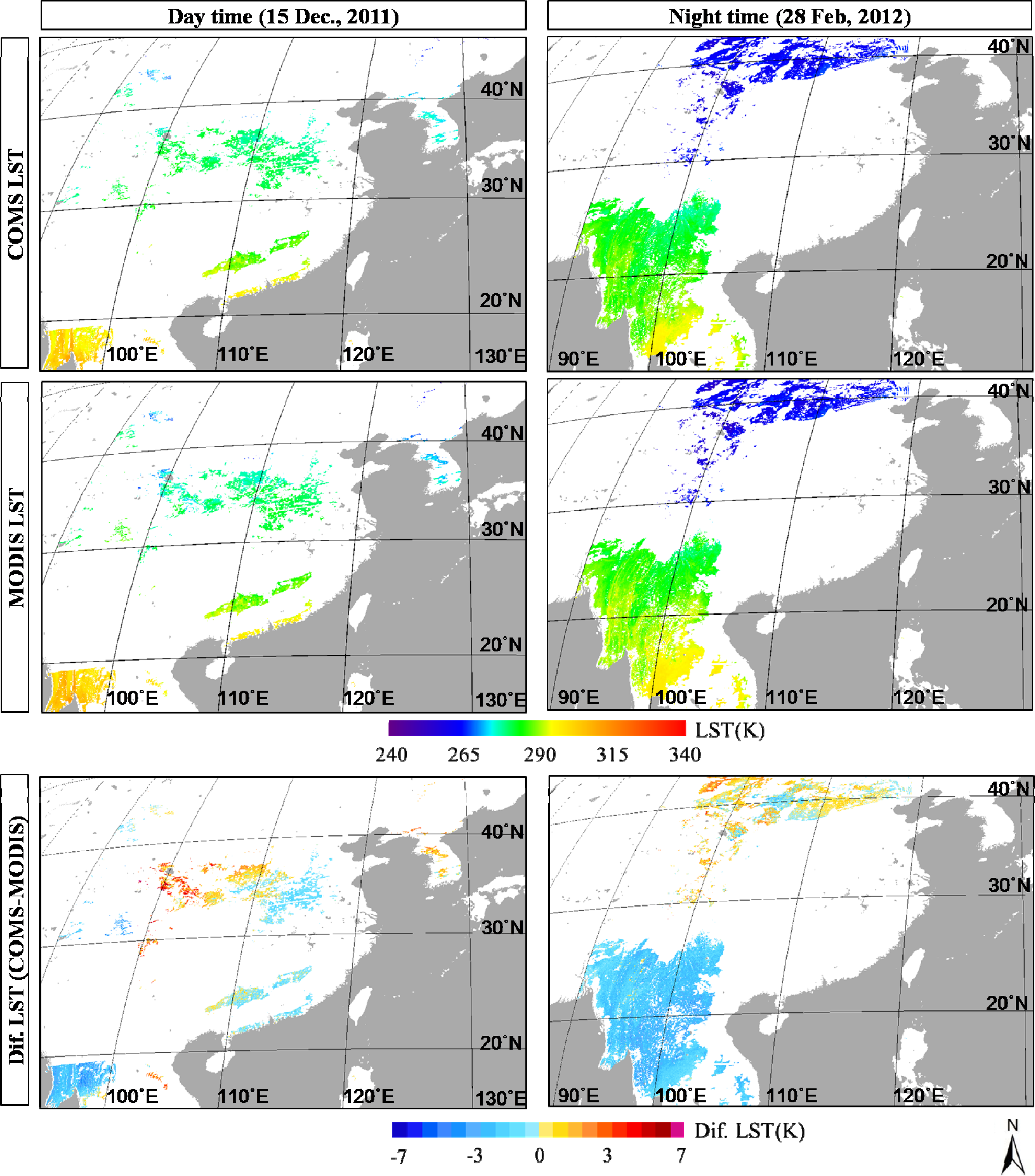
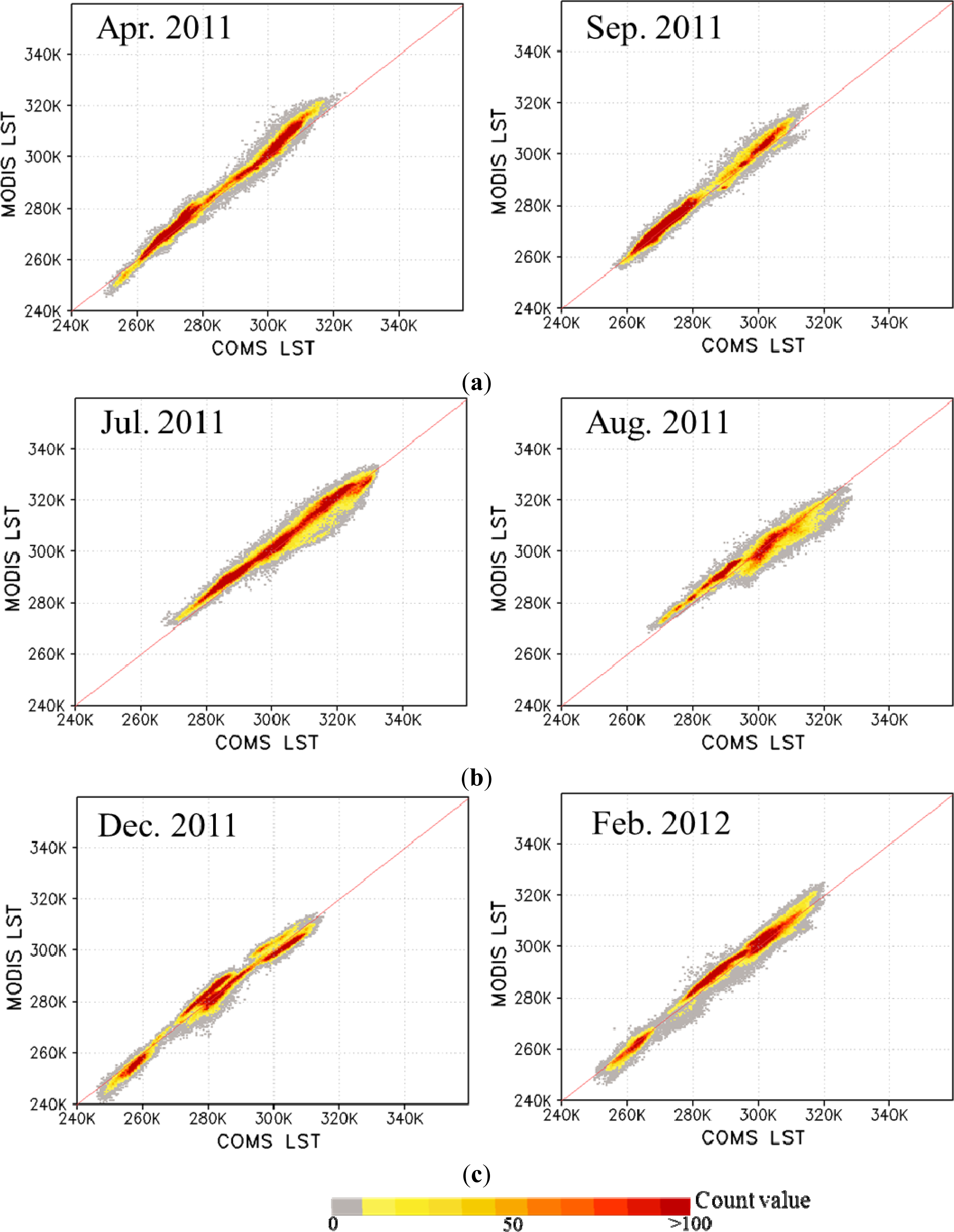
| Characteristics | Visible | Shortwave Infrared | Water Vapor | Infrared1 | Infrared2 |
|---|---|---|---|---|---|
| Band width (μm) | 0.55–0.80 | 3.5–4.0 | 6.50–7.00 | 10.3–11.3 | 11.5–12.5 |
| Band center (μm) | 0.675 | 3.75 | 6.75 | 10.8 | 12.0 |
| Instantaneous Field of View (μrad) | 28 | 112 | 112 × 112 | 112 | 112 |
| Spatial Res. (km) | 1 | 4 | 4 | 4 | 4 |
| Subject | Conditions |
|---|---|
| Atmospheric Profile | 359 profiles of TIGR 2000 database |
| Satellite Zenith Angle | SZA of TIGR point (0° – 50°) |
| Land Surface Temperature | Ta-6 K - Ta + 16 K (in steps of 2 K) |
| Emissivity | εIR1: 0.9478 ∼ 0.9968 (in steps of 0.0049) |
| −0.012 ≤ Δε ≤ 0.012 (in steps of 0.004) | |
| If (εIR2) > 1, εIR2 = 0.9999 |
| Year Month | Total | Daytime | Nighttime | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Corr. Coeff. | Bias (K) | RMSE (K) | Corr. Coeff. | Bias (K) | RMSE (K) | Corr. Coeff. | Bias (K) | RMSE (K) | ||
| 2011 | 4 | 0.995 | −1.506 | 2.477 | 0.973 | −2.177 | 3.187 | 0.982 | −1.080 | 1.892 |
| 5 | 0.995 | −2.421 | 3.056 | 0.966 | −2.870 | 3.686 | 0.956 | −2.024 | 2.363 | |
| 6 | 0.984 | −1.415 | 2.737 | 0.957 | −0.536 | 2.940 | 0.972 | −2.229 | 2.535 | |
| 7 | 0.986 | −1.220 | 2.735 | 0.966 | −0.744 | 2.751 | 0.965 | −2.402 | 2.695 | |
| 8 | 0.968 | −0.010 | 3.175 | 0.920 | 1.189 | 3.385 | 0.983 | −2.440 | 2.70 | |
| 9 | 0.993 | −1.289 | 2.075 | 0.950 | −1.989 | 3.016 | 0.977 | −1.093 | 1.721 | |
| 10 | 0.991 | 0.079 | 1.988 | 0.965 | −1.090 | 2.203 | 0.984 | −0.856 | 1.765 | |
| 11 | 0.991 | −0.166 | 2.136 | 0.986 | 0.981 | 2.086 | 0.994 | −1.171 | 2.178 | |
| 12 | 0.987 | −0.004 | 2.662 | 0.981 | 0.738 | 2.282 | 0.996 | −1.105 | 3.143 | |
| 2012 | 1 | 0.982 | −1.386 | 3.126 | 0.968 | −0.200 | 2.116 | 0.994 | −2.364 | 3.759 |
| 2 | 0.990 | −1.080 | 2.506 | 0.965 | −0.582 | 2.485 | 0.995 | −1.548 | 2.525 | |
| 3 | 0.992 | −1.692 | 2.681 | 0.954 | −2.219 | 3.530 | 0.993 | −1.529 | 2.355 | |
| Average | 0.988 | −1.009 | 2.613 | 0.963 | −0.610 | 2.806 | 0.983 | −1.653 | 2.463 | |
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Cho, A.-R.; Suh, M.-S. Evaluation of Land Surface Temperature Operationally Retrieved from Korean Geostationary Satellite (COMS) Data. Remote Sens. 2013, 5, 3951-3970. https://doi.org/10.3390/rs5083951
Cho A-R, Suh M-S. Evaluation of Land Surface Temperature Operationally Retrieved from Korean Geostationary Satellite (COMS) Data. Remote Sensing. 2013; 5(8):3951-3970. https://doi.org/10.3390/rs5083951
Chicago/Turabian StyleCho, A-Ra, and Myoung-Seok Suh. 2013. "Evaluation of Land Surface Temperature Operationally Retrieved from Korean Geostationary Satellite (COMS) Data" Remote Sensing 5, no. 8: 3951-3970. https://doi.org/10.3390/rs5083951




