Estimating Riparian and Agricultural Actual Evapotranspiration by Reference Evapotranspiration and MODIS Enhanced Vegetation Index
Abstract
:1. Introduction
1.1. Need for Evapotranspiration Estimates for River Basin Irrigation Districts
1.2. Methods to Determine Crop Water Budgets
1.3. Remote Sensing Methods for Estimating ETa
1.4. Applicability of VI-ETo Methods to Dryland Irrigation Districts
1.5. VI-ETo Methods Applied to Crops
1.6. VI Methods Applied to Riparian Vegetation
1.7. Experimental Approach
2. Materials and Methods
2.1. Form of the Algorithm for ETa
2.2. Moisture Flux Tower Data
2.3. ETa and ETo of Selected Crops
2.4. Sources of Validation Data
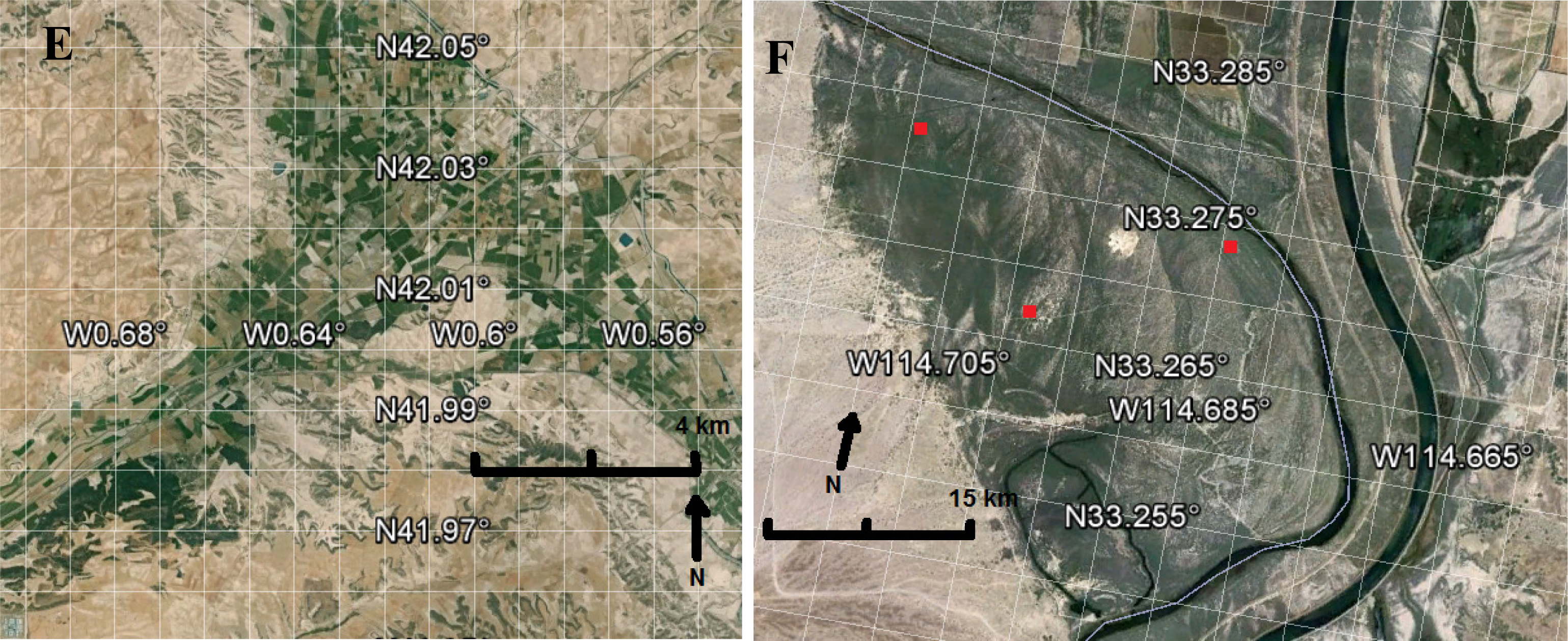
2.5. Acquisition of MODIS EVI Pixels
2.6. Statistical Analyses and Other Methods
3. Results and Discussion
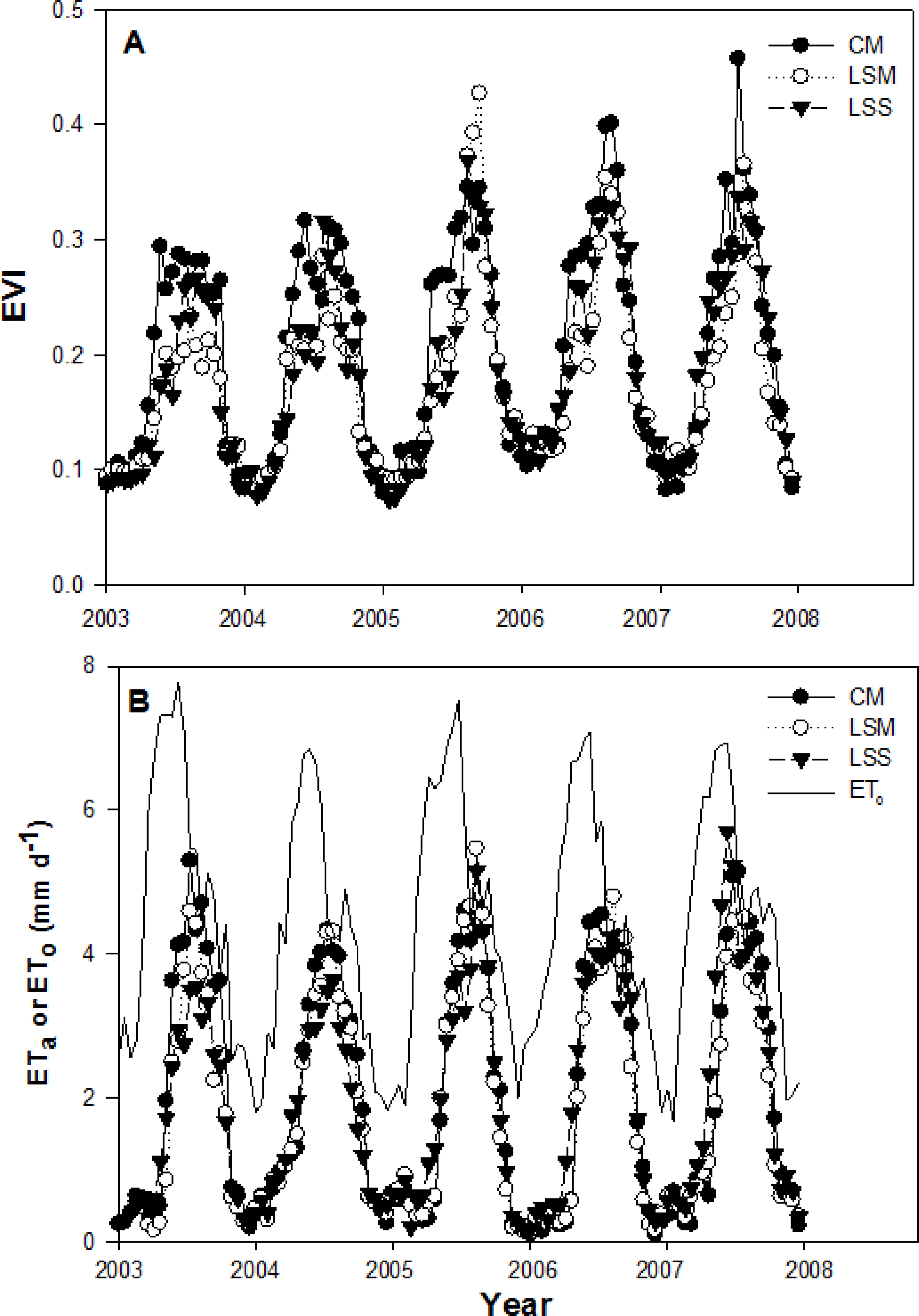
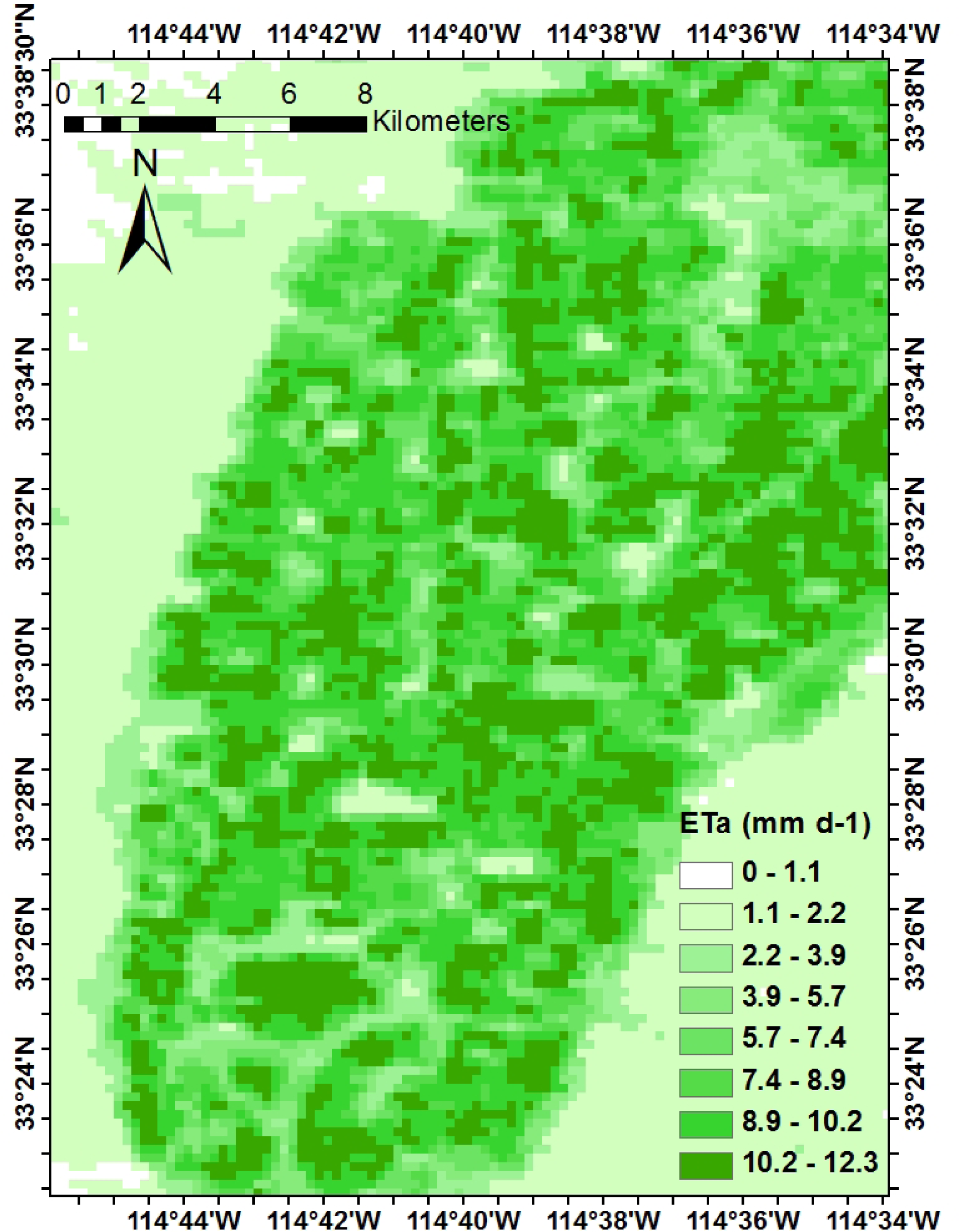
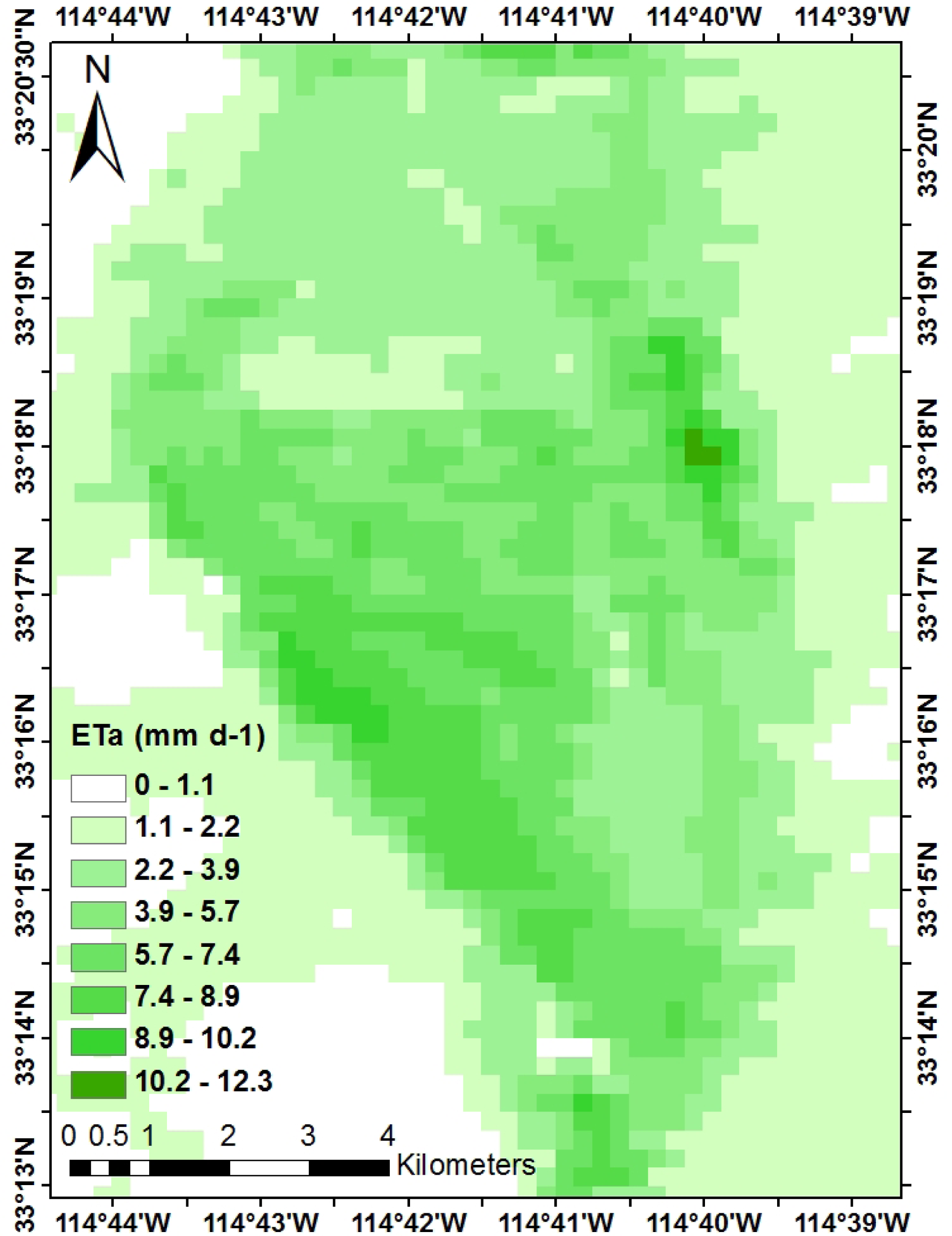
3.1 EVI and ETa Data for San Pedro Riparian Vegetation
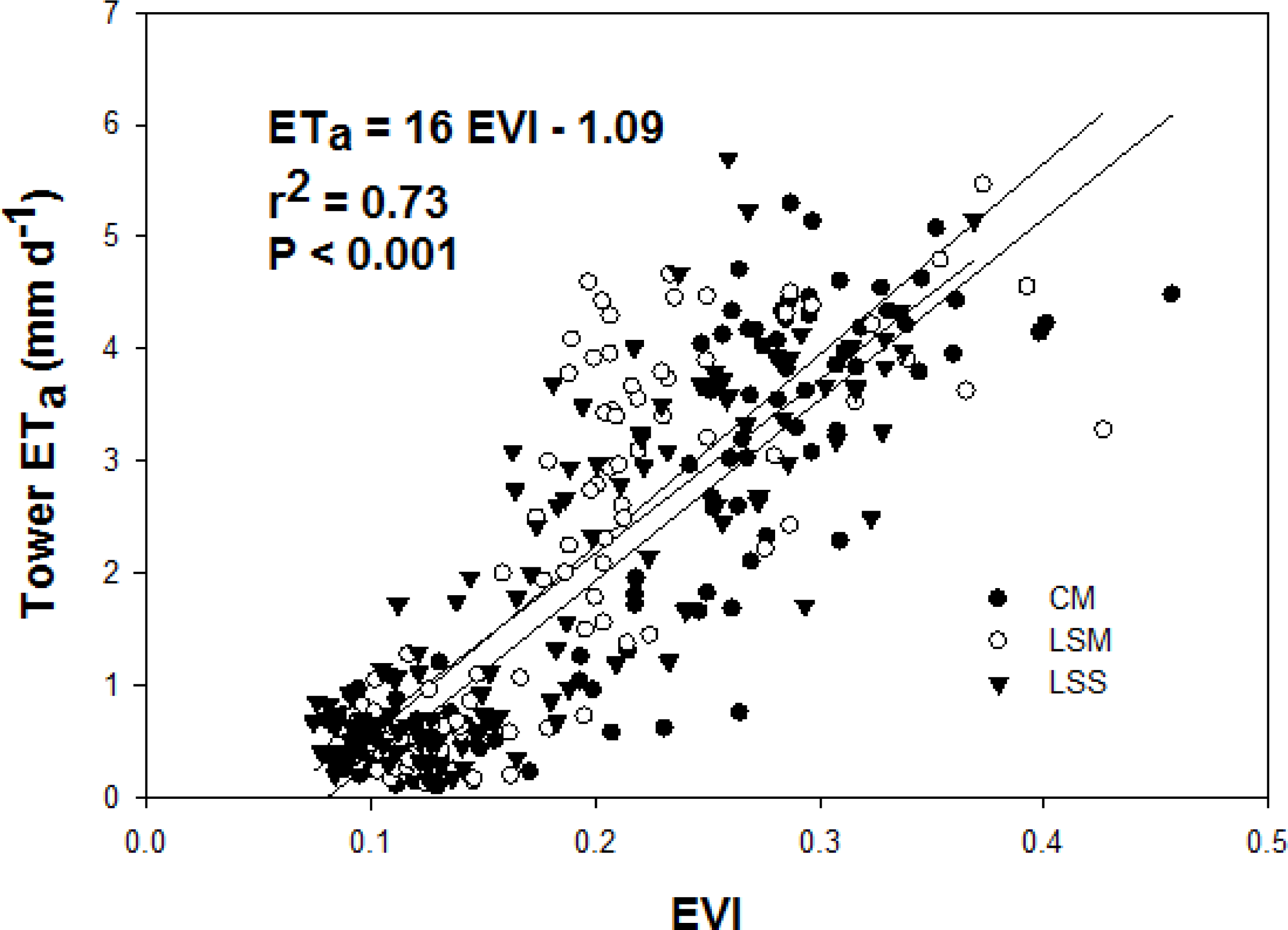
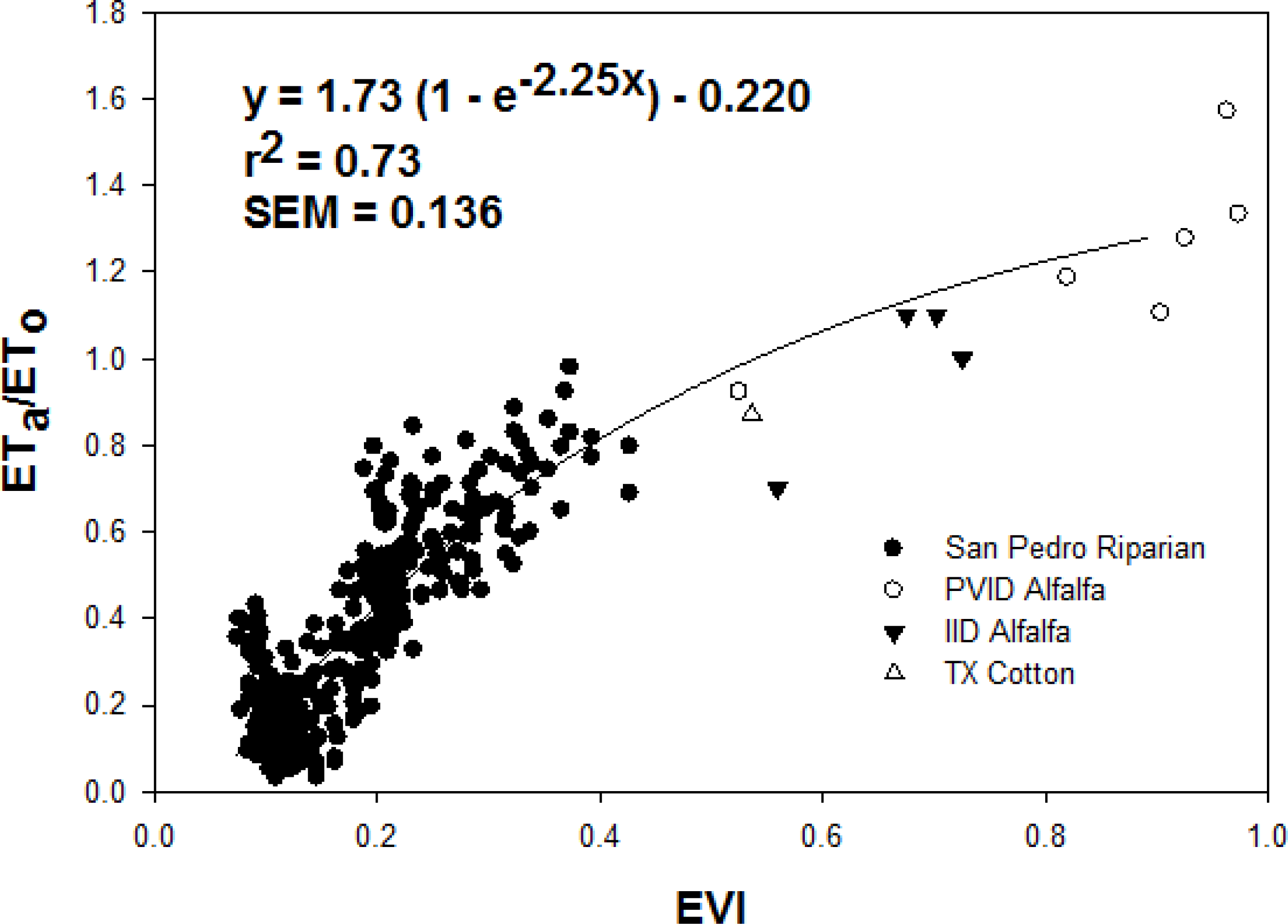
3.2. EVI vs. ETa/ETo for Combined Riparian and Crop Sites
3.3. Validation Data Sets
3.4. Final Equation for ETa
3.5. Limitations and Sources of Error and Uncertainty in ETo and ETa Estimates
3.6. Comparison with Other VI Methods for ETa
3.7. Comparison of VI and Thermal Band Methods to Estimate ETa
4. Conclusion
Acknowledgments
References
- Poff, N.L.; Allan, J.D.; Bain, M.B.; Karr, J.R.; Prestegaard, K.L.; Richter, B.D.; Sparks, R.E.; Stromberg, J.C. The natural flow regime. BioScience 1997, 47, 769–784. [Google Scholar]
- Thenkabail, P.S.; Hanjra, M.A.; Dheeeravath, V.; Gumma, M. A holistic view of global croplands and their water use for ensuring global food security in the 21st Century through advanced remote sensing and non-remote sensing approaches. Remote Sens 2010, 2, 211–261. [Google Scholar]
- Allen, R.G.; Clemmens, A.J.; Burt, C.M. Prediction accuracy for project-wide evapotranspiration using crop coefficients and reference evapotranspiration. J. Irrig. Drain. Eng 2005, 131, 1–24. [Google Scholar]
- Congalton, R.G.; Balough, M.; Bell, C.; Green, K.; Milliken, J.A.; Ottman, R. Mapping and monitoring agricultural crops and other land cover in the Lower Colorado River Basin. Photogram. Eng. Remote Sensing 1998, 64, 1107–1113. [Google Scholar]
- Allen, R.; Pereira, L.; Rais, D.; Smith, M.; Solomon, K.; O’Halloran, T. Crop Evapotranspiration—Guidelines for Computing Crop Water Requirements; FAO Irrigation and Drainage Paper 56; Food and Agriculture Organization of the United Nations: Rome, Italy, 1998. [Google Scholar]
- Glenn, E.; Huete, A.; Nagler, P.; Hirschboek, K.; Brown, P. Integrating remote sensing and ground methods to estimate evapotranspiration. Crit. Rev. Plant Sci 2007, 26, 139–168. [Google Scholar]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating land surface evaporation: A review of methods using remotely sensed surface temperature data. Surv. Geophys 2008, 29, 421–469. [Google Scholar]
- Neale, C.M.U.; Bausch, W.C.; Heermann, D.F. Development of reflectance-based crop coefficients for corn. Irrig. Sci 1989, 22, 95–104. [Google Scholar]
- Hunsaker, D.J.; Fitzgerald, G.J.; French, A.N.; Clarke, T.R.; Ottman, M.J.; Pinter, P.J. Wheat irrigation management using multispectral crop coefficients. I. Crop evapotranspiration prediction. Trans. ASABE 2007, 50, 2017–2033. [Google Scholar]
- Glenn, E.P.; Neale, C.M.U.; Hunsaker, D.J.; Nagler, P.L. Vegetation index-based crop coefficients to estimate evapotranspiration by remote sensing in agricultural and natural ecosystems. Hydrol. Process 2011, 25, 4050–4062. [Google Scholar]
- Choudhury, B.; Ahmed, N.; Idso, S.; Reginato, R.; Daughtry, C. Relations between evaporation coefficients and vegetation indices studies by model simulations. Remote Sens. Environ 1994, 50, 1–17. [Google Scholar]
- Tang, Q.; Huilin, G.; Lu, H. Evapotranspiration by remote sensing. Surv. Geophys 2010, 32, 490–509. [Google Scholar]
- Anderson, M.C.; Allen, R.G.; Morse, A.; Kustas, W.P. Use of Landsat thermal imagery in monitoring evapotranspiration and managing water resources. Remote Sens. Environ 2012, 122, 50–65. [Google Scholar]
- Gonzalez-Dugo, M.P.; Neale, C.M.U.; Mateos, L.; Kustas, W.P.; Anderson, M.C.; Li, F. A comparison of operational remote-sensing based models for estimating crop evapotranspiration. Agric. For. Meteorol 2009, 49, 2082–2097. [Google Scholar]
- Gonzalez-Dugo, M.P.; Escuin, S.; Cano, F.; Cifuentes, V.; Padilla, F.L.M.; Tirado, J.L.; Oyonarte, N.; Fernandez, P.; Mateos, L. Monitoring evapotranspiration of irrigated crops using crop coefficients derived from time series of satellite images. II. Application on basin scale. Agric. Water Manage 2013, 125, 92–104. [Google Scholar]
- Groeneveld, D.P.; Baugh, W.M.; Sanderson, J.S.; Cooper, D.J. Annual groundwater evapotranspiration mapped from single satellite scenes. J. Hydrol 2007, 344, 146–156. [Google Scholar]
- Nagler, P.L.; Morino, K.; Didan, K.; Osterberg, J.; Hultine, K.; Glenn, E. Wide-area estimates of saltcedar (Tamarix spp.) evapotranspiration on the lower Colorado River measured by heat balance and remote sensing methods. Ecohydrology 2009, 2, 18–33. [Google Scholar]
- Nagler, P.L.; Morino, K.; Murray, R.S.; Osterberg, J.; Glenn, E.P. An empirical algorithm for estimating agricultural and riparian evapotranspiration using MODIS Enhanced Vegetation Index and ground measurements of ET. I. Description of method. Remote Sens 2009, 1, 1273–1297. [Google Scholar]
- Allen, R.G. Using the FAO-56 dual crop coefficient method over an irrigated region as part of an evapotranspiration intercomparison study. J. Hydrol 2000, 229, 27–41. [Google Scholar]
- Seller, P.J.; Berry, J.A.; Collatz, G.J.; F. Dield, C.B.; Hall, F.G. Canopy reflectance, photosynthesis, and transpiration. III. A reanalysis using improved leaf models and a new canopy integration scheme. Remote Sens. Environ 1992, 42, 187–216. [Google Scholar]
- Johnson, L.F.; Trout, T.J. Satellite NDVI assisted monitoring of vegetable crop evapotranspiration in California’s San Joaquin Valley. Remote Sens 2012, 4, 439–455. [Google Scholar]
- Melton, F. TOPS Satellite Irrigation Management Support; NASA Ames Research Center: Ames, IA, USA, 2012. Available online: http://ecocast.arc.nasa.gov/sims/ (accessed on 1 August 2013).
- Barros, R.; Isidoro, D.; Aragues, R. Long-term water balances in La Violada irrigation district (Spain): I. Sequential assessment and minimization of closing errors. Agric. Water Manage 2011, 102, 35–45. [Google Scholar]
- Barros, R.; Isidoro, D.; Aragues, R. Long-term water balances in La Violada Irrigation District (Spain): II. Analysis of irrigation performance. Agric. Water Manage 2011, 98, 1569–1576. [Google Scholar]
- Nagler, P.; Scott, R.; Westenburg, C.; Cleverly, J.; Glenn, E.; Huete, A. Evapotranspiration on western US rivers estimated using the Enhanced Vegetation Index from MODIS and data from eddy covariance and Bowen ratio flux towers. Remote Sens. Environ 2005, 97, 337–351. [Google Scholar]
- Scott, R.L.; Cable, W.L.; Huxman, T.E.; Nagler, P.L.; Hernandez, M.; Goodrich, D.C. Multiyear riparian evapotranspiration and groundwater use for a semiarid watershed. J. Arid Environ 2008, 72, 1232–1246. [Google Scholar]
- Nichols, W.D. Groundwater discharge by phreatophyte shrubs in the Great Basin as related to depth to groundwater. Water Resour. Res 1994, 30, 3265–3274. [Google Scholar]
- Nippert, J.B.; Butler, J.J.; Liotemberg, G.J.; Whittemore, D.O.; Arnold, D.; Spal, C.E.; Ward, J.K. Patterns of Tamarix water use during a record drought. Oecologia 2010, 162, 283–292. [Google Scholar]
- Glenn, E.; Nagler, P. Comparative ecophysiology of Tamarix ramosissima and native trees in western US riparian zones. J. Arid Environ 2005, 61, 419–446. [Google Scholar]
- Sperry, J.; Adler, F.; Campbell, G.; Comstock, J. Limitation of plant water use by rhizosphere and xylem conductance: Results from a model. Plant Cell Environ 1998, 21, 347–359. [Google Scholar]
- Guerschman, J.P.; Van Kijk, I.J.M.; Mattersdorf, G.; Beringer, J.; Hutley, L.B.; Leuning, R.; Pipunic, R.C.; Sherman, B.S. Scaling of potential evapotranspiration with MODIS data reproduces flux observations and catchment water balance observations across Australia. J. Hydrol 2009, 369, 107–119. [Google Scholar]
- Nagler, P.; Glenn, E.; Thompson, T.; Huete, A. Leaf area index and Normalized Difference Vegetation Index as predictors of canopy characteristics and light interception by riparian species on the Lower Colorado River. Agric. For. Meteorol 2004, 116, 103–112. [Google Scholar]
- Potithep, S.; Nagai, S.; Nasahara, K.N.; Muraoka, H.; Suzuki, R. Two separate periods of the LAI-Vis relationships using in situ measurements in a deciduous broadleaf forest. Agric. For. Meteorol 2013, 169, 148–155. [Google Scholar]
- Scott, R.L.; Edwards, E.A.; Shuttleworth, W.J.; Huxman, T.E.; Watts, C.; Goodrich, D.C. Interannual and seasonal variation in fluxes of water and carbon dioxide from a riparian woodland ecosystem. Agric. For. Meteorol 2004, 122, 65–84.35. [Google Scholar]
- Scott, R.L.; Huxman, T.E.; Williams, D.G.; Goodrich, D.C. Ecohydrological impacts of woody-plant encrhoachment: Seasonal patterns of water and carbon dioxide exchange within a semiarid riparian environment. Glob. Change Biol 2006, 12, 311–324. [Google Scholar]
- Wilson, K.; Goldstein, A.; Falge, E.; Aubinet, M.; Baldocchi, D.; Berbigier, P.; Bernhofer, C.; Ceulemans, R.; Dolman, H.; Field, C.; et al. Energy balance closure at FLUXNET sites. Agric. For. Meteorol 2002, 113, 223–243. [Google Scholar]
- Twine, T.E.; Kustas, W.P.; Norman, J.M.; Cook, D.R.; Houser, P.R.; Meyers, T.P.; Prueger, J.H.; Starks, P.J.; Wesley, M.L. Correcting eddy-covariance flux underestimates at a grassland site. Agric. For. Meteorol 2000, 103, 279–300. [Google Scholar]
- Chatterjee, S. Estimating Evapotranspiration Using Remote Sensing: A Hybrid Approach between MODIS Derived Enhanced Vegetation Index, Bowen Ratio System, and Ground-based Micrometeorological Data; Ph.D. Dissertation; Wright State University: Dayton, OH, USA, 2010. [Google Scholar]
- Arizona Meteorological Network (AZMET); University of Arizona, College of Agriculture and Life Sciences: Tucson, AZ, USA, 2013. Available online: http://ag.arizona.edu/azmet/ (accessed on 1 August 2013).
- Hanson, B.; Orloff, S.; Bali, K.; Sanden, B.; Putnam, D. Evapotranspiration of Fully-Irrigated Alfalfa in Commercial Fields. 2011 Conference Proceedings: Agricultural Certification Programs-Opportunities and Challenges, Fresno, CA, USA, 1–2 February 2011; pp. 83–86. Available online: http://calasa.ucdavis.edu/files/73479.pdf#page=80 (accessed on 1 August 2013).
- California Irrigation Management System (CIMIS). State of California, 2013. Available online: http://wwwcimis.water.ca.gov/cimis/welcome.jsp (accessed on 1 August 2013).
- Evett, S.R.; Schwartz, R.C.; Howell, T.A.; Baumhardt, R.L.; Copeland, K.S. Can weighing lysimeter ET represent surrounding field ET well enough to test flux station measurements of daily and sub-daily ET? Adv. Water. Resour 2012, 50, 79–90. [Google Scholar]
- Taghvaeian, S.; Neale, C.M.U. Water balance of irrigated areas: A remote sensing approach. Hydrol. Process 2011, 25, 4132–4141. [Google Scholar]
- US Bureau of Reclamation. Compilation of Records in Accordance with Article V of the Decree of the Supreme Court of the United States in Arizona v. California et al. Calendar Year 2001; US Bureau of Reclamation: Boulder City, NV, USA, 2002; Available online: http://www.usbr.gov/lc/region/g4000/4200Rpts/DecreeRpt/2001DecreeRpt.pdf (accessed on 1 August 2013).
- Colorado River Board of California. Report to the California Legislature on the Current Condition and Potential Impacts of Water Transfers; Colorado River Board of California: Glendale, CA, USA, 1992. Available online: http://www.sci.sdsu.edu/salton/PotentialImpactsSaltonSea.html (accessed on 1 August 2013).
- Greenwood, K.L.; Mundya, G.N.; Keyy, B. On-farm measurement of the water use and productivity of maize. Austral. J. Exp. Agric 2008, 48, 274–284. [Google Scholar]
- Lecina, S.; Neale, C.M.U.; Merkley, G.P.; dos Santos, C.A.C. Irrigation evaluation based on performance analysis at the Bear River Irrigation Project (U.S.A.). Agric. Water Manage 2011, 98, 1394–1363. [Google Scholar]
- Imrak, S.; Kabenge, I.; Rudnick, D.; Knezevic, S.; Woodward, D.; Moravek, M. Evapotranspiration crop coefficients for mixed riparian plant community and transpiration crop coefficients for Common reed, Cottonwood and Peach-leaf willow in the Platte River Basin, Nebraska U.S.A. J. Hydrol 2012, 481, 177–190. [Google Scholar]
- Oak Ridge National Laboratory Distributed Active Archive Center (ORNL DAAC). MODIS Subsetted Land Products. Collection 5. 2013. Available online: http://daac.ornl.gov/MODIS/modis.html (accessed on 1 August 2013).
- Fisher, J.B.; Baldocchi, D.D. Global estimates of the land-atmosphere water flux based on monthly AVHRR and ISLSCP-II data, validated at 16 FLUXNET sites. Remote Sens. Environ 2008, 112, 901–919. [Google Scholar]
- Brown, P.; Kopec, D. Converting Reference Evapotranspiration into Turf Water Use. Irrigation Management Series II; University of Arizona Agricultural Extension Service: Tucson, AZ, USA, 2000. Available online: http://ag.arizona.edu/pubs/water/az1195.pdf (accessed on 1 August 2013).
- Allen, R.G.; Pereira, L.S.; Howell, T.A.; Jensen, M.A. Evapotranspiration information reporting: I. Factors governing measurement accuracy. Agric. Water Manage 2011, 98, 899–920. [Google Scholar]
- Yebra, M.; Van Dijk, A.; Leuning, R.; Huete, A.; Guerschman, J.P. Evaluation of optical remote sensing to estimate actual evapotranspiration and canopy conductance. Remote Sens. Environ 2013, 129, 250–261. [Google Scholar]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS global terrestrial evapotranspiration product. Remote Sens. Environ 2011, 115, 1781–1800. [Google Scholar]
- Fisher, J.B.; Whittaker, R.J.; Malhi, Y. ET come home: potential evapotranspiration in geographical ecology. Glob. Ecol. Biogeogr 2011, 20, 1–18. [Google Scholar]
- Glenn, E.P.; Monino, K.; Nagler, P.L.; Hultine, K.R. Phreatophytes under stress: Transpiration and stomatal conductance of saltcedar (Tamarix spp.) in a high-salinity environment. Plant Soil 2013. [Google Scholar] [CrossRef]
- Allen, R.G.; Tasumi, M.; Morse, A.; Trezza, R.; Wright, J.; Nsdyissnddrn, E.; Kramber, W.; Lorite, I.; Robison, C.W. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (METRC)—Applications. J. Irrig. Drain. Eng 2007, 138, 394–406. [Google Scholar]
- King, E.A.; van Niel, T.G.; van Djik, A.; Wang, Z.; Paget, M.J.; Raupach, T.; Guerschman, J.; Haverd, V.; McVicar, T.R.; Miltenberg, I.; et al. Actual Evapotranspiration Estimates for Australia. Intercomparison and Evaluation; CSIRO: Canberra, ACT, Australia, 2011. [Google Scholar]

| Location | MODIS EVI (mm·yr−1) | Ground Measurement (mm·yr−1) | No. Years Data | ETa/ETo | Difference between Means (%) | Ground Method | Ref. |
|---|---|---|---|---|---|---|---|
| PVID Crops | 1,369 | 1,268 | 1 | 0.72 | 7.7 | WB | [43] |
| IID Crops | 1,144 | 1,194 | 1 | 0.65 | 4.3 | WB | [44] |
| VAU Maize2 | 726 | 666 | 2 | 0.72 | 8.6 | WB | [46] |
| BRIP3 | 903 | 877 | 1 | 0.75 | 2.9 | WB | [47] |
| LVSP | 676 | 616 | 8 | 0.66 | 9.3 | WB | [23] |
| CNWR | 886 | 817 | 1 | 0.46 | 8.1 | BR | [38] |
| Riparian | |||||||
| PR Riparian1 | 431 | 370 | 2 | 0.63 | 7.7 | BR | [48] |
| Mean | 876 | 830 | - | - | 5.4 |
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Nagler, P.L.; Glenn, E.P.; Nguyen, U.; Scott, R.L.; Doody, T. Estimating Riparian and Agricultural Actual Evapotranspiration by Reference Evapotranspiration and MODIS Enhanced Vegetation Index. Remote Sens. 2013, 5, 3849-3871. https://doi.org/10.3390/rs5083849
Nagler PL, Glenn EP, Nguyen U, Scott RL, Doody T. Estimating Riparian and Agricultural Actual Evapotranspiration by Reference Evapotranspiration and MODIS Enhanced Vegetation Index. Remote Sensing. 2013; 5(8):3849-3871. https://doi.org/10.3390/rs5083849
Chicago/Turabian StyleNagler, Pamela L., Edward P. Glenn, Uyen Nguyen, Russell L. Scott, and Tanya Doody. 2013. "Estimating Riparian and Agricultural Actual Evapotranspiration by Reference Evapotranspiration and MODIS Enhanced Vegetation Index" Remote Sensing 5, no. 8: 3849-3871. https://doi.org/10.3390/rs5083849
APA StyleNagler, P. L., Glenn, E. P., Nguyen, U., Scott, R. L., & Doody, T. (2013). Estimating Riparian and Agricultural Actual Evapotranspiration by Reference Evapotranspiration and MODIS Enhanced Vegetation Index. Remote Sensing, 5(8), 3849-3871. https://doi.org/10.3390/rs5083849






