Next Article in Journal
Dynamic Assessment of Soil Erosion Risk Using Landsat TM and HJ Satellite Data in Danjiangkou Reservoir Area, China
Next Article in Special Issue
Evaluating and Quantifying the Climate-Driven Interannual Variability in Global Inventory Modeling and Mapping Studies (GIMMS) Normalized Difference Vegetation Index (NDVI3g) at Global Scales
Previous Article in Journal
Application of Landsat to Evaluate Effects of Irrigation Forbearance
Previous Article in Special Issue
Evaluation of Land Surface Models in Reproducing Satellite Derived Leaf Area Index over the High-Latitude Northern Hemisphere. Part II: Earth System Models
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 5
Issue 8
10.3390/rs5083803
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Disentangling the Relationships between Net Primary Production and Precipitation in Southern Africa Savannas Using Satellite Observations from 1982 to 2010

by
Likai Zhu
* and
Jane Southworth
Department of Geography, University of Florida, Gainesville, FL 32611, USA
*
Author to whom correspondence should be addressed.
Remote Sens. 2013, 5(8), 3803-3825; https://doi.org/10.3390/rs5083803
Submission received: 18 June 2013 / Revised: 29 July 2013 / Accepted: 29 July 2013 / Published: 2 August 2013
(This article belongs to the Special Issue Monitoring Global Vegetation with AVHRR NDVI3g Data (1981-2011))
Browse Figures
Versions Notes

Abstract

:
To obtain a better understanding of the variability in net primary production (NPP) in savannas is important for the study of the global carbon cycle and the management of this particular ecosystem. Using satellite and precipitation data sets, we investigated the variations in NPP in southern African savannas from 1982 to 2010, and disentangled the relationships between NPP and precipitation by land cover classes and mean annual precipitation (MAP) gradients. Specifically, we evaluate the utility of the third generation Global Inventory Monitoring and Modeling System (GIMMS3g) normalized difference vegetation index (NDVI) dataset, in comparison with Moderate-resolution Imaging Spectroradiometer (MODIS) derived NPP products, and find strong relationships between the overlapping data periods (2000–2010), such that we can apply our model to derive NPP estimates to the full 29-year NDVI time-series. Generally, the northern portion of the study area is characterized by high NPP and low variability, whereas the southern portion is characteristic of low NPP and high variability. During the period 1982 through 2010, NPP has reduced at a rate of −2.13 g·C·m−2·yr−1 (p < 0.1), corresponding to a decrease of 6.7% over 29 years, and about half of bush and grassland savanna has experienced a decrease in NPP. There is a significant positive relationship between mean annual NPP and MAP in bush and grassland savannas, but no significant relationship is observed in tree savannas. The relationship between mean annual NPP and MAP varies with increases in MAP, characterized as a linear relationship that breaks down when MAP exceeding around 850–900 mm.

1. Introduction

Vegetation over terrestrial ecosystems is a major component of the global carbon cycle since it regulates climate through the exchange of energy, water vapor, and momentum between the land surface and the atmosphere, controls CO2 and currently absorbs about one-third of anthropogenic fossil fuel emissions to the atmosphere [1–3]. Terrestrial net primary production (NPP), known as the difference between carbon gain via gross primary productivity (GPP) and carbon loss through plant respiration, integrates these and other climatic, ecological, geochemical, and human influences on the biosphere [4–6]. Several studies have developed a global and regional understanding of NPP variations though methods, time periods used and results have varied. Nemani et al. [4] has reported a global increase in NPP by 3.4 petagrams of carbon between 1982 and 1999, based on estimates modeled using AVHRR data inputs and climate variables, with 80% of the increase being attributable to ecosystems in tropical regions (mainly rainforests) and those in the high latitudes of the North Hemisphere (NH). Studies have demonstrated that terrestrial NPP has increased in the middle and high latitudes in the NH [3–9] during the 1980–1999 time period. However, Zhao and Running [10] concluded that NPP reduced by 0.55 petagrams of carbon globally from 2000 to 2009, when studied using Moderate-resolution Imaging Spectroradiometer (MODIS) derived input data in association with climate. As such, over the longer time frame of 1980 through 2010 there is still no agreement on global GPP or NPP change [11] and there is still much uncertainty even with the availability of satellite observations for the past three decades. From the studies to date it is clear that location is key, with many northern hemisphere higher latitude regions showing initial (1982–1999) increases in biomass [4,5], but in the latter period of 2000–2010, declines also becoming obvious especially in southern hemisphere and tropical locations [5]. Given the global importance of these trends, in terms of the potential decline in the rate of carbon sequestration in vegetated systems, understanding the multi-decadal patterns of NPP trends is of paramount importance [5].
Atmospheric CO2 is an essential component in photosynthesis, and thus influence vegetation production. Higher concentrations may improve plant growth known as the “fertilization effect”, which is limited by nutrients, air pollution, temperature, and precipitation [12]. Also there is general agreement among scientists that the climate system is changing as a result of increasing atmospheric concentrations of CO2, although the degree to which temperature and precipitation patterns will change is still uncertain. Temperature, radiation, and water interact to impose complex limitations on vegetation activity in different parts of the world, and ultimately determine the spatial and temporal NPP patterns [4]. However, these factors tend to be co-limiting, and differ in their contribution in different ecosystems. In the middle and high latitudes, in the NH, where temperature is limited, higher temperatures have increased NPP by enhancing vegetation growth [4,6,8,13]. In the tropics (23.5°S to 23.5°N) the NPP variation is largely constrained by solar radiation due to severe cloudiness [10,14]. In drier and colder ecosystems NPP increases linearly with the increase in mean annual precipitation and mean annual temperature [15]. In the arid and semi-arid ecosystems and seasonally dry tropical climates NPP is primarily controlled by water availability as precipitation can trigger the emergence of green leaves and controls growth duration [16,17].
Savanna ecosystems, which are characterized by the coexistence of trees and grasses, are more sensitive to climate variability, especially precipitation changes. Savanna is a relatively productive ecosystem with an average of 720 ± 200 g·C·m−2·yr−1 [18], and the entire African savanna biome gives an NPP of 8.9 Pg·C·yr−1, accounting for 13.6% of the global NPP. There are still large uncertainties about the contribution of the African continent to the global carbon budget, since few long-term measurements have been carried out [19]. The degradation of savannas, which is defined as the reduction in vegetation production, will influence the long-term carbon balance and other ecosystem services [20]. There is a pressing need for quantitative assessments of land degradation as savanna ecosystems are essential for local populations [17] and have been changing largely as a result of climate change and overgrazing. Research on long-term NPP change can provide an early warning of land degradation and be used to support policy development for food security and economic development [21].
The emergence and development of remote sensing has provided a powerful instrument to observe, monitor and characterize landscapes, since it is able to offer repeat data of large areas of the terrestrial earth surface at longer temporal scales [22]. Satellite data can provide realistic information on vegetation dynamics, which is helpful to reduce uncertainties in the estimation of the carbon-budget [14]. Based on remote sensing data, partially or entirely, a variety of models have been developed to estimate NPP, e.g., the Carnegie-Ames-Stanford approach (CASA) [1], GLObal Production Efficiency Model (GLO-PEM) [2], the Biosphere model integrating Eco-physiological And Mechanistic approaches (BEAMS) [23], and MODIS daily photosynthesis and annual NPP product (MOD17) [24]. However, a long-term NPP time series is still unavailable, although the introduction of the newly released AVHRR GIMMS3g dataset will invariably help to address this gap. In this study two globally available data sets of the earth’s surface will be analyzed and we will investigate the variations in NPP derived from (1) GIMMS3g NDVI data and (2) the monthly MODIS NPP product (MOD17A2). These datasets will be used initially to compare the products and then to apply developed methods form the comparison to the entire AVHRR GIMMS3g thirty year time-series. We will then link this longer time series of vegetation changes to precipitation variability from 1982 to 2010. We address three main research questions: (1) Can we use the GIMMS3g products to estimate NPP from 1982 to 2010 based only on its relationship to the MODIS MOD17 NPP product? (2) How has NPP changed from 1982 to 2010 across the study area? and (3) What are the relationships between mean annual precipitation (MAP) and annual NPP, as they vary across the main three savanna types and MAP intervals?

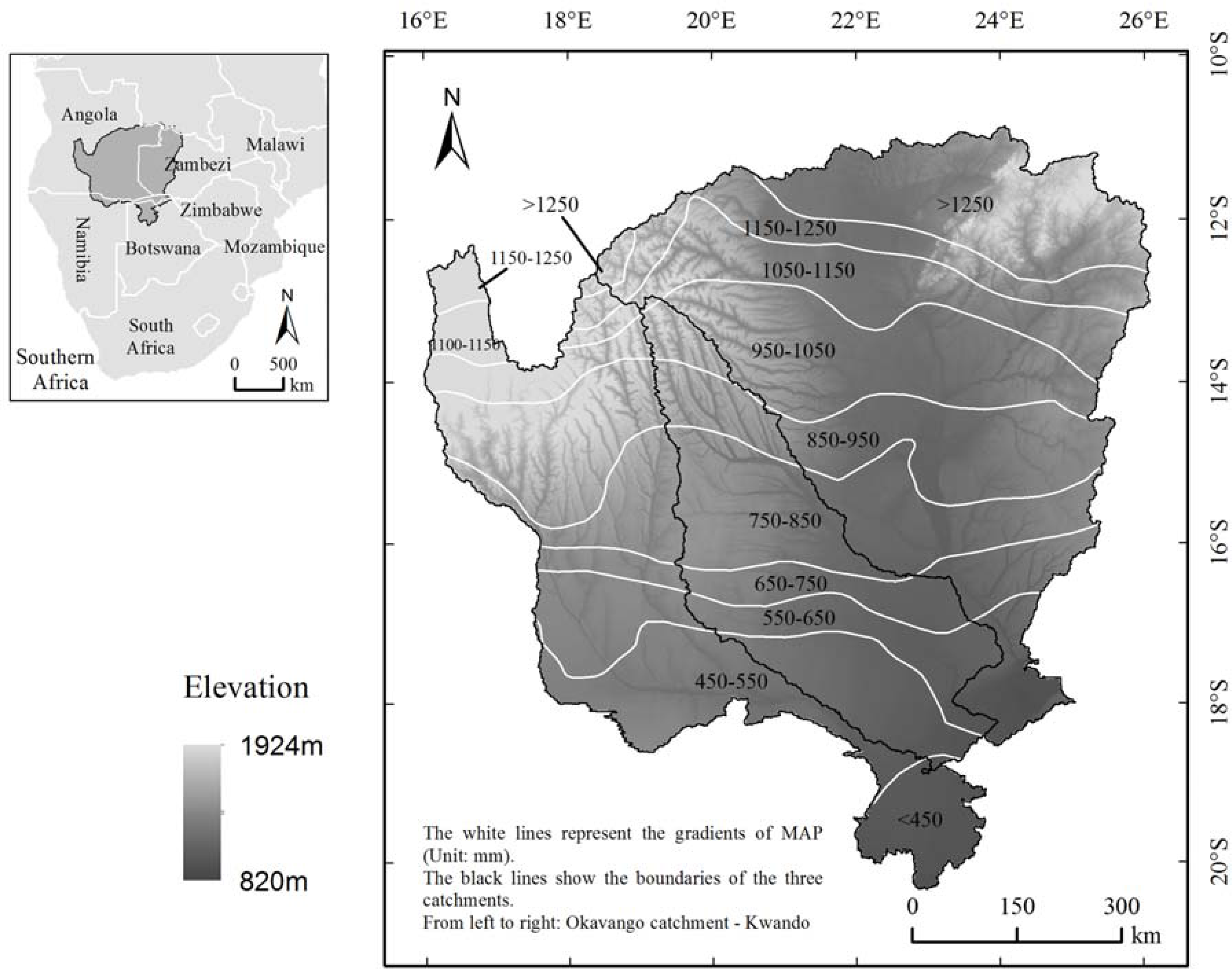
2. Study Area

The Okavango, Kwando, and upper Zambezi (OKZ) catchments cover about 693,000 km2 in Zambia, Angola, Namibia, and Botswana (Figure 1). The elevation in this region ranges from 800 m to 1,900 m. The combined basins have an annual precipitation range from 400 to 1,300 mm·yr−1. The southern portion is semi-arid and is characterized by scarce annual precipitation and high inter-annual variability, while the northern part is characterized by higher annual rainfall and relatively low inter-annual variability. Multi-decadal trends over the latter half of the 20th Century indicates declining MAP, increasing variability, and an increased number of warm phase ENSO events [25]. The majority of the Okavango and Kwando catchments and the headwaters of all three basins are located in Angola. Low topography in the south (especially the Caprivi and northern Botswana) makes clear hydrologic separation of the catchments difficult. Kalahari sand characterizes a large portion of the region’s soil. The upper catchment is characterized by Miombo woodlands, while the lower region is a mixed composition of tree-shrub-grass savannas. This region possesses one of the largest free ranging populations of elephants in Africa. Human settlements are mainly distributed along water courses, especially along rivers in the Caprivi region of Namibia, which makes the human-wildlife conflicts acute in the dry season [26]. The future Kawango-Zambezi Transboundary Conservation Area (KAZA), the largest in Africa, will span nations attempting to achieve regional-scale conservation through cooperative management of shared natural resources [27] and will cover much of this study region.

3. Data and Methods

3.1. Data Sets

The GIMMS3g NDVI data set was used in this study, which has a spatial resolution of about 8 km and a temporal resolution of 15 days. This data set was previously developed by the Global Inventory Modeling and Mapping Studies (GIMMS) group, and is currently available from July 1981 to December 2011 generated in the framework of the Global Inventory Monitoring and Modeling System (GIMMS) project at NASA Goddard Space Flight Center. No atmospheric correction is applied to the GIMMS data except for volcanic stratospheric aerosol periods (1982–1984 and 1991–1994) [22]. A satellite orbital drift correction is performed using the empirical decomposition/reconstruction methods, minimizing effects of orbital drift by removing common trends between time series Solar Zenith Angle and NDVI [17]. Additionally, this data set has been corrected for factors that do not relate to changes in vegetation greenness, and applies an improved cloud masking as compared to older versions of the GIMMS NDVI data set. The GIMMS3g NDVI data use the maximum NDVI value over a 15-day period to represent each 15-day interval to minimize corruption of vegetation signals from atmospheric effects, cloud contamination, scan angle effects and so on at the time of measurement [28]. The maximum value composite (MVC) method was used to obtain monthly NDVI from January 1982 to December 2010 to further reduce cloud effects, and the pixels with mean annual NDVI value less than 0.2 were removed to reduce the effect of non-vegetation cover. Overall, the GIMMS3g archive is considered the best dataset available for long-term trend analysis of vegetation greenness.
A second satellite based dataset, overlapping for 11 years with the AVHRR data was also utilized in this research, the monthly MODIS NPP product (MOD17A2), which spans from January 2000 to December 2010 at a 1-km spatial resolution [5,24]. It is the first regular, near-real-time data set for repeated monitoring of NPP over vegetated land [29]. The principle of the MOD17 algorithm is the application of the radiation conversion efficiency logic to predictions of daily GPP and the subsequent estimation of maintenance and growth respiration terms that are subtracted from GPP to arrive at NPP [24,25]. These data are freely available to the public from the Numerical Terradynamic Simulation Group (NTSG) at the University of Montana. The study area covers three tiles: h19v10, h20v10, and h20v11. Based on the QA information, only the pixels of good quality (labeled with “0”) were considered. To match the grid cell size of MODIS NPP data with other data sets, we adopted a simple but frequently used way to resample. The values of each 9 × 9 grid block were average to create a single pixel, if the values with “good quality” were more than 80% of the total after the values out of 2-time standard deviation were removed.
We chose the Matsuura and Willmott data set of monthly precipitation (1982–2010) which has a spatial resolution of 0.5 degree by 0.5 degree with grid nodes centered on 0.25 degree. These datasets improve upon a previous global mean monthly dataset with a refined Shepard interpolation algorithm and an increased number of neighboring station points included in the analysis [30]. Based on the grid nodes included in the three catchments we interpolated the datasets into continuous surfaces with a spatial resolution of about 0.08 degrees using inverse distance weighted interpolation.
A land cover map of Africa derived by the Global Land Cover (2000) project was used, which has a spatial resolution of 1-km [31]. The map is based on daily observations made from November 1999 to December 2000 by the VEGETATION sensor on the SPOT4 satellite. The thematic accuracy of the map is higher at aggregated levels; thus, leaving the classification at the level of forests, shrublands and grasslands results in a higher class confidence than more specific class labels. In this study, the detailed land cover classes were aggregated into three categories: tree savanna, bush savanna, and grassland savanna (Figure 2). Tree savanna is defined as a tree-dominated savanna with tree canopy cover more than 15% and canopy height more than 5 m, bush savanna is defined as a shrub-dominated savanna type with shrub canopy cover greater than 15% and canopy height less than 5 m with no or sparse tree layer, and grassland savanna is defined as a grass-dominated savanna type with herbaceous cover greater than 15% and tree and shrub canopy cover less than 20%. Tree savanna is mainly distributed in the northern half of the study area, bush savanna is largely distributed in the southeast, and grassland savanna is distributed in the southwest and in the upper reach of Zambezi River (Figure 2). The size of grid is resampled to 0.08 by 0.08 degree to match the spatial resolution of the GIMMS3g NDVI data set.

3.2. Deriving Monthly Net Primary Production (NPP) Data Set

The conversion from the GIMMS3g NDVI into estimated NPP was done from per-pixel correlations between the 11 overlapping years of monthly GIMMS3g NDVI and MODIS NPP (2000–2010) data. The per-pixel strength of the linear relationship between these two data sets was determined by calculating the Pearson correlation coefficient for the 11-year monthly observations (Figure 3). Meanwhile, the significance value of each pixel was used to assess the confidence of its corresponding correlation coefficient. The 11 overlapping years were split into two periods: 7 years for model calibration and 4 years for model validation. A bootstrapping regression model was used for the model calibration, with the pixels of significant and positive correlation coefficient with the monthly MODIS NPP (2000–2006) as the dependent variable and the monthly NDVI as the independent variable. The bootstrapping regression model is a nonparametric approach to statistical inference which is more general and robust than traditional distributional assumptions [32]. The outputs, including per-pixel mean slope and intercept, were then used to validate and predict the per-pixel NPP time series. Figure 4 illustrates the outputs of the bootstrapping regression model for one example pixel (Lat: −15.44°S; Lon: 23.25°E). As such, a monthly time series of estimated NPP pixel level values were created for the GIMMS3g NDVI data, for the entire study area from 1982 to 2010. These data are then utilized in the model evaluation (2007–2010) and the remaining analyses. The eddy covariance data from the CarboAfrica database were used to validate the MODIS NPP dataset which is the benchmark of our estimates. There are two eddy covariance flux sites of savannas within our study area: the Botswana site (Maun, 19.9165°S, 23.5603°E) and the Zambian site (Mongu, 15.4388°S, 23.2525°E). The former is covered by typical mopane woodland, while the vegetation of the latter is broadleaf deciduous miombo woodland. Both vegetation types are representative in our study area. The Level-4 records are available with GPP on varying time intervals including hourly, daily, weekly, and monthly. Although there was still much uncertainty of NPP/GPP ratios of different ecosystem types, here a value of 60% was used to estimate NPP fluxes from Level 4 estimates of GPP based on the empirical relationship from Zhang et al. [33].

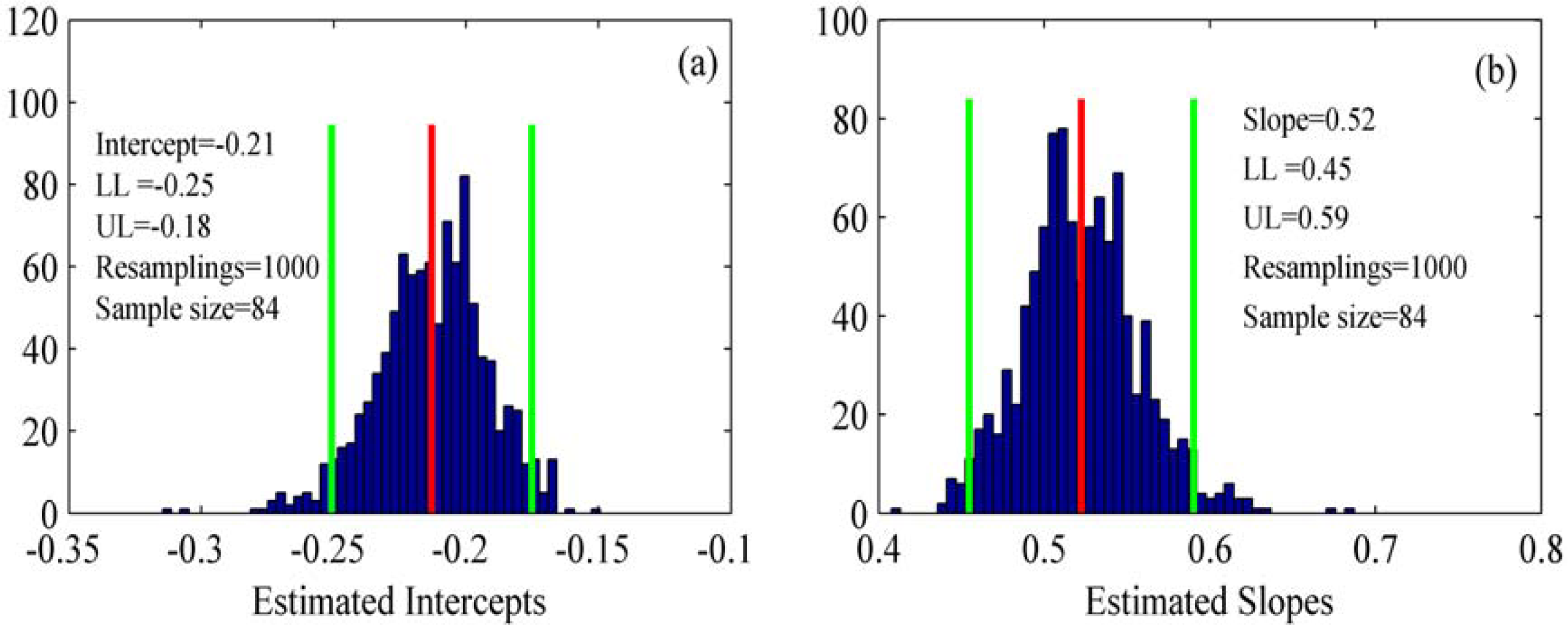
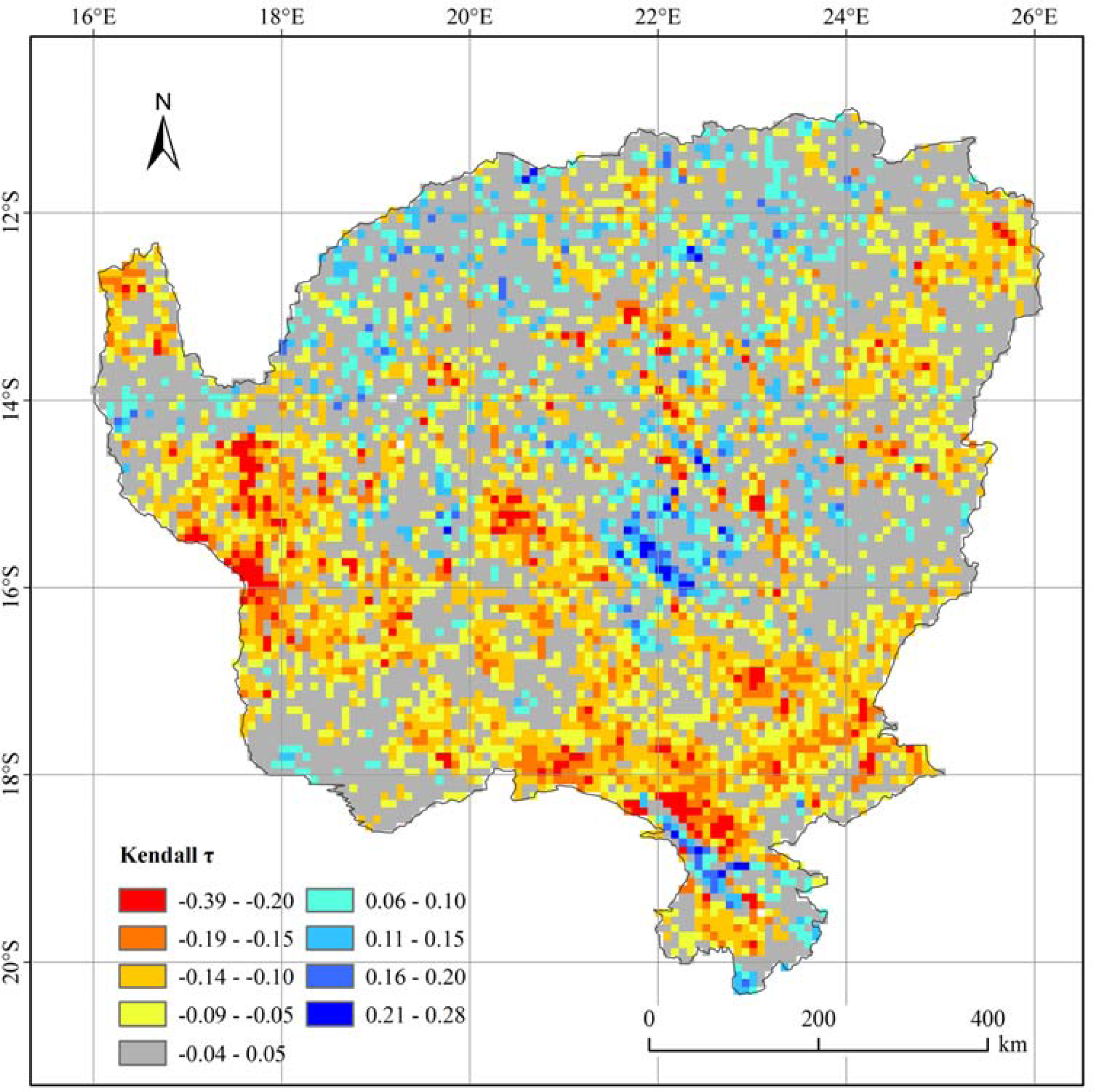
3.3. Net Primary Production (NPP) Trend Analysis

To detect the changing trends in NPP across the study region, the seasonal Kendall test was applied. It is a non-parametric test which can address the time series with seasonal variation, having missing values, tied values, or outliers, and does not require normality of the time series [34]. It is widely used in the field of hydrology to evaluate the significance of trends in time series such as water quality, stream flow, and precipitation [34–36]. This method is developed from the Mann-Kendall test which is based on the correlation between the ranks of a time series and their time order, but is improved to be able to use seasonal data sets to address variability [34]. The seasonal Kendall test was conducted on the per-pixel NPP time series to obtain the spatial pattern of changing trends. The significant and positive Kendall correlation coefficient (τ) value indicates an increasing trend, while the significant and negative τ value suggests a decreasing trend.

4. Results

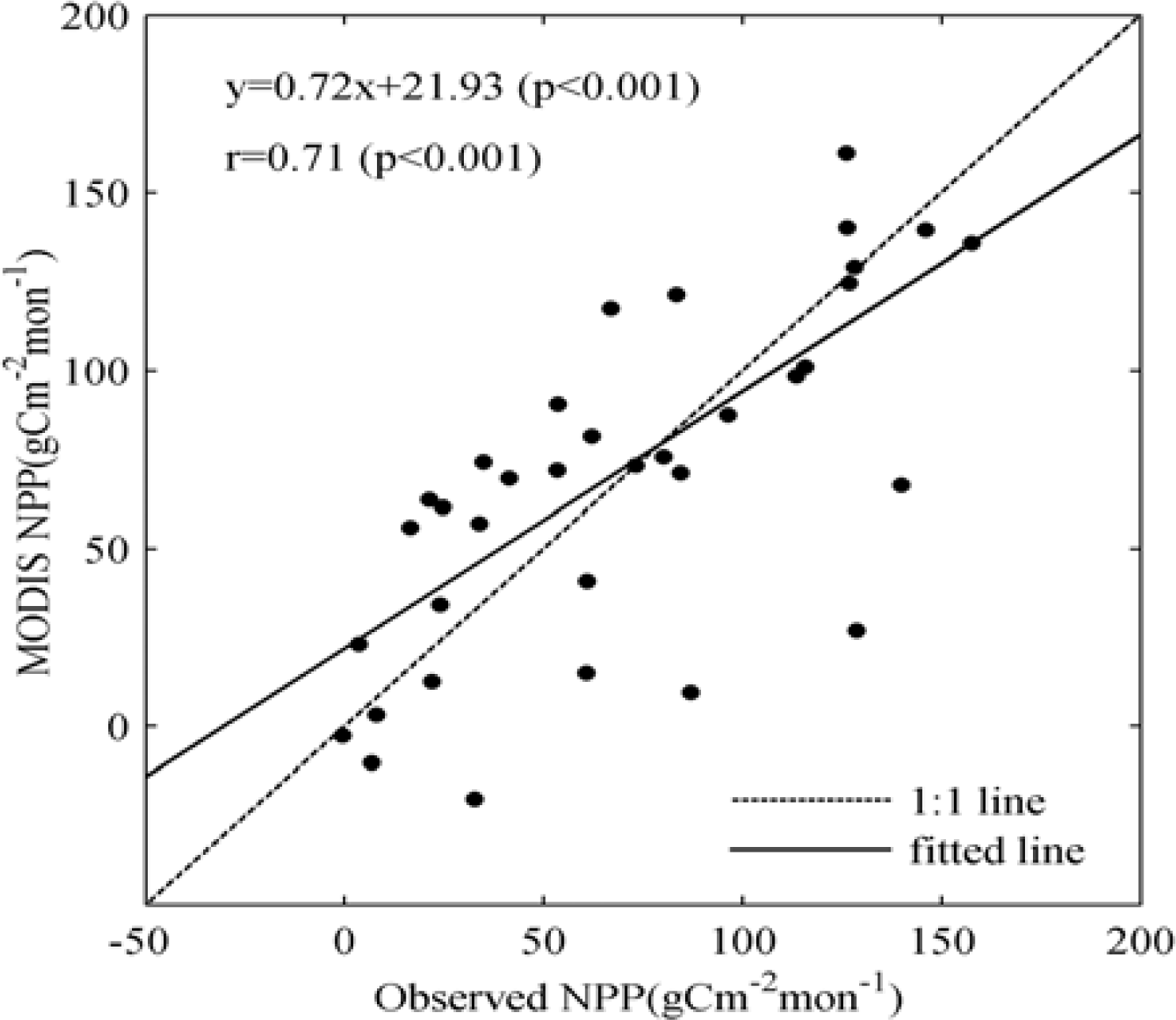
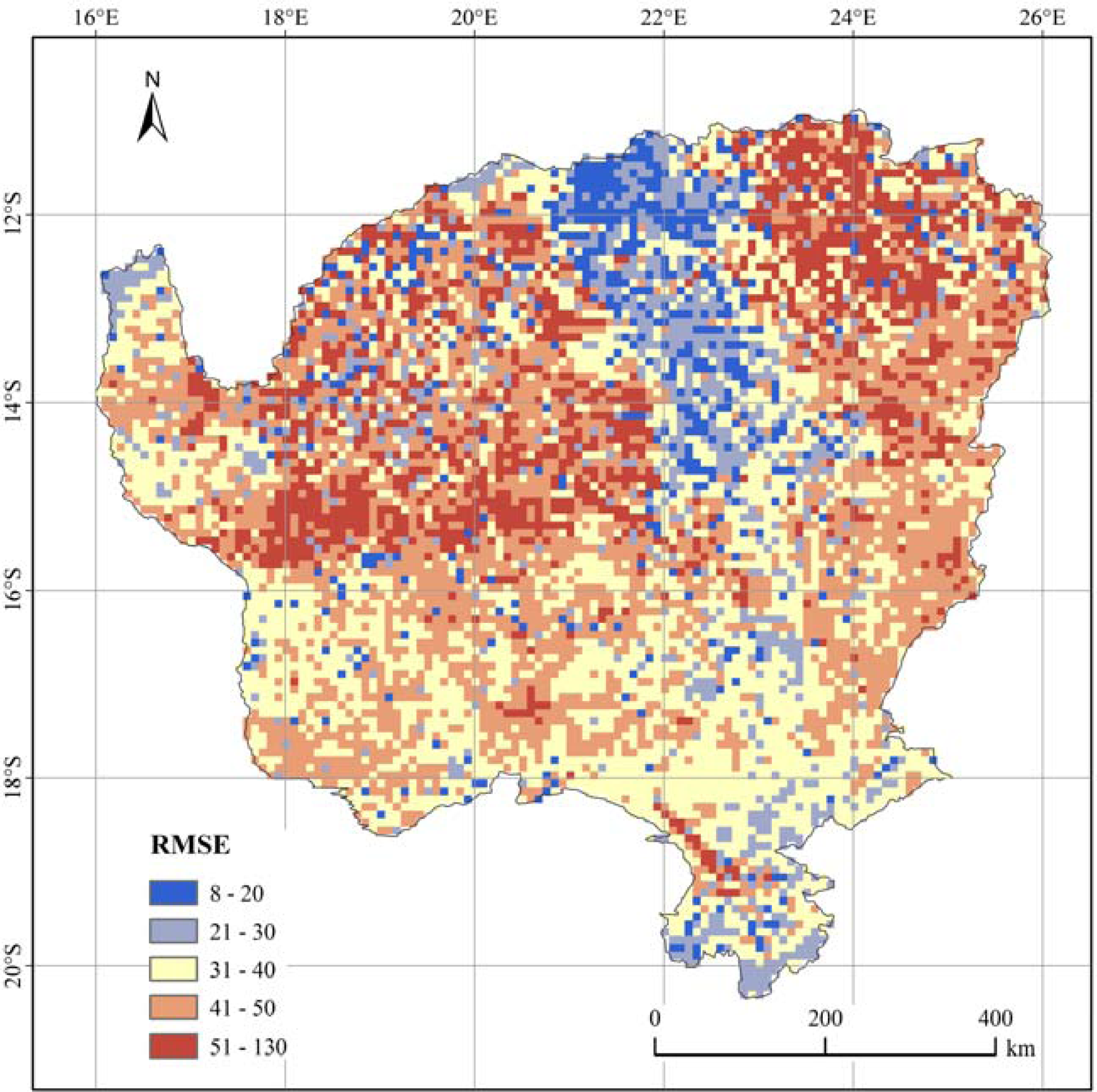
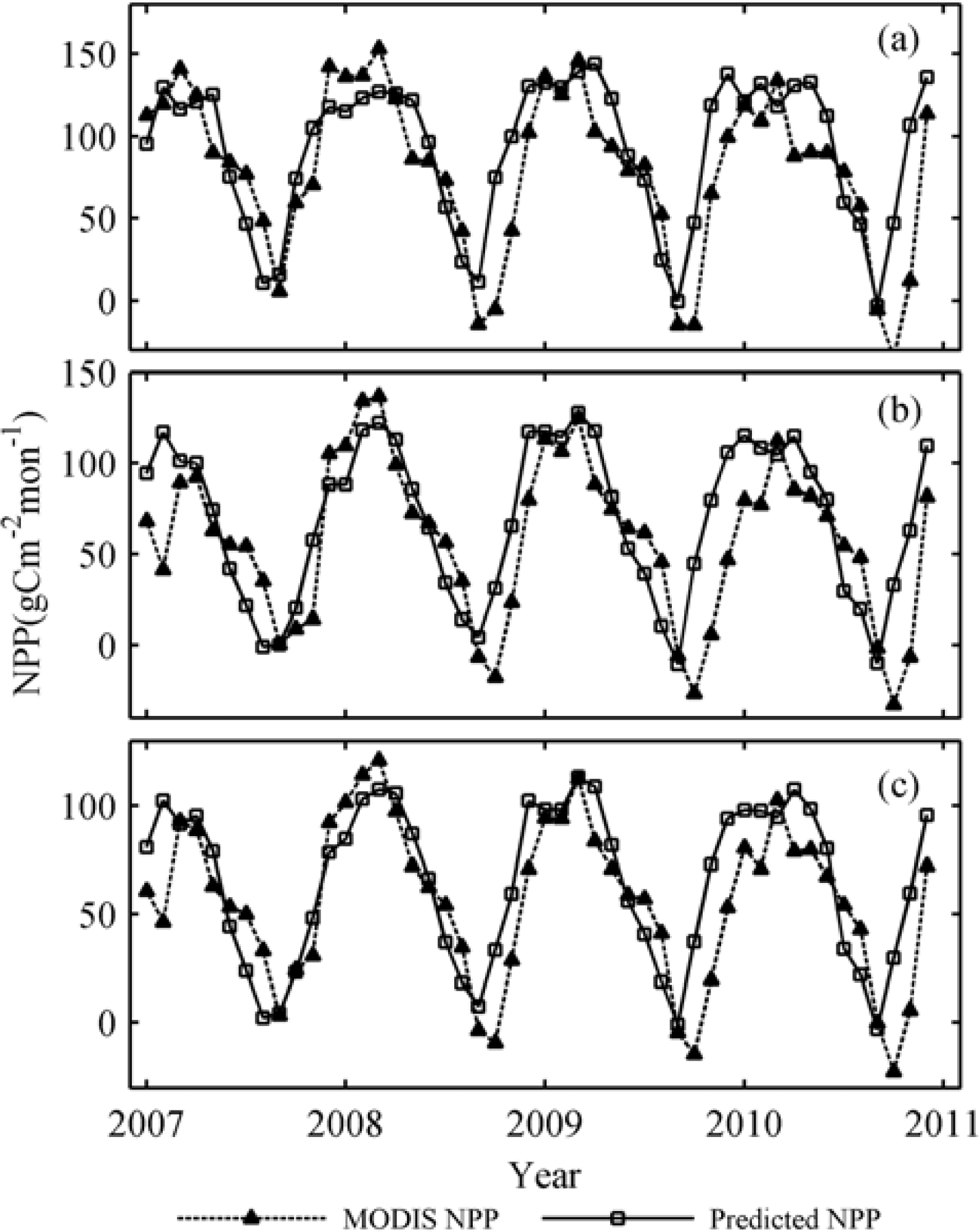
4.1. Assessment of the Derived Monthly Net Primary Production (NPP)

A comparison of monthly NPP from eddy covariance flux sites and MODIS monthly NPP shows that a highly significant and positive correlation exists and a close 1:1 match of field-based and MODIS NPP is observed (Figure 5).
Across the study area, the correlation coefficients between monthly NDVI values and monthly MODIS NPP values (both for 2000–2010) are universally positive, and statistically significant (Figure 3). The mean correlation coefficients of tree, bush, and grassland savanna is 0.71, 0.73, and 0.74, respectively, which indicates that a strong linear relationship for all cover types. As NDVI has strong linear relationship with NPP in the study area, bootstrapping regression can be used to derive estimated or predicted NPP from the NDVI data set [17]. To assess the performance of predictions, we calculated the per-pixel root mean square error (RMSE) based on the predicted NPP and original MODIS NPP from 2007 to 2010 (Figure 6). The RMSE for tree savanna, bush savanna, and grassland savanna is 44.15, 38.78 and 33.03, respectively. This indicates that the predictions of NPP of grassland savanna are more accurate than that of bush and tree savanna, but that all performed well and are more than acceptable for use here. The spatial pattern of mean annual predicted NPP (calculated across water years, from September to August) is consistent with that of mean annual MODIS NPP (Figure 7a,b) for the overlapping 4 years. The predicted NPP value of different land cover classes is also close to the original NPP value.
The model’s seasonal NPP results were evaluated using MODIS NPP from 2007 to 2010. We calculated the mean monthly NPP by land cover classes in the entire study area (Figure 8) and comparisons were made (Figure 9). Model estimates closely follow the seasonality and magnitude of MODIS NPP for each land cover class. It looks that NPP is consistently overestimated in comparison to MODIS NPP during the green-up phase. A period of overestimate suggests the ratio of the increasing rate of NPP to that of NDVI (slope) at this period is lower than the fitted slope. For one thing, the greenness of vegetation which can be better indicated by the NDVI values rises rapidly during the green-up phase; for another, the NPP might not increase as rapid as the greenness during the green-up phase as NPP is significantly controlled by leaf-intercepted photosynthetically active radiation. A highly significant correlation coefficient of 0.78 is observed for all savanna types combined. The performance of the bootstrapping regression model for estimating monthly NPP is slightly different in terms of savanna types as suggested by comparison between model-derived NPP and MODIS NPP. There is a highly significant linear correlation for tree savanna, bush savanna, and grassland savanna with correlation coefficients of 0.77, 0.74, and 0.80, respectively. A close match with 1:1 line for tree savanna, bush savanna, and grassland savanna is observed with slope coefficients of 0.88, 0.76, and 0.81, respectively (Figure 9). To validate annual aggregated NPP, we randomly selected pixels across the study region and extracted annual aggregated NPP of model estimates and MODIS for the 4 overlapping years. On an annual basis, annual total NPP predicted by bootstrapping model correlate positively with annual total MODIS NPP for tree savanna, bush savanna, and grassland savanna with correlation coefficients of 0.86, 0.70, and 0.75, respectively. The fitted line for grassland savanna is closest to 1:1 line with slope coefficient of 0.93, the slope coefficient of fitted line for tree savanna is 0.90, and the slope coefficient of fitted line for bush savanna is 0.73, furthest from the 1:1 line (Figure 10).

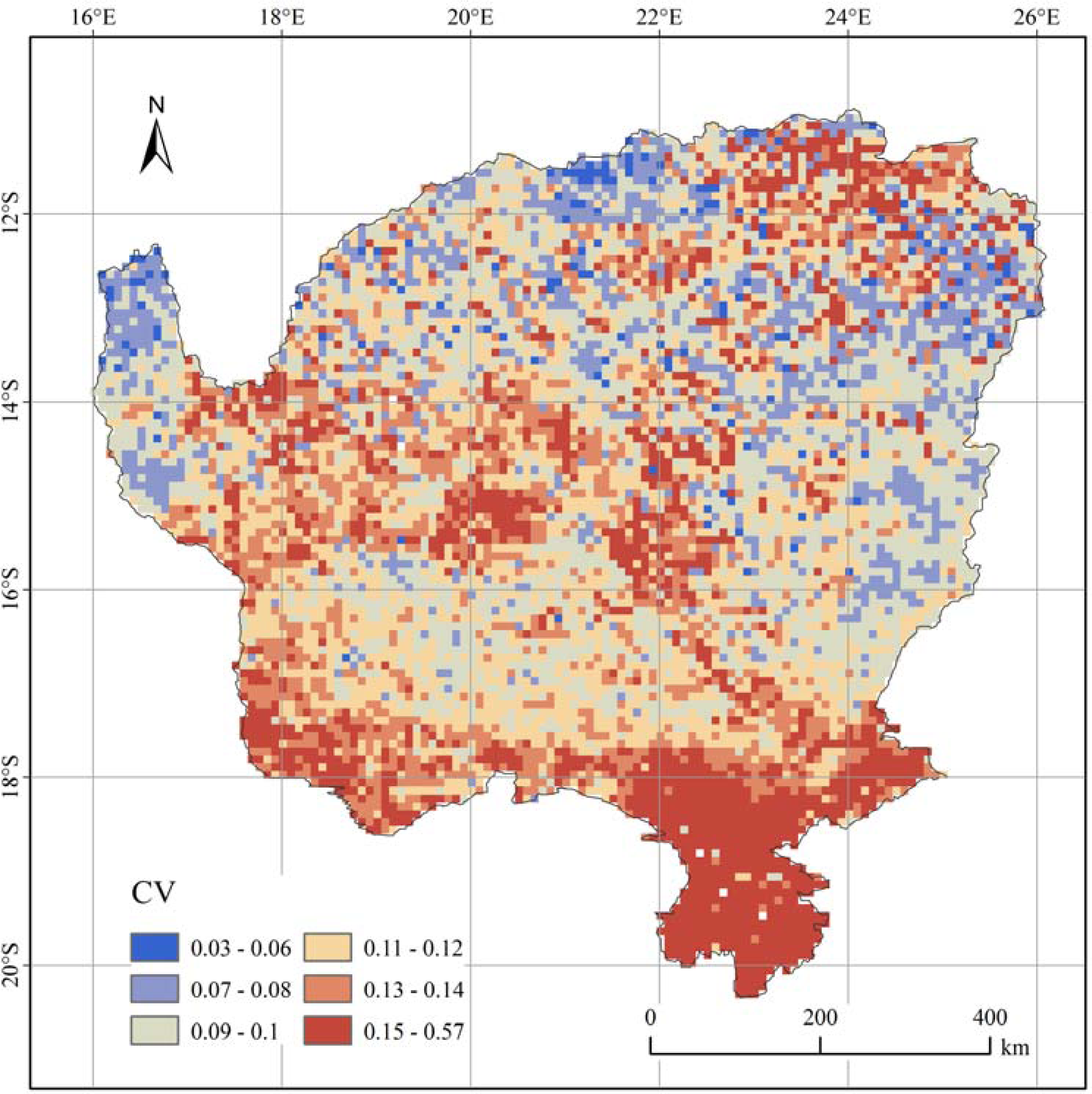
4.2. Spatial Pattern of Net Primary Production (NPP) Variability from 1982 to 2010

Generally, NPP decreases from north to south across the study area (Figure 7b). The NPP of tree savanna is higher than that of bush and grassland savanna (Table 1). NPP in the upper reaches of the Zambezi River is lower than that in the same latitudes as this region is covered by floodplain grasses which have lower NPP (Figure 7b). The northern portion is characterized by a small coefficient of variation (CV), whereas the southern section is characterized by a large CV (Figure 11) which suggests that NPP in the south has experienced higher variability. Bush savanna has a higher variability of NPP and tree savanna has the smallest, which is indicated by the mean CV values of each land cover class (Table 1).
There is a general trend of decreasing NPP across the study region as indicated by the universal significant and negative τ values (Figure 12). About 9% of the study area shows a significant and increasing trend, there is about 40% showing a significant and decreasing trend, and the remaining 48% shows no significant trend at all (Bare lands and water areas are excluded from analysis, so the total is slightly less than 100%). The percentage of increase, decrease, and insignificant pixels for tree savanna is 10%, 33%, and 57%, respectively; the percentage of increase, decrease, and insignificant pixels for bush savanna is 8%, 54%, and 38% respectively; and the percentage of increase, decrease, and insignificant pixels for grassland savanna is 9%, 44%, and 47%, respectively. So in terms of multi-decadal trends, overall the regional NPP has declined across this thirty year period, and when broken down into savanna vegetation types, the decline in tree savanna NPP is the least, the decline in bush savanna NPP is the highest of all the classes and the decline in grassland savanna NPP is between the other two. This suggests that the bush and grassland savanna is potentially representative of a more degraded ecosystem over time, as represented by the NPP decrease during the period 1982–2010, which would also be reflected in the literature, with declining rates of open grasslands and increasing bush encroachment across this region, specifically in the more southern regions dominated by these savanna ecosystems.

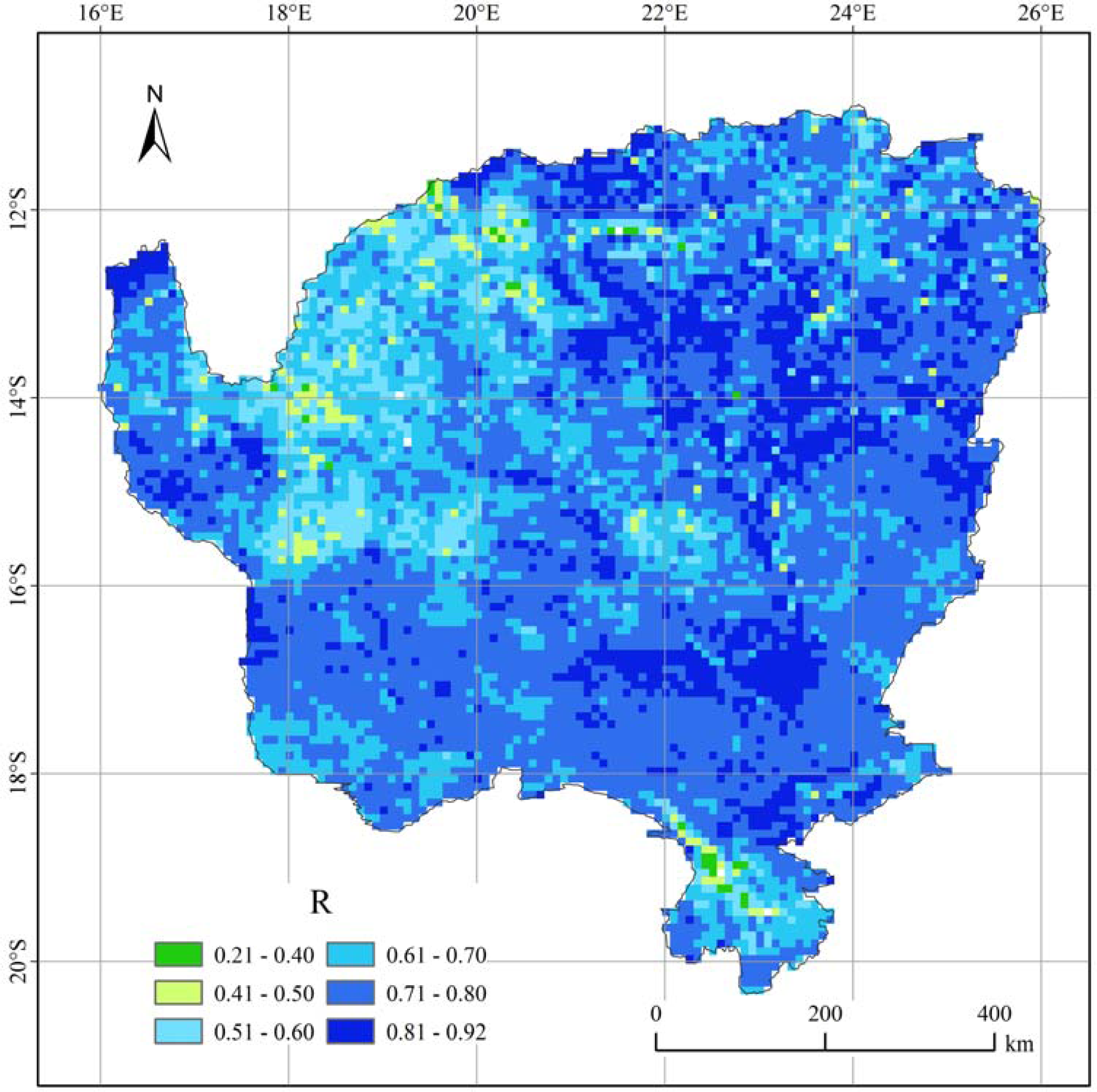
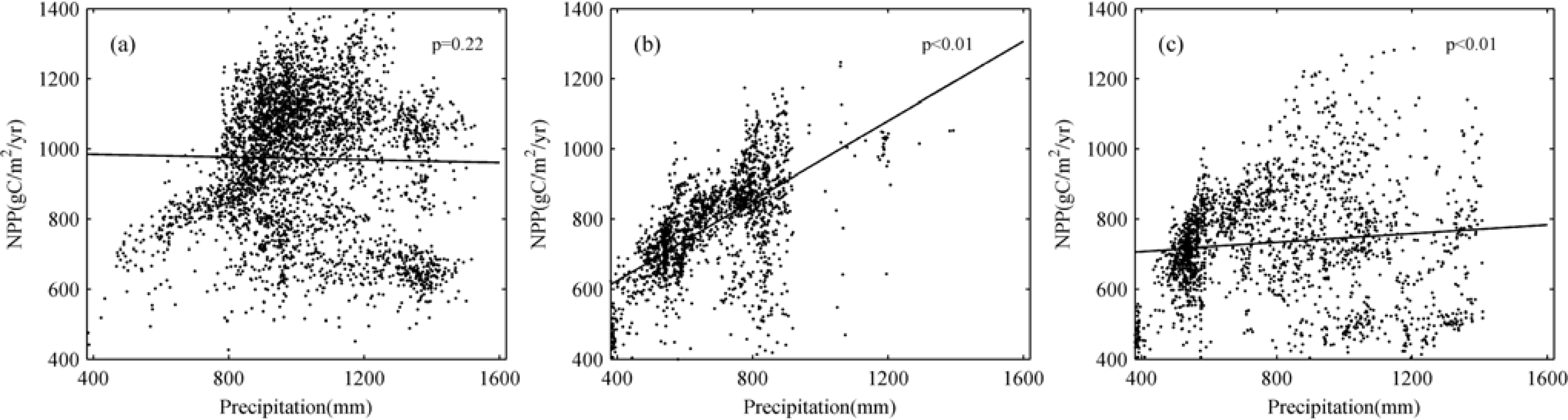
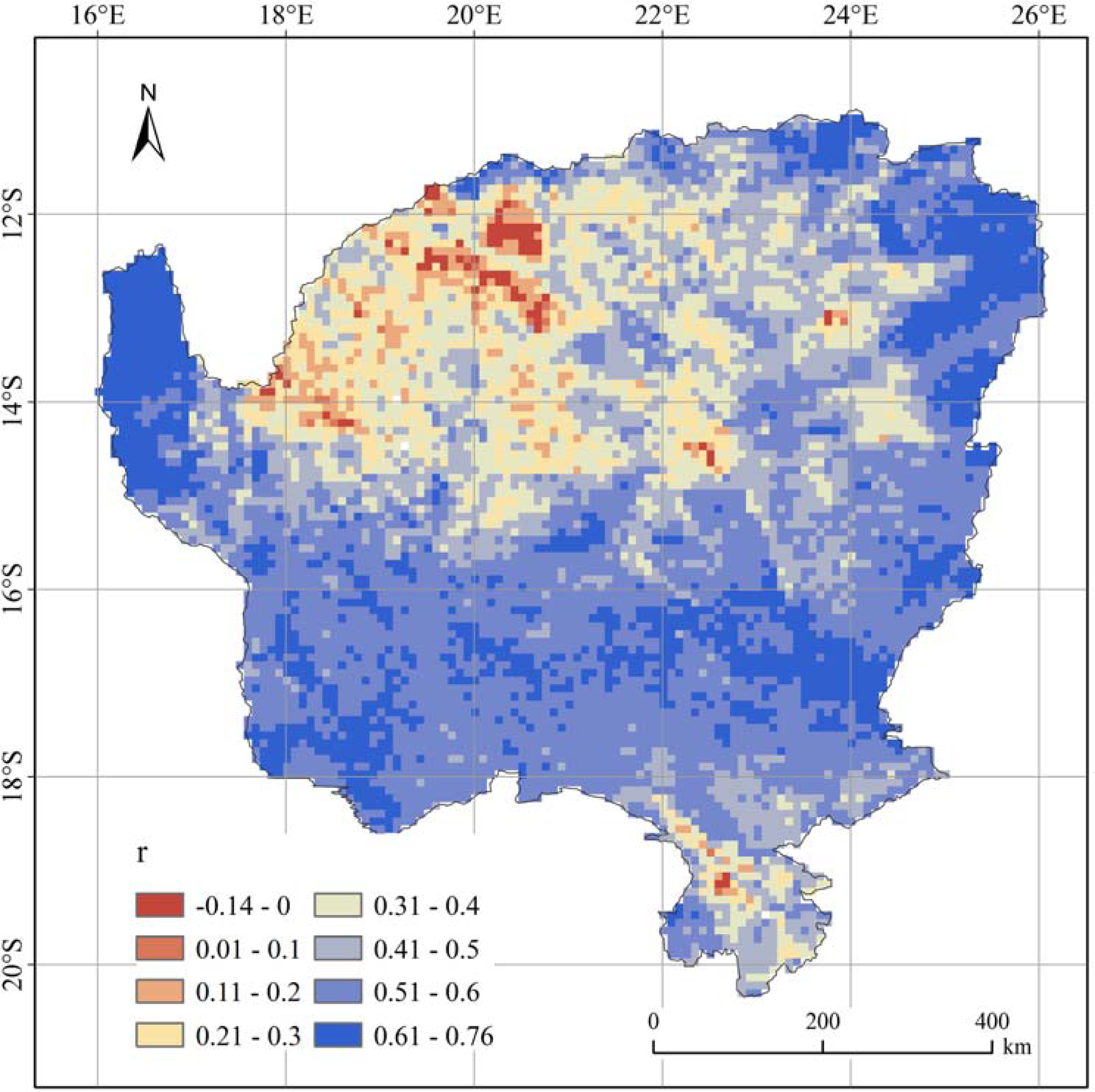
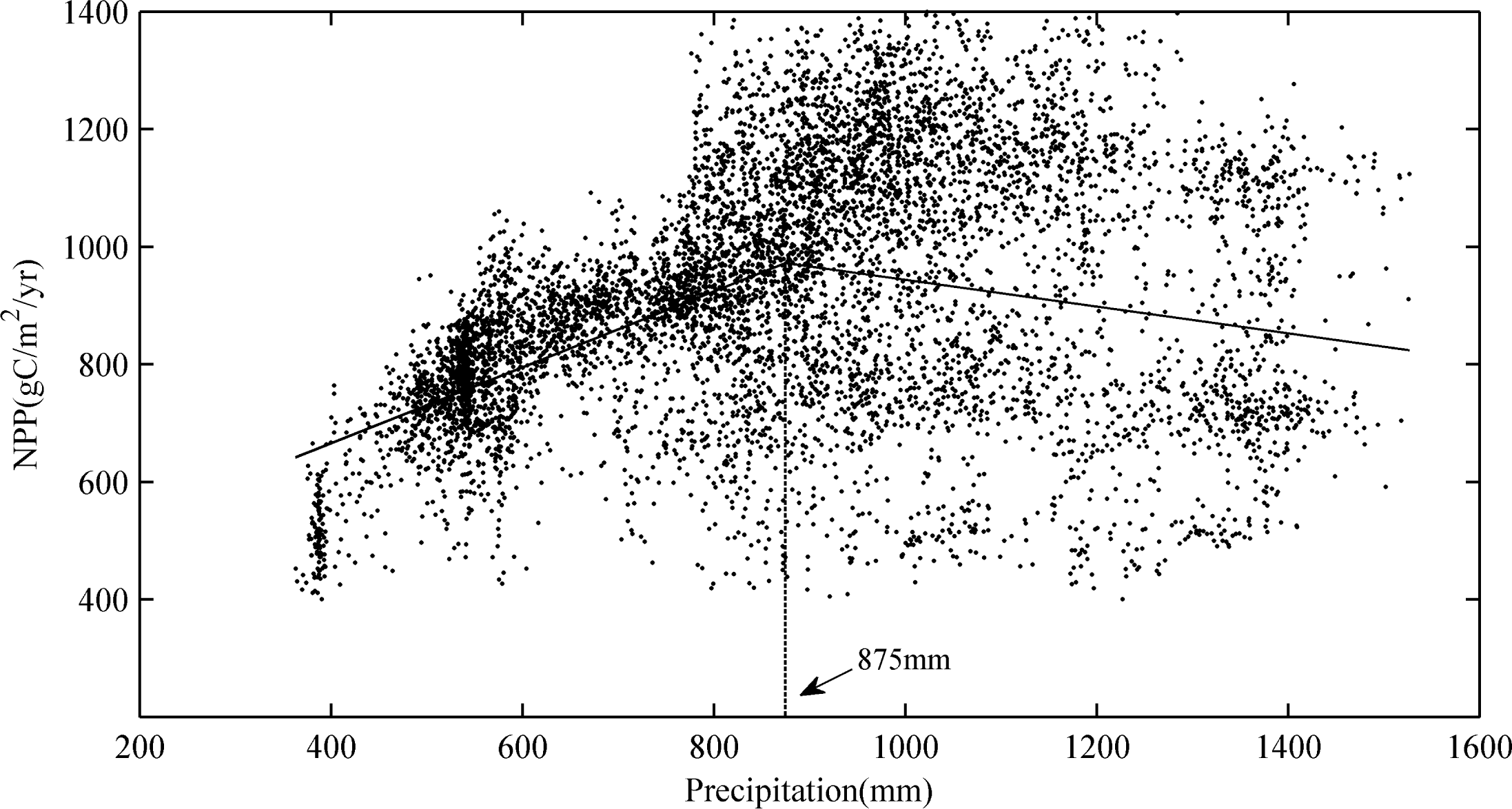
4.3. Relationship between Net Primary Production (NPP) and Precipitation

Monthly precipitation patterns across this region are of the rains beginning in late October, reaching their peak in January, and ending in April. Precipitation for May, June, July, August, and September is less than 10 mm in total and represents the dry season on this landscape. In relation to this, the onset of the increase in NPP is in November, and it peaks in March. The lowest NPP appears in September and October, at the very end of the dry season. There is about a two-month time lag between the seasonal change of precipitation and that of NPP, representing the vegetation response to the precipitation across the landscape. We calculated MAP and mean annual NPP (the water year is represented here by the sum of monthly NPP values from September of one year into August of the next) (1982–2010) of the entire study region and extracted their pixel values using different areas defined by land cover classes. Figure 13a–c shows the scatterplots of mean annual NPP versus MAP for the three savanna land cover classes. The annual NPP of tree savanna has no significant correlation with MAP (p = 0.22). By contrast, the annual NPP of bush and grassland savanna are correlated positively with MAP with correlation coefficients of 0.62 (p < 0.01) and 0.10 (p < 0.01), respectively. The slope of the linear regression model for tree savanna is not statistically significant (Figure 13a), suggesting that annual NPP has no linear relationship with MAP. Annual NPP of bush and grassland savanna are linearly correlated with MAP as indicated by the significant slope coefficients (Figure 13b,c). Figure 14 shows the spatial pattern of correlation between annual totals of precipitation and NPP. Generally the values of correlation decreases from south to north, implying that the linear relationship between precipitation and NPP declines as precipitation increases. The map also shows that the correlation values over grassland and bush savanna are higher than the values over tree savanna.
One important feature of the study area is the precipitation gradients across which MAP increases from south to north. We conducted linear regression analysis on different precipitation intervals of the entire study area and the three catchments (Table 2). The regression results of different precipitation intervals show that annual NPP has a significant and positive relationship with MAP when MAP is less than about 850 mm. However, the relationships are unstable when MAP is more than about 850 mm, which is characteristic of statistical insignificance or a negative regression coefficient. The results of the Okavango and Kwando catchments are similar, which are characterized by an abrupt change in the relationship between annual NPP and MAP. It should be noted that the regression results of the Zambezi catchment are uncertain, which is characterized by generally insignificant relationships between annual NPP and MAP. We applied the piecewise linear regression model to fit all pixel values from the layers of MAP and mean annual NPP (Figure 15). The piecewise linear regression is an effective tool which can be used to identify the turning points (TP) underlying the variations in mean annual NPP with MAP [37]. The results show that the TP occurs at the location with a MAP of 875 mm. This suggests that NPP for savannas is constrained by, and increases linearly with, MAP less than about 875 mm, whereas limited dependence on MAP is shown above this threshold.

5. Discussion

The use of the NDVI has been most widely used as approaches for EO-based monitoring of vegetation productivity. Researchers have derived a variety of relevant measures from NDVI time series as a proxy of vegetation production, such as the sum of positive NDVI values over a given period, the maximum value of the NDVI over a year, or the NDVI integral across growing seasons [17,38]. Researchers also use NDVI or NDVI-derived variables as inputs to process-based models to calculated NPP, such as the Carnegie-Ames-Stanford Approach (CASA), the Terrestrial Observation and Prediction System Model (TOPS) and other light use efficiency models [8,11]. Several studies have suggested the existence of a positive relationship between NDVI and either biomass or NPP. However, the relationship between NDVI and NPP is not always linear. For biomes with high NPP, this relationship becomes saturated, whereas for biomes with low NPP, the relationships are influenced by the spectral characteristics of the bare soil. Our study also shows that a slightly weaker relationship is found over tree savanna where NPP is higher, and the estimated accuracy of tree savanna is lower than that of bush and grassland savanna. The basic assumption to effectively derive NPP from NDVI here is the significant linear relationship. Our results show that MODIS NPP has a significant linear relationship with GIMMS3g NDVI across the entire study area. Paruelo et al. [39] in the central U.S grasslands, found that a positive and statistically significant relationship between NDVI and NPP for areas with MAP between 280 mm and 1,150 mm which overlaps well with our study area. Fensholt et al. [17] successfully converted the GIMMS NDVI into NPP based on per-pixel correlations between overlapping years of GIMMS NDVI and SPOT VGT NPP in the African Sahel. Here we are evaluating the performance of the new AVHRR dataset based on the MODIS NPP product using bootstrapping regression. The accuracy of MODIS NPP especially in the savanna ecosystems potentially has considerable influence on our model estimates. Several studies have highlighted limitations of the MOD17 model such as the uncertainties of coarse resolution DAO meteorological reanalysis data used in the model, and the global trends and regional patterns derived from MODIS NPP have been challenged [11,40–42]. Few studies have been conducted in Africa to evaluate the efficiency of the MOD17 model [43–45]. Fensholt et al. [43] found that the MOD17 model underestimated NPP in the semi-arid Senegal. Sjöström et al. [44] reported that MODIS GPP performed reasonably well in explaining the variability in eddy covariance GPP at a range of African ecosystem, but the model was observed to underestimate GPP, especially in dry savanna ecosystems. Sjöström et al. [45] found that the MODIS GPP can capture the seasonality but the MODIS NPP was underestimated again in dry savanna ecosystems. The possible reasons include the uncertainties of the meteorological data, the inappropriate set of maximum light efficiency, and the insufficiency of vapor pressure deficit (VPD)’s constraint on GPP. However, a comparison of monthly NPP derived from eddy covariance flux sites with monthly NPP from the MOD17 algorithm suggests a better estimate of MODIS NPP in our study area, although the sample number is relatively small.
Although there is some consensus that terrestrial photosynthetic activity has increased over the past two or three decades in the middle and high latitudes in the NH [4,9], no such agreement has been reached on tropical regions and specifically, across the most recent decades some studies have suggested a switch in trends globally [5]. Beyond just this basic interpretation of the trend and patterns over the last thirty years there is also additional confusion regarding interannual variations in NPP at global or regional scales as a result of the selection of model used to derive NPP, the research period selected, or/and the spatial resolution used. Our results found a universal decline in NPP across the study area from 1982 to 2010. These conclusions are in accordance with previous studies which have reported that NPP reduces during both periods 1982–1999 and 2000–2009 in this region of the world [4,10]. Our research highlights the NPP change of land-cover classes in the longer temporal extent (1982–2010) as this new dataset has become available and given the large scale variability, both intra and inter annually within most of these trends a longer time series approach is most definitely required. Almost half of our landscape revealed significant trends in declining NPP amount for bush and grassland savanna, and tree savannas showed declines in about a third of its extent. These trends become more significant in the more southerly areas. There are also a limited number of areas representing increases in NPP though these most often relate to the presence of water bodies and are linked more to flood regime patterns. The overall decline in NPP across this region is −2.13 g·C·m−2·yr−1 (p < 0.1), corresponding to a decrease of 6.7% over 29 years (1982–2010).
Although multiple mechanisms (e.g., nitrogen deposition, CO2 fertilization, climate change) have contributed to the change in NPP, NPP variability has been primarily attributed to water availability in arid and semi-arid areas where water is a limiting resource [12]. Precipitation as the critical importance of water source for plant use is well recognized for savanna ecosystems. Although soil moisture, precipitation—evapotranspiration influence directly plant water availability, it seems to be more useful to disentangle the NPP-precipitation relationship as precipitation is more easily and directly measured at different geographical scales and more frequently as the input for process-based and diagnostic models. Our research found that the NPP of tree savanna is less influenced by MAP, where the NPP of bush and grassland savanna has a significantly positive relationship with MAP. This is consistent with previous studies which have reported that the relationship between NPP and precipitation varies with land cover [14,46]. Savanna ecosystems are characterized by the co-dominance of two contrasting plant life forms, trees and grasses, which are manifest by their relative representation across savanna types. Sankaran et al. [47,48] suggests that MAP is the most important predictor, followed by fire return periods, soil characteristics and herbivory regimes. Woody cover shows a strong positive dependence on MAP between 200 and 700 mm, but no dependence on MAP above this threshold when the effects of other predictors are accounted for. Campo-Bescós et al. [49] find that the impact of a suite of environmental covariates on NDVI varies from grass-dominated regions with MAP < 750 mm to tree-dominated regions with MAP > 950 mm. Our study also found that the relationship between NPP and MAP varies with the increase in MAP. The linear relationship is observed when MAP is less than 750–850 mm, while the linear increase in NPP with MAP levels off when MAP exceeds the range. Whether this range is applicable to other savanna ecosystems still needs further research. For example, Breman and Dewit [50] states that the proportionality breaks down at a precipitation of 300 mm·yr−1.
Estimating the interannual variations in NPP quantitatively is important to support policy development for food security and resource conservation as the degradation of the vegetation cover in savanna ecosystems is increasing. Our study identified the pixels that have experienced a reduction in vegetation production, which may provide an early warning of land degradation. However, our results cannot disentangle the reduction in NPP caused by a number of factors, including climate variations (mainly precipitation), natural disturbances (mainly fire), and human activities (grazing, agriculture, etc.). Methods such as rain use efficiency or RESTREND can be used to tease out the land degradation induced by human influences versus that caused by precipitation variability [21,51]. Future research will attempt to disentangle these influences spatially across this region.

6. Conclusions

Our study used robust bootstrapping regression method to successfully derive monthly net primary production (NPP) of the Okavango, Kwando, and upper Zambezi (OKZ) catchments for the long period 1982–2010 from the third generation Global Inventory Monitoring and Modeling System (GIMMS3g) normalized difference vegetation index (NDVI) data, with the Moderate Resolution Imaging Spectroradiometer (MODIS) NPP product. Then we investigated the variations in NPP over 29 years and disentangled the relationships between NPP and precipitation factor by both savanna types and precipitation intervals. A highly positive correlation between NPP and GIMMS3g NDVI within our study area provides the basic premise for retrieving NPP effectively through relatively simple statistical method. The use of single satellite-derived metric has great appeal for ease of application, assessing the effects of uncertainties caused by input data, and simplifying the exploration of the underlying mechanism [52]. Our findings show that there is a universal decrease in NPP across our study area and NPP of the study area as a whole has reduced significantly at a rate of −2.13 g·C·m−2·yr−1, corresponding to a decrease of 6.7% over 29 years. The reduction in NPP might decrease the food supply for grazing and browsing herbivores, as the ecosystem is known as their habitats and food sources. It is also a possible indicator of the degradation of savanna ecosystem, but degradation expressed by decreasing vegetation coverage, bush encroachment, changes in community composition, and reduced rain-use efficiency is still worthy of special research. Given the importance of carbon sequestration of savannas, a decline in NPP regionally has significant global implications. It remains to be seen if this multi-decadal trend, resulting from the newly available GIMMS3g dataset, is also found in other regions of the globe.
Our research teased out the relationships between NPP and precipitation by different savanna ecosystem types. There is a significant positive relationship between mean annual NPP and mean annual precipitation (MAP) over bush and grassland savanna, but no significant relationship is witnessed over tree savanna. This is useful for understanding landscape level changes in vegetation amounts, and for improving the characterization of the impact of climate change on such landscapes. Our study also got some innovative points in terms of the relationship between mean annual NPP and MAP. Notably, the relationship between mean annual NPP and MAP varies with increases in MAP, characterized as a linear relationship that breaks down when MAP exceeding around 850–900 mm. The existence of this tipping point still needs to be confirmed at other areas and broader extents. The use of such 30-year GIMMS3g NDVI time series will greatly improve our ability to determine trends, shifts and potential landscape level changes in vegetation growth, such as land degradation, and to systematically quantify the relationships between key drivers of vegetation growth and the resultant vegetation cover over different temporal and spatial scales [17,28,53–55].

Acknowledgments

We thank Ranga Myneni, Jorge Pinzón, and Zaicun Zhu for the provision of the GIMMS3g NDVI data set. We thank Werner Kutsch, Almut Arneth, and Elmar Veenendaal for the provision of eddy covariance flux data sets. We also appreciate the four reviewers for giving us very helpful comments and suggestions. The research was funded by the NASA Land Cover/Land Use Change Program, Proposal title: Understanding and predicting the impact of climate variability and climate change on land-use/land-cover change via socio-economic institutions in Southern Africa (No. NNX09AI25G), PI: Jane Southworth, University of Florida.

Conflict of Interest

The authors declare no conflict of interest.

References

  1. Potter, C.S.; Randerson, J.T.; Field, C.B.; Matson, P.A.; Vitousek, P.M.; Mooney, H.A.; Klooster, S.A. Terrestrial ecosystem production: A process model based on global satellite and surface data. Glob. Biogeochem. Cy 1993, 7, 811–841. [Google Scholar]
  2. Field, C.B.; Randerson, J.T.; Malmstrom, C.M. Global net primary production: Combining ecology and remote sensing. Remote Sens. Environ 1995, 88, 74–88. [Google Scholar]
  3. Piao, S.; Fang, J.; Zhou, L.; Zhu, B.; Tan, K.; Tao, S. Changes in vegetation net primary productivity from 1982 to 1999 in China. Glob. Biogeochem. Cy. 2005, 19, GB2027. [Google Scholar]
  4. Nemani, R.R.; Keeling, C.D.; Hashimoto, H.; Jolly, W.M.; Piper, S.C.; Tucker, C.J.; Myneni, R.B.; Running, S.W. Climate-driven increases in global terrestrial net primary production from 1982 to 1999. Science 2003, 300, 1560–1563. [Google Scholar]
  5. Hicke, J.A.; Asner, G.P.; Randerson, J.T.; Tucker, C.; Los, S.; Birdsey, R.; Jenkins, J.C.; Field, C. Trends in North American net primary productivity derived from satellite observations, 1982–1998. Glob. Biogeochem. Cy. 2002. [Google Scholar] [CrossRef]
  6. Lucht, W.; Prentice, I.C.; Myneni, R.B.; Sitch, S.; Friedlingstein, P.; Cramer, W.; Bousquet, P.; Buermann, W.; Smith, B. Climatic control of the high-latitude vegetation greening trend and Pinatubo effect. Science 2002, 296, 1687–1689. [Google Scholar]
  7. Myneni, R.B.; Keeling, C.D.; Tucker, C.J.; Asrar, G.; Nemani, R. Increasing plant growth in the northern high latitude from 1981 to 1991. Nature 1997, 386, 698–702. [Google Scholar]
  8. Piao, S.; Fang, J.; He, J. Variations in vegetation net primary production in the Qinghai-Xizang Plateau, China, from 1982 to 1999. Clim. Change 2006, 74, 253–267. [Google Scholar]
  9. Seaquist, J.W.; Olsson, L.; Ardö, J.; Eklundh, L. Broad-scale increase in NPP quantified for the African Sahel, 1982–1999. Int. J. Remote Sens 2006, 27, 5115–5122. [Google Scholar]
  10. Zhao, M.; Running, S.W. Drought-induced reduction in global terrestrial net primary production from 2000 to 2009. Science 2010, 329, 940–943. [Google Scholar]
  11. Hashimoto, H.; Wang, W.; Milesi, C.; Xiong, J.; Ganguly, S.; Zhu, Z.; Nemani, R. Structural uncertainty in model-simulated trends of global gross primary production. Remote Sens 2013, 5, 1258–1273. [Google Scholar]
  12. Beedlow, P.A.; Tingey, D.T.; Phillips, D.L.; Hogsett, W.E.; Olszyk, D.M. Rising atmospheric CO2 and carbon sequestration in forests. Front. Ecol. Environ 2004, 2, 315–322. [Google Scholar]
  13. Bogaert, J.; Zhou, L.; Tucker, C.J.; Myneni, R.B.; Ceulemans, R. Evidence for a persistent and extensive greening trend in Eurasia inferred from satellite vegetation index data. J. Geophys. Res 2002, 107, D11. [Google Scholar]
  14. Garbulsky, M.F.; Peñuelas, J.; Papale, D.; Ardö, J.; Goulden, M.L.; Kiely, G.; Richardson, A.D.; Rotenberg, E.; Veenendaal, E.M.; Filella, I. Patterns and controls of the variability of radiation use efficiency and primary productivity across terrestrial ecosystems. Glob. Ecol. Biogeogr 2010, 19, 253–267. [Google Scholar]
  15. Chuur, E.A.G. Productivty and global climate revisited: The sensitivity of tropical forest growth to precipitation. Ecology 2003, 84, 1165–1170. [Google Scholar]
  16. Zhang, X.; Friedl, M.A.; Schaaf, C.B.; Strahler, A.H. Monitoring the response of vegetation phenology to precipitation in Africa by coupling MODIS and TRMM instruments. J. Geophys. Res 2005, 110, D12103. [Google Scholar]
  17. Fensholt, R.; Rasmussen, K.; Kaspersen, P.; Huber, S.; Horion, S.; Swinnen, E. Assessing land degradation/recovery in the african sahel from long-term earth observation based primary productivity and precipitation relationships. Remote Sens 2013, 5, 664–686. [Google Scholar]
  18. Grace, J.; Jose, J.S.; Meir, P.; Miranda, H.S.; Montes, R.A. Productivity and carbon fluxes of tropical savannas. J. Biogeogr 2006, 33, 387–400. [Google Scholar]
  19. Ciais, P.; Piao, S.; Cadule, P.; Friedlingstein, P.; Chédin, A. Variability and recent trends in the African terrestrial carbon balance. Biogeosciences 2009, 6, 1935–1948. [Google Scholar]
  20. Jacquin, A.; Sheeren, D.; Lacombe, J.-P. Vegetation cover degradation assessment in Madagascar savanna based on trend analysis of MODIS NDVI time series. Int. J. Appl. Earth Observ. Geoinf 2010, 12, S3–S10. [Google Scholar]
  21. Wessels, K.J.; Prince, S.D.; Frost, P.E.; van Zyl, D. Assessing the effects of human-induced land degradation in the former homelands of northern South Africa with a 1 km AVHRR NDVI time-series. Remote Sens. Environ 2004, 91, 47–67. [Google Scholar]
  22. Tucker, C.; Pinzon, J.; Brown, M.; Slayback, D.; Pak, E.; Mahoney, R.; Vermote, E.; El Saleous, N. An extended AVHRR 8-km NDVI dataset compatible with MODIS and SPOT vegetation NDVI data. Int. J. Remote Sens 2005, 26, 4485–4498. [Google Scholar]
  23. Sasai, T.; Ichii, K.; Yamaguchi, Y.; Nemani, R. Simulating terrestrial carbon fluxes using the new biosphere model “biosphere model integrating eco-physiological and mechanistic approaches using satellite data” (BEAMS). J. Geophys. Res 2005, 110, G02014. [Google Scholar]
  24. Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.; Reeves, M.; Hashimoto, H. A continuous satellite-derived measure of global terrestrial primary production. BioScience 2004, 54, 547–560. [Google Scholar]
  25. Gaughan, A.E.; Waylen, P.R. Spatial and temporal precipitation variability in the Okavango–Kwando–Zambezi catchment, southern Africa. J. Arid Environ 2012, 82, 19–30. [Google Scholar]
  26. Chase, M.J.; Griffin, C.R. Elephants caught in the middle: Impacts of war, fences and people on elephant distribution and abundance in the Caprivi Strip, Namibia. Afr. J. Ecol 2009, 47, 223–233. [Google Scholar]
  27. Vanaarde, R.; Jackson, T. Megaparks for metapopulations: Addressing the causes of locally high elephant numbers in southern Africa. Biol. Conserv 2007, 134, 289–297. [Google Scholar]
  28. Bi, J.; Xu, L.; Samanta, A.; Zhu, Z.; Myneni, R. Divergent arctic-boreal vegetation changes between North America and Eurasia over the past 30 years. Remote Sens 2013, 5, 2093–2112. [Google Scholar]
  29. Zhao, M.; Heinsch, F.A.; Nemani, R.R.; Running, S.W. Improvements of the MODIS terrestrial gross and net primary production global data set. Remote Sens. Environ 2005, 95, 164–176. [Google Scholar]
  30. Legates, D.R.; Willmott, C.J. Mean seasonal and spatial variability in gauge-corrected, global precipitation. Int. J. Climatol 1990, 10, 111–127. [Google Scholar]
  31. Global Land Cover 2000 Database; European Commission, Joint Research Centre: Brussels, Belgium, 2003. Available online: http://bioval.jrc.ec.europa.eu/products/glc2000/glc2000.php (accessed on 1 April 2013).
  32. Efron, B.; Tibshirani, R.J. Regression Models. In An Introduction to the Bootstrap; Chapman & Hall/CRC: Boca Raton, FL, USA, 1993; Chapter 9; pp. 105–121. [Google Scholar]
  33. Zhang, Y.; Xu, M.; Chen, H.; Adams, J. Global pattern of NPP to GPP ratio derived from MODIS data: Effects of ecosystem type, geographical location and climate. Glob. Ecol. Biogeogr 2009, 18, 280–290. [Google Scholar]
  34. Yu, Y.S.; Zou, S.M.; Whittemore, D. Nonparametric trend analysis of water-quality data of rivers in Kansas. J. Hydrol 1993, 150, 61–80. [Google Scholar]
  35. Yue, S.; Pilon, P.; Cavadias, G. Power of the Mann–Kendall and Spearman’s rho tests for detecting monotonic trends in hydrological series. J. Hydrol 2002, 259, 254–271. [Google Scholar]
  36. Kahya, E.; Kalayci, S. Trend analysis of streamflow in Turkey. J. Hydrol 2004, 289, 128–144. [Google Scholar]
  37. Toms, J.D.; Lesperance, M.L. Piecewise regression: A tool for identifying ecological thresholds. Ecology 2003, 84, 2034–2041. [Google Scholar]
  38. Pettorelli, N.; Vik, J.O.; Mysterud, A.; Gaillard, J.-M.; Tucker, C.J.; Stenseth, N.C. Using the satellite-derived NDVI to assess ecological responses to environmental change. Trends Ecol. Evol 2005, 20, 503–510. [Google Scholar]
  39. Paruelo, J.M.; Epstein, H.E.; Lauenroth, W.K.; Burke, I.C. ANPP estimates from NDVI fro the central grassland region of the United States. Ecology 1997, 78, 953–958. [Google Scholar]
  40. Samanta, A.; Costa, M.H.; Nunes, E.L.; Vieira, S.A.; Xu, L.; Myneni, R.B. Comment on “Drought-induced reduction in global terrestrial net primary production from 2000 through 2009”. Science 2011, 333, 1093. [Google Scholar]
  41. Sims, D.A.; Rahman, A.F.; Cordova, V.D.; Elmasri, B.Z.; Baldocchi, D.D.; Bolstad, P.V.; Flanagan, L.B.; Goldstein, A.H.; Hollinger, D.Y.; Misson, L.; et al. A new model of gross primary productivity for North American ecosystems based solely on the enhanced vegetation index and land surface temperature from MODIS. Remote Sens. Environ 2008, 112, 1633–1646. [Google Scholar]
  42. Potter, C.; Klooster, S.; Genovese, V. Net primary production of terrestrial ecosystems from 2000 to 2009. Clim. Change 2012, 115, 365–378. [Google Scholar]
  43. Fensholt, R.; Sandholt, I.; Rasmussen, M.S.; Stisen, S.; Diouf, A. Evaluation of satellite based primary production modelling in the semi-arid Sahel. Remote Sens. Environ 2006, 105, 173–188. [Google Scholar]
  44. Sjöström, M.; Ardö, J.; Arneth, A.; Boulain, N.; Cappelaere, B.; Eklundh, L.; de Grandcourt, A.; Kutsch, W.L.; Merbold, L.; Nouvellon, Y. Exploring the potential of MODIS EVI for modeling gross primary production across African ecosystems. Remote Sens. Environ 2011, 115, 1081–1089. [Google Scholar]
  45. Sjöström, M.; Zhao, M.; Archibald, S.; Arneth, A.; Cappelaere, B.; Falk, U.; de Grandcourt, A.; Hanan, N.; Kergoat, L.; Kutsch, W.; et al. Evaluation of MODIS gross primary productivity for Africa using eddy covariance data. Remote Sens. Environ 2013, 131, 275–286. [Google Scholar]
  46. Churkina Galina, R.S. Contrasting climatic controls on the estimated productivity of global terrestrial biomes. Ecosystems 1998, 1, 206–215. [Google Scholar]
  47. Sankaran, M.; Hanan, N.P.; Scholes, R.J.; Ratnam, J.; Augustine, D.J.; Cade, B.S.; Gignoux, J.; Higgins, S.I.; Le Roux, X.; Ludwig, F.; et al. Determinants of woody cover in African savannas. Nature 2005, 438, 846–849. [Google Scholar]
  48. Sankaran, M.; Ratnam, J.; Hanan, N. Woody cover in African savannas: The role of resources, fire and herbivory. Glob. Ecol. Biogeogr 2008, 17, 236–245. [Google Scholar]
  49. Campo-Bescós, M.A.; Muñoz-Carpena, R.M.; Southworth, J.; Zhu, L.; Waylen, P.R.; Bunting, E. Combined spatial and temporal effects of environmental controls on long-term monthly NDVI in southern Africa savanna. Remote Sens. 2013. under review. [Google Scholar]
  50. Breman, H.; de Wit, C.T. Rangeland productivity and exploitation in the sahel. Science 1983, 221, 1341–1347. [Google Scholar]
  51. Li, A.; Wu, J.; Huang, J. Distinguishing between human-induced and climate-driven vegetation changes: A critical application of RESTREND in inner Mongolia. Landsc. Ecol 2012, 27, 969–982. [Google Scholar]
  52. Hashimoto, H.; Wang, W.; Milesi, C.; White, M.A.; Ganguly, S.; Gamo, M.; Hirata, R.; Myneni, R.B.; Nemani, R.R. Exploring simple algorithms for estimating gross primary production in forested areas from satellite data. Remote Sens 2012, 4, 303–326. [Google Scholar]
  53. Cook, B.; Pau, S. A global assessment of long-term greening and browning trends in pasture lands using the GIMMS LAI3g dataset. Remote Sens 2013, 5, 2492–2512. [Google Scholar]
  54. De Jong, R.; Verbesselt, J.; Zeileis, A.; Schaepman, M. Shifts in global vegetation activity trends. Remote Sens 2013, 5, 1117–1133. [Google Scholar]
  55. Mao, J.; Shi, X.; Thornton, P.; Hoffman, F.; Zhu, Z.; Myneni, R. Global latitudinal-asymmetric vegetation growth trends and their driving mechanisms: 1982–2009. Remote Sens 2013, 5, 1484–1497. [Google Scholar]
Remotesensing 05 03803f1 1024
Figure 1. Geographical location of the study area. Inset map shows the location of the Okavango, Kwando, and upper Zambezi (OKZ) catchment in southern Africa. The white lines show the contours of mean annual precipitation (MAP) with an interval of 100 mm, which illustrates that MAP increases from south to north.
Figure 1. Geographical location of the study area. Inset map shows the location of the Okavango, Kwando, and upper Zambezi (OKZ) catchment in southern Africa. The white lines show the contours of mean annual precipitation (MAP) with an interval of 100 mm, which illustrates that MAP increases from south to north.
Remotesensing 05 03803f1
Remotesensing 05 03803f2 1024
Figure 2. Map of land cover for the Okavango, Kwando, and upper Zambezi (OKZ) catchment.
Figure 2. Map of land cover for the Okavango, Kwando, and upper Zambezi (OKZ) catchment.
Remotesensing 05 03803f2
Remotesensing 05 03803f3 1024
Figure 3. Spatial pattern of correlation coefficient between Moderate-resolution Imaging Spectroradiometer (MODIS) monthly net primary production (NPP) and third generation Global Inventory Monitoring and Modeling System (GIMMS3g) monthly normalized difference vegetation index (NDVI) from 2000 to 2010.
Figure 3. Spatial pattern of correlation coefficient between Moderate-resolution Imaging Spectroradiometer (MODIS) monthly net primary production (NPP) and third generation Global Inventory Monitoring and Modeling System (GIMMS3g) monthly normalized difference vegetation index (NDVI) from 2000 to 2010.
Remotesensing 05 03803f3
Remotesensing 05 03803f4 1024
Figure 4. The histogram of (a) intercepts and (b) slopes derived from the bootstrapping regression model for one example pixel (Lat: −15.44°S; Lon: 23.25°E).
Figure 4. The histogram of (a) intercepts and (b) slopes derived from the bootstrapping regression model for one example pixel (Lat: −15.44°S; Lon: 23.25°E).
Remotesensing 05 03803f4
Remotesensing 05 03803f5 1024
Figure 5. Comparison between monthly net primary production (NPP) from eddy covariance flux towers and Moderate-resolution Imaging Spectroradiometer (MODIS) monthly NPP. The 1:1 line is shown, along with the fitted line of linear regression.
Figure 5. Comparison between monthly net primary production (NPP) from eddy covariance flux towers and Moderate-resolution Imaging Spectroradiometer (MODIS) monthly NPP. The 1:1 line is shown, along with the fitted line of linear regression.
Remotesensing 05 03803f5
Remotesensing 05 03803f6 1024
Figure 6. Spatial pattern of root mean square error between predicted net primary production (NPP) and original Moderate-resolution Imaging Spectroradiometer (MODIS) NPP for 2007–2010.
Figure 6. Spatial pattern of root mean square error between predicted net primary production (NPP) and original Moderate-resolution Imaging Spectroradiometer (MODIS) NPP for 2007–2010.
Remotesensing 05 03803f6
Remotesensing 05 03803f7 1024
Figure 7. Spatial patterns of (a) mean annual Moderate-resolution Imaging Spectroradiometer (MODIS) net primary production (NPP) and (b) mean annual predicted NPP (2007–2010). The mean annual NPP is the summed monthly values of water year from September through August.
Figure 7. Spatial patterns of (a) mean annual Moderate-resolution Imaging Spectroradiometer (MODIS) net primary production (NPP) and (b) mean annual predicted NPP (2007–2010). The mean annual NPP is the summed monthly values of water year from September through August.
Remotesensing 05 03803f7
Remotesensing 05 03803f8 1024
Figure 8. Comparison of model derived monthly net primary production (NPP) with monthly Moderate-resolution Imaging Spectroradiometer (MODIS) NPP from 2007 to 2010 by land cover classes: (a) tree savanna; (b) bush savanna; and (c) grassland savanna.
Figure 8. Comparison of model derived monthly net primary production (NPP) with monthly Moderate-resolution Imaging Spectroradiometer (MODIS) NPP from 2007 to 2010 by land cover classes: (a) tree savanna; (b) bush savanna; and (c) grassland savanna.
Remotesensing 05 03803f8
Remotesensing 05 03803f9 1024
Figure 9. Scatter plot of model-derived monthly net primary production (NPP) with monthly Moderate-resolution Imaging Spectroradiometer (MODIS) NPP by savanna types from 2007 to 2010.
Figure 9. Scatter plot of model-derived monthly net primary production (NPP) with monthly Moderate-resolution Imaging Spectroradiometer (MODIS) NPP by savanna types from 2007 to 2010.
Remotesensing 05 03803f9
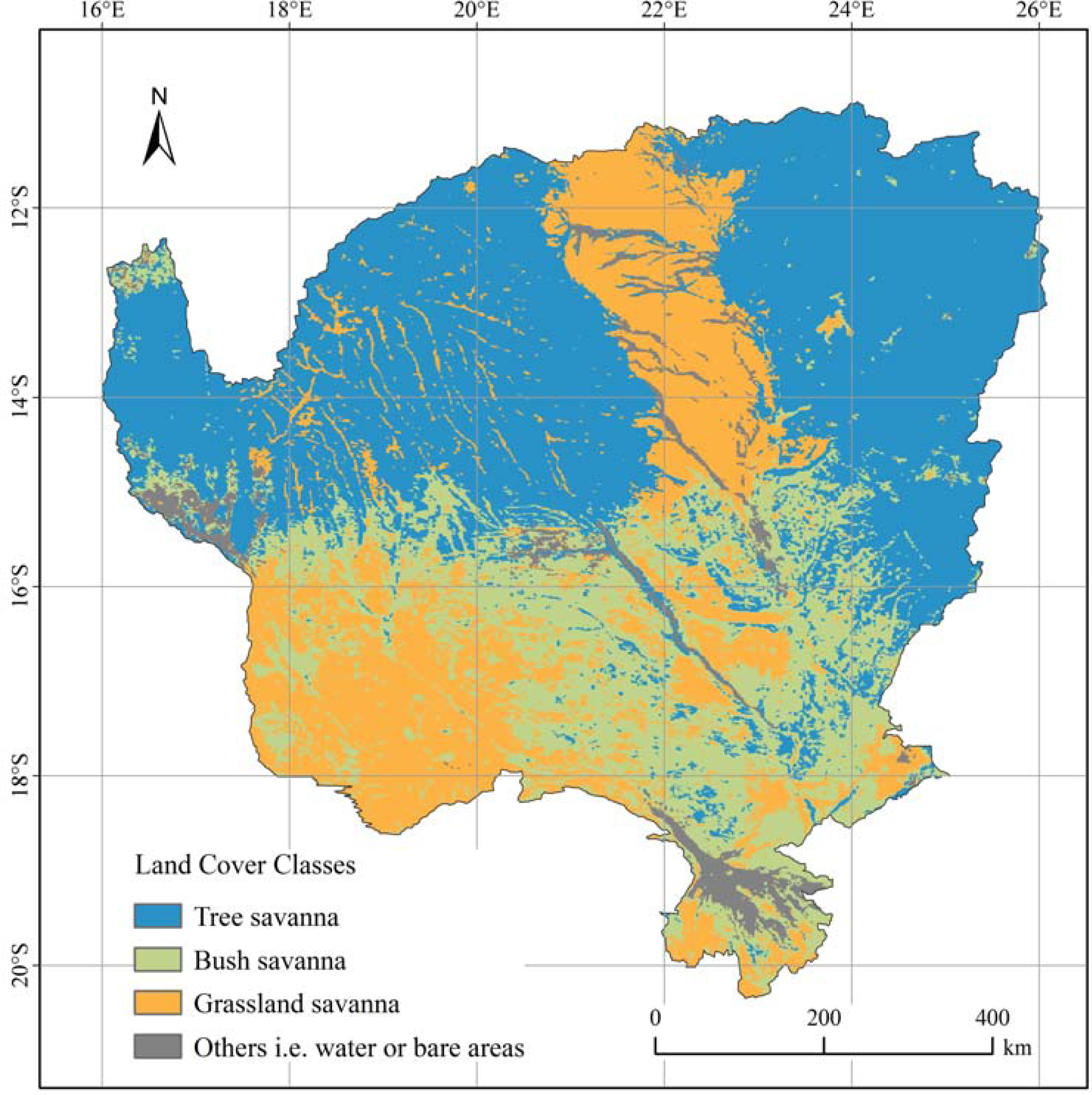
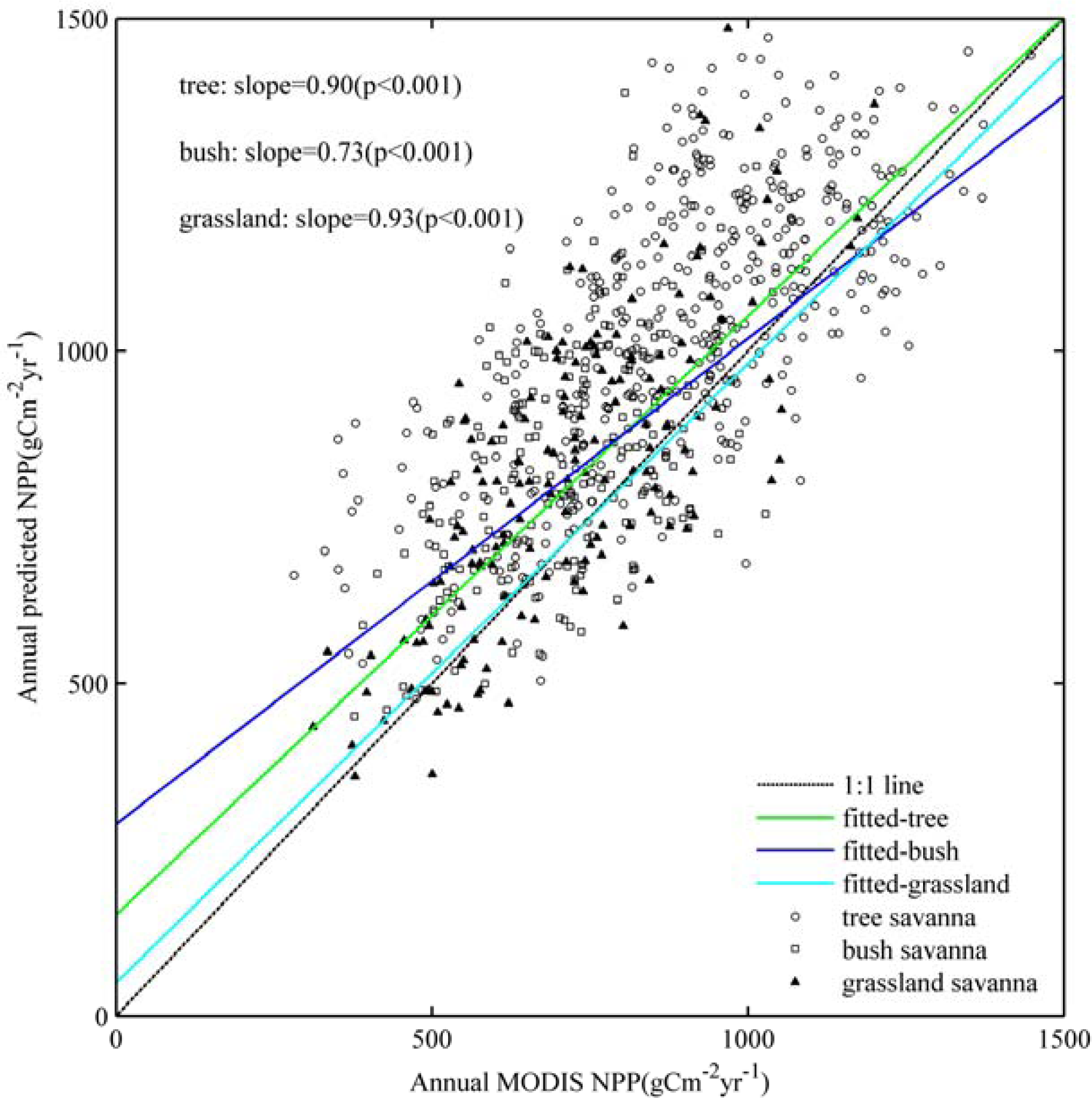
Remotesensing 05 03803f10 1024
Figure 10. Scatter plot of annual aggregated net primary production (NPP) of model estimates with annual Moderate-resolution Imaging Spectroradiometer (MODIS) NPP. These points were randomly selected across our study area.
Figure 10. Scatter plot of annual aggregated net primary production (NPP) of model estimates with annual Moderate-resolution Imaging Spectroradiometer (MODIS) NPP. These points were randomly selected across our study area.
Remotesensing 05 03803f10
Remotesensing 05 03803f11 1024
Figure 11. Spatial pattern of the coefficient of variation (CV) of annual net primary production (NPP) (for water year from September through August) from 1982 to 2010.
Figure 11. Spatial pattern of the coefficient of variation (CV) of annual net primary production (NPP) (for water year from September through August) from 1982 to 2010.
Remotesensing 05 03803f11
Remotesensing 05 03803f12 1024
Figure 12. Spatial pattern of Kendall correlation coefficient (τ) for 1982–2010. The positive τ value indicates an increasing trend, and vice versa.
Figure 12. Spatial pattern of Kendall correlation coefficient (τ) for 1982–2010. The positive τ value indicates an increasing trend, and vice versa.
Remotesensing 05 03803f12
Remotesensing 05 03803f13 1024
Figure 13. The linear relationship between mean annual precipitation (MAP) and mean annual net primary production (NPP) by land cover classes from 1982 to 2010 for (a) tree savanna; (b) bush savanna, and (c) grassland savanna.
Figure 13. The linear relationship between mean annual precipitation (MAP) and mean annual net primary production (NPP) by land cover classes from 1982 to 2010 for (a) tree savanna; (b) bush savanna, and (c) grassland savanna.
Remotesensing 05 03803f13
Remotesensing 05 03803f14 1024
Figure 14. The spatial pattern of correlation coefficients between annual totals of precipitation and net primary production (NPP).
Figure 14. The spatial pattern of correlation coefficients between annual totals of precipitation and net primary production (NPP).
Remotesensing 05 03803f14
Remotesensing 05 03803f15 1024
Figure 15. Scatter plot of mean annual precipitation (MAP) and mean annual net primary production (NPP) for 1982–2010. The piecewise linear regression was used to fit the points to identify the turning point underlying the variations in annual NPP with MAP.
Figure 15. Scatter plot of mean annual precipitation (MAP) and mean annual net primary production (NPP) for 1982–2010. The piecewise linear regression was used to fit the points to identify the turning point underlying the variations in annual NPP with MAP.
Remotesensing 05 03803f15
Table
Table 1. The statistical measures of net primary production (NPP) of different savanna types.
Table 1. The statistical measures of net primary production (NPP) of different savanna types.
TreeBushGrassland
Mean predicted NPP (g·C·m−2·yr−1)1,142.3858.2804.2
Mean MODIS NPP (g·C·m−2·yr−1)985.6743.5711.3
CV0.110.120.12
Increase (%)9.857.579.17
Decrease (%)33.5354.4044.33
Not significant (%)56.6338.0246.50
Table
Table 2. The slope coefficients of linear regression models of different mean annual precipitation (MAP) intervals.
Table 2. The slope coefficients of linear regression models of different mean annual precipitation (MAP) intervals.
Intervals (mm)Study AreaOkavangoKwandoZambezi
SlopeP ValueSlopeP ValueSlopeP ValueSlopeP Value
<4501.37<0.0011.31<0.001----
450–5500.98<0.0010.67<0.0011.16<0.001--
550–6500.94<0.0011.29<0.0010.94<0.012.61<0.001
650–7500.260.0080.290.030.340.020.060.54
750–8500.290.061.10<0.0012.73<0.001−0.87<0.001
850–950−0.090.630.470.140.270.550.460.10
950–1,050−0.290.350.850.032.270.13−0.830.003
1,050–1,1500.390.320.700.21--0.380.38
1,150–1,250−0.0030.991.320.10--−2.10<0.001
>1,250−0.480.0154.380.36--−0.170.38

Share and Cite

MDPI and ACS Style

Zhu, L.; Southworth, J. Disentangling the Relationships between Net Primary Production and Precipitation in Southern Africa Savannas Using Satellite Observations from 1982 to 2010. Remote Sens. 2013, 5, 3803-3825. https://doi.org/10.3390/rs5083803

AMA Style

Zhu L, Southworth J. Disentangling the Relationships between Net Primary Production and Precipitation in Southern Africa Savannas Using Satellite Observations from 1982 to 2010. Remote Sensing. 2013; 5(8):3803-3825. https://doi.org/10.3390/rs5083803

Chicago/Turabian Style

Zhu, Likai, and Jane Southworth. 2013. "Disentangling the Relationships between Net Primary Production and Precipitation in Southern Africa Savannas Using Satellite Observations from 1982 to 2010" Remote Sensing 5, no. 8: 3803-3825. https://doi.org/10.3390/rs5083803

APA Style

Zhu, L., & Southworth, J. (2013). Disentangling the Relationships between Net Primary Production and Precipitation in Southern Africa Savannas Using Satellite Observations from 1982 to 2010. Remote Sensing, 5(8), 3803-3825. https://doi.org/10.3390/rs5083803

Article Metrics

Back to TopTop