1. Introduction
Heterodyne spectroscopy is a powerful tool to observe the atmospheres of terrestrial planets. It provides ultra high spectral resolution of
, yielding the capability to resolve single molecular transition features [
1]. Fully resolved molecular transitions provide information about physical parameters, like temperatures, abundances or dynamical properties. In recent years, this technique has been established to derive ground-based direct wind and temperature measurements by remote sensing of Doppler-shifted and -broadened molecular transitions in the mid-infrared (mid-IR) wavelength regime. Detailed investigations on the dynamical and thermal properties of the upper atmospheres of Titan [
2,
3], Venus [
4–
6] and Mars [
7] have been accomplished. Furthermore, observations of the molecular abundances of Martian ozone were conducted [
8].
High resolution spectroscopy can also be deployed on Earth’s atmosphere. One interesting topic is the tracking of the dynamical behavior in the Earth atmosphere. Hence, investigations to obtain a comprehensive picture are enormous. Ground-based IR heterodyne observations could support ongoing efforts. Analysis of Doppler shifted molecular features is a common technique to observe terrestrial atmospheric dynamics. It is conducted by several airborne and spaceborne instruments,
i.e., the High Resolution Doppler Imager on the Upper Atmosphere Research Satellite, determining winds in an altitude region between 10 km and 40 km [
9], the sub-millimeter limb-sounder S
miles on board the International Space Station (35–60 km) [
10], the ADM-Aeolus (Atmospheric Dynamics Mission) ESA satellite mission (launch 2013) with its Doppler LiDAR instrument A
ladin [
11], which operates at the UV wavelength and probes an altitude region between 26 km and the ground, and the S
wift mission [
12], designed to observe ozone emission features in the mid-infrared. Airborne platforms can provide very high vertical resolution and precision, but they possess spatial limits, due to their orbits.
Recently, ground-based observation by remote sensing with two combined LiDAR instruments between 30 km and 110 km [
13] were conducted. Furthermore, ground-based observations of vertical wind profiles, using a microwave Doppler spectroradiometer [
14], have been performed by probing ozone emission features, originating from an altitude region between 30 km and 70 km.
An additional challenge in observing terrestrial trace gases is the investigation of methane abundances. Methane plays a significant role in the terrestrial greenhouse effect, and its anthropogenic sources are unquestioned. Its sinks, though, are still rarely known, and although its impact is 25-times stronger than that of carbon dioxide, the global distribution is less investigated. The German-French bilateral satellite mission, M
erlin (launched in 2014), is intended to provide better understanding of the global distribution of methane by nadir LiDAR measurements of column densities [
15]. Existing ground-based infrared instruments using direct detection methods are commonly used to probe the terrestrial atmosphere. They also offer high spectral resolution,
, but do not reach the performance of a heterodyne receiver and are significantly larger [
16,
17].
All mid-IR heterodyne investigations on planetary atmospheres, so far, were performed using gas lasers or liquid nitrogen cooled solid-state quantum cascade lasers (QCLs) as local oscillator (LO). QCLs are tunable and provide a continuous spectral tuning range of a few wavenumbers [
18]. Recent improvements on the substrates provide new high-power room temperature QCLs for the mid-IR [
19]. Hence, we developed the first heterodyne receiver that only uses room temperature QCLs. Along with further improvements, this leads to a substantial decrease in the size and weight of the receiver’s framework compared to existing instruments [
1,
20].
2. The Receiver, iChips
The Infrared Compact Heterodyne Instrument for Planetary Science (iChips) is the first heterodyne receiver using room temperature QCLs as LO. In a heterodyne system, the detected signal is coherently superimposed on a reference signal, provided by the LO. The difference, or intermediate frequency (IF), is generated by a mixer that possesses a non-linear characteristic.
The instrument was designed to fit in a two-stage aluminum framework. A schematic view of the beam path can be found in
Figure 1. The dimensions of the receiver are 60 × 42 × 35 cm
3, and it weighs approximately 30 kg, which makes it transportable.
Signal Deck: On the upper, or signal, deck, four radiation sources, needed for calibration purposes, are located, which are a black body radiation source at 673 K as the hot load (4,
Figure 1), a room temperature absorber as the cold load for intensity calibration (5,
Figure 1), a steady state emitter observed through a reference gas cell for spectral calibration and (1,
Figure 1) an input port for the atmospheric signal, provided by the telescope or heliostat, (2 + 3,
Figure 1). The beam selection is provided by a commercially available stepper motor (6,
Figure 1 T
rinamic [
21]). The stepper motor routes the various beam paths through an iris for alignment purposes. The iris (12,
Figure 1) is located in the focal plane of the infrared detector (9,
Figure 1). This is defined by an off-axis parabola (OAP) whose focal length has to be adjusted to the specific input optics. Additionally, a dichroic mirror (DM) (13,
Figure 1) is introduced into the beam to separate the incoming visible and infrared light. The visible signal can be used for active tracking. The infrared signal is forwarded towards the mentioned OAP. Additionally, a visible alignment laser is introduced into the beam path.
LO Deck: The lower deck of the instrument is called the LO deck. Here, the LO (7,
Figure 1), as well as the infrared detector (9,
Figure 1) and the setup of the LO stabilization circuit (10 + 11,
Figure 1) are located along with the beam combining element (beam splitter) (8,
Figure 1). The beam splitter is made of zinc selenite (ZnSe) and has a reflective surface coating with a reflection index of 90%. It is set up such that 90% of the IR signal to be analyzed is reflected onto the mixer, whereas 10% of the LO signal is transmitted, which is sufficient for LO shot noise limited detection.
A QCL operating in continuous wave single mode at room temperature is used as the LO. The device provides an output power of approximately 30 mW and a continuous spectral tuning range of approximately 1% around the central wavenumber [
18,
19]. Such QCLs have recently replaced gas lasers as a state-of-the-art LO in infrared heterodyne spectroscopy [
1]. Currently, two different custom-made QCLs, emitting at 7.8 μm (∼ 1,285 cm
−1), from A
lpes L
asers [
22] and 8.6 μm (∼ 1,160 cm
−1) from M
axion T
echnologies [
23], are available for application.
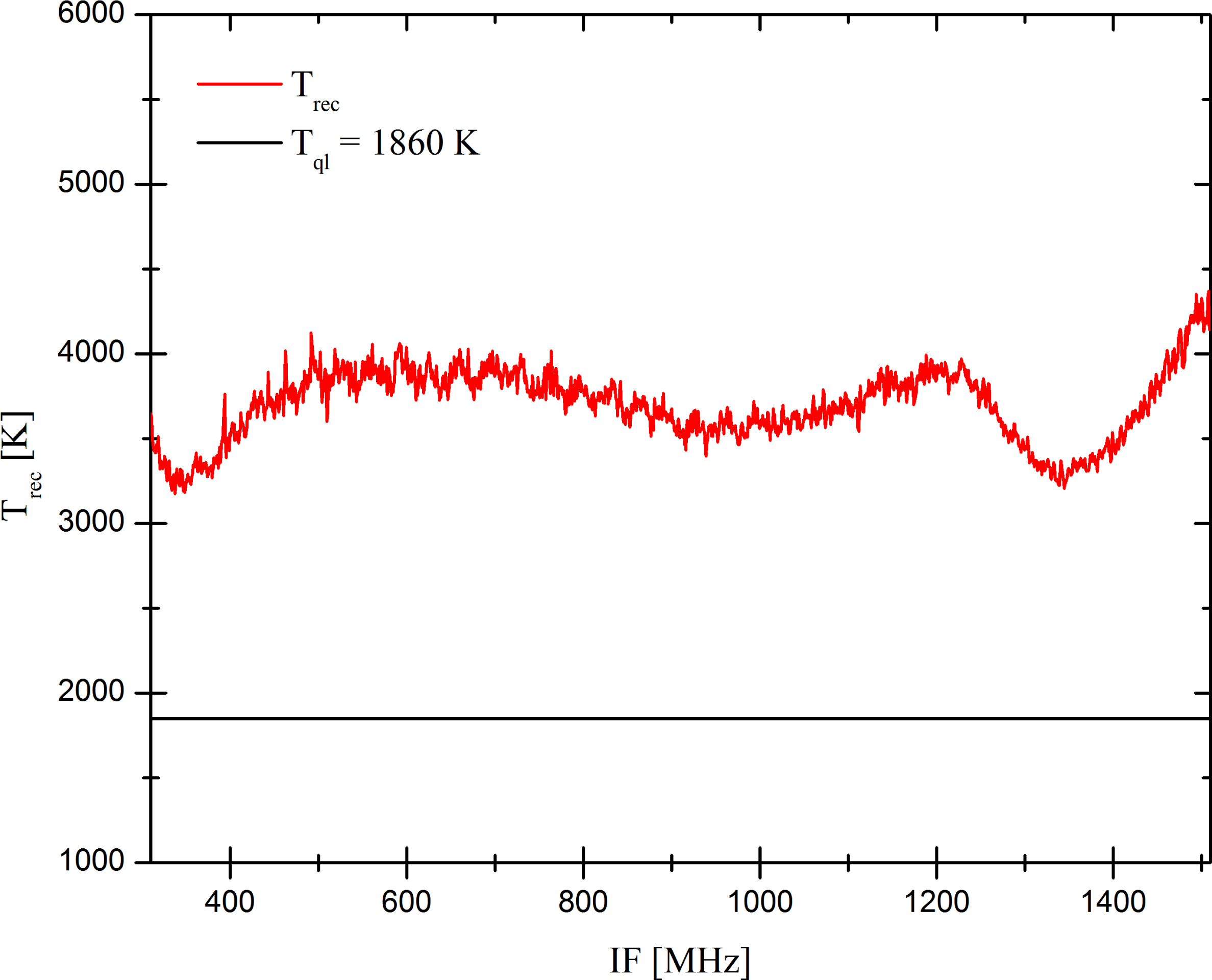
The mixer is a mercury cadmium telluride (MCT)-doped semiconductor pin-photo diode optimized for heterodyne detection between 7.8 μm (∼ 1,285 cm−1) and 12.0 μm (830 cm−1). The diode must be operated at liquid nitrogen temperature of 77 K and has to be biased between 0.5 V and 1.0 V. The mixer has a maximum quantum efficiency of approximately 50%.
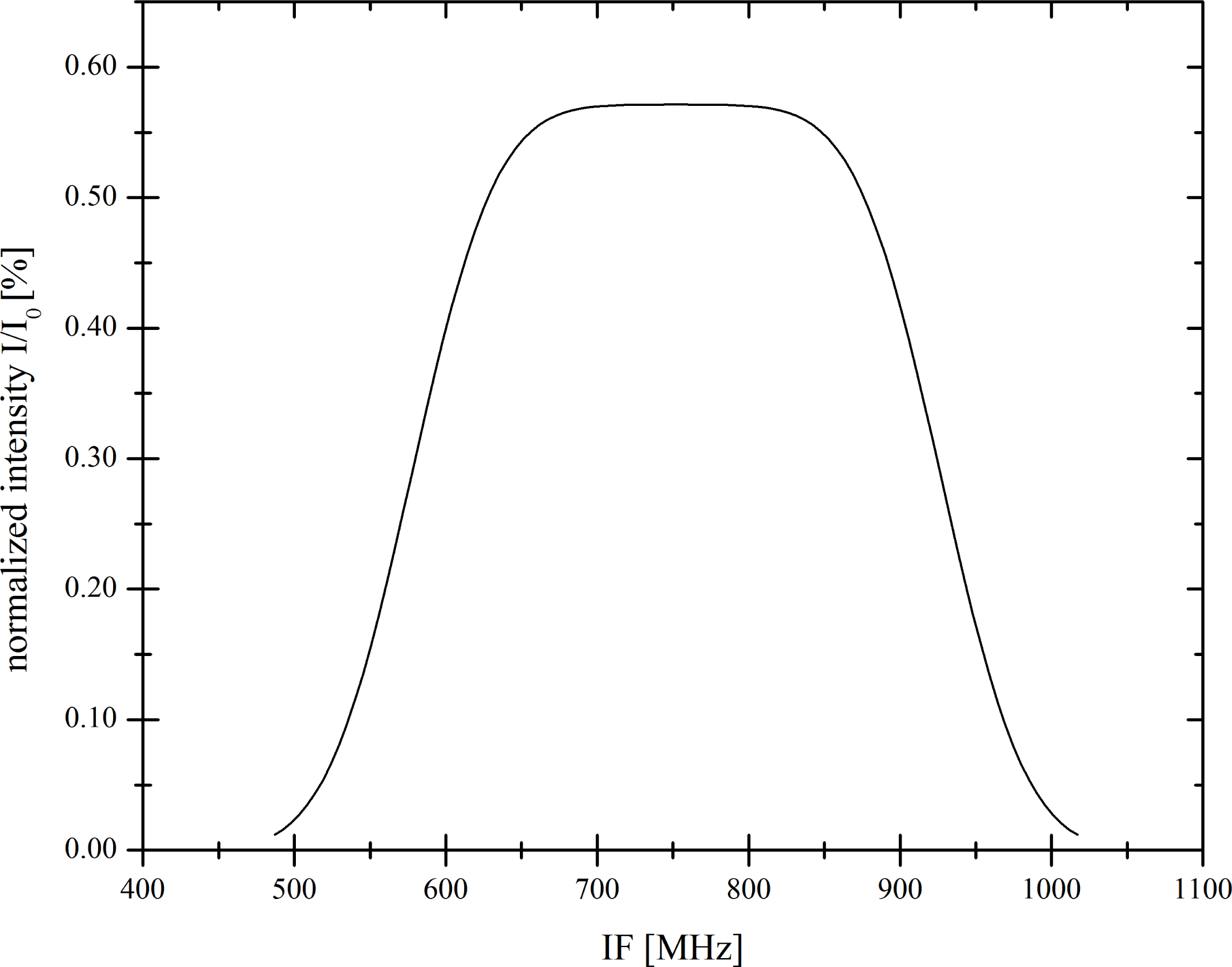
The Signal Processing: The IF signal, generated by the heterodyne mixer, is amplified and shifted to the frequency range of the backend acousto-optical spectrometer (AOS), which is tuned to be sensitive from 250 MHz to 1,650 MHz. It possess a fluctuation bandwidth
δfl of 1.3 MHz and an IF bandwidth
B of 1.4 GHz, defining the IF bandwidth of the entire instrument. AOSs were developed and assembled at our institute [
24] and have been applied successfully for many years for various purposes in the field of radio-astronomy and spectroscopy [
1,
25,
26]. Further analysis and data processing is performed by a PC.
4. Demonstration of Observing Modes: Atmospheric Measurements
As mentioned, the instrument can be operated in two different modes, the staring mode and the scanning mode. Measurements to illustrate the instrument’s capability for atmospheric observation were performed.
To obtain a calibrated spectrum, the ratio of the incident signals from all observed sources is determined:
where
H: hot calibration load,
C: cold calibration load,
S: sky signal,
R: sky reference and
ν̄: wavenumber of observed radiation [
1]. The retrieved dimensionless spectrum,
F, is then multiplied with the difference of the brightness temperature from a hot load and a cold load (
TH−
TC). For hot sources, like the sun, the sky reference,
R, may be substituted by the cold calibration load,
C.
4.1. Staring Mode: Observation of Atmospheric Ozone Features
In staring mode, the LO frequency needs to be stabilized onto an absorption line (see Section 3.1) to investigate single molecular transition features with ultra high resolution of
. A reference line is measured simultaneously to each data set during observation, required for absolute frequency calibration and to verify the stability of the LO spectral line, as demonstrated in Section 3.3.
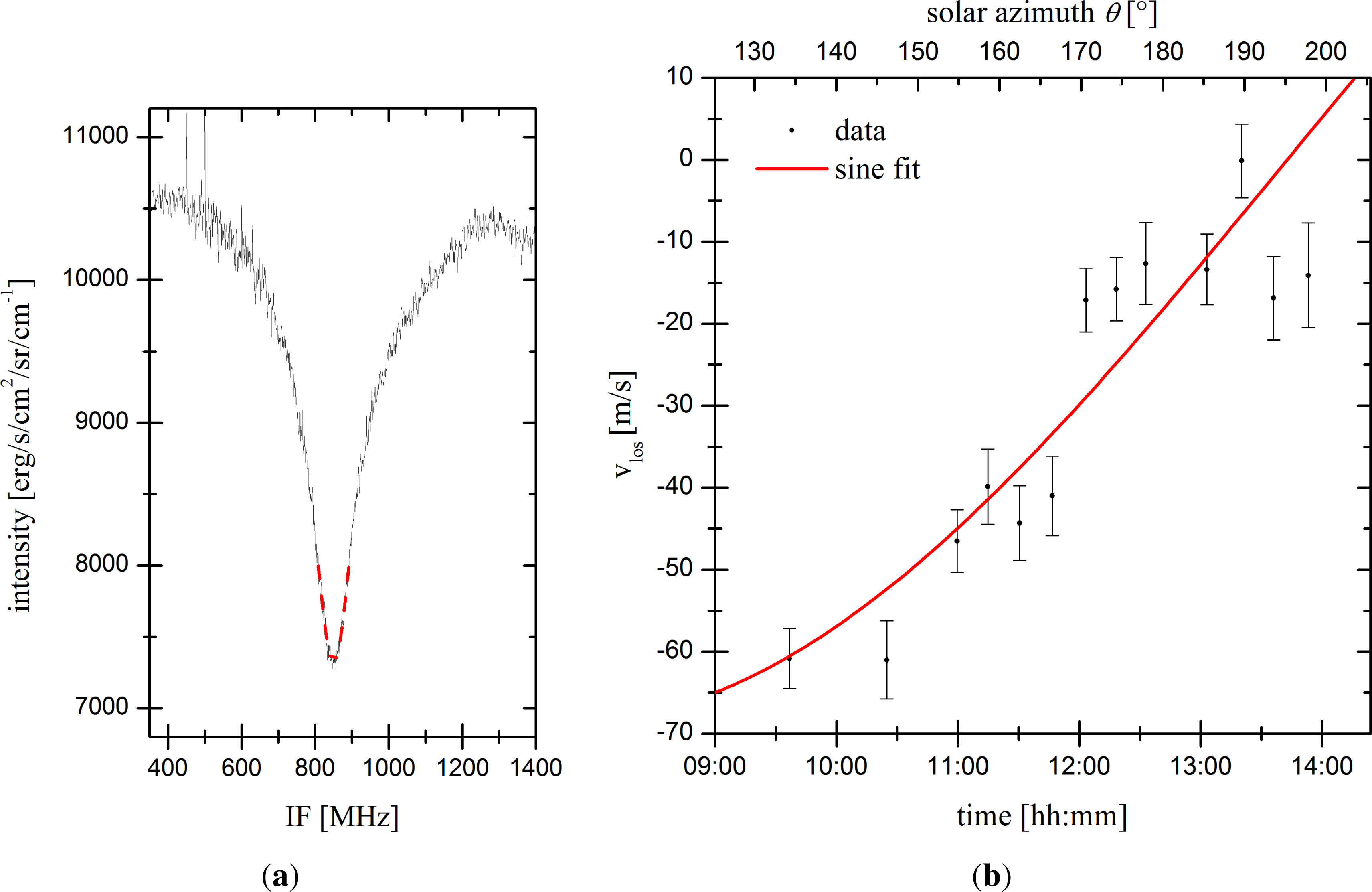
A possible application for the staring mode is the retrieval of atmospheric dynamics. For demonstration purposes, middle atmospheric terrestrial ozone (O3) features were investigated. Since the ozone layer has its peak density at approximately 30 km altitude, the lines are sufficiently narrow to be observed. Initial observations were performed on 10 February 2012, at the I. Physikalisches Institute of the University of Cologne. An ozone line at 1,162.914 cm−1 was observed in absorption, using the sun as the background radiation source. A commercially available solar tracker was used as the heliostat.
During one measuring cycle, the integration time,
τcyc, has to be distributed into appropriate exposure times on each source to minimize the RMS, hence optimizing the signal-to-noise ratio (SNR). The exposure time on the single source can be flexibly adjusted to the specific observational condition. For observations in solar occultation mode, a signal integration time of
is adequate. One example of a measured O
3 absorption line, for a sum of 100 cycles with
τcyc ≈ 3 s, is displayed in
Figure 8a. SO
2 at
≈1 mbar was used as reference to stabilize the LO at 1,162.886 cm
−1. A triangular wave modulation with a bandwidth of Δ
ν = 0.25 FWHM
0, with FWHM
0 = 70 MHz, was applied. In a first step, a Voigt profile was fitted to the line tip (
±50 MHz around the expected IF value) of each measurement to retrieve the precise center frequency of the lines. Thirteen different measurements were performed within 270 min. The shift between the rest IF of the O
3 transition (
νIF,theo in MHz) and the measured IF (
νIF,meas) yields the line of sight (LoS) component of the wind velocity (
vlos) in the stratosphere.
where
νO3 is the absolute frequency of the observed transition. Errors are calculated via Gaussian error propagation from 1-
σ fitting errors and found to be between 0.30 MHz
≤ Δ
νmeas≤ 0.55 MHz for all fits. Thus, fitting errors are smaller than the spectral resolution of the backend spectrometer. In
Figure 8b, the retrieved LoS wind velocities are plotted. In our case, a Doppler shift to a lower frequency yields a negative LoS wind, implying a wind moving away from the observer and
vice versa. LoS wind velocities increase from (
−60.8
± 3.6) m
·s
−1 at 9:36 h local time (LT) to (
−0.1
± 4.5) m
·s
−1 at 13:20 h LT, mainly due to the change in observing geometry.
For further interpretation, a constant horizontal wind field during the time of observation was assumed. The horizontal wind can then be derived by taking the observing geometry into account. Following the sun, a sine wave behavior with a 24 h period of the retrieved LoS wind velocities, in dependency of elevation (
ϕ) and the azimuth (
θ), is expected, by neglecting any up- and down-ward propagation. At the point where the LoS wind velocity is zero, the wind field is perpendicular to the observer (
θvlos=0). Thus, the resulting horizontal wind,
vh, can be expressed as:
A sine fit was applied to the data presented in
Figure 8b. The horizontal wind velocity was found to be
vh = 60.3
± 4.4 m
·s
−1. The uncertainty of the rest frequency of the observed O
3 feature is unreported (H
itran [
31]), which might lead to an offset.
Additionally, in order to investigate a vertically distributed wind in dependence of the altitude, a careful analysis of the full line shape has to be accomplished. Due to the radiative transfer through the atmosphere, different pressure layers, in terms of broadening effects, have a different influence on the spectral shape of the line. This method is successfully applied by Rüfenacht
et al. [
14]. Thus, the tip of the line originates in a specific pressure layer in the Earth’s atmosphere.
4.2. Scanning Mode: Observation of Terrestrial Transmission
The second observing mode of the instrument is the scanning mode. The QCL is capable of sweeping continuously through its whole spectral tuning range (∼ 5–6 wavenumber, depending on the operating temperature) within several seconds. This enables scanning the atmospheric transmission within a short time span.
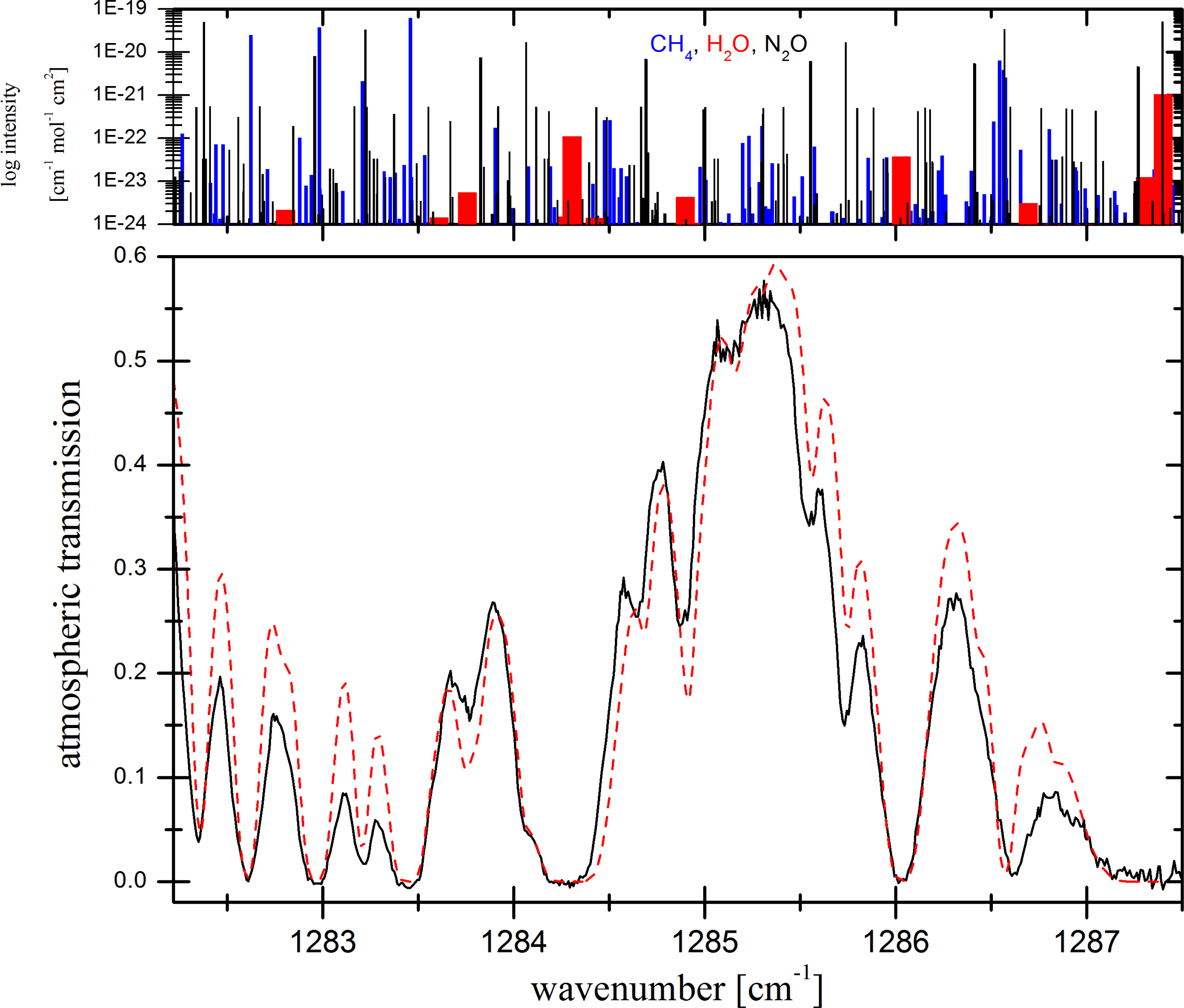
First measurements using the scanning mode were performed during an observing campaign in June 2011, at the McMath-Pierce Solar Telescope East Auxiliary at Kitt Peak National Observatory in Arizona, USA. In
Figure 9, the measured atmospheric transmission between ∼ 1,282.0 cm
−1 and ∼1,287.5 cm
−1 is displayed. The data were acquired by rectifying the heterodyne signal using a Schottky-barrier diode with a bandwidth of approximately 1.4 GHz. The total integration time was 360 s. The solar zenith angle (SZA) for the measurement was 41°, corresponding to an airmass of 1.3 (an airmass of one corresponds to zenith observations). The obtained transmission spectrum is compared to the mid-summer latitude atmosphere model [
32]. The model spectrum was computed using the online database
spectralcalc [
33]. Since the atmospheric parameters during observation (
i.e., water abundance, air pressure,
etc.), were not fully known, a set of standard values was taken to acquire the model. This is the main reason for any intensity deviation of the model from the data. Another, yet neglected, effect is the temperature change of the LO, which affects the output frequency during the scan, yielding small systematic shifts in the spectrum. Nevertheless, absorption features of methane, water and nitrous oxide can be unambiguously assigned.
Further progress will be made to optimize this application mode by implementing variable spectral resolution and instantaneous calibration, taking thermal drifts of the LO into account.
5. Discussion
Room temperature QCLs were successfully applied as LOs in a heterodyne spectrometer for the first time. Spectral analysis of trace gases can be conducted in two different operational modes.
Initial measurements in staring mode of LoS wind velocities were performed by probing stratospheric ozone. The presented results are yet preliminary, since the accuracy of the rest of the frequency of the observed ozone line is unreported. Assuming good knowledge about the observed transition, the horizontal wind can be calculated by considering the observing geometry. Ground-based remote sensing wind measurements in the lower terrestrial stratosphere are quite rare, but have recently been performed by Rüfenacht
et al. [
14] using a microwave spectrometer. Hence, infrared heterodyne spectroscopy can provide complementary studies for ground-based observations on the dynamics in the telluric stratosphere. The observed lines originate in an altitude region around 30 km, where the ozone layer has its peak density. However, a sophisticated retrieval algorithm has to be established, in order to obtain information on the exact observing altitude. Nevertheless, initial observations prove the feasibility of the instrument for the investigation of stratospheric dynamics.
The usage of tunable room temperature QCLs allows one to scan the terrestrial atmosphere over several wavenumbers. A first transmission spectrum, taken at around 7.8 μm (∼ 1,285 cm
−1), is, in principle, in agreement with an average mid-summer latitude atmosphere model [
32] and proves the general performance of the instrument for this operational mode. By using the scanning mode, highly pressure broadened methane transition can be observed with a high spectral resolution and good SNR. Although, the Schottky-barrier diode, used for the initial measurements, limits the resolution to its intrinsic bandwidth. Future work will be performed to discard the diode and to establish the AOS for data acquisition in the scanning mode, enabling the possibility to increase the resolution of the spectra by averaging over an arbitrary and adjustable frequency range (
≤340 MHz) easily to
Additionally, a careful frequency calibration will be performed by simultaneously measuring a reference gas, comparable to the staring mode calibration.
The scanning mode offers the capability to scan the terrestrial atmosphere within a few minutes. Thus, ground-based observing campaigns may provide valuable and continuous input on the distribution of terrestrial methane. From the line shape and the depth of the absorption, it is possible to retrieve an abundance of methane in different altitudes using an inversion method, given a decent knowledge of additional atmospheric parameters, like atmospheric temperatures. With an SNR of 1,000, an accuracy of 0.1 ppmv can be achieved if the temperature and water vapor profile is known [
34].
Besides the molecules mentioned above, many more molecular transitions in the mid-infrared wavelength regime are accessible. Measurements of sulfur and carbon dioxide (SO2, CO2), nitrous oxide (N2O) and ethylene (C2H4) are just some examples of such gases.
In comparison to radiosondes, a tunable heterodyne spectrometer provides a relatively easy and cost-efficient ground-based technique for long-term monitoring of atmospheric parameters.
6. Conclusions
In the present paper the setup of a new compact infrared heterodyne receiver, named iChips, is specified. iChips is the first infrared heterodyne receiver using room temperature quantum cascade lasers as local oscillators. Two different operating modes honor the instrument.
In the staring mode, iChips can be used to observe single fully resolved molecular features. This is demonstrated by the observation of a telluric ozone line around 8.6 μm (∼ 1,160 cm−1). Due to the ultra high spectral resolution of
, such lines can be used to retrieve Doppler winds by determination of the precise frequency position. Applying the second operation mode, the scanning mode iChips can be used to cover a broader wavelength region with resolution,
. Demonstrative measurements of the terrestrial atmosphere around 7.8 μm (∼1,285 cm−1) are shown.
The results validate the capability of iChips for observations of terrestrial and extraterrestrial atmospheres. The instrument’s compactness allows its deployment in flexible field measurement campaigns, even in remote locations, and a broad range of applications for the instrument is available. Further observations of terrestrial ozone to track abundances and stratospheric dynamics and the observation of terrestrial methane are planned.