Multiple Cost Functions and Regularization Options for Improved Retrieval of Leaf Chlorophyll Content and LAI through Inversion of the PROSAIL Model
Abstract
:1. Introduction
2. Methodology
2.1. Cost Functions
2.1.1. Information Measures
- This measure is called the Kullback Leibler divergence and it also corresponds to the maximum likelihood distance in probabilistic space:
- This measure is called Pearson chi-square:
- Squared-Hellinger measure:
- Neyman chi-square divergence:
- Jeffreys-Kullback-Leibler:
- K-divergence of Lin:
- L-divergence of Lin is a symmetric version of K-divergence:
- The harmonique Toussaint measure:
- The negative exponential disparity measure:
- Bhattacharyya divergence:
- Shannon (1948):
2.1.2. Nonlinear Regression and M-Estimates
2.1.3. Minimum Contrast Estimation
- Let ,
- let K(x) = −logx + x, then
- let K(x) = (logx)2, then
- let K(x) = xlogx − x, then
2.2. SPARC Validation Dataset
2.3. Sentinel-2
2.4. LUT Generation
2.5. Regularization Options
- Various standalone cost functions from three mathematically different families.
- Insertion of Gaussian noise on simulated spectra: 0–50%.
- Use of multiple sorted best solutions in the inversion: 0–50%.
- Impact of normalization for CFs in M-estimates and Minimum Contrast Estimates families.
3. Results
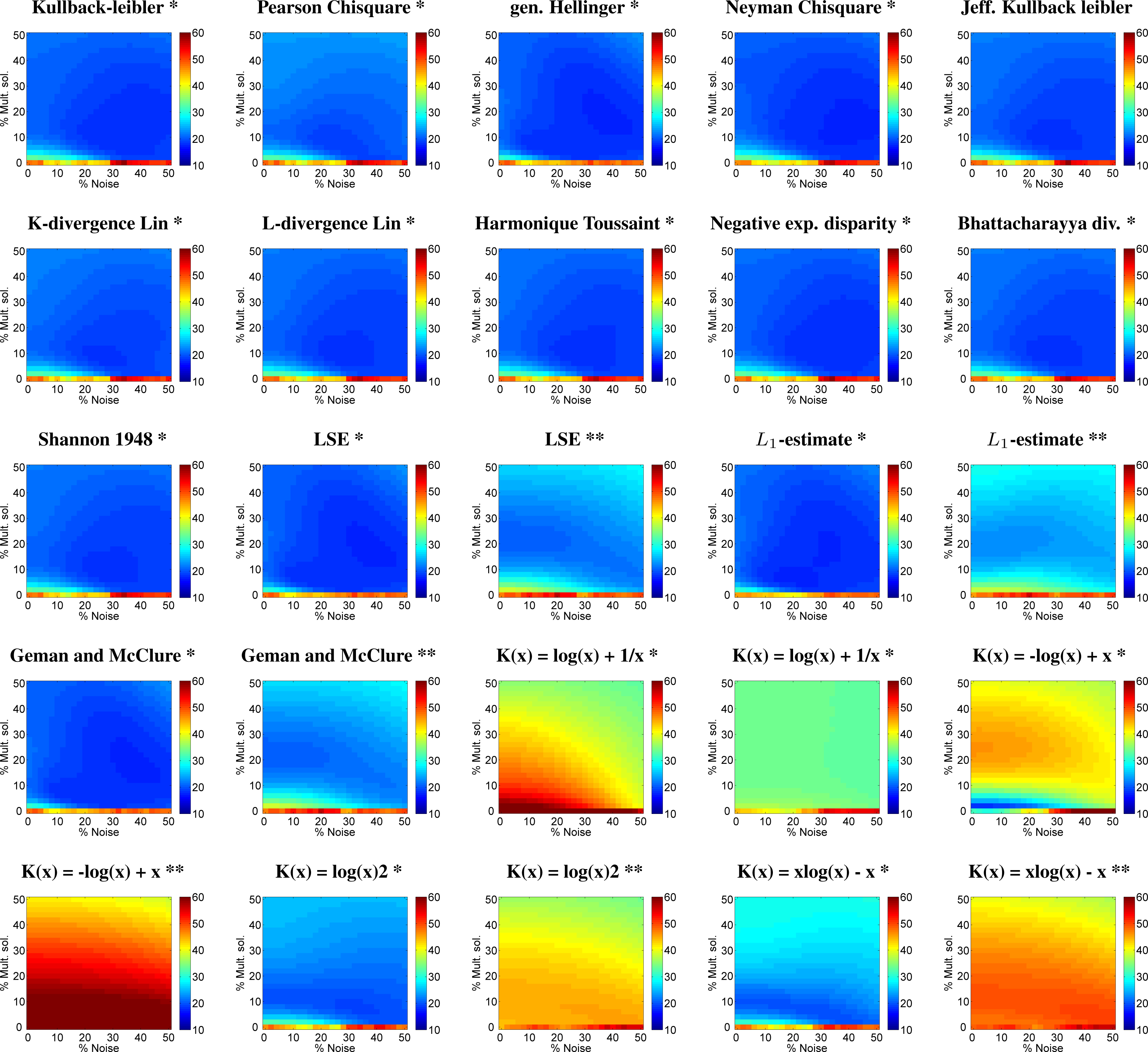
3.1. Evaluation of Cost Functions and Regularization Options
3.1.1. Leaf Chlorophyll Content (LCC) Retrieval
3.1.2. Leaf Area Index (LAI) Retrieval
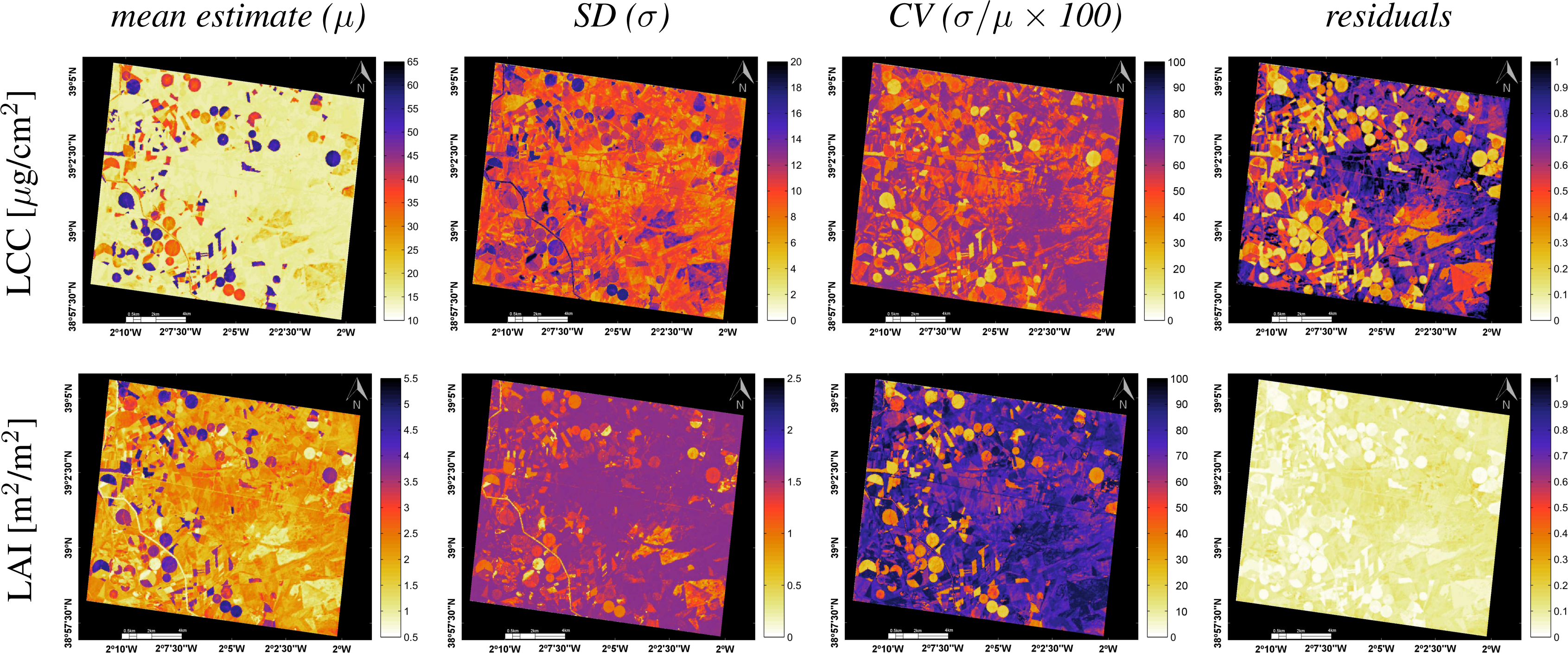
3.2. Biophysical Parameters Mapping
4. Discussion
4.1. Cost Functions and Regularization Options
4.2. Inversion Performance
5. Conclusions
- All evaluated CFs and biophysical parameters gained from regularization options such as adding some noise and multiple solutions in the inversion. These options with proper adjustment can significantly reduce relative errors.
- With introduction of multiple solutions and noise information measures CFs proved to be successful for deriving LCC. However best LCC results were achieved with the M-estimate L1 (NRMSE of 17.6% at 6% multiple solutions and 18% noise) when data is normalized.
- Data normalization appeared to be unsuccessful for retrieving LAI. Here, the classical LSE yielded best results for non-normalized data; NRMSE of 15.3% at 6% multiple solutions and 18% noise, and 16.4% at 16% multiple solutions and 0% noise, respectively.
Acknowledgments
Conflict of Interest
References
- Whittaker, R.H.; Marks, P.L. Methods of Assessing Terrestrial Productivity. In Primary Productivity of the Biosphere; Springer Verlag: Berlin/Heidelberg, Germany, 1975; pp. 55–118. [Google Scholar]
- Lichtenthaler, H.K. Chlorophylls and carotenoids: Pigments of photosynthetic biomembranes. Methods Enzymol 1987, 148, 350–382. [Google Scholar]
- Malenovský, Z.; Rott, H.; Cihlar, J.; Schaepman, M.; García-Santos, G.; Fernandes, R.; Berger, M. Sentinels for science: Potential of Sentinel-1, -2, and -3 missions for scientific observations of ocean, cryosphere, and land. Remote Sens. Environ 2012, 120, 91–101. [Google Scholar]
- Lichtenthaler, H.K.; Lang, M.; Sowinska, M.; Heisel, F.; Miehe, J.A. Detection of vegetation stress via a new high resolution fluorescence imaging system. J. Plant Physiol 1996, 148, 599–612. [Google Scholar]
- Sampson, P.H.; Zarco-Tejada, P.J.; Mohammed, G.H.; Miller, J.R.; Noland, T.L. Hyperspectral remote sensing of forest condition: Estimating chlorophyll content in tolerant hardwoods. For. Sci 2003, 49, 381–391. [Google Scholar]
- Dorigo, W.A.; Zurita-Milla, R.; de Wit, A.J.W.; Brazile, J.; Singh, R.; Schaepman, M.E. A review on reflective remote sensing and data assimilation techniques for enhanced agroecosystem modeling. Int. J. Appl. Earth Obs. Geoinf 2007, 9, 165–193. [Google Scholar]
- Delegido, J.; Verrelst, J.; Meza, C.; Rivera, J.; Alonso, L.; Moreno, J. A red-edge spectral index for remote sensing estimation of green LAI over agroecosystems. Eur. J. Agron 2013, 46, 42–52. [Google Scholar]
- Gianquinto, G.; Orsini, F.; Fecondini, M.; Mezzetti, M.; Sambo, P.; Bona, S. A methodological approach for defining spectral indices for assessing tomato nitrogen status and yield. Eur. J. Agron 2011, 35, 135–143. [Google Scholar]
- Baret, F.; Hagolle, O.; Geiger, B.; Bicheron, P.; Miras, B.; Huc, M.; Berthelot, B.; Niço, F.; Weiss, M.; Samain, O.; et al. LAI, fAPAR and fCover CYCLOPES global products derived from VEGETATION. Part 1: Principles of the algorithm. Remote Sens. Environ 2007, 110, 275–286. [Google Scholar]
- Myneni, R.; Hoffman, S.; Knyazikhin, Y.; Privette, J.; Glassy, J.; Tian, Y.; Wang, Y.; Song, X.; Zhang, Y.; Smith, G.; et al. Global products of vegetation leaf area and fraction absorbed PAR from year one of MODIS data. Remote Sens. Environ 2002, 83, 214–231. [Google Scholar]
- Ganguly, S.; Nemani, R.; Zhang, G.; Hashimoto, H.; Milesi, C.; Michaelis, A.; Wang, W.; Votava, P.; Samanta, A.; Melton, F.; et al. Generating global leaf area index from landsat: Algorithm formulation and demonstration. Remote Sens. Environ 2012, 122, 185–202. [Google Scholar]
- Dash, J.; Curran, P. The MERIS terrestrial chlorophyll index. Int. J. Remote Sens 2004, 25, 5403–5413. [Google Scholar]
- Bacour, C.; Baret, F.; Béal, D.; Weiss, M.; Pavageau, K. Neural network estimation of LAI, fAPAR, fCover and LAI × Cab, from top of canopy MERIS reflectance data: Principles and validation. Remote Sens. Environ 2006, 105, 313–325. [Google Scholar]
- Houborg, R.; Boegh, E. Mapping leaf chlorophyll and leaf area index using inverse and forward canopy reflectance modeling and SPOT reflectance data. Remote Sens. Environ 2008, 112, 186–202. [Google Scholar]
- Houborg, R.; Anderson, M.; Daughtry, C. Utility of an image-based canopy reflectance modeling tool for remote estimation of LAI and leaf chlorophyll content at the field scale. Remote Sens. Environ 2009, 113, 259–274. [Google Scholar]
- Stuffler, T.; Kaufmann, C.; Hofer, S.; Förster, K.; Schreier, G.; Mueller, A.; Eckardt, A.; Bach, H.; Penné, B.; Benz, U.; et al. The EnMAP hyperspectral imager-An advanced optical payload for future applications in Earth observation programmes. Acta Astronaut 2007, 61, 115–120. [Google Scholar]
- Labate, D.; Ceccherini, M.; Cisbani, A.; De Cosmo, V.; Galeazzi, C.; Giunti, L.; Melozzi, M.; Pieraccini, S.; Stagi, M. The PRISMA payload optomechanical design, a high performance instrument for a new hyperspectral mission. Acta Astronaut 2009, 65, 1429–1436. [Google Scholar]
- Roberts, D.; Quattrochi, D.; Hulley, G.; Hook, S.; Green, R. Synergies between VSWIR and TIR data for the urban environment: An evaluation of the potential for the Hyperspectral Infrared Imager (HyspIRI) decadal survey mission. Remote Sens. Environ 2012, 117, 83–101. [Google Scholar]
- Darvishzadeh, R.; Skidmore, A.; Schlerf, M.; Atzberger, C. Inversion of a radiative transfer model for estimating vegetation LAI and chlorophyll in a heterogeneous grassland. Remote Sens. Environ 2008, 112, 2592–2604. [Google Scholar]
- Knyazikhin, Y.; Kranigk, J.; Myneni, R.; Panfyorov, O.; Gravenhorst, G. Influence of small-scale structure on radiative transfer and photosynthesis in vegetation canopies. J. Geophys. Res. D 1998, 103, 6133–6144. [Google Scholar]
- Durbha, S.; King, R.; Younan, N. Support vector machines regression for retrieval of leaf area index from multiangle imaging spectroradiometer. Remote Sens. Environ 2007, 107, 348–361. [Google Scholar]
- Combal, B.; Baret, F.; Weiss, M.; Trubuil, A.; Mace, D.; Pragnère, A.; Myneni, R.; Knyazikhin, Y.; Wang, L. Retrieval of canopy biophysical variables from bidirectional reflectance using prior information to solve the ill-posed inverse problem. Remote Sens. Environ 2003, 84, 1–15. [Google Scholar]
- Richter, K.; Atzberger, C.; Vuolo, F.; Weihs, P.; D’Urso, G. Experimental assessment of the Sentinel-2 band setting for RTM-based LAI retrieval of sugar beet and maize. Can. J. Remote Sens 2009, 35, 230–247. [Google Scholar]
- Weiss, M.; Baret, F.; Myneni, R.; Pragnère, A.; Knyazikhin, Y. Investigation of a model inversion technique to estimate canopy biophysical variables from spectral and directional reflectance data. Agronomie 2000, 20, 3–22. [Google Scholar]
- Fang, H.; Liang, S. A hybrid inversion method for mapping leaf area index from MODIS data: Experiments and application to broadleaf and needleleaf canopies. Remote Sens. Environ 2005, 94, 405–424. [Google Scholar]
- Qu, Y.; Wang, J.; Wan, H.; Li, X.; Zhou, G. A Bayesian network algorithm for retrieving the characterization of land surface vegetation. Remote Sens. Environ 2008, 112, 613–622. [Google Scholar]
- Walthall, C.; Dulaney, W.; Anderson, M.; Norman, J.; Fang, H.; Liang, S. A comparison of empirical and neural network approaches for estimating corn and soybean leaf area index from Landsat ETM+ imagery. Remote Sens. Environ 2004, 92, 465–474. [Google Scholar]
- Weiss, M.; Baret, F. Evaluation of canopy biophysical variable retrieval performances from the accumulation of large swath satellite data. Remote Sens. Environ 1999, 70, 293–306. [Google Scholar]
- Jacquemoud, S.; Baret, F.; Andrieu, B.; Danson, F.; Jaggard, K. Extraction of vegetation biophysical parameters by inversion of the PROSPECT+SAIL models on sugar beet canopy reflectance data. Application to TM and AVIRIS sensors. Remote Sens. Environ 1995, 52, 163–172. [Google Scholar]
- Baret, F.; Buis, S. Estimating Canopy Characteristics from Remote Sensing Observations. Review of Methods and Associated Problems. In Advances in Land Remote Sensing: System, Modeling, Inversion and Application; Liang, S., Ed.; Springer: Berlin, Germany, 2008; pp. 173–201. [Google Scholar]
- Combal, B.; Baret, F.; Weiss, M. Improving canopy variables estimation from remote sensing data by exploiting ancillary information. Case study on sugar beet canopies. Agronomie 2002, 22, 205–215. [Google Scholar]
- Dorigo, W.; Richter, R.; Baret, F.; Bamler, R.; Wagner, W. Enhanced automated canopy characterization from hyperspectral data by a novel two step radiative transfer model inversion approach. Remote Sens 2009, 1, 1139–1170. [Google Scholar]
- Koetz, B.; Baret, F.; Poilvé, H.; Hill, J. Use of coupled canopy structure dynamic and radiative transfer models to estimate biophysical canopy characteristics. Remote Sens. Environ 2005, 95, 115–124. [Google Scholar]
- Richter, K.; Atzberger, C.; Vuolo, F.; D’Urso, G. Evaluation of Sentinel-2 spectral sampling for radiative transfer model based LAI estimation of wheat, sugar beet, and maize. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens 2011, 4, 458–464. [Google Scholar]
- Darvishzadeh, R.; Matkan, A.A.; Dashti Ahangar, A. Inversion of a radiative transfer model for estimation of rice canopy chlorophyll content using a lookup-table approach. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, PP, 1–9. [Google Scholar]
- Leonenko, G.; North, P.; Los, S. Statistical distances and their applications to biophysical parameter estimation: Information measures, M-estimates, and minimum contrast methods. Remote Sens 2013, 5, 1355–1388. [Google Scholar]
- Verrelst, J.; Rivera, J.; Leonenko, G.; Moreno, J. Optimizing LUT-based RTM inversion for semiautomatic mapping of crop biophysical parameters from Sentinel-2 and -3 data: Role of cost functions. IEEE Trans. Geosci. Remote Sens. 2013, in press.. [Google Scholar]
- Atzberger, C.; Richter, K. Spatially constrained inversion of radiative transfer models for improved LAI mapping from future Sentinel-2 imagery. Remote Sens. Environ 2012, 120, 208–218. [Google Scholar]
- Chen, J.; Pavlic, G.; Brown, L.; Cihlar, J.; Leblanc, S.; White, H.; Hall, R.; Peddle, D.; King, D.; Trofymow, J.; et al. Derivation and validation of Canada-wide coarse-resolution leaf area index maps using high-resolution satellite imagery and ground measurements. Remote Sens. Environ 2002, 80, 165–184. [Google Scholar]
- Kullback, S.; Leibler, R. On information and sufficiency. Ann. Math. Stat 1951, 22, 79–86. [Google Scholar]
- Pardo, L. Statistical Inference Based on Divergence Measures, Statistics: A Series Textbooks and Monographs; Chapman and Hall/CRC: Boca Raton, FL, USA, 2006. [Google Scholar]
- Staudte, R.; Sheather, S. Robust Estimation and Testing; Wiley: New York, NY, USA, 1990. [Google Scholar]
- Taniguchi, M. On estimation of parameters of Gaussian stationary processes. J. Appl. Probab 1979, 16, 575–591. [Google Scholar]
- Gandía, S.; Fernández, G.; Garcia, J.C.; Moreno, J. Retrieval of Vegetation Biophysical Variables from CHRIS/PROBA Data in the SPARC Campaign. Proceedings of the 2nd CHRIS/PROBAWorkshop, Frascati, Italy, 28–30 April 2004.
- Fernández, G.; Moreno, J.; Gandía, S.; Martínez, B.; Vuolo, F.; Morales, F. Statistical Variability of Field Measurements of Biophysical Parameters in SPARC-2003 and SPARC-2004 Campaigns. Proceedings of the SPARC Workshop WPP-250, Enschede, The Netherlands, 4–5 July 2005.
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s optical high-resolution mission for GMES operational services. Remote Sens. Environ 2012, 120, 25–36. [Google Scholar]
- Barnsley, M.J.; Settle, J.J.; Cutter, M.A.; Lobb, D.R.; Teston, F. The PROBA/CHRIS mission: A low-cost smallsat for hyperspectral multiangle observations of the earth surface and atmosphere. IEEE Trans. Geosci. Remote Sens 2004, 42, 1512–1520. [Google Scholar]
- Alonso, L.; Moreno, J. Advances and Limitations in A Parametric Geometric Correction of CHRIS/PROBA Data. Proceedings of the 3rd CHRIS/Proba Workshop, Frascati, Italy, 21–23 March 2005.
- Guanter, L.; Alonso, L.; Moreno, J. A method for the surface reflectance retrieval from PROBA/CHRIS data over land: Application to ESA SPARC campaigns. IEEE Trans. Geosci. Remote Sens 2005, 43, 2908–2917. [Google Scholar]
- Verrelst, J.; Rivera, J.; Alonso, L.; Moreno, J. ARTMO: An Automated Radiative Transfer Models Operator Toolbox for Automated Retrieval of Biophysical Parameters through Model Inversion. Proceedings of EARSeL 7th SIG-Imaging Spectroscopy Workshop, Edinburgh, UK, 11–13 April 2011.
- Verrelst, J.; Romijn, E.; Kooistra, L. Mapping vegetation density in a heterogeneous river floodplain ecosystem using pointable CHRIS/PROBA data. Remote Sens 2012, 4, 2866–2889. [Google Scholar]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.; Asner, G.; François, C.; Ustin, S. PROSPECT + SAIL models: A review of use for vegetation characterization. Remote Sens. Environ 2009, 113, S56–S66. [Google Scholar]
- Feret, J.B.; François, C.; Asner, G.P.; Gitelson, A.A.; Martin, R.E.; Bidel, L.P.R.; Ustin, S.L.; le Maire, G.; Jacquemoud, S. PROSPECT-4 and 5: Advances in the leaf optical properties model separating photosynthetic pigments. Remote Sens. Environ 2008, 112, 3030–3043. [Google Scholar]
- Garrigues, S.; Lacaze, R.; Baret, F.; Morisette, J.; Weiss, M.; Nickeson, J.; Fernandes, R.; Plummer, S.; Shabanov, N.; Myneni, R.; et al. Validation and intercomparison of global leaf area index products derived from remote sensing data. J. Geophys. Res.-Biogeosci. 2008, 113. [Google Scholar] [CrossRef]
- Pinty, B.; Lavergne, T.; Vobbeck, M.; Kaminski, T.; Aussedat, O.; Giering, R.; Gobron, N.; Taberner, M.; Verstraete, M.; Widlowski, J.L. Retrieving surface parameters for climate models from Moderate Resolution Imaging Spectroradiometer (MODIS)-Multiangle Imaging Spectroradiometer (MISR) albedo products. J. Geophy. Res.-Atmos. 2007, 112. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F.; Garrigues, S.; Lacaze, R. LAI and fAPAR CYCLOPES global products derived from VEGETATION. Part 2: validation and comparison with MODIS collection 4 products. Remote Sens. Environ 2007, 110, 317–331. [Google Scholar]
- Clevers, J.; Gitelson, A. Remote estimation of crop and grass chlorophyll and nitrogen content using red-edge bands on Sentinel-2 and -3. ITC J. 2013; in press. [Google Scholar]
- Delegido, J.; Verrelst, J.; Alonso, L.; Moreno, J. Evaluation of sentinel-2 red-edge bands for empirical estimation of green LAI and chlorophyll content. Sensors 2011, 11, 7063–7081. [Google Scholar]
- Verrelst, J.; Muñoz, J.; Alonso, L.; Delegido, J.; Rivera, J.; Camps-Valls, G.; Moreno, J. Machine learning regression algorithms for biophysical parameter retrieval: Opportunities for Sentinel-2 and -3. Remote Sens. Environ 2012, 118, 127–139. [Google Scholar]
- Richter, K.; Hank, T.; Vuolo, F.; Mauser, W.; D’Urso, G. Optimal exploitation of the Sentinel-2 spectral capabilities for crop leaf area index mapping. Remote Sens 2012, 4, 561–582. [Google Scholar]
- Gitelson, A.; Merzlyak, M.; Lichtenthaler, H. Detection of red edge position and chlorophyll content by reflectance measurements near 700 nm. J. Plant Physiol 1996, 148, 501–508. [Google Scholar]
- Si, Y.; Schlerf, M.; Zurita-Milla, R.; Skidmore, A.; Wang, T. Mapping spatio-temporal variation of grassland quantity and quality using MERIS data and the PROSAIL model. Remote Sens. Environ 2012, 121, 415–425. [Google Scholar]
- Baret, F. Biophysical vegetation variables retrieval from remote sensing observations. Proc. SPIE 2010, 7824, 17–19. [Google Scholar]
- Drusch, M.; Gascon, F.; Berger, M. Sentinel-2 Mission Requirements Document, 2010. Available online: http://esamultimedia.esa.int/docs/GMES/Sentinel-2_MRD.pdf (accessed on 27 April 2013).
- Atzberger, C. Object-based retrieval of biophysical canopy variables using artificial neural nets and radiative transfer models. Remote Sens. Environ 2004, 93, 53–67. [Google Scholar]
- Meroni, M.; Colombo, R.; Panigada, C. Inversion of a radiative transfer model with hyperspectral observations for LAI mapping in poplar plantations. Remote Sens. Environ 2004, 92, 195–206. [Google Scholar]
- Brown, L.; Chen, J.; Leblanc, S.; Cihlar, J. A shortwave infrared modification to the simple ratio for LAI retrieval in boreal forests: An image and model analysis. Remote Sens. Environ 2000, 71, 16–25. [Google Scholar]

| Band # | B1 | B2 | B3 | B4 | B5 | B6 | B7 | B8 | B8a | B9 | B10 | B11 | B12 |
| Band center (nm) | 443 | 490 | 560 | 665 | 705 | 740 | 783 | 842 | 865 | 945 | 1375 | 1610 | 2190 |
| Band width (nm) | 20 | 65 | 35 | 30 | 15 | 15 | 20 | 115 | 20 | 20 | 30 | 90 | 180 |
| Spatial resolution (m) | 60 | 10 | 10 | 10 | 20 | 20 | 20 | 10 | 20 | 60 | 60 | 20 | 20 |
| Model Parameters | Units | Range | Distribution | |
|---|---|---|---|---|
| Leaf parameters: PROSPECT-4 | ||||
| N | Leaf structure index | unitless | 1.3–2.5 | Uniform |
| LCC | Leaf chlorophyll content | (μg/cm2) | 5–75 | Gaussian (x̄: 35, SD: 30) |
| Cm | Leaf dry matter content | (g/cm2) | 0.001–0.03 | Uniform |
| Cw | Leaf water content | (cm) | 0.002–0.05 | Uniform |
| Canopy variables: 4SAIL | ||||
| LAI | Leaf area index | (m2/m2) | 0.1–7 | Gaussian (x̄: 3, SD: 2) |
| αsoil | Soil scaling factor | unitless | 0–1 | Uniform |
| ALA | Average leaf angle | (○) | 40–70 | Uniform |
| HotS | Hot spot parameter | (m/m) | 0.05–0.5 | Uniform |
| skyl | Diffuse incoming solar radiation | (fraction) | 0.05 | - |
| θs | Sun zenith angle | (○) | 22.3 | - |
| θv | View zenith angle | (○) | 20.19 | - |
| φ | Sun-sensor azimuth angle | (○) | 0 | - |
| Cost Function | Mult. Sol. (%) | Noise (%) | r2 | abs. RMSE | NRMSE (%) | 0,0 NRMSE (%) |
|---|---|---|---|---|---|---|
| Kullback leibler * | 10 | 26 | 0.71 | 7.34 | 19.47 | 47.54 |
| Chi square * | 8 | 24 | 0.69 | 7.57 | 18.64 | 48.94 |
| Generalised Hellinger * | 20 | 36 | 0.74 | 7.16 | 17.63 | 47.55 |
| Neyman Chi square * | 16 | 44 | 0.73 | 7.16 | 17.63 | 46.62 |
| Jeffreys Kullback leibler * | 10 | 26 | 0.70 | 7.41 | 18.25 | 48.36 |
| K-divergence Lin * | 8 | 26 | 0.70 | 7.43 | 18.30 | 48.01 |
| L-divergence Lin * | 10 | 26 | 0.70 | 7.39 | 18.20 | 48.25 |
| Harmonique Toussaint * | 10 | 26 | 0.71 | 7.37 | 18.15 | 48.36 |
| Negative exp. disparity * | 10 | 26 | 0.71 | 7.31 | 18.01 | 47.43 |
| Bhattacharyya divergence * | 10 | 28 | 0.70 | 7.40 | 18.22 | 48.18 |
| Shannon 1948 * | 10 | 26 | 0.70 | 7.39 | 18.20 | 48.18 |
| LSE * | 20 | 36 | 0.74 | 7.16 | 17.63 | 47.55 |
| LSE ** | 22 | 0 | 0.68 | 8.23 | 20.27 | 46.99 |
| L1-estimate * | 6 | 18 | 0.73 | 7.14 | 17.59 | 45.88 |
| L1-estimate ** | 20 | 12 | 0.61 | 9.14 | 22.52 | 45.58 |
| Geman and McClure * | 20 | 36 | 0.74 | 7.16 | 17.63 | 47.55 |
| Geman and McClure ** | 22 | 0 | 0.68 | 8.24 | 20.30 | 46.99 |
| K(x) = log(x) + 1/x * | 50 | 50 | 0.68 | 13.43 | 33.09 | 70.96 |
| K(x) = log(x) + 1/x ** | 16 | 50 | 0.62 | 13.36 | 32.91 | 43.86 |
| K(x) = −log(x) + x * | 2 | 0 | 0.70 | 7.45 | 18.34 | 31.82 |
| K(x) = −log(x) + x ** | 50 | 50 | 0.48 | 15.76 | 38.83 | 83.15 |
| K(x) = log(x)2 * | 8 | 32 | 0.68 | 7.76 | 19.11 | 46.68 |
| K(x) = log(x)2 ** | 50 | 50 | 0.31 | 13.87 | 34.15 | 44.14 |
| K(x) = x(log(x)) − x * | 6 | 30 | 0.66 | 7.95 | 19.58 | 47.19 |
| K(x) = x(log(x)) − x ** | 50 | 50 | 0.30 | 15.05 | 37.06 | 48.99 |
| Cost Function | Mult. Sol. (%) | Noise (%) | r2 | abs. RMSE | NRMSE (%) | 0,0 NRMSE (%) |
|---|---|---|---|---|---|---|
| Kullback leibler * | 4 | 50 | 0.63 | 1.25 | 22.74 | 45.59 |
| Chi square * | 8 | 50 | 0.62 | 1.29 | 23.53 | 45.74 |
| Generalised Hellinger * | 2 | 42 | 0.62 | 1.17 | 21.34 | 44.59 |
| Neyman Chi square * | 4 | 50 | 0.62 | 1.24 | 22.48 | 45.51 |
| Jeffreys Kullback leibler * | 6 | 50 | 0.62 | 1.26 | 22.93 | 45.60 |
| K-divergence Lin * | 6 | 50 | 0.62 | 1.27 | 23.06 | 45.67 |
| L-divergence Lin * | 10 | 26 | 0.70 | 1.26 | 22.92 | 45.54 |
| Harmonique Toussaint * | 6 | 50 | 0.62 | 1.26 | 22.91 | 45.60 |
| Negative exp. disparity * | 4 | 50 | 0.63 | 1.25 | 22.72 | 45.53 |
| Bhattacharyya divergence * | 6 | 50 | 0.62 | 1.26 | 22.93 | 45.53 |
| Shannon 1948 * | 6 | 50 | 0.62 | 1.26 | 22.92 | 45.54 |
| LSE * | 2 | 42 | 0.62 | 1.17 | 21.34 | 44.58 |
| LSE ** | 2 | 14 | 0.74 | 0.84 | 15.32 | 25.45 |
| L1-estimate * | 2 | 50 | 0.62 | 1.22 | 22.25 | 44.93 |
| L1-estimate ** | 2 | 12 | 0.73 | 0.91 | 16.57 | 25.31 |
| Geman and McClure * | 2 | 42 | 0.62 | 1.17 | 21.34 | 44.59 |
| Geman and McClure ** | 2 | 14 | 0.74 | 0.85 | 15.39 | 25.45 |
| K(x) = log(x) + 1/x * | 2 | 42 | 0.63 | 0.91 | 16.51 | 34.02 |
| K(x) = log(x) + 1/x ** | 10 | 50 | 0.50 | 1.35 | 24.57 | 46.17 |
| K(x) = −log(x) + x * | 50 | 50 | 0.52 | 1.53 | 27.80 | 51.69 |
| K(x) = −log(x) + x ** | 2 | 0 | 0.64 | 1.09 | 19.86 | 51.17 |
| K(x) = log(x)2 * | 12 | 50 | 0.54 | 1.40 | 25.42 | 45.13 |
| K(x) = log(x)2 ** | 2 | 46 | 0.66 | 1.13 | 20.47 | 37.94 |
| K(x) = x(log(x)) − x * | 6 | 50 | 0.63 | 1.42 | 25.82 | 45.11 |
| K(x) = x(log(x)) − x ** | 2 | 40 | 0.63 | 1.08 | 19.56 | 35.57 |
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Rivera, J.P.; Verrelst, J.; Leonenko, G.; Moreno, J. Multiple Cost Functions and Regularization Options for Improved Retrieval of Leaf Chlorophyll Content and LAI through Inversion of the PROSAIL Model. Remote Sens. 2013, 5, 3280-3304. https://doi.org/10.3390/rs5073280
Rivera JP, Verrelst J, Leonenko G, Moreno J. Multiple Cost Functions and Regularization Options for Improved Retrieval of Leaf Chlorophyll Content and LAI through Inversion of the PROSAIL Model. Remote Sensing. 2013; 5(7):3280-3304. https://doi.org/10.3390/rs5073280
Chicago/Turabian StyleRivera, Juan Pablo, Jochem Verrelst, Ganna Leonenko, and José Moreno. 2013. "Multiple Cost Functions and Regularization Options for Improved Retrieval of Leaf Chlorophyll Content and LAI through Inversion of the PROSAIL Model" Remote Sensing 5, no. 7: 3280-3304. https://doi.org/10.3390/rs5073280







