1. Introduction
Sunshine duration (SD), together with surface temperature and precipitation, is one of the most important and widely used parameters in climate monitoring and a key variable for various sectors, including tourism, public health, agriculture [
1], vegetation modeling [
2], and solar energy. Although not specifically defined as an Essential Climate Variable by the Global Climate Observing System, SD is strongly related to the Essential Climate Variables cloud properties and surface radiation budget. SD is also used as an input parameter for hydrological modeling [
3] and is a good predictor for the estimation of global radiation (e.g., [
4–
8]) where it can be also used for quality control of measured global radiation data [
9].
Historical records of SD date back more than a century. In the mid-19th century, the Campbell–Stokes sunshine recorder was invented—much earlier than the first pyranometer. Even today, Campbell–Stokes recorders are still used by many national weather services. The continuation of these long time series is of importance e.g., for climatological studies. As sunshine duration data are a good proxy for global and direct solar radiation (e.g., [
6–
8]), the observed decadal variation of sunlight at the Earth’s surface is, for example, an object of research in the context of global dimming and brightening [
10,
11]. Trends and variability of SD have recently been described for several regions of the world, e.g., South America [
12], India [
13] and Western Europe [
14].
Another very important reason for the use of SD is that it is easy to understand. SD is very established in media, and the public is used to this parameter. The hours of sunshine per day are much easier to handle for most non-scientific people than a value in W/m2. Thus, SD is especially important for national weather services and federal authorities to communicate with the public or decision makers.
SD is a standard parameter at meteorological stations and its measurement is specified by the World Meteorological Organization (WMO) [
15]. The possibility of mapping SD by using station observations is limited, given that the density of stations is very heterogeneous and many regions suffer from a coarse station network. Also, station observations are point measurements with a limited representativeness for larger regions. To extend the spatial information of station data, some national meteorological and hydrological services produce gridded maps of interpolated SD station measurements, e.g., the UK Met Office [
16] and the German Meteorological Service DWD [
17]. For the WMO region VI (Europe and the Middle East), operational station-based SD maps are produced by the WMO Regional Climate Centre on Climate Monitoring [
18], and the Climatic Research Unit provides a global SD climatology over land areas [
19].
Station-based gridded products incorporate spatial interpolation techniques. For example, Dolinar [
20] used Kriging for the generation of SD maps for Slovenia. Hogewind and Bissolli [
21] described several interpolation methods for the construction of operational climate maps for Europe and the Middle East. Station-based products are subjected to several problems. For example, the uncertainty of the interpolation strongly increases in areas with a low station density and the interpolation has to account for the influence of topographic features. Moreover, SD itself is highly variable as it depends on cloud fraction, which is highly heterogeneous and exhibits strong temporal dynamics.
Due to the ability of space-borne instruments to detect clouds and the correlation of SD with cloud cover [
22], satellite data can be used for the estimation of SD and add valuable information to station-based products. For instance, Kandirmaz [
23] used a statistical relationship between daily mean cloud cover index and measured SD to derive daily global SD from geostationary satellite data. Kandirmaz [
23] tested this method on data from the Meteosat First Generation. Journée
et al. [
24] derived SD maps for Belgium and Luxembourg from Meteosat First Generation global and direct solar radiation by help of the Ångström–Prescott equation [
25]. More recently, Good [
26] used 15-minute time series of cloud type (CTY) data from Meteosat Second Generation (MSG) to compute daily SD for the United Kingdom. The study by Good [
26] is the first one that used the high potential of the MSG SEVIRI (Spinning Enhanced Visible and Infrared Imager) instrument to derive SD. This imager offers a larger selection of channels for more complex products with a higher spatial resolution compared with Meteosat First Generation. However, Good [
26] applied this method to the relatively small region of United Kingdom, which allowed no conclusions for other European regions with different climatic influences, high mountains, or limited ground-based observations.
The aims of this study are:
- (i)
to extend the Good [
26] CTY method to the wider region of Europe in order to enable the provision of sunshine duration products for the whole region and to support countries with limited ground-based observations or lacking adequate production systems,
- (ii)
to propose a new method where SD is computed using solar incoming direct radiation (SID) and the WMO threshold for sunshine of 120 W/m2, and
- (iii)
to compare the results against station-based SD data, and each other.
The 120 W/m
2 threshold for SID is based on Campbell–Stokes recorders, which were used for SD measurements since the mid-19th century. Investigations showed that the threshold irradiance for burning the cards was on average 120 W/m
2[
15]. In 1981, this threshold was recommended by the Commission for Instruments and Methods of Observation [
15] to distinguish bright sunshine.
Both the CTY and SID datasets used here are provided by the European Organisation for the Exploitation of Meteorological Satellites (EUMETSAT) Climate Monitoring Satellite Application Facility (CM SAF). Daily and monthly sums of the satellite-based products will be compared with station data as well as gridded station data. Our analysis focuses on the year 2008 and examines the feasibility and validity of both daily and monthly satellite SD totals. The MSG SEVIRI instrument offers a temporal resolution of up to 15 minutes in operational mode. Thus, it is also of interest to establish whether there is a significant change in the satellite SD estimates when the temporal resolution changes from 15 min (as used by Good [
26]) to 1 h, which would be substantially less computationally demanding.
Sections 2 and 3 give a description of the applied data and retrieval methods. Examples of both the CTY- and SID-based products are shown in Section 4. Additionally, in Section 4 the satellite SD products are compared with point and gridded station observations, to estimate the uncertainties, advantages, and disadvantages of satellite-based SD. Finally, the difficulties in retrieving SD from satellites are discussed.
3. Methods: Generation of Satellite-Based SD Estimates
For derivation of satellite-based SD two different methods were applied to generate daily SD estimates. The first method is based on CTY observations, following Good [
26], and is described in Section 3.1. The second method is similar, but uses sub-daily SID data (Section 3.2). Although the native temporal resolution of SEVIRI is 15 min, the satellite SD product generation was trialed using both 15-minute and hourly data. Using hourly data is preferable as the data volumes are significantly smaller and processing less computationally expensive. The results of this trial are presented in Section 3.3.
Monthly satellite SD totals are also calculated in this study and are compared with the SD-RCC product described in Section 2. The monthly satellite SD data are generated from the daily sums on a pixel-by-pixel basis. Due to more than three missing days, the monthly totals of May and December 2008 are unavailable for this study. If there are one to three missing days, the monthly totals are scaled up to account for that by using the daily average SD for that month.
3.1. SD Derivation Using CTY Data (SD-CTY Product)
The method proposed by Good [
26] is based on the Satellite Applications Facility on Nowcasting CTY product. In essence, the method takes a sub-daily time series of CTY observations during daylight hours to estimate the SD for each day. For each observation slot, each pixel is assigned either bright sunshine or no sunshine. The daily SD total (SD
Total) is then calculated according to:
where N is the number of SEVIRI observation slots and H is the number of hours of daylight.
The CTY product has 19 different cloud classes. If there is no cloud, bright sunshine is assumed. For opaque clouds there is no sunshine. In case of fractional clouds a factor of 0.5 is assumed following Good [
26]. For semi-transparent clouds, bright sunshine is assumed if the solar elevation angle exceeds a specific threshold.
The biggest challenge in the context of deriving SD by using CTY products is the treatment of fractional and semi-transparent clouds. Good [
26] used the online available Fu–Liou radiation code to derive the solar elevation angle thresholds for assumed cloud properties of three different cirrus clouds. To cover a wider variety of cirrus clouds, in this study, the solar elevation angle thresholds for the three classes of semi-transparent clouds were derived using a linear regression between the solar elevation angle and the normalized SID, using hourly data for each month of the year 2008. The normalization is done to be consistent with
in situ observations, which are done for the perpendicular component of SID. Good [
26] did not use this normalization, which could lead to uncertainties. The normalized SID (SID
Norm) is the ratio of SID and the cosine of the solar zenith angle (SZA):
In deriving the thresholds for each cirrus cloud class of the CTY product (15: very thin, 16: thin, 17: thick), data with solar elevation angle <2.5° were not used, following Good [
26], who reports ground-based instruments are unlikely to record bright sunshine for solar elevation angles less than this value. Also we did not use data with SID
Norm < 50 W/m
2, so as to capture the thresholds better by a linear regression. The solar elevation threshold is the angle below which SID
Norm is less than the WMO criterion of 120 W/m
2 according to these regressions.
For each day, all pixels that fulfilled these requirements were collected and a linear regression between SID
Norm and the corresponding solar elevation angle applied. The resulting thresholds were averaged over each month (
Table 1). The thresholds demonstrate an annual cycle, with a maximum in summer. The explained variances (R
2) for the regressions between SID
Norm and the corresponding solar elevation angle are high (typically 0.8–0.9) and quite consistent throughout the year for cloud classes 15 and 16 (
Table 1, in brackets). The R
2 for class 17 is lower (0.5–0.6), but with higher values in winter (∼0.8).
3.2. SD Derivation Using SID Data (SD-SID Product)
The SID method is based on a sub-daily time series of the CM SAF SID product. According to the WMO, bright sunshine occurs when the solar direct radiation exceeds 120 W/m
2[
15]. Modern Kipp and Zonen sunshine detectors measure in the direction of the sun, while the satellite-based SID product assumes a horizontal plane [
28]. To account for this directional discrepancy, the SID product was normalized by the solar zenith angle to ensure consistency with
in situ observations.
The solar elevation angle limit of 2.5° was adopted for consistency with the CTY method (Section 3.1). Owing to problems with the CM SAF SID retrieval at low solar elevation angles (SEA), there is a sharp transition in the twilight zone of this product, which causes some artifacts in the resulting SD product. Varying the 2.5° solar elevation angle threshold was found to have only minor effects on these artifacts. These artificial patterns are visible mainly in daily totals, but are also visible in some monthly totals, and can influence the quality of the SD products. In the twilight zone of the SID product there are values cut, which were larger than 0. Thus, it is possible that the resulting SDSID product has values that are too low in these areas.
The CM SAF validation report specifies for the SID product an accuracy within 15 W/m
2. To investigate the impact of this uncertainty the SD-SID product was generated for SID
Norm thresholds of 105 W/m
2 and 135 W/m
2.
Table 2 shows the impact of varying this threshold on monthly SD totals from 2008, and demonstrates that the effect of this uncertainty on the resulting SD-SID product is negligible.
3.3. Comparison of Hourly and 15 Min Satellite SD Products
Clouds, which show strong temporal dynamics, are the main influencing factor for calculation of SD using both the CTY and SID methods. Good [
26] used 15-minute data to generate daily SD-CTY estimates from SEVIRI. In this section, example satellite SD products were generated using both 15-minute and hourly input data to assess any impact of using the lower temporal resolution input data. Results for the months of March 2009 for SD-CTY, and August 2007 for SD-SID are presented. The CM SAF generally stores CTY and SID products only on an hourly basis, and these two months were chosen due to the availability of 15-minute CTY and SID data.
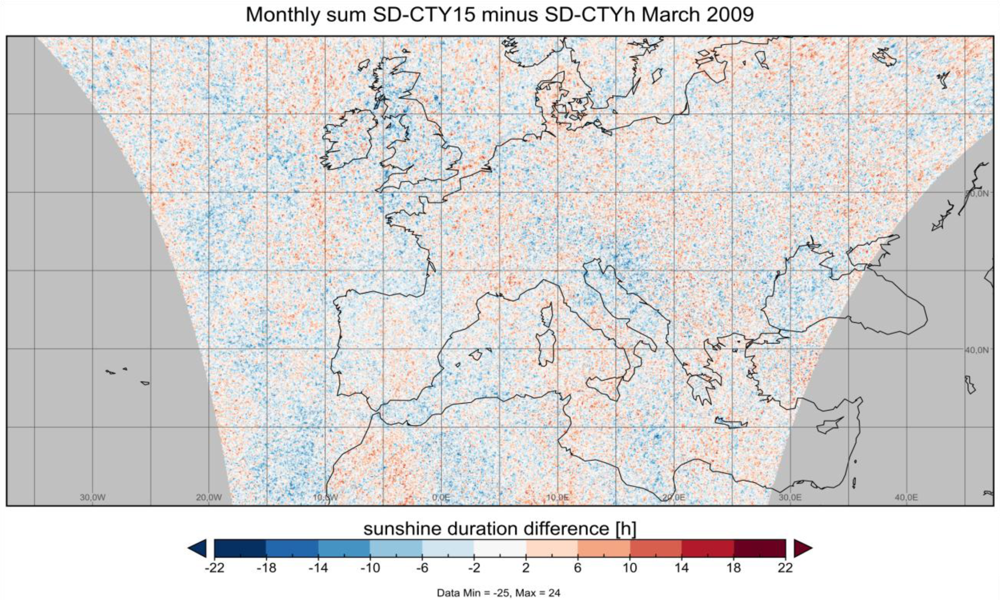
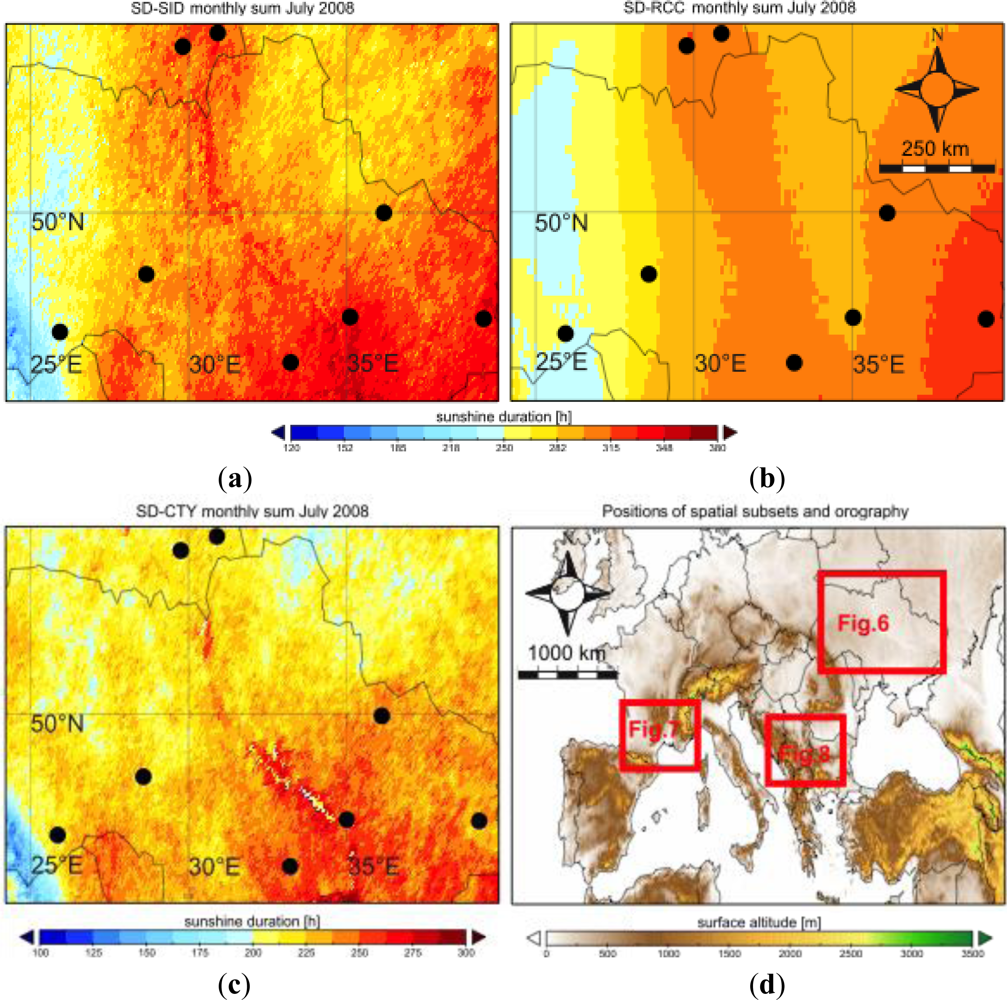
Table 3 shows some simple statistics comparing the monthly satellite SD totals generated using the 15-minute and hourly input data. In each case the mean difference is around 30 min, which equates to less than 0.4% of the monthly mean SD total. The spatial pattern of these differences is non-systematic (
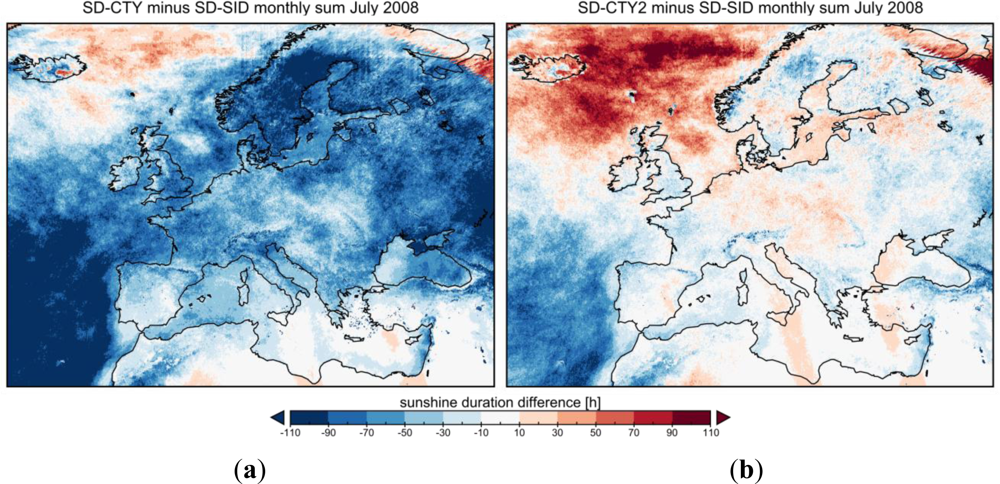
Figure 1), with no clear tendency for higher or lower SD values for one of the two time resolutions.
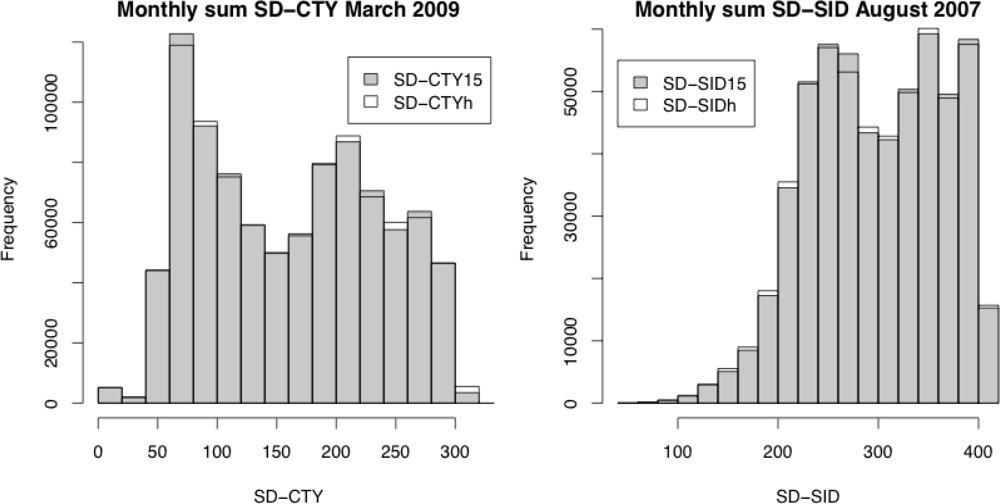
Figure 2 shows the distributions of monthly SD totals for each product, using input data with both temporal resolutions. The results show that changing the temporal resolution from 15 min to 1 h has only a very tiny effect on the overall monthly SD distributions.
In light of these findings, the satellite SD products used in the remainder of this article were generated using input data at hourly resolution, as the additional computational expense required to process the 15-minute data cannot be justified.
6. Conclusions and Outlook
Within this study, new daily and monthly satellite-based sunshine duration (SD) products for Europe were developed. Two different methods were applied using data from the SEVIRI instrument onboard the geostationary Meteosat Second Generation platform. Basing on a method of Good [
26], the first method used sub-daily time series of cloud-type (CTY) data to identify sunny and non-sunny periods during each day in order to estimate daily bright sunshine duration (SD-CTY). In the second method, sub-daily time series of surface incoming direct radiation (SID) were used to establish the proportion of each day where the radiation exceeded the WMO definition of bright sunshine (120 W/m
2) (SD-SID). For both products, the input satellite data were hourly. It was demonstrated that the benefit of using 15-minute data in preference to hourly was too small to justify the additional computational expense required to process the higher resolution data.
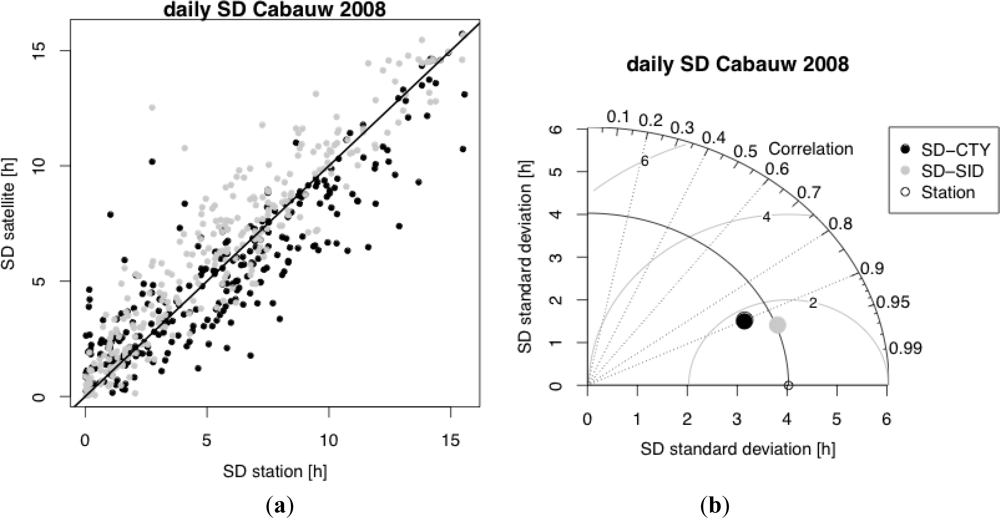
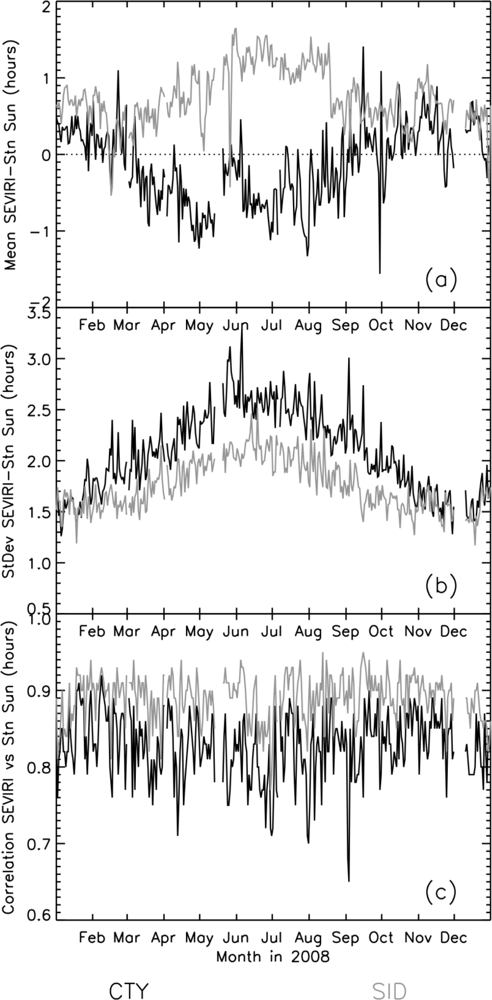
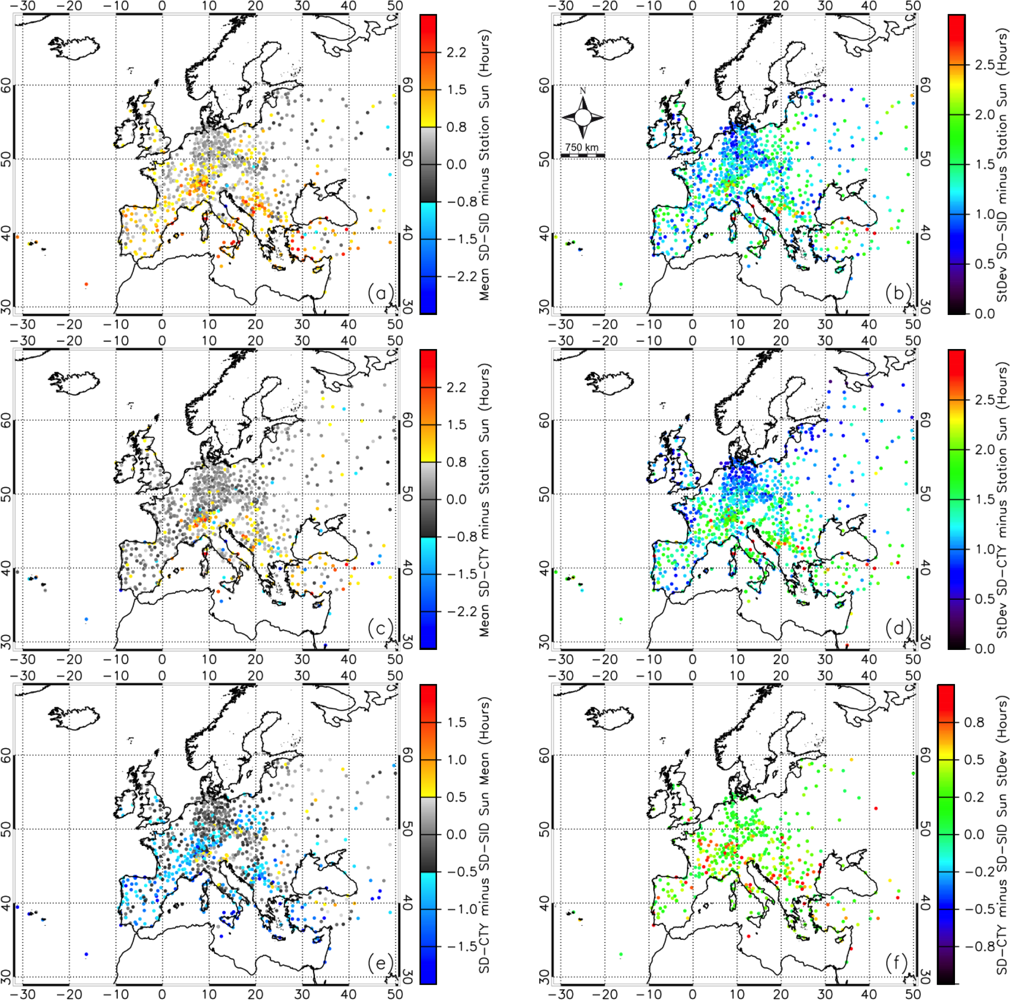
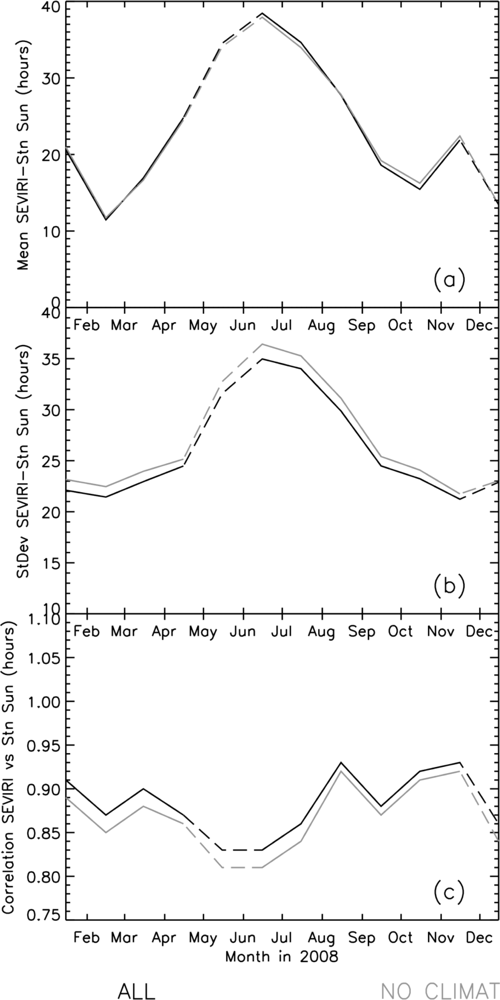
The satellite SD products were intercompared and validated against station measurements over land. This comparison and validation process highlighted some uncertainties in the satellite products. Differences between the products were found to be considerable over ocean regions, sometimes approaching 70%. However, the daily satellite SD products were found to agree well over land with high quality BSRN station data (correlation >90%, RMS difference between 1 to 2 h, mean difference within ±1 h). Both satellite-based SD products also showed good agreement with lower-quality SYNOP station data, where SD-SID mainly overestimated SD and SD-CTY underestimated SD. In this case, the mean daily bias for 2008 across the ∼900 European stations used ranges between −1.6 and 1.4 h (95% within ±1 h) for SD-CTY and −0.5 and 1.7 h (74% within ±1 h) for SD-SID (
Figure 9). The corresponding standard deviations were between 1.3 and 3.3 h (45% within 2 h) for SD-CTY and 1.2 and 2.5 h (80% within 2 h) for SD-SID. The station-satellite correlations for these daily data are also high, ranging between 0.65 and 0.92 for SD-CTY and 0.77 and 0.95 for SD-SID. Both products exhibited seasonal cycles in the daily agreement with the highest standard deviations observed in summer. The seasonal cycle in the mean daily biases was found to be opposite in sense for each product, with the most positive (negative) biases being observed during the summer for the SD-SID (SD-CTY) product. Overall, the SD-SID product showed the most consistent and stable agreement with the station data, although biases for this method were slightly larger.
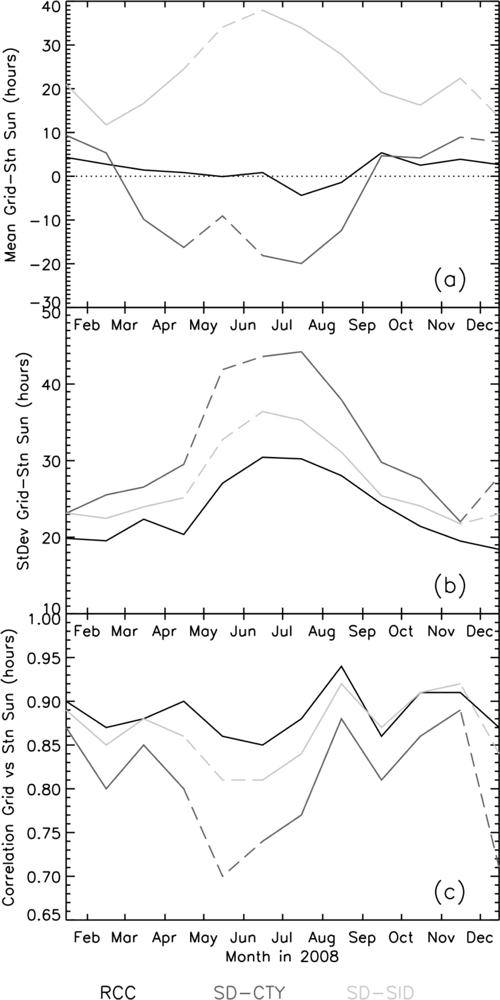
Compared to station-based gridded SD data, it was expected that the satellite-based SD products would perform better, particularly in regions with a sparse station network. Comparison with the monthly 0.1-degree SD-RCC gridded station SD product was limited because the SYNOP stations used to evaluate the product were generally in the same areas as the CLIMAT stations used to generate the SD-RCC product. Thus, the number of SYNOP reference stations in regions with a low density of CLIMAT stations was too low to confirm this assumption in a statistically robust way.
In summary, the satellite-based SD datasets presented in this paper can help to improve the spatial and temporal information of gridded SD datasets. The high spatial resolution offers a variety of possibilities for applications in agriculture, solar technologies, or tourism. Combined with a good accuracy over land, it can also be a basis for scientific studies. Another advantage compared to other gridded state-of-the-art SD datasets is the daily temporal resolution (e.g., SD-RCC is only available on a monthly basis) and availability over ocean regions. However, there are uncertainties in the satellite products and in the interpolated station data, which should be considered in any application. In particular, the uncertainty of the satellite SD products over ocean may be large, but cannot be properly assessed owing to lack of
in situ observations in these areas. Besides the unknown uncertainty of the CM SAF CTY product, the uncertainty of the SD-CTY method results mainly from the treatment of fractional clouds whose impact is quite strong. The uncertainty of the SD-SID method results mainly from the SID product, whose accuracy for monthly means is estimated by CM SAF to be better than 15 W/m
2[
31] (for instantaneous SID values, the uncertainty may be larger). The variation of the SID threshold of ±15 W/m
2 showed only minor influences on the retrieval of SD-SID. This leads to the assumption that the overall uncertainty of SD-SID is lower than for SD-CTY.
SD-SID, being superior to SD-CTY, was selected to become an operational product within the Regional Climate Centre on Climate Monitoring. Monthly maps of sums and anomalies will be freely provided in the near future based on CM SAF Near-Real-Time data in an operational mode. CM SAF recently released a Thematic Climate Data Record for SID covering the years 1983–2005. Deriving sunshine duration based on this dataset for the generation of a long-term record, which can be used as reference climatology and for climate studies, has been planned.
It is also conceivable to use other SAF products, such as cloud fractional cover, or cloud optical thickness, to derive a satellite-based SD. However, just as for SID, the basis for these products is the underlying cloud mask. Thus, the accuracy of the resulting SD product is strongly dependent on the accuracy of the cloud mask. Because SD-SID is insensitive to the ±15 W/m2 uncertainty of SID, the cloud mask will be the limiting factor, and it is not expected that products, such as cloud fractional cover or cloud optical thickness, will give better SD estimates. Finally, a very promising option is the merging of satellite data and station data. In this way, the advantages of both methods could be combined.