Comparing Two Methods of Surface Change Detection on an Evolving Thermokarst Using High-Temporal-Frequency Terrestrial Laser Scanning, Selawik River, Alaska
Abstract
:1. Introduction
1.1. Change Detection via TLS
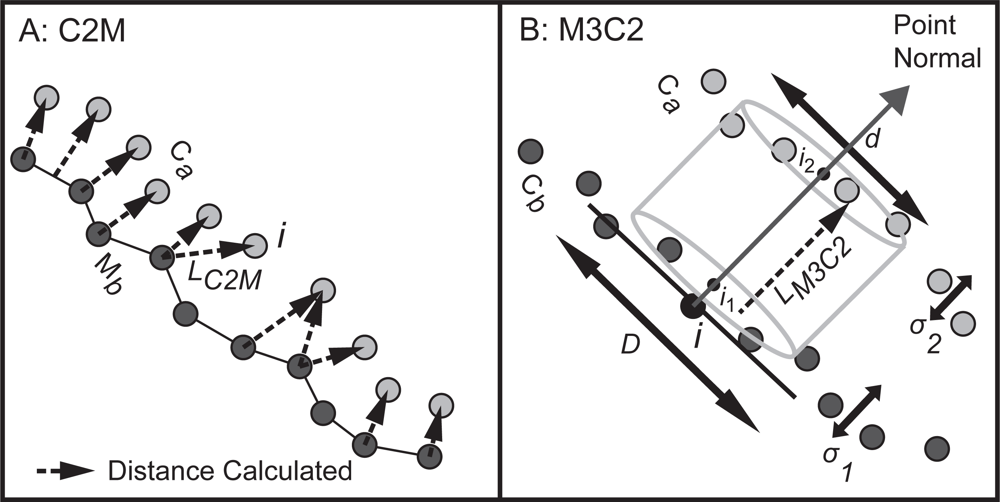
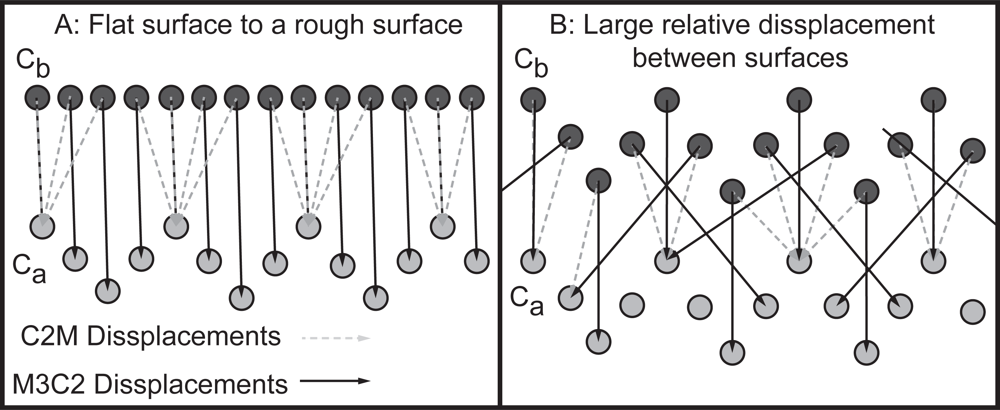
1.1.1. C2M Analyses
1.1.2. M3C2 Analyses
1.2. Objective
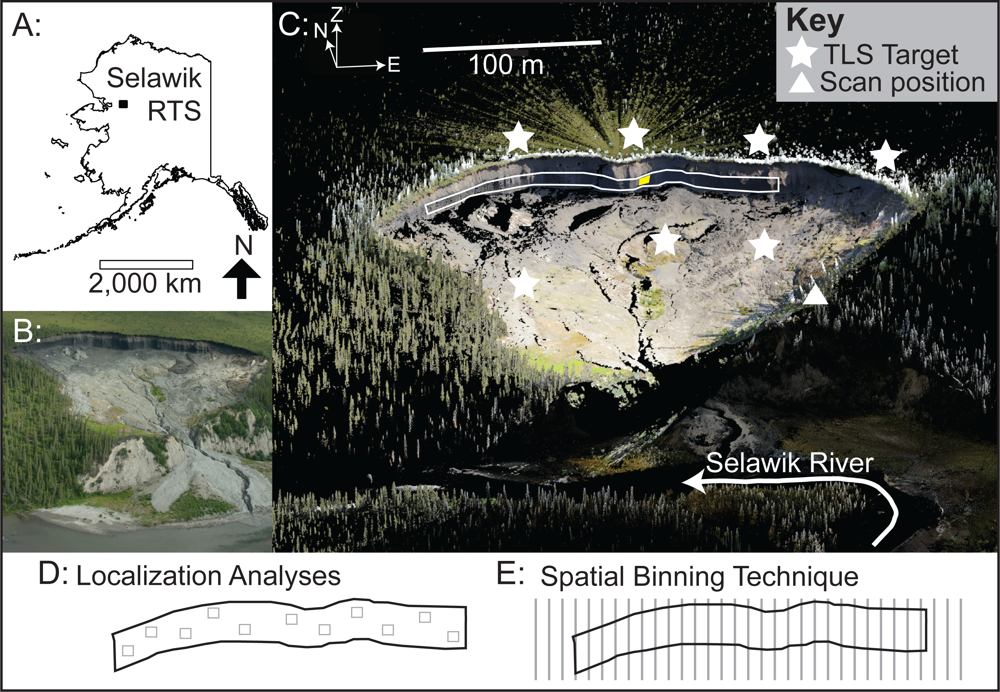
1.3. Site Description and Significance
2. Methods
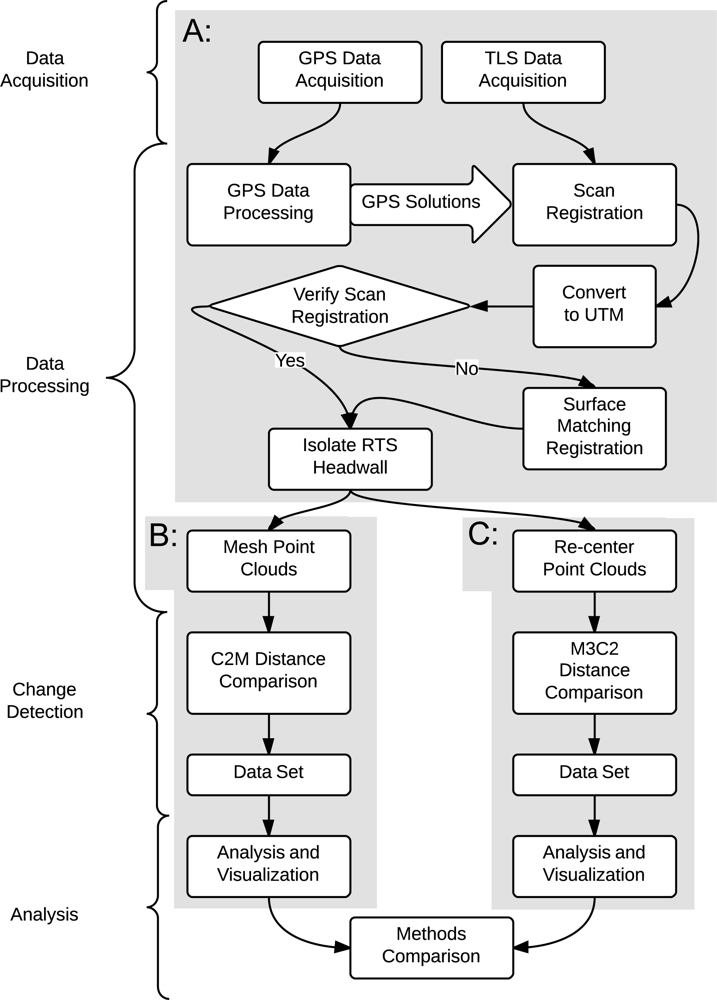
2.1. Data Acquisition and Processing
2.2. Change Detection Method I: C2M
2.2.1. Additive RMS Error Analysis
2.2.2. Empirical Error Analysis
2.2.3. Application of the Error Analysis Results
2.3. Change Detection Method II: M3C2
2.3.1. Error Analysis: Spatially Variable Confidence Interval
2.3.2. Application of the M3C2 SVCI
3. Results and Discussion
3.1. Comparison of Error Analysis Methods
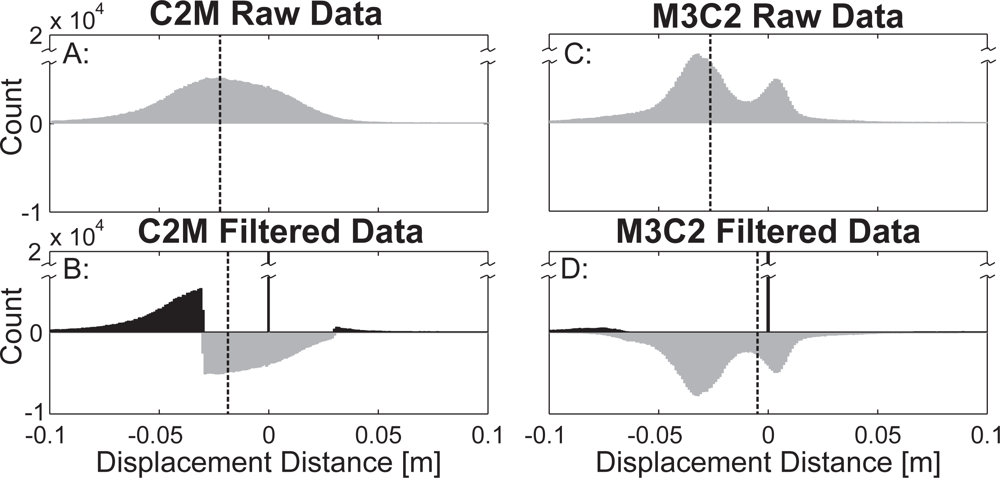
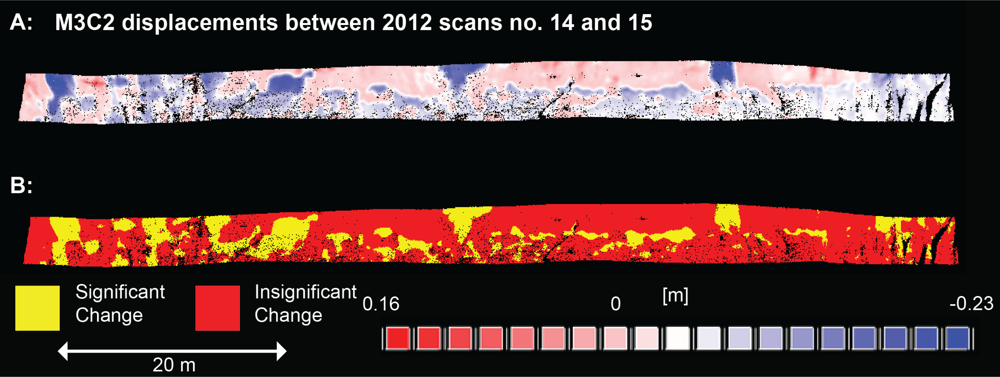
3.2. Comparison of Change Detection Methods
3.3. Comparison of Cumulative Change
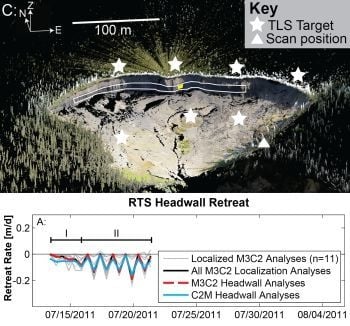
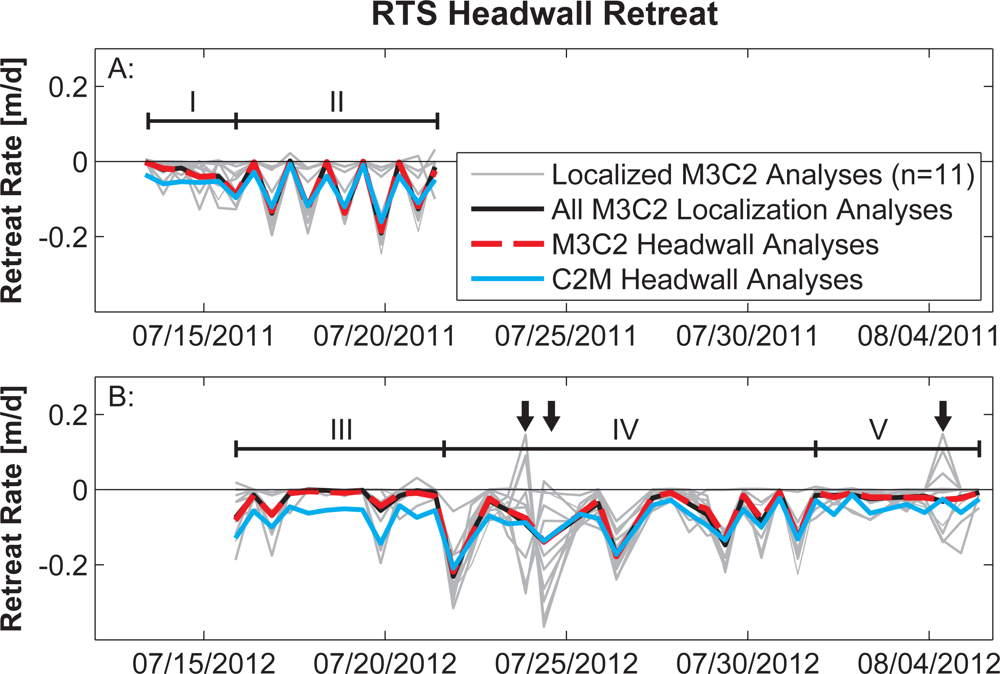
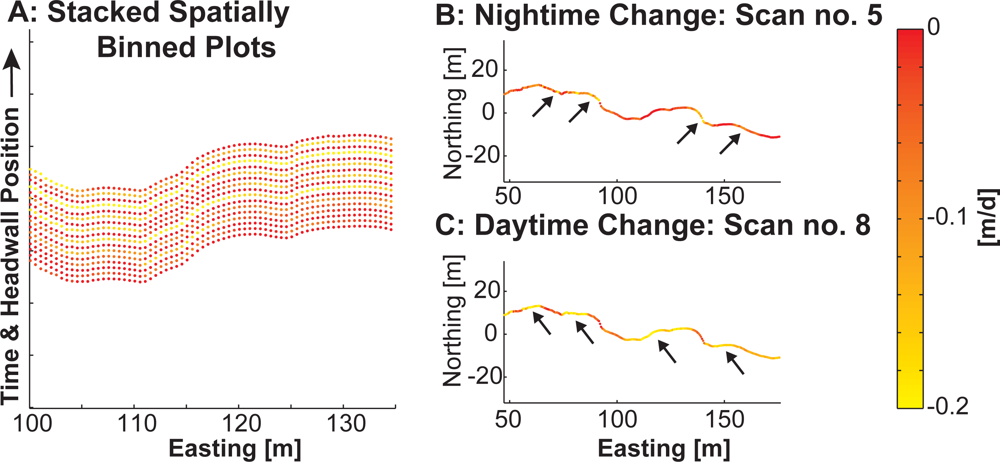
3.4. Capturing Spatial and Temporal Variability in RTS Headwall Retreat Rate
3.5. Unconstrained Sources of Uncertainty
4. Conclusions
Acknowledgments
- Conflict of InterestThe authors declare no conflict of interest.
References
- Webb, R.; Boyer, D.; Turner, R. Repeat Photography: Methods and Applications in the Natural Sciences; Island Press: Washington, DC, USA, 2010. [Google Scholar]
- Williams, G. The Case of the Shrinking Channels: The North Platte and Platte Rivers in Nebraska; Geological Survey Circular 781; US Department of the Interior: Arlington, VA, USA, 1978. [Google Scholar]
- Tape, K.; Sturm, M.; Racine, C. The evidence for shrub expansion in northern Alaska and the Pan-Arctic. Glob. Change Biol 2006, 12, 686–702. [Google Scholar]
- Bierman, P.R.; Howe, J.; Stanley-Mann, E.; Peabody, M.; Hilke, J.; Massey, C.A. Old images record landscape change through time. GSA Today 2005, 15, 4–10. [Google Scholar]
- Kaab, A.; Lefauconnier, B.; Melvold, K. Flow field of Kronebreen, Svalbard, using repeated Landsat 7 and ASTER data. Ann. Glaciol 2005, 42, 7–13. [Google Scholar]
- Nichol, J.; Wong, M. Satellite remote sensing for detailed landslide inventories using change detection and image fusion. Int. J. Remote Sens 2005, 26, 1913–1926. [Google Scholar]
- Frankl, A.; Nyssen, J.; de Dapper, M.; Haile, M.; Billi, P.; Munro, R.; Deckers, J.; Poesen, J. Linking long-term gully and river channel dynamics to environmental change using repeat photography (Northern Ethiopia). Geomorphology 2011, 129, 238–251. [Google Scholar]
- Mackay, J. Segregated epigenetic ice and slumps in permafrost Mackenzie Delta area, NWT. Geogr. Bull 1966, 8, 59–80. [Google Scholar]
- Ruhlman, M.; Nutter, W. Channel morphology evolution and overbank flow in the Georgia Piedmont. J. Am. Water Resour. Assoc 1999, 35, 277–290. [Google Scholar]
- Wheaton, J.; Brasington, J.; Darby, S.; Sear, D. Accounting for uncertainty in DEMs from repeat topographic surveys: Improved sediment budgets. Earth Surf. Process. Landf 2010, 35, 136–156. [Google Scholar]
- Lane, S.; Westaway, R.; Murray Hicks, D. Estimation of erosion and deposition volumes in a large, gravel-bed, braided river using synoptic remote sensing. Earth Surf. Process. Landf 2003, 28, 249–271. [Google Scholar]
- Charlton, M.; Large, A.; Fuller, I. Application of airborne LiDAR in river environments: The River Coquet, Northumberland, UK. Earth Surf. Process. Landf 2003, 28, 299–306. [Google Scholar]
- Gordon, S.; Lichti, D.; Stewart, M. Application of a High-Resolution, Ground-Based Laser Scanner for Deformation Measurements. Proceedings of 10th International FIG Symposium on Deformation Measurements, Orange, CA, USA, 19–22 March 2001; pp. 23–32.
- Rosser, N.; Petley, D.; Lim, M.; Dunning, S.; Allison, R. Terrestrial laser scanning for monitoring the process of hard rock coastal cliff erosion. Q. J. Eng. Geol. Hydrogeol 2005, 38, 363–375. [Google Scholar]
- Girardeau-Montaut, D.; Roux, M.; Marc, R.; Thibault, G. Change detection on points cloud data acquired with a ground laser scanner. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2005, 36, 30–35. [Google Scholar]
- Heritage, G.; Hetherington, D. Towards a protocol for laser scanning in fluvial geomorphology. Earth Surf. Process. Landf 2007, 32, 66–74. [Google Scholar]
- Abellán, A.; Jaboyedoff, M.; Oppikofer, T.; Vilaplana, J. Detection of millimetric deformation using a terrestrial laser scanner: Experiment and application to a rockfall event. Nat. Hazards Earth Syst. Sci 2009, 9, 365–372. [Google Scholar]
- Abellán, A.; Calvet, J.; Vilaplana, J.; Blanchard, J. Detection and spatial prediction of rockfalls by means of terrestrial laser scanner monitoring. Geomorphology 2010, 119, 162–171. [Google Scholar]
- Brodu, N.; Lague, D. 3D terrestrial lidar data classification of complex natural scenes using a multi-scale dimensionality criterion: Applications in geomorphology. ISPRS J. Photogramm 2012, 68, 121–134. [Google Scholar] [Green Version]
- Kociuba, W.; Kubisz, W.; Zagórski, P. Use of terrestrial laser scanning (TLS) for monitoring and modelling of geomorphic processes and phenomena at a small and medium spatial scales in Polar environment (Scott River–Spitsbergen). Geomorphology 2013. In press.. [Google Scholar]
- Krieger, K.E. A Topographic Form Evolution of Thermal Erosion Features: A First Analysis Usinig Airborne and Ground-Based LiDAR in Arctic Alaska. 2012. [Google Scholar]
- Lague, D.; Brodu, N.; Leroux, J. Accurate 3D comparison of complex topography with terrestrial laser scanner: Application to the Rangitikei canyon (N-Z). ISPRS J. Photogramm 2013. [Google Scholar] [CrossRef]
- Brasington, J.; Langham, J.; Rumsby, B. Methodological sensitivity of morphometric estimates of coarse fluvial sediment transport. Geomorphology 2003, 53, 299–316. [Google Scholar]
- Ghoshal, S.; James, L.A.; Singer, M.B.; Aalto, R. Channel and floodplain change analysis over a 100-year period: Lower Yuba River, California. Remote Sens 2010, 2, 1797–1825. [Google Scholar]
- Vaaja, M.; Hyyppä, J.; Kukko, A.; Kaartinen, H.; Hyyppä, H.; Alho, P. Mapping topography changes and elevation accuracies using a mobile laser scanner. Remote Sens 2011, 3, 587–600. [Google Scholar]
- Pesci, A.; Teza, G.; Casula, G.; Fabris, M.; Bonforte, A. Remote sensing and geodetic measurements for volcanic slope monitoring: Surface variations measured at northern flank of La Fossa Cone (Vulcano Island, Italy). Remote Sens 2013, 5, 2238–2256. [Google Scholar]
- Olsen, M.J.; Kuester, F.; Chang, B.J.; Hutchinson, T.C. Terrestrial laser scanning-based structural damage assessment. J. Comput. Civil Eng 2010, 24, 264–272. [Google Scholar]
- Monserrat, O.; Crosetto, M. Deformation measurement using terrestrial laser scanning data and least squares 3D surface matching. ISPRS J. Photogramm 2008, 63, 142–154. [Google Scholar]
- Collins, B.; Corbett, S.; Fairly, H.; Minasian, D.; Kayen, R.; Dealy, T.; Bedford, D. Topographic Change Detection at Select Archeological Sites in Grand Canyon National Park, Arizona, 2007–2010; US Geologic Survey Scientific Investigation Report 2012-5133; US Geological Survey: Reston, VA, USA, 2012. [Google Scholar]
- Glennie, C.; Brooks, B.; Ericksen, T.; Hauser, D.; Hudnut, K.; Foster, J.; Avery, J. Compact multipurpose mobile laser scanning system—Initial tests and results. Remote Sens 2013, 5, 521–538. [Google Scholar]
- Schürch, P.; Densmore, A.L.; J Rosser, N.; Lim, M.; McArdell, B.W. Detection of surface change in complex topography using terrestrial laser scanning: Application to the Illgraben debris-flow channel. Earth Surf. Process. Landf 2011, 36, 1847–1859. [Google Scholar]
- Lewkowicz, A. Use of an ablatometer to measure short-term ablation of exposed ground ice. Can. J. Earth Sci 1985, 22, 1767–1773. [Google Scholar]
- Matsuoka, N. Monitoring periglacial processes: Towards construction of a global network. Geomorphology 2006, 80, 20–31. [Google Scholar]
- Lewkowicz, A. Nature and importance of thermokarst processes, Sand Hills moraine, Banks Island, Canada. Geografiska Annaler 1987, 69A, 321–327. [Google Scholar]
- Lantz, T.; Kokelj, S. Increasing rates of retrogressive thaw slump activity in the Mackenzie Delta region, NWT, Canada. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Burn, C.R.; Friele, P.A. Geomorphology, vegetation succession, soil characteristics and permafrost in retrogressive thaw slumps near Mayo, Yukon Territory. Arctic 1989, 42, 31–40. [Google Scholar]
- Gooseff, M.; Balser, A.; Bowden, W.; Jones, J. Effects of hillslope thermokarst in northern Alaska. Eos Trans. AGU 2009, 90, 29–30. [Google Scholar]
- Schuur, E.; Bockheim, J.; Canadell, J.; Euskirchen, E.; Field, C.; Goryachkin, S.; Hagemann, S.; Kuhry, P.; Lafleur, P.; Lee, H.; et al. Vulnerability of permafrost carbon to climate change: Implications for the global carbon cycle. BioScience 2008, 58, 701–714. [Google Scholar]
- Overpeck, J.; Hughen, K.; Hardy, D.; Bradley, R.; Case, R.; Douglas, M.; Finney, B.; Gajewski, K.; Jacoby, G.; Jennings, A.; et al. Arctic environmental change of the last four centuries. Science 1997, 278, 1251–1256. [Google Scholar]
- ACIA. Arctic Climate Impact Assessment; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Barnhart, T.B. Morphodynamics of the Selawik Retrogressive Thaw Slump, Northwest Alaska. 2013. [Google Scholar]
- Brown, J.; Ferrians, O., Jr.; Heginbottom, J.; Melnikov, E. Circum-Arctic Map of Permafrost and Ground-Ice Conditions; The National Snow and Ice Data Center and The World Data Center for Glaciology: Boulder, CO, USA, 1998. Available online: http://nsidc.org/data/docs/fgdc/ggd318mapcircumarctic/ (accessed on 10 February 2013).
- Jorgenson, M.T.; Roth, J.E.; Miller, P.F.; Macander, M.J.; Duffy, M.S.; Pullman, E.R.; Miller, E.A.; Attanas, L.B.; Wells, A.F. An Ecological Land Survey and Landcover Map of the Selawik National Wildlife Refuge; ABR, Inc.: Fairbanks, AK, USA; US Fish and Wildlife Service: Anchorage, AK, USA, 2009. [Google Scholar]
- USFWS. Selawik National Wildlife Refuge Newsletter; USFWS Selawik NWR: Kotzebue, AK, USA, 2007. [Google Scholar]
- Hamilton, T. Late Cenozoic Glaciation of Alaska. In The Geology of Alaska; Plafker, G., Berg, H.C., Eds.; The Geological Society of America: Boulder, CO, USA, 1994; Volume G-1,; pp. 813–844. [Google Scholar]
- Lanan, K.M. Glacial and Geomorphic History of the Upper Selawik Valley, Northwest Alaska, with Implications for Thermokarst Formation. 2013. [Google Scholar]
- NOAA. OPUS: Online Positioning User Service. 2012. Available online: http://geodesy.noaa.gov/OPUS/ (accessed on 5 September 2012).
- Trimble Geomatics Office; Trimble Navigation LTD.: Sunnyvale, CA, USA, 2000.
- Trimble Business Center; Trimble Navigation LTD.: Sunnyvale, CA, USA, 2005.
- Oldow, J. Assessment of Uncertainty Budget in TLS Characterization of Fault Scarps. Proceedings of Charting the Future of Terrestrial Laser Scanning (TLS) in the Earth Sciences, Boulder, CO, USA, 17–19 October 2011.
- RiScan Pro; Riegl LMS: Orlando, FL, USA, 2012.
- MATLAB; Mathworks: Natick, MA, USA, 2012.
- I-Site Studio; Maptek.: Denver, CO, USA, 2012.
- Yang, C.; Medioni, G. Object Modelling by Registration of Multiple Range Images. Proceedings of the International Conference on Robotics and Automation, Sacramento, CA, USA, 9–11 September 1991; pp. 2724–2729.
- Riegl, LMS. Data Sheet, Riegl VZ-400. 2012. Available online: http://products.rieglusa.com/Asset/10_DataSheet_VZ400_29-11-2012.pdf (accessed on 12 February 2013).
- Hodge, R. Using simulated terrestrial laser scanning to analyse errors in high-resolution scan data of irregular surfaces. ISPRS J. Photogramm 2010, 65, 227–240. [Google Scholar]
| Year | GPS (2σ) (m) | Instrumental * (1σ) (m) | Georeferencing (2σ) (m) | RMS Error (2σ) (m) | Empirical Error (m) | M3C2 SVCI (2σ) (m) |
|---|---|---|---|---|---|---|
| 2011 | 0.008 | 0.01 | 0.015 | 0.02 | 0.028 | 0.052 |
| 2012 | 0.014 | 0.01 | 0.022 | 0.03 | 0.019 | 0.069 |
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Barnhart, T.B.; Crosby, B.T. Comparing Two Methods of Surface Change Detection on an Evolving Thermokarst Using High-Temporal-Frequency Terrestrial Laser Scanning, Selawik River, Alaska. Remote Sens. 2013, 5, 2813-2837. https://doi.org/10.3390/rs5062813
Barnhart TB, Crosby BT. Comparing Two Methods of Surface Change Detection on an Evolving Thermokarst Using High-Temporal-Frequency Terrestrial Laser Scanning, Selawik River, Alaska. Remote Sensing. 2013; 5(6):2813-2837. https://doi.org/10.3390/rs5062813
Chicago/Turabian StyleBarnhart, Theodore B., and Benjamin T. Crosby. 2013. "Comparing Two Methods of Surface Change Detection on an Evolving Thermokarst Using High-Temporal-Frequency Terrestrial Laser Scanning, Selawik River, Alaska" Remote Sensing 5, no. 6: 2813-2837. https://doi.org/10.3390/rs5062813