1. Introduction
Spectral images acquired from the same area at different times contain valuable information for regular monitoring of the Earth’s surface, allowing us to describe the land-cover evolution, vegetation phenology, and natural hazard events. However, it is difficult to maintain radiometric accuracy in orbital images due to changes in atmospheric conditions, Earth-Sun distance, detector calibration, illumination angles, viewing angles, and sensor oscillation, as are required in order to highlight the spectral changes of interest. Another common problem in change-detection analysis from different sensors, such as Landsat Thematic Mapper (TM) and Landsat Enhanced Thematic Mapper plus (ETM+) images is that they, additionally, require the evaluation of radiometric consistency between sensors to ensure comparability between the temporal images [
1,
2]. Thus, methods for ensuring radiometric consistency among temporal images are necessary to remove, or compensate for, all the above effects, except for actual changes on the land surface, allowing the surface reflectance or normalized digital numbers obtained under different conditions to be placed on a common scale [
3].
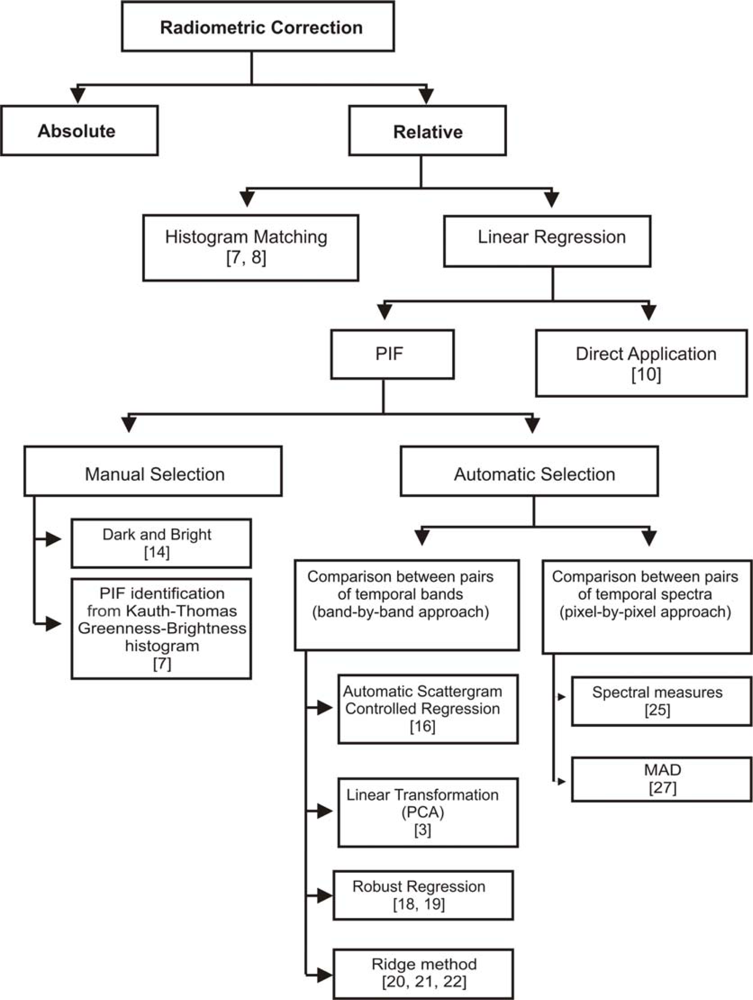
In previous studies, two levels of radiometric correction were developed: absolute and relative [
1,
4–
6] (
Figure 1). In absolute radiometric correction, atmospheric radiative-transfer codes are used to obtain the reflectance at the Earth’s surface from the measured spectral radiances. The absolute method corrects for following factors: changes in satellite sensor calibration over time, differences among in-band solar spectral irradiance, solar angle, variability in Earth-Sun distance, and atmospheric interferences. In contrast, relative correction by normalization does not find the true radiance of the surface or remove atmospheric errors, but instead transforms the digital numbers to a common scale [
3]. Thus, the radiometric properties of an image are adjusted to match a reference image [
7,
8], image normalization uses a histogram-matching method [
9] or a linear-regression method [
10].
The linear regression method is the most widely used approach for relative correction. Initially, the technique was based on simple regression that considered all the pixels of temporal images [
10]. Subsequently, normalization was performed considering landscape elements with reflectance values that are nearly constant over time, ‘pseudo-invariant features’, or PIFs [
7,
11–
13]. Therefore, the key problem of the image regression is to obtain an appropriate procedure for a selection of PIFs. For the regression model to be reliable, selection of radiometric control targets must consider the following characteristics [
11,
14,
15]: small changes in elevation for which the thickness of the atmosphere over each target is approximately the same; minimal amounts of vegetation due to high susceptibility changes over time; positioning in flat areas in order to minimize the influence of changes in sun angle between the images; and a large range of brightness values. PIF selection can be made by visual inspection or through computational methods.
PIF selection through visual inspection establishes regions of interest for the dark and bright (DB) areas [
14]. In this objective, the PIFs can be selected using scatterplots with Kauth-Thomas (KT) greenness-brightness components [
7]. However, visual inspection methods are subjective and dependent on the analyst’s selection, which can decrease accuracy.
Computational methods for PIF selection are more accurate, considering an automatic extraction. There are two main strategies, which consider the different dimensions of the image (X, Y, and Z components): (a) band-by-band methods that compare a pair of bands at different times (X and Y dimensions of the image), and (b) pixel-by-pixel methods that compare a pair of spectra at different times for a pixel (Z dimension of the image).
PIF detection methods that perform comparisons between pairs of bands are the most commonly used. These include no-change buffer zone around a fitted line from linear regression [
16] or principal components [
2,
3,
17]; robust-regression [
18,
19]; scatter-plot density [
20–
22]. Generally, two attributes are used to identify the PIFs: invariant point density and residual values obtained from differences between observed and estimated values from the linear model.
Elvidge
et al.[
16] proposed a method called automatic scattergram controlled regression (ASCR), which performs a linear regression between the temporal image pairs and calculates a no-change buffer zone from the orthogonal distances between the points and the fitted straight-line. Du
et al.[
3] selected the PIFs using principal component analysis (PCA) and a no-change buffer zone. The authors consider the most probable linear relationship between two individual bands is described by the first principal component. The pattern of pixel distribution resembles an ellipse, described adequately by the major and minor PC axes. The quality control of the method establishes a range around the primary major axis (no-change buffer zone), until obtaining an acceptable linear correlation coefficient (r) of candidate PIFs from the two images. This procedure limits the no-change buffer zone from the minor PC axes (orthogonal to the first axis) which shows the deviations to the main axis. In addition, the user can apply thresholds for rejecting cloudy and water pixels. Although the method improves the optimal linear regression model, it still has problems. If the invariant point density is too low the sample will not be well-represented in first component. Thus, there is a tradeoff between the sample size and the correlation coefficient. The main limitation of these two methods is the elimination of outliers in a single step (no-change buffer zone). If the initial data contain many outliers, the first estimate of the linear regression or PCs can be wrong, as the subsequent steps of buffer zone and the elimination of outliers. The reliability of the first straight-line is of high importance for the solution, however, this is not always possible. Furthermore, a marked reduction in the buffer zone can have a result similar to the first straight-line.
Limitation in the use of the buffer zone indicates the need for a different approach, already described in statistical science in the 1970s [
23,
24]. The theory of multidimensional robust estimators searches the identification of outliers by successive interactions. Robust-regression is a form of the regression analysis insensitive to outliers,
i.e., observations, which do not follow the pattern of the other observations, and they have serious effects on statistical inference. Thus, this procedure is an improvement to least squares, which fit a model from the valid observations. Heo and FitzHugh [
18] developed an optimal linear regression model with a robust criterion for effective outlier rejection. Their procedure consists of a robust statistical method in that the change points are concentrated in residual outliers. Similarly, Olthof
et al.[
19] adopted a simple robust regression method, called Theil-Sen to radiometric correction. This method is a non-parametric, rank-based regression technique that uses the median of all slopes of unique pairwise observations separated by a minimum distance as the maximum-likelihood slope for the regression.
The density scatter plot method (ridge method) compares two images made at different times in a scatter plot and calculates the point density. The PIFs describe a high-density ridge along a straight line near the 1:1 line (the ridge), while areas with pronounced change (clouds and land cover changes) are characterized as having low density [
20]. In summary, the methods attempt to identify the regression line, along which unchanging pixels plot, because everything else (plots off the ridge) are pixels that have changed. So the key is to eliminate outliers and then to regress a line of no change and finally to establish a density threshold within which a point can deviate from the ridge without being considered as significantly changed.
However, PIF detection methods using band comparisons (simple linear regression, robust regression, density scatter plot, and linear transformations) present errors when there are few PIFs in the image. If the preponderance of pixels contains systemic changes, the identification of PIF may contain biased distortions. Thus, the use of these methods must adopt a “PIF assumption” for their implementation [
3], considering the premise that the consistently changed targets are not the majority of targets in each scene.
This problem in PIF detection can be avoided by ignoring the relationship between bands (X and Y dimension) and focusing instead on the particular spectral relationship between each pair of temporal pixel (Z dimension). PIF detection methods, using spectral comparison, consider the distance measures (Euclidean and Mahalanobis distance) and similarity measures (cosine correlation and Pearson’s correlation) [
25,
26]. In this approach, PIF detection is independent of its neighbors, unlike other methods that are only possible from a set of pixels. Thus, errors in the detection of temporal points from weakly correlated images are eliminated.
Canty
et al.[
27] proposed a new approach for the calculation of spectral measures, instead of considering the original images they adopted the canonical variates, calculated from Canonical Correlation Analysis (CCA). CCA establishes a linear combination between two groups of temporal images, such that their mutual correlations are showed in their pairs of canonical variates. The change detection is determinate by the differences between the pairs of CCA components, which are called by authors, Multivariate Alteration Detection (MAD). The metric used for the selection of PIFs was the square of the normalized Euclidean distance. Selected PIFs are used for radiometric normalization using linear regression.
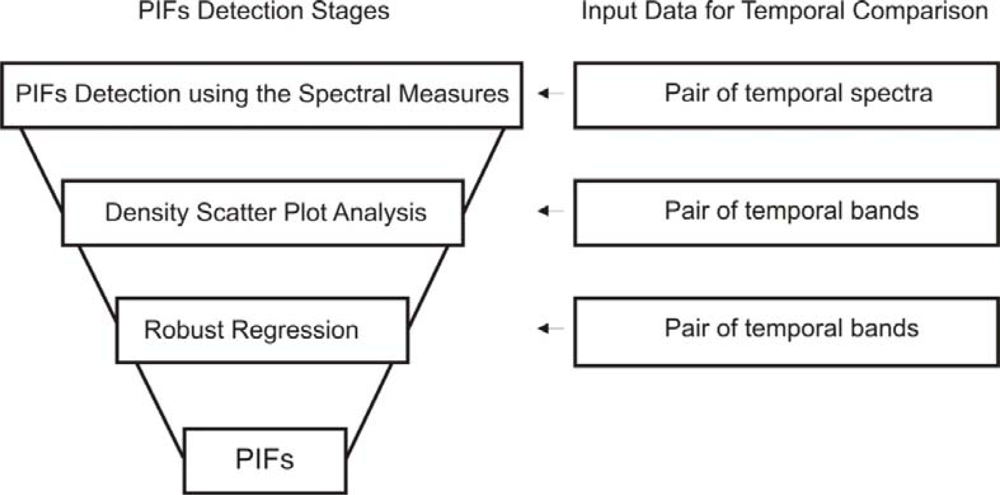
In this study, a new algorithm is formulated for radiometric normalization that combines three methods for the detection of PIFs: similarity and distance measures, a density scatter plot method, and robust linear regression. The methods presented are complementary and can be used together in consecutive steps that improve the selection of PIFs. The method was implemented in software developed in C++.
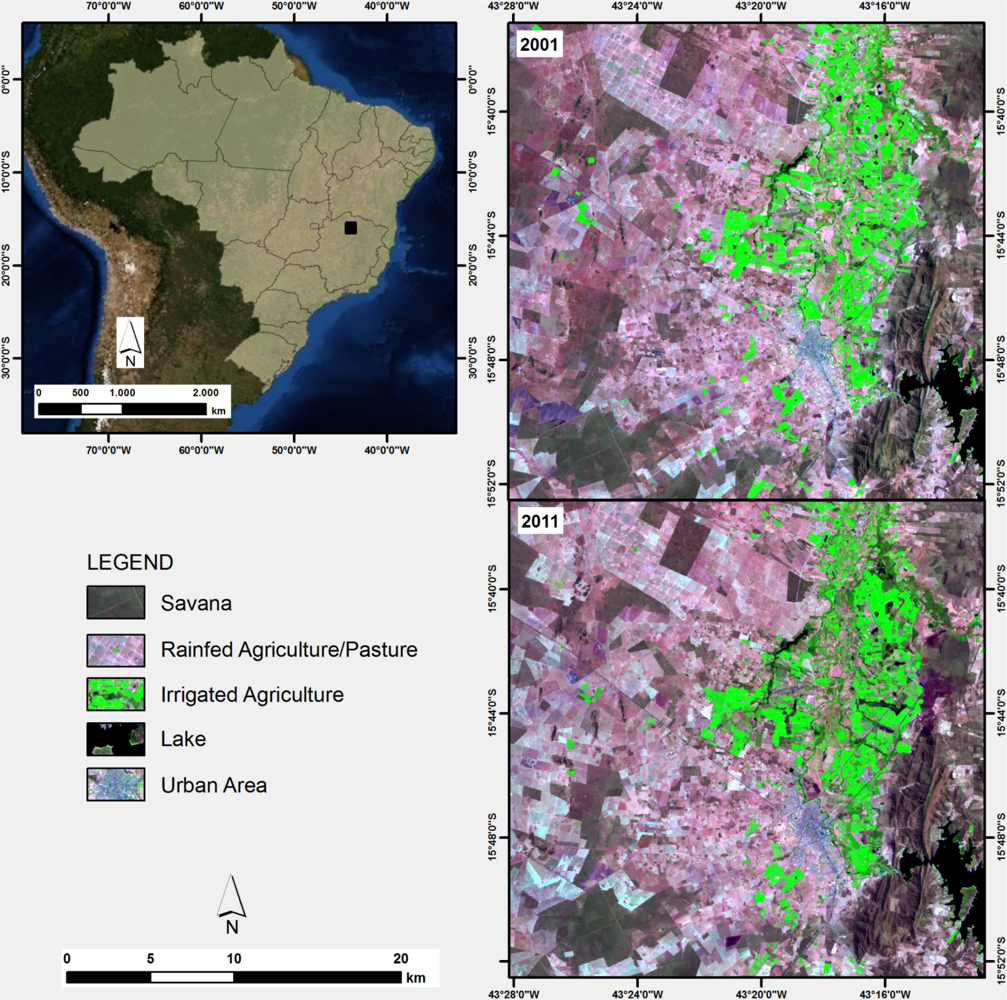
The proposed methods have been applied in an extensive irrigation project located in the Gorutuba region, Central Brazil. The irrigation project has established an important economic growth vector to agricultural activities and agro-industries, keeping the production under a high climate risk. The São Francisco River provides a steady water flow for use in irrigated farming. The topography is generally very flat, which favors the development of agriculture irrigation, involving the establishment of dikes and regulations. The agriculture irrigated produces mainly fruits; species include banana, pineapple, and mango. Thus, this area is suitable for this study because it presents different targets such as: lake, city, cultivated area, and natural vegetation.
3. Results
3.1. Results of the Pixel-by-Pixel Procedures
3.1.1. Distance and Similarity Measures from Original Images
Initially, the PIFs detection using different spectral measures from original images were evaluated.
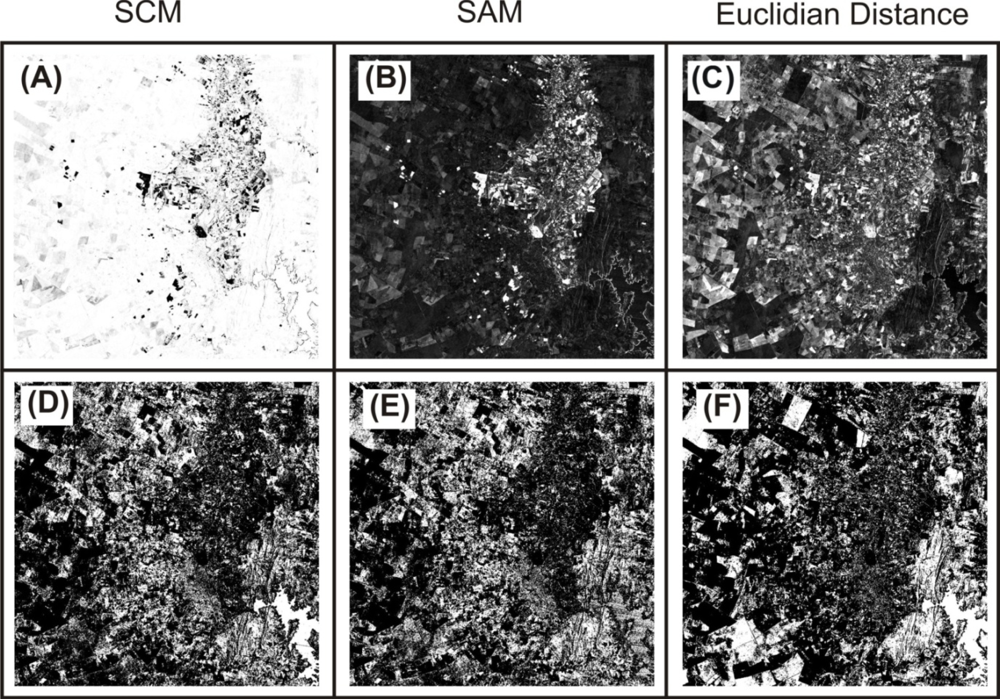
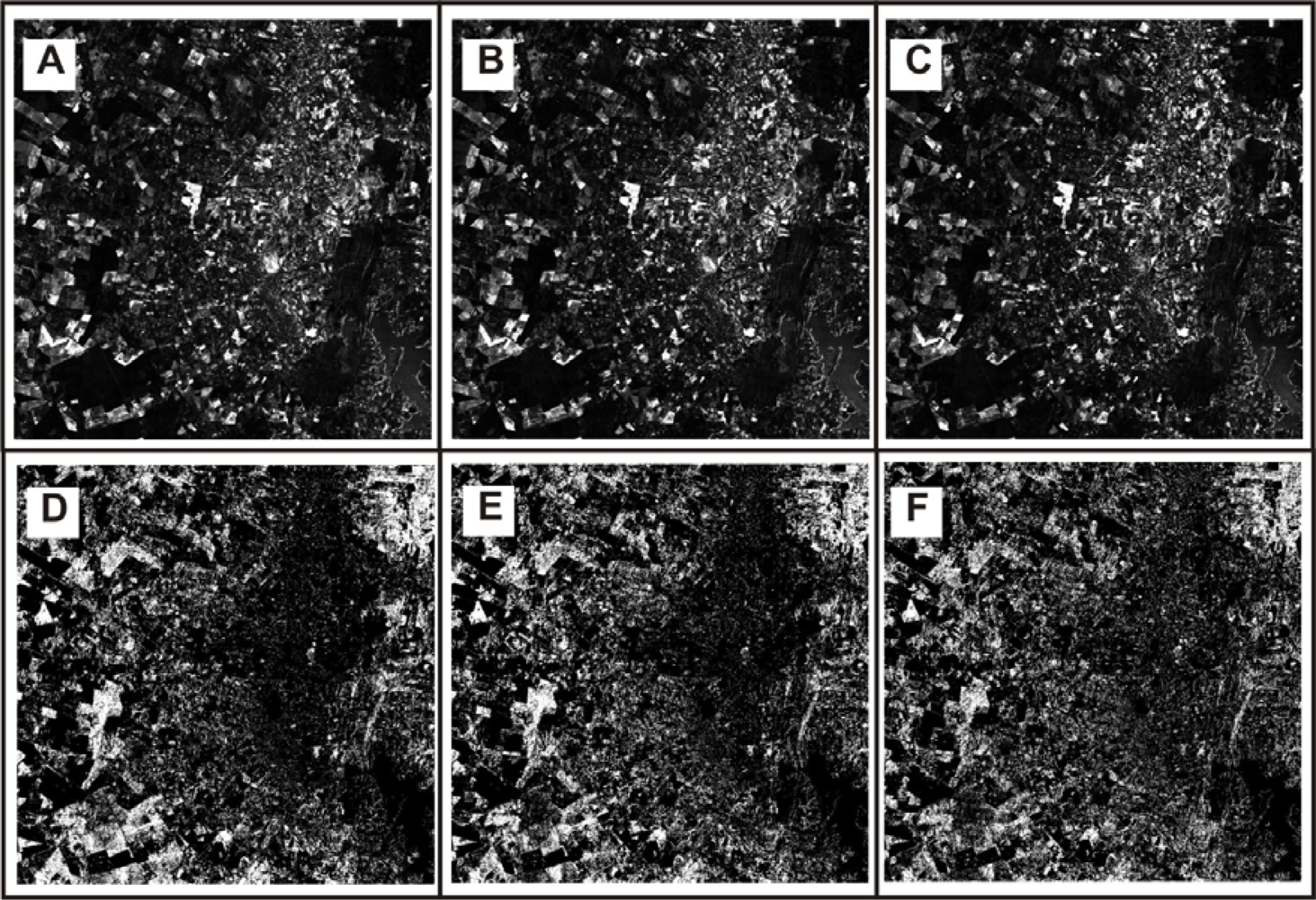
Figure 4 shows the spectral measure images in a gray-scale format and PIF images in a binary format. The SCM
CD image (
Figure 4(a)) shows the most likely invariant points as bright, while the SAM
CD and distance images (
Figure 4(b,c)) show them as dark. A PIF selection with less points should adopt a threshold with a high value to the SCM
CD method; low angles from SAM
CD, and low ED
CD values. As an example, a threshold value of 20% (200,000 pixels) was evaluated for the study area. PIFs identified with them are represented with bright colors for each of the three approaches (
Figure 4(d–f)). The PIFs have been well distributed in the image considering the different targets of the scene.
Most of the invariant points are identified independently using the three different measures; however there are differences among the results and these can be visualized from the intersection PIFs among the methods (
Table 2). The most pronounced differences occur between the similarity measures and Euclidean distance, where nearly half of the PIFs are coincidental. The SAM
CD and SCM
CD show a high PIFs overlap,
i.e., approximately 80% of pixels.
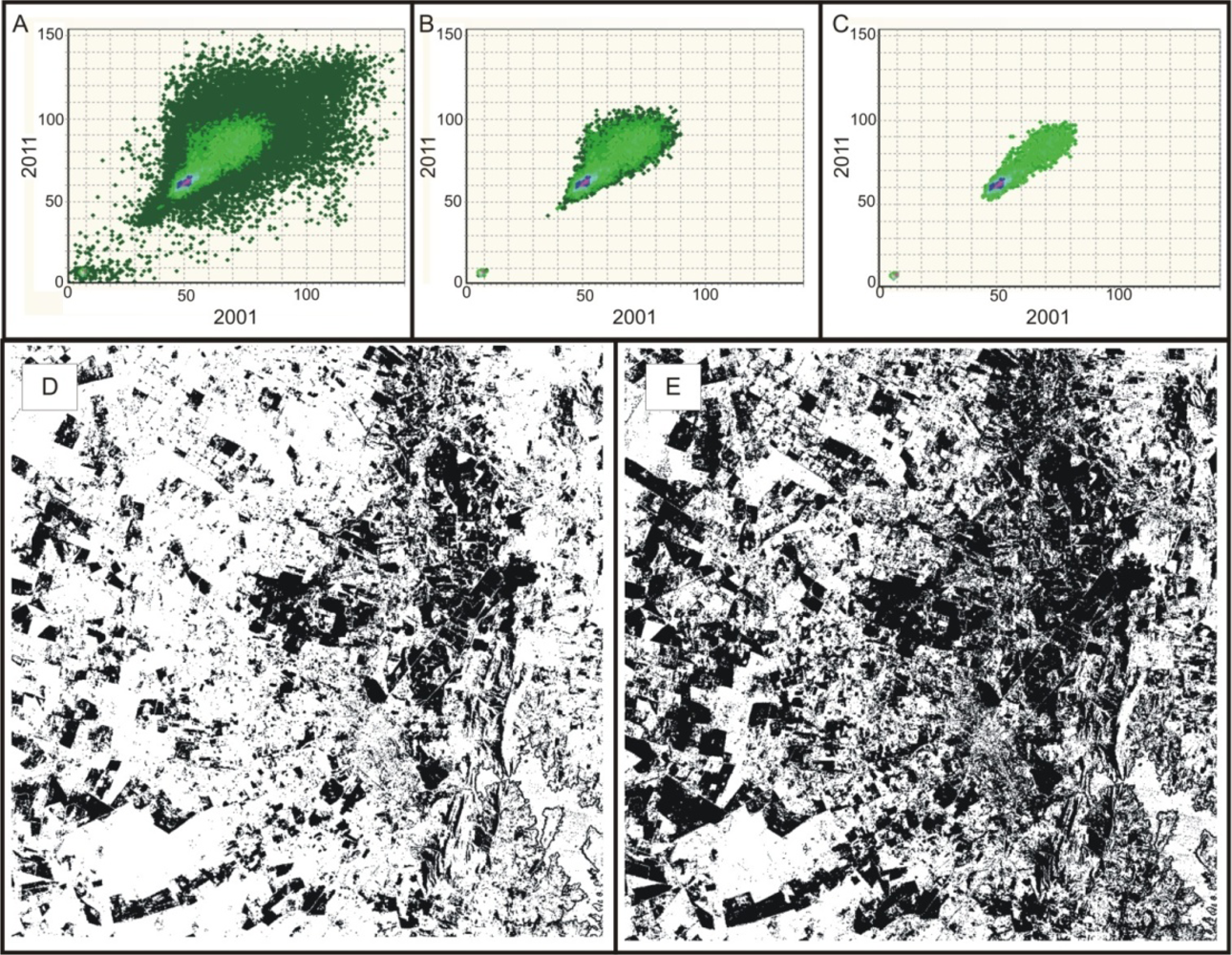
The spatial location of PIFs from the different methods can be performed by color composite images (
Figure 5(a)). In the color composite, the invariant points identified by all three methods are white, and change points are black. Primary colors (red, green, and blue) indicate identification by a single method; secondary colors (cyan, magenta, and yellow) indicate identification by two methods. The similarity measures (SCM
CD and SAM
CD) have greater amounts of common invariant points (yellow color).
Figure 5(b) shows a PIF image with the intersection of all methods, where the PIFs are represented with bright colors.
Figure 6 shows an example of the differences between the spectral measures of similarity and distance. In
Figure 6(a) two temporal spectra that have the same shape and offset difference are identified as invariant point using the SAM
CD and SCM
CD measures, and as a change point by the ED
CD. In contrast,
Figure 6(b) demonstrates two temporal spectra identified as invariant point using the Euclidean distance, and as a change point by the SAM
CD and SCM
CD measures. These differences emphasize that the methods are complementary and their combinations allow a greater constraint for PIFs and a significant number of the pixels are change targets between the temporal images (
Figure 6(b)).
Statistical data from the simple linear regression for the selected PIFs are compared in order to evaluate the different spectral measures (
Tables 3,
4 and
5). A comparison of the spectral measures adopted a simple linear regression to avoid interference from other methods (ridge and robust regression).
Table 3 gives the corresponding information about regression statistics. PIFs-ED
CD shows the best-fit linear regressions for all bands with the lowest root-mean-square errors (RMSE) and highest correlation coefficients (R). This behavior was expected because the minimum Euclidean distance tends to be more aligned to a straight line; unlike the similarity measures that can have greater variability. PIFs-SCM
CD provides better correlation coefficients than the PIFs-SAM
CD, however the PIFs-SAM
CD presents best RMSE values.
Table 4 shows the means of the 2011 scene (reference image) and 2001 scenes, before and after normalizations, using least squares regression line. The differences between the means of reference and normalized images are always close to 0.5. SCM
CD has the lowest average differences for the infrared bands (4,5,7). SAM
CD shows a lowest difference value for band 3, while the ED
CD for bands 1 and 2.
Measures of dispersion differ among PIFs from ED and measures of similarities (SCM and SAM) (
Table 5). The PIFs from ED have lower differences of variance and coefficient of variation between the reference image and the images uncorrected and corrected. These measurements, between SAM and SCM are similar, but SAM presents variance values closest between the reference image and the normalized image, whereas SCM shows variation coefficients, which are slightly closer. The range of values varies greatly although the SCM and ED present more homogeneous values than the SAM.
3.1.2. Distance Measures from Canonical Variates (CVs)
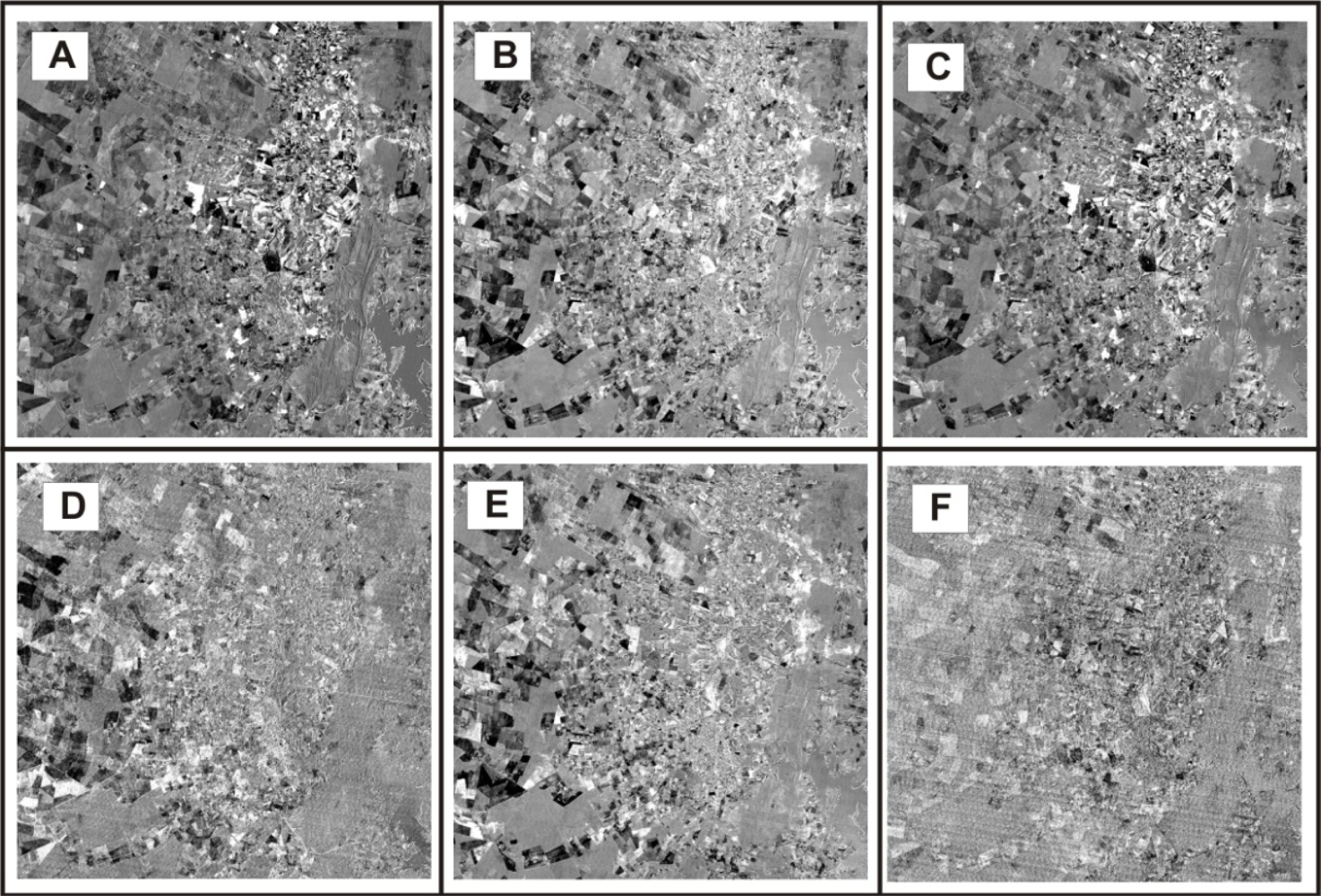
MAD components have an ordering image that highlights the reduction of intercorrelation between the CV pairs and increased noise interference (
Figure 7). The last component concentrates the noise fraction (
Figure 7(f)).
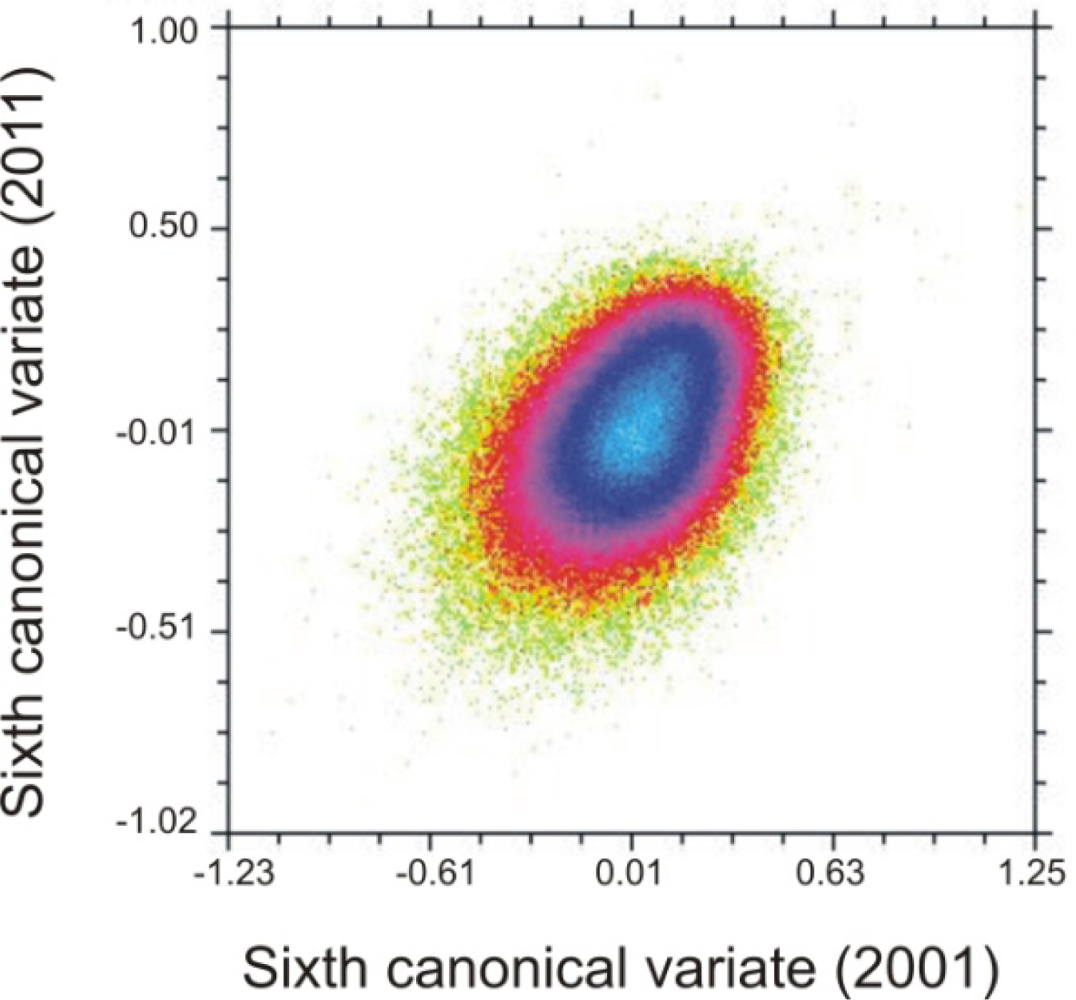
The scatterplot between the pair of the latest CV-pair appears spherically distributed around the data. This is evidence of the predominance of the uncorrelated noises with equal variance in all bands (
Figure 8). This optimal ordering of image quality (when the noise variances in all bands are equal) is similar with the standard principal components transformation. However, CCA transformation is not suitable for other types of spatial noise, such as salt-and-pepper noise. The amount of noise reduction depends on the degree of temporal-band correlation, the relative noise in each input band, and the type of noise performed on the transformed components.
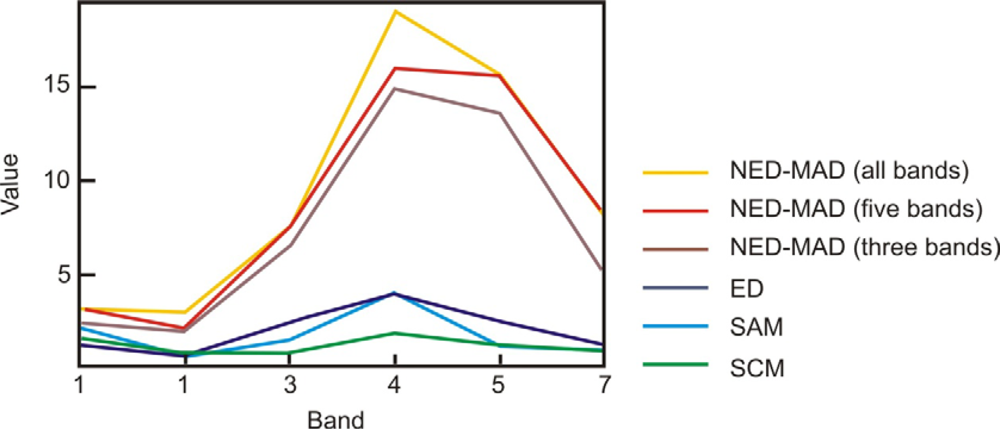
The high correlation frequently exists in multi-temporal data provides a redundancy reduction and increasing the signal magnitudes in the first CVs. Once data have been transformed into canonical variates with decreasing noise, the subsequent calculation of the distance measures between the temporal variables can disregard the noisiest components. This practice should be emphasized with the use of the NED or Mahalanobis distance that lead to data normalization,
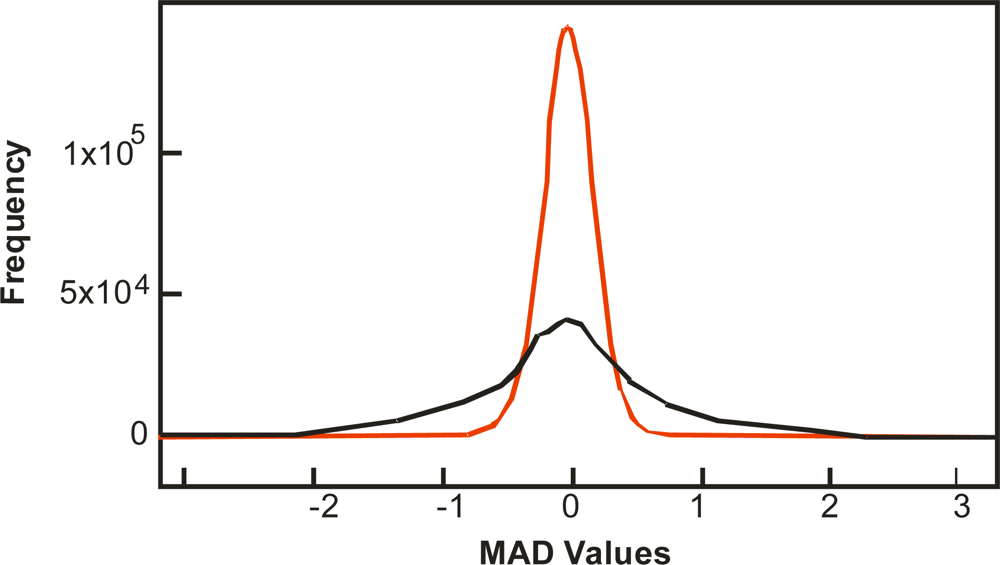
i.e., MAD components are converted to a common scale (standard deviation equal to 1). Noise bands that have smaller value range (
Figure 9), with the use of NED are amplified in comparison with other bands.
In this work we calculated the NED measures considering two scenarios: with all MAD components and removing the noisy components. The NED
2 image originally described by Canty [
27] is not shown due to interference from very high values and because the PIF result is equal to the NED considering a same threshold by image percentage.
Figure 10 demonstrates the NED-MAD images and its PIFs images (20%) considering: all bands, first five MAD components, and first three MAD components.
Table 6 shows the number of similar PIFs among the NED-MAD images (considering different amounts of MAD components) and spectral measures applied to original images (SAM, SCM, and ED). PIFs from NED-MAD, using all components, have an overlap of approximately 80% (160, 923 pixels) with the PIFs using five MAD components, and around 70% (139,654 pixels) with the PIF using three MAD components.
The number of coincident PIFs from the spectral measures (SCM, SAM, and ED) using the original images and the NED using the MAD components are extremely low, indicating a significant difference between the two procedures (
Table 6). The smaller intersections are among the PIFs from ED and NED-MAD. PIFs from the similarity measures (SCM and SAM) have an overlap of approximately 25% (50,000 pixels) with the PIFs from NED-MAD.
Table 7 shows the fitted intercepts, slopes, correlation coefficient and RMSE for least squares regression on the 200,000 PIFs from NED-MAD images. The removal of the noisiest component provides the best fit regression line, with higher correlation coefficient and lower RMSE for all bands, except for band 7. Thus, the noise reduction provides a more homogeneous PIF selection. In opposition, PIF from NED using only the first three MAD components causes a loss of signal, decreasing the fits of regression lines for bands 3, 5, and 7.
PIFs from NED-MAD compared to PIFs from EDCD exhibit higher correlation coefficients for linear regression in the first and second bands and the lower for the rest. An inverse behavior is found for the RMSE values, where PIFs from NED-MAD presents lower values for bands 1, 2, 3, and 4. PIFs from NED-MAD show best fit regression line compared to the two similarity measures (SCMCD and SAMCD) applied to the original images.
Table 8 shows the means of PIFs from the NED-MAD method considering all-components, first five components and first three components for the 2011 scene (reference image) and 2001 scene before and after normalizations using least squares regression line. The differences between the means of reference and normalized images are always close to 0.5.
The NED-MAD, considering all the bands, shows the smallest differences for bands 1, 2, and 5. However, the differences of the means of PIFs from NED-MAD procedures are larger in all bands compared to PIFs from EDCD (
Table 4).
Table 9 shows the dispersion measures of hold-out test PIFs for the three NED-MAD procedures. The variance and correlation coefficient between the reference and normalized image present the lowest differences distributed in different procedures: NED-MAD with all bands (bands 4 and 7); NED-MAD with the first 5 components (band 3), and NED-MAD with the first 3 components (bands 1, 2, and 5). The range of values shows greater differences for PIFs from NED-MAD using first three bands.
3.1.3. Spectral Analysis from the Dark Radiometric Control Target
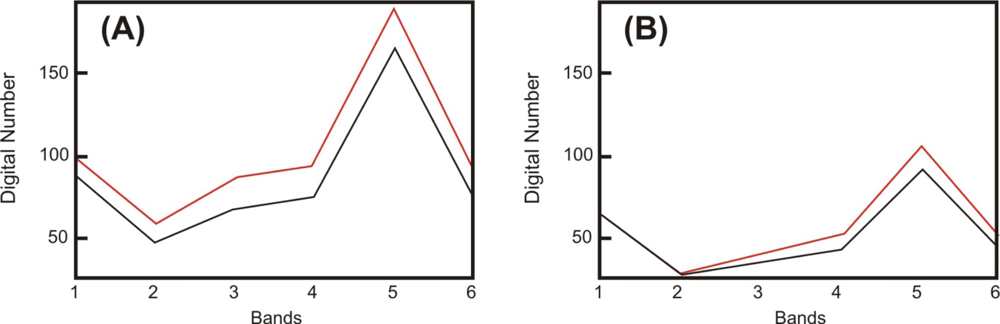
Spectral analysis between the reference and normalized images was made from the dark radiometric control targets, considering water body. Dimension of the water body may be important, and small sizes may not be representative [
12]. The present study adopted 55 pixels present in the center of the water body of a dam. Mean of the absolute deviations between the reference and normalized images demonstrates the adequacy of different measures in the PIF selection (
Figure 11). Normalized data considering the SCM, SAM, and ED methods showed results very close to the reference data. The best result is obtained by using the SCM method followed by SAM and ED methods. In contrast, the normalized spectra considering the NED-MAD, method show the highest deviations (
Figure 11).
Results show a different behavior of the fitting information of the linear regression model from PIFs, where for example the distance measures have lower RMSE values and higher R values (
Tables 3 and
7). These apparently contradictory results can be explained. The distance measures (ED and NED) describe a deviation from an ideal condition where there is equality between the temporal spectra (null condition),
i.e., a regression with a slope of 1 and intercept of zero. Therefore, the selection of pixels consider deviations from this ideal condition, even extending the limit of distance, and mismatches can occur. However, the distance measures by considering only values close to the ideal line (
Xt1 =
Xt2) always provide points fitted to straight line.
The similarity measures are not consistently related to the accuracy of the prediction, i.e., the degree to which the spectrum of time 1 approaches time 2. Statistically, SCM and partially SAM values are often unrelated to the sizes of the difference between the temporal spectra. The similarity measures are usually found to be a value that describes the quality or relative accuracy of the PIF samples. For example, the correlation is not affected by gain and offset effects, which makes high correlations possible even when the distance accuracy tends to be too weak or too strong. Thus, the similarity measures show a selection of points with larger dispersion measures. This feature allows the SCM to detect points without the restriction of an idealized model (α = 0 and β = 1). However, if the scattering is appreciable the line-fitting becomes subjective and unreliable. Therefore, the combined use of the two measures is the best solution.
The worst results for the NED-MAD measures are probably derived from the susceptibility of CCA to be influenced by the correlation of current changes in the ground target. CCA generates eigenvectors that describes the linear relations from the effects of atmosphere, illumination, and sensor calibration (that are external to the ground target). Temporal images with the majority of consistently changed ground targets generate eigenvalues conditioned to it, which interferes and modify the true PIFs, damaging their detection.
These results demonstrate that statistical data from the fits of the linear regression (RMS, correlation coefficient, and measures of central tendency and dispersion restricted to selected points) does not evidence necessarily the PIFs quality.
3.2. Results of the Band-by-Band Procedures
The use of ridge method on the previously selected PIFs allows a supplementary pixels reduction.
Figure 12 shows scatter plots and PIF images for band 4 made using two density thresholds, 12 and 26. In order to emphasize the results of this method for the figure, the original data are regarded as input, rather than points previously selected using spectral measurements. The PIFs eliminated for each band can be viewed in binary images (
Figure 12(d,e)).
One problem in density thresholds is the elimination of points having low density that are positioned along the line (ridge). These are usually points at each end of the ridge. Therefore, this processing step needs to be done carefully to avoid loss of relevant information. The pixels eliminated in a particular band can be eliminated in all five other bands.
The final step is to perform the robust regression for determining the line of best fit to the data from the reference and subject image for each image band. Robust regression procedure automatically omits eventual outliers in the calculations considering an absolute deviation value. The robust procedures fit the calibration line through the dark and bright targets.
Figure 13 shows the robust approach based on M-estimation regarding all bands, considering 106 PIFs from intersection of SCM and ED methods. In practice, with a good set of targets from the previous methods, there is very little difference between the least squares and M-estimation calibration lines.
The proposed combination of methods enables one to extract points from various conditions that can be applied from image to image. Thus, areas labeled as invariant points in a method can be described as change point in the next methods. The method allows one to select a number of targets to cover the range from bright to dark data values. This highlights the importance of using difference techniques.
Statistical analyses of these complementary methods (ridge and robust regression), following pixel-by-pixel, always provide the best fit straight line since it eliminates outliers, making the demonstration unnecessary.
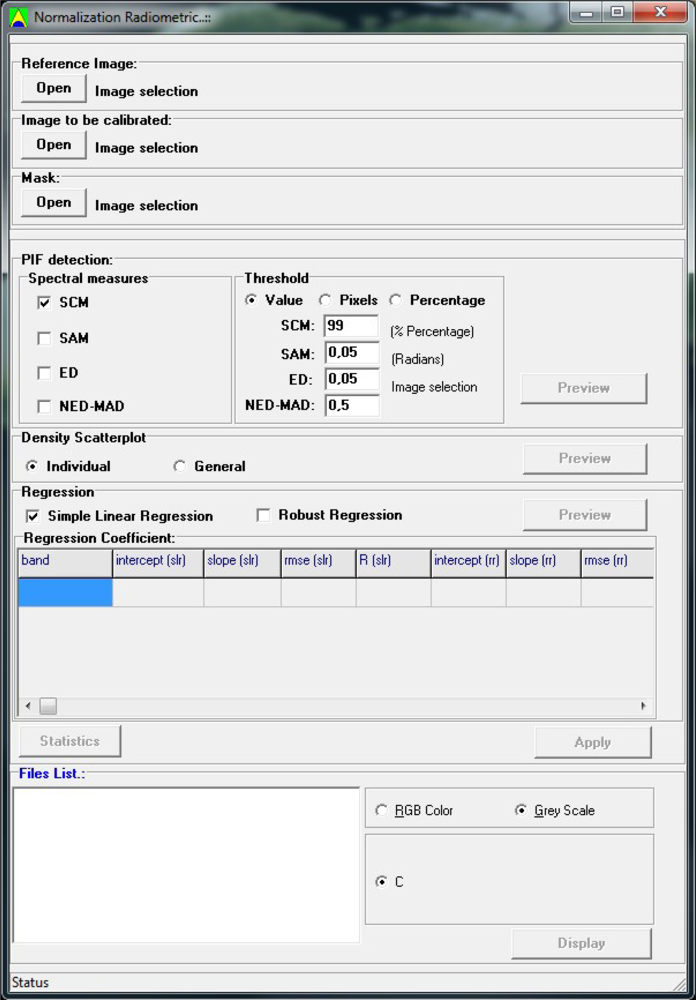
3.3. Program
The main functions of the program are organized in the main window interface, which contains the temporal image input boxes, mask image input box, spectral measures box, density scatter plot box, robust regression box, and image display (
Figure 14).
Input files are required for the two temporal images (Xt1 and Xt2), which must be co-registered and have the same number of rows, columns, and bands. The first image is used as a reference while the second is the image to be corrected. The program reads general raster data stored as an interleaved binary stream of bytes in the Band Sequential Format (BSQ) and Band Interleaved by Pixel Format (BIP). Each image is accompanied by a header file in ASCII (text) containing information to read data file, such as: sample numbers, line numbers, bands, interleave code (BIP or BSQ), and data type (byte, signed and unsigned integer, long integer, floating point, 64-bit integer, and unsigned 64-bit integer). This configuration combining image and header file allows versatility in the use of different image formats. When the user tries to open an image without the header file, an interface requesting the necessary information about the input image structure automatically appears. Optionally, a binary mask can be used as an input file to disregard some variants targets over time.
Four options for the automatic detection of PIFs using spectral measures are provided: SCM, SAM, Euclidean distance, and NED-MAD. The user can select the measures and their threshold values. The program allows the user to select different spectral measures simultaneously. The PIFs are only selected if they meet all conditions set out in the spectral measures. The program allows a preview of PIF images, obtained by the spectral measures, facilitating the user to, if necessary, reset the threshold values.
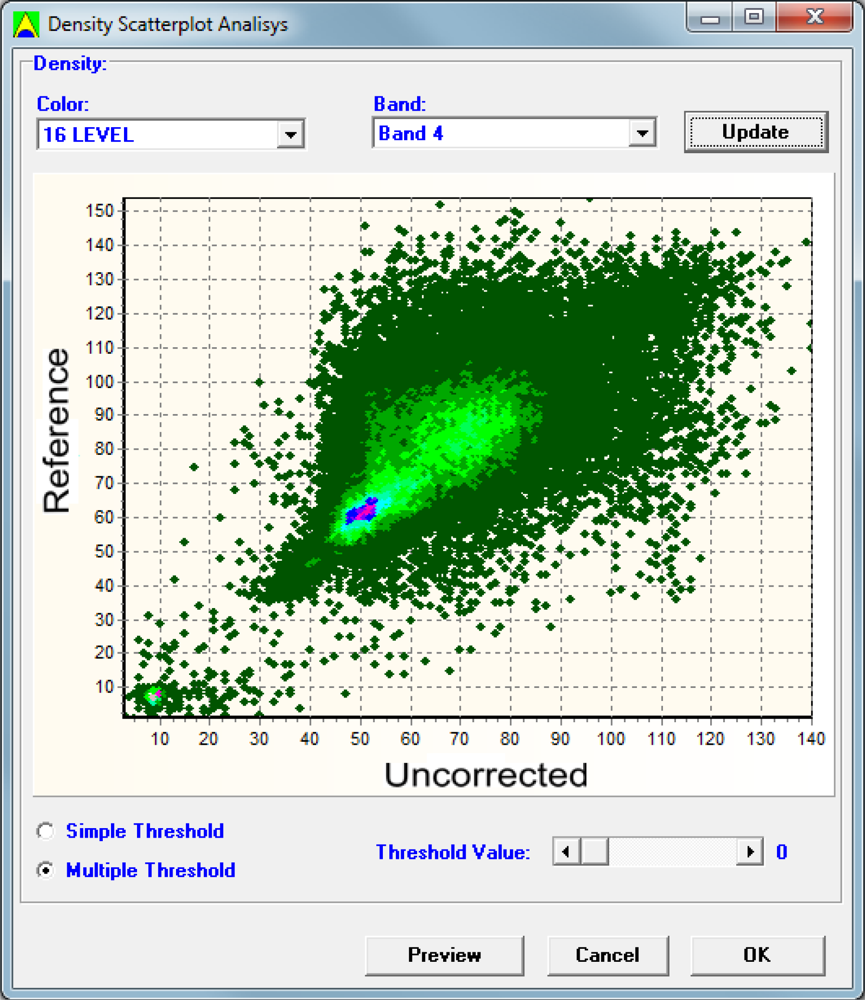
The ridge method can be applied from pre-selected PIFs from the previous step. The density scatter plot can be visualized from the preview button, which opens a window interface for the ridge method (
Figure 15).
In the scatter-plot density window, the user can choose to display the pair of bands and a pre-saved color table. At the bottom of the window, the user can set the density threshold value in order to eliminate the outliers. The elimination of the targets can be made by considering a single value for each pair of bands (multiple thresholds) or a single value for all scatter plots (single threshold). Density threshold value can be set with a scrollbar ranging from 0 to 255, derived by linear conversion of density values.
Finally, the robust regression using PIFs can be applied. In the main window the user can choose between the simple linear regression and robust regression from a check box. Thus, both method results can be compared. In the robust regression, the user must set the absolute deviation value between the regression line and the points in order to select the outliers. When the absolute deviation is greater than the set value, the observation is removed and the procedure is repeated. The decrease in the absolute deviation value by the user increases the number of outliers.
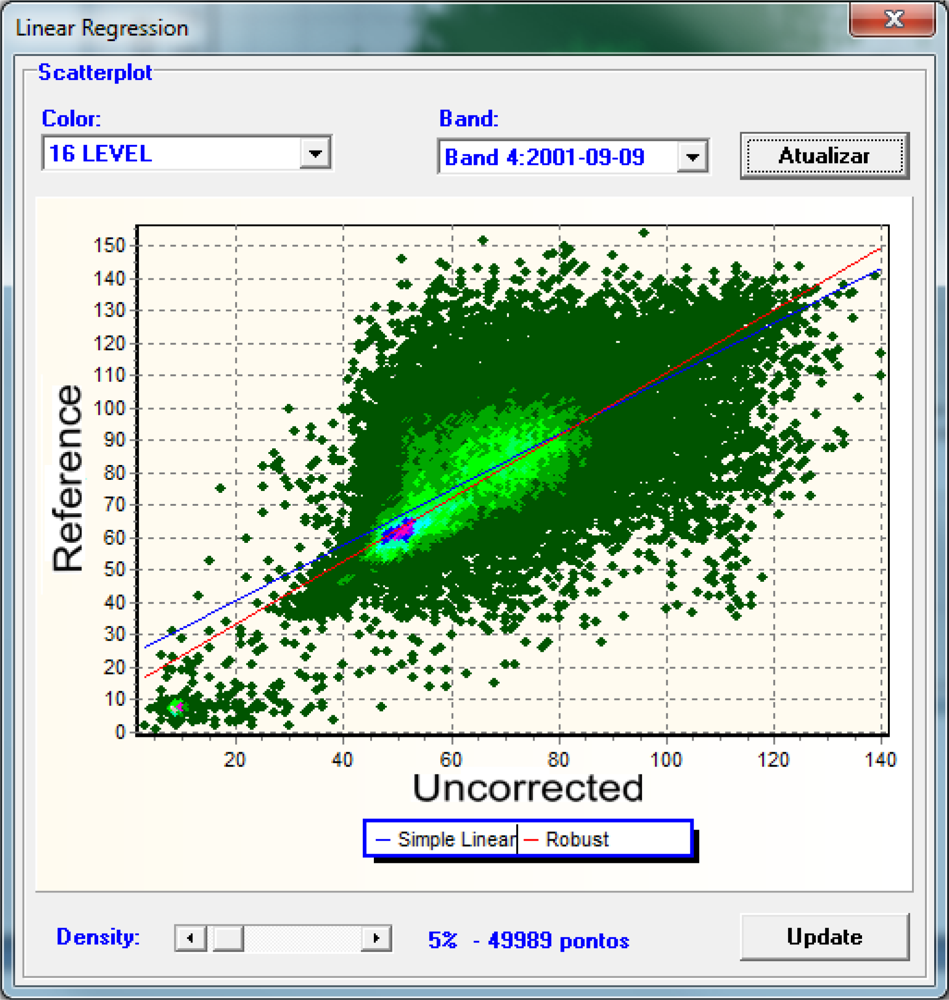
The linear regression window can be visualized with the preview button (
Figure 16). The user must select the band and color table for the density scatter-plot window. Moreover, the program allows the visualization of the regression line and the distribution of its points. In the case of a wrong selection of points, the program allows the absolute deviation threshold to be modified. Once the threshold has been determined, the slope and intercept values are applied for each subject band, obtaining the calibrated images.
After the generation of calibrated images, the program generates statistics on the following images: reference, uncalibrated, and calibrated, considering the following statistical values: mean, variance, range, and coefficient of variation.
The program generates the following output files: radiometrically normalized images and PIF images. All inputs and results are shown in the File List, so it is possible to visualize them by choosing “Gray Scale” or “RGB” composite. The display interface provides basic functions for image visualization such as zoom areas and pixel values. Moreover, the results (output files) can be read with other images viewers.
4. Discussion
4.1. Comparison among Spectral Measures
The spectral measures can be performed on the original images, or on CVs from CCA. The use of CCA aims to correct temporal images (gain and offset). Thus CCA generates matrices of eigenvectors for both temporal sets that are invariants to linear and affine scaling, provided that the linear transformations are homogeneous for the entire image (such as band-by-band method). CCA operates throughout the bands; consequently specific effects in different parts of the image are not corrected. In addition, the calculation of eigenvectors in CCA is influenced, not only by the gain and offset from sensor-illumination-atmospheric effects, but also by systematic changes in the ground. Therefore, the contributions of other correlated attributes though the temporal bands (e.g., seasonal changes in vegetation, planting cycle) are difficult to determine due to mathematical formulation. The issue of the CCA application is to introduce a bias associated with correlations of surface changes to the true PIFs, hindering their detection. The canonical analysis (such as the principal components and factor analysis) should use images with a prevalence of unchanged targets. Moreover, CVs images have a spatial noise that should be considered in the calculation of the distance measures. The elimination of noisy components of CVs should be explored as an improvement to the method.
Spectral measures on the original temporal images consider both land cover changes as undesirable effects (e.g., different atmospheric conditions, variations in the solar illumination angles, and sensor calibration trends). Normally, the relative radiometric correction adopts the assumption that the linear effects are much greater than nonlinear effects [
3,
16,
27]. In this case, SCM measure is completely invariant to linear transformations, even considering different behaviors on parts of the image. The use of distance measures on the pre-selected data by SCM measure enables the decrease the scattering data and outliers. Thus, combining similarity and distance measures on the original images have greater simplicity and control over the generated information.
Statistical data of the linear regression (RMSE, correlation coefficient, and measures of central tendency, and dispersion restricted to selected points) does not always describe the PIFs quality.
4.2. Advantages and Drawbacks of the Proposed Method
The present method integrates different radiometric normalization algorithms with distinct mathematical and statistical operations that provide a set of alternatives according to the characteristics of the data. The methods can be combined in different ways, not needing to use all available methods. Compared to some previous relative radiometric normalization methods, this new method offers several improvements and advantages because a single method cannot be used in all situations. The best combination of methods is to adopt a pixel-by-pixel method followed by the band-by-band method. Thus, PIFs selection accuracy is distributed in the different methods that provide a sequential selection, taking into account, not only, the statistical behavior of the samples but also their physical properties, such as surface moisture, shadow, etc.. This method can be used for the pre-processing of different multispectral images (e.g., ASTER, SPOT, CBERS, among others) concerning bi-temporal data with the same spectral bands and radiometric resolution. Radiometric normalization of panchromatic images can be done considering only ridge and robust regression methods. This relative normalization algorithm is wide-ranging and can be used for most operational applications, different images and conditions.
While this approach is straightforward and brings together different algorithms, it still shows problems, especially with the effects of heterogeneous aerosol scattering and water vapor content in a scene. All methods of PIFs detection presume a uniform behavior for atmospheric effects; being suitable for molecular scattering and absorption by ozone and oxygen because their concentrations are quite stable over both time and space. Contrary to this, most aerosols are heterogeneously distributed which makes this task more difficult and requires the development of new algorithms.
Furthermore, atmospheric effects on the two images can be different, not only spatially, but also in the spectral dimension damaging PIFs detection by pixel-by-pixel methods. Considering aerosol effects, a simple procedure is used with infrared bands that are less contaminated, in the specific case of TM/ETM+ imagery the bands 4, 5, and 7. However, this procedure is ineffective if there are thick aerosols and thin clouds. Therefore, a challenge in improving the methods of relative correction is the development of procedures to consider the heterogeneity of the image, i.e., specific linear regressions for different portions of the image.