Landslide Displacement Monitoring Using 3D Range Flow on Airborne and Terrestrial LiDAR Data

Abstract

An active landslide in Doren, Austria, has been studied by multitemporal airborne and terrestrial laser scanning from 2003 to 2012. To evaluate the changes, we have determined the 3D motion using the range flow algorithm, an established method in computer vision, but not yet used for studying landslides. The generated digital terrain models are the input for motion estimation; the range flow algorithm has been combined with the coarse-to-fine resolution concept and robust adjustment to be able to determine the various motions over the landslide. The algorithm yields fully automatic dense 3D motion vectors for the whole time series of the available data. We present reliability measures for determining the accuracy of the estimated motion vectors, based on the standard deviation of components. The differential motion pattern is mapped by the algorithm: parts of the landslide show displacements up to 10 m, whereas some parts do not change for several years. The results have also been compared to pointwise reference data acquired by independent geodetic measurements; reference data are in good agreement in most of the cases with the results of range flow algorithm; only some special points (e.g., reflectors fixed on trees) show considerably differing motions.

1. Introduction

In many environmental applications, monitoring change of the geomorphic surface is important. Internal and external forces shape and reshape the surface over various timescales, including that of the human time scale. Increased or sudden erosion (e.g., gully head retreat), sedimentation and, in particular mass movements belong to the category that is important not only from the point of view of geomorphology or surface processes, but they may also have a severe impact on the human environment, or in extreme cases, they may even endanger property or human lives. The latter possibility justifies the efforts invested in change monitoring, change detection and prediction of such events or estimations on rates of such processes. Techniques that are able to detect small motions, slow deformations, displacements, or incipient motion are particularly valuable. Usually, multitemporal remotely sensed data are used as input for these techniques. In the case of mass movements, even if the processes originate from the same source or the process itself is well known, the actual motion pattern may turn to be complex and composed of many different acting factors that affect the actual surface in various ways. Soil creep, small rock falls and sapping combined with gravity-driven slow deformation result in a multi-rate, differential motion pattern that is difficult to study, even if the (dormant) landslide is known. There may be human impact or intentional countermeasures that also modify the surface. In order to detect changes and derive deformation patterns, advanced remote sensing techniques and data evaluation procedures are required. Many techniques are able to detect change; some of them are capable to quantify it. This paper goes beyond that: besides the quantification of the change, the magnitude and the direction of complete 3D motion is extracted. Furthermore, we would like to decipher not just the deviation of the temporal phases of the surface, but we aim to follow the history of the motion of the surface elements and particles that allow deeper insight to the dynamics of the landslide.

Studying surface processes quantitatively and spatially requires a digital model of the terrain surface. Optical methods with area wide data acquisition (photographic imaging, laser scanning) are capable of providing the resolution required for analyzing movements and deformations within a landslide. Because of the (i) direct line of sight and (ii) the range resolution within a beam, laser scanning is advantageous in forested areas for capturing the ground. While this has been demonstrated for airborne laser scanning data (ALS) [1,2], it has not been investigated intensively for terrestrial laser scanning (TLS) data. In the first case, the stem direction is, more or less, aligned with the viewing direction. Acquiring a notable portion of a slope by terrestrial laser scanning typically requires a viewing position from the opposite slope. Thus, the growing direction of vegetation is, more or less, perpendicular to the viewing direction. In aerial and terrestrial laser scanning, both resolution and accuracy depend on the distance from the sensor to the object. In a very generalized formulation, an accuracy better than 1:10,000 can be achieved, depending on the georeferencing of the scan positions and object reflectivity.

In this paper, we propose a method based on range flow [3–5] to estimate the 3D displacements of the landslide. We calculate dense motion fields by applying range flow on the digital terrain models (DTMs) generated from the ALS and TLS data available for the landslide. The motion vectors are estimated in between the two consecutive epochs (here, epoch refers to the reference date when the data was acquired) of the ALS and TLS data, and this process is applied over all the epochs to estimate motion of the landslide for the whole time series of the available data. Hence, we obtain dense 3D motion information for several years over an active landslide that exhibits largely varying motion patterns over different parts of the landslide.

For the study of a landslide, spatially and temporally resolved analysis is required. The object of study is located in Vorarlberg, Austria. Three epochs of airborne laser scanning and five epochs of terrestrial laser scanning data are available. Using this LiDAR time series data enables us to discern spatial and temporal variations in the surface processes. In this paper, we demonstrate the feasibility of range flow to derive dense 3D flow fields for tracking landslide deformation. The quantitative analysis of the results are performed against reference data.

2. Related Work

Historic landslides were mapped by Bell et al. [6] in forested areas using ALS. The landslides were identified in one epoch by the irregular surface and other geomorphic features. Typical extracted parameters of the landslide are the scarp length or the affected area. Using a number of epochs (often two), surface variations, such as volume change resulting from geomorphic processes, can be studied from digital surface models. Miller et al. [7] used optical satellite imagery for terrain model generation over glaciers. For scaling and as a reference method, airborne laser scanning data were used. In such a case, the correct georeferencing across the epochs needs to be assured, but no identification of corresponding points between epochs is necessary. This naturally does not provide movement in planimetry. Similarly, radar interferometry, as applied, e.g., in [8,9], provides change information along the line of sight, thus in one direction. Baldo et al. [10] derive altitude and volumetric changes through elevation differences of the DTMs. Kasperski et al. [11] determine the active region of the landslide by subtracting the terrain models derived from TLS data. Quantification of the displacement was performed by analyzing the 2D transects over TLS point clouds.

Dewitte et al. [12] used sequential DTMs generated from aerial images and laser scanning over a landslide. Distinct features were identified and positioned manually in the DTMs. Thus, motion is determined at only a few points. Feng et al. [13] detect motion of a landslide model using image feature matching in a stereo pair. The 3D motion of the points were computed by the SIFT [14] feature matching at each epoch in the calibrated stereo pair. Arjun et al. [15] estimate displacement fields from TLS data by cross correlating the height raster images. The cross correlation method gives the 2D displacement fields of the surface, and large motions were computed by first estimating motion at coarser grid resolution and then at subsequent finer grid resolutions. Abdalati and Krabill [16] estimated velocity of a glacier captured by ALS by cross correlation of features, e.g., crevasses. In this case, the geometric texture is used for finding corresponding patches.

A 3D velocity field of a glacier surface was determined by Schwalbe and Maas [17] using long range (4 km) terrestrial laser scanning. Point cloud matching (e.g., iterative closest point (ICP) algorithm [18]) could directly be used to estimate the movement of corresponding features. In a similar setup ([19]), images were taken from one position and features tracked automatically. Scale was determined with the aid of GPS and a photogrammetric bundle. Teza et al. [20] determine the displacement field of a landslide using piecewise application of the ICP on a point cloud data of a landslide acquired by TLS. The landslide is divided into sub-areas and six translational and rotational parameters are derived by minimizing point to surface distance in the ICP. Monserrat and Crosetto [21] estimate landslide deformation using least squares surface matching (LSM) [22,23]. An elaborate study on the use of LiDAR for landslide investigation, not restricted to displacement monitoring, is available in [24].

These approaches differ in automation and in the results, from vertical differences to 3D motion vectors. Automatic determination of flow fields was demonstrated for landslides and glaciers. The methods using geometric or image texture either provide the full motion vector or fail, due to a singularity. For example, this occurs if a straight edge is moving. While movement across the edge direction may be determined and picked up visually, movements in edge direction cannot be derived (this is also known as the aperture problem [25]).

Our approach to estimate the displacements of the subject landslide is based on the range flow [3–5], which refers to motion fields derived from range image sequences. A closely related algorithm used for estimating 2D image motion from color or gray scale images is known as optical flow [26]. The flow algorithms were developed in the context of video analysis. Range flow has been used for motion estimation of a leaf [5], human arm [27,28], deformable paper [4], rubber balloon [4] and detection of independently moving objects [29].

To this end, it should be pointed out that the methods of ICP [18,30] and the least squares surface matching (LSM) [22,23] are very similar to the range flow. ICP and LSM were developed for a pair of point clouds or surfaces, and this was extended to multiple point clouds and surfaces. This extension, however, is in the context of a large baseline in the sense that point cloud acquisition positions may be far apart, as long as the same object is in the field of view. ICP is applied to point cloud data, and the point to point or point to plane distance is minimized. In LSM, commonly, a raster or a triangulated mesh is generated from each point cloud, and the orthogonal or the Euclidean distances between the surfaces are minimized. Different formulation may arise from use of different transformation parameters, e.g., a Euclidean, a similarity or an affine transformation that may depend on the application. For example, in [22], six parameters of a Euclidean transformation were estimated for point cloud registration, and in [31], 12 parameters of a 3D affine transformation were estimated for airborne laser scanning strip adjustment. When only a 3D shift is computed between two regularly interpolated rasters, the range flow and LSM are basically the same (e.g., [32,33]). Further information about LSM and ICP can be found in [22,34] respectively.

The methods based on ICP (e.g., the piecewise alignment method of Teza et al. [20]) suffers from problem of large movements and different point densities that may arise from using different scanning techniques (e.g., ALS, TLS) for two epochs or occlusions caused by different view points. Image feature matching approaches have the disadvantage of estimating only sparse motion, and the correlation based approaches can estimate 2D motion only. Compared to point-based techniques, range flow can compute dense motion fields of a moving surface. Therefore, a more detailed motion analysis can be performed on the landslide surface using range flow compared to feature-based or point-based techniques. The range flow is applied on the interpolated surface, and point data acquired from different sensors can be utilized. In range flow, large motions can be estimated using the well-known coarse to fine strategy [35,36]. In addition, range flow can estimate 3D motion at sub-pixel level, and input data with different point densities and temporal resolution can be used. As range flow is usually applied in a least squares framework, the accuracy measures for the least squares adjustment are also well-defined [37]. These accuracy measures are essential for the correct interpretation of the results.

3. Data and Methods

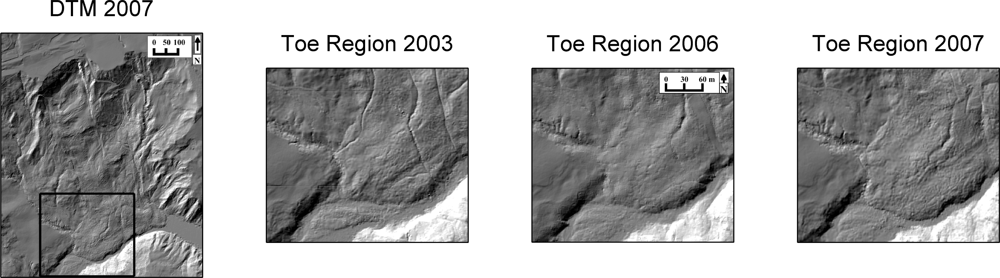
3.1. Study Site

The site of the landslide (Figure 1) is located in Doren, Western Austria, in the federal state of Vorarlberg. Geographically, the area belongs to the Bregenzer Wald, a hilly to mountainous region characterized by relatively mild climate, due to the effect of the Lake Constance, but also influenced by the Alpine environment. The high precipitation (ca. 1, 030 mm/yr) with a rainy summer season (> 150 mm/month for May–Aug—data for Oberstdorf, Germany, 30 km SE of Doren; [38]) implies high runoff and often well saturated soils. Geologically speaking, the area is a part of the Foreland Molasse Zone. Freshwater molasse sediments are the most abundant surface lithology; however, because the area was glaciated during the Last Glacial Maximum [39], Würmian glacial moraine also occurs (Herrmann et al. [40]). The lower freshwater molasse units consist of the Weißach and Steigbach formations (representing the Oligocene) and the Miocene Kojen formation, respectively [41].

The glaciation is also partly responsible for the current disequilibrium of the landscape; it is continuously adjusting to balance internal and external forcing. Basically, the system is continuously adjusting to the last deglaciation, which left behind a higher relief topography that is unstable in the long-term with the given conditions. The watercourses of various sizes incise intensively into the host rocks, forming rapidly evolving valleys, evacuating large amounts of sediments from the area. The slopes of the river valleys are often steeper near to the thalweg, whereas slopes are gentler in higher uphill regions.

The dynamic equilibrium at the toe of the landslide is maintained by the river Weißach: it is eroding the material of the lobate spreading with various rates. The discharge of the Weißach may vary considerably, tending occasionally to flash floods; therefore, the settlements are situated on the higher valley slopes, such as the village of Doren. The continuous evacuation of sediments by the Weißach combines with the active tectonic setting, due to the N-S shortening, causes unstable valley slopes on both sides of the valley. The landslide itself is a long-lasting problem of the local community and has become increasingly dangerous ([42]). The active area is continuously evolving, but major mass movements occurred in the 1980s and in 2005 and 2007. As the landslide mass evolves, the material of toe of the landslide protrudes to the channel of the Weißach, partly blocking the flow of the river. Consequently, in some years, the damming effect of the landslide is observable (e.g., prior to 2010, this was the case, and in 2011, large parts of the toe had been washed away). As this dynamic situation also generates redistribution of material, various types of material movements can be observed on many scales.

3.2. Data Acquisition and Basic Processing

The airborne LiDAR data have been acquired in the years of 2003, 2006 and 2007 on behalf of the Vorarlberg Surveying Authority (Landesvermessungsamt Vorarlberg [43]) in the frame of various measuring campaigns. The processing of the data has been carried out in a standard manner (see Roncat et al. [44] for details). The terrestrial laser scanning data have been acquired through the ÖAW (Österreichische Akademie der Wissenschaften (Austrian Academy of Sciences)) project; the data have been acquired yearly using mostly a Riegl LMS-Z420i laser scanner during the late summer or early autumn (leaf-on state, due to a foggy autumn and the high risk of early snowing in the study area). Georeferencing of the individual point clouds has been conducted using multiple external reflectors; the positions of the reflectors have been measured by an RTK GPS receiver with ca. 2 cm positional accuracy. The georeferenced point clouds have been integrated for further processing. The DTMs have been calculated using the software packages SCOP++ [45] and OPALS [46]. During the data processing, in most of the processing steps, the point cloud has been treated as if it were measured by the airborne technique. Densely forested areas were excluded using a mask. This processing made it possible that the landslide scarp, the grass-covered meadows above and below the main scarp and most of the anthropogenic features are well-modelled independent of airborne or terrestrial acquisition.

In order to obtain a digital terrain model (DTM) from the laser scanning point clouds, a classification of the measured points into ground points and off-terrain points is necessary. This was performed using the hierarchic robust interpolation ([47]). For airborne and terrestrial laser scanning point clouds, the parameters had to be adjusted accordingly.

3.3. Range Flow Methodology

The range flow algorithm computes the 3D velocity fields of a moving surface [5]. The surface is defined as a function of the spatial location and time, Z = f(X, Y, t). The total change in the elevation (range) over time is given by:

$$\frac{dZ}{dt}=\frac{\partial Z}{\partial X}\frac{dX}{dt}+\frac{\partial Z}{\partial Y}\frac{dY}{dt}+\frac{\partial Z}{\partial t},$$

(1)

$$W=Z_X\hspace{0.17em}U+Z_Y\hspace{0.17em}V+Z_t,$$

(2)

where Z_X and Z_Y are the spatial derivatives and Z_t is the time derivative of the surface and (U, V, W) = (dX/dt, dY/dt, dZ/dt) is the unknown velocity vector. In the current context, (U, V, W) correspond to the motion along west-east, south-north and the zenith direction between the two epochs, respectively. The time derivative, Z_t, is the height difference per time unit. Equation (2) is known as the range flow constraint equation [5]. In [3], it has been called the elevation rate constraint equation. The same equation has been used in LSM for laser scanning strip adjustment [33].

Equation (2) provides one constraint for each grid point and contains three unknowns. Therefore, additional constraints are added by using a window of size m by m grid points and solving the resulting overdetermined system of equations, which is written in the form:

$$\mathbf{Ax}=\mathbf{y}+\mathbf{e}$$

(3)

The unknowns, x = (U, V, W)^⊤, are estimated using the least squares solution, which minimizes the height differences at each grid point. A window of m × m provides m² observation equations. The observations, y, are the height differences between two epochs (i.e., Z_t), and e is the vector of residuals. The solution of the above equation system is given as:

$$\mathbf{x}={\left({\mathbf{A}}^{\top }\mathbf{A}\right)}^{-1}{\mathbf{A}}^{\top }\mathbf{y}$$

(4)

$${\mathbf{Q}}_{\mathbf{xx}}={\sigma }_0^2{\left({\mathbf{A}}^{\top }\mathbf{A}\right)}^{-1},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\sigma }_0^2=\frac{{\mathbf{e}}^{\top }\mathbf{e}}{n-3},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\mathbf{e}=\mathbf{Ax}-\mathbf{y}$$

(5)

where n is the number of observations. Q_xx is a 3 × 3 matrix, whose diagonal elements are variances of the three components of the estimated motion vector. The standard deviations derived from these diagonal elements are used as an accuracy measure for the estimated flow vectors. High deformation and surface changes caused by human activity will result in high σ₀, and consequently, the diagonal elements of the Q_xx matrices will also be high. Further causes of errors in the estimation process are the presence of moving and non-moving pixels within one window and low ground coverage due to vegetation, erosion and incision. Therefore, a robust least squares adjustment is performed by iteratively reducing the weight of the observations with high residuals.

The evaluation of range flow constraint, Equation (2) requires small motion between the two surfaces, because it is based on the first order approximation of the surface. However, it cannot be assured that the motion is small in between two time frames. The common strategy to overcome this problem is to use a coarse to fine scheme [35,36]. Therefore, we employ a hierarchical scheme, i.e., estimating motion from lower resolution to higher resolution for areas with large motion. Large motion in W (the zenith direction) can be estimated without the need of the pyramid scheme.

The window size is also an essential factor in the estimation of the 3D motion fields. A small window size may not provide enough variations in the surface normals and would result in a lower determinability of the motion vectors. A larger window may include areas with very different motion. Therefore, an appropriate window size is often empirically selected.

In the context of landslides, large movement may result in large deformations. The changes in the surface caused by large deformations result in lower accuracy of the estimated motion vectors. However, the resulting motion vector may still hold reliable motion information. Therefore, the magnitude of the motion vector is analyzed along with its estimated accuracy.

The variance estimates in Q_xx from the least squares adjustment of the range flow may not be an exact representation of the accuracy of the estimated motion. In Equation (3) the coefficients of the design matrix, A, are the derivatives of the surface, and these coefficients are assumed to be error-free in the least squares adjustment. As a result, the uncertainties in the generation of the surface model and the subsequent slope estimation are not taken into account. Furthermore, the coefficients in the A matrix are the derivatives of the surface, which are estimated using a local point neighbourhood. Hence, the coefficients in A and the observations are strongly correlated with each other. Therefore a more rigorous approach for strict modeling of the errors in the range flow constraint can be investigated using total least squares adjustment [48] and the Gauss-Helmert model [37], which allows modeling of the errors in A and the correlation between the coefficients in A and the observations. However, in the context of the landslides, the deviations in the functional model caused by deformations and the changes in the surface roughness makes the problem ill-posed. Furthermore, the correlations induced by generation of the digital surface model from original distance observations and the use of the coarse to fine strategy for large motion estimation are difficult to model. Therefore, in this paper, we use a simpler model for motion estimation (i.e., Equation (3)), which allows the results to be interpreted with high confidence and reliability.

3.4. Motion Detection Framework

Range flow is applied from lower resolution DTMs (e.g., 8 m resolution) to higher resolution DTMs (e.g., 1 m resolution). The application of the coarse to fine strategy is necessary, due to the presence of “large” movements (>10 m) in the active areas of the landslide. In the coarse to fine application of the range flow, a warped DTM of the first epoch is computed using the motion vectors at each grid location for each resolution. The time derivative, Z_t, between the two epochs is then computed by taking the difference of the height values between the warped DTM of the first epoch and the DTM of the second epoch [36]. The resulting motion between the warped DTM at one epoch and the DTM in the second epoch is smaller in magnitude. The fine scale of the motion is then estimated using the finer resolution DTMs.

The motion is computed from each dataset to the next temporal dataset, and no distinction between the ALS and the TLS dataset is necessary for the motion estimation, as the derived DTMs are used as the input to the range flow algorithm. However, the area coverage and the point densities vary significantly in the ALS and TLS datasets, and the point densities may serve as an attribute in defining the accuracy of the generated DTMs. In the current work, we use point density only to filter out the areas with no ground point in one of the epochs.

4. Results

Figures 2 and 3 show the DTMs of the landslide from 2003 to 2012, generated from the ALS and the TLS data. In order to apply the range flow algorithm on the ALS and TLS datasets, DTMs with different resolutions (1 m, 2 m, 4 m, 8 m and 16 m) were generated. The TLS datasets provide high point densities in certain parts of the landslide (e.g., > 30 points/m² at the scarp area). However, the ground point densities in the vegetated areas are significantly lower, with some areas without any ground point. In comparison, ALS data provide more uniform distribution of points, and the average ground point density is 1.2 points/m². Therefore, we have used 1 m resolution as the finest resolution for the motion estimation. Figure 4 shows the point density maps for TLS datasets from 2009 to 2012. As visible in Figure 4, point density in the southern part of the landslide is very low, due to the presence of vegetation. For better visual correspondence, interpolation was performed over these areas when generating the DTMs. The smoothing effect due to interpolation is clearly visible in the DTMs from the TLS campaigns (Figure 3). However, for motion estimation, these areas would give erroneous results, due to the lack of sufficient terrain information. Therefore, no motion vector has been computed over these areas with no ground point in a one meter cell. A window size of 11 × 11 pixels is used at each resolution for local motion estimation. This window size was empirically selected, and most areas of the landslide have a sufficient topographic variation within this window size.

In general, the absolute and the relative accuracy of the registration was below a std. dev. of 1 dm for the TLS data and 2 dm for ALS data. The magnitude of the motion in the non-moving parts of the landslide is negligible within the accuracy of the data. However, in the TLS dataset from 2008, we observed large errors in the georeferencing of the point cloud, and therefore, we have omitted the 2008 TLS dataset from our analysis. 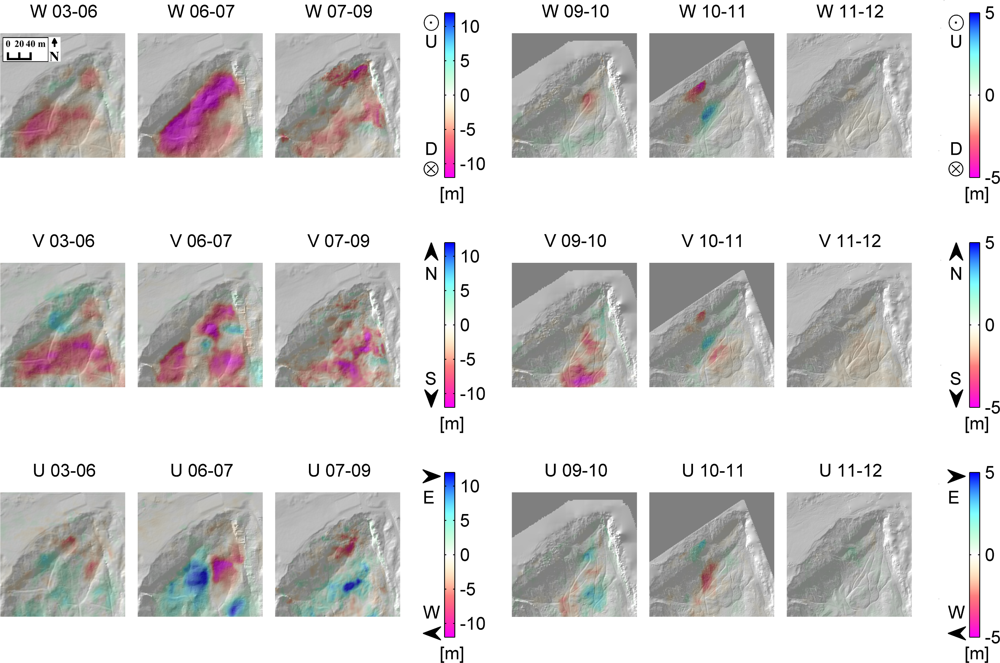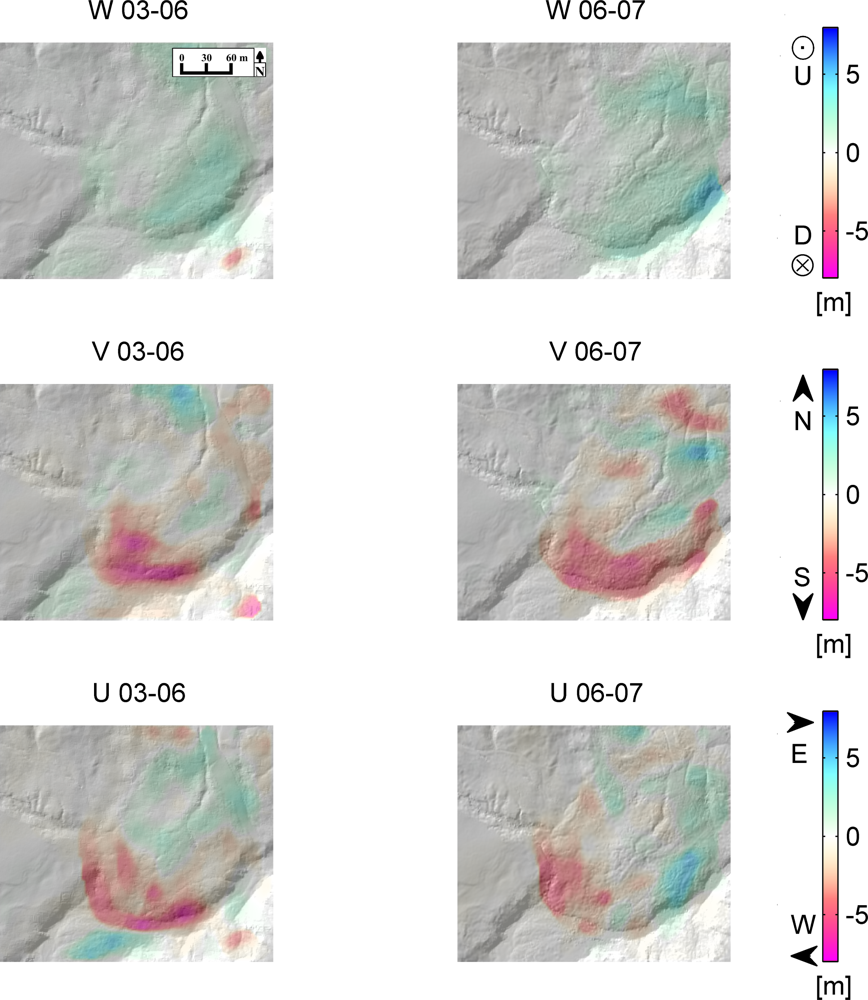The estimated motion vectors have been compared manually with traceable features in the DTMs, and the estimated motion vectors correspond well to the manually traced features in the DTMs.

4.1. Flow Vectors

Figure 5 shows the motion of the landslide for the whole time series. The motion vectors for different parts of the landslide are discussed in detail later in the current section.

In Figure 5, it can be seen that different parts of the landslide show very different magnitudes of motion in the (U, V, W) components of the range flow. The standard deviation of the estimated flow vectors are shown in Figure 6. It is important to analyze the motion vectors in conjunction with their estimated standard deviation. The average σ of the motion vectors from 2003 to 2009 is higher in comparison to the motion vectors from 2009 to 2012. The main reason for the low accuracy of the motion vectors is the deformation resulting from large movements that occurred in between the respective epochs. The range flow constraint is based on the local rigidity of the surface. Therefore, large deformation and complex motion patterns in the local window result in deviations from the functional model and result in lower accuracy. The high σ values in the scarp are results not only from deformations, but also from the presence of non-moving areas, which are included in the window of local motion estimation.

It is important to note that even though different parts of the landslide exhibit different motions, the non-uniformity of the estimated motion vectors, in part, also arise from the aperture problem [25]. In areas where the slope of the surface remains constant, the local application of the range flow cannot estimate motion along the slope of the terrain. Furthermore, human activity has also caused significant changes in the terrain, and this leads to unreliable and non-uniform motion vectors. In some parts of landslide, especially in the mid-slope area from 2003 to 2007, it is very difficult to visually verify the results, because of the surface changes resulting from human influence. This influence is visible in orthophotos of the area (Figure 7), which show considerable changes in the terrain in between epochs. However, in most areas, the magnitude of the motion in comparison to its accuracy is large enough to be deemed reliable.

Figure 8 shows the motion at the scarp of the landslide. From years 2003 to 2009 there have been large movements around the scarp area, with maximum magnitude of around 15 m in W, V and U components (down and in south-east direction, resp.). The standard deviation is also high in large moving areas (up to 70 cm, see Figure 6).

Figure 9 shows the west toe area of the landslide, and Figures 10 and 11 show the motion vectors over this area. The motion vectors at the tip of the toe correspond well to the observed motion of the mass. However, it can be noted that the motion is not fully estimated in the landslide area north-east of the tip of the toe. The reason for this is the aperture problem, because the movements along the slope are not discernible, and only the motion perpendicular to the local slope can be well estimated. At the tip of the toe, the significant change in the slope increases the determinability of the horizontal movement, and as a result, the motion corresponds well with the visually observed motion. The aperture problem can be solved by using a regularization strategy [5,49], which is an essential part of the state of the art motion estimation algorithms. The regularization scheme can utilize more global information by assuming similar motion between neighboring grid points. In the current work, we do not utilize the regularization scheme, due to the presence of a very large difference between the accuracy of the estimated motion vectors at different parts of the landslide. The situation is further complicated, due to the presence of vegetation and anthropogenic influence, which may lead to undesired results.

Figure 12 shows the mid-slope part of the landslide, and Figure 13 shows the motion vectors over this area. In the mid-slope part, we see large difference in the V component of the motion between the north and south areas. This motion gradient is also apparent in the respective DTMs. The average standard deviation of the estimated components of motion vectors is about 4 cm in the mid-slope area.

4.2. Interpretation and Assessment of the Results

The results show the applicability of the method at different parts of the landslide. In the following discussion, parts of the landslide are pinpointed where the detection of the motion is most conspicuous and the motion is contrasted to the landslide behavior.

The apparent motion at the scarp of the landslide is due to the loss of material rather than downslope movement (Figure 8). This is reflected in the vertical component, whereas in the area between the scarp rim and the boundary to the incipient motion, the vertical component represents the real motion of the material (Figure 8, post 2009 years). The displacement here is expectedly small; the rates are low; however, the motion affects the whole area, and it shows the expected characteristics of this part of the landslide.

The lower parts of the scarp that have been covered by very young (a few years old) debris are gradually exhumed by the motion (and, partly erosion) of the debris; this process is also reflected in the vertical component (Figure 8), but in large areas, gravitational movement also affects it, so some components of the detected motion are really due to the displacement of material blocks or patches. The rate of the displacement also varies in time: the measured, as well as the visually observed deformation in the years 2006–2008, both horizontally and vertically, were considerably larger in this area as during the subsequent years. (This is the reason why the repeated ALS campaigns were carried out between 2003 and 2007.)

At the foot of the scarp, the averaged vertical rate turned to positive from 2009 onwards, because large areas are affected by the accumulation of debris falling from the upper slopes. (Here, human interference cannot be ruled out: the farming activity above the landslide also produces various types of material that are deposited at the rim; this material falls down together with the natural processes.) This is, of course again, an apparent component of the motion, but its detection is an important result.

At the toe of the landslide (Figures 9, 10 and 11), practically only the ALS data are applicable, mostly because of the vegetation cover and partly because of the restricted visibility from the measurement station points on the opposite side. Therefore, the processing provided reliable values only for the years 2003–2007.

The elevation change is moderate and almost uniform, except for a patch during 2006–2007. (This transitional year can be characterized as a high-activity period for the landslide.) The pattern of the horizontal components are similar to a lobate spreading with forward and lateral extension, since in this area, there are no constraining walls that would confine the motion of the material, as in the upper parts of the landslide. Figure 11 shows clearly the pattern of the motion: in the left panel (2003–2006), the south-westward drift of the material dominates the toe, and the material in the river bed moves downstream (westwards); whereas, in the right panel (2006–2007), despite the shorter period, the protruding lobe of the material invades a considerable part of the river valley, overprinting the downstream pattern with a southward movement. This motion is a real material movement, during which the individual material blocks/units are deformed and displaced. This area is the best example for the applicability of the method.

Figure 13 shows the development of a mid-slope part (Figure 12) of the landslide that was very active in the early 2000s and is still in continuous motion up to now. Four phases (three differential flow phases) of TLS data (acquired almost exactly yearly) have been analyzed in detail. Here, the deformation rate can be calculated almost precisely, because the TLS campaign was performed at similar times of the year, and the results show a non-uniform pattern. 2010 was a wet year that caused many subsequent changes (including the increased ponding of Weißach and, later, large-scale erosional material loss of the toe; Figure 3, right panels). The infiltration of precipitation lubricating the slide plane and altering internal stress-strain relationships lead to the landslide gliding on its shear surface, as well as facilitating internal deformation. It enhanced the SSE-ward (i.e., downhill) movement rate of the mid-slope part. An internal “toe” of a smaller, embedded landslide has been forming, deforming the existing paths and de-watering channels (limited artificial countermeasures also took place).

4.3. Methodological Consequences

Figure 14 shows the sum of incremental motion vectors (computed by summing motions vectors from each consecutive epoch from 2003 to 2012; Figure 14, left panel), direct motion estimation between the first and the last phase (Figure 14, middle panel) and the difference of the two motion estimation results (Figure 14, right panel) at the scarp (here, we use the scarp as an example, because it is the most visible part; therefore, the most reliable DTMs can be generated both for ALS and TLS). In Figure 14, W and V components are shown, because the main motion is down and in the southward direction. The large differences in the result of the two approaches emphasizes the need for higher temporal sampling of the rapidly moving surface. The incremented motion vectors conform well with the visual analysis of the landslide motion. In comparison, there is a large underestimation of the motion in the direct estimation of the motion from 2003 and 2012. This can be attributed to large motion (> 30 m in some areas) in between the 2003 and 2012 epochs. At coarser spatial resolutions, fine details of the terrain are no longer visible, because large motions present at finer scales cannot be well estimated ([50]). Furthermore, at a coarse resolution, significant areas of the local window overlap with the non-moving parts of the scarp. Therefore, the large underestimation of the motion can be attributed to these factors. Due to combination of these factors, there is a large underestimation of the motion, especially in the horizontal component. This implies that the large motions should be handled carefully, and in some cases, it may be very difficult to automatically and reliably estimate large motion.

The rate of deformation can be calculated for certain parts of the scene for the shortest time elapsed between two phases, for instance, for one year. (Here, it is assumed that these two phases provide interpretable results.) However, it is often the case that the displacement of material in the landslide is inhomogeneous, both in time and space; consequently, the estimated displacement rates may differ by an order of magnitude for the different parts of the landslide at different time intervals. For example, in the subject landslide, large movements occurred within 24 h in 2007. Therefore, in the current work, only the motion vectors between laser scanning epochs are provided instead of stating the yearly displacement rates.

In our study area, a further complication should be taken into account: as it was earlier mentioned, at the toe of the landslide, the river Weißach erodes the material away with varying transport capacity depending on its water discharge. This has a seasonal and long-term variation. This reshaping activity is mostly independent of the landslide itself, but sometimes, the damming effect of the slumped material means a feedback for the erosive power of the river. Considering our method, this implies that in some cases, the respective parts of a later DTM phase cannot be found in the later landform, because the material that would correspond to that of the previous phase has been removed. This was the case in 2011 and in 2012, when even TLS station points of the previous year were washed away in the SE corner of the landslide. (Anthropogenic influence can also be considered here, as well, e.g., countermeasures carried out between two phases.) This behavior may spoil the method from working in some parts of the toe, where the motion otherwise is the largest; therefore, interesting results would be expected there.

In the future, these types of problems that are presumably present in many or most gravity-driven movements should be addressed. Our suggestion is to make use of the pyramidal results in a dynamic manner combined with other methods discussed in the introduction to detect areas of considerable material loss.

The elimination of vegetation from airborne laser scanning point clouds is a well established method ([47]). Using these methods with adapted parameters provides DTMs also for TLS point clouds. However, as it is visible in the shaded relief maps (Figure 3), the lower measurement distance did not lead to more terrain details displayed, but at some places, even to fewer details. We interpret this as a consequence of the rather horizontal viewing direction in the TLS campaigns versus the vertical growth of vegetation. The last TLS campaign was performed with a full waveform TLS. In Gaurnieri et al. [51], it was demonstrated that full waveform TLS can penetrate vegetation better than single return discrete TLS. In our case, low vegetation (bushes) partly covered the landslide, and we could not notice a comparable improvement.

4.4. Comparison with Reference Data

The Surveying Office (Landesamt für Vermessung und Geoinformation) of the Federal State of Vorarlberg, Austria, has carried out ground-based geodetic measurements of target points (prisms), placed at different positions on the landslide from year 2010 to 2012. The prisms are placed mostly on a metal rod, or in some cases, on a tree trunk, as shown in Figure 15. The change in the position of these points gives the motion between two epochs, which can be used as reference data for comparing the results of the range flow method. For years 2011 and 2012, the geodetic measurements of these points were performed synchronously with the laser scanning campaigns. However, for year 2010, there is a difference of several weeks between the laser scanning campaign and the measurement of the target points. Thus, a correction in the form of linear interpolation has been applied to compensate for the time shift. Figure 16 and

Table 1. Comparison between the estimated motion (U,V,W) and the reference data.

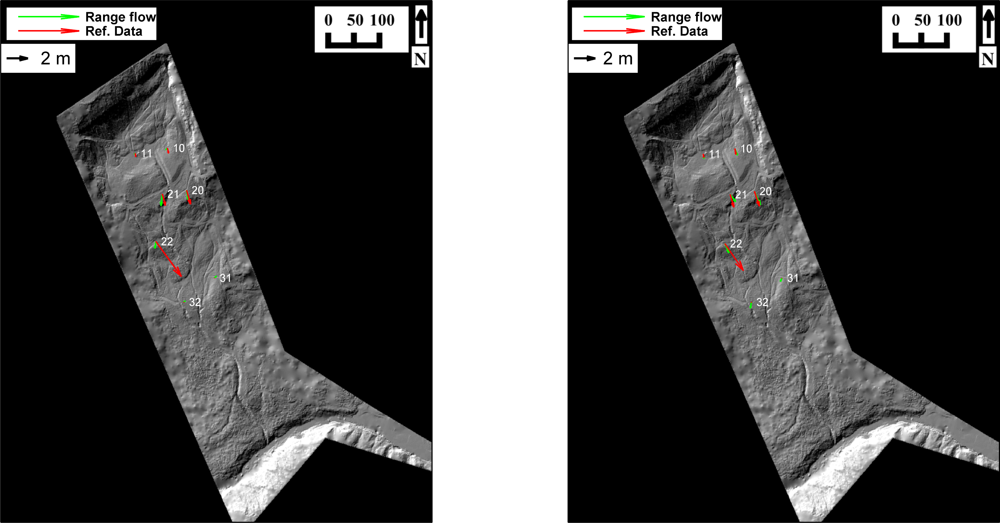
Pts.	Range Flow 10–11 (m)	Ref. Vector 10–11 (m)	Difference 10–11 (m)	Range Flow 11–12 (m)	Ref. Vector 11–12 (m)	Difference 11–12 (m)
#10	−0.15, −0.11, −0.10	0.10, −0.49, −0.02	−0.26, 0.38, −0.08	0.28, −0.59, −0.14	0.11, −0.56, 0.00	0.17, −0.02, −0.14
#11	0.15, −0.16, 0.46	0.05, −0.32, −0.16	0.10, 0.17, 0.62	0.05, −0.38, −0.07	0.06, −0.35, −0.15	−0.01, −0.03, 0.08
#20	0.22, −0.86, −0.32	0.38, −1.31, −0.32	−0.16, 0.46, 0.01	0.64, −1.26, −0.46	0.48, −1.41, −0.33	0.16, 0.15, −0.13
#21	−0.14, −1.15, −0.35	0.31, −1.10, −0.27	−0.44, −0.05, −0.08	0.55, −0.69, −0.46	0.35, −1.20, −0.21	0.21, 0.50, −0.25
#22	−0.20, −0.58, −0.01	2.41, −3.32, −0.21	−2.61, 2.74, 0.20	0.41, −0.84, −0.25	1.76, −2.56, 0.05	−1.34, 1.72, −0.31
#31	0.23, 0.23, 0.14	−0.00, −0.03, −0.00	0.24, 0.26, 0.14	−0.08, −0.36, −0.07	−0.01, −0.03, 0.00	−0.07, −0.33, −0.08
#32	0.07, 0.07, 0.21	0.01, −0.03, −0.00	0.06, 0.10, 0.22	−0.01, −0.29, −0.13	0.01, −0.03, 0.00	−0.02, −0.26, −0.13

give the comparison between the estimated motion vectors from the range flow and the motion computed from point-based measurements.

It is important to note that the results of the point-based measurements and range flow can be very different especially due to placement of these target points on tree trunks. e.g., the inclination of tree is clearly visible in Figure 15, which in combination with the offset between ground and the target prisms would result in motion that may be different from the motion of the surface. Furthermore, the motion estimated from range flow corresponds to surface changes arising from processes like debris flow, erosion and incision. These surfaces changes may not be reflected in point-based measurement. Therefore these point-based measurements can be somewhat biased by the actual placement of the prisms. However, they still serve as a reference for comparing the results since a measurement to an identified point (the prism) provides 3D motion at high accuracy, while a single point measurement in TLS provides only displacement along line of sight.

In general, the point-based measurement is in good agreement with the range flow results especially considering the 1 m DTM resolution. However, there is only one case, of point 22 where we found large deviation between the motion vector from the range flow and the motion vector derived from geodetic measurements. This reference vector is by far the largest (exceeding 5 m for two years); however, the geodetic vertical displacement is only 16 cm. Taking into account the slope of the terrain (Figure 17), it seems that the motion of the prism is somewhat decoupled from that of the ground (Figure 17 right panel). It seems that the tree protects its local neighborhood from erosion; its roots became exposed in 2012 (Figure 17 right panel). For this reason, we treat this point as an outlier; all other points behave consistent with our results.

5. Conclusions

The method of range flow estimates the movement of surface between epochs. Physical constraints, e.g., the conservation of material, is not considered in the computation. Geomorphic processes in a landslide can be pronouncedly visualized by the results of the method; however, the two types of motions should be separated. The estimated motion vectors are based on morphological changes in the surface arising from several geomorphological processes like debris flow, erosion and incision. Therefore, the motion vectors do not have a 1:1 relationship to landslide mass movement. Range flow results provide a qualitative and quantitative approach for measuring surface change (geomorphic and/or anthropogenic change). These changes can then be directly tied to geomorphic processes and used to infer material dynamics and impacts of landslide movement.

Growth of small vegetation is typically eliminated by laser scanning data (ALS) filtering for ground detection; however, in the case of terrestrial laser scanner (TLS) the growth of tall vegetation may remain in the calculation of the digital terrain model (DTM) at places with problematic geometry. Therefore, it may constitute an apparent deformation that must be taken into account.

Gully deepening or filling can be detected only if the characteristic width is larger than the analysis scale; if the width is less then this scale, gullies belong to the features that are used to detect the change and are treated as other features suffering deformation (they may appear or disappear during the evolution).

Range flow is proven to be a method that is (i) automatic and (ii) reliably describes the movement of surface. The importance of the results is twofold: (a) we were able to demonstrate the applicability of the method mainly used for motion estimation in range video sequences; furthermore, (b) the technique gave us reliable estimates on motion rates at important regions of the Doren landslide. The latter achievement is particularly valuable if we consider that the ground-based geodetic measurements of the Landesamt für Vermessung und Geoinformation Vorarlberg that were intended to quantify the displacement are only carried out for some established points (cf.[52]), mostly irrespective to the changing (and often unexpected) behavior of the landslide. Although the algorithm automatically estimates motion over the entire landslide area, the interpretation of the motion results should be undertaken carefully in combination with the confidence measures presented in this paper.