Topographic Correction of Wind-Driven Rainfall for Landslide Analysis in Central Taiwan with Validation from Aerial and Satellite Optical Images
Abstract
:1. Introduction
2. Study Area and Rainfall Event for an Experiment
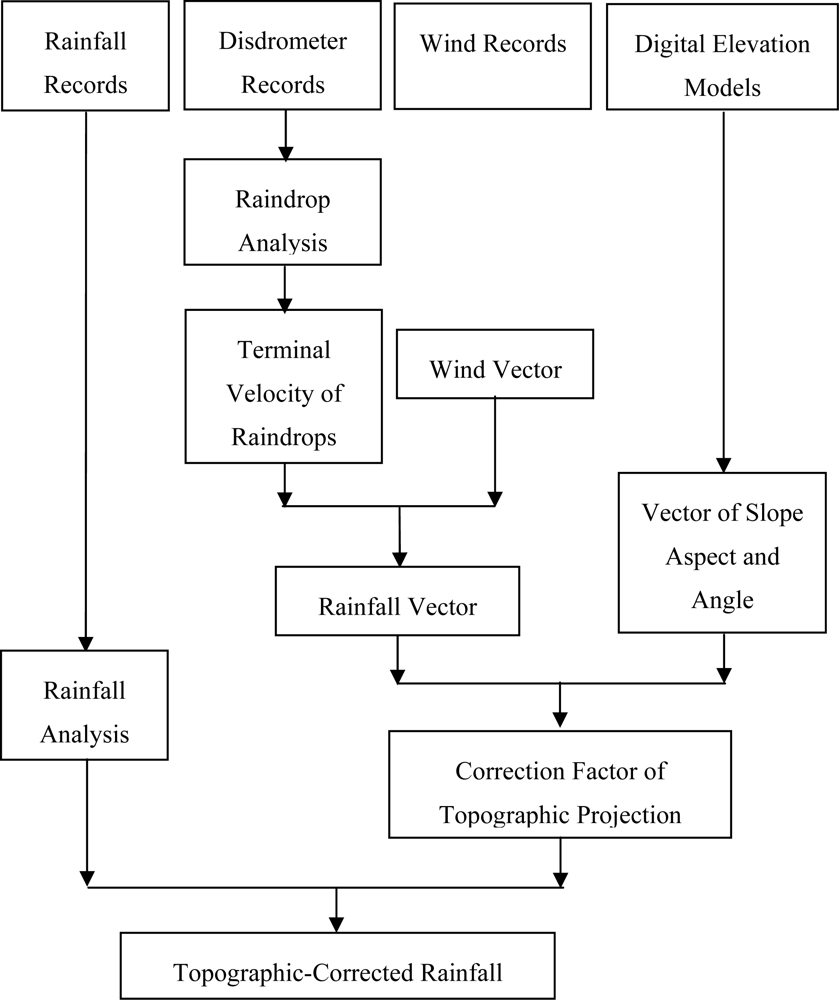
3. Methodology
3.1. Determining the Terminal Velocity of Raindrops
| V | the terminal velocity (m/s), |
| D | the raindrop size (mm), |
| R | the regression coefficient. |
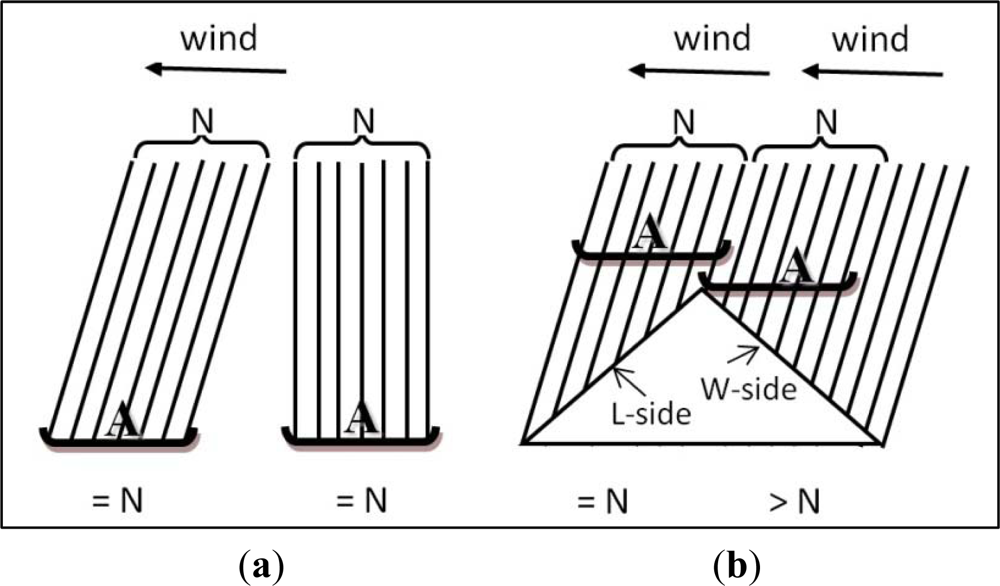
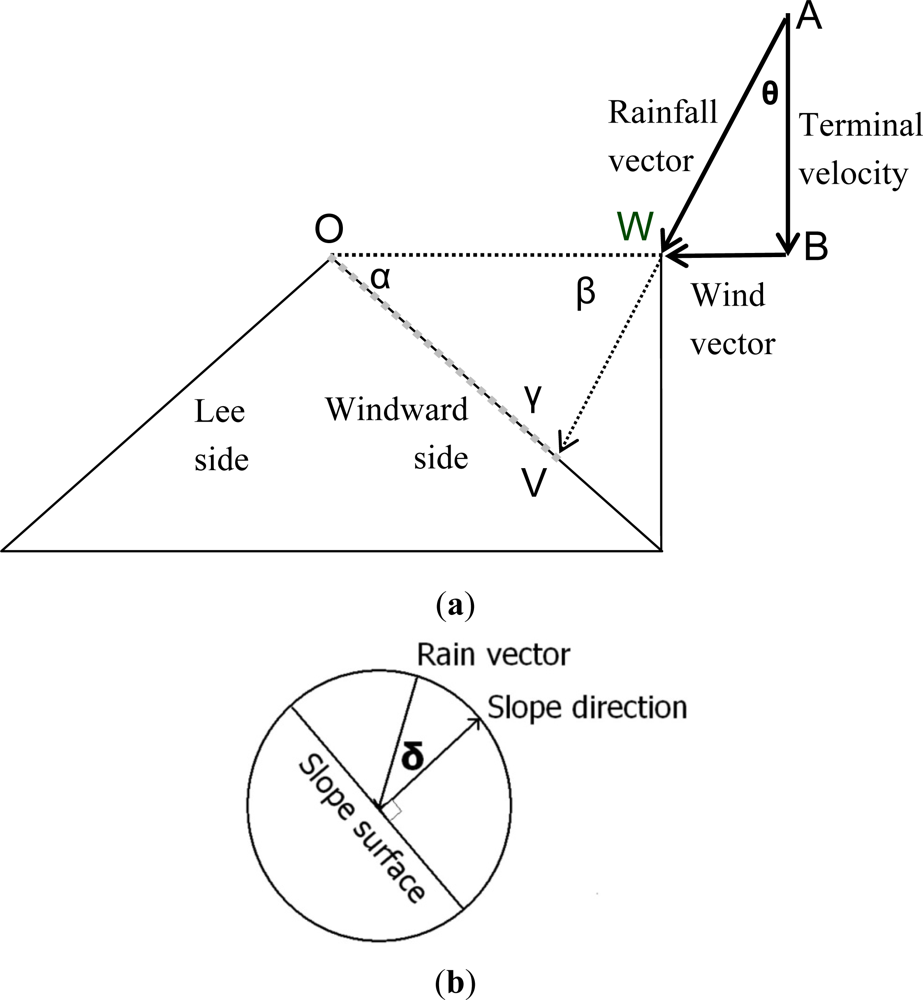
3.2. Determining the Wind Vector
3.3. Determine the Rainfall Vector
- (a). the average rainfall vector of the highest 24-h rainfall intensity;
- (b). the accumulated rainfall vector of hourly average rainfall vectors in the highest 24-h rainfall intensity;
- (c). the average rainfall vector of the 12 h prior to the peak intensity of the event;
- (d). the accumulated rainfall vector of the hourly average rainfall vectors in the 12 h prior to the peak intensity of the event; and,
- (e). the accumulated rainfall vector of the hourly average rainfall vectors in the all hours of the event.
3.4. Determining the Correction Factor of Topographic Projection
3.5. Kernel Density Analysis of Landslides
| τ | radius of circle neighborhood, |
| hi | distance between the point s and the observation point si, |
| n | number of observation points, |
| D(s) | density at point s (grid cell center), |
| si | observation point i (equals 1 or a quantity). |
4. Experimental Results and Discussion
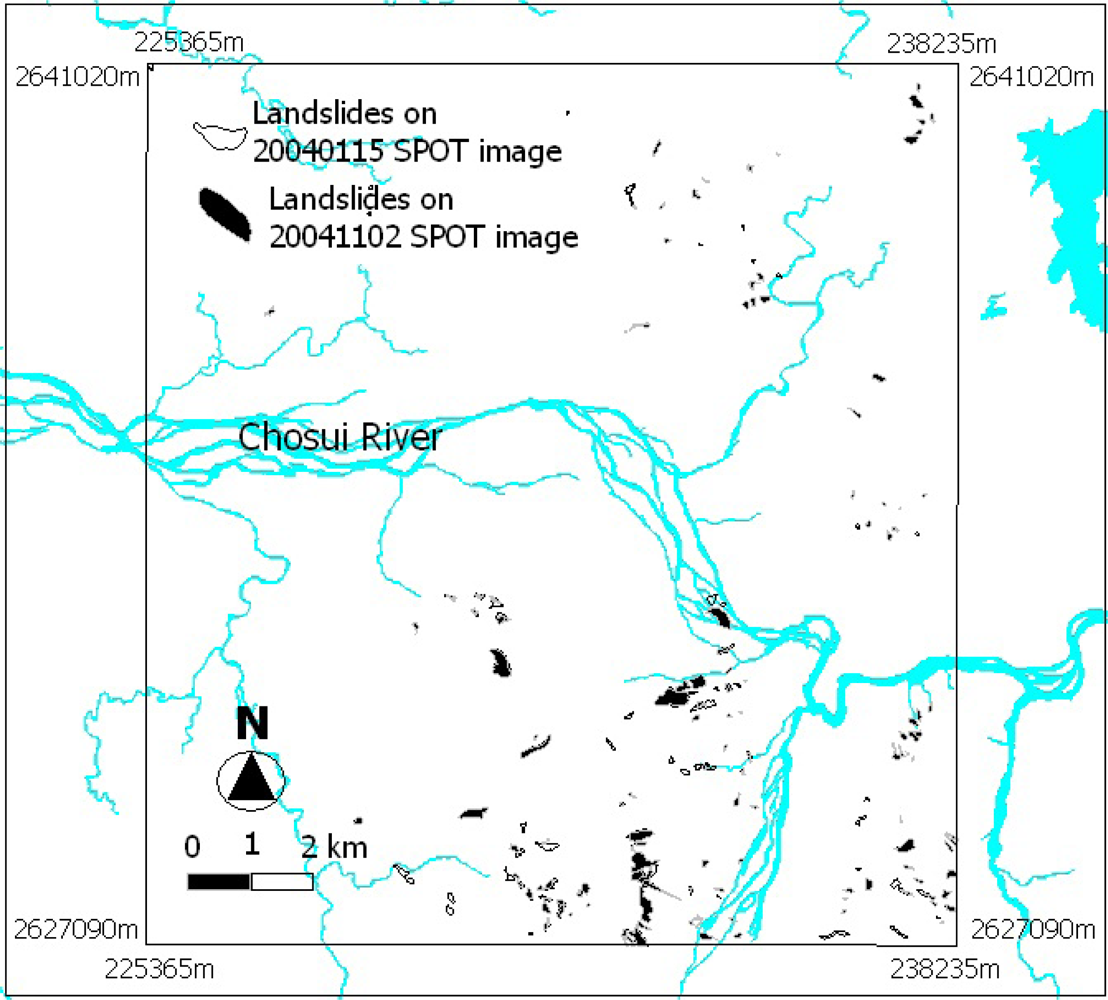
4.1. The Generation of Reference Data for Evaluation
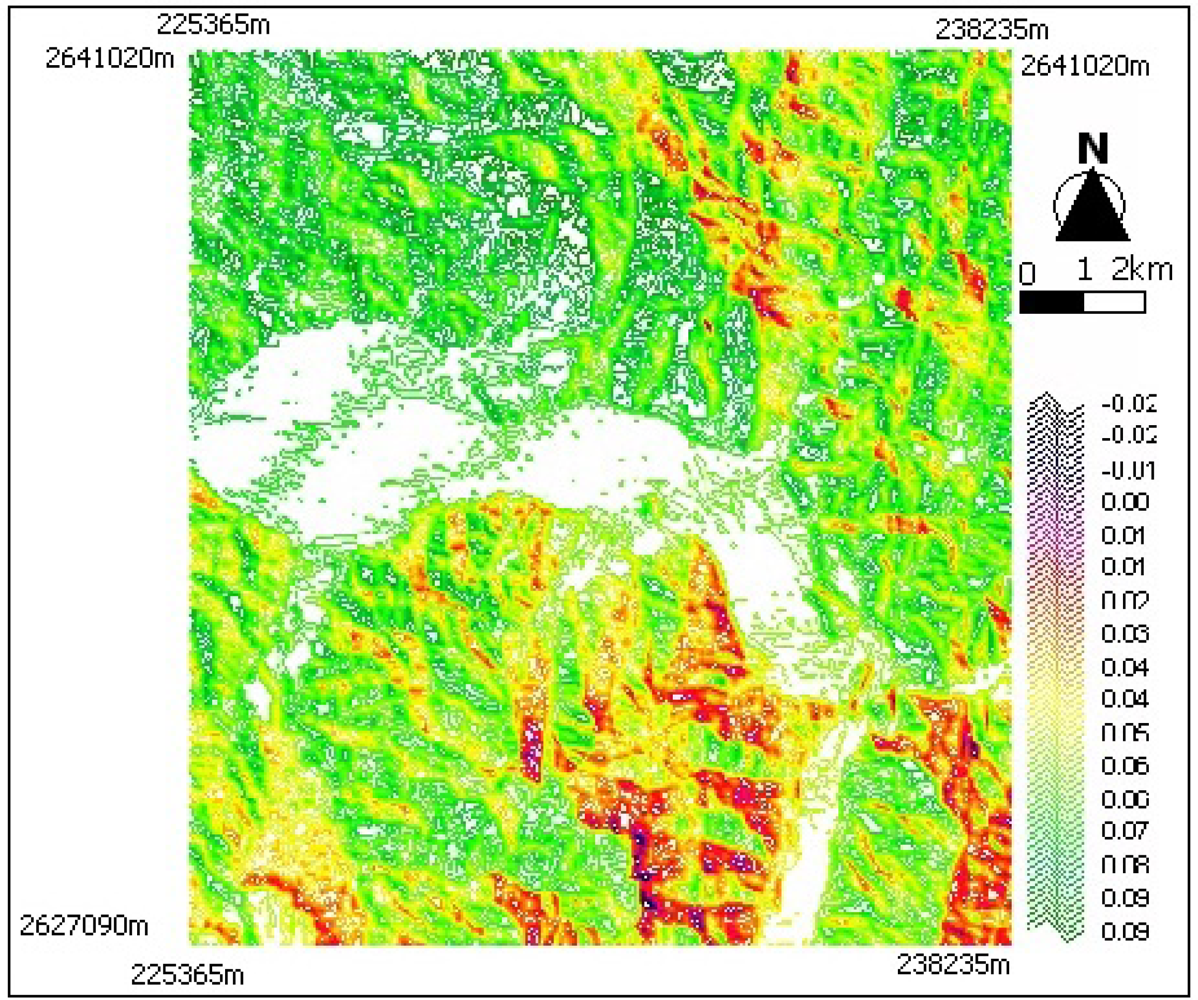
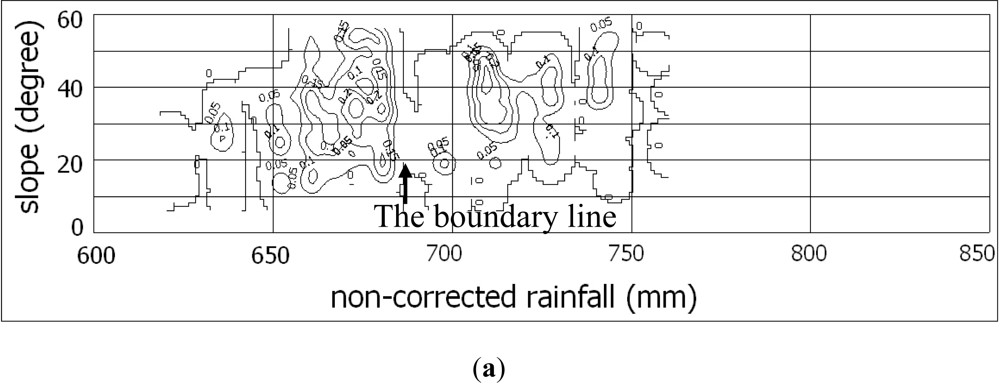
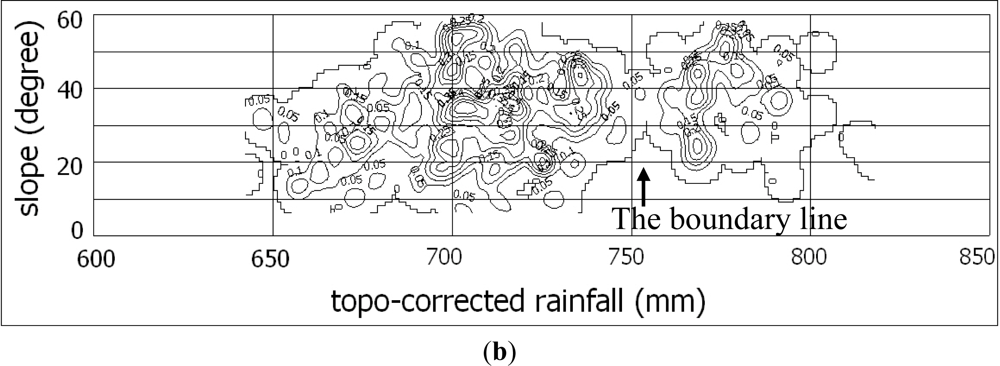
4.2. Effects of Topographic Correction with Rainfall Vectors
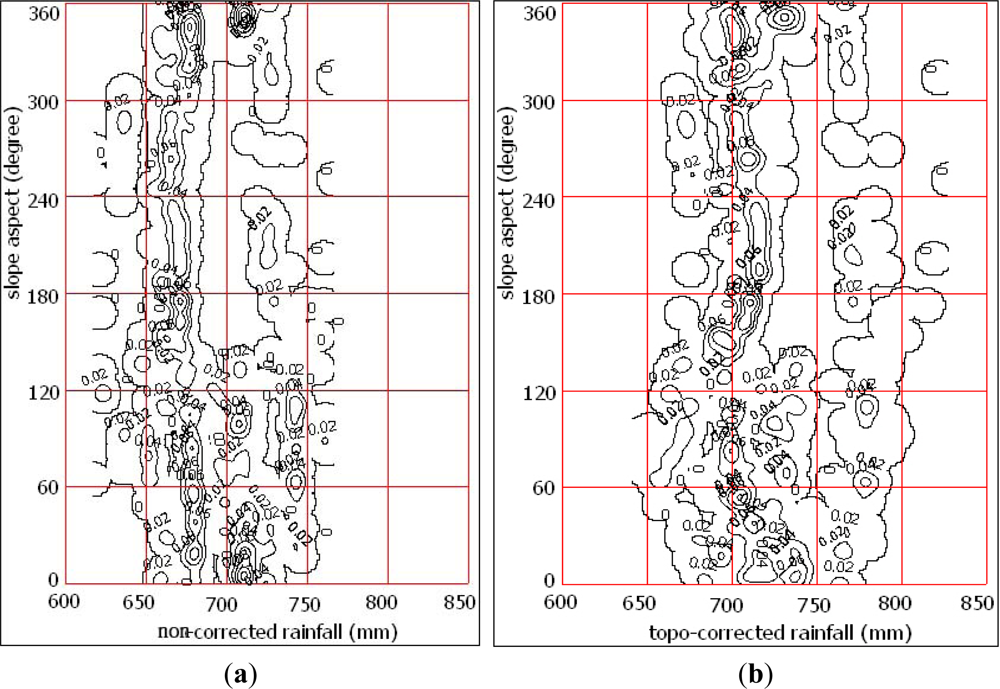
4.3. Landslide Distribution in Various Slope Aspects and Rainfall
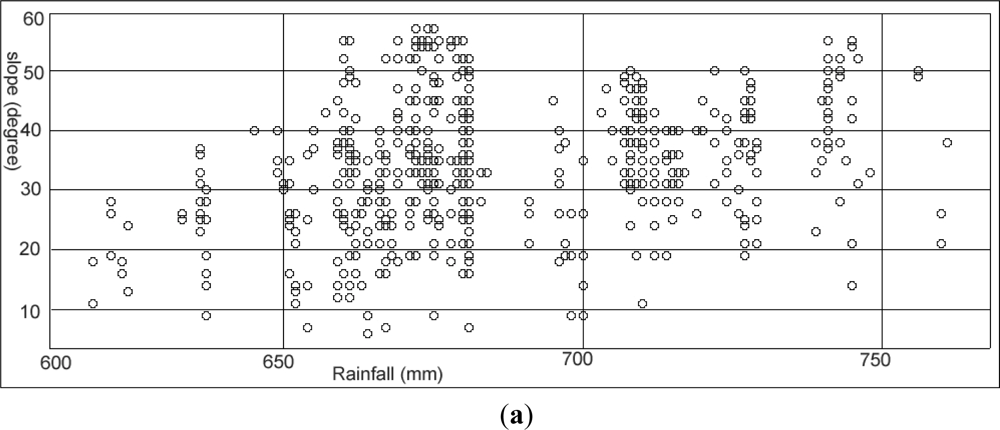
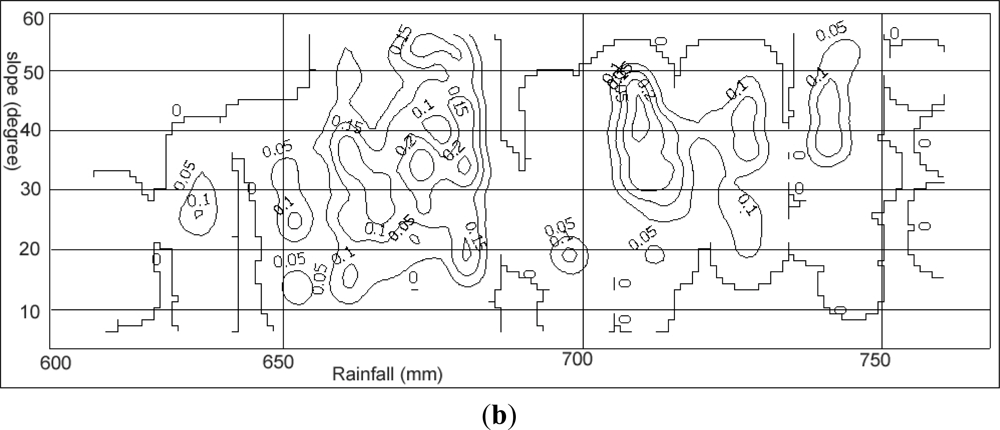
4.4. Landslide Distribution in Various Slope Angles and Rainfall
5. Conclusions and Future Work
Acknowledgments
- Conflict of InterestThe authors declare no conflict of interest.
References
- Brocca, L.; Ponziani, F.; Moramarco, T.; Melone, F.; Berni, N.; Wagner, W. Improving landslide forecasting using ASCAT-derived soil moisture data: A case study of the Torgiovannetto landslide in Central Italy. Remote Sens 2012, 4, 1232–1244. [Google Scholar]
- Holbling, D.; Fureder, P.; Antolini, F.; Cigna, C.; Casagli, N.; Lang, S. A semi-automated object-based approach for landslide detection validated by persistent scatterer interferometry measures and landslide inventories. Remote Sens 2012, 4, 1310–1336. [Google Scholar]
- Kasperski, J.; Delacourt, C.; Allemand, P.; Potherat, P.; Jaud, M.; Varrel, E. Application of a Terrestrial Laser Scanner (TLS) to the study of the Sechilienne Landslide (Isere, France). Remote Sens 2010, 2, 2785–2802. [Google Scholar]
- Othman, A.A.; Gloaguen, R. River courses affected by landslides and implications for hazard assessment: A high resolution remote sensing case study in NE Iraq–W Iran. Remote Sens 2013, 5, 1024–1044. [Google Scholar]
- Tofani, V.; Raspini, F.; Catani, F.; Casagli, N. Persistent Scatterer Interferometry (PSI) technique for landslide characterization and monitoring. Remote Sens 2013, 5, 1045–1065. [Google Scholar]
- Yonezawa, C.; Watanabe, M.; Saito, G. Polarimetric decomposition analysis of ALOS PALSAR observation data before and after a landslide event. Remote Sens 2012, 4, 2314–2328. [Google Scholar]
- De Lima, J. The effect of oblique rain on inclined surfaces: A nomograph for the rain-gauge correction factor. J. Hydrol 1990, 115, 407–412. [Google Scholar]
- Helming, K. Wind Speed Effects on Rain Erosivity. Sustaining the Global Farm: Selected Papers from the 10th International Soil Conservation Organization Meeting; Stott, D.E., Mohtar, R.H., Steinhardt, G.C., Eds.; ISCO: West Lafayette, IN, USA, 1999; pp. 771–776. [Google Scholar]
- Sharon, D. The distribution of hydrologically effective rainfall incident on sloping ground. J. Hydrol 1980, 46, 165–188. [Google Scholar]
- Schulz, W.H. Landslide Susceptibility Estimated From Mapping Using Light Detection and Ranging (LIDAR) Imagery and Historical Landslide Records; Open-File Report 2005-1405; USGS: Seattle, WA, USA, 2005. [Google Scholar]
- Schulz, W.H. Landslide susceptibility revealed by LIDAR imagery and historical records, Seattle, Washington. Eng. Geol 2007, 89, 67–87. [Google Scholar]
- Liu, J.K.; Liao, Z.Y.; Lau, C.C.; Shih, T.Y. A Study on Rainfall-Induced Landslides in Alishan Area Using Airborne Lidar and Digital Photography. Proceedings of the 28th Asian Conference on Remote Sensing, Kuala Lumpur, Malaysia, 12–16 November 2007.
- Varnes, D. J. Slope Movement Types and Processes. In Special Report 176: Landslides: Analysis and Control; Schuster, R.L., Krizek, R.J., Eds.; Transportation and Road Research Board, National Academy of Science: Washington, DC, USA, 1978; pp. 11–33. [Google Scholar]
- Assilzadeh, H.; Levy, J.K.; Wang, X. Landslide catastrophes and disaster risk reduction: A GIS framework for landslide prevention and management. Remote Sens 2010, 2, 2259–2273. [Google Scholar]
- Debella-Gilo, M.; Kääb, A. Measurement of surface displacement and deformation of mass movements using least squares matching of repeat high resolution satellite and aerial images. Remote Sens 2012, 4, 43–67. [Google Scholar]
- Metternicht, G.; Hurni, L.; Gogu, R. Remote sensing of landslides: An analysis of the potential contribution to geo-spatial systems for hazard assessment in mountainous environments. Remote Sens. Environ 2005, 98, 284–303. [Google Scholar]
- Yang, S.J.; Lin, J.J.; Cheng, C.T.; Pan, K.L.; Tsai, J.J.; Lee, C.L. Landslide Classification in Common Use in Taiwan. Proceedings of The 14th Conference On Current Researches In Geotechnical Engineering In Taiwan, Taoyuan, Taiwan, 25–6 August 2011.
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. The rainfall intensity-duration control of shallow landslides and debris flows: and update. Landslides 2008, 5, 3–17. [Google Scholar]
- Li, M.; Shao, Q.; Renzullo, L. Estimation and spatial interpolation of rainfall intensity distribution from the effective rate of precipitation. Stoch. Environ. Res. Risk Assess 2010, 24, 117–130. [Google Scholar]
- Salciarini, D.; Tamagnini, C.; Conversini, P.; Rapinesi, S. Spatially distributed rainfall thresholds for the initiation of shallow landslides. Nat. Hazards 2012, 61, 229–245. [Google Scholar]
- CWB. List of Typhoons of Which Official Warning Notices Have Been Issued; Central Weather Bureau: Taiwan. Available online: http://rdc28.cwb.gov.tw/data.php (accessed on 20 July 2008).
- Lin, J.Y. Use Radar Echoes to Analyze Three Dimensional Structure of Rainfalls. M.Sc. Thesis, Institute of Civil Engineering, National Taiwan University, Taipei, Taiwan,. 2001. [Google Scholar]
- Wu, S.H.; Lin, P.L. Seasonal Change of Rainfall Types Observed by Disdrometers. Proceedings of Taiwan Geoscience Union Conference in 2004, Longtan Aspire Learning Complex, Taoyuan, Taiwan, 17–20 May 2004.
- Gunn, R.; Kinzer, G.D. Terminal velocity of water droplets in stagnant air. J Meteorol 1949, 6, 243–248. [Google Scholar]
- Lin, L.L.; Lin, H.W. The measurement of erodibility of red soils. J Chin Soil Water Conserv 1998, 30, 41–58. [Google Scholar]
- Sheppard, B.E. Measurement of raindrop size distributions using a small Doppler radar. J Atmos. Oceanic Tech 1990, 7, 255–268. [Google Scholar]
- Lin, P.L.; Jian, C.L.; Hsu, Y.C. The rain-drop distributions of Northern Taiwan. Proceedings of Taiwan Geoscience Union conference in 2007, Longtan Aspire Learning Complex, Taoyuan, Taiwan, 15–18 May 2007.
- Su, C.L.; Chu, Y.H.; Chen, C.Y. Analyzing the relationship between terminal velocity of raindrops and VHF backscatter from precipitation. TAO 2004, 15, 629–645. [Google Scholar]
- Tokay, A.; Short, D.A. Evidence from tropical raindrop spectra of the origin of rain from stratiform versus convective clouds. J. Appl. Meteorol 1996, 35, 355–371. [Google Scholar]
- Tokay, A.; Short, D.A.; Williams, C.R.; Ecklund, W.L.; Gage, K.S. Tropical rainfall associate with convective and stratiform clouds: Intercomparison of disdrometer and profiler measurements. J. Appl. Meteorol 1999, 38, 302–320. [Google Scholar]
- Maki, M.; Keenan, T.D.; Sasaki, Y.; Nakamura, K. Characteristics of the raindrop size distribution in tropical continental squall lines observed in Darwin, Australia. J. Appl. Meteorol 2001, 40, 1939–1412. [Google Scholar]
- Wu, S.H. Use Disdrometer to Analyze Different Precipitation Type. M.Sc. Thesis, Institute of Atmospheric Physics, National Central University, Chungli, Taiwan,. 2006. [Google Scholar]
- Mao, Y.Y. The Characteristics of Drop Size Distribution of Stratiform and Convective Rains in Northern Taiwan. M.Sc. Thesis, Institute of Atmospheric Physics, National Central University, Chungli, Taiwan,. 2007. [Google Scholar]
- Arden, W.B. Medical Geography in Public Health and Tropical Medicine: Case Studies from Brazil. Ph.D. Dissertation, Louisiana State University and Agricultural and Mechanical College, Baton Rouge, LA, USA,. 2008. [Google Scholar]
- De Smith, M.J.; Goodchild, F.M.; Longley, P.A. Geospatial Analysis; The Winchelsea Press: London, UK, 2007. [Google Scholar]
- Longley, P.A.; Goodchild, F.M.; Maguire, D.J.; Rhind, D.W. Geographic Information Systems and Science; John Wiley & Sons: West Sussex, UK, 2005. [Google Scholar]
- Teo, T.A.; Chen, L.C.; Chan, A.J.; Liu, C.L. The Development of Geometric Corrections System for Multi-Satellite Imagery. Proceeding of the 30th Asian Conference on Remote Sensing, Beijing, China, 18–23 October 2009.
- Shih, H.Y.; Shih, T.Y. Error analysis of the 40m-grid DTM in the catchment of Pachang River. J. Chin. Institute Civil Hydraulic Eng 1997, 24, 46–55. [Google Scholar]



| Type of Movements | Type of Materials | |||
|---|---|---|---|---|
| Bed Rock | Engineering Soils | |||
| Debris | Soils | |||
| Falls | Rock falls | Shallow-seated slide | ||
| Topples | ||||
| Slide | Translational | Dip-slope and wedge slide | ||
| Rotational | Deep-seated slide | |||
| Flows | (not applicable) | Debris flow | (not applicable) | |
| Taken before Mindulle | Taken after Mindulle | |
|---|---|---|
| Image ID | CSR_P0000358_SP5G1J_20040115 | CSR_P0000787_SP5G1J_20041102 |
| Receiving time | 2004/01/15_02:40:31 | 2004/11/02_02:26:21 |
| Viewing incidence angle | −3.088 | −30.333551 |
| Path/Row | 299/300 | 299/301 |
| Width/Height (Km) | 121/324 | 149.5/391 |
| Lines/pixels | 32400(lines)/12100(pixels) | 39100(lines)/14950(pixels) |
| Sun Elevation | 39.607085 | 39.607085 |
| Sun Azimuth | 154.07631 | 153.53001 |
| Orientation | 12.9894 | 11.6754 |
| Class | Lower Bound (m2) | Upper Bound (m2) | By Image on 20040115 | By Image on 20041102 | ||
|---|---|---|---|---|---|---|
| Slide Number | Slide Area | Slide Number | Slide Area | |||
| 1 | 0 | 1,600 | 16 | 17,332 | 20 | 21,748 |
| 2 | 1,600 | 3,200 | 8 | 19,323 | 19 | 42,971 |
| 3 | 3,200 | 6,400 | 21 | 109,372 | 27 | 130,225 |
| 4 | 6,400 | 12,800 | 23 | 210,572 | 24 | 222,137 |
| 5 | 12,800 | 25,600 | 9 | 156,715 | 14 | 243,953 |
| 6 | 25,600 | 51,200 | 4 | 151,399 | 6 | 221,090 |
| 7 | 51,200 | 80,437 | 3 | 212,585 | 3 | 173,041 |
| Total | 84 | 877,298 | 113 | 1,055,165 | ||
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Liu, J.-K.; Shih, P.T.Y. Topographic Correction of Wind-Driven Rainfall for Landslide Analysis in Central Taiwan with Validation from Aerial and Satellite Optical Images. Remote Sens. 2013, 5, 2571-2589. https://doi.org/10.3390/rs5062571
Liu J-K, Shih PTY. Topographic Correction of Wind-Driven Rainfall for Landslide Analysis in Central Taiwan with Validation from Aerial and Satellite Optical Images. Remote Sensing. 2013; 5(6):2571-2589. https://doi.org/10.3390/rs5062571
Chicago/Turabian StyleLiu, Jin-King, and Peter T.Y. Shih. 2013. "Topographic Correction of Wind-Driven Rainfall for Landslide Analysis in Central Taiwan with Validation from Aerial and Satellite Optical Images" Remote Sensing 5, no. 6: 2571-2589. https://doi.org/10.3390/rs5062571




