Evaluating Ecohydrological Impacts of Vegetation Activities on Climatological Perspectives Using MODIS Gross Primary Productivity and Evapotranspiration Products at Korean Regional Flux Network Site
Abstract
:1. Introduction
2. Materials
2.1. Site Description
2.2. Eddy Covariance System
2.3. The Properties of the MODIS Satellite
2.4. MODIS 17 GPP/NPP Algorithm and Estimated Products
2.5. MODIS 16 Global ET Products
2.6. Estimating the WUE Based on Remote Sensing Technology
3. Results and Discussion
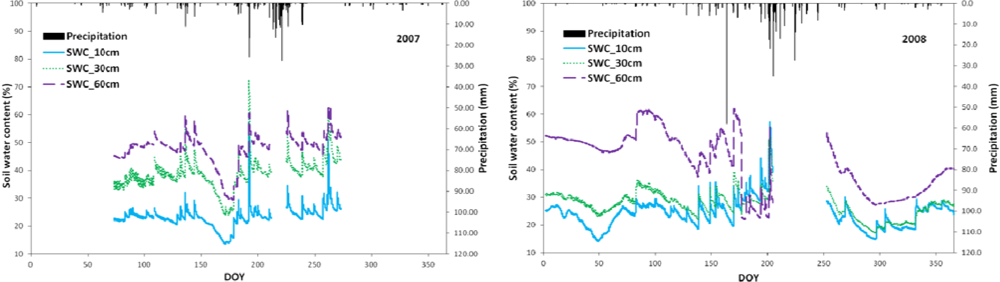
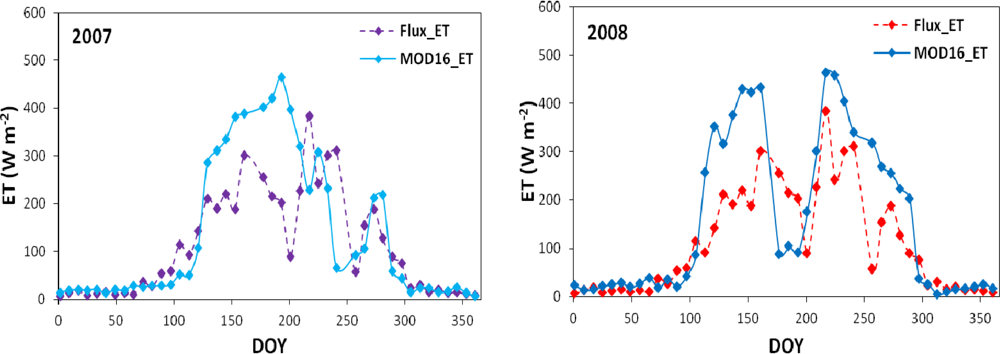
3.1. Temporal Variation of Hydrometeorological Conditions
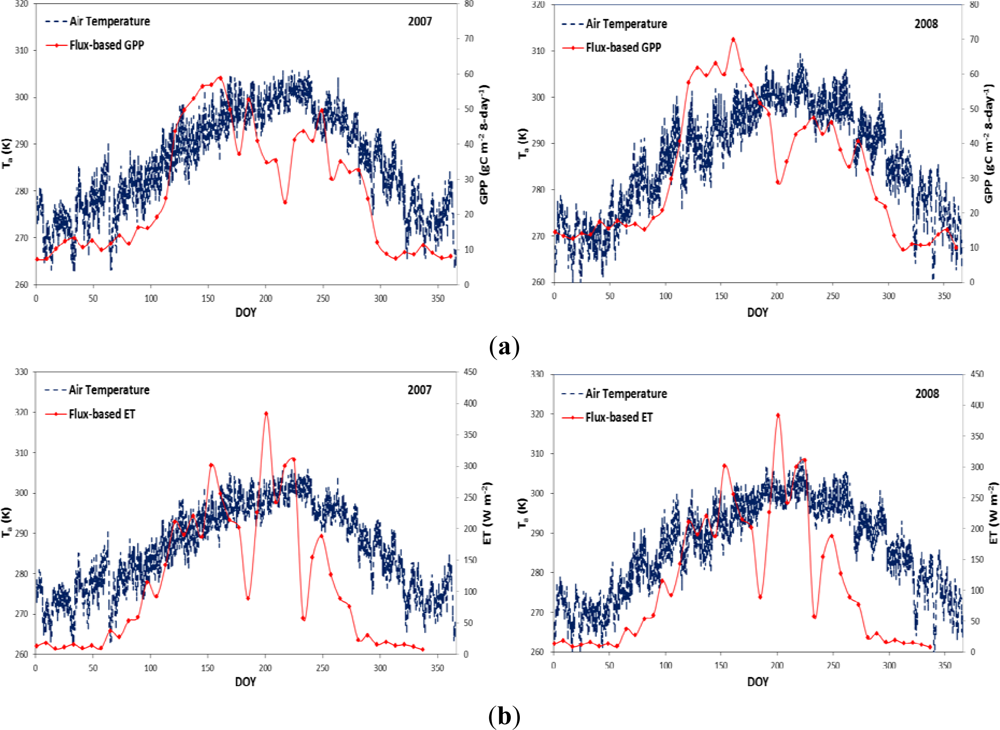
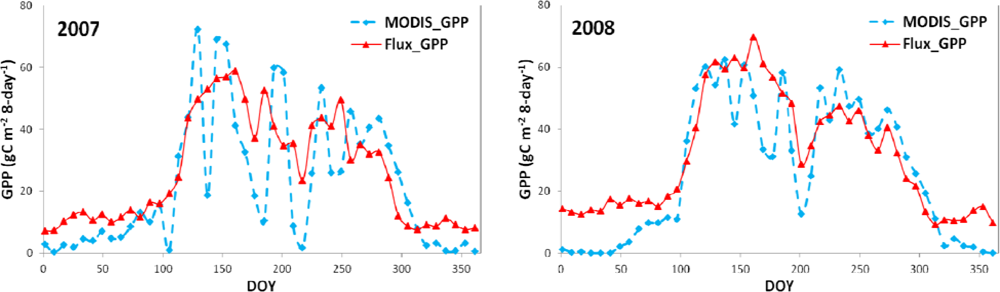
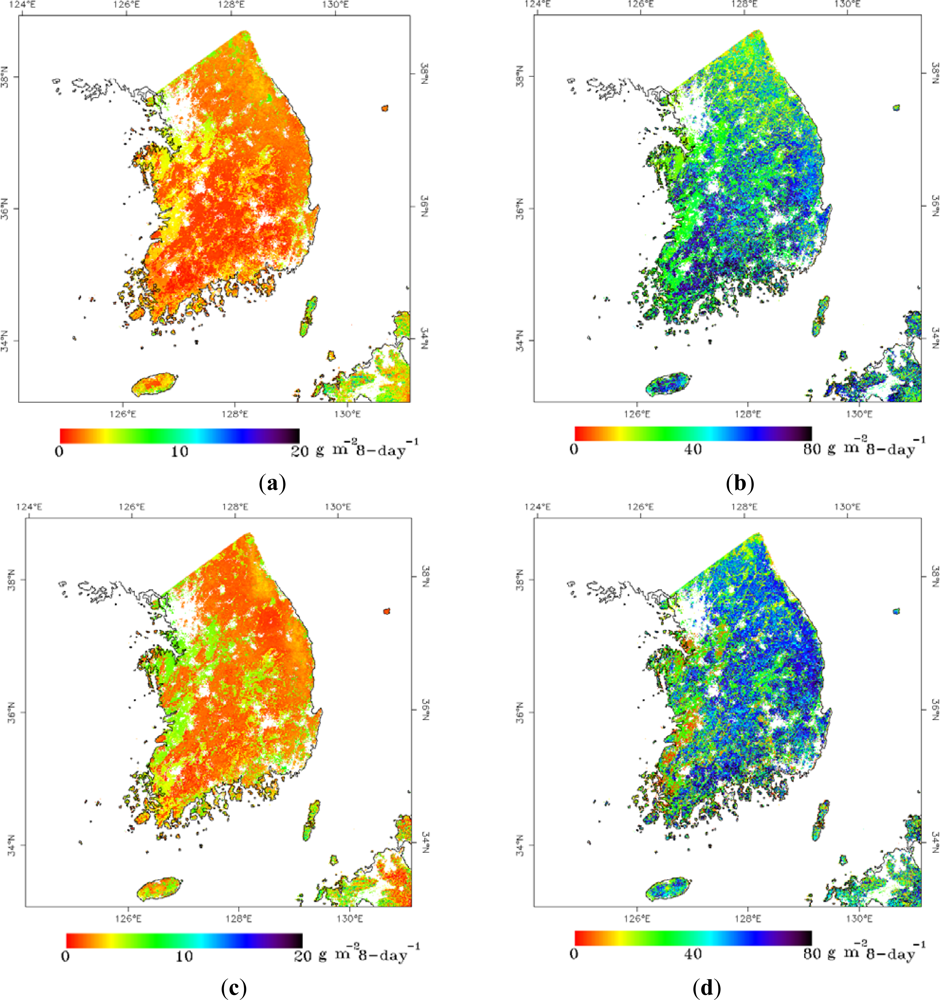
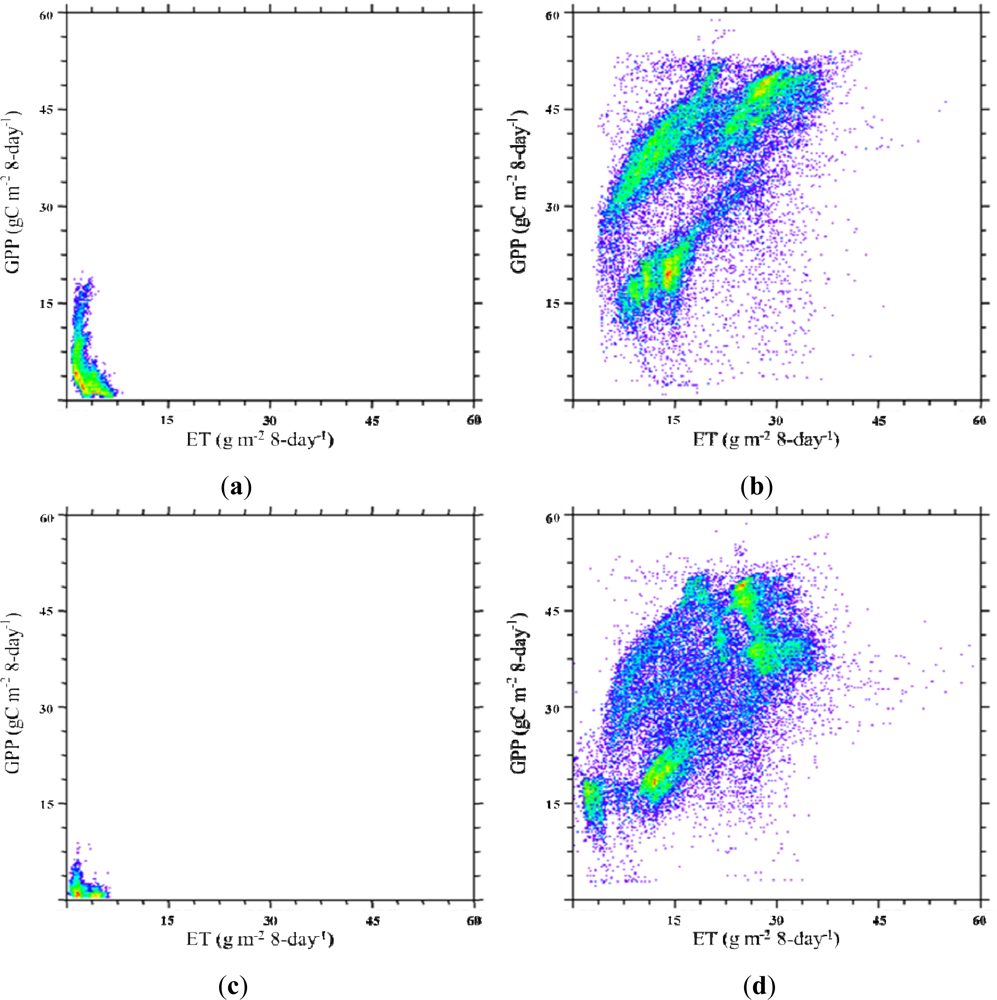
3.2. Spatio-Temporal Variation of Terrestrial Ecosystems’ GPP, ET, and WUE
4. Conclusions
- Conflict of InterestThe authors declare no conflict of interest.
References and Notes
- Nemani, R.R.; Keeling, C.D.; Hashimoto, H.; Jolly, W.M.; Piper, S.C.; Tucker, C.J.; Myneni, R.B.; Running, S.W. Climate-Driven increases in global terrestrial net primary production from 1982 to 1999. Science 2003, 300, 1560–1563. [Google Scholar]
- Cook, B.D.; Davis, K.J.; Wang, W.; Desai, A.R.; Berger, B.W.; Teclaw, R.M.; Martin, J.G.; Bolstad, P.V.; Bakwin, P.S.; Yi, C.; Heilman, W. Carbon exchange and venting anomalies in an upland deciduous forest in northern Wisconsin, USA. Agr. For. Meteorol. 2004, 126, 271–295. [Google Scholar]
- Goodale, C.L.; Apps, M.J.; Birdsey, R.A.; Field, C.B.; Heath, L.S.; Houghton, R.A.; Jenkins, J.C.; Kohlmaier, G.H.; Kurz, W.; Liu, S.; Nabuurs, G.-J.; Nilsson, S.; Shvidenko, A.Z. Forest carbon sinks in the northern hemisphere. Ecol. Appl. 2002, 12, 891–899. [Google Scholar]
- McCaughey, J.H.; Pejam, M.R.; Arain, M.A.; Cameron, D.A. Carbon dioxide and energy fluxes from a boreal mixedwood forest ecosystems in Ontario, Canada. Agr. For. Meteorol. 2006, 140, 79–96. [Google Scholar]
- Cox, P.M.; Betts, R.A.; Jones, C.D.; Spall, S.A.; Totterdell, I.J. Acceleration of global warming due to carbon-cycle feedbacks in a coupled climate model. Nature 2000, 408, 184–187. [Google Scholar]
- Matsushita, B.; Tamura, M. Integrating remotely sensed data with an ecosystem model to estimate net primary productivity in East Asia. Remote Sens. Environ. 2002, 81, 58–66. [Google Scholar]
- Climate Change 2007: Synthesis Report. Contribution of Working Groups Groups I, II and III to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; IPCC: Geneva, Switzerland, 2007.
- Churkina, G.; Running, S.W.; Schloss, A.L. Comparing global models of terrestrial net primary productivity (NPP): The importance of water availability. Glob. Change Biol. 2000, 5, 46–55. [Google Scholar]
- Morisette, J.T.; Heinsch, F.A.; Running, S.W. Monitoring global vegetation using moderate-resolution satellites. Eos Trans. AGU 2006, 87, 214–231. [Google Scholar]
- Running, S.W.; Thornton, P.E.; Nemani, R.; Glassy, J. Global Terrestrial Gross and Net Primary Productivity from the Earth Observing System. In Methods in Ecosystem Science; Sala, O.E., Jackson, R.B., Eds.; Springer-Verlag: New York, NY, USA, 2000; pp. 44–57. [Google Scholar]
- Yuan, W.; Liu, S.; Yu, G.; Bonnefond, J.-M.; Chen, J.; Davis, K.; Desai, A.R.; Goldstein, A.H.; Gianelle, D.; Rossi, F.; et al. Global estimates of evapotranspiration and gross primary production based on MODIS and global meteorology data. Remote Sens. Environ. 2010, 114, 1416–1431. [Google Scholar]
- Polley, H.W.; Phillips, R.L.; Frank, A.B.; Bradford, J.A.; Sims, P.L.; Morgan, J.A.; Kiniry, J.R. Variability in light-use efficiency for Gross Primary Productivity on great plains grasslands. Ecosystems 2011, 14, 15–27. [Google Scholar]
- Tum, M.; Gunther, K.P. Validating modelled NPP using statistical yield data. Biomass Bioenerg. 2011, 35, 4665–4674. [Google Scholar]
- Webb, W.; Szarek, S.; Lauenroth, W.K.; Kinerson, R.; Smith, M. Primary productivity and water use in native forest, grassland, and desert ecosystems. Ecology 1978, 59, 1239–1247. [Google Scholar]
- Cao, M.; Prince, S.D.; Small, J.; Goetz, S.J. Remotely sensed interannual variations and trends in terrestrial net primary productivity 1981–2000. Ecosystems 2004, 7, 233–242. [Google Scholar]
- Singh, R.P.; Rovshan, S.; Goroshi, S.K.; Panigrahy, S.; Parihar, J.S. Spatial and temporal variability of Net Primary Productivity (NPP) over terrestrial biosphere of India using NOAA-AVHRR Based GloPEM Model. J. Indian Soc. Remote Sens. 2011, 39, 345–353. [Google Scholar]
- Xiao, X.; Hollinger, D.; Aber, J.; Goltz, M.; Davidson, E.A.; Zhang, Q.; Moore, B. Satellite-Based modeling of gross primary production in an evergreen needleleaf forest. Remote Sens. Environ. 2004, 89, 519–534. [Google Scholar]
- Yu, G.; Song, X.; Wang, Q.; Liu, Y.; Guan, D.; Yan, J.; Sun, X.; Zhang, L.; Wen, X. Water-Use efficiency of forest ecosystems in eastern China and its relations to climatic variables. New Phytol. 2008, 177, 927–937. [Google Scholar]
- Tian, H.; Chen, G.; Liu, M.; Zhang, C.; Sun, G.; Lu, C.; Xu, X.; Ren, W.; Pan, S.; Chappelka, A. Model estimates of net primary productivity, evapotranspiration, and water use efficiency in the terrestrial ecosystems of the southern United States during 1895–2007. Forest Ecol. Manage. 2010, 259, 1311–1327. [Google Scholar]
- Allen, L.H., Jr; Kakani, V.G.; Vu, J.C.V.; Boote, K.J. Elevated CO2 increase water use efficiency by sustaining photosynthesis of water-limited maize and sorghum. J. Plant Physiol. 2011, 168, 1909–1918. [Google Scholar]
- Jassal, R.S.; Black, T.A.; Spittlehouse, D.L.; Brummer, C.; Nesic, Z. Evapotranspiration and water use efficiency in different-aged Pacific Northwest Douglas-fir stands. Agr. For. Meteorol. 2009, 149, 1168–1178. [Google Scholar]
- Hwang, T.; Kang, S.; Kim, J.; Kim, Y.; Lee, D.; Band, L. Evaluating drought effect on MODIS Gross Primary Production (GPP) with an eco-hydrological model in the mountainous forest, East Asia. Glob. Change Biol. 2008, 14, 1037–1056. [Google Scholar]
- Law, B.; Falge, E.; Gu, L.; Baldocchi, D.D.; Bakwin, P.; Berbigier, P.; Davis, K.; Dolman, A.J.; Falk, M.; Fuentes, J.D.; et al. Environmental controls over carbon dioxide and water vapor exchange of terrestrial vegetation. Agr. For. Meteorol. 2002, 113, 97–120. [Google Scholar]
- Sakamoto, T.; Gitelson, A.A.; Wardlow, B.D.; Verma, S.B.; Suyker, A.E. Estimating daily gross primary production of maize based only on MODIS WDRVI and shortwave radiation data. Remote Sens. Environ. 2011, 115, 3091–3101. [Google Scholar]
- Jongen, M.; Pereira, J.S.; Aires, L.M.I.; Pio, C.A. The effects of drought and timing of precipitation on the inter-annual variation in ecosystem-atmosphere exchange in a Mediterranean grassland. Agr. For. Meteorol. 2011, 151, 595–606. [Google Scholar]
- Ponton, S.; Flanagan, F.B.; Alstad, K.P.; Johnson, B.G.; Morgenstern, K.; Kljun, N.; Black, T.A.; Barr, A.G. Comparison of ecosystem water use efficiency among Douglas-fir forest, aspen forest and grassland using eddy covariance and carbon isotope techniques. Glob. Change Biol. 2006, 12, 294–310. [Google Scholar]
- Drolet, G.G.; Middleton, E.M.; Huemmrich, K.F.; Hall, F.G.; Amiro, B.D.; Barr, A.G.; Black, T.A.; McCaughey, J.H.; Margolis, H.A. Regional mapping of gross light-use efficiency using MODIS spectral indices. Remote Sens. Environ. 2008, 112, 3064–3078. [Google Scholar]
- Zhao, M.; Heinsch, F.A.; Nemani, R.R.; Running, S.W. Improvements of the MODIS terrestrial gross and net primary production global data set. Remote Sens. Environ. 2005, 95, 164–176. [Google Scholar]
- Cleugh, H.A.; Leuning, R.; Mu, Q.; Running, S.W. Regional evaporation estimates from flux tower and MODIS satellite data. Remote Sens. Environ. 2007, 106, 285–304. [Google Scholar]
- Mu, Q.; Heinsch, F.A.; Zhao, M.; Running, S.W. Development of a global evapotranspiration algorithm based on MODIS and global meteorology data. Remote Sens. Environ. 2007, 111, 519–536. [Google Scholar]
- Lim, J.-H.; Shin, J.H.; Jin, G.Z.; Chun, J.H.; Oh, J.S. Forest stand structure, site characteristics and carbon budget of the Kwangneung Natural Forest in Korea (in Korean). Korean J. Agr. Forest Meteorol. 2003, 5, 101–109. [Google Scholar]
- Ryu, Y.; Kang, S.; Moon, S.-K.; Kim, J. Evaluation of land surface radiation balance derived from moderate resolution imaging spectroradiometer (MODIS) over complex terrain and heterogeneous landscape on clear sky days. Agr. For. Meteorol. 2008, 148, 1538–1552. [Google Scholar]
- Kim, J.; Lee, D.; Hong, J.; Kang, S.; Kim, S.-J.; Moon, S.-K.; Lim, J.-H.; Son, Y.; Lee, J.; Kim, S. HydroKorea and CarboKorea: Cross-scale studies of ecohydrology and biogeochemistry in a heterogeneous and complex forest catchment of Korea. Ecol. Res. 2006, 21, 881–889. [Google Scholar]
- Heinsch, F.A.; Reeves, M.; Bowker, C.F.; Votava, P.; Kang, S.; Milesi, C.; Zhao, M.; Glassy, J.; Jolly, W.M.; Kimball, J.S.; et al. User’s Guide: GPP and NPP (MOD17A2/A3) Products. NASA MODIS Land Algorithm.. 2003. Available online: http://www.ntsg.umt.edu/sites/ntsg.umt.edu/files/modis/MOD17UsersGuide.pdf (accessed on 4 November 2012).
- Monteith, J.L. Evaporation and environment. Symp. Soc. Exp. Biol. 1965, 19, 205–234. [Google Scholar]
- Friedl, M.; McIver, D.; Hodges, J.; Zhang, X.; Muchoney, D.; Strahler, A.; Woodcock, C.; Gopal, S.; Schneider, A.; Cooper, A. Global land cover mapping from MODIS: Algorithms and early results. Remote Sens. Environ. 2002, 83, 287–302. [Google Scholar]
- Huete, A.R.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar]
- Huete, A.R.; Didan, K.; Shimabukuro, Y.E.; Ratana, P.; Saleska, S.R.; Hutyra, L.R.; Yang, W.; Nemani, R.R.; Myneni, R. Amazon rainforests green-up with sunlight in dry season. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Myneni, R.B.; Hoffman, S.; Knyazikhin, Y.; Privette, J.L.; Glassy, J.; Tian, Y.; Wang, Y.; Song, X.; Zhang, Y.; Smith, G.R.; et al. Global products of vegetation leaf area and fraction absorbed PAR from year one of MODIS data. Remote Sens. Environ. 2002, 83, 214–231. [Google Scholar]
- Jin, Y.; Schaaf, C.B.; Gao, F.; Li, X.; Strahler, A.H.; Lucht, W.; Liang, S. Consistency of MODIS surface bidirectional reflectance distribution function and albedo retrievals: 1. Algorithm performance. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Lucht, W.; Schaaf, C.B.; Strahler, A.H. An Algorithm for the retrieval of albedo from space using semiempirical BRDF models. IEEE Trans. Geosci. Remote Sens. 2000, 38, 977–998. [Google Scholar]
- Salomon, J.; Schaaf, C.B.; Strahler, A.H.; Gao, F.; Jin, Y. Validation of the MODIS bidirectional reflectance distribution function and albedo retrievals using combined observations from the aqua and terra platforms. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1555–1565. [Google Scholar]
- Schaaf, C.B.; Gao, F.; Strahler, A.H.; Lucht, W.; Li, X.; Tsang, T.; Strugnell, N.C.; Zhang, X.; Jin, Y.; Muller, J.-P; et al. First operational BRDF, Albedo and Nadir Reflectance Products from MODIS. Remote Sens. Environ. 2002, 83, 135–148. [Google Scholar]
- Bai, Y.; Wu, J.; Qi, X.; Pan, Q.; Huang, J.; Yang, D.; Han, X. Primary production and rain use efficiency across a precipitation gradient on the Mongolia plateau. Ecology 2008, 89, 2140–2153. [Google Scholar]
- Huxman, T.E.; Smith, M.D.; Fay, P.A.; Knapp, A.K.; Shaw, M.R.; Loik, M.E.; Smith, S.D.; Tissue, D.T.; Zak, J.C.; Weltzin, J.F.; et al. Convergence across biomes to a common rain use efficiency. Nature 2004, 429, 651–654. [Google Scholar]
- Kang, S.; Kim, Y.; Kim, Y. Errors of MODIS product of Gross Primary Productivity by using Data Assimilation Office Meteorological data (in Korean). Korean J. Agr. Forest Meteorol. 2005, 7, 171–183. [Google Scholar]
- Kim, Y.; Kang, S.; Kim, J. Enhancing the reliability of MODIS Gross Primary Productivity (GPP) by improving input data (in Korean). Korean J. Agr. Forest Meteorol. 2007, 9, 132–139. [Google Scholar]
- Lee, H.W.; Kim, E.J.; Park, S.S.; Choi, J.H. Effects of climate change on the thermal structure of lakes in the Asian Monsoon Area. Climatic Change 2012, 112, 859–880. [Google Scholar]
- Zhang, Z.; Xu, C.-Y.; El-Tahir, M.E.H.; Cao, J.; Singh, V.P. Spatial and temporal variation of precipitation in Sudan and their possible cause during 1948–2005. Stoch. Environ. Res. Risk Assess. 2012, 26, 429–441. [Google Scholar]
- Kim, H.W.; Hwang, K.; Mu, Q.; Lee, S.O.; Choi, M. Validation of MODIS 16 global terrestrial evapotranspiration products in various climates and land cover types in Asia. KSCE J. Civil Eng. 2012, 16, 229–238. [Google Scholar]
- Monteith, J.L. Principles of Environmental Physics, 1st ed.; Edward Arnold: London, UK, 1973. [Google Scholar]
- Moon, B.-K.; Hong, J.; Lee, B.-R.; Yun, J.I.; Park, E.W.; Kim, J. CO2 and Energy Exchange in a Rice Paddy for the Growing season of 2002 in Hari, Korea. Korean J. Agr. Forest Meteorol. 2003, 5, 51–60. [Google Scholar]
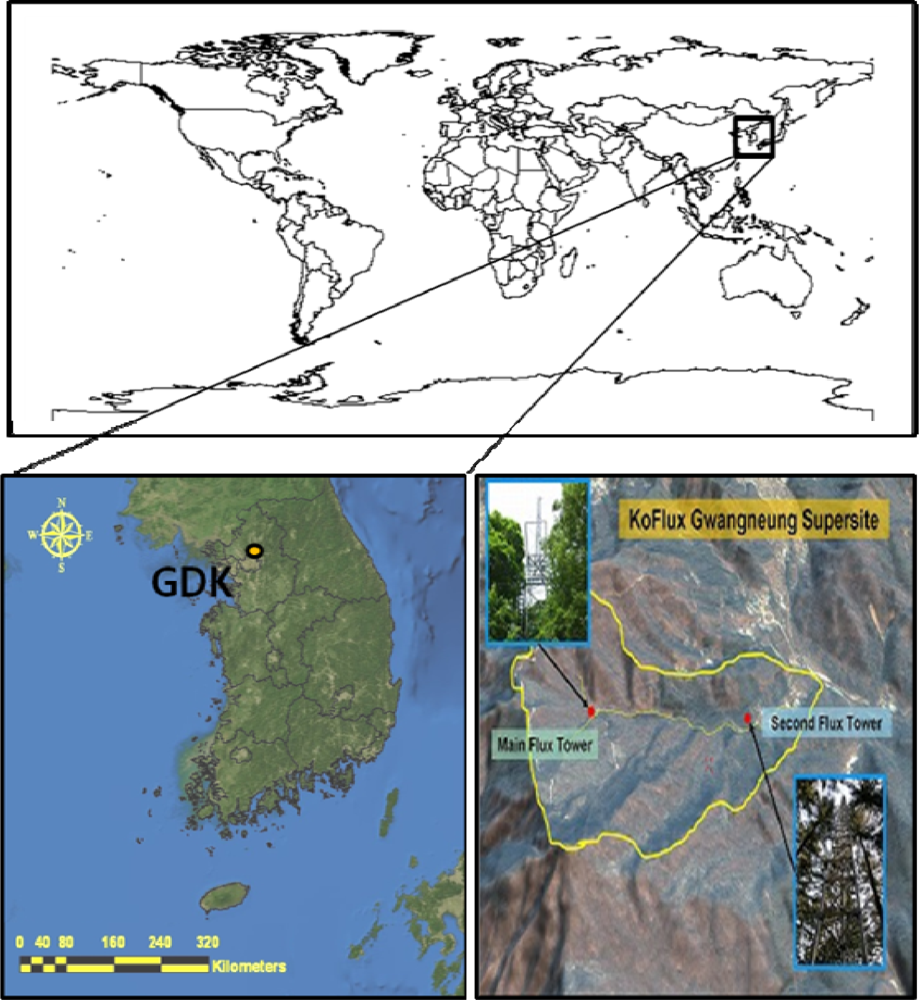





| Properties | KoFlux Gwangneung Supersite (GDK) |
|---|---|
| Latitude | 37.75°N |
| Longitude | 127.15°E |
| Elevation | 340 m |
| Slope | 10–20° |
| Land cover | Mixed forests |
| Soil texture | Sandy loam |
| Predominant species | Quercus sp., Carpinus sp. (80–200 years old) |
| Depth of soil moisture | 10, 30, 60 cm |
| Canopy height | 18 m |
| Maximum Leaf Area Index (LAI) | 6 |
| Mean annual temperature | 11.5 °C |
| Mean annual precipitation | 1,365 mm |
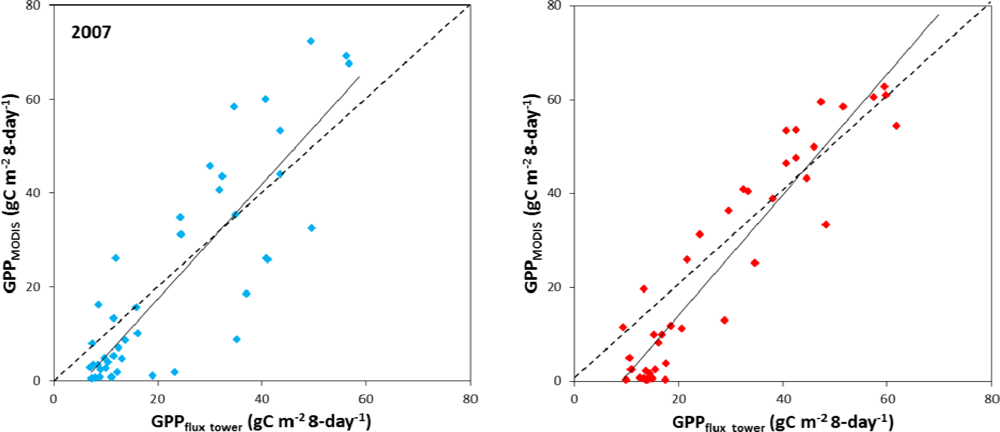
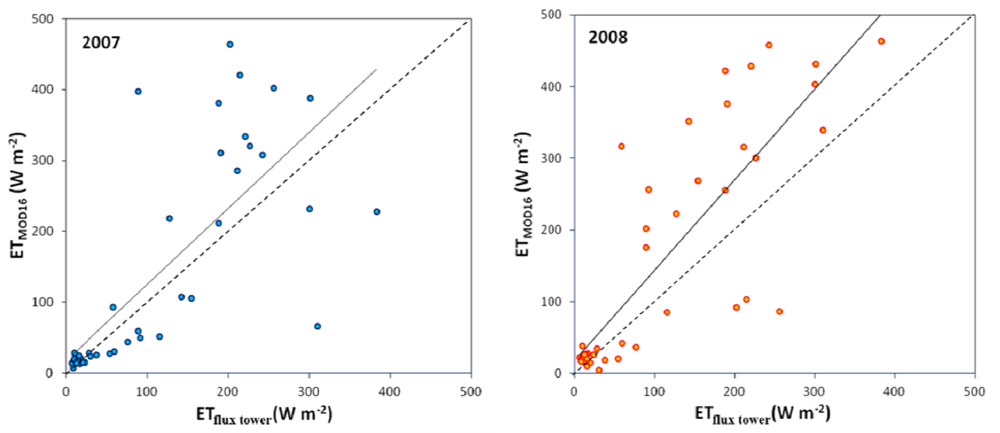
| GDK | Average | Bias | RMSE | Regression Slope | Correlation Coefficient (R) | |
|---|---|---|---|---|---|---|
| GPP (gC·m−2·8-day−1) | 2007 | 21.70 | 2.94 | 14.12 | 1.22 | 0.85 |
| 2008 | 24.63 | 3.63 | 9.64 | 1.28 | 0.94 | |
| ET (g·m−2·8-day −1) | 2007 | 13.85 | 2.52 | 9.84 | 1.07 | 0.76 |
| 2008 | 15.84 | 4.70 | 10.41 | 1.26 | 0.83 | |
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Sur, C.; Choi, M. Evaluating Ecohydrological Impacts of Vegetation Activities on Climatological Perspectives Using MODIS Gross Primary Productivity and Evapotranspiration Products at Korean Regional Flux Network Site. Remote Sens. 2013, 5, 2534-2553. https://doi.org/10.3390/rs5052534
Sur C, Choi M. Evaluating Ecohydrological Impacts of Vegetation Activities on Climatological Perspectives Using MODIS Gross Primary Productivity and Evapotranspiration Products at Korean Regional Flux Network Site. Remote Sensing. 2013; 5(5):2534-2553. https://doi.org/10.3390/rs5052534
Chicago/Turabian StyleSur, Chanyang, and Minha Choi. 2013. "Evaluating Ecohydrological Impacts of Vegetation Activities on Climatological Perspectives Using MODIS Gross Primary Productivity and Evapotranspiration Products at Korean Regional Flux Network Site" Remote Sensing 5, no. 5: 2534-2553. https://doi.org/10.3390/rs5052534




