Geometric Accuracy Investigations of SEVIRI High Resolution Visible (HRV) Level 1.5 Imagery
Abstract
:1. Introduction
1.1. Motivation and Background
- (a)
- Investigation of the relative geometric accuracy within one image, between different channels, and for multi-temporal imagery;
- (b)
- Investigation of the absolute geometric accuracy using reference data;
- (c)
- Investigation of the temporal stability of the absolute as well as the relative geometric accuracy (e.g., from different orbital overpasses, in case of satellite maneuvers, etc.);
- (d)
- First analysis of the impact of geometric errors on the derivation of climate parameters.
1.2. MSG-SEVIRI
2. Data and Methodology
2.1. Data and Software
2.2. Relative Accuracy Evaluation
2.3. Absolute Accuracy Evaluation
- 39 large lakes (except the Garda Lake) in and around Switzerland are digitized manually and saved as vector polygons in Swiss Coordinate System.
- The Garda Lake in Italy is digitized manually on the Landsat 5 orthophoto of USGS and transformed into the Swiss Coordinate System.
- All 40 lakes are first transformed from the Swiss Coordinate System into the GEOS, and then into the HRV image space.
- A cartographic generalization is applied to all lakes to reduce the level of detail of the polygons by removing dense vertices (e.g., forming edges with a length of less than 0.1 pixel).
- After a visual inspection and initial tests for matching, small lakes, which cover an area of smaller than 7 pixels, are removed from the evaluation. The remaining 20 lakes are used for the investigations.
3. Results and Discussion
3.1. Relative Accuracy Investigations
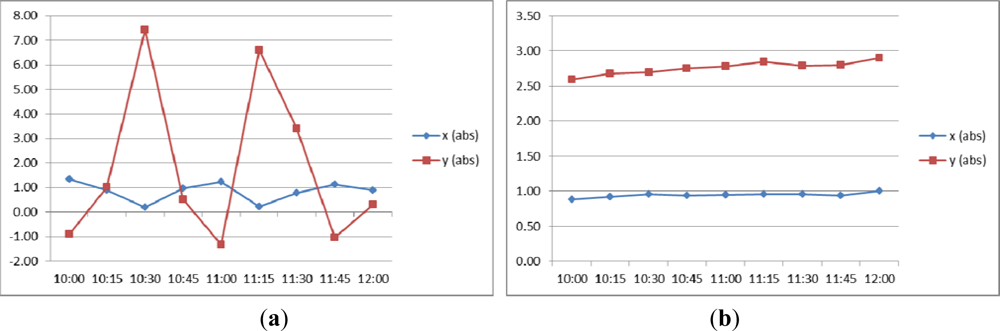
3.2. Absolute Accuracy Investigations
4. Conclusions and Future Work
- The large shifts observed on the Meteosat-8 data shall be analyzed in more detail, and in coordination with EUMETSAT, to detect potential error sources of the problems (e.g., instrument moves, etc.).
- Band-to-band registration accuracy between the HRV channel and a number of MS channels of SEVIRI, which are relevant to the climate variable estimations, shall be investigated.
- Similar investigations will be performed with the data of two other satellite sensors, i.e., MODIS and AVHRR.
Acknowledgments
- Conflict of InterestThe author declares no conflict of interest.
References and Notes
- GCOS. Available online: http://www.wmo.int/pages/prog/gcos/ (accessed on 09 March 2013).
- Seiz, G.; Foppa, N.; Meier, M.; Paul, F. The role of satellite data within GCOS Switzerland. Remote Sens 2011, 3, 767–780. [Google Scholar]
- Swiss GCOS Office. GCOS Satellite Component. Available online: http://www.meteoschweiz.admin.ch/web/en/meteoswiss/international_affairs/gcos/Satellites.html (accessed on 10 March 2013).
- WMO. Systematic Observation Requirements for Satellite-Based Products for Climate. Supplemental Details to the Satellite-Based Component of the Implementation Plan for the Global Observing System for Climate in Support of the UNFCCC (Update); GCOS-154; WMO: Geneva, Switzerland, 2011. [Google Scholar]
- Arnold, G.T; Hubanks, P.A.; Platnick, S.; King, M.D.; Bennartz, R. Impact of Aqua Misregistration on MYD06 Cloud Retrieval Properties. Presented at MODIS Science Team Meeting, Washington, DC, USA, 26–28 January 2010; Available online: http://modis.gsfc.nasa.gov/sci_team/meetings/201001/presentations/posters/atmos/arnold.pdf (accessed on 10 May 2013).
- Hanson, C.G.; Mueller, J.; Pili, P.; Aminou, D.M.A.; Jacquet, B.; Bianchi, S.; Coste, P.; Faure, F. Meteosat Second Generation: SEVIRI Imaging Performance Results From The MSG-1 Commissioning Phase. In Proceedings of The 2003 EUMETSAT Meteorological Satellite Conference, Weimar, Germany, 29 September–3 October 2003.
- Hanson, C.; Mueller, J. Status of the SEVIRI Level 1.5 Data. In Proceedings of the Second MSG RAO Workshop (ESA SP-582, November 2004), Salzburg, Austria, 9–10 September 2004; Available online: http://earth.esa.int/workshops/msg_rao_2004/papers/4_hanson.pdf (last accessed on 20 March 2013).
- Gieske, A.S.M.; Hendrikse, J.H.M.; Retsios, V.; van Leeuwen, B.; Maathuis, B.H.P.; Romaguera, M.; Sobrino, J.A.; Timmermans, W.J.; et al. Processing of MSG-1 SEVIRI Data in the Thermal Infrared-Algorithm Development with the Use of the SPARC2004 Data Set. In Proceedings of the ESA WPP-250 SPARC Final Workshop, Enschede, The Netherlands, 4–5 July 2005.
- Dürr, B.; Zelenka, A. Deriving surface global irradiance over the Alpine region from Meteosat Second Generation by supplementing the HELIOSAT method. Int. J. Remote Sens 2009, 30, 5821–5841. [Google Scholar]
- Deneke, H.M.; Roebeling, R. A. Downscaling of METEOSAT SEVIRI 0.6 and 0.8 μm channel radiances utilizing the high-resolution visible channel. Atmos. Chem. Phys 2010, 10, 9761–9772. [Google Scholar]
- Aminou, D.M.A.; Luhmann, H.J.; Hanson, C.; Pili, P.; Jacquet, B.; Bianchi, S.; Coste, P.; Pasternak, F.; et al. Meteosat Second Generation: A Comparison of On-Ground and On-Flight Imaging and Radiometric Performances of SEVIRI on MSG-1. In Proceedings of the 2003 EUMETSAT Meteorological Satellite Conference, Weimar, Germany, 29 September–3 October 2003.
- EUMETSAT. MSG Level 1.5 Image Data Format Description. Available online: http://www.eumetsat.int/groups/ops/documents/document/pdf_ten_05105_msg_img_data.pdf (accessed on 14 March 2013).
- Just, D. SEVIRI Level 1.5 Data. In Proceedings of the First MSG RAO Workshop (ESA SP-452, October 2000), Bologna, Italy, 17–19 May 2000.
- EUMETSAT. Typical Geometrical Accuracy for MSG-1/2. EUMETSAT Report EUM/OPS/TEN/07/0313 v1;. 26 February 2007. Available online: http://www.eumetsat.int/groups/ops/documents/document/pdf_typ_geomet_acc_msg-1-2.pdf. (Accessed on 08 March 2013).
- EUMETSAT. Central Operations Report: January to June 2008. EUMETSAT Report EUM/OPS/VWG/08/2808 v1B;. 9 September 2008. Available online: http://www3.eumetsat.int/website/home/Data/ServiceStatus/CentralOperationsReports/index.html (accessed on 16 May 2013).
- EUMETSAT. Central Operations Report: July to December 2008. EUMETSAT Report UM/OPS/VWG/09/0389 v1D. 3 March 2009. Available online: http://www3.eumetsat.int/website/home/Data/ServiceStatus/CentralOperationsReports/index.html (accessed on 16 May 2013).
- Python. Python Programming Language. Available online: http://www.python.org/ (accessed on 11 March 2013).
- OpenCV. Available online: http://opencv.willowgarage.com/wiki/ (accessed on 15 February 2013).
- Shi, J.; Tomasi, C. Good Features to Track. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 21–23 June 1994; pp. 593–600.
- Lucas, B.; Kanade, T. An Iterative Image Registration Technique with an Application to Stereo Vision. In Proceedings of 7th International Joint Conference on Artificial Intelligence (IJCAI), Vancouver, BC, Canada, 24–28 August 1981.
- Wessel, P.; Smith, W.H.F. A global, self-consistent, hierarchical, high-resolution shoreline database. J. Geophys. Res 1996, 101, 8741–8743. [Google Scholar]
- Swisstopo. Landsat Mosaic. Available online: http://www.swisstopo.admin.ch/internet/swisstopo/en/home/products/images/ortho/landsat.html (accessed on 18 February 2013).
- Global Land Survey (GLS). USGS. Available online: http://eros.usgs.gov/#/Find_Data/Products_and_Data_Available/GLS (accessed on 19 February 2013).
- Coordination Group for Meteorological Satellites (CGMS). LRIT/HRIT Global Specification. CGMS 03;. 12 August 1999, pp. 20–25. Available online: http://www.eumetsat.int/groups/cps/documents/document/pdf_cgms_03.pdf (accessed on 14 March 2013).
- EUMETSAT. Navigation Software for Meteosat-9 (MSG)-Level 1.5 VIS/IR/HRV Data. Available online: http://www.eumetsat.int/Home/Main/DataAccess/SupportSoftwareTools/index.htm (accessed on 19 February 2013).
- Median Absolute Deviation. Wikipedia. Available online: http://en.wikipedia.org/wiki/Median_absolute_deviation (accessed on 15 March 2013).
Appendix







| Channel ID | Absorption Band/Channel Type | Spectral Bandwidth (m) | Spectral Bandwidth As % of energy actually detected within spectral band |
|---|---|---|---|
| HRV | Visible/High Resolution | 0.6 to 0.9 | Precise spectral characteristics not critical |
| VIS 0.6 | VNIR/Core Imager | 0.56 to 0.71 | 98.0 % |
| VIS 0.8 | VNIR/Core Imager | 0.74 to 0.88 | 99.0 % |
| IR 1.6 | VNIR/Core Imager | 1.50 to 1.78 | 99.0 % |
| IR 3.9 | IR/Window Core Imager | 3.48 to 4.36 | 98.6 % (1) |
| IR 6.2 | Water Vapour/Core Imager | 5.35 to 7.15 | 99.0 % |
| IR 7.3 | Water Vapour/Pseudo-Sounding | 6.85 to 7.85 | 98.0 % |
| IR 8.7 | IR/Window Core Imager | 8.30 to 9.10 | 98.0 % |
| IR 9.7 | IR/Ozone Pseudo-Sounding | 9.38 to 9.94 | 99.0 % |
| IR 10.8 | IR/Window Core Imager | 9.80 to 11.80 | 98.0 % |
| IR 12.0 | IR/Window Core Imager | 11.00 to 13.00 | 98.0 % |
| IR 13.4 | IR/Carbon Dioxide | 12.40 to 14.40 | 96.0 % |
| Pseudo-Sounding |
| Geometric Quality Criterion | Specification (km SSP/Pixel Size at SSP) | Meteosat-8/9 Performance (km) |
|---|---|---|
| Absolute accuracy | <3.0 (3 pixels for HRV) | 1.2 |
| Relative accuracy between two consecutive images | <1.2 (3 pixels for HRV) | 0.3 |
| Relative accuracy within an image (over 500 samples) | <3.0 (3 pixels for HRV) | 1.2 |
| Mean (x) | Mean (y) | Mean (xy) | MED (x) | MED (y) | σ (x) | σ (y) | MAD (x) | MAD (y) | |
|---|---|---|---|---|---|---|---|---|---|
| Min | −0.86 | −8.11 | 0.01 | −0.91 | −8.11 | 0.03 | 0.03 | 0.02 | 0.02 |
| Max | 1.01 | 6.90 | 8.15 | 0.99 | 6.92 | 0.27 | 0.22 | 0.13 | 0.13 |
| Mean | −0.02 | 0.01 | 0.46 | −0.03 | 0.01 | 0.09 | 0.11 | 0.05 | 0.07 |
| Shift x (pixel) | Shift y (pixel) | Shift xy (pixel) | |
|---|---|---|---|
| Min/Max | 0.3/1.5 | 0.3/3.3 | 0.9/3.3 |
| Mean/Median | 0.9/1.0 | 2.2/2.2 | 2.4/2.4 |
| σ/MAD | 0.3/0.1 | 0.6/0.2 | 0.5/0.2 |
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Aksakal, S.K. Geometric Accuracy Investigations of SEVIRI High Resolution Visible (HRV) Level 1.5 Imagery. Remote Sens. 2013, 5, 2475-2491. https://doi.org/10.3390/rs5052475
Aksakal SK. Geometric Accuracy Investigations of SEVIRI High Resolution Visible (HRV) Level 1.5 Imagery. Remote Sensing. 2013; 5(5):2475-2491. https://doi.org/10.3390/rs5052475
Chicago/Turabian StyleAksakal, Sultan Kocaman. 2013. "Geometric Accuracy Investigations of SEVIRI High Resolution Visible (HRV) Level 1.5 Imagery" Remote Sensing 5, no. 5: 2475-2491. https://doi.org/10.3390/rs5052475




