Optical and Thermal Remote Sensing of Turfgrass Quality, Water Stress, and Water Use under Different Soil and Irrigation Treatments
Abstract
:1. Introduction
- To investigate the sensitivity of several vegetation indices to soil preparation and water application treatments in order to explore the possibility of replacing them with the traditional visual rating, performed by human assessors;
- To estimate the GWSI based on the empirical approach and to identify the effects of experimental treatments on this stress indicator;
- To compare the performance of several turfgrass species under limited levels of water availability; and,
- To estimate turfgrass water use based on the GWSI approach, as well as a complex surface energy balance model.
2. Methods and Materials
2.1. Study Area
- (i)
- Warm-season mix, WSM: a mixture of 70% blue grama (Bouteloua gracilis L.) and 30% buffalograss (Bouteloua dactyloides L.);
- (ii)
- Aggressive Kentucky bluegrass (Poa pratensis L.), AKB: a blend of cultivars ‘Rampart’ (50%), ‘Touchdown’ (25%), and ‘Orfeo’ (25%);
- (iii)
- Texas hybrid bluegrass (Poa arachnifera L.), THB: a blend of cultivars ‘Reveille’ (50%) and ‘SPF 30’ (50%);
- (iv)
- Fine fescue, FF: a mixture of 25% ‘Covar sheep fescue’ (Festuca ovina L.), 25% ‘Intrigue Chewings fescue’ (Festuca rubra subp. Commutata), 25% ‘Cindy Lou Creeping Red fescue (Festuca rubra subp. Rubra), and 25% ‘Durar Hard fescue (Festuca trachyphylla (Hack.) Krajina); and,
- (v)
- Tall fescue (Festuca arundinacea L.), TF: 100% ‘Major League’ cultivar.
2.2. Remote Sensing Data
2.3. Vegetation Indices
2.4. Grass Water Stress Index
2.5. Turfgrass Water Use
2.5.1. GWSI-Based Water Use
2.5.2. METRIC-Based Water Use
3. Results and Discussion
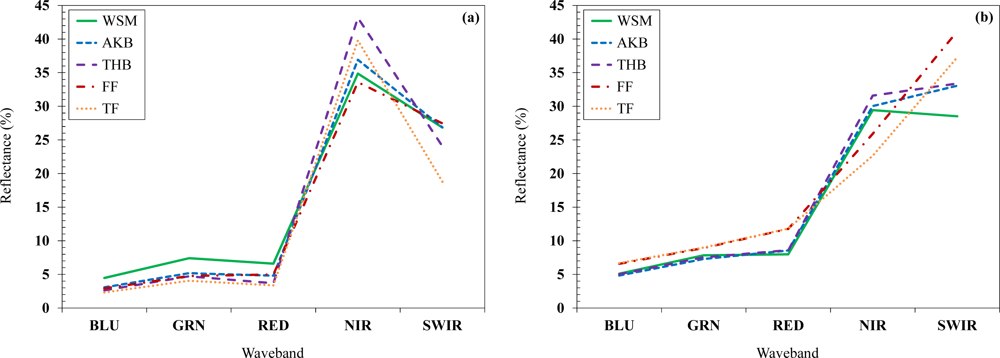
3.1. Spectral Characteristics of Turfgrass
- (i)
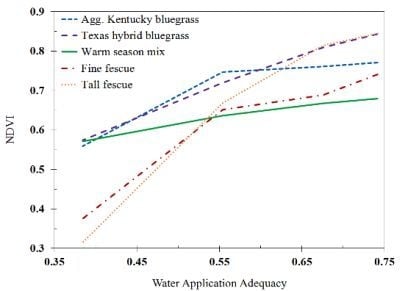
- The range of variation in NDVI and SAVI was largest for TF, followed in order by FF, THB, AKB, and WSM. This means that Festuca species were the most sensitive and the mixture of warm season grasses was the most tolerant to water limitation.
- (ii)
- Except for the WSM plots, the NDVI-vs.-WAA and the SAVI-vs.-WAA relationships were non-linear, having different slopes at WAA levels below and above 0.55. In case of VARI, plots of WSM, THB, and TF appeared to have linear graphs, while other species demonstrated a non-linear pattern. Other studies have reported similar non-linear relationships between turfgrass quality indicators and water availability [8,40].
- (iii)
- Pairwise multiple comparison analysis (Holm-Sidak method) revealed that NDVI estimates at the two highest WAA levels were not statistically different. In comparison with the highest WAA (closest distance to sprinklers), NDVI values at the third highest WAA level were not significantly different for WSM, AKB, and THB. The difference was significant only for TF and FF. At the lowest WAA level (farthest distance), all turfgrass species had a NDVI that was statistically different that the values for the highest WAA level. SAVI estimates had a similar behavior, suggesting that considerable water conservation can be achieved before turfgrass quality is significantly degraded. This is similar to a previous finding that irrigation depths can be reduced by 15% at a golf course without affecting the turf quality [13].
- (iv)
- According to all VIs, the quality and growth of WSM was poorer under high WAA levels and better under low WAA level in comparison to other species.
- (v)
- Treatment S did not cause any significant variation in estimated VIs, with average NDVI, SAVI, and VARI values of 0.88, 0.65, and 0.23, respectively. Since WAA was 95% at this treatment, the mentioned values can be regarded as the upper limits that respected VIs can reach over a non-water-stressed Kentucky bluegrass turf under conditions similar to those of this experiment.
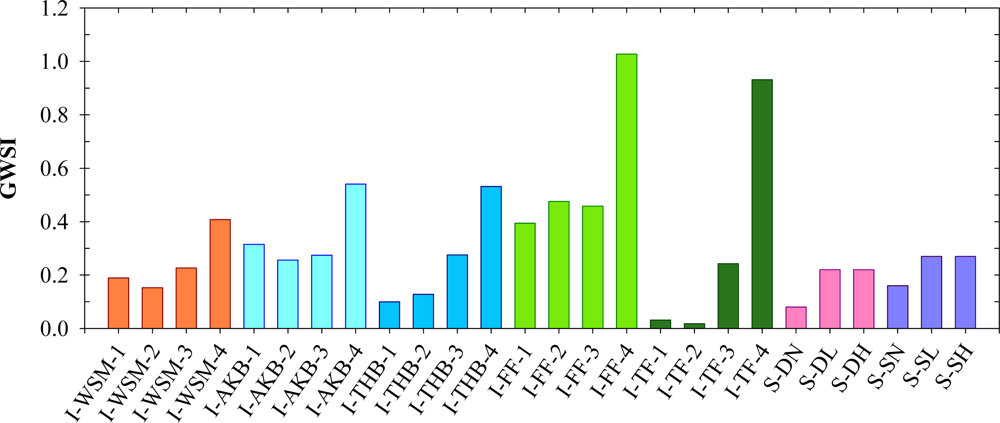
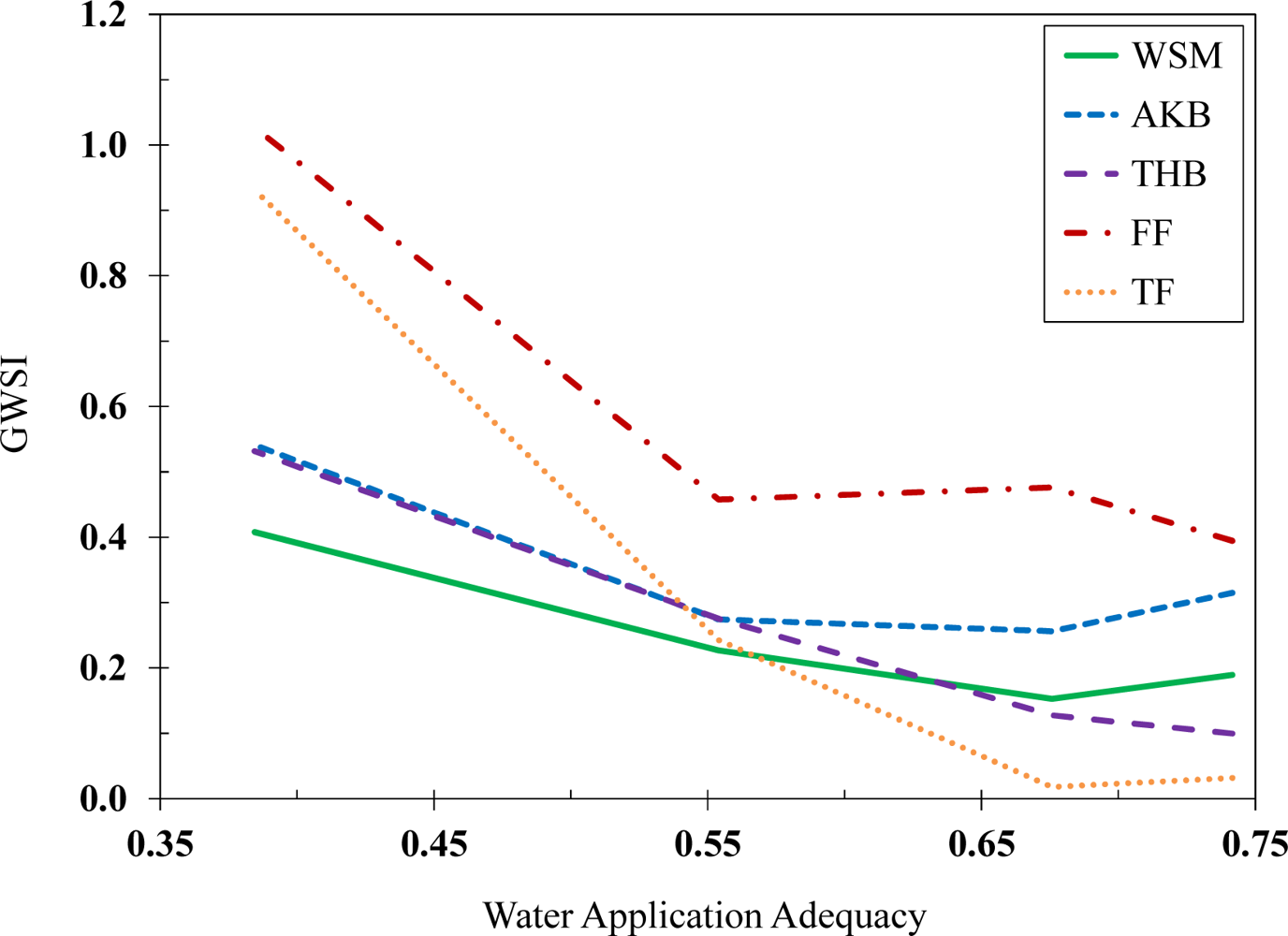
3.2. Grass Water Stress Index
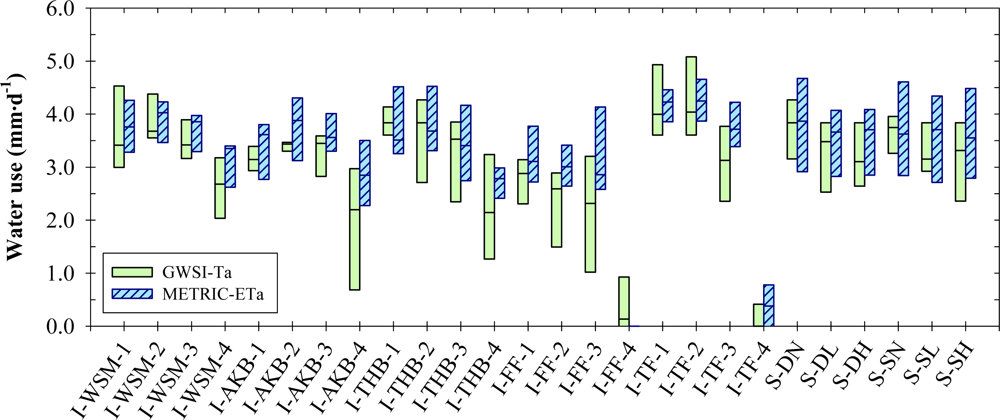
3.3. Turfgrass Water Use
3.3.1. GWSI-Based Water Use
3.3.2. METRIC-Based Water Use
4. Conclusions
Acknowledgments
- Conflict of InterestThe authors declare no conflict of interest.
References and Notes
- Boland, J.J. Assessing urban water use and the role of water conservation measures under climate uncertainty. Climatic Change 1997, 37, 157–176. [Google Scholar]
- Kjelgren, R.; Rupp, L.; Kilgren, D. Water conservation in urban landscape. HortScience 2000, 35, 1037–1040. [Google Scholar]
- Cooley, H.; Gleick, P.H. Urban Water-Use Efficiencies: Lessons from United States Cities. In The World’s Water 2008–2009: The Biennial Report on Freshwater Resources; Gleick, P.H., Ed.; Island Press: Washington, DC, USA, 2009; pp. 101–122. [Google Scholar]
- Hilaire, R.S.; Hall, S.; Cruces, L.; Arnold, M.A.; Wilkerson, D.C.; Devitt, D.A.; Hurd, B.H.; et al. Efficient water use in residential urban landscapes. HortScience 2008, 43, 2081–2092. [Google Scholar]
- Wu, J.; Bauer, M.E. Estimating net primary production of Turfgrass in an urban-suburban landscape with QuickBird imagery. Remote Sens. 2012, 4, 849–866. [Google Scholar]
- Carrow, R.N. Turfgrass Irrigation Scheduling by Infrared Thermometry. Proceedings of the 1989 Georgia Water Resources Conference, Athens, GA, USA, 16–17 May 1989; pp. 63–65.
- Bell, G.E.; Martin, D.L.; Wiese, S.G.; Dobson, D.D.; Smith, M.W.; Stone, M.L.; Solie, J.B. Vehicle-mounted optical sensing: An objective means for evaluating turf quality. Crop Sci. 2002, 42, 197–201. [Google Scholar]
- McKenney, C.B.; Zartman, R.E. Response of Buffalograss and Bermudagrass to reduced irrigation practices under semiarid conditions. J. Turf. Manag. 1997, 2, 45–54. [Google Scholar]
- Trenholm, L.E.; Schlossberg, M.J.; Lee, G.; Parks, W.; Geer, S.A. An evaluation of multi-spectral responses on selected turfgrass species. Int. J. Remote Sens. 2000, 21, 709–721. [Google Scholar]
- Martin, D.L.; Wehner, D.J.; Throssell, C.S.; Fermanian, T.W. Evaluation of four crop water stress index models for irrigation scheduling decisions on Penncross Creeping Bentgrass. Int. Turf Soc. Res. J. 2005, 10, 373–386. [Google Scholar]
- Fitz–Rodríguez, E.; Choi, C.Y. Monitoring turfgrass quality using multispectral radiometry. Trans. ASAE 2002, 45, 865–871. [Google Scholar]
- Baghzouz, M.; Devitt, D.A.; Morris, R.L. Evaluating temporal variability in the spectral reflectance response of annual ryegrass to changes in nitrogen applications and leaching fractions. Int. J. Remote Sens. 2006, 27, 4137–4157. [Google Scholar]
- Bastug, R.; Buyuktas, D. The effects of different irrigation levels applied in golf courses on some quality characteristics of turfgrass. Irrig. Sci. 2003, 22, 87–93. [Google Scholar]
- Fenstermaker-Shaulis, L.K.; Leskys, A.; Devitt, D.A. Utilization of remotely sensed data to map and evaluate turfgrass stress associated with drought. J. Turf. Manag. 1997, 2, 65–81. [Google Scholar]
- Park, D.M.; Cisar, J.L.; Williams, K.E.; McDermitt, D.K.; Miller, W.P.; Fidanza, M.A. Using spectral reflectance to document water stress in Bermudagrass grown on water repellent sandy soils. Hydrol. Process. 2007, 21, 2385–2389. [Google Scholar]
- Johnsen, A.R.; Horgan, B.P.; Hulke, B.S.; Cline, V. Evaluation of remote sensing to measure plant stress in Creeping Bentgrass (L.) fairways. Crop Sci. 2009, 49, 2261–2274. [Google Scholar]
- Throssell, C.S.; Carrow, R.N.; Milliken, G.A. Canopy temperature-based irrigation scheduling indices for Kentucky Bluegrass turf. Crop Sci. 1987, 27, 126–131. [Google Scholar]
- Jackson, R.D.; Idso, S.B.; Reginato, R.J. Canopy temperature as a crop water stress indicator. Water Resour. Res. 1981, 17, 1133–1138. [Google Scholar]
- Idso, S.B.; Jackson, R.D.; Pinter, P.J., Jr.; Reginato, R.J.; Hatfield, J.L. Normalizing the stress-degree-day parameter for environmental variability. Agric. Meteorol. 1981, 24, 45–55. [Google Scholar]
- Jalali-Farahani, H.R.; Slack, D.C.; Kopec, D.M.; Matthias, A.D. Crop water stress index models for Bermudagrass turf: a comparison. Agron. J. 1993, 85, 1210–1217. [Google Scholar]
- Martin, D.L.; Wehner, D.J.; Throssell, C.S. Models for predicting the lower limit of the canopy-air temperature difference of two cool season grasses. Crop Sci. 1994, 34, 192–198. [Google Scholar]
- Al-Faraj, A.; Meyer, G.E.; Horst, G.L. A crop water stress index for tall fescue (Festuca arundinacea Schreb.) irrigation decision-making—A traditional method. Comput. Electron. Agr. 2001, 31, 107–124. [Google Scholar]
- Payero, J.O.; Neale, C.M.U.; Wright, J.L. Non-water-stressed baselines for calculating crop water stress index (CWSI) for alfalfa and tall fescue grass. Trans. ASAE 2005, 48, 653–661. [Google Scholar]
- Idso, S.B. Non-water-stressed baselines: A key to measuring and interpreting plant water stress. Agric. Meteorol. 1982, 27, 59–70. [Google Scholar]
- CropScan. Available online: http://www.cropscan.com/ (accessed on 12 November 2012).
- Deering, D.W. Rangeland Reflectance Characteristics Measured by Aircraft and Spacecraft Sensors. Ph.D. Dissertation, Texas A & M University, College Station, TX, USA. 1978. [Google Scholar]
- Huete, A.R. A soil-adjusted vegetation index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar]
- Gitelson, A.A.; Stark, R.; Grits, U.; Rundquist, D.; Kaufman, Y.; Derry, D. Vegetation and soil lines in visible spectral space: A concept and technique for remote estimation of vegetation fraction. Int. J. Remote Sens. 2002, 23, 2537–2562. [Google Scholar]
- Baghzouz, M.; Devitt, D.A.; Morris, R.L. Assessing canopy spectral reflectance of hybrid Bermudagrass under various combinations of nitrogen and water treatments. Appl. Eng. Agric. 2007, 23, 763–774. [Google Scholar]
- Allen, R.G.; Tasumi, M.; Trezza, R. Satellite-based energy balance for mapping evapotranspiration with internalized calibration (METRIC)-model. J. Irrig. Drain. Eng. 2007, 133, 380–394. [Google Scholar]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration: Guidelines for Computing Crop Requirements; Irrigation and Drainage Paper No. 56; FAO: Rome, Italy, 1998. [Google Scholar]
- ASCE-EWRI. The ASCE Standardized Reference Evapotranspiration Equation. Report by the American Society of Civil Engineers Task Committee on Standardization of Reference Evapotranspiration; Allen, R.G., Walter, I.A., Elliot, R.L., Howell, T.A., Itenfisu, D., Jensen, M.E., Snyder, R.L., Eds.; ASCE: Reston, VA, USA, 2005. [Google Scholar]
- Brest, C.L.; Goward, S.N. Driving surface albedo measurements from narrow band satellite data. Int. J. Remote Sens. 1987, 8, 351–367. [Google Scholar]
- Bastiaanssen, W.G.M.; Menenti, M.; Feddes, R.A.; Holtslang, A.A. A remote sensing surface energy balance algorithm for land (SEBAL): 1. Formulation. J. Hydrol. 1998, 212–213, 198–212. [Google Scholar]
- Chávez, J.; Gowda, P.; Howell, T.; Garcia, L.; Copeland, K.; Neale, C. ET Mapping with high-resolution airborne remote sensing data in an advective semiarid environment. J. Irrig. Drain. Eng. 2012, 138, 416–423. [Google Scholar]
- Chávez, J.L.; Neale, C.M.U.; Prueger, J.H.; Kustas, W.P. Daily evapotranspiration estimates from extrapolating instantaneous airborne remote sensing ET values. Irrig. Sci. 2008, 27, 67–81. [Google Scholar]
- Colaizzi, P.D.; Evett, S.R.; Howell, T.A.; Tolk, J.A. Comparison of five models to scale daily evapotranspiration from one-time-of day measurements. Trans. ASABE 2006, 49, 1409–1417. [Google Scholar]
- Taghvaeian, S.; Chávez, J.L.; Hansen, N.C. Infrared thermometry to estimate crop water stress index and water use of irrigated maize in Northeastern Colorado. Remote Sens. 2012, 4, 3619–3637. [Google Scholar]
- Tucker, C.J. Remote sensing of leaf water content in the near infrared. Remote Sens. Environ. 1980, 10, 23–32. [Google Scholar]
- Feldhake, C.M.; Danielson, R.E.; Butler, J.D. Turfgrass evapotranspiration. II. Responses to deficit irrigation. Agron. J. 1984, 76, 85–89. [Google Scholar]
- Carrow, R.N. Canopy temperature irrigation scheduling indices for turfgrasses in humid climate. In International Turfgrass Society Research Journal 7; Carrow, R.N., Christians, N.E., Shearman, R.C., Eds.; Intertec Publishing Corp: Overland Park, KS, USA, 1993; pp. 594–599. [Google Scholar]
- Bastiaanssen, W.G.M.; Noordman, E.J.M.; Pelgrum, H.; Davids, G.; Thoreson, B.P.; Allen, R.G. SEBAL model with remotely sensed data to improve water-resources management under actual field conditions. J. Irrig. Drain. Eng. 2005, 131, 85–93. [Google Scholar]





| Parameter | Value | Units |
|---|---|---|
| Average daily minimum air temp. | 12.6 | °C |
| Average daily mean air temp. | 20.9 | °C |
| Average daily maximum air temp. | 29.3 | °C |
| Average daily mean wind speed | 1.5 | m·s−1 |
| Average daily vapor pressure | 1.1 | kPa |
| Average daily solar radiation | 20.6 | MJ·d−1 |
| Total precipitation | 54.0 | mm |
| Average daily ETo | 4.7 | mm·d−1 |
| Total ETo | 329.0 | mm |
| Treatment | Experimental plots | Abb. | Irr. (mm) |
|---|---|---|---|
| Irrigation depth (I) | Warm Season Mix, 1.0* | I-WSM-1 | 190 |
| Warm Season Mix, 2.1 | I-WSM-2 | 169 | |
| Warm Season Mix, 3.3 | I-WSM-3 | 129 | |
| Warm Season Mix, 4.5 | I-WSM-4 | 73 | |
| Agg. Kent. Bluegrass, 1.0 | I-AKB-1 | 190 | |
| Agg. Kent. Bluegrass, 2.1 | I-AKB-2 | 169 | |
| Agg. Kent. Bluegrass, 3.3 | I-AKB-3 | 129 | |
| Agg. Kent. Bluegrass, 4.5 | I-AKB-4 | 73 | |
| Texas Hyb. Bluegrass, 1.0 | I-THB-1 | 190 | |
| Texas Hyb. Bluegrass, 2.1 | I-THB-2 | 169 | |
| Texas Hyb. Bluegrass, 3.3 | I-THB-3 | 129 | |
| Texas Hyb. Bluegrass, 4.5 | I-THB-4 | 73 | |
| Fine Fescue, 1.0 | I-FF-1 | 190 | |
| Fine Fescue, 2.1 | I-FF-2 | 169 | |
| Fine Fescue, 3.3 | I-FF-3 | 129 | |
| Fine Fescue, 4.5 | I-FF-4 | 73 | |
| Tall Fescue, 1.0 | I-TF-1 | 190 | |
| Tall Fescue, 2.1 | I-TF-2 | 169 | |
| Tall Fescue, 3.3 | I-TF-3 | 129 | |
| Tall Fescue, 4.5 | I-TF-4 | 73 | |
| Soil Preparation (S) | Deep tillage, No compost | S-DN | 259 |
| Deep tillage, Low compost | S-DL | 259 | |
| Deep tillage, High compost | S-DH | 259 | |
| Shallow tillage, No compost | S-SN | 259 | |
| Shallow tillage, Low compost | S-SL | 259 | |
| Shallow tillage, High compost | S-SH | 259 | |
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Taghvaeian, S.; Chávez, J.L.; Hattendorf, M.J.; Crookston, M.A. Optical and Thermal Remote Sensing of Turfgrass Quality, Water Stress, and Water Use under Different Soil and Irrigation Treatments. Remote Sens. 2013, 5, 2327-2347. https://doi.org/10.3390/rs5052327
Taghvaeian S, Chávez JL, Hattendorf MJ, Crookston MA. Optical and Thermal Remote Sensing of Turfgrass Quality, Water Stress, and Water Use under Different Soil and Irrigation Treatments. Remote Sensing. 2013; 5(5):2327-2347. https://doi.org/10.3390/rs5052327
Chicago/Turabian StyleTaghvaeian, Saleh, José L. Chávez, Mary J. Hattendorf, and Mark A. Crookston. 2013. "Optical and Thermal Remote Sensing of Turfgrass Quality, Water Stress, and Water Use under Different Soil and Irrigation Treatments" Remote Sensing 5, no. 5: 2327-2347. https://doi.org/10.3390/rs5052327