Deformation Trend Extraction Based on Multi-Temporal InSAR in Shanghai
Abstract
:1. Introduction
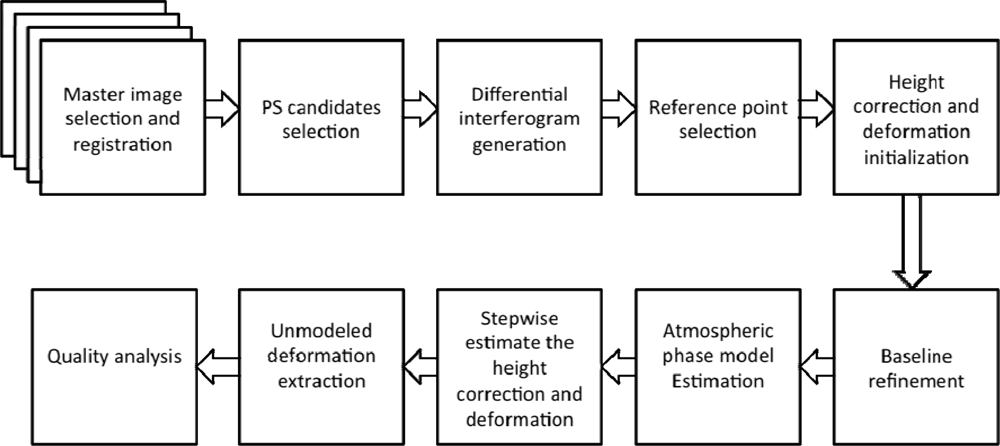
2. Methodology
3. Experimental Result and Analysis
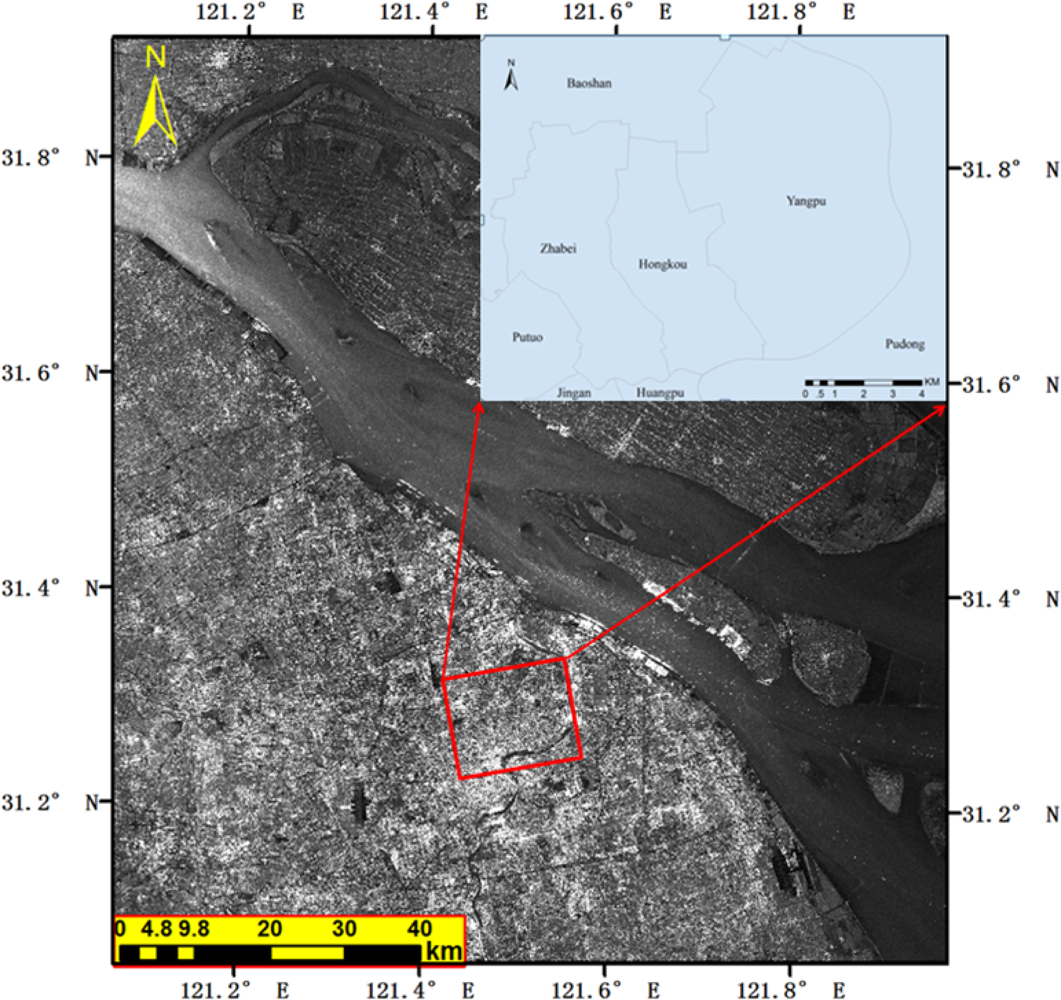
3.1. Data Selection
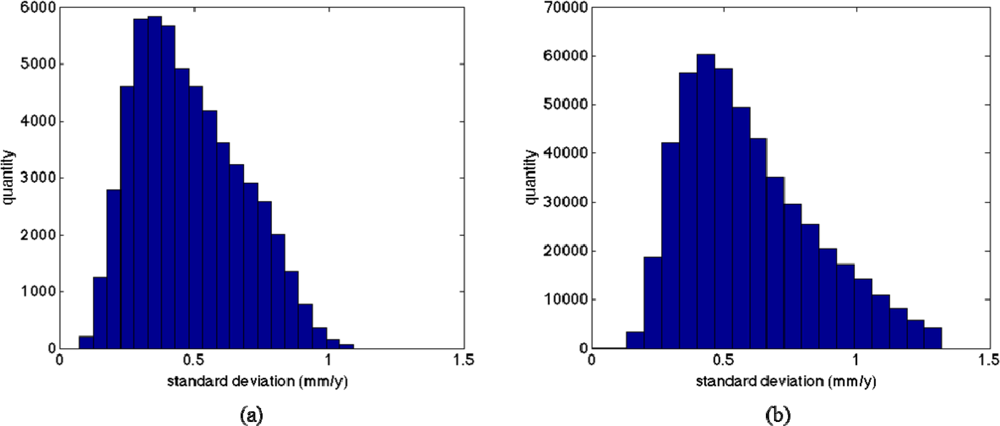
3.2. Subsidence Results
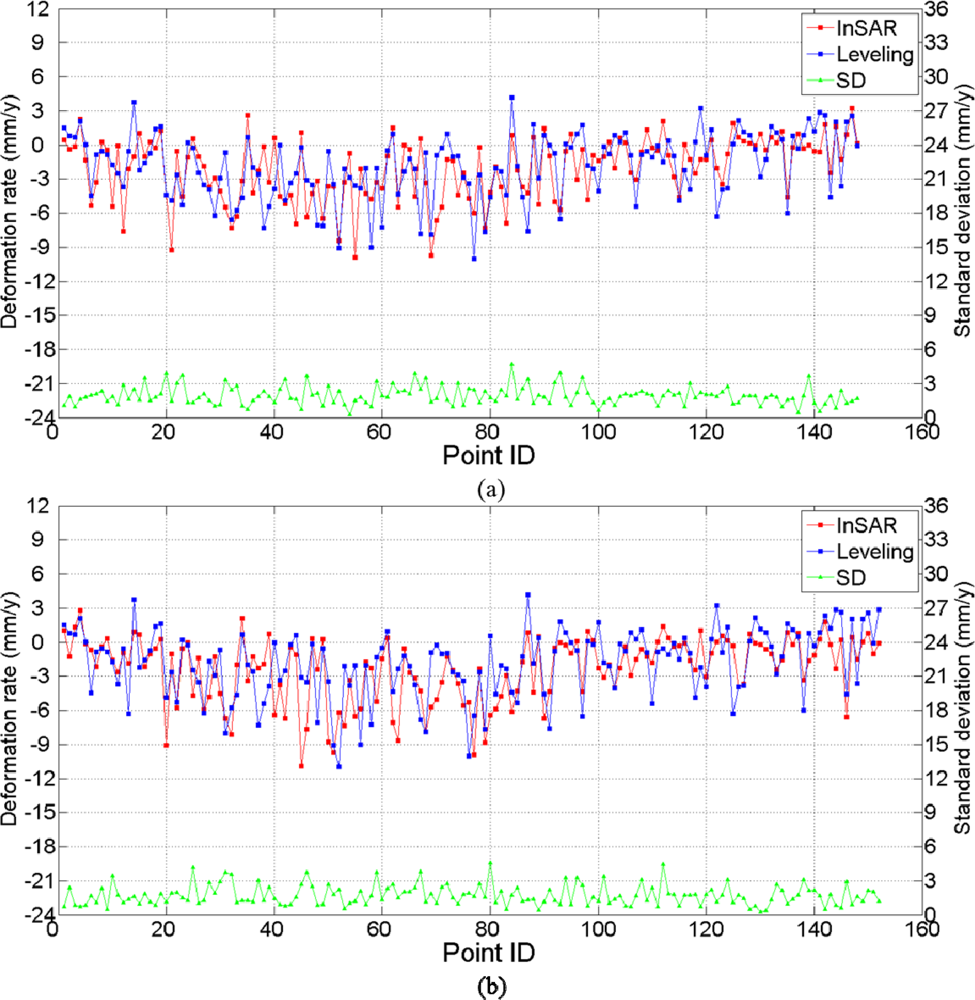
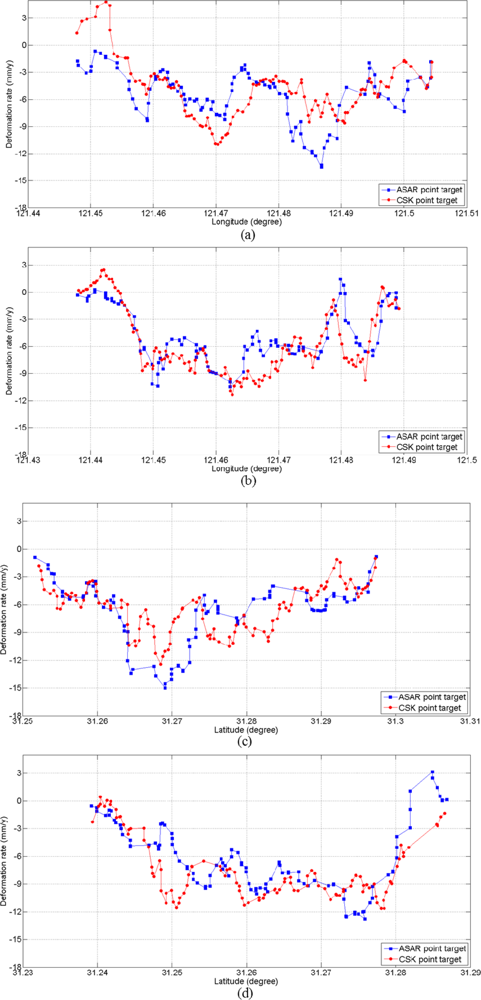
3.3. Validation
- For ASAR, t = 0.38
- For CSK, t = 0.83
4. Comparison and Discussion
5. Conclusions
Acknowledgments
References
- Liu, Y.; Zhang, X.L.; Wan, G.F.; Han, Q.D. The situation of land subsidence within Shanghai in recent years and its countermeasure (in Chinese). Chinese J. Geol. Hazard Control 1998, 9, 13–17. [Google Scholar]
- Liu, Y. Preventive measures for land subsidence in Shanghai and their effects. Volcanol. Miner. Resour 2000, 21, 107–111. [Google Scholar]
- Wang, Y.; Liao, M.S.; Li, D.R.; Wei, Z.X.; Fang, Z. Subsidence velocity retrieval from long-term coherent targets in radar interferometric stacks (in Chinese). Chinese J. Geophys 2007, 50, 598–604. [Google Scholar]
- Liu, G.X.; Luo, X.J.; Chen, Q.; Huang, J.F.; Ding, X.L. Detecting land subsidence in Shanghai by PS-networking SAR interferometry. Sensors 2008, 8, 4725–4741. [Google Scholar]
- Luo, X.J.; Huang, D.F.; Liu, G.X. On urban ground subsidence detection based on PS-DInSAR: A case study for Shanghai (in Chinese). Bull. Surv. Mapp 2009, 4, 4–8. [Google Scholar]
- Damoah-Afari, P.; Ding, X.L.; Lu, Z.; Li, Z.W.; Makoto, O. Magnitude and Extent of Six Years of Land Subsidence in Shanghai Revealed by JERS-1 SAR Data. In Geoscience and Remote Sensing New Achievements; Pasquale, I., Daniele, R., Eds.; InTech: New York, NY, USA, 2010; pp. 477–496. [Google Scholar]
- Wang, Z.Y.; Perissin, D.; Lin, H. Subway Tunnels Identification through Cosmo-SkyMed PSInSAR Analysis in Shanghai. Processing of IEEE Geoscience and Remote Sensing Symposium 2011, Vancouver, BC, Canada, 24–29 July 2011; pp. 1267–1270.
- Leighton, J.M. Methodology and Results. GPS and PSI Integration for Monitoring Urban Land Motion, 2010; pp. 154–155. [Google Scholar]
- Bamler, R.; Hartl, P. Synthetic aperture radar interferometry. Inverse Probl 1998, 14, R1–R54. [Google Scholar]
- Gabriel, A.K.; Goldstein, R.M.; Zebker, H.A. Mapping small elevation changes over large areas: Differential radar interferometry. J. Geophys. Res 1989, 94, 9183–9191. [Google Scholar]
- Zebker, H.A.; Villaseno, J. Decorrelation in interferometric radar echoes. IEEE Trans. Geosci. Remote Sens 1992, 30, 950–959. [Google Scholar]
- Zebker, H.A.; Rosen, P.A.; Hensley, S. Atmospheric effects in interferometric synthetic aperture radar surface deformation and topographic maps. J. Geophys. Res 1997, 102, 7547–7563. [Google Scholar]
- Sanchez, P.; Mallorquí, J.J.; Duque, S.; Monells, D. The coherent pixels technique (CPT): An advanced DInSAR technique for nonlinear deformation monitoring. Pure Appl. Geophys 2008, 165, 1167–1194. [Google Scholar]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens 2011, 39, 8–20. [Google Scholar]
- Berardino, P.; Fornaro, G.; Lanari, R. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens 2002, 40, 2375–2383. [Google Scholar]
- Werner, C.; Wegmuller, U.; Strozzi, T.; Wiesmann, A. Interferometric Point Target Analysis for Deformation Mapping. Processing of IEEE Geoscience and Remote Sensing Symposium 2003, Toulouse, France, 21–25 July 2003; 7, pp. 4362–4364.
- Kampes, B. The STUN Algorithm. In Radar Interferometry: Persistent Scatterer Technique; Springer: Dordrecht, The Netherlands, 2006; pp. 47–48. [Google Scholar]
- Chen, Q.; Ding, X.L.; Liu, G.X. Method for optimum selection of common master acquisition for PS-DInSAR (in Chinese). Bull. Surv. Mapp 2007, 36, 395–399. [Google Scholar]
- Gamma Remote Sensing. GAMMA Interferometric Point Target Analysis: Users Guide. 2003; Gamma Remote Sensing: Gümligen, Switzerland, 2003. [Google Scholar]


| L1 | L2 | L3 | L4 | |
|---|---|---|---|---|
| RMSE (mm/yr) | 3.15 | 2.49 | 2.79 | 2.74 |
Share and Cite
Chen, J.; Wu, J.; Zhang, L.; Zou, J.; Liu, G.; Zhang, R.; Yu, B. Deformation Trend Extraction Based on Multi-Temporal InSAR in Shanghai. Remote Sens. 2013, 5, 1774-1786. https://doi.org/10.3390/rs5041774
Chen J, Wu J, Zhang L, Zou J, Liu G, Zhang R, Yu B. Deformation Trend Extraction Based on Multi-Temporal InSAR in Shanghai. Remote Sensing. 2013; 5(4):1774-1786. https://doi.org/10.3390/rs5041774
Chicago/Turabian StyleChen, Jie, Jicang Wu, Lina Zhang, Junping Zou, Guoxiang Liu, Rui Zhang, and Bing Yu. 2013. "Deformation Trend Extraction Based on Multi-Temporal InSAR in Shanghai" Remote Sensing 5, no. 4: 1774-1786. https://doi.org/10.3390/rs5041774






