1. Introduction
Automatic building reconstruction from Digital Surface Models (DSMs) with or without using other data sources is still an active research area in Photogrammetry and GIS institutions. In this context, providing a 3D CAD model that represents the overall shape of the building and containing the most significant parts has boosted many applications in the GIS area such as urban planning. In the past few years, several algorithms have been proposed for automated 3D building reconstruction. The algorithms comprise methods that only employ elevation data such as high resolution airborne LIDAR for model generation while some methods use other additional sources of data. An additional data source plus DSM is usually employed when the quality or resolution of the elevation data is not appropriate for model generation. Segmentation based approaches for a 3D building model generation from grid data are proposed by [
1,
2] to find planar regions that determine a polyhedral model. Gorte [
3] employed another segmentation approach using Triangulated Irregular Network (TIN) structures for the data and the segments are generated by iteratively merging the triangles based on similarity measurements. Verma
et al. [
4] also proposed a method based on integration of model-driven and data-driven algorithms to detect and construct a 3D building models from LIDAR data. The method consists of three main steps, namely, segmentation of building roofs, region adjacency graph for shape roof topology, and parametric roof reconstruction.
Rotensteiner [
5] described a model for consistent estimation of building parameters, which is part of the 3D building reconstruction. Geometric regularities were included as soft constraints in the adjustment of the model. Robust estimation can then be used to eliminate false hypotheses about geometric regularities. A comparison between data- and model-driven approaches for building reconstruction have been made, which states that the model-driven approach is faster and does not visually deform the building model. In contrast, the data-driven approach tends to model each building detail to obtain the nearest polyhedral model, but it usually visually deforms the real shape of the building [
6].
Khoshelham [
7] proposed a method for the reconstruction of the buildings in suburban areas by employing combined height and aerial images. The method is based on the matching of a CAD model of a building against the image, while the selection of the CAD model is based on the features extracted from the height data. The straight lines are extracted from the aerial image and grouped based on proximity and parallelism assumptions.
A projection based approach for 3D model generation of the buildings from high resolution airborne LIDAR data was proposed by [
8]. The building blocks have been divided to smaller parts according to the location and direction of the ridge lines. A projection based method was applied to generate CAD models of each building parts.
Kada [
9] utilized a library of parametrized standard shapes of models to reconstruct building blocks. The buildings are partitioned into non-intersecting sections, for which roof shapes are then determined from the normal directions of the LIDAR points. Sohn [
10] presented a data-driven algorithm based on Binary Space Partitioning Tree (BSP-Tree) for modeling 3D buildings. The method integrates linear- and area-features extracted from LIDAR and IKONOS data for generating the BSP-tree, which is used for the reconstruction of prismatic and parametric roofs.
Kabolizadeh [
11] proposed a model-driven approach for building reconstruction from LIDAR data based on genetic algorithm (GA). The method works in three steps, namely detection, extraction, and reconstruction. Accordingly, the initial building boundaries are detected and then a GA-based method is used for reconstructing the building models. Another recent approach is developed for the 3D reconstruction of the flat roof buildings by integrating the LIDAR data and orthophoto [
12]. The linear features such as building edges are extracted from orthophoto and refined by LIDAR data. The lines are merged together to shape roof polygons, and then using RANSAC technique plane parameters are extracted. Accordingly the 3D roof patches are determined and merged to form 3D prismatic building model.
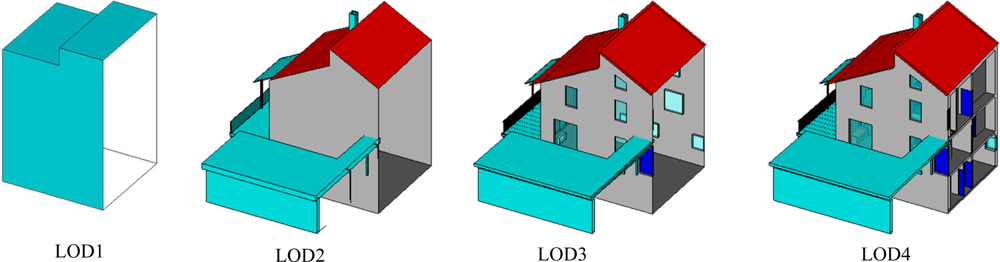
In this paper we propose a method that aims at simplifying the 3D reconstruction of the building blocks by decomposing the overall model into several smaller ones corresponding to each building part. The focus is on the generation of 3D models of parametric building roofs as the basis for creating Level of Detail 2 (LOD2) according to City Geography Markup Language (CityGML) standard [
13]. In contrast to LOD1 in which the geometry of a building is represented as a prismatic model, in LOD2 the outer facade of the building is modeled with greater detail. The LOD2 model enables representing the parametric roof shapes such as gable and hip models. Accordingly, LOD3 shapes the building model including external architectural details and LOD4 represents the building model including the interior architecture (
cf. Figure 1).
A similar method has been already reported [
15] by the author for automated generation of the 3D building models from high resolution LIDAR data. In contrast to LIDAR data, the DSMs generated by stereo matching of satellite imagery have a lower quality, particularly on the building ridge lines and boundaries. Therefore, a method that solely employs stereo-matched DSMs for 3D building reconstruction often produces lower geometric accuracy especially on the building walls. Accordingly, in this study the Worldview-2 orthorectified image is included as additional data source to enhance the model accuracy. Due to a smooth behavior and lower quality of the height gray values of worldview DSM on the building edges (
cf. Figure 2), an appropriate and accurate edge line extraction by using only DSM is not perfect. Therefore, the orthoimage has been employed to improve the location of the linear features (such as eave and ridge) of buildings.
Figure 2 illustrates two sample images that have been selected to show the quality of the building edge representation in Worldview DSM against the Ortho-rectified image.
Figure 2(a) shows a sample area in Munich city center containing several isolated buildings. As shown, the building edges become smoother if we go from center to the image border. Particularly, it can be seen that about the three isolated and parallel buildings located on the left side of the scene the edges connected to the shadow side of the buildings are completely smoothed. Obviously, in those areas the building edges cannot be extracted correctly. In contrast, the same locations in the ortho-rectified image are still in good quality and discrimination between the buildings eave and shadows are visible. Therefore, the edges can be extracted in a much better quality.
Figure 2(b) illustrates another example representing a spacious building,
i.e., central train station in Munich. It shows that even for such big buildings, not all edges are correctly recognizable.
The novelty of the approach proposed in this paper in comparison with [
8] is that it shows the potential of the projection-based algorithm for 3D building reconstruction from satellite based data, which is in lower quality comparing with the airborne data. On the other hand, two model based approximation techniques have been proposed for the approximation of the building boundary polygons with rectangular or non-rectangular shapes.
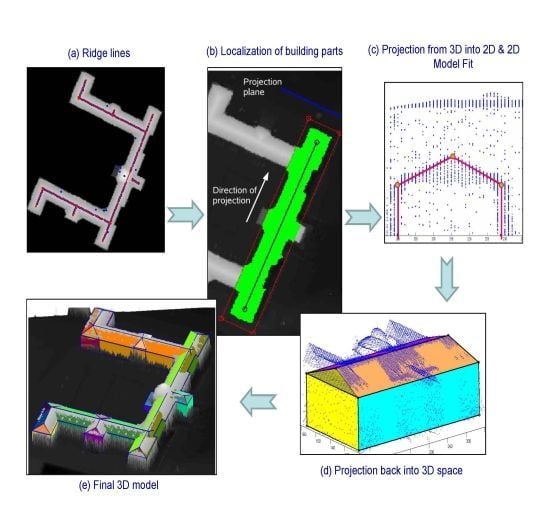
The process begins with the extraction of building ridge lines using orthoimage and height information. According to each ridge line, a projection-based algorithm is employed to transfer the 3D points into 2D space by orthogonal projection of the corresponding pixels of each building part onto a 2D plane that is defined based on the orientation of the ridge line. Based on the type of the roofs, a predefined 2D model is fitted to the data, and in the next step, the 2D model is extended to 3D by analyzing the third dimension of the points. A final model regarding the parametric roof structures of the building block is defined by merging all the individual models and employing some post-processing refinements regarding the coinciding nodes and corners to shape the appropriate model. Additionally prismatic models with flat roof are provided regarding to the remaining areas that are not containing ridge lines. Finally, all parametric and prismatic models are merged to form a final 3D model of the building.
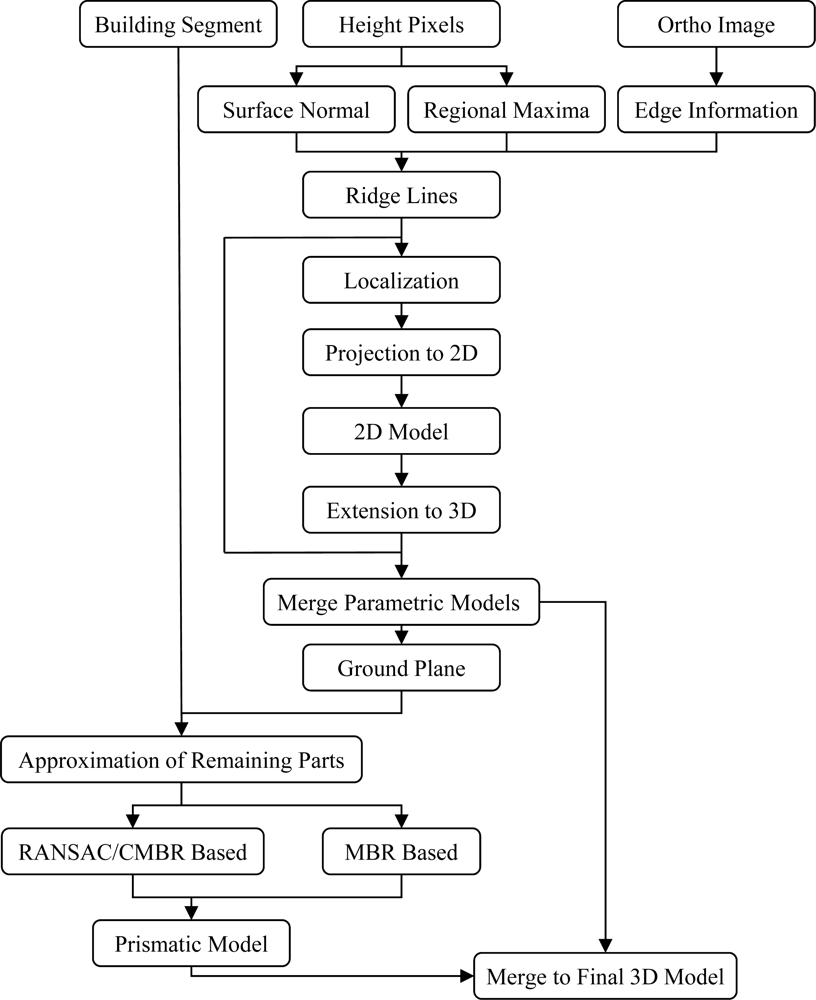
2. Proposed Method
In this section, a new method is proposed for the reconstruction of buildings by integrating DSMs and orthorectified image information produced from Worldview-2 stereo satellite imagery. Worldview-2 provides panchromatic images with 50 cm Ground Sampling Distance (GSD) as well as eight-band multispectral images with 2 m GSD. A DSM is produced from panchromatic Worldview-2 images with 50 cm image resolution using a fully automated method [
16] based on semiglobal stereo matching algorithm using mutual information proposed by [
17].
In this article, the main focus is on the reconstruction of the buildings with tilted roof shapes, including hipped and gabled parametric roof models, although modeling of the flat roof segments (prismatic models), which is reported in a former work of the authors, is utilized in this study as well.
The preliminary and also the most critical issue on all the building reconstruction approaches is building segmentation, which is still an unsolved problem particularly based on only geometric data such as DSMs. During the past year, many algorithms have been proposed for building classification and segmentation from remotely sensed data. Some of these algorithms work properly for some special areas and fail in others. In this paper we do not focus on building segmentation issue, and therefore we assume that the building masks have been extracted using a successful algorithm with any degree of automation.
Accordingly, the automatic 3D building reconstruction algorithm proposed in this paper comprises the following major steps:
Ridge-based decomposition of building parts
Projection-based reconstruction of parametric roofs
Prismatic model generation related to flat roof segments
Merge parametric and prismatic models and refine the corner nodes
Figure 3 presents the proposed workflow for the automatic generation of building models using a projection based algorithm. Detailed explanations are given in the following sections.
2.1. Ridge-Based Decomposition of Building Parts
The idea of the 3D building reconstruction algorithm proposed in this article is to simplify the modeling procedure by decomposing the overall building model into smaller tiles based on the location of the ridge lines. The building parts containing ridge lines are individually modeled and merged to shape the overall model of the entire building. Accordingly, the location of the ridge lines in buildings with tilted roof structures should be carefully extracted. The quality of the final model has a direct relation to the quality of extracted ridge lines,
i.e., a high quality ridge lines leads to a high quality 3D model. The location of ridge line has two major roles in the proposed modeling approach:
Therefore, the first and the most important and sensitive part of the proposed approach is extracting ridge lines. Arefi [
15] proposed an algorithm to extract the ridge location from high resolution airborne LIDAR data using morphological geodesic reconstruction [
18]. Due to the lower quality of DSMs created from Worldview-2 stereo images compared with the LIDAR data, a method relying only on height data does not produce appropriate ridge pixels. In this paper, orthorectified Worldview images are employed as additional data source to assist DSM data for an appropriate extraction of the ridge points (
cf. Figure 3). The procedure to extract all the ridge lines corresponding to a building with tilted roofs begins with feature extraction. For this purpose, three feature descriptors are extracted from DSM and orthoimage as follows (
cf. Figure 4):
Surface normals of DSM: The surface normal is a vector perpendicular to a surface, which represents the orientation of a surface. It can be estimated by determining the best fitting plane over a small neighborhood. A normal vector can also be computed by means of the cross product of any two non-collinear vectors that are tangent to the surface at a targeted pixel [
19].
Figure 4(c) shows the surface normals generated from the Worldview DSM. This feature descriptor is employed to eliminate the pixels with a sharp height discontinuity, e.g., eaves, from other edge pixels.
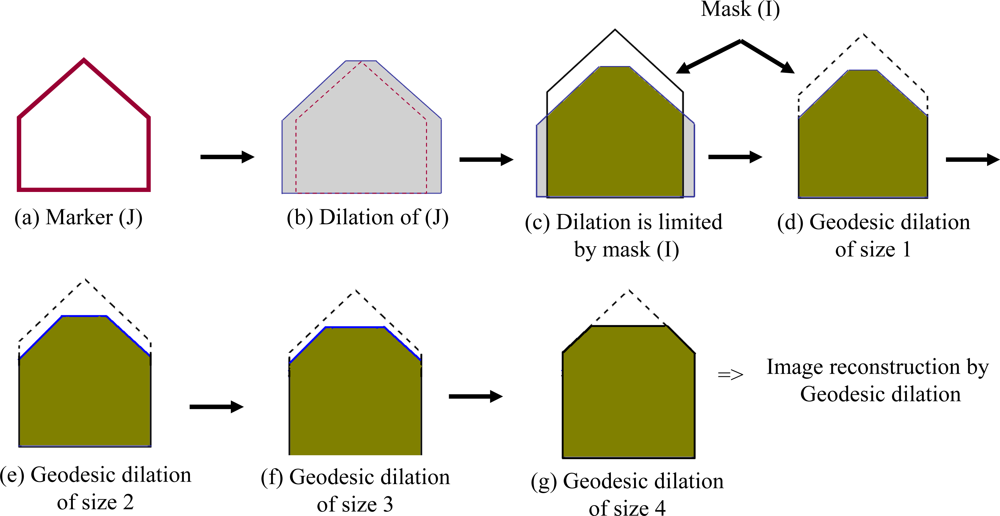
Regional maxima from DSM: Here, an algorithm based on image reconstruction using geodesic morphological dilation [
20] is employed to reformulate the regional maxima regions. The geodesic dilation differs from basic dilation where an image and a structuring element are involved in the filtering process. In geodesic dilation additionally the dilated image is masked (or limited) by a predefined “mask” image.
Equation 1 shows the geodesic dilation of image J as
marker using
mask I. In this study the marker image is defined by a height offset to the mask image, which generally represents the original DSM.
Figure 5 illustrates the difference between geodesic and basic image dilation as well as reconstruction based on geodesic dilation in a profile view of a simple building with tilted roof. The input image
Figure 5(a), called
marker, is enlarged by dilation
Figure 5(b), and limited by the
mask image (I) (
cf. Figure 5(c)). The result of geodesic dilation is shown as the green area in
Figure 5(d) and a dashed line around it depicts the mask image. If this process,
i.e., dilation and limitation by mask, is iteratively continued, it stops after
n iterations (here four) to reach stability. The result provided by this step is called reconstruction of marker (J) by mask (I) using geodesic dilation (
cf. Figure 5(g)). The number of iteration
n in
Equation 2 varies from one sample to another. In the example presented in
Figure 5 the reconstruction procedure stops after four iterations.
Accordingly, geodesic dilation (δ
I) and image reconstruction are defined as:
Equation (2) defines the morphological reconstruction of the marker image (J) based on geodesic dilation (
δI) (
cf. Equation (1)). The basic dilation (
δ) of marker and point-wise minimum (∧) between dilated image and mask (I) is employed iteratively until stability (
i.e., no more pixel value modifications). In other words, morphological reconstruction can be thought as repeated dilations of the marker image while the contour of the marker image fits under the mask image.
Considering the reconstructed image of the example depicted in
Figure 5(g) shows that the upper part of the object,
i.e., the difference between marker and mask, is suppressed during image reconstruction. Therefore, the result of gray scale reconstruction depends on the height offset between the marker and the mask images and accordingly, different height offset suppress different parts of the object. More information regarding the segmentation of the DSMs by gray scale reconstruction using geodesic dilation can be found in [
15] where similar algorithms are employed for extracting the 3D objects as well as the ridge lines from high resolution LIDAR DSMs. In a segmentation algorithm based on geodesic reconstruction, selecting an appropriate “marker” image plays the main role and has a direct effect on the quality of the final reconstructed image. A marker image with a small offset, e.g., a few meters, from the mask can suppress mainly local maxima regions similar to the artifacts above the ground.
Canny edges from orthorectified image:
Figure 4(e) represents the result of applying the Canny edge detector on the orthorectified image of the selected building. As shown, the Canny edge extraction method looks for local maxima of the gradient of the image.
The above mentioned three feature descriptors are employed to classify and extract the potential ridge points using DSM and orthorectified image as follows:
The image provided by surface normal (
cf. Figure 4(c)) is thresholded to eliminate the pixels located on the inclined part of the roof. The surface normal image is often normalized with the gray values in [0,1]. The pixels with gray values 1 are flat regions. Here we employ a threshold of
t > 0.96 since the ridge points are not exactly located in a flat surface (locally).
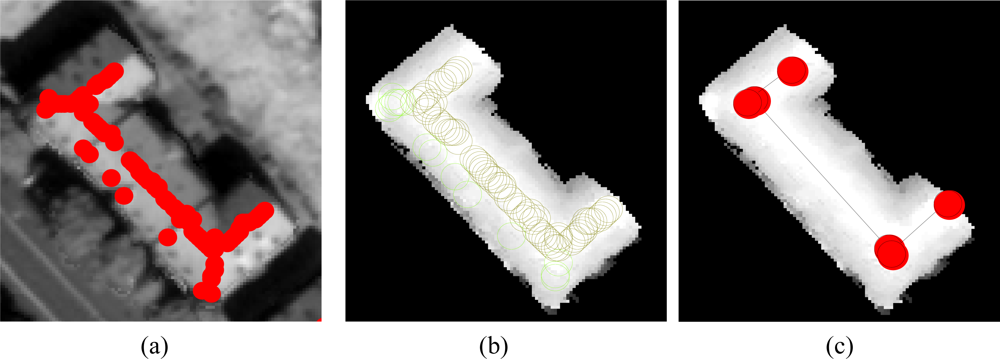
Intersection of the three binary images,
i.e., binarized surface normal, binarized regional maxima, and Canny edges, provide the potential ridge pixels, which still need to be refined (
cf. Figure 6(a)).
Figure 6(a) illustrates the pixels that are classified as ridge pixels plotted by red points. As shown, all the red pixels do not correspond to the ridges and therefore, an additional procedure is included to separate horizontal pixels (
i.e., pixels with almost same gray value) from the other pixels. For this aim, the pixels located in almost the same heights are extracted (
cf. Figure 6(b)).
Next, the RANdom SAmple Consensus (RANSAC) algorithm [
21] is employed to extract corresponding ridge lines from the classified pixels (
cf. Figure 6(c)).
2.2. Projection-Based Reconstruction of Parametric Roofs
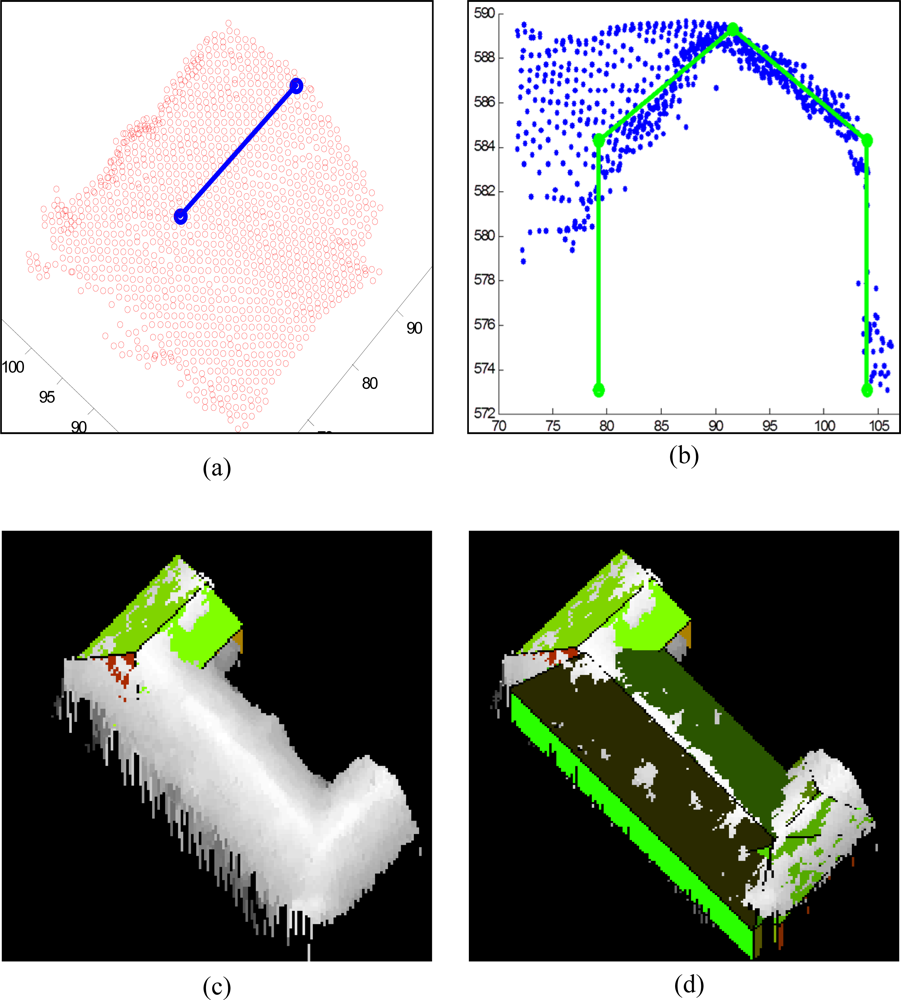
In this paper, it is assumed that an individual building part exists according to each ridge line. Therefore, for each ridge line and the pixels located in its buffer zone, a 3D model is fitted. For a rectangle buffer zone parallel (or perpendicular) to the main orientation, the points located inside it are extracted using the point-in-polygon algorithm. This step is necessary for buildings containing more than one part. A rectangle parallel to the main orientation (parallel to ridge line) is created. A rectangle is defined around the ridge line with equal distances of the edges to the ridge line. The limits of the rectangle are selected in this way that detected building pixels are all included. In
Figure 7(a) the red points represent the localized points corresponding to the blue ridge line.
The procedure continues by projecting the localized points onto a 2D plane perpendicular to the ridge direction (
cf. Figure 7(b)). In this step, the overall aim is to decrease one dimension from the 3D data and continue the further processing in 2D space. In 2D space, which is shown in
Figure 7(b), a 2D model containing four lines (green lines) that are supported by a maximum number of points (blue) related to the front- and back-side of the building part is extracted. Therefore, two vertical lines relating to the walls and two inclined lines relating to the roof faces are defined (
cf. Figure 7(b)). The quality of the 2D model in this step depends on the existence of a sufficient number of height points relating to each side of the wall. It is common in complex buildings that the number of supporting height points is not sufficient to extract the corresponding vertical line. To cope with this problem, a vertical line located symmetrically to the side with maximum supporting points is defined. Hence, the algorithm in this step only extracts the side walls having equal distances to the ridge position (symmetry constraint).
In order to shape the final 3D model relating to the building part, the 2D model is converted back to 3D space by extruding it orthogonally to the projection plane. The 3D model consists of four walls plus one to four roof planes: two inclined planes in addition to two vertical triangular planes for a gable roof, and four inclined planes for a hipped roof (
cf. Figure 7(c)).
After reconstructing 3D models for all building parts, they are merged to form the overall 3D model of the building.
Figure 7(d) displays a building model produced by merging three building parts. The three ridge lines lead to three parametric building models with hipped roofs.
The method contains some extra processes to refine the nodes and the walls that represent common locations. In this context, the following refinements are applied (
cf. Figure 8):
If neighboring segments are nearly parallel and close to each other, the parallel sides are shifted to a location with equal distance to each other.
If the end point of a ridge line is close to the end point of the other ridge line, the intersection of two lines is replaced to both end points.
Figure 9 represents the final 3D model of the selected building after refining the polygons plotted on the orthorectified image as well as the DSM.
2.3. Approximation of the Remaining Polygons and Generating Prismatic Models
Two algorithms are proposed for the approximation of the building polygons based on the main orientation of the buildings [
22]. The algorithms are selected according to the number of main orientations of the buildings and implemented as follows:
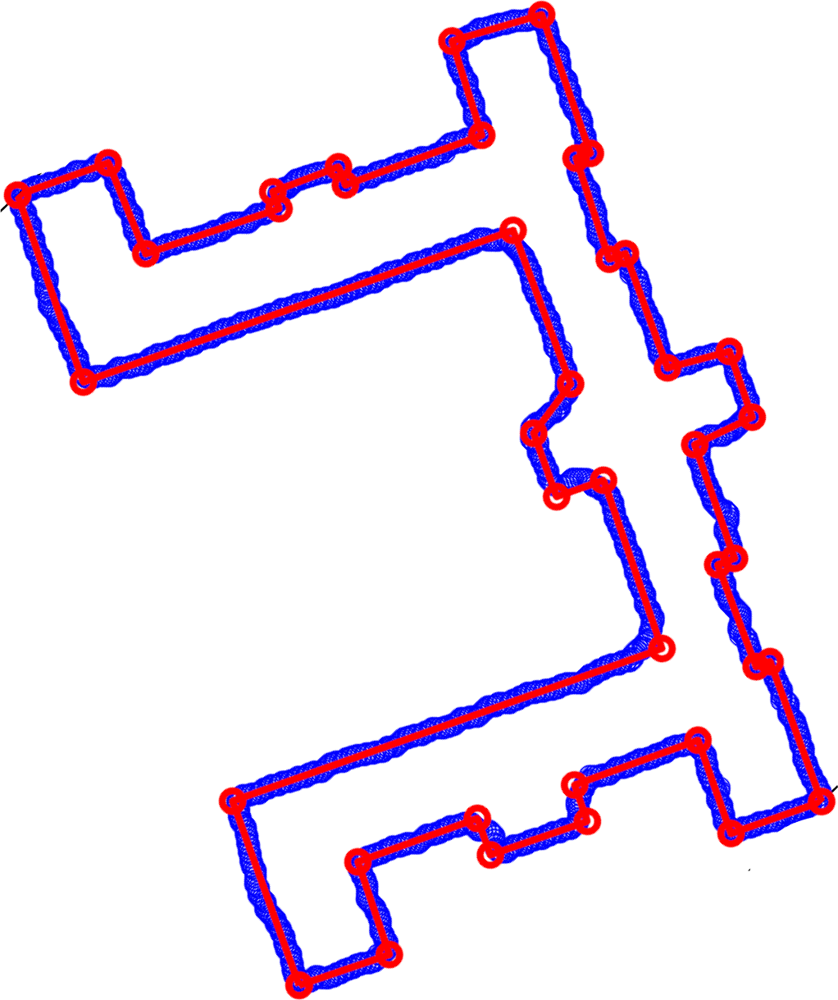
If the building is formed by a rectilinear polygon,
i.e., sides are perpendicular to each others from the top view, a method based on Minimum Bounding Rectangle (MBR) is applied for approximation. The MBR is computed by the classical Rotating Calipers algorithm [
23]. The original polygon is sequentially rotated in small steps around its center of gravity, e.g., in steps of 0.5 degree. In each step the bounding box is determined and its area is calculated. The rotation angle that results in the minimum bounding box provides the MBR. The MBR-based method is a top-down, model-based approach that hierarchically optimizes the initial rectilinear model by fitting MBR to all details of the data set. Principles of MBR based polygon approximation is presented in
Figure 10.
If the building is not rectilinear,
i.e., at least one side is not perpendicular to the other sides, a method based on RANSAC [
24] is applied for approximation.
RANSAC was originally devised to robustly fit one single model to noisy data. It turns out, however, that it can also be successfully used to fit a beforehand unknown number of models to the data: In the case of the ground plan boundaries, the number of line segments is initially unknown. We simply apply the method repeatedly—always deleting the already fitted given points from the input data—until either:
- (a)
we consider the lines found so far sufficient to construct the ground plan completely, or
- (b)
the number of points fitting to the best line segment with respect to the current iteration step falls below a chosen threshold t.
In this algorithm the straight lines are repeatedly extracted using the RANSAC algorithm and merged to form the final polygon.
Figure 11 shows the RANSAC based approximation of the same building represented in
Figure 10.
As an alternative to the RANSAC-based approximation algorithm, a method similar to MBR-based is proposed for the buildings containing several orientation directions. The method called Combined Minimum Bounding Rectangle (CMBR) based algorithm for hierarchical approximation of non-rectangular polygons. In this method, based on each orientation, a MBR (rectangle) polygon is estimated as first approximation level, as shown in
Figure 12(a,b). The intersection of the rectangles corresponding to each orientation produces the first approximation of non-rectangular building (
cf. Figure 12(e), yellow region). The first approximation area is subtracted from the original binary region to generate the remaining regions that should be approximated. The process is continued, similar to the MBR-based method but using all orientation directions, until no more regions remain or the remaining regions contain small number of pixels.
Figure 12(f) illustrates the final approximation result of the sample building by using two main orientations. The approximation result could be improved by taking into account more significant orientations.
All approximation methods are containing the parameters as “stopping criteria”, which could be tuned to provide desired level-of-detail for 2D approximation. The MBR- and CMBR-based methods are both iterative algorithms and in each iteration the remaining regions are checked if they have sufficient number of pixels for approximation or they can be neglected.
Figure 10(b) provides first approximation level of the building, which is an optimal rectangle. After generating remaining the details (
cf. Figure 10(c) or
Figure 10(e)), the size of the regions are compared with the predefined minimum size of accepted detail for further processing. The same procedure is included in CMBR-based method for further processing from
Figure 12(c) to
Figure 12(e). Likewise, in RNASAC algorithm, several parameters and thresholds are included, which assists to determine specific straight lines containing different consensus (number of inliers) or line size.
In order to include the other structures (here, with flat roof) into the merged parametric model generated in Section 2.2, the ground plan of the merged model is compared with an approximated polygon. The overall area of the approximated polygon is subtracted from the corresponding area of the parametric models. The positive pixels belong to protrusions and the negative pixels are related to indentations. The areas corresponding to the protrusions and indentations are again approximated. The average of the heights of the internal points of protrusion area is used as the height of the building part. Although, this does not mean that the protrusion parts have always flat roofs, but since their corresponding roof types cannot be distinguished by the proposed algorithm, a prismatic model is fitted to the points.
Figure 13 shows an example about a complex building containing several parts with different types of roof classes as tilted, flat, and dome shapes. The corresponding procedures and results to obtain approximated polygons to form prismatic model is represented in
Figure 10. Prismatic model (LOD1) is generated by giving an average height corresponding to all internal pixels of the approximated polygon and creating the roof and wall polygons (
cf. Figure 14).
In
Figure 15(a) the corresponding area related to the parametric models plotted as blue lines and approximated polygon by MBR based method is illustrated using red lines.
2.4. Merge Parametric and Prismatic Models
A final model of the building block is provided by including the prismatic model corresponding to the protrusion area to the parametric models and excluding the indentation area from it. The corresponding polygon nodes of indentation and protrusion regions are included in the overall 3D model. Finally, the inclinations of the building roofs are adapted after including the indentation nodes.
Figure 15(b) shows the final 3D reconstruction model of the building block after merging parametric and prismatic models. As shown, the building contains a dome shaped part that is not properly modeled.
3. Results and Discussion
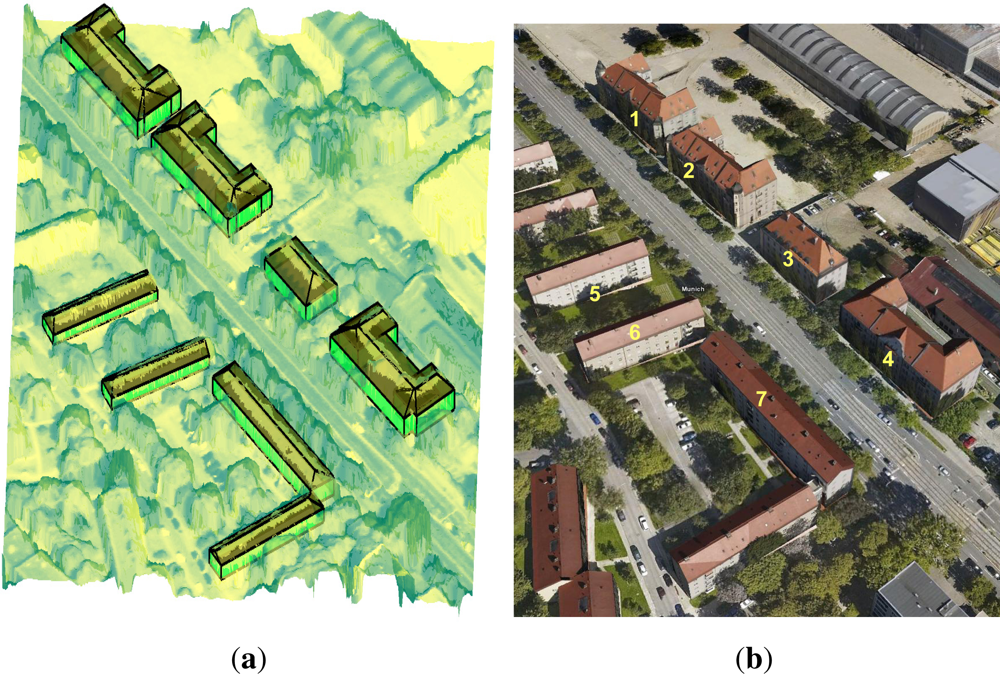
The proposed algorithm for the 3D reconstruction of buildings from Worldview-2 DSM by integrating image information has been tested in an area located at the city center of Munich, Germany. The area contains 7 buildings with different shapes that are all modeled using the projection-based approach.
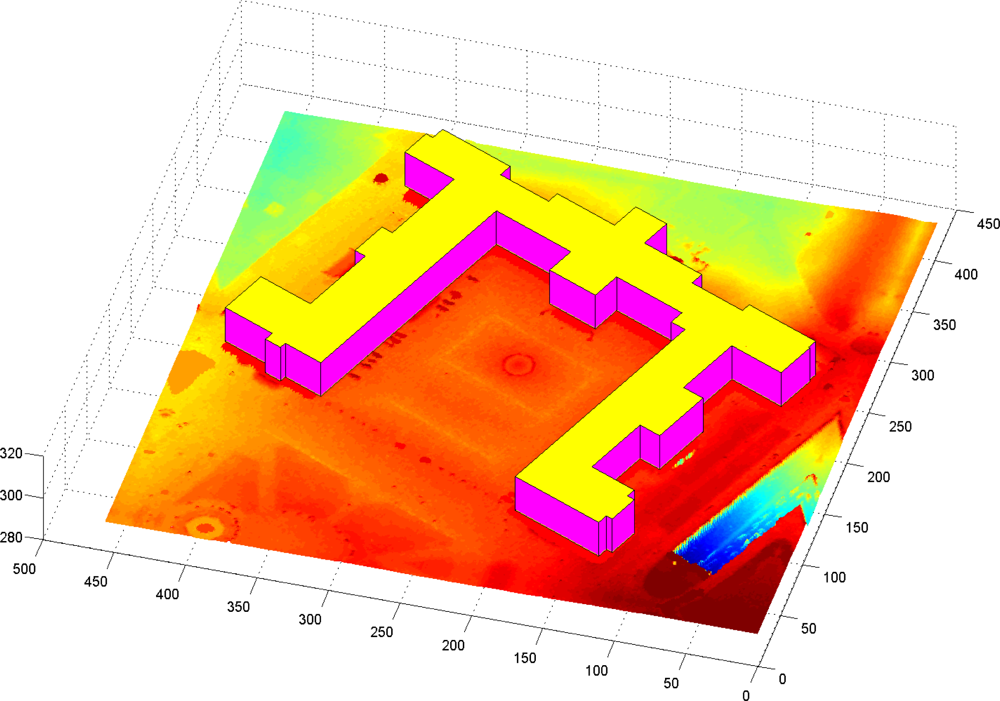
Figure 16 illustrates the vector polygons corresponding to the 3D models plotted on the orthorectified image (
Figure 16(a)) as well as the Digital Surface Model (
Figure 16(b)). The visual interpretation of the models from the top view (2D), comparing the orthorectified image with the DSM, shows that almost all the extracted eave and ridge lines of the buildings are located on their correct locations. As mentioned, the model still can be refined to generate coinciding corners.
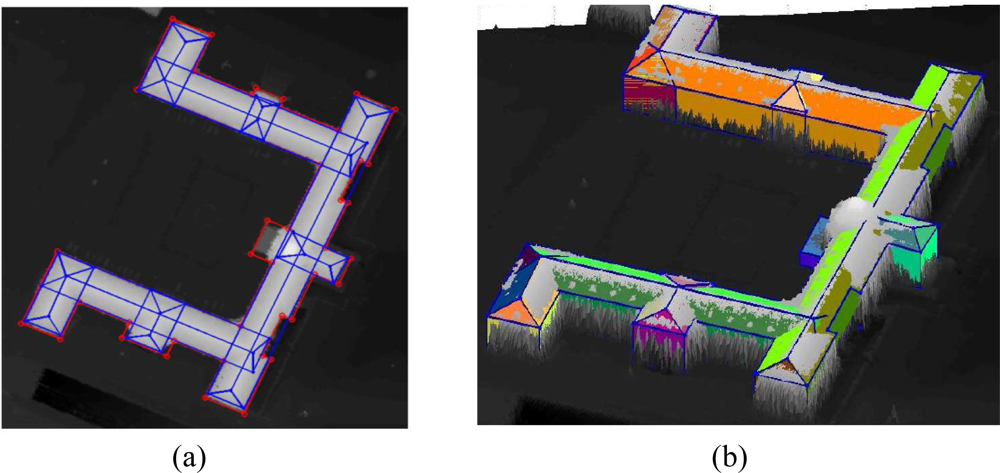
Additionally the comparison can be extended in 3D by superimposing the representation of the parametric models on a 3D surface generated from the DSM (
cf. Figure 17(a)). In this figure the roof and wall polygons are filled by green and red colors, respectively.
Accordingly, the quality of the model can be evaluated by the rate of visible colors against gray (height) pixels. In areas where the green colors are visible, the produced roof model is higher than the height pixels in the DSM. In contrast, the visible gray pixels on the roofs show that the roof model is located below the DSM in those areas. A similar conclusion describes the quality of the walls against DSM pixels.
Figure 17(b) shows a picture provided from “Google Earth” corresponding to the test area. It is captured from perspective view, which also proves the quality of the produced 3D model. The comparison of the model represented in
Figures 16 and
17(a) with this figure shows that there are still some small 3D structures such as dormers and cone shaped objects that are not modeled. This is due to insufficient allocated pixels for model generation corresponding to those regions in the DSM.
In addition to visual interpretation and comparisons, a quantitative assessment proves the high quality of the fitted models. In order to measure the statistical parameters, the corresponding heights of the walls and ridges are taken from official construction plans of the buildings.
Table 1 illustrates the corresponding heights of the walls and ridges of the buildings with the numbers given in
Figure 17(b). The table also shows the heights extracted from Ground Truth (GT), which are taken from building plan, versus the corresponding heights from 3D parametric models. The average and standard deviations of the differences between GT and model values are computed and added extra rows in
Table 1. It shows that the quality of the 3D model on the ridge points is much higher where the mean of the height differences is about 5 cm. The average between the height differences on the walls is about 45 cm. Due to a lower quality and smoothed behavior of the building walls in DSMs, a lower quality of the location of the eave lines compared with the ridge lines were expected. However, a standard deviation of about 40–50 cm for eave and ridge lines extraction from Worldview-2 DSMs proves that the methodology leads to very good results.
It is necessary to mention that due to the lack of a ground truth related to the horizontal coordinates (X and Y) of the model corners, only the height values can be evaluated using statistical parameters, and the evaluation of the horizontal accuracies can only be performed by visual interpretation.
4. Summary and Conclusions
An algorithm for the automatic 3D reconstruction of buildings using both the Worldview-2 DSM and the edge information from orthorectified images is proposed. According to the ridge information, the building block is decomposed into several parts depending on the number of ridge lines. For each ridge, a projection plane is defined and all points located on the buffer zone of the ridge line are projected onto that plane. Next, a 2D model supported by maximum number of projected points is modeled and then extended to 3D to shape a hipped- or gabled-roofs (parametric model). Integrating all 3D models corresponding to each ridge line produces the parametric model of the building block.
Additionally, prismatic models with flat roofs are provided regarding the remaining areas of the buildings, which are not already modeled by the projection-based method. Finally, all parametric and prismatic models are merged to form the final 3D models of the buildings. Here it is important to mention that all parameters, such as thresholds for binarization steps, thresholds for RANSAC line fitting, size and area thresholds, and other parameters, are empirically selected and defined in the program, which can be almost used for other Worldview DSM and orthorectified images with same resolution.
The example used in the previous section to illustrate the developed algorithm shows that the concept for building reconstruction provides an appropriate result in particular about the buildings isolated from the neighboring trees. Since the data used are only satellite data, it also shows that it is possible to derive already LOD2 building models from these data, which has a lower resolution in comparison with airborne data. It follows that for areas where no airborne measurements are available, satellite data could serve as the source for city modeling. Further applications could be 3D change analysis or damage assessment after earthquakes or other hazards.
However, from the quantitative assessment provided by
Table 1 and also
Figure 17(a), we can conclude that:
Boundary approximation using MBR and CMBR methods are efficient and robust techniques that employ rectangular and non-rectangular boundary polygons. In a future work we aim to expand the algorithm by the approximation of more complex building shapes such as buildings boundaries containing curves and lines.
Automatic ridge line extraction method using the combination of image and DSM data is an appropriate method and provides high quality ridge line with standard deviation of about 50 cm.
Detecting the building walls is more critical than detecting the ridges, particularly when the building is connected to a tree or the building wall is smoothed due to spatial interpolation after image matching. Nevertheless, if the buildings are isolated from the neighboring buildings or other 3D objects, the building wall could be extracted with a proper quality as seen in
Table 1.
Here it should be mentioned that the existence of the 3D model of roof superstructures containing tilted faces (such as attic windows) depends on whether the corresponding ridge line is extracted or not. As mentioned, if the corresponding ridge line contains enough number of pixels (depending on the image resolution and size of the ridge line), the line can be extracted by the RANSAC algorithm. This happens usually for very big castles containing sufficient number of pixels for a roof superstructure. A similar reason exists about other small structures such as chimneys, whether they contain enough number of pixels (area threshold) to be modeled or not.
Compared with previous methods, the strength of the proposed algorithm include: (a) it is a model-driven approach, i.e., the aim is to provide a simple model that is as close as possible to reality beside satisfying most of the applications; (b) it decomposes the building block to individual building parts, which makes the modeling simpler and also faster; (c) the most important description of this method is “projection-based”, i.e., projecting the 3D point cloud onto the 2D plane, which causes the preliminary model to be generated in 2D space and then extruded into the 3D space. This makes the process more robust and much faster due to this dimension reduction step.
On the other hand, the drawback of the algorithm is its sensitivity to the location and accuracy of the extracted ridge lines. The quality of the final model is directly related to the quality of the extracted ridge line. Other limitation concerns the buildings connected to a tree from one side or surrounded by trees, which makes wall detection inaccurate.