Recent Trend and Advance of Synthetic Aperture Radar with Selected Topics
Abstract
: The present article is an introductory paper in this special issue on synthetic aperture radar (SAR). A short review is presented on the recent trend and development of SAR and related techniques with selected topics, including the fields of applications, specifications of airborne and spaceborne SARs, and information contents in and interpretations of amplitude data, interferometric SAR (InSAR) data, and polarimetric SAR (PolSAR) data. The review is by no means extensive, and as such only brief summaries of of each selected topics and key references are provided. For further details, the readers are recommended to read the literature given in the references theirin.1. Introduction
In the 1985 Pioneer Award story [1], Carl Wiley, the inventor of SAR, stated with his modest manner:
I had the luck to conceive of the basic idea, which I called Doppler Beam Sharpening (DBS), rather than Synthetic Aperture Radar (SAR). Like all signal processing, there is a dual theory. One is a frequency-domain explanation. This is Doppler Beam Sharpening. If one prefers, one can analyze the system in the time domain instead. This is SAR.
The conception of SAR was recorded in a Goodyear Aircraft report in 1951 by Wiley (note that the origin of the aperture synthesis technique was an early phased array antenna called “bedspring antenna” developed by Sir Watson-Watt in 1938 [2]), followed by the first SAR operation in 1952. Experiments continued with airborne SARs, and it was in 1978 when the first spaceborne SAR for earth observation on board the SEASAT satellite was put into orbit. Despite its short lifetime of 106 days, SEASAT-SAR [3] was the pioneering mission which has lead the SAR technology to the present and future state-of-the-art status [4].
SAR is an imaging radar, which can produce high-resolution radar images of earth’s surface from airborne and spaceborne platforms [5]. Since SAR is an active sensor and uses the microwave band in the broad radio spectrum as in Figure 1, it has a day-and-night imaging capability, and an ability of penetrating could cover, and to some extent, rain (see Figure 2). Further, L-band and P-band SAR has relatively long penetration depth into vegetation and soil, enabling to extract information on the interior of the targets. Because of these characteristics, SAR has been used in various fields of research [6], ranging from oceanography to archeology as listed in Table 1.
After the launch of SEASAT, scientists realized the potential of SAR in the variety of fields of geoscience and engineering applications. The second spaceborne SAR following SEASAT-SAR was ERS-1 SAR [8] in 1991 (see Table 2 and Figure 3). During the 13 years of interval between these two spaceborne SARs, much effort was made to develop and experiment new techniques with airborne SARs and Shuttle Imaging Radar (SIR) series. The SIR-A mission was in 1981 with a L-band HH-polarization SAR on board similar to SEASAT-SAR. The SIR-B mission [9] followed in 1984 with SAR operating at the same frequency and polarization as those of SIR-A, but varying incidence angles by a mechanically steered antenna [10].
The SIR missions continued, and in 1994 the SIR-C/X-SAR was in orbit, which, for the first time for its kind, operating at multi-frequency X-, C- and L-bands with a full polarimetric mode [11,12]. The Shuttle Radar Topography Mission (SRTM) [13–15] in 2000 carried X- and C-band main antennas on the cargo bay and a second outboard antenna separated by a 60 m long mast (see the illustration in Figure 4). With its interferometric system using the two antennas the SRTM produced a digital elevation model (DEM) of approximately 80% of land.
Increasing number of spaceborne SARs have been launched recently and further missions are being planned. A recent special issue of IEEE Proceedings describes the details and applications of ALOS-PALSAR [16–18] (and its predecessor JERS-1 SAR in [19]), RADARSAT-2 [20] (see also RADARSAT-1 [21]), and the formation flight of TerraSAR-X and TanDEM-X [22]. It should also be mentioned on the Cosmo-SkyMed constellation [23–25], and RADARSAT constellation [26–28] programs. The general trends are that the spatial resolution is becoming finer, and different beam modes are available including high-resolution spotlight and wide-swath scan modes with coarser resolution (see Figure 5 for different bean modes). The conventional single-polarization mode is becoming dual or full polarimetric modes.
There are many airborne SARs developed by various organizations as in Table 3 with examples in Figure 4, and almost all current systems operate at multi-frequency full polarization mode, some of which are equipped with cross-track and/or along-track interferometric modes. The spatial resolution is order of meters or less.
Apart from spatial resolution and altitude, the main difference of airborne SARs is the requirement of motion compensation. The platform of spaceborne SARs is relatively stable, but the airborne SARs often suffer from platform instability caused by varying speed and/or motion of aircrafts. Since the azimuth reference signal assumes a stable platform path, the azimuth reference signal does not “match” the signal in raw data, and the images are degraded. It is, therefore, necessary to estimate the platform movement to produce a correct azimuth reference signal in order to form images of high quality by airborne SARs. There exist several motion compensation (also called autofocus) algorithms based on, for example, the onboard measurements, optimizing the image intensity of point-like targets, and the difference in inter-look image position in multi-look images e.g., [29,30]. These early post-processing algorithms (apart from the direct estimation by onboard sensors) include the multi-look registration or multi-look map drift algorithms [31,32], multi-look contrast optimization [33], prominent point processing [34], phase difference algorithm [35], and phase gradient algorithm [36,37]. These algorithms often suffer from long processing times. To shorten the processing time and/or to be applicable to scenes without prominent point-like targets, several algorithms have been proposed, including the phase adjustment by contrast enhancement [38,39], autofocus by minimum-entropy [40], coherent map drift [41,42], and others [43,44]. It should be mentioned that spaceborne SARs, in particular interferometric SARs, sometimes suffer from image degradation by tropospheric and ionospheric effects as will be described in Section 4.1.3. High-frequency airborne SARs may have some effects when imaging through dense rain cells (see Figure 2 for microwave transmission rate), but in general, they are not affected by the atmospheric effects.
At the time of SEASAT, amplitude or intensity images were of main concern, and little consideration was given to preserving the phase in SAR processors. Of course, amplitude data containing much information on scattering media are the basis of SAR image analysis, and the utilization of amplitude data is still a subject of current active research. The additional potential information presented by SEASAT-SAR was the information in phase and polarization state in the coherently processed complex images.
The potential information in the phase of SAR complex images has led a new technology of interferometric SAR (InSAR) [45,46]. Today, InSAR is an established technology, and the cross-track InSAR (CT-InSAR) has been used for producing topographic maps [47–51], and measurements of crust movement caused by earthquakes and volcanic activity, and those of glacier movement [52,53].
PS-InSAR (Permanent Scatterer InSAR), InSAR CTM (Coherent Target Monitoring), and CPT (Coherent Pixel Technique) use the temporal phase changes of semi-permanent scatterers that consistently give rise to strong backscatter, and the measurement accuracy is of the order of several millimeters per year [54–62].
The along-track InSAR (AT-InSAR) can measure the velocity of ocean surface currents associated with tides, internal waves, and other oceanic features [63–73], and can also be used as a moving target indicator (MTI) to detect such deterministic (hard) targets as moving vehicles [74–79].
The polarization information has lead another new technology of polarimetric SAR (PolSAR) [80–87], which is a considerable current interest. PolSAR data contain information on scattering mechanisms by different objects’ structure and material, and as such, they can be used to distinguish the scattering objects and to improve image classification [88–127]. The details on the aforementioned references will be given in Section 5.
Linearly polarized microwave changes its polarization angle when it goes through dense electron clouds in the ionosphere. It is known as the “Faraday effect” or “ Faraday rotation”, and PolSAR can be a useful tool for the investigation of such effect [128–135]. Attempts have also been made to combine SAR polarimetry and interferometry. Pol-InSAR (Polarimetric-Interferometric SAR), first introduced by Cloude and Papathanassiou [136], is expected to achieve microwave tomography and information extraction in the forestry application [137–156].
Thus, the pioneering SEASAT-SAR has guided us to establish a new paradigm in radar remote sensing, and at present the state-of-the-art technologies developed in the new paradigm are taking a central role in the wide range of applications in earth science and related fields.
At this stage, it is useful to remind the geometry and terms used for the SAR systems as shown in Figure 6. An antenna transmits a series of FM (Frequency Modulation) pulses also known as chirp pulses at an off-nadir angle θoff off in the plane normal to the satellite trajectory as it travels in the azimuth direction with a constant velocity V. The illumination direction is called the slant-range direction, and the ground-range direction is the illuminating direction on the ground. The angle between the illumination direction and the direction vertical to the surface is called incidence angle θi, and is almost the same as the off-nadir angle for airborne systems. For spaceborne systems, the Earth’s curvature needs to be taken into consideration, and therefore the incidence angle becomes several degrees larger than the off-nadir angle. As is well known for most of SAR systems, the fine resolution in the range direction is achieved by pulse compression, and that in the azimuth direction by aperture synthesis [5].
In the followings, the recent trend on SAR technologies is briefly described, followed by a summary on SAR applications in the selected fields of earth science is described. In the third part, the principle of InSAR is presented, and that of PolSAR is summarized in the fourth part with concluding remarks in the final part.
2. Recent Trend
2.1. Platform Weight
Tables 2 and 3 (for further details, see [157]) show the parameters of selected spaceborne and airborne SARs respectively. One of the recent trend is the lighter weights of spaceborne SARs. The very first SEASAT-SAR weighted approximately 2.3 tons, while that of recent SAR-Lupe is mere 0.77 tons. To reduce the weight, SAR-Lupe uses a fixed solar panel, and a parabola antenna with a diameter of 3 m for both the signal transmission and reception and also for downlink. Thus, in a strict sense, SAR-Lupe does not make real-time observation, but the data collected by the parabola antenna are stored in a recorder and then downlinked later by the same antenna.
The heaviest satellite carrying SAR was ENVISAT which weighted approximately 8.2 tons; the Japanese ALOS was the second-heaviest with 3.85 tons. The main reason for the heavy weight is that the satellite carries many sensors on board. ENVISAT (ceased its mission in May 2012), for example, carried 10 optical/infrared and microwave instruments including ASAR (Advanced SAR). ALOS (ceased its mission in May 2011) carried PALSAR and two optical sensors. Multiple sensors on a same platform such as ALOS can be useful for simultaneous data acquisition by different types of sensors, but at the same time, there is a conflict of the data acquisition priority. The priority of ALOS-PALSAR was given to the descending mode because the optical sensors could be operated during daytime only. Cosmo-SkyMed, TerraSAR-X, and SAR-Lupe are “sole-SAR” satellites, and as such, their weights are considerably reduced. As for the sole-SAR satellites of KOMPSAT-5 (Korea in 2012), Sentinel-1 (ESA in 2013), ALOS-2 (Japan in 2013), and AstroSAR-Light (ESA, in TBD), this trend may well continue in the future spaceborne SAR missions.
2.2. Revisit Time and Bistatic SAR
These sole-SAR satellites are compact, and several SARs of the same type can be put into orbit. This, in turn, reduces the revisit times which have been one of the major problems in satellite remote sensing. The revisit time of a single SAR can be reduced by changing the beam modes and dual-sided imaging: the latter being adopted by RADARSAT-2. As in Table 2, there are four identical Cosmo-SkyMed (reconnaissance and civil applications) and five SAR-Lupe (reconnaissance), with their revisit time of 7 h and less than 10 h respectively, as compared with, for example, 24, 35, and 46 days of the nominal revisit times of RADARSAT-2, ENVISAT-ASAR, and ALOS-PALSAR respectively. Note that the revisit time depends on the incidence angle, beam mode, and geographic location of the swath. It is, in general, shorter for the wide-swath mode than narrow-swath beam mode, and in the polar regions than the equator areas. Reduction of the revisit time for the wide-swath mode, however, is achieved at the expense of spatial resolution. Currently, a new generation of spaceborne SAR systems is being planned to provide a wide-swath coverage without loosing spatial resolution using a digital beam forming (DBF) technique (for DBF, see Section 2.7). TanDEM-L, for example, will cover a swath width of 350 km with spatial resolution of 10 m, and the revisit time will be 8 days [22,158].
As to the number of identical SARs, the revisit time (strip map mode) would be 1 h if 14 identical SARs are used, and it would be 10 min for 36 SARs. Further, a bistatic SAR system consisting of 3–4 geostationary satellites equipped with transmission-only antennas and 24–26 low-altitude reception-only SARs (of which the movement will be used for azimuth compression) will reduce the revisit time to 10 s [159].
The present SAR systems can be transformed to bistatic systems by launching (and using existing) conventional SARs with reception-only satellites and/or aircrafts at lower altitudes. Indeed, recent studies indicate increasing effort on the feasibility of bistatic SAR systems [160–170].
2.3. Interferometry
It was in 1974 when the concept of SAR interferometry for Earth observation was first proposed [47]. SAR interferometry is now a well known established technique. Cross-track InSAR (CT-InSAR), or generally referred to as InSAR, can produce a digital elevation model (DEM) for spatial changes of surface height; the crust movement and deformation caused by, for example, earthquakes and volcanic activities, and glacier flows can be measured by differential InSAR (DInSAR). For repeat-pass InSAR, where multiple data are acquired with a single SAR antenna using multiple baselines at different acquisition times, short revisit times are important to avoid temporal decorrelation, and the fine control of baselines is also essential. The temporal decorrelation caused by the changes in shape of scattering surfaces is large for high-frequency SAR such as TerraSAR-X and RADARSAT-1/2 in comparison with L-band SARs. For example, high temporal coherence was achieved by L-band JERS-1 SAR between the interval of 2 years 5 months for the surface height change caused by the 1995 Great Hanshin earthquake, Japan (see Figure 7). In order to achieve high temporal correlation and short baseline separation at X-band, a bistatic system is employed using TerraSAR-X and TanDEM-X [22,171]. For bistatic InSAR, fine positioning of two satellites and baseline control are required.
Other applications of CT-InSAR are also being sought for image classification and change detection using the coherence information.
Along-track InSAR can measure the line-of-sight velocity of ocean current. This technique can be applied to moving target indicator (MTI) including ocean current and hard targets such as vehicles and ships. AT-InSAR was restricted to the airborne systems because of technical difficulty. The first spaceborne AT-InSAR is made by TerraSAR-X and TanDEM-X, and the work is in progress. AT-InSAR with two antennas placed along the platform can measure the velocity in the range direction only, but the University of Massachusetts developed an airborne AT-InSAR consisting of four antennas, two of which are looking at forward direction and the other two at rear direction, and thus, the current vector can be measured [68,71].
The combination of interferometry with polarimetry has been studied since late 1990s. Pol-InSAR is still in the developing stage, with its main theme of SAR tomography, tree height and biomass estimations, and improvement of classification accuracy. RAMSES in Table 3, for example, includes a Pol-InSAR mode at X-band with which simultaneous interferometric polarimetric data can be acquired.
2.4. Polarimetry
As mentioned earlier, there is a strong trend of utilizing polarimetric information in the polarized SAR data. From Table 2, it can be noticed that the earlier spaceborne SARs from SEASAT-SAR to RADARSAT-1 operated with a single polarization, and that the recent SARs including ALOS-PALSAR operate with quad- (full) polarization. SAR polarimetry using quad-polarization data is the HV-polarization base in which an antenna transmits and receives horizontally and vertically polarized signals. A single set of image, therefore, consists of four complex images of different polarization combinations, i.e., HH- (transmit and receive horizontally polarized signals), HV- (transmit horizontally polarized signal, receive vertically polarized signal), VH-, and VV-polarization images. The dual-polarization implies the combination of two polarizations such as HH and HV or HH and VV. Once the quad-polarization data on the HV-polarization base are acquired, the scattering matrix (composed of HH-, HV-, VH-, and VV-polarization elements) can be transformed into those on different polarization bases, such as the circular polarization base, where the same polarimetric information can be interpreted from different viewpoints.
Another technique recently suggested is the hybrid polarization imaging mode known as the compact polarimetric SAR (CP-SAR) [172–178]. In this mode, the transmitting signals are either circularly polarized or linearly polarized with 45° (or π/4) rotation from the horizontal or vertical axes, and horizontally and vertically polarized backscattered signals are received. Although CP-SAR does not completely provide the information of scattering targets that can be obtained by fully polarimetric SAR, it has an advantage of transmitting only a single polarization signal instead of two (H and V) signals of fully polarimetric SAR, and thus reducing the power and hardware requirements. Further, for spaceborne circular polarized CP-SAR, the signals would not be affected by the ionospheric effect of Faraday rotation on longer wavelengths such as L- and P-bands. Another advantage of CP-SAR is on the swath width. The pulse repetition frequency (PRF) needs to be increased for the full-polarization mode, which in turn has the effect of narrowing the swath as compared with, for example, the strip-map mode. CP-SAR can be used with no increase of the PRF, and hence without narrowing the swath width.
As to airborne SARs, almost all systems including those listed in Table 3 are capable of operating in the quad-polarization mode, except the Swedish CALABAS-II in HH-polarization only, and DBSAR in HH/VV dual-polarization. The further details on SAR polarimetry will be given in Section 5.
2.5. Spatial Resolution
Table 2 also shows that the resolution of spaceborne SARs is improving fast. At L-band, the spatial resolution of SEASAT-SAR was 6 m in single-look azimuth direction and 25 m in range direction; while that of ALOS-PALSAR, the only L-band spaceborne SAR at that time, was 4.5 m (full single-look) in azimuth and 9 m in range directions. At X-band, TerraSAR-X, TanDEM-X, and COSMO-SkyMed have achieved 1 m resolution in both directions. Even finer submetric resolution of 0.5 m is achieved by SAR-Lupe. The fine resolutions of latter three SARs are in the SpotLight mode. Note that unlike the phase array antenna used by general SpotLight SARs, beam-steering of SAR-Lupe is made by rotating the parabola antenna. The resolution of the X-band TecSAR (Israel) launched in 2008 is said to be 0.1–1.0 m in the SpotLight mode.
The resolution of the most airborne SARs is of the order of 1 m or submetric as listed in Table 3. The frequency band ranges from the high frequency W-band (frequency 100 GHz: wavelength 0.3 cm) of RAMSES (Regional earth observation Application for Mediterranean Sea Emergency Surveillance) by the French ONERA (Office National dfEtudes et Recherches Aérospatiales) to low frequency VHF (frequency 22–80 MHz: wavelength 3.8–13.6 m) of CARABAS-II operated by Swedish Defence Research Establishment. The Ka-band UAV-borne SAR has the spatial resolution as high as 10 cm in the SpotLight mode.
Higher resolution is, of course, desirable for increased accuracies in deterministic and statistical measurements of physical and biophysical quantities of scattering targets, including classification, detection and identification.
2.6. UAV-Borne SAR
SARs on board of UAVs (Unmanned/Uninhabited Aerial Vehicle) have been studied and developed since the end of the last century, and are gaining strong attention in the recent years [179–184]. Many UAV-borne SARs (which can also be on board of airborne platforms), including Lynx in Table 3 and those in Table 4 are capable of operating in both the Strip and SpotLight modes. A X-band SAR on board of Global Hawk (USA) manufactured by Northrop Grumman operates at high altitude up to 20 km well above the commercial air traffic with little turbulence which reduces the requirements of motion compensation. It has a Strip mode MTI (Moving Target Indicator) with 6 m resolution and a SpotLight mode with 1.8 m resolution. Lynx developed by Sandia Laboratory and TESAR (Tactical Endurance SAR) in the Predator system are the medium altitude UAV-SARs at Ku-band having spatial resolution of 0.1 m and 0.3 m at SpotLight and Strip modes respectively. The recent Ka-band SAR has 10 cm resolution as noted earlier. Initially, these UAV-SARs have been developed and used for military reconnaissance, change detection, target detection and identification, but technology transfer, such as the case of JPL/NASA’s UAVSAR, to civil applications has been in progress [185,186].
2.7. Digital Beam Forming
With some exceptions of parabola antennas used in the SAR-Lupe constellation, the most current SAR systems use phased array antennas for beam forming using analogue electrical circuits. An alternative method of beam forming is to use digital circuits, known as digital beam forming (DBF). DBF is a technique of producing multiple beams by dividing an antenna into multiple sub-apertures, and digitally processing the signals of each sub-apertures independently [187]. The technique has been used in HF radars, sonar, and communication systems [188–191]; the idea of multiple-beam wide-swath SAR has also been suggested since 1980s [192–194]. Currently, DBF is considered to be a promising concept for future spaceborne SAR systems for solving the trade-off between the swath width and spatial resolution due to the limitation imposed by range and azimuth ambiguities. In the conventional SAR systems based on the analogue RF beam forming, the swath width and resolution are inversely proportional. For example, for TerraSAR-X, the azimuth resolution of 1–2 m can be achieved in the spotlight mode but with a narrow swath width of 10 km, while the swath width of the scan mode is 100 km, but the azimuth resolution is reduced to 16 m (e.g., [195,196]). A basic design of achieving high resolution in wide swath is DBF on receive with the conventional analogue beam forming on transmit, where a wide swath is illuminated using either a small part of an antenna or a small separate antenna, and the scattered signal is received by multiple independent sub-apertures; these signals are then processed independently to produce images of multiple swaths and to produce a wide-swath image by combining them. Several different approaches have been proposed, including a squinted geometry, a displace phase center antenna technique, both of which use sub-apertures aligned in the azimuth direction, a quad-element rectangular array system, and a high-resolution wide-swath (HRWS) system employing multiple sub-aperture elements split into both the azimuth and range directions [192–194,197–199], as well as the use of a large reflector antenna with feed arrays [158,200,201]. As mentioned in Section 2.2, Tandem-L will have 10 m resolution covering 350 km swath with repeat cycle of 8 days [22,158]. A new different approach to the DBF-based HRWS SAR system has also been proposed using a staggered illumination by continuously varying pulse repetition frequency with a full aperture on both transmission and reception [198,202,203].
DBF has not yet been realized on the spaceborne platform, but tested on the airborne platform. The digital beamforming SAR (DBSAR) listed in Table 2 is a state-of-the-art L-band HH/VV dual polarization SAR employing the DBF technique with multi-function capability of scatterometer and altimeter [204]. Based on DBSAR, a P-band DBF SAR with cross-tack interferometric capability is being planned [205,206].
3. Amplitude Information
When SAR raw data are processed, the resultant image is in a complex format, containing amplitude and phase (angle) in a single pixel. In this article, one pixel is assumed to be the same size as a single resolution cell, but it should be noted that a pixel size depends on the sampling interval in the processed complex SAR image, and it does not always correspond to a resolution cell. The phases of a complex image are randomly distributed over the interval (0, 2π], so that the phases do not carry information on the scattering objects, provided that there are more than 4–8 randomly distributed elementary scatterers within a resolution cell on the surface.
The amplitudes of each pixels are proportional to the magnitude of radar backscatter and they depend on SAR geometry, wavelength, polarization and the electrical properties of scattering objects. The conventional method of utilizing the SAR data is the inverse problem to retrieve the physical quantities from the amplitude dependence on the properties of scattering objects. Although these SAR data are of a single set of a single wavelength and at a single polarization, the image amplitude is one of the important parameters, containing the most basic information on the scattering objects; and the research on the quantitative relation between the amplitude and the scattering objects is considered to continue alongside with the new technologies of InSAR and PolSAR.
3.1. Land Surface Features
3.1.1. Different Backscattering Mechanisms
Figure 8 is an amplitude image around Mt. Fuji, Japan, acquired by ALOS-PALSAR L-band SAR. This amplitude image contains wealth of information on the scattering objects. For example, there is no backscatter from the shadowed part in the mouth of Mt. Fuji, and the image consists of just system noise. Normalized radar cross section (NRCS) is little from dead-calm water surface of lakes and sea, because, under no wind or very low wind speed, the most of the incident microwave is reflected in the specular direction and little is backscattered. However, NRCS increases with increasing wind speed since the surface becomes increasingly rough. NRCS from bare soil and weed in the maneuvering grounds is slightly larger than NRCS from the water surface due to backscattering from random rough surfaces. Vegetation in agricultural fields has larger NRCS than the former areas, and NRCS from forests is very large. Increased NRCS from vegetation and even larger NRCS from forests are mainly caused by volume and multiple scattering. The largest NRCS is from buildings in the cities because of multiple reflections between the ground and building walls. The very large NRCS from urban areas arises if the roads and building walls are aligned orthogonal to the radar illumination direction. Thus, if the urban structures are not in the orthogonal to the line-of-sight direction, the incident microwave does not backscatter toward the radar antenna and the images appear dark. In order to compensate this effect, polarimetric analyses can be applied to enhance the images of urban areas [118]. Another way of compensating this effect is to use SAR images acquired from different geometries.
3.1.2. Geometrical Effects
Apart from the image amplitude modulation by the microwave scattering process, the image modulation by geometrical effects inherent to the side-looking radar takes an important role. The areas surrounding Mt. Fuji are bare soil, but the face of Mt. Fuji in the radar direction appears very bright, partly because the surface is tilted toward the radar illuminating direction giving rise to increased radar backscatter by so-called tilt modulation, and partly because of the geometrical effect known as foreshortening. The latter geometrical effect, including shadowing and layover, can be seen in the mountain areas of high relief in Figure 8. The details of the geometrical effects are well known and can be found in any literature e.g., [5,207].
3.1.3. Forest Information Extraction
Monitoring of deforestation and regrowth is a one of the major issues of the earth environmental problems because of the role of forests for the carbon cycle and global warming, as discussed in COP13 [208] and also described in detail in the REDD (Reduced Emissions from Deforestation and Forest Degradation) Program [209].
The main theme of forest information extraction by SAR is the estimation of carbon stock through aboveground tree biomass for the study on the carbon cycle. Note that classification of tree species is difficult by SAR compared with optical sensors, and the fusion of both types of data should improve the measurement accuracy.
A simple theory of microwave backscatter from forests can be traced back to the water-cloud model for vegetation [210]. In this model, a vegetation canopy is modeled as a cloud of randomly distributed water droplets for its high water content, and the backscatter is expressed in terms of the moisture content of soil and vegetation, and plant height. The principle can equally be applied and extended to model the radar backscatter from forests [211–213]. However, it is not trivial in practice to use these numerical models directly to retrieve forest information and computing above-ground tree biomass, since many parameters, such as number of branches, orientations, and sizes, are required for computation. The practical approach is the empirical and model-based semi-empirical methods utilizing the relation between the SAR data and in situ sample data measured by field survey. There are four main empirical and model-based approaches to date. The first is to use the relationship between the NRCS and biomass or stem volume, and there exist a substantial number of reports on this issue for various locations and species [214–222] (see also a good review paper [223]). The second approach is based on SAR interferometry [224–235], (see also a recent study using UAVSAR [236]), and the third approach is based on PolSAR and Pol-InSAR [141,144,147–150,152–156,237]. The fourth approach is to use the relation between biomass and image texture [238–243].
The method based on NRCS has been studied since 1980s. The general trend is that NRCS increases with increasing aboveground biomass in both conifer and deciduous trees, but saturates at certain biomass levels. This saturation biomass increases with increasing radar wavelengths. Since the microwave of longer wavelength can penetrate deeper into forest interior, the backscattered microwave contains more information on the forest such as branches and trunks that are the major constituents of aboveground biomass. The dominant scatterers at X- and C-bands are the canopy layer; while those at L-band are the canopy and branches as well as the ground-volume (branches/trunks) reflection. The P-band backscatter has similar contributions as those of L-band, but with increased ground-volume contribution. It is also known that the cross-polarization data have higher correlation with tree biomass than the co-polarization data. Since the present scattering theories are not practical, regression analyses are usually made using the NRCS and sample biomass data acquired by field survey, and from the regression model function the average tree biomass of forests can be estimated from the NRCS of SAR data only. The model function is not universally applicable to all types of forests, but it depends on the forests types and locations, e.g., conifers, deciduous, broad or needle leaves, rain forests, or boreal forests, and ground topography, so that the corresponding model function needs to be recalculated for the forests of interest.
Although the topic of this section is the amplitude information, it is appropriate, at this stage, to provide a brief account on the techniques of InSAR and Pol-InSAR for the forest information extraction.
The general approach of interferometric SAR is based on the relation of the coherence of complex interferogram and stem volume, i.e., InSAR coherence decreases with increasing stem volume (Biomass), and also the relation of the InSAR phase with effective tree height. The coherence-based method uses a semi-empirical water cloud model, and the repeat-pass InSAR coherence of a forest is considered as the sum of the ground and volume contributions, which are expressed in terms of stem volume and tree height. There are several unknown parameters in this model, and they are empirically determined and approximated under appropriate assumptions. The model is trained with sample data and stem volume is estimated. For a given tree species, the stem volume is closely related to the tree height, and biomass using allometric equations e.g., [244].
The phase-based method originates from the early study using the C-band repeat-pass ERS-1 inteferometric data over boreal forests, suggesting that the coherence was high enough under stable environmental condition in winter to estimate the InSAR phase center (effective scattering center) which is close to the forest height, and hence the tree height (and biomass) could be estimated [224,225]. However, Santoro et al.[233] reported that the tree height estimation by InSAR phase is less accurate than that by InSAR coherence.
The upper limits of measurable biomass by the multi-temporal InSAR technique appear to be higher than those of NRCS saturation biomass. However, the technique is limited by the baseline decorrelation, and environmental conditions, including wind speed, temperature, rain, and snow. The results of the C-band InSAR coherence over boreal forests suggest that the most suitable conditions for the stem volume estimation is under stable winter conditions with a snow cover and an at least moderate breeze [235].
The recent studies suggest that Pol-InSAR (and tomography) is an effective means of retrieving forest information such as tree height [141,144,147–150,152,153], and to estimate above-ground tree biomass with increased accuracy compared with the PolSAR technique [155]. Estimated tree heights appear to be in good agreement with lidar measurements [141,147,148,152,152,156], suggesting a potential of combining lidar and Pol-InSAR for forestry and related applications.
On the other hand, several reports indicate the limitation of multi-temporal Pol-InSAR and InSAR methods imposed by the temporal decorrelation caused by the environmental conditions [231,233,235], which cannot easily be quantified in terms of interferometric coherence even if the information on these conditions are available [237].
The technique of biomass estimation by Pol-InSAR uses the Random Volume over Ground (RVoG) model which is also based on the water cloud mode. In this model, a covariance matrix is produced from the multiple polarimetric data sets acquired from slightly different baseline separations. The covariance matrix (see Equation (7) in Section 5) describes the degree of correlation between different polarization images that are directly related to the physical elements of scattering objects. This covariance matrix is decomposed into the ground and volume contributions; the former corresponds to the surface and double-bounce scattering contributions, and the latter the scattering contribution from vertically distributed canopy layer. In both covariance matrices, each elements (i.e., cross-covariance matrices) are proportional to the interferometric coherence or decorrelation between interferometric pairs of different baseline combinations. The forest height can be inferred from the different combinations of interferometric coherence under the same assumptions as those for InSAR technique, where the dielectric constant of canopy layers are statistically uniform and that the volume component obeys a negative exponential function in the vertical (forest height) direction (it is based on the negative exponential transmissibility).
The texture-based approach makes use of the non-Gaussianity of amplitude fluctuations in a high-resolution SAR images of forests. The principal idea of this approach is that the images of sparsely distributed trees have statistically high non-Gaussianity, and they tend to be Gaussian distributed as the forests become increasingly dense, i.e., increasing biomass. Thus, the model uses the relation between the parameter(s) of the amplitude distribution function that fits best to the data and sample biomass. Wang et al.[241,242] reported that the K-distribution [238,240,245–247] is a versatile distribution function that describes the non-Gaussian amplitude fluctuations in the high-resolution SAR images of forests. The robust model based on the regression relation between the amplitude or intensity moments and tree biomass does not require a distribution function [243]. Both the models have larger saturation biomass than the NRCS model. In the texture-based technique of Wang et al.[241] and Wang and Ouchi [242], only coniferous forests were used to test the algorithms, and thus, further studies using different types of forests are required for their validity.
It has been shown that the L-band NRCS depends also on the soil moisture [234,248]. It was found that the highest correlation was observed when the soil moisture was highest, that the influence of soil moisture on NRCS was biomass dependent, and that the effect was large for smaller tree biomass for the simple reason that the ground contribution increases with decreasing biomass. From the study over the Alaskan coniferous forests, Kasischke et al.[248] suggest that to use the L-band NRCS for the biomass estimation and monitoring forest regrowth will require development of approaches to account for the variations of soil moisture, particularly, for the forests of low levels of aboveground biomass.
In the most studies mentioned above, the forests are located on flat ground or ground of gentle slope. In the areas of large topographic undulations or mountainous regions, there exist the effects of foreshortening and layover, resulting in the increased NRCS and hence spurious relation between the above ground biomass and NRCS. Thus, the removal of topographic contribution to NRCS is required for such cases [207,249,250].
3.1.4. Soil Moisture
Estimation of soil moisture is one of the top-priority subjects in agriculture and in the study on the interaction between atmosphere and land surface. Apart from the SAR parameters (radar incidence angle, wavelength, and polarization), there are two main contribution to radar backscatter from bare soil; surface roughness and dielectric constant, the latter of which yields the soil moisture. In order to retrieve the soil moisture content, it is necessary to eliminate the contribution from surface roughness, and the problem is ill-posed such that it is not a straightforward task from a single set of SAR data without prior knowledge. It becomes even more difficult for the fields covered by vegetation and the ploughed fields which give rise to the directional and surface-tilt dependencies on microwave backscatter.
To date, three types of models for soil moisture retrieval have been proposed: physical-based theoretical model, semi-empirical model, and empirical model. In the physical-based model, the NRCS is computed using scattering theories that take into account the dielectric constant of the scattering surface [251] (see also [252]). The generally used theory is the integral equation model (IEM) first developed by Fung et al.[253], which is based on the combination of the Kirchhhoff or physical optics model (KM, POM) [254] and the small perturbation model (SPM) [255,256]. In principle, the former is applicable to the surface (single-bounce) scattering from the perfectly conducting surface and is independent of polarization. The latter is polarization-dependent and is a function of the dielectric constant of the scattering media of slightly rough surface. Although improved IEM [257,258] and several different approximations [259–262] (see also a recent comprehensive book by Fung and Chen [263]) have been proposed, it is rather difficult to estimate soil moisture from theoretical models alone without prior knowledge such as surface roughness, and it is rarely used in practice.
Empirical models such as those of [264–266] are based on the empirical relation between the NRCS and soil moisture, and as such, they are site-limite, dependent on radar parameters and surface roughness, and require a large amount of datasets. The empirical models can be useful for the areas where sample data are collected, but they are not, in principle, applicable to other sites.
Semi-emperical models overcome the difficulty of the theoretical models by combining the scattering theories and empirical models [267–270], which do not require prior information on surface roughness [271]. The model developed by Oh et al.[267,270] appears to be most widely used. In this model, the ratio of σHH / σVV and that of σHV/ σVV are expressed as functions of the Fresnel reflection coefficient and surface roughness, where σmn is the NRCS of mn polarization with m, n = H, V. Since there are two functions (polarization ratios) and two unknown parameters (dielectric constant and surface roughness), the dielectric constant and hence soil moisture can be estimated by solving these two equations with the empirical datasets of different polarizations. This model, therefore, requires fully polarimetric data.
The semi-empirical model of Dubois et al.[268] uses the functional expressions for σHH and σVV in terms of dielectric constant and surface roughness for specific radar parameters, and thus, requiring only the dual-polarization data sets. While, the model of Shi et al.[269] is based on the regression analysis of simulation of the IEM at a single polarization.
Numerous experimental studies have been reported on the soil moisture retrieval by active microwave sensors since mid 1970s, some of which agree and some disagree with the theoretical models and semi-empirical models. Examples include those of [272–282]. See also the techniques based on DInSAR data [283], CP-SAR data [135], PolSAR data [284], and the combination of optical with SAR data [285] and with PolSAR data [286]. For further details, please see the special issues on SMEX 2004 (Soil Moisture Experiments 2004) [287] and Retrieval of Bio- and Geophysical Parameters from SAR Data for Land Applications [288]; also the operational performance [289]. An excellent and comprehensive review article with extensive reference papers by Brian et al.[290] is also available.
It may be of some interest, although SAR sensors are not onboard, that the SMOS (Soil Moisture and Ocean Salinity) mission [291–293] was launched in 2009 to provide maps of soil moisture and ocean salinity by a passive L-band 2-dimensional microwave interferometric radiometer which is the first of its kind in the spacebone platform.
3.1.5. Vegetation
Another important topic in the field of agriculture is monitoring of staple foods such as rice, maze, wheat, and soybeans. Since rice, among those staple foods, is the major staple food for over the half the world population, monitoring of rice ecosystems by SAR is briefly described here as an example. On this topic, substantial numbers of studies have been reported to date using the test sites mainly in Asia [120,294–315].
From those studies, it is understood that the microwave backscatter at high frequencies such as K- to X-bands from rice fields is dominated by canopy scattering, while the microwave at lower frequencies such as L-band has contributions both from canopy and soil or water surface (when irrigated) due to longer penetration depth. The general trend of the temporal variation of NRCS from rice fields is that there is a certain amount of backscatter from bare soil before irrigation, and the NRCS drops to almost a system noise level after irrigation due to specular reflection by water surface. The area of rice plantation, and possibly yields, can be estimated from this information. The NRCS increases with the growth of crops, and the decreases slightly in the heading stage.
From the theoretical point of view, the temporal and spatial variations of NRCS can be computed by using models based on the radiative transfer theory [294,297]. However, due to the local variation and complexity of the theory, the empirical approach based on the regression analysis of NRCS and in situ data on the rice fields is generally used to monitor the rice ecosystems.
Measurements based on a multifrequency polarimetric scatterometer indicate that the backscattering coefficients of the high frequency bands (K- to X-bands) correlated poorly with LAI (leaf area index) and biomass of rice plants, while LAI is best correlated with the backscattering coefficients of C-band HH- and HV-polarizations, and the biomass is best correlated with those of L-band HH-polarization data. SAR measurements also showed that C-band HV-polarization data have a significant correlation with the development of rice plants [314,315]. In general, C-band microwave backscatter seems to show good correlation with rice plants with high signal-to-noise ratio (SNR), and it is also suggested the HH/VV polarization ratio is a useful parameter for monitoring rice during growing season and classification of rice and non-rice fields [308,309]. Similarly, a recent study using TerraSAR-X data showed a significant correlation of the X-band HH/VV ratio with the development of rice plants [313]. At L-band, it was reported that little radar backscatter from rice fields was observed in JERS-SAR and airborne Pi-SAR L-band data, and occasionally it yielded the Bragg resonant backscatter from regularly planted bunches of rice plants [301,305,307]. A recent report [311], however, showed some promise of utilizing L-band HV-polarization data by avoiding the Bragg scattering. Wang et al.[310] also showed the possible use of PALSAR L-band HH-polarization data that are sensitive to the structure of rice plants than VV-polarization data. Polarimetric analyses have been studied for the application to rice monitoring, and Li et al.[120] concluded that the Touzi decomposition [108] is best for classification of rice fields, requiring only a single date of imagery. Based on the analyses of RADARSAT-2 quad-polarization data, Wu et al.[314] suggested a good set of parameters to classify rice fields are those at HH- and HV-polarizations, and HH/VV ratio.
3.1.6. Other Land Features
Measurement of surface topography by radar is generally made by InSAR (see Section 4 and references therein). Another technique is radargrammetry [316–319] which is based on the photogrammetry utilizing the parallax of stereoscopic pairs of images of a same area acquired with two different viewing angles. The main difference between the two approaches is that the parallax measurements are made using the phase difference in InSAR and amplitude in radargrammetry. Radargrammetry has been used for producing the surface relief of the planet Venus by the S-band Magellan-SAR [320–322] and Earth by RADARSAT [323] with recent examples by TerraSAR-X [324], Cosmo-SkyMed [325], and the combination of the both [326]. These techniques require multiple sets of complex (InSAR) or amplitude (radargrammetry) SAR data. While, radarclinometry [327–333], based on the optical shape-from-shading [334], uses only a single SAR image to estimate local terrain slope by inversion of the radiometric incidence angle correction. Radarclinometry originates from photoclinometry (see [328] and references therein), and has been studied in the field of computer vision [335]. Radarclinometry using SAR data was first proposed by Wildey [327,328] for producing landscapes of Venus by the Venera-15 [336], where stereoscopic SAR data were not available. Since radarclinometry relies on the relation between the image intensity (or amplitude) and local surface slope, modeling of intensity distribution is crucial. The Lambertian model, generally used in the photoclinometry [334], assumes a random rough and statistically uniform surface yielding the image intensity proportional to the cosine of the local tilt angle. However, this model is not generally applicable to SAR data, and various distribution functions have been used to model SAR image statistics, including Gaussian [329,337], Rayleigh [338], Gamma [339,340], and Rayleigh-Bessel composite [332] distributions (see also [238]). Radarclinometry is simple and easy to implement, but the technique is considered as a qualitative relief reconstruction method for its accuracy is marred by large errors caused by the geometric effect of foreshortening and speckle noise [333].
Amplitude data can be applied to monitoring and estimation of parameters of other land features including those listed in Table 1. The progress and present status in these fields of applications can be found in recent journals and proceedings (e.g., [341–344]). Note that the aforementioned references contain SAR applications to land surfaces using not only amplitude information but also applications to other fields such as oceanography, as well as technology and methodology.
3.2. Oceanic Features
The research and development on SAR applications to oceanography are matured to a certain level, and a large number of papers and documentations are available elsewhere (see, for example, [345,346], and the proceedings on ESA documents from the series of SEASAR Workshop [347–350]).
3.2.1. Scattering from Sea Surface
Figure 9 is the ERS-1 C-band SAR image of the English Channel. The microwave backscattering process from sea surface is predominantly surface scattering (apart from volume scattering from forms and sprays, and man-made targets such as vessels), and NRCS depends on surface roughness and dielectric constant of the water, e.g., [345,351,352]. The elementary scatterers are small-scale waves whose wavelength satisfies the Bragg resonance condition, LBragg = λ/(2 sin θi), where LBragg is the wavelength of small-scale waves, λ is the radar wavelength and θi is the incidence angle. It may be of historic interest, but as the name suggests, the Bragg resonance scattering was first discovered by Bragg in the X-ray diffraction from crystals in 1913 [353,354]. It was 42 years later in 1955 that the phenomenon of the Bragg scattering in the microwave backscatter from the sea surface was first found by Crombie [355]. There are numerous experimental evidence to support the theory of Bragg waves as the main elementary scatterers on the sea surface. Temporal and spatial changes of the Bragg waves caused by, for example, ocean waves, internal waves, and ocean wind, modulate the radar backscatter, and thus, these oceanic features can be made visible in SAR images.
At this stage, the criterion of surface roughness is introduced. The criterion, whether a surface is rough or smooth, is dependent on the radar wavelength and incidence angle. According to the Rayleigh criterion, the surface is considered as rough yielding large radar backscatter if the standard deviation σH of vertical undulation is large compared to the reference roughness λ/(8 cos θi), the surface is moderately rough and smooth if σH is comparable with and much smaller than the reference roughness respectively (σH should not be confused with NRCS σHH,VV,HV). This criterion applies any surface over water and land. Since the roughness depends on the radar wavelength, a surface which is rough for X-band and C-band SARs becomes intermediately rough or smooth for L-dand and P-band SARs.
3.2.2. Oil Slicks
The dark areas near the shore in Figure 9 are the smooth surface under no or little wind. The surface is “mirror-like” without Bragg waves, and most of the incident microwave is reflected away in the specular direction. Oil has larger surface tension than water, so that if oil slicks are present, they damp small-scale Bragg waves, resulting in reduced NRCS as compared with oil-free surface. The dark linear feature in Figure 9 is considered as the oil spill by a moving ship. Monitoring oil slick is an important issue in marine environment, but also it has been used to discover submarine oil fields by observing oil slicks constantly leaking from the oil fields [356–359].
In general, high frequency bands such as X- and C-band are used mainly because the damping effect is larger for the Bragg waves of shorter wavelengths. Note, however, that L-band can also be used to extract the dark features as demonstrated using ALOS-PALSAR e.g., [360,361] (see also oil detection by L-band UAVSAR [362]). VV-polarization is preferred due to larger radar backscatter than HH-polarization from sea surface [351], yielding larger difference between the images of oil slicks and surrounding waters. The wind speeds under which the dark features of oil spill can be distinguished from surrounding waters are approximately 3–14 m/s [363,364]. If the wind speed is less than ∼3 m/s, both the surfaces with and without oil slicks become equally smooth, and indistinguishable in SAR images. With increasing wind speeds above ∼14 m/s, oil is dispersed by mixing with sea water; surface also becomes very rough and the dumping effect becomes negligible. Oil dispersion is also caused by dissolution, oxidization, and biodegradation. Thus, with increasing time from the oil discharge and with increasing wind speed, oil slicks become undetectable. The time that takes oil to disperse varies from day to weeks, depending on several factors such as the types of oil, amount of discharge, and meteorological conditions.
The main problem in the detection of oil slick features is to separate the dark features caused by oil slick from other look-alikes such as calm sea surfaces, rain cells, upwelling, and biogenic slicks [365,366]. If oil is discharged from a moving ship, a linear dark oil trail appears in SAR images, but the shapes of slicks become complex if the oil is discharged from a maneuvering ship and strong non-uniform currents are present [367].
Several approaches have been proposed to solve this problem, including the algorithms based on neural network and fuzzy logic [368–376]. A recent study proposed a trained one-class classification approach [377] which appeared superior over the two-class classification algorithms such as those based on neural network. Further advances have been made recently using polarimetric analysis [378–380]. For further details, see comprehensive review articles with extensive reference papers by Topouzelis [381] and by Leifer et al.[382].
There are several operational systems for oil slick detection by SAR, such as GNOME (General NOAA Operational Modeling Environment) [383] and ISTOP (Integrated Satellite Tracking of Polluters) [384,385].
3.2.3. Ocean Winds
The wind-dependent radar backscatter as seen in Figure 9 is the basis of estimating the wind speed over the oceans. There are two approaches to the wind speed measurements by SAR. The first approach utilizes the standard algorithm based on the empirical geophysical model function (GMF) used in the microwave wind scatterometers [8,386–389]. There are well-defined GMFs at Ku-band to L-band, in particular, the Ku- and C-band GMFs are very accurate for the reasons that these bands are generally used for wind scatterometers [390]. The function relates NRCS at different incidence angles to the wind speeds (10 m above the sea surface) and wind directions with respect to the line-of-sight direction. The technique requires a precise radiometric calibration of the SAR image, and the estimation accuracy decreases with increasing wind speeds.
The second approach is based on the azimuth cut-off (or correlation) algorithm [391–393]. As will be described in the following section of ocean waves, the SAR image spectrum of a two-dimensional wave field is constrained in the azimuth direction by the non-linear image modulation process of ocean waves, and the smallest measurable wavelength, that is, the cut-off wavelength, is dependent on the wind and sea state conditions, where the relation can be described by a quasi-linear ocean-to-SAR transform model [394]. Based on this rationale, a semi-emperical model was developed to estimate the wind speed from the azimuth cut-off wavelength without requiring the wind direction and precise calibration of NRCS [391–393]. Although further validation tests are required, the model appears to show sufficient accuracy under some limited conditions.
Wind speed can be measured from SAR data, but, unlike scatterometers that use multiple beams at different look angles, the direction cannot be estimated directly by the single-beam SAR. In general, wind directions are estimated by other sources such as inter-look cross-spectra [395], wind streaks in SAR images [396–398], and polarimetric analysis [399,400]. The SAR-based wind data are used to fill the gap in the scatterometer data [401–405], and to study climate, atmosphere-ocean interaction and extreme events such as hurricanes and cyclones [406–408]. They are also used in coastal zones where the measurements are difficult to make by wind scatterometers of low spatial resolution ranging from several kilometers to few tens of kilometers. One of the interesting applications of SAR-based wind data is the search for suitable areas for constructing offshore wind farms [409–411].
3.2.4. Ocean Waves
Monitoring ocean waves is a main and practical application in oceanography for improving wave forecast model and providing real-time wave information. The interest on the SAR image analysis of ocean waves on a global scale started since the launch of SEASAT, and considerable efforts were made on the theoretical and experimental studies during late 1970s to early 2000s (see, for example [345,346,351,412–435], and references therein. See below for further details of these references). As a result, the imaging process is considered to be well understood, and, despite the criticism [436], the technique of estimating wave directional spectra is established as a routine wave monitoring system [437]. However, SAR is considered to be unsuitable for waveheight estimation due to the non-linerality of imaging process.
There are four image modulation processes of ocean waves [345]. The first is the tilt modulation in which the Bragg waves on the tilted surface toward and away from the radar give rise to large and small NRCS respectively, and therefore this image modulation is largest for range-travelling waves [414]. Image modulations by range-bunching [418,422] and hydrodynamic interaction [345] are also characteristics of range-traveling waves. The former is caused by foreshortening of waveheight undulation and the latter is associated with water movement. These modulations are small compared with the RCS modulation. These three range-dependent modulations become weaker as the wave propagation direction approaches to the azimuth direction, and they disappear for azimuth-traveling waves.
For azimuth-traveling waves, a very strong non-linear image modulation known as velocity bunching appears [412,413]. Velocity bunching is a result of orbital motion of Bragg-waves which move in the vertical direction as a long gravity wave propagates. The slant-range velocity component of the up-and-down motion of Bragg waves gives rise to their images displaced in the positive and negative azimuth directions by different amounts. The images of Bragg waves are thus dispersed in one image area and bunched in another area to yield a periodic image modulation. The modulation, however, is highly non-linear in that double peaks, 180° phase shift, or uniform modulations may appear depending on the SAR and wave parameters [420,421]. Because of this non-linearity, it has been suggested that wave information extracted from SAR data is not enough for operational use [436], including the possibility of detecting freak or rogue waves by SAR [438–440], claimed to have been observed by ERS-2 wave mode [441,442].
3.2.5. Internal Waves
Oceanic internal waves [443–449], whose existence is known as “dead water” in the Viking age [450,451], are subject of great interest for oceanographers for their strong energy transport between continental shelf and deep water, their effects on phytoplankton and fishery, and the effects on ships, submarines, marine architecture, oil platforms, underwater communications, and sonar, as well as the effects on underwater workers. A comprehensive report on the oceanic internal waves is available with the principles and examples in [452]. Internal waves are generated at the boundary of a stratified water layers, e.g., light (warm or low saline) water on top of dense (cold or high saline) water. When this boundary is disturbed by ships, submarines, or the interaction between current and bottom topography, internal waves are produced on the boundary. As the waves propagate, the water particles take circular motion, and this motion in the upper water layer gives rise to converging and diverging surface currents. The surface of current convergence becomes rough, while that of diverging current becomes smooth. These smooth and rough surfaces can be imaged by SAR as a manifestation of internal waves [453]. The another mechanism is the dumping of small-scale waves by surface films in the current convergence zone which appear dark in SAR images [454–457].
Internal waves appear either as solitary waves (solitons) or a wave packet containing multiples of waves of increasing wavelength with increasing distance from the source of wave generation. Unlike ocean surface waves of wavelengths up to several hundreds of meters, the wavelengths of internal waves range from hundreds of meters to tens of kilometers with phase velocities from about 0.1 m/s to several m/s with periods ranging from several minutes to several hours, and propagate long distance.
The general theoretical interpretation is based on the non-linear Korteweg-De Vries (K-dV) equation that describes the interface displacement between the two layers in terms of phase velocity, non-linear coefficient, and dispersion coefficient [458,459]. The K-dV equation, under certain conditions, has an analytical solution that describes nonlinear solitary internal waves (solitons) in the water of constant depth [460,461]. The amplitude, phase velocity of solitons, and horizontal velocities of water particles can then be calculated. Because of the nonlinear nature of the K-dV equation, its solutions and approximations under different conditions have been a subject of much interest in the fields of mathematics and nonlinear studies as well as fluid dynamics. The modified K-dV equation takes into account the effects of water depth and nonuniform medium, which can also be used to simulate the evolution of internal waves [462–470].
Given the spatial and temporal variations of the surface current induced by the internal wave, the changes of surface waves can be approximated by using the action balance equation [471–474] that describes the waveheight spectrum in terms of the varying surface current, wind speed and direction. Scattering models such as POM is then used to compute the NRCS from the water surface perturbed by the interaction of surface waves and currents [475–477].
Observations of internal waves by optical sensors onboard aircrafts and satellites were reported in the 1950s to 1970s [478,479], and by airborne SARs [480]. Research of internal waves by spaceborne SAR was initiated again by the launch of SEASAT in 1978. Since then numerous studies have been reported on the naturally occurring internal waves often observed at the boundaries of deep waters and continental shelfs as a result of current-botoom interaction e.g., [481–493], as well as ship-generated internal waves [494–498]. Detection of submarines by SAR has interested military sectors for over 20 years [454], but no clear evidence of detection ability has been reported to date.
3.2.6. Bottom Topography
The shallow waters in Figure 9 have large radar backscatter because the surface is rough caused by the interaction of currents and bottom topography. The image amplitude has strong correlation with bottom topography [499–503], and using this relation, attempts have been made to map the depth of coastal waters [504]. A general approach is to measure first the depths at several reference points by other instruments like acoustic sensors, and using these depths as calibration data the contours of depth are computed from NRCS. The effect of bottom topography to the surface currents appears to be limited to the waters of depth less than approximately 30–40 m. The shallow waters in Figure 9 ranges from 2–33 m according to the sea chart.
3.2.7. Fronts
The linear feature of oceanic fronts between the warm water mass and cold water is known as the thermal front. Fronts are often associated with fisheries and the data can be used to locate good fishing waters around the oceanic fronts. SAR can be a suitable sensor to locate oceanic fronts for its all-weather and day-and-night observation ability [505–510]. Monitoring warm and cold waters, major currents and fronts can also be made by optical and thermal sensors, and thus, complementary use of these sensors can be a possible future approach to increase the detection accuracy and information content in the data.
3.2.8. Ship Detection and Identification
Ship detection and identification by airborne radar were the major issue during the World War II, but the research on ship detection by spaceborne SAR started when SEASAT was launched in 1978 [511]. Since then a substantial number of papers and review articles have been published, including those of [512–532], and also good review articles are available [533–536].
The reasons for the active research on ship detection are due to the increasing international maritime problems and requirements, such as monitoring of maritime traffic and fishing activity, tracking and identifying illegally operating ships, ships intruding into territorial waters, those responsible for oil spill, and surveillance of piracy [537].
At present, AIS (Automatic Identification System) is mandatory to all passenger ships and ships over 300 tonnage cruising international waters. In the European Union, VMS (Vessel Monitoring System) is mandatory to all fishing boats longer than 15 m. AIS and VMS are the systems for cruising ships and monitoring stations to exchange information on their positions, types, nationalities, cruising speeds and directions through direct or through satellite communications. The conventional AIS system uses ground-based monitoring stations, so that AIS signals can be received from only ships within 50–70 km from coasts. In order to extend the AIS signal reception on a global scale, some commercial satellite-borne AIS systems are being operated [538,539], and real-time vessel positions and information are available online [540]. However, small boats and illegally operating ships are not equipped AIS/VMS transponders, and in order to detect and identify these vessels, development of vessel detection systems incorporating spaceborne and airborne SARs has been in progress.
Algorithms for ship detection include the amplitude based Constant False Alarm Rate (CFAR) which is the standard and most widely used algorithm [541–543], multi-look cross-correlation [515,525], along-track InSAR [521,527], polarimetric analysis (with and without CFAR) [516,518,523,524,526,528,529,531,532], and others (see review papers [533–536] for further information).
The progress of ship identification by SAR is rather slow in comparison with that of ship detection due mainly to low resolution of spaceborne SAR. Indeed, the DECLIM report in 2006 stated “To derive a vessel’s type (tanker, fishing boat, etc.) is beyond today’s capabilities” [519]. However, with increasing maritime problems by vessels and increasing SAR resolution in recent years, need has been raised by coast guards and related organizations for ship identification, which initiated the research and development of integrated ship detection and identification systems. There are three main approaches to ship identification: (1) Decision-based classification [544–546]; (2) Classification by pattern matching [547]; and (3) Multi-channel classification [516,548–552], excluding the use of ISAR (Inverse SAR) [553]. Probably, the most practical algorithm at present may be the decision-based classification by GMV Aerospace and Defense in Spain [546].
Currently, AIS/VIS with SAR has been used in practice by several European and Canadian communities. For example, MARISS (Maritime Security Services) by ESA/NASA/JPL covers the north Atlantic sea to east-Atlantic sea as well as Baltic and Mediterranean seas [554]. Others include the MEOS SAR Ship Detection system by Kongsberg Spacetec (Norway) [555], SIMONS (Ship Monitoring System) developed by GMV Aerospace, S.A. [556], DECLIM (Detection and Classification of Maritime Traffic from Space) project by Joint Research Center (JRC) [514,517,519,520], and that by Defence Research and Development Canada [557]. These commercial and institutional systems also include algorithms for oil spill monitoring. Further details can be found in the corresponding websites.
4. Interferometry
The concept of interferometric SAR, which is the microwave version of optical holographic interferometry [558–560], was first applied to the planet Venus [561] and later Moon [562,563] by the ground-based radars of MIT Lincoln Laboratory operating at 7.84 GHz (wavelength 3.83 cm) on Earth (termed as “delay-doppler method”). Its application to Earth was first suggested by Graham in 1974 [47], and the practical study on SAR interferometry started in 1980s, with the pioneering study using the airborne JPL SAR (currently AIRSAR) data by Zebker and Goldstein [564] followed by SIR-B data [565], and those of SEASAT-SAR [566,567]. Unlike the techniques using amplitude data or polarimetry, SAR interferometry can provide strictly quantitative measurements. Although there is some space for basic research such as phase unwrapping, the InSAR technology is now almost at a complete stage and has been used as a practical tool. The principle of InSAR is to extract quantitative information on the scattering objects from complex interferograms produced by two or more sets of mutually correlated complex SAR images of a same scene. There are two types of InSAR depending on measurable quantities. The first is CT-InSAR including DInSAR (Differential InSAR) [48,51–53], and the second is AT-InSAR e.g., [63,71] as illustrated in Figure 10. The details of these systems are beyond the scope of this article, but brief summaries are presented as follows.
4.1. Cross-Track InSAR
4.1.1. Digital Elevation Model Generation
The left of Figure 10 shows two-pass CT-InSAR (also known as repeat-pass CT-InSAR), in which two complex images of a same area on land are formed using a single antenna, and a complex interferogram is produced by multiplying one of the complex images and the complex conjugate of the other image. In order to produce interferograms and InSAR-DEM of high quality, several procedures are required, including co-registration, phase unwrapping from the wrapped phase extracted from the complex interferogram, orbital phase (due to antenna separation) removal, the conversion from phase to height, and ortho-rectification.
Figure 11 illustrates the process of InSAR-DEM generation.
The procedure of InSAR-DEM production is illustrated in Figure 11. Two SLC (Single Look Complex) images acquired at slightly different antenna separation are first produced. The Doppler centers of the SLC images in the azimuth direction should be the same in order to produce an inteferogram with high coherence. If the Doppler centers are different, one of the SLC image needs to be re-produced from raw data using a SAR processor with an adjusted Doppler center. The next step is the geometrical correction called co-registration with the sub-pixel (1/8 to 1/20 pixel) accuracy for the purpose of, again, increasing interferometric coherence. Interferograms of relatively high quality without co-registration may be produced by a single-pass InSAR, but this correction is required for most cases of repeat-pass InSAR. The image that co-registration is applied is called a “slave” image, while the reference image is called a “master” image.
A complex interferogram is then computed by multiplying the complex master image and co-registered slave image. There are two types of information in the interferogram: interferometric phase and coherence (also known as InSAR phase and InSAR coherence respectively). The latter is a measure of correlation between two images. The former is the phase difference between the two complex images, and this phase information is used for contour generation. The phase difference is proportional to the path difference between the two antennas and a surface position, and therefore, the InSAR phase depends, apart from the radar wavelength and antenna separation, on the ground-range distance and surface height as in Figure 12. The InSAR phase that depends on the ground-range distance is called the orbital or flat phase, and the corresponding interferometric fringes are called the orbital fringes. The InSAR phase that depends on the surface height is the topographic phase to yield the topographic fringes. In order to compute the topographic phase, the flat phase needs to be removed from the InSAR phase.
As noted above, the InSAR phase ψ is computed from the two complex images A1 and A2 as
Well known phase unwrapping algorithms include, among others, the branch-cut or path-following method [566,570], least-square method [569,571]. In the former method, residues are first sought, and each positive and negative residues (which generally appear as a pair) are connected by a cut-line. Starting from a pixel with high coherence, the principal phase is retrieved by adding the phases of neighboring pixels without crossing these cut-lines. The phases along the cut-lines are estimated later by interpolation. The branch-cut method is fast to compute and the errors are small for local phase errors do not propagate to other pixels. The main problem is that the method cannot be used for the InSAR data with many residues. In the least-square method, on the other hand, the principal phase is computed by minimizing the phase difference between the neighboring pixels of the wrapped phase and the corresponding ideal principal phase. Since unwrapping is carried out irrespective of residues, solutions are always obtained, but local phase errors are carried over to neighboring pixels, resulting in the unwrapped phases of large errors. For this reason the least-square method is not often used except for “quick look” phase images. Several improved least-square algorithms have been proposed in which certain weight is applied to the areas of residues to mitigate the effects at the expense of computational time. These algorithms include the preconditioned conjugate gradient algorithm [575], multi-grid algorithm [579], and minimum Lp-norm algorithm [578]. There is no such “universal” algorithm that can be applied to all types of InSAR data, but a suitable algorithm depends on the density of residues and applications.
As in Figure 12 of simple geometry, the unwrapped phase ϕ and surface height Hs are related by ϕ = k BCT sin(θi – γCT) and Hs = HSAR – R1 cos θi, where k = 2π/λ is the wavenumber. The surface height can, in principle, be estimated by eliminating θi and solving these two equations. In practice, however, the orbital information is not accurate enough to estimate the surface height directly from these relations, so that each equation is differentiated with respect to θi to yield the following expression for the height difference ΔHs in terms of the differential phase Δϕ.
Using single-pass CT-InSAR with two-antennas separated by 30 m in the horizontal direction, the Shuttle Radar Topography Mission (SRTM) [13,587–589] in the year 2000 produced the InSAR-DEM of 80% of land with the absolute accuracy of 16 m in vertical height and 30 m in horizontal direction corresponding to the DTED-2 standard shown in Table 5. The data can freely be downloaded from the SRTM Website [590]. Note that the standard accuracy of airborne single-pass InSAR-DEM is the DTED-2, but most of airborne InSAR systems have higher accuracy of approximately 2–5 m in vertical height.
Currently, a global-scale DEM with the HRTI-3 standard is being made using TerraSAR-X and TanDEM-X [22,171,593–597]. The data acquisition is by the strip (map) mode for the repeat-pass InSAR and bistatic mode for the tandem formation. The main problem of InSAR operating at X-band is that the interferometric coherence is not very high over forests and the surfaces of heavy vegetation cover. Therefore, the DEM by TerraSAR-X and TanDEM-X may be limited to barren areas and those of light vegetation cover, and otherwise, some other means is required to increase the interferometric coherence [598,599].
4.1.2. Differential InSAR
Figure 13 illustrates the flow for the measurements of surface height change by DInSAR. In the figure, JERS-1 SAR data were used for the case of the M7 earthquake on Sakhalin Island in 1995 [600]. If the surface height changes during the passes due to earthquake or volcanic activity, and if the two passes are identical, the height change can be estimated from the phase of the interferogram. In general, the satellite passes are different, so that the interferogram contains the topographic and orbital phase information as well as the temporal change as in Figure 13. In order to achieve DInSAR, the former two phases need to be subtracted from the interferogram, and it is done either by using an existing external DEM or another inteferogram produced before the event. Since the latter method uses the SAR data from three orbits, it is known as three-pass DInSAR. After removal of topographic phase, the interferometric phase is expressed as ϕ = 2k δRH, where δRH is the surface height change in the slant-range direction. By putting ϕ=2π, the wavelength or width of interferometric fringes is given by λ/2. Thus, the accuracy of DInSAR is of the order of a half the radar wavelength, provided that the correct removal of the baseline and topographic components is made. For example, the number of interferometric fringes over the Awaji Island in Figure 7 is 10, implying the surface displacement of 1.175 m; while the displacement measured by ground survey is 1.2 m at the Nojima fault located at the top-left (center of the semi-circular fringes) of the island.
The conventional technique of DInSAR measures the surface deformation only in the slant-range direction. Multiple aperture interferometry (MAI), first proposed by Bechor and Zebker [601] followed by an improved version [602], can measure two-dimensional surface displacement. MAI uses a pair of multi-temporal SAR data before and after an event, each of which is produced by multi-look (2-look in general) processing in the azimuth direction, resulting in four sub-images: two sub-images in the forward-looking and two sub-images in the backward-looking before and after the event. Then, two different looking interferograms (one using the forward-looking sub-images and one using the backward-looking sub-images) are produced. The phases of the forward-looking and backward-looking interferograms are proportional to the forward-looking and backward-looking displacements respectively. Subtraction of these phases, therefore, yields the surface displacement in the azimuth direction. Bechor and Zebker [601] tested the algorithm using ERS-2 C-band SAR data over the Hector Mine earthquake in 1999, and compared with with GPS and offset-derived displacements data, resulting in the accuracy of 3–11 cm for coherence 0.8–0.4. The technique has been used by several researchers for the measurements of surface deformation by the 2003 Mw7.2 Altai earthquake [603], and seismic analyses e.g., [604,605].
4.1.3. Atmospheric and Ionospheric Effects
Occasionally, a phenomenon associated with microwave propagation delay caused by spatial and temporal atmospheric variations in the troposphere is observed [606–609], in particular, in DInSAR phase images. As in Figure 12, InSAR and DInSAR techniques are based on the measurements of two-way path difference ΔR = 2(R1 – R2) in a radar wavelength scale. If microwave pulses pass through locally dense vapor in the troposphere, there appears a time delay caused by the vapor, and the path difference becomes ΔR+ ΔRT where ΔRT is the path difference corresponding to this time delay [610,611]. The path difference ΔRT may be as large as tens of centimeters in spatial scale [608], and therefore, the interferometric phase corresponding to this delay causes erroneous measurements of surface topography or deformation [612,613]. It is common to separate the tropospheric delays into two components: one related to turbulent mixing processes and the other related to tropospheric stratification.
The phase delay associated with the atmospheric turbulence can be corrected or mitigated by stacking or averaging a large number of interfetograms, since the turbulence has short spatial correlation length with virtually no temporal correlation between data acquisition times e.g., [608,614–616]. Tropospheric stratification is associated with temperature, pressure, and water vapor, and it introduces phase delays correlated with topography, leading to misinterpreted InSAR data in the areas of steep topography e.g., [617]. To correct these effects, stacking of multiple interferograms is not, in general, successful, due to the periodic nature of the perturbation in the interferometric phase. Several correction methods have been proposed, including those utilizing external independent data such as local atmospheric models [618], GPS (Ground Positioning System) [619–621], spaceborne optical data [622,623], a stack of small baseline SAR interferograms [624,625], and a multi-scale time-series approach [626]. Among those, an approach utilizing global scale atmospheric models appears very promising [627,628]. It was also suggested that the removal of the atmospheric effects before phase unwrapping reduces the errors in phase unwrapping in the areas of high relief [628]. For further details, see a good review article on the issue of atmospheric effects and their mitigation [612,613].
Spatial and temporal variations of electron density in the ionosphere have a significant impact on SAR, InSAR, and DInSAR as well as PolSAR [629–631]. The effects of ionospheric delays become significant at lower frequencies, since the variance of the refractive index fluctuations is approximately proportional to λ4, as observed in the RADARSAT C-band and JERS-1 L-band SAR amplitude images over the auroral zones in Alaska, showing kilometer-scale linear or banding patterns in the azimuth direction, termed as “azimuth streaks” [632]. The effects of ionospheric fluctuation have been observed near the magnetic poles [632,633], particularly during strong magnetic disturbances, but also in the areas away from the polar regions, such as the ALOS-PALSAR L-band data over Japan and Brazil [634], and the 2008 Sichuan Earthquake [635,636]. In addition to azimuth streaks, ionospheric delays caused by the variations of total electron content (TEC) introduce Faraday rotation (see the polarization paragraphs in Section 1 and references therein), relative range delay between interferometric data acquisition times, range and azimuth defocusing, loss of interferometric coherence, and phase errors. Azimuth streaks and range shifts cause misregistration in the subpixel correlation in both the azimuth and range directions in interferometry, and decorrelation as reported in the study on the 2008 Sichuan Earthquake [635].
Due to the dispersive nature, the effects of ionospheric delays can, in principle, be separated from non-dispersive features of surface deformation and atmosphere. The range split-spectrum method [637] is based on this separation of dispersive and non-dispersive effects on the InSAR phase [638]. In this method, the range spectrum of an InSAR dataset is split into two parts of high and low frequency sub-bands, and each part is used to form an inteferogram. Assuming that the two interferograms have the same non-dispersive effects with different dispersive contributions depending on the inter-band center frequency, the relative TEC can be estimated by subtracting the phases of these interferograms. The split-spectrum method, however, can estimate only the relative values of TEC but not the absolute values.
Matter and Gray [639] suggested a method of estimating and reducing the effect of azimuth streaks on the InSAR phase from a map of azimuth offset. Improved versions [635,636] have been proposed based on the relation between the ionospheric contributions to the azimuth offset and interferometric phase derived by Mayer et al.[640,641]. From this relation the interferometric phase errors caused by the spatial variation of TEC, i.e., azimuth streaks, can be estimated empirically using the azimuth offset values [639] and removed, enhancing surface topography and coseismic deformation measures. Another technique is based on Faraday rotation. The angle of Faraday rotation can be measured from fully polarimetric data [642,643]. Then from the relation of the rotation angle and TEC [128] (and with known SAR geometry), 2-dimensional distribution of TEC and hence maps of phase delay can be estimated [633,644].
These observations of atmospheric and ionospheric effects, on the other hand, may lead to new techniques to study the high-resolution troposphere turbulence and stratification and TEC by InSAR and DInSAR.
4.1.4. Examples of DInSAR Applications
The first experimental result of DInSAR was reported by Gabriel et al.[52] using the SEASAT-SAR data, detecting small elevation change caused by increased soil moisture by irrigation in the agricultural area of California. The first DInSAR measurements of crustal movement by earthquakes were made using the ERS-1 SAR data over the Landers earthquake, California in 1992 [645–647]; and the first measurement of glacier flow in Antarctica by the JPL group [648]. These early studies initiated the study on geodetic dynamics by DInSAR that followed.
Examples of DInSAR measurements of deformation by earthquakes also include the 1994 Northridge earthquake in California [649], the Great Hanshin-Awaji earthquake, Japan in 1995 [650] also shown in Figure 7, the Sichuan earthquake, China [651], the L’Aquila earthquake, Italy both in 2009 [652], and the recent Tohoku-Oki earthquake in 2011 [653,654].
Surface deformation by volcanic activity was reported, such as the case of Kilauea volcano, Hawaii by SIR-C data [655] and the discovery of fore active volcanoes in the central Andes mountains previously considered to be dormant using ERS-1 and ERS-2 data [656]. Other applications include landslide and subsidence monitoring [657,658], surface deformation by constructing dams [659], underground excavations [660,661] and by groundwater extraction [662–664], and topographic changes and flow of glaciers [665–669]. Examples and details on the InSAR and related techniques can be found in the ESA website [670], and also the selected papers of the ESA Fringe 2007 Workshop a special issue of Journal of Applied Geophysics [671].
4.1.5. PS-InSAR
PS-InSAR was developed by Politechnico di Milano (Italy) in 2000 [54–56,59]. In 2003, GAMMA REMOTE SENSING (Switzerland) developed a similar software Interferometric Point Target Analysis (IPTA) combined with Persistent Scatterer InSAR [58]. A similar algorithm known as InSAR CTM (Coherent Target Monitoring) [57,60] was developed by Vexcel Corp. (currently in Microsoft Corp.), and also CPT (Coherent Pixels Technique) by the Universitat Politecnica de Catalunya, Spain [61].
The principle of PS-InSAR is to measure the phase difference of particular point-like targets which yield consistent strong backscatter over a year or years. In general, at least 10–20 image sets are required to achieve PS-InSAR. Stacks of multi-temporal SAR data mitigate the phase distortion caused by atmospheric effect. The accuracy of estimating surface height deformation is of the order of few millimeters per year (see also [54–62]). Stacking of multiple interferograms has also been used for conventional DInSAR. An example is SBAS (small baseline subset) InSAR [624,625] which uses only interferograms produced with short baseline separation in order to reduce both spatial and temporal decorrelation, and mitigate atmospheric effects and topographic errors.
Examples of PS-InSAR include the measurements of subsidence by groundwater extraction, underground mining, and tunneling of underground railways [672–675]. PS-InSAR is very accurate and effective in urban areas where many point-like targets exist, but not effective in natural fields without many permanent (or persistent) scatterers. For such cases, several corner reflectors can be deployed as semi-permanent scatterers.
Recently, a new algorithm termed as “SqueeSAR” was proposed to utilize not only permanent (deterministic) scatterers but also distributed scatterers using their statistical property [676]. The algorithm is capable of measuring surface deformation over non-urban areas of sparsely distributed deterministic scatterers. Prior to SqueeSAR, another (free) software package “StaMPS (Stanford Method for Persistent Scatters)” was developed [677]. As for SqueeSAR, StaMPS can be applied to persistent scatterers as well as distributed scatterers by incorporating the small baseline and persistent scatterer methods.
4.1.6. Ground-Based InSAR
The principle of the ground-based InSAR is the same as that of multi-temporal InSAR and DInSAR for generating DEM [678–681], and measurements of small surface movement [682–684]. Instead of airborne or spaceborne SARs, the system consists of (X-band in general) T/R horn antennas fixed on a platform that slides along the horizontal axis to achieve aperture synthesis. Targets of ground-based DInSAR are generally sloped surfaces which are suspected to subside, and many differential interferograms are made over a certain period of time, depending the magnitude of movement. The fixed rail on which the platform slides is considered as stationary during the observation, otherwise motion compensation is required. The system has been used to monitor the subsidence of cliffs over which an ancient monument is standing, and suspected subsidence and hazardous areas. Note that a recent work showed that a ground-based real-aperture radar can as well be effective for DEM generation [685].
4.1.7. Interferometric Coherence
Another property of complex interferograms is the interferometric coherence or degree of correlation defined as
ΓT is the temporal decorrelation due to the interaction of the incident microwave with the scattering objects. This coherence loss includes the decorrelation by the temporal changes of scattering objects and the volume (multiple) scattering associated with different incidence angles. For example, the surface of water changes between passes and hence the coherence over the water surface is theoretically zero (in real data, it is non-zero due to statistical averaging). On the other hand, the surface of a solid ground does not, in general, change significantly, so that the coherence is very high. Vegetation and forests have moderate to low coherence due to volume scattering. As to the dependence of radar wavelength on ΓT, the X- and C-band radar backscatter from forests and vegetation are predominantly from the crown parts that are susceptible to changes, and hence the temporal coherence takes small values. While, the backscatter of longer wavelengths (L- and P-bands) is mainly from stable ground, branches, and trunks, penetrating vegetation cover, and therefore, higher temporal coherence than X- and C-band can be obtained. These factors causing the temporal decorrelation are the random changes of the backscattered fields (and hence the speckle patterns) between the data takes, arising from the changes in the shapes of surfaces for the case of surface scattering. In optical speckle interferometry, it is known as “speckle boiling” [686–688].
ΓB is the decorrelation caused by the baseline separation. Higher interferometric coherence can be obtained with shorter baseline separation, but at the expense of interferometric resolution. As in Equation (2) and discussion with it, the ambiguity height is inversely proportional to the baseline separation, and hence the accuracy of height measurements decreases with decreasing baseline separation. A good measure for the limit of baseline separation is known as the critical baseline (separation) defined as the distance with which the corresponding interference fringes are resolved, i.e., fringe separation equals the spatial resolution cell. Then, assuming ρR as the slant-range resolution cell, the critical baseline is defined, by setting ΔH = ρR cos θi and Δϕ = 2π in Equation (2), as . For C-band spaceborne SAR of λ = 5.7 cm, R1 = 800 km, θi = 35°, and ρR = 25 m, the critical baseline is . For L-band SAR of λ = 23.5 cm, for the same geometry and resolution.
ΓS describes the coherence as a function of surface slope. With reference to Figure 12, if a flat surface is tilted toward the radar at an angle θS, the effective incidence angle becomes (θi – θS), and hence . Thus, the critical baseline becomes smaller, and the coherence decreases. For the surface tilted away from the radar, the reverse process increases the coherence. Another simple way to look at this effect is the width (or wavelength) of interferometric fringes, given by λR1 tan(θi – θS)/(2BCT), where γCT = 0 is assumed for simplicity. It can be seen that the fringe width decreases as the tilt angle θS increases. It means that the “effective” baseline separation increases, and therefore, the coherence decreases. For the surface tilted away from the radar, the fringe width increases, so that the effective baseline separation decreases to yield higher interferometric coherence. It should be mentioned that higher interferometric coherence can be gained by increasing off-nadir (incidence) angles, but at the expense of reduced NRCS, i.e., reduced SNR.
It can further be noticed that the fringe width increases as the radar wavelength λ increases, and the accuracy of height estimation decreases as also mentioned with reference to the ambiguity height and Equation (2). On the other hand, the interferometric coherence increases with increasing λ since the critical baseline increases. There is a trade-off between the interferometric coherence and the accuracy of height measurements. Although X- and C-band SARs are useful for DEM generation (and indeed is being in progress using TerraSAR-X and TanDEM-X [22,171,593–597]), L-band SAR has an advantage for its high coherence over the surfaces covered by vegetation and insensitivity to the changes over long time periods, in particular, for the measurements of temporal surface height changes by DInSAR.
In DInSAR, smaller or ideally no baseline separation is desirable to reduce the baseline decorrelation ΓB in Equation (4). The effects of SNR and surface slope on the coherence are the same as for InSAR described above. The effect of volume scattering in the temporal decorrelation ΓT is also the same. Another factor which causes the temporal decorrelation is the amount of surface displacement. If a surface translates or changes its height due, for example, to earthquakes, in such a way that the phase changes more than one cycle within the slant-range resolution cell, then interference does not occur. This critical displacement in the slant-range distance corresponds to δRH = λ/2. The equivalent phenomenon has been known in optical speckle interferometry as “speckle translation” [688,689].
It is of some interest that for large translation such as glacier flows and large deformation by earthquakes or volcanic activity, the conventional DInSAR cannot be applied due to the loss of coherence by speckle translation. In such cases, a technique called “speckle-tracking” (also called “sub-pixel image correlation”) is often used [690–694]. It is a kind of pattern matching, in which the patch of a same speckle image is sought between two SAR images and a flow vector is produced, provided that there is no speckle boiling. This subject matter may belong to amplitude information in Section 3, but a brief note is given here for the sake of continuity. The second approach to tackle large deformation was the two-step hybrid algorithm based on a rubber-sheeting coregistration to improve interferometric coherence and range offset image subtraction to mitigate steep phase gradient [695]. Unlike the conventiona methods of InSAR, the rubber-sheeting coregistration is a non-parametric method, in which a slave image is projected on a rubber sheet which is overlaid with a master image. Then, the slave image is distorted to match the features of the master image. A range offset image is then produced, smoothed, and subtracted from the interferogram before phase unwrapping. Finally, the interferogram is unwrapped, and the offset field is added back to recover the true phase. Using ENVISAT-ASAR data over the Galapagos Islands, Yun et al. [695] retrieved an interferogram inside the caldera of an erupted volcano, which other conventional InSAR algorithms could not.
As mentioned in the forestry application of Section 3.1.3, InSAR coherence has some correlation with tree biomass to yield the coherence-based biomass retrieval algorithm [225,226,228,229,231,235].
4.2. Along-Track InSAR
The geometry of AT-InSAR is shown in Figure 10. AT-InSAR consists of two (or more) antennas placed along the body of an aircraft platform, and can measure the range velocity component of moving scatterers [63–72]. In general, a forward (or aft) antenna transmits signals and return signals are recived by both antennas. If the scatterers have a slant-range velocity component vR, the signals received by the two antennas have different Doppler centers, and the phase difference is given by ψ = k tBvR, where tB = BAT/ V is the time lag between the two antennas separated by the distance BAT, and V is the platform velocity.
The system was limited to the airborne platform due to technical difficulty. In 2000, however, an experimental AT-InSAR was carried out by Shuttle-borne SRTM. SRTM was designed originally for CT-InSAR with two antennas separated by 60 m in the cross-track direction, but in addition, they were separated by 7 m in the along-track direction. Further, TerraSAR-X has two antennas split in the along-track direction to experiment AT-InSAR from space for ocean current measurements [73]. The measurement accuracy of SRTM AT-InSAR is approximately 0.2 m/s [70], and the accuracy of 0.1 m/s is expected by TerraSAR-X. In 2009, TanDEM-X, identical to TerraSAR-X, was launched, and AT-InSAR by the formation flight is one of the secondary mission objectives [22].
The interferometric coherence is another aspect of AT-InSAR. In the same way as for CT-InSAR, the coherence decreases with increasing baseline separation (or time-lag tB); while increasing tB increases interferometric phase ψ and hence increases the measurement accuracy. Thus, there is a trade-off between the accuracy of estimating InSAR phase (and hence velocity) and coherence. In general, the interferometric phase of AT-InSAR does not exceed 2π for the case of ocean currents, so that phase unwrapping is not required. The measurement accuracies of airborne AT-InSAR are few centimeters per second, depending on the radar wavelength and antenna separation. The interferometric coherence is also a function of the time duration (surface coherence time) over which the principal scatterers, i.e., Bragg waves, retain the same shape. Longer the wavelength of ocean waves is, longer the coherence time becomes. For AT-InSAR operating at X- to L-bands, the coherence time is estimated as approximately 0.2–0.02 ms [65,66,696–699].
As mentioned briefly in Section 2.3, the conventional AT-InSAR system with two antennas measures only the velocity in the range direction, while an airborne AT-InSAR equipped with four antennas was developed to produce current vectors [71].
AT-InSAR can also detect and measure the slant-range velocity of a moving hard targets such as vehicles and ships [74–79]. The principle of this technique known as moving target indicator (MTI) by AT-InSAR is essentially the same as that for current measurements. It utilizes the difference in the interferometric phase between a moving hard target and a stationary target, in that the velocity and acceleration components in the azimuth and range directions give rise to the phase difference to the return signals.
5. Polarimetry
SAR polarimetry is a current “hot topic”. Expectation of polarimetry to extend the current SAR and InSAR technologies has lead increasing number of spaceborne SARs equipped with the quad-polarimeric mode as listed in Table 2 and almost all airborne SARs are able to acquire quad-polarization data. This enthusiasm stems from the fact that polarimetric data contain more information on the scattering objects than the conventional single- and dual-polarization data. PolSAR data describe the changes of polarization states of received microwave by the structures and dielectric constants of the objects, so that these properties can, in principle, be extracted from the polarimetric data. However, at present, SAR polarimetry and possible applications need further stringent validation using ground-truth data, and it has not yet been used in practice as much as the DEM generation and measurements of surface deformation by SAR interferometry.
5.1. Principle of Polarimetry
A part of the reason for slow development of PolSAR in routine practice may be its mathematical complexity in comparison with SAR interferometry. Much of PolSAR data analysis is based on the matrix manipulation, so that it deters researchers in some fields of geoscience and related applications, who are not accustomed to using complex matrix manipulation. Reflecting this, a free software is provided by ESA to promote and expand the utilization of PolSAR data [700]. In the following, the principles of PolSAR are briefly summarized with least mathematics.
Polarimetric SAR measures the complex scattering matrix of a scattering object with different polarizations. On the linear polarization base, the microwave pulses of alternating horizontal and vertical polarizations are transmitted from either a single antenna or multiple antennas, and the horizontal and vertical polarization components of the backscattered signals are received. There are four possible combinations of transmitted and received polarizations, i.e., HH: horizontal transmission and reception, HV: horizontal transmission and vertical reception, VV: vertical transmission and vertical reception, and VH: vertical transmission and horizontal reception. The scattering matrix [S] describes this relation of the polarization states before and after the microwave scattering by the objects, and is expressed by
To date, many algorithms have been proposed for polarimetric analyses e.g., [85–87]. Among them, three most used techniques, i.e., polarization signature, model-based scattering power decomposition analysis, and eigenvalue analysis, are summarized here.
5.2. Polarization Signature
A conventional well known method of expressing the changes of polarization states by scattering objects is by the polarization signature [80,82,83]. The polarization signature is a three-dimensional or two-dimentional visualization technique in which the normalized power is expressed in terms of the tilt angles and ellipticity angles as shown in Figure 14. Using the polarimetric signature, different scattering processes can be classified. Typical scattering processes that can be identified by the polarimetric signature include those by a plate, a sphere or a trihedral reflector, double-reflection, dipoles, crossed wires (helix scattering), and others.
Depending on the polarimetric signature of co- and cross-polarization channels, there appear stationary points of peaks, valleys, and saddle points of which the positions are inherent to scattering objects. Using these characteristic polarization states, polarimetric filters can be produced for image enhancement, contrast optimization, and classification e.g., [88–91,94,100,102,114].
5.3. Model-Based Scattering Power Decomposition Analysis
In 1998, Freeman and Durden [98] proposed a three-component scattering power decomposition analysis based on fitting the observed scattering matrix to the model-based matrix. In this analysis, the total received power P is considered as a sum of the three types of scattering powers, namely, those by single-bounce surface scattering, double-bounce scattering, volume (multiple) scattering as follows.
From Equation (5), the covariance of different polarization combinations can be estimated. The three- (and four-) component scattering powers are computed from the covariance or coherency matrices. The three-component decomposition analysis assumes the reflection symmetry of the polarimetric covariance matrix elements, i.e., the co- and cross-polarized scattering coefficients are statistically uncorrelated, so that the assumption of holds. The reflection symmetry occurs, for example, in L- and P-band data from forests where the phases of and are random and uniformly distributed between (0, 2π].
The HV-base scattering matrix in Equation (5) can be represented by the covariance matrix
In order to deduce the individual scattering power contributions, the scattering matrix of Equation (5) is first rotated by an angle around the radar line-of-sight direction, and expressions corresponding to the scattering elements of the covariance matrix of Equation (7) are calculated by assuming a suitable probability density function (PDF) for the orientation angles of elementary scatterers. In the three-component decomposition analysis, this PDF is assumed to be uniform. From comparison of the covariance matrix elements of Equation (7) and those derived from the scattering matrix under the reflection symmetry, the following set of equations can be derived.
The volume scattering contribution fv can be estimated directly from 〈|SHV|2〉 in the second of Equation (8), so that there remain three equations and four unknown parameters. Equation (8) cannot be solved unless one of the unknown parameters is known. An assumption is then made that if the real component of is positive, the surface scattering is dominant and put a = −1; but if it is negative, the double-bounce scattering is dominant and put b = 1. Once the values of a, b, fs, and fd are known, the powers, Ps, Pd, and Pv corresponding respectively to the surface, double-bounce, and volume scattering can be estimated from
The three-component scattering decomposition assumes the reflection symmetry [98]. This assumption is generally valid for natural targets such as forests and vegetation, but it is often violated for urban scenes where, for example, the double-reflection scattering from the ground-building orientated in non-orthogonal directions to the radar line-of-sight. The generalized four-component scattering decomposition analysis is valid without the assumption of the reflection symmetry and includes the helix scattering [104]. Helix scattering changes the linearly polarized incidence microwave to a circularly polarized backscattered wave. This change in polarization state may be caused by, for example, crossed wires and quarter wave plates. In the four-component approach, the modified PDF takes into account the vertical structures of tree trunks and branches and also vegetation, depending on the 〈|SHH|2〉 / 〈|SVV|2〉 ratio.
Figure 15 shows the L-band and X-band Pi-SAR images decomposed into three scattering powers [305,307]. The area (the Kojima district in Okayama, Japan) is covered predominantly by rice paddies. The image size is approximately 3.5 km in both the azimuth (from top to bottom) and range (from right to left) directions. The bunches of rice plants were mechanically transplanted in a regular interval, and almost fully grown with height approximately 60–90 cm at the data acquisition date of the 13th of July 1999.
At L-band, double-bounce scattering can be seen between roads and houses, and canal water and banks. The dominant backscattering by double-bounce appears in the triangular district at the center of the image, where the walls of the houses, roads and canals that are orthogonal to the range (illumination) direction, but little double bounce scattering can be observed in other districts, where they are not non-orthogonal to the range direction. Double-bounce scattering as a result of the Bragg resonance scattering between the bunches of rice plants and water is indicated in red in the ground survey map in the top-left of Figure 15[307]. Apart from the Bragg scattering, little radar backscatter is observed from other rice paddies due to long penetration depth of L-band microwave. Lotus plants of height approximately 1.5–2 m over the water indicate a mixture of double-bounce and volume scattering. Volume scattering is mainly from trees and bushes, and interestingly from vegetation in the green houses composted of frames of metal pipes covered by polyolefin films that are transparent to microwave.
At X-band, the dominant backscatter is volume scattering with some surface scattering. Double-bounce between the roads and houses are seen in the central triangular district, but much less than the L-band image. The backscatter from the canal water and banks also includes surface scattering as well as double-bounce. The rice paddies that give rise to the double-bounce Bragg scattering at L-band do not now satisfy the Bragg condition. Lotus fields are dominated by volume scattering, and the volume scattering contribution from the green houses is greater than the L-band image.
As can be noticed in Figure 15, the double-bounce scattering occurs between the ground and flanks of houses facing toward the radar, and also the water surface and canal banks that are orthogonal to the radar line-of-sight. If the flanks and faces of banks are not alined in other directions, the incident microwave is reflected away from the radar and little backscatter is received by the antenna, as in the upper and lower districts of the images in Figure 15. To compensate this effect and to enhance the double-bounce scattering contribution, a four-component scattering power decomposition with rotation of coherency matrix is proposed [118] (see also [125] based on the equivalent covariance matrix). In this classification scheme, the coherence matrix is rotated along the radar line-of-sight, and then the rotation angle that minimizes the cross-polarization (volume scattering) component is sought. Since the rotation is a unitary transform of the coherency matrix, the four-component (or three-component) scattering power decomposition can be applied to the rotated matrix without loss of generality. This algorithm is particularly useful for improving the classification accuracy in urban areas by distinguishing the double-bounce scattering from volume scattering.
5.4. Eigenvalue Analysis
Unlike the covariance matrix (and coherence matrix) which is a measure of the complex degree of coherence between different combinations of polarization data, this classification algorithm is based on the eigenvalue analysis.
The mathematical formulation of the eigenvalue analysis is usually given in terms of the coherency matrix 〈[T]〉 which is related to the covariance matrix through the unitary transform
The coherency matrix can also be expressed in a diagonal form using the unitary matrix [U3] as follows.
The degree of randomness of scattering is determined by the entropy defined by
The average of alpha angles is given by
Anisotropy is also defined as
A classification scheme based on the scattering process using the entropy and alpha angles was proposed as illustrated in Figure 16. The curve shows the boundary that the values of ᾱ and H can take, and they always fall within the left-hand side of the curve, so that no values fall in the right-hand side of the boundary.
In the H/α classifier shown in Figure 16, the scattering mechanisms are defined into nine zones. The zone 1 is the class of the high entropy with multiple scattering, and the zone 2 is the high entropy category with H > 0.9 and alpha angles in the range 40°–55°. This zone includes single scattering from a cloud of anisotropic scatterers or multiple/volume scattering from a cloud of low-loss symmetric scatterers, such as those from forest canopies and vegetation with randomly orientated anisotropic scatterers. The zone 4 belongs to the dihedral scattering such as the double-bounce between ground and flanks of buildings, and L- and P-band double-bounce between the ground and tree trunks passing through a cloud of branches. The zones 4–6 have medium entropy indicating the additional secondary scattering caused by increased surface roughness and wave penetration into vegetation. The zone 5 is the dipole scattering category with medium entropy, corresponding to vegetation with anisotropic scatterers. The zones 7–9 are all in the low entropy category of surface scattering, where the zone 7 corresponds to low entropy multiple scattering, including the scattering from isolated dihedral scatterers. The alpha angles in the zone 8 indicate the dipole scattering with large co-polarization amplitude difference. Sparsely distributed vegetation with anisotropic scatterers falls into this category. The zone 9 has small alpha angles so that it corresponds to the surface scattering from rough soil and water surfaces.
In case of λ2 ≠ λ3, λ2 and λ3 yield a same H, and they cannot be determined. The anisotropy of Equation (19) can then be used to distinguish these two eigenvalues. Taking the anisotropy as the vertical axis, the H/α space can be extended to a three-dimensional H/A/α space. It is then possible to classify the targets in a same zone into new classes of different anisotropy values [101]. The total power instead of the anisotropy can also be used to extend the two-dimensional H/α space into a three-dimensional space.
Many image classifiers using PolSAR data have been proposed, most of which are based on the feature vector in feature space. These methods are extensively used in image processing of optical remote sensing data, including the maximum likelihood and minimum distance classifiers. A classifier known as the Whishart classifier has also been proposed as a promising tool, utilizing the coherency matrix which obeys the Whishart distribution [99,101,121].
Figure 17 shows an example of the eigenvalue-based classification scheme. The data were acquired by ALOS-PALSAR in the polarimetric mode over the Tokyo Bay, Japan. The image size is approximately 44 km and 28 km in azimuth and range directions respectively. The left and middle images are the classified images using the H/α classifier only and with the Whishart distribution (5 iterations) respectively. It can be seen that urban areas and numerous ships are better identified by using the Whishart distribution than the H/α alone.
There are several parameters introduced for improving the eigenvalue-based classification accuracy, such as the Shannon entropy (SE) [143] and radar vegetation index (RVI) [93].
5.5. Pol-InSAR
Pol-InSAR uses the combination of SAR interferometry and polarimetry. One of the emerging techniques is forest information extraction, in particular, measurements of vertical structure of forests as described in Section 3.1.3. The basic idea of Pol-InSAR in its simplest form is that two sets of polarimetric images with diffrent incidence angles are produced from two passes. Polarimetric analysis can identify the scattering mechanisms; while the heights of scattering centers can be estimated by interferometry, Thus, by combining SAR polarimetry and interferometry, the heights of volume scattering centers can be estimated. In order to obtain the scattering from the forest interior, SARs operating with L- and P-band bands of long penetration depths are preferred. The measured heights are those of scattering centers, related to the lidar rh100 height, and therefore forest biomass can be estimated [155].
Another application of Pol-InSAR is in image classification. Pol-InSAR can provide the combination of three polarization data, SHH, SHV, and SVV (assuming SHV = SVH for the monostatic SAR) from, in its simplest case, two passes at different times, and hence, the total of nine sets of data in different combinations are available. The degree of interferometric temporal coherence was found to improve the accuracy of the classification algorithms by the conventional InSAR. The relevant references on Pol-InSAR are cited in Section 1 and Section 3.1.3.
The main application of PolSAR is target classification and that of Pol-InSAR is tomography. However, the measurement accuracies have not yet been fully proven in a strictly quantitative manner as those of InSAR and DInSAR, since there are not enough reports on the comparisons using ground-truth data, in particular, for image classification. Nevertheless, there is no doubt that quad-polarization SAR data contain much information on the scattering targets in comparison with single- and dual-polarization data, and radar polarimetry is expected to provide a new tool for the various fields of science and engineering in the near future.
6. Conclusions
Recent trend and advances of the state-of-the-art SAR technologies are described in this article with selected applications ranging from the conventional SAR, InSAR and DInSAR to polarimetric SAR. As is well known, increasing number of airborne SARs have been built and increasing numbers of spaceborne SARs have been launched during the last several decades. This is due to the all-weather and day-and-night imaging capabilities of SAR, and because the spatial resolution is improving (up to submetric) and becoming comparable with that of optical sensors. One of the interesting trends is the increasing number of light-weight SARs. Although satellites with multiple sensors have their own advantages, a constellation of these compact sole-SAR satellites enables to reduce revisit intervals that have been a major problem in satellite remote sensing. The feasibilities of bistatic SARs and digital beam forming are also tested using airborne SAR systems.
Amplitude is the most basic parameter in SAR data, containing information on the electric and structural properties of scattering objects. Alongside with interferometry and polarimetry, utilization of amplitude data in single polarization and combination of different polarizations will be continued in various applications such as measurements of forest biomass and soil moisture, monitoring of agricultural crops, extraction of geological features, disaster monitoring and mitigation, and those listed in Table 1. Applications of amplitude information in oceanography include the spectral estimation of ocean waves leading to improvement in wave forecast and providing real or semi-real time wave information, and measurements of oceanic internal waves leading to deeper understanding of the interaction between continental shelf and deep water, their effects on phytoplankton and fishery, and the effects on marine architecture and underwater communications. Measurements of ocean wind field by SAR can be made in much finer scale than wind scatterometers. Although further study is required for the determination of wind direction, this application is particularly useful in estimating wind field near coastal waters where the measurements are difficult to make by scatterometers of coarse resolution (order of several to few tens of kilometers). Amplitude data can also be used to monitor the spatial and temporal variations of oil slicks, major currents, fronts, and icebergs and sea ice in cryosphere. Ship detection and identification by SAR and combined with AIS are another application for combating increasing maritime crimes, monitoring and controlling of maritime traffics, and fishery.
Cross-track InSAR and DInSAR utilize the phase information of complex SAR images. This technology is matured to an established technique for producing DEM and measurements of surface movement and deformation caused by earthquakes, volcanic activities, and glacier flows. Following the DEM of the earth by the SRTM mission in 2000, a higher resolution digital elevation model of which the characteristics are listed in Table 5 is currently being made using TerraSAR-X and TanDEM-X data. DInSAR has been used extensively to evaluate the surface deformation associated with major earthquakes from the 1992 Landers earthquake in California to the recent 2011 Tohoku-Oki earthquake in the north-east Japan. Improved accuracy of the order of few millimeters per year can be achieved by PS-InSAR and related techniques for the deformation measurements over discrete persistent scatterers as well as distributed scatterers. Cross-track DInSAR measures the surface deformation only in the line-of-sight (slant-range) direction, but MAI (multiple aperture interferometry) can measure the along-track (azimuth) displacement by making forward- and backward-looking interferograms from multi-look (2-looks in general) processed sub-images before and after an event. By combining with the conventional DInSAR technique, two-dimensional surface deformation can then be measured. The use of InSAR is not limited to the DEM generation and measurements of surface deformation, but can also be applied to forestry. Although the technique and its accuracy are under study, the InSAR coherence is shown to be a useful parameter for tree height estimation. Unlike the CT-InSAR system using multiple antennas (for airborne systems) or multiple baselines (for both airborne and spaceborne systems) separated in the cross-track direction, the along-track InSAR system uses multiple antennas along the platform direction, and measures current fields over oceans and rivers; it can also be used for MTI (moving target indicator). AT-InSAR has been limited to the airborne system due to the technical difficulty of placing multiple antennas on a satellite, but the antennas of TerraSAR-X and TanDEM-X are split into two sections in the along-track direction, enabling AT-InSAR from space. The current velocity measured by AT-InSAR is proportional to the time lag between the two antennas, so that the measurable lower velocity is limited by the small separation of the split antenna of TerraSAR-X (and TanDEM-X). However, the formation flight by these two satellites, currently being experimented, should yield flexible and extended range of velocity measurements.
Polarimetry is a recent emerging state-of-the-art technology, and expanding the present SAR technology to the field of new dimension. PolSAR and Pol-InSAR have been used by airborne systems, but with the launch of the first spaceborne fully polarimetric ALOS-PALSAR in 2006, interest has accelerated with great enthusiasm resulting in substantial numbers of research publications. In the model-based scattering power decomposition analysis, the backscattered power can be decomposed into three or four components of different scattering mechanisms, and thus the technique is used for a new type of image classification, which cannot be achieved by amplitude data alone. Eigenvalue analysis can determine the randomness of scattering by the entropy, and different scattering processes by the alpha angle. Using these two parameters in Cartesian coordinates, a new classification scheme based on the scattering process has been proposed, which can be expanded to a three-dimensional space using the anisotropy or total power. Many other classifiers based on feature vector in feature space using PolSAR data have been proposed, including one based on the Whishart distribution. While these techniques are based on statistical averaging, pixel-based non-statistical analyses such as the Pauli decomposition have been used for target detection and classification. Pol-InSAR is a new technique combining polarimetry and interferometry. The former is used for classification of scattering mechanisms, and the latter for height measurements. Thus, Pol-InSAR can be applied to estimating the height of a target having a particular scattering process, e.g., surface, double-bounce, or volume scattering, and as such, can be used to measure tree height. Pol-InSAR using L-band or P-band of long penetration depth can also be used for tomography. A recent interesting new scheme is compact polarimetric SAR (CP-SAR). CP-SAR cannot provide the full polarimetric information that can be obtained by the conventional quad-polarization data, but it has advantages of reducing the transmission power and hardware requirements, and also mitigating the ionospheric effects. SAR polarimetry is at a developing stage, and for practical applications, it requires further effort for stringent validation of its methodology.
As to the present status of spaceborne SARs, CosmoSkyMed and SAR-Lupe series, and RADARSAT-2 are in operation, and TanDEM-X with TerraSAR-X has started to produce new results. Reflecting these recent trends, new spaceborne and airborne SARs are being planned by the agencies and institutes of various countries. Using the great amount of these data, much advance is expected in research, developing and validating new SAR technologies, and in applications to geoscience and related fields.
Acknowledgments
The author should like to thank the two reviewers and external editor for very constructive comments and suggestions to improve this paper. The author is also grateful to M. Sugimoto of National Defense Academy, Japan for processing ALOS-PALSAR data, and to G.M. Martin of GMV Aerospace, Spain for providing information on ship detection and identification. Thanks are also due the Japan Aerospace Exploration Agency (JAXA) and European Space Agency (ESA) for cordially providing ALOS-PALSAR and ERS-1 SAR data respectively. Pi-SAR data were provided by the National Institute of Information and Communications Technology (NICT), and JAXA.
References
- Wiley, C.A. Synthetic aperture radars—A paradigm for technology evolution. IEEE Trans. Aerosp. Electron. Syst 1985, 21, 440–443. [Google Scholar]
- Watson-Watt, R., Sir. Three Steps to Victory; Odhams Press: London, UK, 1957. [Google Scholar]
- Jordan, R.L. The Seasat—A synthetic aperture radar system. IEEE J. Ocean. Eng 1980, 5, 154–164. [Google Scholar]
- Evans, D.L.; Alpers, W.; Cazanave, A.; Elach, C.; Farr, T.; Glakin, D.; Holt, B.; Jones, L.; Liu, W.T.; McCandless, W.; et al. Seasat—A 25-year legacy of success. Remote Sens. Environ 2005, 94, 384–404. [Google Scholar]
- Curlander, J.C.; McDonough, R.N. Synthetic Aperture Radar: Systems and Signal Processing; Wiley: New York, NY, USA, 2001. [Google Scholar]
- Elachi, C. Spaceborne Radar Remote Sensing: Applications and Technologies; IEEE Press: New York, NY, USA, 1988. [Google Scholar]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave Remote Sensing: Active and Passive; Addison-Wesley: Reading, MA, USA, 1986; Volume I, pp. 2–3. [Google Scholar]
- Attema, E.P.W. The active microwave instrument on-board the ERS-1 satellite. Proc. IEEE 1991, 79, 791–799. [Google Scholar]
- Cimino, J.; Elachi, C.; Settle, M. SIR-B-the second Shuttle Imaging Radar experiment. IEEE Trans. Geosci. Remote Sens. 1986, GE-24, 445–452. [Google Scholar]
- Granger, J.L. Shuttle Imaging Radar-A/B Sensors. Proceedings of First Spaceborne Imaging Radar Symposium, Pasadena, CA, USA, 17–20 January 1983; JPL Pub. 83–11. pp. 26–31.
- Jordan, R.L.; Huneycutt, B.L.; Werner, M. The SIR-C/X-SAR synthetic aperture radar system. Proc. IEEE 1991, 79, 827–838. [Google Scholar]
- Evans, D.L. Spaceborne imaging radar-C/X-band synthetic aperture radar (SIR-C/X-SAR): A look back on the tenth anniversary. IEEE Proc. Radar Son. Nav 2006, 153, 81–85. [Google Scholar]
- Farr, T.G.; Kobrick, M. Shuttle radar topography mission produces a wealth of data. EOS Trans. AGU 2000, 81, 583–585. [Google Scholar]
- Werner, M. Shuttle Radar Topography Mission (SRTM), Mission overview. Frequenz 2001, 55, 75–79. [Google Scholar]
- Rabus, B.; Eineder, M.; Roth, A.; Bamler, R. The shuttle radar topography mission—A new class of digital elevation models acquired by spaceborne radar. ISPRS J. Photogramm 2003, 57, 241–262. [Google Scholar]
- Shimada, M. SAR programmes in JAXA: From JERS-1 to the future. IEE Proc. Radar Son. Navig 2006, 153, 122–128. [Google Scholar]
- Rosenqvist, A.; Shimada, M.; Ito, N.; Watanabe, M. ALOS PALSAR: A pathfinder mission for global-scale monitoring of the environment. IEEE Trans. Geosci. Remote Sens 2007, 45, 3307–3316. [Google Scholar]
- Shimada, M.; Tadono, T.; Rosenqvist, A. Advanced Land Observing Satellite (ALOS) and monitoring global environmental change. Proc. IEEE 2010, 98, 780–799. [Google Scholar]
- Nemoto, Y.; Nishino, H.; Ono, M.; Mizutamari, H.; Nishikawa, K.; Tanaka, K. Japanese Earth Resources Satellite-1 synthetic aperture radar. Proc. IEEE 1991, 79, 800–809. [Google Scholar]
- Moon, W.M.; Staples, G.; Kim, D.-J.; Park, S.-E.; Park, K.-A. RADARSAT-2 and coastal applications: Surface wind, waterline, and intertidal flat roughness. Proc. IEEE 2010, 98, 800–815. [Google Scholar]
- Raney, R.K.; Luscombe, A.P.; Langham, E.J.; Ahmed, S. RADARSAT. Proc. IEEE 1991, 79, 839–849. [Google Scholar]
- Krieger, G.; Hajnsek, I.; Papathanassiou, P.; Younis, N.; Moriera, A. Interferometric synthetic aperture radar (SAR) missions employing formation flying. Proc. IEEE 2010, 98, 816–843. [Google Scholar]
- COSMO-SkyMed Web Site, Available online: http://www.cosmo-skymed.it/en/index.htm (accessed on 14 November 2012).
- Torre, A.; Capece, P. COSMO-SkyMed: The Advanced SAR Instrument. Proceedings of 2011 5th International Conference on Recent Advances in Space Technologies (RASAT), Rome, Italy, 9–11 June 2011; pp. 865–868.
- Reale, D.; Nitti, D.O.; Peduto, D.; Nutricato, R.; Bovenga, F.; Fornaro, G. Postseismic deformation monitoring with the COSMO/SKYMED constellation. IEEE Geosci. Remote Sens. Lett 2011, 8, 696–700. [Google Scholar]
- The RADARSAT Constellation Program, Available online: http://www.asc-csa.gc.ca/pdf/radarsat_constellation_eng.pdf (accessed on 14 November 2012).
- Colinas, J.; Séguin, G.; Plourde, P. Radarsat Constellation, Moving toward Implementation. Proceedings of IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25– 30 July 2010; pp. 3232–3235.
- Thompson, A.A. Innovative Capabilities of the RADARSAT Constellation Mission. Proceedings of 8th European Conference on Synthetic Aperture Radar (EUSAR), Aachen, Germany, 7–10 June 2010.
- Stevens, D.R.; Cumming, I.G.; Gray, A.L. Options for airborne interferometric SAR motion compensation. IEEE Trans. Geosci. Remote Sens 1995, 3, 409–420. [Google Scholar]
- Prats, P.; de Macedo, K.A.C.; Reigber, A.; Scheiber, R.; Mallorquí, J.J. Comparison of topography-and aperture-dependent motion compensation algorithms for airborne SAR. IEEE Geosci. Remote Sens. Lett 2007, 4, 349–353. [Google Scholar]
- Brown, W.D.; Ghiglia, D.C. Some methods for reducing propagation-induced phase errors in coherent imaging systems. Part I. Formalism. J. Opt. Soc. Am 1988, A5, 924–942. [Google Scholar]
- Ghiglia, D.C.; Mastin, G.A. Two-dimensional phase correction of synthetic-aperture-radar imagery. Opt. Let 1989, 14, 1104–1106. [Google Scholar]
- Oliver, C.J. Synthetic-aperture radar imaging. J. Phys. D 1989, 22, 871–980. [Google Scholar]
- Werness, S.; Carrara, W.; Joyce, L.; Franczak, D. Moving target imaging algorithms for SAR data. IEEE Trans. Aerosp. Electron. Syst 1990, 26, 57–67. [Google Scholar]
- Yoji, G.N. Phase Difference Auto Focusing for Synthetic Aperture Radar Imaging, US Patent 4,999,635. 12 March 1991.
- Eichel, P.H.; Jakpwatz, G.V., Jr. Phase-gradient algorithm as an optimal estimator of the phase derivative. Opt. Let 1989, 14, 1101–1103. [Google Scholar]
- Wahl, D.E.; Eichel, P.H.; Ghiglia, D.C.; Jakpwatz, G.V., Jr. Phase gradient autofocus—A robust tool for high resolution SAR phase correction. IEEE Trans. Aerosp. Electron. Syst 1994, 30, 827–834. [Google Scholar]
- Kolman, J. PACE: An Autofocus Algorithm for SAR. Proceedings of 2005 IEEE International Radar Conference, Arlington, VA, USA, 9– 12 May 2005; pp. 310–314.
- Yang, J.; Huang, X.; Jin, J.; Xue, G.; Zhou, Z. An interpolated phase adjustment by contrast enhancement algorithm for SAR. IEEE Geosci. Remote Sens. Lett 2011, 8, 211–214. [Google Scholar]
- Wang, J.; Liu, X. SAR minimum-entropy autofocus using an adaptive-order polynomial model. IEEE Geosci. Remoe Sens. Lett 2006, 3, 512–516. [Google Scholar]
- Samczynski, P.; Kulpa, K.S. Coherent MapDrift technique. IEEE Trans. Geosci. Remote Sens 2010, 48, 1505–1517. [Google Scholar]
- Samczynski, P. Superconvergent velocity estimator for an autofocus coherent MapDrift Technique. IEEE Geosci. Remote Sens. Lett 2012, 9, 204–208. [Google Scholar]
- Kersten, P.R.; Jansen, R.W.; Luc, K.; Ainsworth, T.L. Motion analysis in SAR images of unfocused objects using time-frequency methods. IEEE Geosci. Remote Sens. Lett 2007, 4, 527–531. [Google Scholar]
- Ash, J.N. An autofocus method for backprojection imagery in synthetic aperture radar. IEEE Geosci. Remote Sens. Lett 2012, 9, 104–108. [Google Scholar]
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Massonnet, D.; Souyris, J.-C. SAR Interferometry: Towards the Ultimate Ranging Accuracy. In Imaging with Synthetic Aperture Radar; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2008; Chapter 4; pp. 177–228. [Google Scholar]
- Graham, L.C. Synthetic interferometer radar for topographic mapping. Proc. IEEE 1974, 62, 763–768. [Google Scholar]
- Rodriguez, E.; Martin, J.M. Theory and design of interferometric SARs. Proc. IEEE 1992, 139, 147–159. [Google Scholar]
- Gens, R.; van Genderen, J.L. SAR interferometry-Issues, techniques, applications. Int. J. Remote Sens 1996, 17, 1803–1835. [Google Scholar]
- Bamler, R.; Hartl, P. Synthetic aperture radar interferometry. Inverse Probl 1998, 14, R1–R54. [Google Scholar]
- Rosen, P.; Hensley, S.; Joughin, I.R.; Li, F.K.; Madsen, S.N.; Rodriguez, E.; Goldstein, R. Synthetic aperture radar interferometry. Proc. IEEE 2000, 88, 333–382. [Google Scholar]
- Gabriel, A.K.; Goldstein, R.M.; Zebker, H.A. Mapping small elevation changes over large areas: Differential radar interferometry. J. Geophys. Res 1989, 94, 9183–9191. [Google Scholar]
- Massonnet, D.; Feigl, K. Radar interferometry and its application to changes in the earth’s surface. Rev. Geophys 1998, 36, 441–500. [Google Scholar]
- Ferretti, A.; Prati, C.; Rocca, F. Nonlinear subsidence rate estimation using permanent scatterers in differential SAR interferometry. IEEE Trans. Geosci. Remote Sens 2000, 38, 2202–2212. [Google Scholar]
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens 2001, 39, 8–20. [Google Scholar]
- Hilley, G.E.; Bergmann, R.; Ferretti, A.; Novali, F.; Rocca, F. Dynamics of slow-moving landslides from permanent scatter analysis. Science 2004, 304, 1952–1955. [Google Scholar]
- Van der Kooij, M.; Hughes, W.; Sato, S.; Poncos, V. Coherent Target Monitoring at High Spatial Density: Examples of Validation Results. Proceedings of the Advances in the Science and Applications of SAR Interferometry, ESA Fringe 2005, Workshop, ESA, Frascati, Italy, 28 November–2 December 2005; Available online: http://earth.esa.int/fringe05/proceedings/ (accessed on 15 November 2012).
- Kampes, B.M. Radar Interferometry—Persistent Scatterer Technique; Springer: Dordrecht, The Netherlands, 2006. [Google Scholar]
- Rocca, F. Modeling interferogram stacks. IEEE Trans. Geosci. Remote Sens 2007, 45, 3289–3299. [Google Scholar]
- InSAR CTM, Available online: http://www.gisat.cz/images/upload/6185b_ev-ctm.pdf (accessed on 15 November 2012).
- Blanco-Sanchez, P.; Mallorquí, J.J.; Duque, S.; Monells, D. The coherent pixels technique (CPT): An advanced DInSAR technique for nonlinear deformation monitoring. Pure Appl. Geophys 2008, 165, 1167–1194. [Google Scholar]
- Crosetto, M.; Monserrat, O.; Cuevas, M.; Crippa, B. Spaceborne differential SAR interferometry: Data analysis tools for deformation measurement. Remote Sens 2011, 3, 305–318. [Google Scholar]
- Goldstein, R.M.; Zebker, H.A. Interferometric radar measurements of ocean surface currents. Nature 1987, 328, 707–709. [Google Scholar]
- Shemer, L.; Marom, M.; Markman, D. Estimates of currents in the nearshore ocean region using interferometric synthetic aperture radar. J. Geophys. Res 1993, 98, 7001–7010. [Google Scholar]
- Shemer, L.; Marom, M. Estimates of ocean coherence time by an interferometric SAR. Int. J. Remote Sens 1993, 14, 3021–3029. [Google Scholar]
- Carande, R.E. Estimating ocean coherence time using dual-baseline interferometric synthetic aperture radar. IEEE Trans. Geosci. Remote Sens 1994, 32, 846–854. [Google Scholar]
- Ainsworth, T.L.; Chubb, S.R.; Fusina, R.A.; Goldstein, R.M.; Jansen, R.W.; Lee, J.-S.; Valenzuela, J.S. INSAR imagery of surface currents, wave fields, and fronts. IEEE Trans. Geosci. Remote Sens 1995, 33, 1117–1123. [Google Scholar]
- Frasier, S.J.; Camps, A.J. Dual-beam interferometry for ocean surface current vector mapping. IEEE Trans. Geosci. Remote Sens 2001, 39, 404–414. [Google Scholar]
- Siegmund, R.; Bao, M.; Lehner, S.; Mayerle, R. First demonstration of surface currents imaged by hybrid along- and cross-track interferometric SAR. IEEE Trans. Geosci. Remote Sens 2004, 42, 511–519. [Google Scholar]
- Romeiser, R.; Breit, H.; Eineder, M.; Runge, H.; Flament, P.; Karin, de Jong; Vogelzang, J. Current measurements by SAR along-track interferometry from a Space Shuttle. IEEE Trans. Geosci. Remote Sens 2005, 43, 2315–2324. [Google Scholar]
- Toporkov, J.V.; Perkovic, D.; Farquharson, G.; Sletten, M.A.; Frasier, S.J. Sea surface velocity vector retrieval using dual-beam interferometry: First demonstration. IEEE Trans. Geosci. Remote Sens 2005, 43, 2494–2502. [Google Scholar]
- Romeiser, R.; Runge, H. Current Measurements in Coastal Waters and Rivers by Along-Track InSAR. In Remote Sensing of the European Seas; Barale, V., Gade, M., Eds.; Springer: Berlin, Germany, 2008; pp. 411–422. [Google Scholar]
- Romeiser, R.; Suchandt, S.; Runge, H.; Steinbrecher, U.; Grünler, S. First analysis of TerraSAR-X along-track InSAR-derived current fields. IEEE Trans. Geosci. Remote Sens 2010, 48, 820–829. [Google Scholar]
- Breit, H.; Eineder, M.; Holzner, J.; Runge, H.; Bamler, H. Traffic Monitoring Using SRTM Along-Track Interferometry. Proceedings of IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Toulouse, France, 21– 25 July 2003; II, pp. 1187–1189.
- Lombardo, P.; Colone, F.; Pastina, D. Monitoring and surveillance potentialities obtained by splitting the antenna of the COSMO-SkyMed SAR into multiple sub-apertures. IEE Proc. Radar Son. Navig 2006, 153, 104–116. [Google Scholar]
- Meyer, F.; Hinz, S.; Laika, A.; Weihing, D.; Bamler, R. Performance analysis of the TerraSAR-X traffic monitoring concept. ISPRS J. Photogramm 2006, 61, 225–242. [Google Scholar]
- Kohlleppel, R.; Gierull, C.H. Enhancement of Along-Track Interferometry for Ground Moving Target Indication. Proceedings of IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Boston, MA, USA, 7– 11 July 2008; II, pp. 229–232.
- Yang, L.; Wang, T.; Bao, Z. Ground moving target indication using an InSAR system with a hybrid baseline. IEEE Geosci. Remote Sens. Lett 2008, 5, 373–377. [Google Scholar]
- Suchandt, S.; Runge, H.; Breit, H.; Steinbrecher, U.; Kotenkov, A.; Balss, U. Automatic extraction of traffic flows using TerraSAR-X along-track interferometry. IEEE Trans. Geosci. Remote Sens 2010, 48, 807–819. [Google Scholar]
- Van Zyl, J.J. Imaging radar polarization signatures: Theory and observation. Radio Sci 1987, 22, 529–543. [Google Scholar]
- Ulaby, F.T.; Elachi, C. Radar Polarimetry for Geoscience Applications; Artech House: Norwood, MA, USA, 1990. [Google Scholar]
- Zebker, H.A.; van Zyl, J.J. Imaging radar polarimetry: A review. Proc. IEEE 1991, 79, 1583–1605. [Google Scholar]
- Mott, H. Remote Sensing with Polarimetric Radar; Wiley: New York, NY, USA, 2007. [Google Scholar]
- Massonnet, D.; Souyris, J.-C. SAR Polarimetry: Towards the Ultimate Characterization of Targets. In Imaging with Synthetic Aperture Radar; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2008; Chapter 5; pp. 229–272. [Google Scholar]
- Lee, J.-S.; Pottier, E. Polarimetric Radar Imaging—From Basics to Applications; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2009. [Google Scholar]
- Cloude, S.R. Polarisation: Application in Remote Sensing; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Van Zyl, J.J.; Kim, Y.J. Synthetic Aperture Radar Polarimetry; Wiley: New York, NY, USA, 2011. [Google Scholar]
- Kostinski, A.B.; James, B.D.; Boerner, W.-M. Polarimetric matched filter for coherent imaging. Can. J. Phys 1988, 66, 817–877. [Google Scholar]
- Swarts, A.A.; Yueh, H.A.; Kong, J.A.; Novak, L.M.; Shin, R.T. Optimal polarization for achieving maximum contrast in radar images. J. Geophys. Res 1988, 93, 15252–15260. [Google Scholar]
- Boerner, W.-M.; Yan, W.L.; Xi, A.-Q.; Yamaguchi, Y. On the basic principles of radar polarimetry: The target characteristic polarization state theory of Kennauugh, Huynen’s polarization fork concept, and its extension to the partially polarized case. Proc. IEEE 1991, 79, 1538–1550. [Google Scholar]
- Boerner, W.-M.; Walther, M.; Segal, A.C. The concept of the polarimetric matched signal & image filters: Application to radar target versus speckle reduction & optimal background clutter discrimination in microwave sensing and imaging. EARSeL Adv. Remote Sen 1993, 2, 219–252. [Google Scholar]
- Rignot, E.; Chellappa, R.; Dubois, P. Unsupervised segmentation of polarimetric SAR data using the covariance matrix. IEEE Trans. Geosci. Remote Sens 1992, 30, 697–705. [Google Scholar]
- Van Zyl, J.J. Application of Cloude’s target decomposition theorem to polarimetric imaging radar. Proc. SPIE 1993, 184, 184–191. [Google Scholar]
- Yamaguchi, Y.; Takayanagi, Y.; Boerner, W.-M.; Eom, H.J.; Sengoku, M. Polarimetric enhancement in radar channel imagery. IEICE Trans. Commun 1995, E78, 1571–1579. [Google Scholar]
- Cloude, S.R.; Pottier, E. A review of target decomposition theorems in radar polarimetry. IEEE Trans. Geosci. Remote Sens 1996, 34, 498–518. [Google Scholar]
- Cloude, S.R.; Pottier, E. An entropy based classification scheme for land applications of polarimetric SAR. IEEE Trans. Geosci. Remote Sens 1997, 35, 68–78. [Google Scholar]
- Boerner, W.-M.; Mott, H.; Lunenburg, E.; Livingstone, C.; Brisco, B.; Brown, R.J.; Patterson, J.S. Polarimetry in Remote Sensing: Basic and Applied Concepts. In Manual of Remote Sensing, Volume 2: Principles and Applications of Imaging Radar, 3rd ed.; Wiley: New York, NY, USA, 1998; Chapter 5; pp. 271–358. [Google Scholar]
- Freeman, A.; Durden, S.L. A three-component scattering model for polarimetric SAR data. IEEE Trans. Geosci. Remote Sens 1998, 36, 963–973. [Google Scholar]
- Lee, J.-S.; Grunes, M.R.; Anisoworth, T.L.; Du, L.J.; Schuler, D.L.; Coulde, S.R. Unsupervised classification using polarimetric decomposition and the complex Whishart classifier. IEEE Trans. Geosci. Remote Sens 1999, 35, 2249–2258. [Google Scholar]
- Yang, J.; Yamaguchi, Y.; Yamada, H.; Sengoku, M.; Lin, S.-M. The optimal problem for contrast enhancement in polarimetric radar remote sensing. IEICE Trans. Commun. 1999, E82-B, 174–183. [Google Scholar]
- Ferro-Famil, L.; Pottier, E.; Lee, J.-S. Unsupervised classification of multifrequency and fully polarimetric SAR images based on H/A/Alpha-Whishart classifier. IEEE Trans. Geiosci. Remote Sens 2001, 39, 2332–2342. [Google Scholar]
- Pottier, E.; Lee, J.-S.; Ferro-Famil, L. Advanced Concepts in Polarimetry—Part 1 (Polarimetric Target Description, Speckle Filtering and Decomposition Theorems); RTO-EN-SET-081; NATO Science and Technology Organization: Paris, France, 2004. [Google Scholar]
- Lumsdon, P.; Cloude, S.R.; Wright, G. Polarimetric classification of land cover for Glen Affric radar project. IEEE Proc. Radar Son. Navig 2005, 152, 404–412. [Google Scholar]
- Yamaguchi, Y.; Moriyama, T.; Ishido, M.; Yamada, H. Four-component scattering model for polarimetric SAR image decomposition. IEEE Trans. Geosci. Remote Sens 2005, 43, 1699–1706. [Google Scholar]
- Xu, F.; Jin, Y.-Q. Deorientation theory of polarimetric scattering targets and application to terrain surface classification. IEEE Trans. Geosci. Remote Sens 2005, 43, 2351–2364. [Google Scholar]
- Cameron, W.L.; Rais, H. Conservative polarimetric scatterers and their role in incorrect extensions of the Cameron decomposition. IEEE Trans. Geosci. Remote Sens 2006, 44, 3506–3516. [Google Scholar]
- Lee, J.-S.; Krogager, E.; Ainsworth, T. L.; Boerner, W.-M. Polarimetric analysis of radar signature of a manmade structure. IEEE Geosci. Remote Sens. Lett 2006, 3, 555–559. [Google Scholar]
- Touzi, R. Target scattering decomposition in terms of roll-invariant target parameters. IEEE Trans. Geosci. Remote Sens 2007, 45, 73–84. [Google Scholar]
- Yajima, Y.; Yamaguchi, Y.; Sato, R.; Yamada, H.; Boerner, W.-M. POLSAR image analysis of wetlands using a modified four-component scattering power decomposition. IEEE Trans. Geosci. Remote Sens 2008, 46, 1667–1673. [Google Scholar]
- Zhang, L.; Zou, B.; Cai, H.; Zhang, Y. Multiple-component scattering model for polarimetric SAR image decomposition. IEEE Geosci. Remote Sens. Lett 2008, 5, 603–607. [Google Scholar]
- McNairn, H.; Shang, J.L.; Jiao, S.F.; Champagne, C. The contribution of ALOS PALSAR multipolarization and polarimetric data to crop classification. IEEE Trans. Geosci. Remote Sens 2009, 47, 3981–3992. [Google Scholar]
- Praks, J.; Koeniguer, E.C.; Hallikainen, M.T. Alternatives to target entropy and alpha angle in SAR polarimetry. IEEE Trans. Geosci. Remote Sens 2009, 47, 2262–2274. [Google Scholar]
- Touzi, R.; Deschamps, A.; Rother, G. Phase of target scattering for wetland characterization using polarimetric C-band SAR. IEEE Trans. Geosci. Remote Sens 2009, 47, 3241–3261. [Google Scholar]
- Li, P.; Deng, S.; Zhang, J.; Huang, G.; Zhao, Z. A Framework of Polarimetric SAR Filter Based on Independence of Intensity and Polarimetric Information. Proceedings of ISPRS TC VII Symposium—100 Years ISPRS, Vienna, Austria, 5–7 July 2010; XXXVIII, Part 7A. pp. 117–121.
- Marino, A.; Cloude, S.R.; Woodhouse, I.H. A polarimetric target detector using the Huynen fork. IEEE Trans. Geosci. Remote Sens 2010, 48, 2357–2366. [Google Scholar]
- Antropov, O.; Rauste, Y.; Hame, T. Volume scattering modeling in PolSAR decompositions: Study of ALOS PALSAR data over boreal forest. IEEE Trans. Geosci. Remote Sens 2011, 49, 3838–3848. [Google Scholar]
- Arii, M.; van Zyl, J.J.; Kim, Y. Adaptive model-based decomposition of polarimetric SAR covariance matrices. IEEE Trans. Geosci. Remote Sens 2011, 49, 1104–1113. [Google Scholar]
- Yamaguchi, Y.; Sato, A.; Boerner, W.M.; Sato, R.; Yamada, H. Four-component scattering power decomposition with rotation of coherency matrix. IEEE Trans. Geosci. Remote Sens 2011, 49, 2251–2258. [Google Scholar]
- Van Zyl, J.J.; Arii, M.; Kim, Y. Model-based decomposition of polarimetric SAR covariance matrices constrained for nonnegative eigenvalues. IEEE Trans. Geosci. Remote Sens 2011, 49, 3452–3459. [Google Scholar]
- Li, K.; Brisco, B.; Yun, S.; Touzi, R. Polarimetric decomposition with RADARSAT-2 for rice mapping and monitoring. Can. J. Remote Sens 2012, 38, 169–179. [Google Scholar]
- Pajares, G.; López-Martinez, C.; Sánchez-Lladó, F.J.; Molina, I. Improving Wishart classification of polarimetric SAR data using the Hopfield Neural Network optimization approach. Remote Sens 2012, 4, 3571–3595. [Google Scholar]
- Ramsey, E., III; Rangoonwala, A.; Suzuoki, Y.; Jones, C.E. Oil detection in a coastal marsh with polarimetric synthetic aperture radar (SAR). Remote Sens 2011, 3, 2630–2662. [Google Scholar]
- Sato, A.; Yamaguchi, Y.; Singh, G.; Park, S.-E. Four-component scattering power decomposition with extended volume scattering model. IEEE Geosci. Remote Sens. Lett 2012, 9, 166–170. [Google Scholar]
- Shan, Z.; Wang, C.; Zhang, H.; An, W. Improved four-component model-based target decomposition for polarimetric SAR data. IEEE Geosci. Remote Sens. Lett 2012, 9, 75–79. [Google Scholar]
- Sugimoto, M.; Ouchi, K.; Nakamura, Y. Four-component scattering power decomposition algorithm with rotation of covariance matrix using ALOS-PALSAR polarimetric data. Remote Sens 2012, 4, 2199–2209. [Google Scholar]
- Watanabe, M.; Yonezawa, C.; Iisaka, J.; Sato, M. ALOS/PALSAR full polarimetric observations of the Iwate-Miyagi Nairiku earthquake of 2008. Int. J. Remote Sens 2012, 33, 1234–1245. [Google Scholar]
- Yonezawa, C.; Watanabe, M.; Saito, G. Polarimetric decomposition analysis of ALOS-PALSAR observation data before and after a landslide event. Remote Sens 2012, 4, 2314–2328. [Google Scholar]
- Wright, P.A.; Quegan, S.; Wheadon, N.S.; Hall, C.D. Faraday rotation effects on L-band spaceborne SAR data. IEEE Trans. Geosci. Remote Sens 2003, 41, 2735–2744. [Google Scholar]
- Jehle, M.; Ruegg, M.; Small, D.; Meier, E.; Nuesch, D. Estimation of ionospheric TEC and Faraday rotation for L-band SAR. Proc. SPIE 2005. [Google Scholar] [CrossRef]
- Qi, R.-Y.; Jin, Y.-Q. Analysis of the effects of Faraday rotation on spaceborne polarimetric SAR observations at P-band. IEEE Trans. Geosci. Remote Sens 2007, 45, 1115–1122. [Google Scholar]
- Meyer, F.J.; Nicoll, J.B. Prediction, detection, and correction of Faraday rotation in full-polarimetric L-band SAR data. IEEE Trans. Geosci. Remote Sens 2008, 46, 3076–3086. [Google Scholar]
- Jehle, M.; Ruegg, M.; Zuberbuhler, L.; Small, D.; Meier, E. Measurement of ionospheric Faraday rotation in simulated and real spaceborne SAR data. IEEE Trans. Geosci. Remote Sens 2009, 47, 1512–1523. [Google Scholar]
- Kimura, H. Calibration of polarimetric PALSAR imagery affected by Faraday rotation using polarization orientation. IEEE Trans. Geosci. Remote Sens 2009, 47, 3943–3950. [Google Scholar]
- Takeshiro, A.; Furuya, T.; Fukuchi, H. Verification of polarimetric calibration method including Faraday rotation compensation using PALSAR data. IEEE Trans. Geosci. Remote Sens 2009, 47, 3960–3968. [Google Scholar]
- Truong-Loi, M.-L.; Freeman, A.; Dubois-Fernandez, P.C.; Pottier, E. Estimation of soil moisture and Faraday rotation from bare surfaces using compact polarimetry. IEEE Trans. Geosci. Remote Sens 2009, 47, 3608–3615. [Google Scholar]
- Cloude, S.R.; Papathanassiou, K.P. Polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Sens 1998, 36, 1551–1563. [Google Scholar]
- Reigber, A.; Moriera, A. First demonstration of airborne SAR tomography using multibaseline L-band data. IEEE Trans. Geosci. Remote Sens 2000, 38, 2142–2152. [Google Scholar]
- Treuhaft, R.N.; Siqueira, P.R. Vertical structure of vegetated land surfaces from interferometric and polarimetric radar. Radio Sci 2000, 53, 141–177. [Google Scholar]
- Papathanassiou, K.P.; Cloude, S.R. Single-baseline polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Sens 2001, 39, 2352–2363. [Google Scholar]
- Cloude, S.R.; Papathanassiou, K.P. Three-stage inversion process for polarimetric SAR interferometry. IEEE Proc. Radar Son. Navig 2003, 150, 125–134. [Google Scholar]
- Aulinger, T.; Mette, T.; Papathanassiou, K.P.; Hajnsek, I.; Heurich, M.; Krzystek, P. Validation of Heights from Interferometric SAR and Lidar over the Temperate Forest Site “National Park Bayerischer Wald”. Proceedings of the 2nd International Workshop POLINSAR 2005 (ESA SP-586), ESRIN, Frascati, Italy, 17–21 January 2005.
- Boerner, W.-M. Applications of Polarimetric and Interferometric SAR to Environmental Remote Sensing and Its Activities: Recent Advances in Extrawideband Polarimetry, Interferometry and Polarimetric Interferometry in Synthetic Aperture Remote Sensing and Its Applications, Available online: http://www.cso.nato.int/ (accessed on 15 November 2012).
- Morio, J; Réfrégier, P.; Goudail, F.; Dubois-Fernandez, P.; Dupuis, X. Application of Information Theory Measures to Polarimetric and Interferometric SAR Images. Proceedings of 5th International Conference on Physics in Signal & Image Processing (PSIP), Mulhouse, France, 30 January–2 February 2007.
- Praks, J.; Kugler, F.; Papathanassiou, K.P.; Hajnsek, I.; Hallikainen, M. Tree height estimation for boreal forest by means of L- and X- band POLInSAR and HUTSCAT profiling scatterometer. IEEE Geosci. Remote Sens. Lett 2007, 4, 466–470. [Google Scholar]
- Lambardini, F.; Pardini, M. 3-D SAR tomography: The multibaseline sector interpolation approach. IEEE Geosci. Remote Sens. Lett 2008, 5, 630–634. [Google Scholar]
- Garestier, F.; Dubois-Fernandez, P.C.; Papathanassiou, K.P. Pine forest height inversion using single-pass X Band PolInSAR data. IEEE Trans. Geosci. Remote Sens 2008, 46, 59–68. [Google Scholar]
- Hajnsek, I.; Kugler, F.; Lee, S.-K.; Papathanassiou, K.P. Tropical-forest-parameter estimation by means of Pol-InSAR: The INDREX-II campaign. IEEE Trans. Geosci. Remote Sens 2009, 47, 481–493. [Google Scholar]
- Tebaldini, S. Algebraic synthesis of forest scenarios from multibaseline PolInSAR data. IEEE Trans. Geosci. Remote Sens 2009, 47, 4132–4142. [Google Scholar]
- Gama, F.F.; Santos, J.R.D.; Mura, J.C. Eucalyptus biomass and volume estimation using interferometric and polarimetric SAR data. Remote Sens 2010, 2, 939–956. [Google Scholar]
- Neumann, M.; Ferro-Famil, L.; Reigber, A. Estimation of forest structure, ground, and canopy layer characteristics from multibaseline polarimetric interferometric SAR data. IEEE Trans. Geosci. Remote Sens 2010, 48, 1086–1104. [Google Scholar]
- Tebaldini, S. Single and multipolarimetric SAR tomography of forested areas: A parametric approach. IEEE Trans. Geosci. Remote Sens 2010, 48, 2375–2387. [Google Scholar]
- Tabaldini, S.; Guarieri, A.M. On the role of phase stability in SAR multibaseline applications. IEEE Trans. Geosci. Remote Sens 2010, 48, 2953–2966. [Google Scholar]
- d’Alessandro, M.M.; Tebaldini, S. Phenomenology of P-band scattering from a tropical forest through three-dimensional SAR tomography. IEEE Geosci. Remote Sens. Lett 2012, 9, 442–446. [Google Scholar]
- Kobayashi, S.; Omura, Y.; Sanga-Ngoie, K.; Widyorini, R.; Kawai, S.; Supriadi, B.; Yamaguchi, Y. Characteristics of decomposition powers of L-band multi-polarimetric SAR in assessing tree growth of industrial plantation forests in the tropics. Remote Sens 2012, 4, 3058–3077. [Google Scholar]
- Neumann, M.; Saatchi, S.S.; Ulander, L.M.H.; Fransson, R.E.S. Assessing performance of L- and P-band polarimetric interferometric SAR data in estimating boreal forest above-ground biomass. IEEE Trans. Geosci. Remote Sens 2012, 50, 714–726. [Google Scholar]
- Tebaldini, S.; Rocca, F. Multibaseline polarimetric SAR tomography of a boreal forest at P- and L-bands. 2012, 50, 232–246. [Google Scholar]
- Keydel, W. Present and Future Airborne and Space-Borne Systems, Available online: http://www.dtic.mil/cgi-bin/GetTRDoc?AD=ADA470890 (accessed on 22 January 2013).
- Krieger, G.; Hajnsek, I.; Papathanassiou, K.; Eineder, M.; Younis, M.; De Zan, F.; Lopez-Dekker, P.; Huber, S.; Werner, M.; Prats, P.; et al. Tandem-L: A Mission for Monitoring Earth System Dynamics with High Resolution SAR Interferometry. Proceedings of 8th European Conference on Synthetic Aperture Radar (EUSAR), Aachen, Germany, 7–10 June 2010; pp. 506–509.
- Corcoran, K.M. Higher Eyes in the Sky-The Feasibility of Moving AWACS and JSTARS Functions into Space; Air University Press: Montgomery, AL, USA, 1999. [Google Scholar]
- Cherniakov, M., Ed.; Bistatic Radar: Emerging Technology; John Wiley & Sons: Chechester, UK, 2007.
- Cherniakov, M. Bistatic Radar: Theory and Practice; John Wiley & Sons: Chechester, UK, 2007. [Google Scholar]
- Nies, H.; Loffeld, O.; Natroshvili, K. Analysis and focusing bistatic airborne SAR data. IEEE Trans. Geosci. Remote Sens 2007, 45, 3342–3349. [Google Scholar]
- Bamler, R.; Meyer, F.; Liebhart, W. Processing bistatic SAR data from quasi-stationary configuration. IEEE Trans. Geosci. Remote Sens 2007, 45, 3350–3358. [Google Scholar]
- Antoniou, M.; Saini, R.; Cherniakov, M. Results of a space-surface bistatic SAR imaging formation algorithm. IEEE Trans. Geosci. Remote Sens 2007, 45, 3359–3371. [Google Scholar]
- Arnold-Bos, A.; Khenchaf, A.; Martin, A. Bistatic radar imaging of the marine environment—Part I: Theoretical background. IEEE Trans. Geosci. Remote Sens 2007, 45, 3372–3383. [Google Scholar]
- Arnold-Bos, A.; Khenchaf, A.; Martin, A. Bistatic radar imaging of the marine environment—Part II: Simulation and results analysis. IEEE Trans. Geosci. Remote Sens 2007, 45, 3384–3396. [Google Scholar]
- Goh, A.S.; Preiss, M.; Stacy, N.J.S.; Gray, S.A. Bistatic SAR experiment with the Ingara imaging radar. IET Radar Sonar Navig 2010, 4, 426–437. [Google Scholar]
- Rodriguez-Cassola, M.; Baumgartner, S.V.; Krieger, G.; Moreira, A. Bistatic TerraSAR-X/F-SAR spaceborne-airborne SAR experiment: Description, data processing, and results. IEEE Trans. Geosci. Remote Sens 2010, 48, 781–794. [Google Scholar]
- Walterscheid, I.; Espeter, T.; Brenner, A.R.; Klare, J.; Ender, J.H.G.; Nies, H.; Wang, R.; Loffeld, O. Bistatic SAR experiments with PAMIR and TerraSAR-X-Setup, processing, and image results. IEEE Trans. Geosci. Remote Sens 2010, 48, 3268–3279. [Google Scholar]
- Rodriguez-Cassola, M.; Prats, P.; Schulze, D.; Tous-Ramon, N.; Steinbrecher, U.; Marotti, L.; Nannini, M.; Younis, M.; Lopez-Dekker, P.; Zink, M.; et al. First bistatic spaceborne SAR experiments with TanDEM-X. IEEE Geosci. Remote Sens. Lett 2012, 9, 33–37. [Google Scholar]
- Krieger, G.; Moreira, A.; Fielder, H.; Hajnsek, I.; Werner, M.; Younis, M.; Zink, M. TenDEM-X: A satellite formation for high-resolution SAR interferometry. IEEE Trans. Geosci. Remote Sens 2007, 45, 3317–3341. [Google Scholar]
- Souyris, J.-C.; Imbo, P.; Fjortoft, R.; Mingot, S.; Lee, J.-S. Compact polarimetry based on symmetry properties of geophysical media: The π/4 mode. IEEE Trans. Geosci. Remote Sens 2005, 43, 634–646. [Google Scholar]
- Raney, R.K. Hybrid-polarity SAR architecture. IEEE Trans. Geosci. Remote Sens 2007, 45, 3397–3404. [Google Scholar]
- Dubois-Fernandez, P.; Souyris, J.-C.; Angelliaume, S.; Garestier, F. The compact polarimetry alternative for spaceborne SAR at low frequency. IEEE Trans. Geosci. Remote Sens 2008, 46, 3208–3222. [Google Scholar]
- Nord, M.; Ainsworth, T.L.; Lee, J.-S.; Stacy, N. Comparison of compact polarimetric synthetic aperture radar modes. IEEE Trans. Geosci. Remote Sens 2009, 47, 174–188. [Google Scholar]
- Ainsworth, T.L.; Kelly, J.P.; Lee, J.-S. Classification comparisons between dual-pol, compact polarimetric and quad-pol SAR imagery. ISPRS J. Photogramm 2009, 64, 464–471. [Google Scholar]
- Charbonneau, F.J.; Brisco, B.; Raney, R.K.; McNairn, H.; Liu, C.; Vachon, P.; Shang, J.; DeAbreu, R.; Champagne, C.; Merzouki, A.; et al. Compact polarimetry overview and applications assessment. Can. J. Remote Sens 2010, 36, S298–S315. [Google Scholar]
- Cloude, S.R.; Goodenough, D.G.; Chen, H. Compat decomposition theory. IEEE Geosci. Remote Sens. Lett 2012, 9, 28–32. [Google Scholar]
- Tsunoda, S.I.; Pace, P.; Stence, J.; Woodring, M.; Hensley, W.H.; Doerry, A.W.; Walker, B.C. Lynx: A high-resolution synthetic aperture radar. Proc. SPIE 1999, 3704, 20–27. [Google Scholar]
- Tsunoda, S.I.; Pace, P.; Stence, J.; Woodring, M.; Hensley, W.H.; Doerry, A.W.; Walker, B.C. Lynx: A High-Resolution Synthetic Aperture Radar. Proceedings of 2000 IEEE Aerospace Conference, Big Sky, MT, USA, 18– 25 March 2000; 5, pp. 51–58.
- Doerry, A.W.; Dubbert, D.E.; Thompson, M.E.; Gutierrez, V.D. A portfolio of fine resolution Ka-band SAR images: Part I. Proc. SPIE 2005, 5788, 13–24. [Google Scholar]
- Doerry, A.W.; Dubbert, D.E.; Thompson, M.E.; Gutierrez, V.D. A portfolio of fine resolution Ka-band SAR images: Part II. Proc. SPIE 2005, 5788, 185–196. [Google Scholar]
- Patterson, M.C.L.; Brescia, A. Integrated Sensor Systems for UAS. Proceedings of the 23rd Bristol UAV System Conference, Bristol, UK, 7–9 April 2008.
- Wang, W.-Q.; Peng, Q.; Cai, J. Waveform-diversity-based millimeter-wave UAV SAR remote sensing. IEEE Trans. Geosci. Remote Sens 2009, 47, 691–700. [Google Scholar]
- Madsen, S.N.; Hensley, S.; Wheeler, K.; Sadowy, G.A.; Miller, T.; Muellerschoen, R.; Lou, Y.; Rosen, P.A. UAV-based L-band SAR with precision flight path control. Proc. SPIE 2005, 5659, 51–60. [Google Scholar]
- Rosen, P.A.; Hensley, S.; Wheeler, K.; Sadowy, G.A.; Miller, T.; Shaffer, S.; Muellerschoen, R.; Jones, C.; Zebker, H.; Madsen, S.N. UAVSAR: A New NASA Airborne SAR System for Science and Technology Research. Proceedings of IEEE Radar Conference, Verona, NY, USA, 24– 27 April 2006; Available online: http://uavsar.jpl.nasa.gov/index.html (accessed on 14 November 2012).
- Kuhnert, C.; Wiesbeck, W. Overview Beamforming Principle. Proceedings of 6th European Conference on Synthetic Aperture Radar (EUSAR), Dresden, Germany, 16–18 May 2006.
- Barton, P. Digital beam forming for radar. IEE Proc. F. Commun. Radar Signal Process 1980, 127, 266–277. [Google Scholar]
- Curtis, T.E. Digital beam forming for sonar systems. IEE Proc. F. Commun. Radar Signal Process 1980, 1. [Google Scholar]
- Steyskal, H. Digital beam forming antenna, an introduction. Microwave J 1987, 30, 107–124. [Google Scholar]
- Chiba, I.; Miura, R.; Tanaka, T.; Karasawa, T. Digital beam beam forming (DGF) antenna for mobile communications. IEEE Aerosp. Electron. Syst. Magazine 1997, 12, 31–41. [Google Scholar]
- Jean, B.R.; Rouse, J.W., Jr. A multiple beam synthetic aperture radar design concept for geoscience applications. IEEE Trans. Geosci. Remote Sens. 1983, GE-21, 201–207. [Google Scholar]
- Currie, A.; Brown, M.A. Wide-swath SAR. IEE Proc. F. Commun. Radar Signal Process 1992, 139, 122–135. [Google Scholar]
- Callaghan, G.D.; Longstaff, I.D. Wide-swath space-borne SAR using a quad-element array. IEE Proc. Radar Son. Navig 1999, 146, 159–165. [Google Scholar]
- Buckreuss, S.; Balzer, W.; Mühlbauer, P.; Werninghaus, R.; Pitz, W. The TerraSAR-X Satellite Project. Proceedings of IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Toulouse, France, 21– 25 July 2003; pp. 3096–3098.
- Herrmann, J. TerraSAR-X Mission: The New Generation in High Resolution Satellites. Procedings of the Anais XIII Simpósio Brasilerio de Sensoriamento Remote, Florianópolis, Brazil, 21–26 April 2007; pp. 7063–7070. Available online: http://marte.dpi.inpe.br/col/dpi.inpe.br/sbsr80/2006/11.10.14.00/doc/7063-7070.pdf (accessed on 27 November 2012).
- Younis, M.; Fischer, C.; Wiesbeck, W. Digital beamforming in SAR systems. IEEE Trans. Geosci. Remote Sens 2003, 41, 1735–1739. [Google Scholar]
- Krieger, G.; Gebert, N.; Moreira, A. Multidimensional waveform encoding: A new digital beamforming technique for synthetic aperture radar remote sensing. IEEE Trans. Geosci. Remote Sens 2008, 46, 31–46. [Google Scholar]
- Krieger, G.; Younis, M.; Gebert, N.; Huber, S.; Bordoni, F.; Patyuchenko, A.; Moreira, A. Advanced Digital Beamforming Concepts for Future SAR Systems. Proceedings of IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25– 30 July 2010; pp. 245–248.
- Freeman, A.; Krieger, G.; Rosen, P.; Younis, M.; Johnson, W.; Huber, S.; Jordan, R.; Moreira, A. SweepSAR: Beam-forming on Receive Using a Reflector-Phased Array Feed Combination for Spaceborne SAR. Proceedings of IEEE Radar Conference, Pasadena, CA, USA, 4– 8 May 2009.
- Younis, M.; Huber, S.; Patyuchenko, A.; Bordoni, F.; Krieger, G. Performance comparison of reflector- and planner-antenna based digital beam-forming SAR. Int. J. Antenn. Propagat. 2009. [Google Scholar] [CrossRef]
- Gebert, N.; Krieger, G.; Moreira, A. Digital beamforming on receive: Techniques and optimization strategies for high-resolution wide-swath SAR imaging. IEEE Trans. Aerosp. Electron 2009, 45, 564–592. [Google Scholar]
- Villano, M.; Krieger, G.; Moreira, A. Staggered-SAR: A New Concept for High-Resolution Wide-Swath Imaging. Proceedings of 2012 IEEE GOLD Remote Sensing Conference, Rome, Italy, 4– 5 June 2012; Available online: http://elib.dlr.de/75767/ (accessed on 15 November 2012).
- Rincon, R.F.; Vega, M.A.; Buenfil, M.; Geist, A.; Hilliard, L.; Racette, P. NASA’s L-band digital beamforming synthetic aperture radar. IEEE Trans. Geosci. Remote Sens 2011, 49, 3622–3628. [Google Scholar]
- Fatoyinbo, T.; Ricon, R.F.; Sun, G.; Ranson, K.J. ECOSAR: A P-band Beamforming Polarimetric Interferometric SAR Instrument to Measure Ecosystem Structure and Biomass. Proceedings of IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Vancouver, Canada, 24– 29 July 2011; pp. 1524–1527.
- Rincon, R.F.; Fatoyinbo, T.; Sun, G.; Ranson, K.J.; Perrine, M.; Deshapnde, M.; Bonds, Q. The ECOSAR P-band Synthetic Aperture Radar. Proceedings of IEEE International Geoscience and Remote Sensing Symposium. (IGARSS), Vancouver, BC, Canada, 24– 29 July 2011; pp. 1512–1515.
- Shimada, M. Ortho-rectification and slope correction of SAR data using DEM and its accuracy evaluation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens 2010, 3, 657–671. [Google Scholar]
- Angelsen, A.; Boucher, D.; Brown, S.; Merckx, V.; Streck, C.; Zarin, D. Guidelines for REDD+ Reference Levels: Principles and Recommendations; Meridian Institute: Washington, DC, USA, 2011. Available online: http://www.REDD-OAR.org (accessed on 15 November 2012).
- UN-REDD Programme, Available online: http://www.un-redd.org/ (accessed on 15 November 2012).
- Attema, E.P.W.; Ulaby, F.T. Vegetation modeled as a water cloud. Radio Sci 1978, 13, 357–364. [Google Scholar]
- Ulaby, F.T.; Sarabandi, K.; McDonald, K.; Whitt, M.; Dobson, M.C. Michigan microwave canopy scattering model. Int. J. Remote Sens 1990, 11, 1223–1253. [Google Scholar]
- Imhoff, M.L. A theoretical analysis of the effect of forest structure on synthetic aperture radar backscatter and the remote sensing of biomass. IEEE Trans. Geosci. Remote Sens 1995, 33, 341–352. [Google Scholar]
- Saatchi, S.S.; McDonald, K.C. Coherent effects in microwave backscattering models for forest canopies. IEEE Trans. Geosci. Remote Sens 1997, 35, 1032–1044. [Google Scholar]
- Dobson, M.C.; Ulaby, F.T.; Le Toan, T.; Beaudoin, A.; Kasischke, E.S.; Christensen, N. Dependence of radar backscatter on coniferous forest biomass. IEEE Trans. Geosci. Remote Sens 1992, 30, 412–415. [Google Scholar]
- Le Toan, T.; Beaudoin, A.; Riom, J.; Guyon, D. Relating forest biomass to SAR data. IEEE Trans. Geosci. Remote Sens 1992, 30, 402–411. [Google Scholar]
- Ranson, K.J.; Sun, Q. Mapping biomass of a northern forest using multifrequency SAR data. IEEE Trans. Geosci. Remote Sens 1994, 32, 388–396. [Google Scholar]
- Beaudoin, A.; Le Toan, T.; Goze, S.; Nezry, E.; Lopes, A.; Mougin, E.; Hsu, C.C.; Han, H.C.; Long, J.A.; Shin, R.T. Retrieval of forest biomass from SAR data. Int. J. Remote Sens 1994, 15, 2777–2796. [Google Scholar]
- Rauste, Y.; Häme, T.; Pulliainen, J.; Heiska, K.; Hallikainen, M. Radar-based forest biomass estimation. Int. J. Remote Sens 1994, 15, 2797–2808. [Google Scholar]
- Imhoff, M.L. Radar backscatter and biomass saturation: Ramifications for global biomass inventory. IEEE Trans. Geosci. Remote Sens 1995, 33, 511–518. [Google Scholar]
- Rignot, E.J.; Zimmermann, R.; van Zyl, J.J. Spaceborne applications of P band imaging radars for measuring forest biomass. IEEE Trans. Geosci. Remote Sens 1995, 33, 1162–1169. [Google Scholar]
- Watanabe, M.; Shimada, M.; Rosenqvist, A.; Tadono, T.; Matsuoka, M.; Romshoo, S.A.; Ohta, K.; Furuta, R.; Nakamura, K.; Moriyama, T. Forest structure dependency of the relation between L-band σ0 and biophysical parameters. IEEE Trans. Geosci. Remote Sens 2006, 44, 3154–3165. [Google Scholar]
- Mohan, S.; Das, A.; Halder, D.; Maity, S. Monitoring and Retrieval of Vegetation Parameter Using Multi-Frequency Polarimetric SAR Data. Proceedings of the 3rd International Asia-Pacific Conference on Synthetic Aperture Radar (APSAR), Seoul, Korea, 26–30 September 2011.
- Kasischke, E.S.; Melack, J.M.; Dobson, M.C. The use of imaging radars for ecological applications—A review. Remote Sens. Environ 1997, 59, 141–156. [Google Scholar]
- Hagberg, J.O.; Ulander, L.M.H.; Askne, J. Repeat-pass SAR interferometry over forested terrain. IEEE Trans. Geosci. Remote Sens 1995, 33, 331–340. [Google Scholar]
- Askne, J.; Dammert, P.; Ulander, L.; Smith, G. C-band repeat-pass interferometric SAR observations of the forest. IEEE Trans. Geosci. Remote Sens 1997, 35, 25–35. [Google Scholar]
- Hyyppä, J.; Hyyppä, H.; Inkinen, M.; Engdahl, M.; Linko, S.; Zhu, Y.-H. Accuracy comparison of various remote sensing data sources in the retrieval of forest stand attributes. For. Ecol. Manage 2000, 128, 109–120. [Google Scholar]
- Fransson, J.E.S.; Smith, G.; Askne, J.; Olsson, H. Stem volume estimation in boreal forests using ERS-1/2 coherence and SPOT XS optical data. Int. J. Remote Sens 2001, 22, 2777–2791. [Google Scholar]
- Koskinen, J.; Pulliainen, J.; Hyyppä, J.; Engdahl, M.; Hallikainen, M. The seasonal behavior of interferometric coherence in boreal forest. IEEE Trans. Geosci. Remote Sens 2001, 39, 820–829. [Google Scholar]
- Santoro, M.; Askne, J.; Smith, G.; Fransson, J.E.S. Stem volume retrieval in boreal forests from ERS 1/2 interferometry. Remote Sens. Environ 2002, 81, 19–35. [Google Scholar]
- Askne, J.; Santoro, M.; Smith, G.; Fransson, J.E.S. Multitemporal repeat-pass SAR interferometry of boreal forests. IEEE Trans. Geosci. Remote Sens 2003, 41, 1540–1550. [Google Scholar]
- Pulliainen, J.; Engdahl, M.; Hallikainen, M. Feasibility of multitemporal interferometric SAR data for stand-level estimation of boreal forest stem volume. Remote Sens. Environ 2003, 85, 397–409. [Google Scholar]
- Askne, J.; Santoro, M. Multitemporal repeat pass SAR interferometry of boreal forests. IEEE Trans. Geosci. Remote Sens 2005, 43, 1219–1228. [Google Scholar]
- Santoro, M.; Askne, J.; Dammert, P.B.G. Tree height influence on ERS interferometric phase in boreal forest. IEEE Trans. Geosci. Remote Sens 2005, 43, 207–217. [Google Scholar]
- Drezet, P.M.L.; Quegan, S. Environmental effects on the interferometric repeat-pass coherence of forests. IEEE Trans. Geosci. Remote Sens 2006, 44, 825–837. [Google Scholar]
- Santoro, M.; Shvidenko, A.; McCallum, I.; Askne, J.; Schmullius, C. Properties of ERS-1/2 coherence in the Siberian boreal forest and implications for stem volume retrieval. Remote Sens. Environ 2007, 106, 154–172. [Google Scholar]
- Pinto, N.; Simard, M.; Dubayah, R. Using InSAR coherence to map stand age in a boreal forest. Remote Sens 2013, 5, 42–56. [Google Scholar]
- Lee, S.K.; Papathanassiou, K.P.; Moreira, A. Forest Height Estimation by Means of Pol-InSAR, Limitations Posed by Temporal Decorrelation. In ALOS Kyoto & Carbon Initiative Science Report- Phase 1; JAXA TKSC: Tsukuba, Japan; 13–16; January; 2009; Available online: http://www.eorc.jaxa.jp/ALOS/en/kyoto/phase_1/KC-Phase1-report_DLR_v2.pdf (accessed on 16 November 2012). [Google Scholar]
- Oliver, C.; Quegan, S. Data Models. In Understanding Synthetic Aperture Radar Images; Artech House: Norwood, MA, USA, 1998; Chapter 5; pp. 123–156. [Google Scholar]
- Kurvonen, L.; Hallikainen, M.T. Textural information of multitemporal ERS-1 and JERS-1 SAR images with applications to land and forest type classification in boreal zone. IEEE Trans. Geosci. Remote Sens 1999, 37, 680–689. [Google Scholar]
- Oliver, C.J. Rain forest classification based on SAR texture. IEEE Trans. Geosci. Remote Sens 2000, 38, 1095–1104. [Google Scholar]
- Wang, H.; Ouchi, K.; Watanabe, M.; Shimada, M.; Tadono, T.; Rosenqvist, A.; Romshoo, S.A.; Matsuoka, M.; Moriyama, T.; Uratsuka, S. In search of the statistical properties of high-resolution polarimetric SAR data for the measurements of forest biomass beyond the RCS saturation limits. IEEE Geosci. Remote Sens. Lett 2006, 3, 495–499. [Google Scholar]
- Wang, H.; Ouchi, K. Accuracy of the K-distribution regression model for forest biomass estimation by high-resolution polarimetric SAR: Comparison of model estimation and field data. IEEE Trans. Geosci. Remote Sens 2008, 46, 1058–1064. [Google Scholar]
- Wang, H.; Ouchi, K. A simple moment method of forest biomass estimation from non-Gaussian texture information by high-resolution polarimetric SAR. IEEE Geosci. Remote Sens. Lett 2010, 7, 811–815. [Google Scholar]
- Zianis, D.; Muukkonen, P.; Mäkipää, R.; Mencuccinii, M. Biomass and stem volume equations for tree species in Europe. Silva Fennica 2005, Monographs 4, 1–63. [Google Scholar]
- Jakeman, E.; Pusey, P.N. A model for non-Rayleigh sea echo. IEEE Trans. Antennas Propagat. 1976, AP-24, 806–814. [Google Scholar]
- Jakeman, E. On the statistics of K-distributed noise. I. Phys. A: Math. Gen 1980, 13, 31–48. [Google Scholar]
- Jakeman, E.; Tough, R.J.A. Generalized K-distribution: A statistical model for weak scattering. J. Opt. Soc. Am. A 1987, 4, 1764–1772. [Google Scholar]
- Kasischke, E.S.; Tanase, M.A.; Bourgeau-Chavez, L.L.; Borr, M. Soil moisture limitations on monitoring boreal forest regrowth using spaceborne L-band SAR data. Remote Sens. Environ 2011, 115, 227–232. [Google Scholar]
- Sun, G.; Ranson, K.J.; Kharuk, V.I. Radiometric slope correction for forest biomass estimation from SAR data in the western Sayani Mountains, Siberia. Remote Sens. Environ 2002, 79, 279–287. [Google Scholar]
- Soja, M.J.; Sandberg, G.; Ulander, L.M.H. Topographic Correction for Biomass Retrieval from P-band SAR Data in Boreal Forests. Proceedings of IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25– 30 July 2010; pp. 4776–4779.
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Physical Mechanisms and Empirical Models for Scattering and Emission. In Microwave Remote Sensing: Active and Passive; Addison-Wealey: Reading, MA, USA, 1982; Volume II, Chapter 11. [Google Scholar]
- Dobson, M.C.; Ulaby, F.T. Active microwave soil moisture research. IEEE Trans. Geosci. Remote Sens 1986, 24, 23–36. [Google Scholar]
- Fung, A.K.; Li, Z.; Chen, K.S. Backscattering from a randomly rough dielectric surface. IEEE Trans. Geosci. Remote Sens 1992, 30, 356–369. [Google Scholar]
- Born, M.; Wolf, E. Principles of Optics, 7th ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Rice, S.O. Reflection of electromagnetic waves from slightly rough surfaces. Commun. Pure Apply. Math 1951, 4, 351–378. [Google Scholar]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Introduction to Random Surface Scattering and Emission. In Microwave Remote Sensing: Active and Passive; Addison-Wealey: Reading, MA, USA, 1982; Volume II, Chapter 12; pp. 922–1033. [Google Scholar]
- Fung, A.K. Microwave Scattering and Emission Models and Their Applications; Artech House: Norwood, MA, USA, 1994. [Google Scholar]
- Wu, T.-D.; Chen, K.-S. A reappraisal of the validity of the IEM model for backscattering from rough surfaces. IEEE Trans. Geosci. Remote Sens 2004, 42, 743–753. [Google Scholar]
- Altese, E.; Bolognani, O.; Mancini, M.; Troch, P.A. Retrieving soil moisture over bare soil from ERS 1 synthetic aperture radar data: Sensitivity analysis based on a theoretical surface scattering model and field data. Water Resour. Res 1996, 32, 653–661. [Google Scholar]
- Hsieh, C.-Y.; Fung, A.K.; Nesti, G.; Sieber, A.J.; Coppo, P. A further study of the IEM surface scattering model. IEEE Trans. Geosci. Remote Sens 1997, 35, 901–909. [Google Scholar]
- Chen, K.S.; Tzong-Dar, W.; Mu-King, T.; Fung, A.K. Note on the multiple scattering in an IEM model. IEEE Trans. Geosci. Remote Sens 2000, 38, 249–256. [Google Scholar]
- Song, K.; Zhou, X.; Fan, Y. Empirically adopted IEM for retrieval of soil moisture from radar backscattering coefficients. IEEE Trans. Geosci. Remote Sens 2009, 47, 1662–1672. [Google Scholar]
- Fung, A.K.; Chen, K.S. Scattering and Emission Models for Users; Artech House: Norwood, MA, USA, 2010. [Google Scholar]
- Chen, K.S.; Yen, S.K.; Huang, W.P. A simple model for retrieving bare soil moisture from radarscattering coefficients. Remote Sens. Environ 1995, 54, 121–126. [Google Scholar]
- Mathieu, R.; Sbih, M.; Viau, A.; Anctil, F.; Parent, L.; Boisvert, J. Relationships between Radarsat SAR data and surface moisture content of agricultural organic soils. Int. J. Remote Sens 2003, 24, 5265–5281. [Google Scholar]
- Holah, N.; Baghdadi, N.; Zribi, M.; Bruand, A.; King, C. Potential of ASAR/ENVISAT for the characterization of soil surface parameters over bare agricultural fields. Remote Sens. Environ 2005, 96, 78–86. [Google Scholar]
- Oh, Y.; Sarabandi, K.; Ulaby, F.T. An empirical model and an inversion technique for radar scattering from bare soil surfaces. IEEE Trans. Geosci. Remote Sens 1992, 30, 370–381. [Google Scholar]
- Dubois, P.C.; van Zyl, J.J.; Engman, T. Measuring soil moisture with imaging radars. IEEE Trans. Geosci. Remote Sens 1995, 33, 915–926. [Google Scholar]
- Shi, J.; Wang, J.; Hsu, A.Y.; O’fNeill, P.E.; Engman, E.T. Estimation of bare surface soil moisture and surface roughness parameter using L-band SAR image data. IEEE Trans. Geosci. Remote Sens 1997, 35, 1254–1266. [Google Scholar]
- Oh, Y.; Sarabandi, K.; Ulaby, F.T. Semi-empirical model of the ensemble-averaged differential Mueller matrix for microwave backscattering from bare soil surfaces. IEEE Trans. Geosci. Remote Sens 2002, 40, 1348–1355. [Google Scholar]
- D’Urso, G.; Minacapilli, M. A semi-empirical approach for surface soil water content estimation from radar data without a-priori information on surface roughness. J. Hydrol 2006, 321, 297–310. [Google Scholar]
- Ulaby, F.T.; Batlivala, P.P. Optimum radar parameters for mapping soil moisture. IEEE Trans. Geosci. Electron 1976, 14, 81–93. [Google Scholar]
- Ulaby, F.T.; Batlivala, P.P.; Dobson, M.C. Microwave backscatter dependence on surface roughness, soil moisture, and soil texture: Part I—Bare soil. IEEE Trans. Geosci. Electron 1978, 16, 286–295. [Google Scholar]
- Jackson, T.J.; Chang, A.; Schmugge, T.J. Active microwave measurements for estimating soil moisture. Photogramm. Eng. Remote Sensing 1981, 47, 801–805. [Google Scholar]
- Wang, J.R.; Engmen, E.T.; Shiue, J.C.; Rusek, M.; Steinmeier, C. The SIR-B observations of microwave backscatter dependence on soil moisture, surface roughness, and vegetation covers. IEEE Trans. Geosci. Remote Sens 1986, 24, 510–516. [Google Scholar]
- Wang, J.R.; Hsu, A.; Shi, J.C.; O’Neill, P.E.; Engman, E.T. A comparison of soil moisture retrieval models using SIR-C measurements over the Little Washita River watershed. Remote Sens. Environ 1997, 59, 308–320. [Google Scholar]
- Oh, Y. Quantitative retrieval of soil moisture content and surface roughness from multipolarized radar observations of bare soil surfaces. IEEE Trans. Geosci. Remote Sens 2004, 42, 596–601. [Google Scholar]
- Baghdadi, N.; Holah, N.; Zribi, M. Soil Moisture estimation using multi-incident and multi-polarization ASAR data. Int. J. Remote Sens 2006, 27, 1907–1920. [Google Scholar]
- Baghdadi, N.; Zribi, M.; Loumagne, C.; Ansart, P.; Anguela, T.P. Analysis of TerraSAR-X data and their sensitivity to soil moisture parameters over bare agricultural fields. Remote Sens. Environ 2008, 112, 4370–4379. [Google Scholar]
- Rahman, M.M.; Moran, M.S.; Thoma, D.P.; Bryant, R.; Holifield Collins, C.D.; Jackson, T.; Orr, B.J.; Tischler, M. Mapping surface roughness and soil moisture using multi-angle radar imagery without ancillary data. Remote Sens. Environ 2008, 112, 391–402. [Google Scholar]
- Pathe, C.; Wagner, W.; Sabel, D.; Doubkova, M.; Basara, J.B. Using ENVISAT ASAR global mode data for surface soil moisture retrieval over Oklahoma, USA. IEEE Trans. Geosci. Remote Sens 2009, 47, 468–480. [Google Scholar]
- Baghdadi, N.; Aubert, M.; Zribi, M. Use of TerraSAR-X data to retrieve soil moisture over bare soil agricultural fields. IEEE Geosci. Remote Sens. Lett 2012, 9, 512–516. [Google Scholar]
- Nolan, M.; Fatland, D.R.; Hinzman, L. DInSAR measurement of soil moisture. IEEE Trans. Geosci. Remote Sens 2003, 41, 2802–2813. [Google Scholar]
- Hajnsek, I.; Jagdhuber, T.; Schon, H.; Papathanassiou, K.P. Potential of estimating soil moisture under vegetation cover by means of PolSAR. IEEE Trans. Geosci. Remote Sens 2009, 47, 442–454. [Google Scholar]
- Lakhankar, T.; Ghedira, H.; Temimi, M.; Azar, A.E.; Khanbilvardi, R. Effect of land cover heterogeneity on soil moisture retrieval using active microwave remote sensing data. Remote Sens 2009, 1, 80–91. [Google Scholar]
- Notarnicola, C.; Angiulli, M.; Posa, F. Use of radar and optical remotely sensed data for soil moisture retrieval over vegetated areas. IEEE Trans. Geosci. Remote Sens 2006, 44, 925–935. [Google Scholar]
- Jackson, T.J.; Moran, M.S.; O’Neill, P. Introduction to Soil Moisture Experiments 2004 (SMEX04) special issue. Remote Sens. Environ 2008, 112, 301–303. [Google Scholar]
- Mattia, F.; Floury, N.; Moriera, A. Foreword to the special issue on the retrieval of bio- and geophysical parameters from SAR data for land applications. IEEE Trans. Geosci. Remote Sens 2009, 47, 379–380. [Google Scholar]
- Baghdadi, N.; Cerdan, O.; Zribi, M.; Auzet, V.; Darboux, F.; Hajj, M.E.; Kheir, R.B. Operational performance of current synthetic aperture radar sensors in mapping soil moisture characteristics: Application to hydrology and erosion modeling. Hydrol. Process 2008, 22, 9–20. [Google Scholar]
- Brian, W.B.; Dwyer, E.; Whelan, P. Soil moisture retrieval from active spaceborne microwave observations: An evaluation of current techniques. Remote Sens 2009, 1, 210–242. [Google Scholar]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.J.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS mission: New tool for monitoring key elements of the global water cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar]
- Kerr, Y.H.; Waldteufel, P.; Richaume, P.; Wigneron, J.P.; Ferrazzoli, P.; Mahmoodi, A.; Bitar, A.A.; Cabot, F.; Gruhier, C.; et al. The SMOS soil moisture retrieval algorithm. IEEE Trans. Geosci. Remote Sens 2012, 50, 1384–1403. [Google Scholar]
- ESA Website, Available online: http://www.esa.int/esaLP/LPsmos.html (accessed on 6 December 2012).
- Le Toan, T.; Laur, H.; Mougin, E.; Lopes, A. Multitemporal and dualpolarization observations of agriculture vegetation covers by X-band SAR images. IEEE Trans. Geosci. Remote Sens 1989, 27, 709–717. [Google Scholar]
- Kurosu, T.; Fujita, M.; Chiba, K. Monitoring of rice crop growth from space using ERS-1 C-band SAR. IEEE Trans. Geosci. Remote Sens 1995, 33, 1092–1096. [Google Scholar]
- Durden, S.L; Morrisey, L.A.; Livingston, G.P. Microwave backscatter and attenuation dependence on leaf area index for flooded rice fields. IEEE Trans. Geosci. Remote Sens 1995, 33, 807–810. [Google Scholar]
- Le Toan, T.; Ribbes, F.; Wang, L.-F.; Floury, N.; Ding, K.-H.; Kong, J.A.; Fujita, M.; Kurosu, T. Rice crop mapping and monitoring using ERS-1 data based on experiment and modeling results. IEEE Trans. Geosci. Remote Sens 1997, 35, 41–56. [Google Scholar]
- Brisco, B.; Brown, R.J. Agricultural Applications with Radar. In Principles and Applications in Imaging Radar; Henderson, F.H., Lewis, A.J., Eds.; Wiley: New York, NY, USA, 1998; pp. 381–406. [Google Scholar]
- Frei, U.; Sporri, S.; Stebler, O.; Holecz, F. Rice field mapping in Sri Lanka using ERS SAR data. Earth Obs. Quart. 1999, 63, 30–35. [Google Scholar]
- Ribbes, F.; Le Toan, T. Rice field mapping and monitoring with Radarsat data. Int. J. Remote Sens 1999, 20, 745–765. [Google Scholar]
- Rosenqvist, A. Temporal and spatial characteristics of irrigated rice in JERS-1 L-band SAR data. Int. J. Remote Sens 1999, 20, 1567–1587. [Google Scholar]
- Shao, Y.; Fan, X.; Liu, H.; Xiao, J.; Ross, S.; Brisco, B.; Brown, R.; Staples, G. Rice monitoring and production estimation using multi-temporal RADARSAT. Remote Sens. Environ 2001, 76, 310–325. [Google Scholar]
- Inoue, Y.; Kurosu, T.; Maeno, H.; Uratsuka, S.; Kozu, T.; Dabrowska-Zielinska, K.; Qi, J. Season-long daily measurements of multifrequency (Ka, Ku, X, C and L) and full-polarization backscatter signatures over paddy rice field and their relationship with biological variables. Remote Sens. Environ 2002, 81, 194–204. [Google Scholar]
- Davidson, G.; Ouchi, K. Segmentation of SAR images using multitemporal information. IEE Proc. Radar Son. Navig 2003, 150, 367–374. [Google Scholar]
- Ishitsuka, N.; Saito, G.; Ouchi, K.; Uratsuka, S. Observation of Japanese rice paddy fields using multi wavelength and full polarimetric SAR. Adv. Astronaut. Sci 2004, 117, 565–575. [Google Scholar]
- Choudhury, I.; Chakraborty, M. SAR signature investigation of rice crop using Radarsat data. Int. J. Remote Sens 2006, 27, 519–534. [Google Scholar]
- Ouchi, K.; Wang, H.; Ishitsuka, N.; Saito, G.; Mohri, K. On the Bragg scattering observed in L-band synthetic aperture radar images of flooded rice fields. IEICE Trans. Commun. 2006, E89-B, 2218–2225. [Google Scholar]
- Bouvet, A.; Le Toan, A.; Lam-Dao, N. Monitoring of the rice cropping system in the Mekong Delta using ENVISAT/ASAR dual polarization data. IEEE Trans. Geosci. Remote Sens 2009, 47, 517–526. [Google Scholar]
- Lam-Dao, N.; Apan, A.; Le-Toan, T.; Young, F.; Le-Van, T.; Bouvet, A. Towards an Operational System for Rice Crop Inventory in the Mekong River Delta, Vietnam Using ENVISAT-ASAR data. Proceedings of the 7th FIG Regional Conference, Spatial Data Serving People: Land Governance and the Environment- Building the Capacity, Hanoi, Vietnam, 19–22 October 2009.
- Wang, C.; Wu, J.; Zhang, Y.; Pan, G.; Qi, J.; Salas, W.A. Characterizing L-band scattering of paddy rice in southeast China with radiative transfer model and multitemporal ALOS/PALSAR imagery. IEEE Trans. Geosci. Remote Sens 2009, 47, 988–998. [Google Scholar]
- Ling, F.; Li, Z.; Chen, E.; Tian, X.; Bai, L.; Wang, F. Rice Areas Mapping Using ALOS PALSAR FBD Data Considering The Bragg Scattering in L-band SAR Images of Rice Fields. Proceedings of IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25– 30 July 2010; pp. 1461–1464.
- Bouvet, A.; Le Toan, T. Use of ENVISAT/ASAR wide-swath data for timely rice fields mapping in the Mekong River Delta. Remote Sens. Environ 2011, 114, 1090–1101. [Google Scholar]
- Lopez-Samchez, J.M.; Ballester-Berman, J.D.; Hajnsek, I. First results of rice monitoring practice in Spain by means of time series of TerraSAR-X dual-pol images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens 2011, 4, 412–422. [Google Scholar]
- Wu, F.; Wang, C.; Zhang, H.; Zhang, B.; Tang, X. Rice crop monitoring in South China with RADARSAT-2 quad-polarization SAR data. IEEE Geosci. Remote Sens. Lett 2011, 8, 106–200. [Google Scholar]
- Yang, S.; Zhao, X.; Li, B.; Hua, G. Interpreting RADARSAT-2 quad-polarization SAR signatures from rice paddy based on experiments. IEEE Geosci. Remote Sens. Lett 2012, 9, 65–69. [Google Scholar]
- Schanda, E. A radargrammetry experiment in a mountain region. Int. J. Remote Sens 1985, 6, 1113–1124. [Google Scholar]
- Paillou, P.; Gelautz, M. Relief reconstruction from SAR stereo pairs: The “Optimal Gradient” matching method. IEEE Trans. Geosci. Remote Sens 1999, 37, 2099–2107. [Google Scholar]
- Li, Z.; Zhu, Q.; Gold, C. Digital Terrain Modeling: Principles and Methodology; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Meric, S.; Fayard, F.; Pottier, E. Radargrammetric SAR Image Processing. In Geoscience and Remote Sensing; Ho, P.-G.P., Ed.; InTech: Rijeka, Croatia, 2009; pp. 421–454. [Google Scholar]
- Johnson, W.T.K. Magellan imaging radar mission to Venus. Proc. IEEE 1991, 79, 777–790. [Google Scholar]
- Leberl, F.W.; Maurice, K.E.; Thomas, J.K.; Leff, C.E.; Wall, S.D. Images and topographic relief at the North Pole of Venus. J. Geophys. Res. Planet 1992, 97, 13667–13674. [Google Scholar]
- Leberl, F.W.; Thomas, J.K.; Maurice, K.E. Initial results from the Magellan stereo experiment. J. Geophys. Res. Planet 1992, 97, 13675–13689. [Google Scholar]
- Toutin, T. Evaluation of radargrammetric DEM from RADARSAT images in high relief areas. IEEE Trans. Geosci Remote Sens 2000, 38, 782–789. [Google Scholar]
- Raggam, H.; Gutjahr, K.; Perko, R.; Schardt, M. Assessment of the stereo-radargrammetric mapping potential of TerraSAR-X multibeam spotlight data. IEEE Trans. Geosci. Remote Sens 2010, 48, 971–977. [Google Scholar]
- Capaldo, P.; Crespi, M.; Fratarcangeli, F.; Nascetti, A.; Pieralice, F. High-resolution SAR radargrammetry: A first application with COSMO-SkyMed SpotLight imagery. IEEE Geosci. Remote Sens. Lett 2011, 8, 1100–1104. [Google Scholar]
- Perko, R.; Raggam, H.; Deutscher, J.; Gutijahr, K.; Schardt, M. Forest assessment using high resolution SAR data in X-band. Remote Sens 2011, 3, 792–815. [Google Scholar]
- Wildey, R.L. Topography from single radar images. Science 1984, 224, 153–156. [Google Scholar]
- Wildey, R.L. Radarclinometry. Earth Moon Planets 1986, 36, 217–247. [Google Scholar]
- Frankot, R.T.; Chellappa, R. Estimation of surface topography from SAR imagery using shape from shading techniques. Artif. Intel 1990, 43, 271–310. [Google Scholar]
- Guindon, B. Development of a shape-from-shading technique for the extraction of topographic models from individual spaceborne SAR images. IEEE Trans. Geosci. Remote Sens 1990, 28, 654–661. [Google Scholar]
- Wildey, R.L. Radarclinometry of the earth and venus from space-shuttle and venera-15 imagery. Earth Moon Planets 1990, 48, 197–231. [Google Scholar]
- Bors, A.G.; Hancok, E.R.; Wilson, R.C. Terrain analysis using radar shape-from-shading. IEEE Trans. Pattern Anal 2003, 25, 974–992. [Google Scholar]
- Maître, H. Radioclinometry. In Processing of Synthetic Aperture Radar Images; Maître, H., Ed.; Wiley-ISTE: London, UK, 2010; Chapter 11; pp. 261–278. [Google Scholar]
- Ikeuchi, K.; Horn, B.K.P. Numerical shape from shading and occluding boundaries. Artif. Intell 1981, 17, 141–184. [Google Scholar]
- Horn, B.K.P.; Brooks, M.J. The variational approach to shape from shading. Comput. Vision Graph. Image Process 1986, 33, 174–208. [Google Scholar]
- Ronca, L.B.; Basilevski, A.T. Maxwell Montes and Thessera Fortuna: A study of Venera 15 and 16 radar images. Earth Moon Planet. 1986, 36, 23–39. [Google Scholar]
- Bayer, T.; Winter, R.; Schreier, G. Terrain influences in SAR backscatter and attempts to their correction. IEEE Trans. Geosci. Remote Sens 1991, 29, 451–462. [Google Scholar]
- Zito, R.N. The shape of SAR histogram. Comput. Vision Graph. Image Process 1988, 43, 281–293. [Google Scholar]
- Oliver, C.J.; Blacknell, D.; White, R.G. Optimum edge detection in SAR. IEE Proc. Radar Son. Navig 1996, 143, 31–40. [Google Scholar]
- Caves, R.; Quegan, S.; White, R.G. Quantitative comparison of the performance of SAR segmentation algorithms. IEEE Trans. Image Process 1998, 7, 1534–1546. [Google Scholar]
- EUSAR 2010, Available online: http://www.vde-verlag.de/books/453272/eusar-2010.html (accessed on 15 November 2012).
- 2011 3rd International Asia-Pacific Conference on Synthetic Aperture Radar (APSAR 2011), Available online: http://www.proceedings.com/13505.html (accessed on 15 November 2012).
- Kunkee, D.; Gamba, P.; Smits, P.; St. Germain, K. Foreword to the special issue on the 2010 international geoscience and remote sensing symposium. IEEE Trans. Geosci. Remote Sens 2011, 49, 4683–4685. [Google Scholar]
- EUSAR 2012, Available online: http://www.vde-verlag.de/books/453404/eusar-2012.html (accessed on 15 November 2012).
- Hasselmann, K.; Raney, R.K.; Plant, W,J.; Alpers, W.; Shuchman, R.A.; Lyzenga, D.R.; Rufenach, C.L.; Tucker, M.J. Theory of synthetic aperture radar radar ocean imaging: A MAESEN view. J. Geophys. Res 1985, 90, 4659–4686. [Google Scholar]
- Kerbaol, V.; Collard, F. SAR-derived coastal and marine applications: From research to operational products. IEEE J. Ocean. Eng 2005, 30, 472–486. [Google Scholar]
- The 1st International Workshop on Advances in SAR Oceanography from ENVISAT and ERS Missions, Available online: http://earth.esa.int/seasar06/ (accessed on 10 September 2012).
- The 2nd International Workshop on Advances in SAR Oceanography from ENVISAT and ERS Missions, Available online: http://earth.esa.int/workshops/seasar2008/ (accessed on 10 September 2012).
- The 3rd International Workshop on Advances in SAR Oceanography from ENVISAT, ERS and ESA Third Party Missions, Available online: http://earth.eo.esa.int/workshops/seasar2010/ (accessed on 10 September 2012).
- The 4th International Workshop on Advances in SAR Oceanography, Available online: https://earth.esa.int/web/guest/seasar-2012 (accessed on 10 September 2012).
- Valenzuela, G.R. Theories for the interaction of electromagnetic and ocean waves—A review. Boundary-Layer Meteorol 1978, 13, 61–85. [Google Scholar]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave Remote Sensing: Active and Passive; Addison-Wesley: Reading, MA, USA, 1982; Volume II. [Google Scholar]
- Bragg, W.L. Structure of some crystals as indicated by their diffraction of X-rays. Proc. R. Soc. A (Lond.) 1913, 89, 248–277. [Google Scholar]
- Bragg, W.H.; Bragg, W.L. The structure of the diamond. Proc. R. Soc. A (Lond.) 1923, 89, 277–292. [Google Scholar]
- Crombie, D.D. Doppler spectrum of sea echo at 13.56 Mc/s. Nature 1955, 175, 681–682. [Google Scholar]
- Jordan, R.E.; Payne, J.R. Fate and Weathering of Petroleum Spills in the Marine Environment: A Literature Review and Synopsis; Ann Arbor Science Pub.: Ann Arbor, MI, USA, 1980. [Google Scholar]
- Lu, J.; Kwoh, L.K.; Lim, H.; Liew, S. C.; Bao, M. Mapping oil pollusion from space. Backscatter 2000, 11, 23–26. [Google Scholar]
- Wahl, T; Skøelv, A.; Pedersen, J.P.; Seljelv, L.-G.; Andersen, J.H.; Follum, O.A.; Anderssen, T.; Strøm, G.D.; Bern, T.-I.; Espedal, H.H.; et al. Radar satellites: A new tool for pollusion monitoring in coastal waters. Coast. Manage 2008, 24, 61–71. [Google Scholar]
- Migliaccio, M. Sea Oil Field Satellite Monitoring: An Operational View; 2011 STAR Seminars. NOAA: Camp Springs, MD, USA, 2011. Available online: http://www.star.nesdis.noaa.gov/star/documents/seminardocs/2011/Migliaccio20110721.pdf (accessed on 5 August 2012).
- Kim, D.-J.; Kang, J.; Yoon, B.; Kim, Y.; Kim, Y. Observation of Crude Oil Spill off the West Coast of Korea Using TerraSAR-X, ENVISAT ASAR and ALOS PALSAR. Proceedings of IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Boston, MA, USA, 7– 10 July 2008; III, pp. 1398–1401.
- Migliaccio, M.; Gambardella, A.; Nunziata, F.; Shimada, M.; Isoguchi, O. The PALSAR polarimetric mode for sea oil slick observation. IEEE Trans. Geosci. Remote Sens 2009, 47, 4032–4041. [Google Scholar]
- Ranmsey, E., III; Rangoonwala, A.; Suzuoki, Y.; Jones, C.E. Oil detection in a coastal marsh with polarimetric synthetic aperture radar (SAR). Remote Sens 2011, 3, 2630–2662. [Google Scholar]
- Gade, M.; Ufermann, S. Using ERS-2 SAR Images for Routine Observation of Marine Pollution in European Coastal Waters. Proceedings of IEEE International Geoscience and Remote Sensing Symposium (IGARSS), 6– 10 July 1998; Seattle, WA, USA; II, pp. 757–759.
- Ivanov, A. Oil pollution of the sea on Kosmos-1870 and Almaz-1 radar imagery. Earth Obs. Remote Sens 2000, 15, 949–966. [Google Scholar]
- Huehnerfuss, H.W.; Alpers, W.; Garret, W.D.; Lange, P.A.; Stolte, S. Attenuation of capillary and gravity waves at sea by monomolecular organic surface films. J. Geopyhs. Res 1983, 88, 9809–9816. [Google Scholar]
- Gade, M.; Alpers, W.; Huhnerfuss, H.; Masuko, H.; Kobayashi, T. Imaging of biogenic andanthropogenic ocean surface films by the multifrequency/multipolarization SIR-C/X-SAR. J. Geophys. Res 1998, 103, 18851–18866. [Google Scholar]
- Orchadlick, A.R.; Cho, P.; Evans-Morgis, J. Synthetic aperture radar observations of current colocated with slicks. J. Geophys. Res 1992, 97, 5325–5333. [Google Scholar]
- Espedal, H.A.; Wahl, T. Satellite SAR oil spill detection using wind history information. Int. J. Remote Sens 1999, 20, 49–65. [Google Scholar]
- Frate, F.D.; Petrocchi, A.; Lichtenegger, J.; Calabresi, G. Neural networks for oil spill detection using ERS-SAR data. IEEE Trans. Geosci. Remote Sens 2000, 38, 2282–2287. [Google Scholar]
- Karathanassi, V.; Topouzelis, K.; Pavlakis, P.; Rokos, D. An object-oriented methodology to detect oil spills. Int. J. Remote Sens 2006, 27, 5235–5251. [Google Scholar]
- Mercier, G.; Girard-Ardhuin, F. Partially supervised oil-slick detection by SAR imagery using kernel expansion. IEEE Trans. Geosci. Remote Sens 2006, 44, 2839–2846. [Google Scholar]
- Derrode, S.; Mercier, G. Unsupervised multiscale oil slick segmentation from SAR images. Pattern Recog 2007, 40, 1135–1147. [Google Scholar]
- Solberg, A.H.S.; Brekke, C.; Husøy, P.O. Oil spill detection in Radarsat and ENVISAT SAR images. IEEE Trans. Geosci. Rem. Sens 2007, 45, 746–755. [Google Scholar]
- Solberg, A.H.S.; Brekke, C. Oil Spill Detection in Northern European Waters: Approaches and Algorithms. In Remote Sensing of the European Seas; Barale, V., Gade, M., Eds.; Springer: Dordrecht, The Netherlands; pp. 359–370.
- Topouzelis, K.N.; Stathakis, D.; Karathanassi, V. Investigation of genetic algorithms contribution to feature selection for oil spill detection. Int. J. Remote Sens. 2009, 30, 611–625. [Google Scholar]
- Fana, K.; Zhanga, Y.; Lina, H. Satellite SAR analysis and interpretation of oil spill in the offshore water of Hong Kong. Ann. GIS 2011, 16, 269–275. [Google Scholar]
- Gambardella, A.; Giacinto, G.; Migliaccio, M.; Andrea Montali, A. One-class classification for oil spill detection. Pattern Anal. Appl 2010, 13, 349–366. [Google Scholar]
- Velotto, D.; Migliaccio, M.; Nunziata, F.; Lehner, S. Dual-polarized TerraSAR-X data for oil-spill observation. IEEE Trans. Geosci. Remote Sens 2011, 49, 4751–4762. [Google Scholar]
- Zhang, B.; Perrie, W.; Li, X.; Pichel, W.G. Mapping sea surface oil slicks using RADARSAT-2 quad-polarization SAR image. Geophys. Res. Lett. 2011. [Google Scholar] [CrossRef]
- Migliaccio, M.; Nunziata, F.; Brown, C.E.; Holt, B.; Li, X.; Pichel, W.G.; Shimada, M. Polarimetric synthetic aperture radar utilized to track oil spills. EOS Trans. AGU 2012, 93, 161–162. [Google Scholar]
- Topouzelis, K.N. Oil spill detection by SAR images: Dark formation detection, feature extraction and classification algorithms. Sensors 2008, 8, 6642–6656. [Google Scholar]
- Leifer, I.; Lehrb, W.J.; Simecek-Beatty, D.; Bradley, E.; Clark, R.; Dennison, P.; Hu, Y.; Matheson, S.; Jones, C.E.; Holt, B.; et al. State of the art satellite and airborne marine oil spill remote sensing: Application to the BP Deepwater Horizon oil spill. Remote Sens. Environ 2012, 124, 185–209. [Google Scholar]
- GNOME (General NOAA Operational Modeling Environment), Available online: http://response.restoration.noaa.gov/oil-and-chemical-spills/oil-spills/response-tools/gnome.html (accessed on 6 August 2012).
- Integrated Satellite Tracking of Polluters (ISTOP), Available online: http://www5.asc-csa.gc.ca/eng/programs/grip/project.asp-Id=110719 (accessed on 5 August 2012).
- Keramitsoglou, L.; Asimakopoulos, D.N.; Cartalis, C.; Petrakis, M.; Argiriou, A.; Sifakis, N; Kassomenos, P; Theophilopoulos, N.; Ntziou, L.; Herrero, A.M. An operational system for monitoring oil spills in the Mediterranean Sea: The PROMED system. Mediterr. Marine Sci 2003, 4, 65–72. [Google Scholar]
- Grantham, W.L.; Bracalente, E.M.; Jones, W.L.; Johnson, J.W. The SeaSat—A satellite scatterometer. IEEE J. Ocean. Eng. 1977, OE-2, 200–206. [Google Scholar]
- Naderi, F.; Freilich, M.H.; Long, D.G. Spaceborne radar measurement of wind velocity over the ocean—An overview of the NSCAT scatterometer system. Proc. IEEE 1991, 79, 850–866. [Google Scholar]
- Tsai, W.-Y.; Graf, J.E.; Winn, C.; Huddleston, J.N.; Dunbar, S.; Freilich, M.H.; Wentz, F.J.; Long, D.G.; Jones, W.L. Postlaunch sensor verification and calibration of the NASA scatterometer. IEEE Trans. Geosci. Remote Sens 1999, 37, 1517–1542. [Google Scholar]
- Figa-Saldan̈a, J.; Wilson, J.J.W.; Attema, E.; Gelsthorpe, R.; Drinkwater, M.R.; Stoffelen, A. The advanced scatterometer (ASCAT) on the meteorological operational (MetOp) platform: A follow on for European wind scatterometers. Can. J. Remote Sens 2002, 28, 404–412. [Google Scholar]
- Yang, X.; Li, X.; Pichel, W.G.; Li, Z. Comparison of ocean surface winds from ENVISAT ASAR, MetOp ASCAT scatterometer, buoy measurements, and NOGAPS model. IEEE Trans. Gosci. Remote Sens 2011, 49, 4743–4750. [Google Scholar]
- Kerbaol, V.; Chapron, B.; Vachon, P.W. Analysis of ERS-1/2 synthetic aperture radar wave mode imagettes. J. Geophys. Res 1998, 103, 7833–7846. [Google Scholar]
- Korsbakken, E.; Johannessen, J.A.; Johannessen, O.M. Coastal wind field retrievals from ERS synthetic aperture radar image. J. Geophys. Res 1998, 103, 7857–7874. [Google Scholar]
- Montuori, A.; de Ruggiero, P.; Migliaccio, M.; Pierini, S.; Spezie, G. X-band COSMO-SkyMed wind field retrieval, with application to coastal circulation modeling. Ocean Sci. Discuss 2012, 9, 3251–3279. [Google Scholar]
- Vachon, P.W.; Krogstad, H.E.; Paterson, J.S. Airborne and spaceborne synthetic aperture radar observations of ocean waves. Atmos. Ocean 1994, 32, 83–112. [Google Scholar]
- Johnson, H.; Engen, G. Ocean Winds from SLC SAR Data-Processing System Description and Intial Validation Results; Norut IT Report: IT550/2-00, Version 1.0; NORUT: Tromso, Norway, 2000. [Google Scholar]
- Vachon, P.W.; Dobson, F.W. Validation of wind vector retrieval from ERS-1 SAR images over the ocean. Global Atmos. Ocean Syst 1996, 5, 177–187. [Google Scholar]
- Horstmann, J.; Koch, W.; Lehner, S.; Tonboe, R. Computation of wind vectors over the ocean using spaceborne synthetic aperture radar. Johns Hopkins APL Tech. Dig 2000, 21, 100–107. [Google Scholar]
- Koch, W.; Feser, F. Relatioship between SAR-derived wind vectors and wind at 10-m height represented by a mesoscale model. Mon. Weather Rev 2006, 134, 1505–1517. [Google Scholar]
- Zhang, B.; Perrie, W.; Vachon, P.W.; Li, X.; Pichel, W.G.; Guo, J.; He, Y. Ocean vector winds retrieval from C-band fully polarimetric SAR measurements. IEEE Trans. Geosci. Remote Sens 2012, 50, 4252–4261. [Google Scholar]
- Zhang, B.; Perrie, W. Cross-polarized synthetic aperture radar: A new potential technique for hurricanes. Bull. Amer. Meteorol. Soc 2012, 93, 531–541. [Google Scholar]
- Horstmann, J.; Koch, W.; Lehner, S.; Tonboe, R. Wind retrieval over the ocean uasing synthetic aperture radar with C-band HH polarization. IEEE Trans. Geosci. Remote Sens 2000, 38, 2122–2131. [Google Scholar]
- Monaldo, F.M.; Thompson, D.R.; Beal, R.C.; Pichel, W.G.; Clemente-Colón, P. Comparison of SAR-derived wind speed with model predictions and ocean buoy measurements. IEEE Trans. Geosci. Remote Sens 2001, 39, 2587–2600. [Google Scholar]
- Horstmann, J.; Schiller, H.; Schulz-Stellenfleth, J.; Lehner, S. Global wind speed retrieval from SAR. IEEE Trans. Geosci. Remote Sens 2003, 41, 2277–2286. [Google Scholar]
- Monaldo, F.M.; Thompson, D.R.; Pichel, W.G.; Clemente-Colón, P. A systematic comparison of QuikSCAT and SAR ocean surface wind speeds. IEEE Trans. Geosci. Remote Sens 2004, 42, 283–291. [Google Scholar]
- Vachon, P.; Wolfe, J. C-band cross-polarization wind speed retrieval. IEEE Geosci. Remote Sens. Lett 2011, 8, 456–459. [Google Scholar]
- Lehner, S.; Horstmann, J.; Koch, W.; Rosenthal, W. Mesoscale wind measurements using recalibrated ERS SAR images. J. Geophys. Res 1998, 103, 7847–7856. [Google Scholar]
- Reppucci, A.; Lehner, S.; Schulz-Stellenfleth, J. Tropical Cyclone Parameters Derived from Synthetic Aperture Radar (SAR) Images. Proceedings of IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Denver, CO, USA, 31 July– 4 August 2006; pp. 2220–2223.
- Shen, H.; Perrie, W.; He, Y. A new hurricane wind retrieval algorithm for SAR images. Geophys. Res. Lett. 2006. [Google Scholar] [CrossRef]
- Johannessen, O.M.; Bjorgo, E. Wind energy mapping of coastal zones by synthetic aperture radar (SAR) for siting potential windmill locations. Int. J. Remote Sens 2000, 21, 1781–1786. [Google Scholar]
- Badger, M.; Badger, J.; Nielsen, M.; Hasager, C.B.; Peña, A. Wind class sampling of satellite SAR imagery for offshore wind resource mapping. J. Appl. Meteorol. Climatol 2010, 49, 2474–2491. [Google Scholar]
- Hasager, C.B.; Badger, M.; Peña, A.; Larsén, X.G.; Bingöl, F. SAR-based wind resource statistics in the Baltic Sea. Remote Sens 2011, 3, 117–144. [Google Scholar]
- Alpers, W.R.; Rufenach, C.L. The effect of orbital motions on synthetic aperture radar imagery of ocean waves. IEEE Trans. Antennas Propagat. 1979, AP-27, 685–690. [Google Scholar]
- Swift, C.T.; Wilson, L.R. Syntheic aperture radar imaging of ocean waves. IEEE Trans. Antennas Propag 1979, 27, 725–729. [Google Scholar]
- Alpers, W.; Ross, D.B.; Rufenach, C.L. On the detectability of ocean surface waves by real and synthetic aperture radar. J. Geophys. Res 1981, 86, 6481–6498. [Google Scholar]
- Beal, R.C.; DeLeonibus, P.S.; Katz, I. Spaceborne Synthetic Aperture Radar for Oceanography; Johns Hopkins University Press: Baltimore, MD, USA, 1981. [Google Scholar]
- Alpers, W. Monte Carlo simulations for studying the relationship between ocean wave spectra and synthetic aperture radar image spectra. J. Geophys. Res 1983, 88, 1745–1759. [Google Scholar]
- Beal, R.C.; Tilley, D.G.; Monaldo, F.M. Large- and small-scale spatial evolution of digitally processed ocean wave spectra from Seasat synthetic aperture radar. J. Geophys. Res 1983, 88, 1761–1778. [Google Scholar]
- Gower, J.F.R. ‘Layover’ in satellite radar imagery of ocean waves. J. Geophys. Res 1983, 88, 7719–7720. [Google Scholar]
- Ouchi, K. Two-dimensional imaging mechanisms of ocean waves by synthetic aperture radars. J. Phys. D: Appl. Phys 1994, 17, 25–42. [Google Scholar]
- Lyzenga, D.R.; Shuchman, R.A.; Lyden, J.D. SAR imaging of waves in water and ice: Evidence for velocity bunching. J. Geophys. Res 1985, 90, 1031–1036. [Google Scholar]
- Ouchi, K. Multilook images of ocean waves by synthetic aperture radars. IEEE Trans. Antennas Propagat. 1987, AP-35, 313–317. [Google Scholar]
- Ouchi, K. Synthetic aperture radar imagery of range traveling waves. IEEE Trans. Geosci. Remote Sens. 1988, GE-26, 30–37. [Google Scholar]
- Hasselmann, K.; Hasselmann, S. On the nonlinear mapping of an ocean wave spectrum into a synthetic aperture radar image spectrum and its inversion. J. Geophys. Res 1991, 96, 10713–10729. [Google Scholar]
- Krogstad, H.E.; Samset, O.; Vachon, P.W. Generalizations of the nonlinear ocean-SAR transformation and simplified SAR inversion algorithm. Atmos. Ocean 1994, 32, 61–82. [Google Scholar]
- Ouchi, K.; Burridge, D.A. Resolution of a controversy surrounding the focusing mechanisms of synthetic aperture radar images of ocean waves. IEEE Trans. Geosci. Remote Sens 1994, 32, 1004–1016. [Google Scholar]
- Engen, G.; Johnson, H. SAR-ocean wave inversion using image cross spectra. IEEE Trans. Geosci. Remote Sens 1995, 33, 1047–1056. [Google Scholar]
- Hasselmann, S.; Brüning, C.; Hasselmann, K.; Heimbach, P. An improved algorithm for the retrieval of oceanwave spectra from synthetic aperture radar image spectra. J. Geophys. Res 1996, 101, 16615–16629. [Google Scholar]
- Heimbach, P.; Hasselmann, S.; Hasselmann, K. Statistical analysis and intercomparison of WAM model data with global ERS-1 SAR wave mode spectral retrieval over 3 years. J. Geophys. Res 1998, 103, 7931–7977. [Google Scholar]
- Ouchi, K.; Maedoi, S.; Mitsuyasu, H. Determination of ocean wave propagation direction by split-look processing using JERS-1 SAR data. IEEE Trans. Geosci. Remote Sens. 1999, GE-37, 849–855. [Google Scholar]
- Ouchi, K. A theory on the distribution function of backscatter radar cross section from ocean waves of individual wavelength. IEEE Trans. Geosci. Remote Sens 2000, 38, 811–822. [Google Scholar]
- Mastenbroek, C.; de Valk, C.F. A semi-parametric algorithm to retrieve ocean wave spectra from synthetic aperture radar. J. Geophys. Res 2000, 105, 3497–3516. [Google Scholar]
- Dowd, M.; Vachon, P.W. Ocean wave extraction from Radarsat synthetic aperture inter-look image cross-spectra. IEEE Trans. Geosci. Remote Sens 2001, 39, 21–37. [Google Scholar]
- Violante-Carvalho, N.; Robinson, I.S. Comparison of the two-dimensional wave spectra retrieved from spaceborne synthetic aperture radar images using MPI scheme against directional buoy measurements. Sci. Mar 2004, 68, 317–330. [Google Scholar]
- Collard, F.; Ardhuin, F.; Chapron, B. Extraction of coastal ocean wave fields from SAR images. IEEE J. Ocean. Eng 2005, 30, 526–533. [Google Scholar]
- Kanevsky, M. Radar Imaging of Ocean Waves; Elsevier: London, UK, 2008. [Google Scholar]
- Janssen, P.; Alpers, W. Why SAR Wave Mode Data of ERS and Envisat are Inadequate for Giving the Probability of Occurrence of Freak Waves, Available online: http://earth.esa.int/seasar06/proceedings/ (accessed on 14 September 2012).
- European Centre for Medium-Range Weather Forecasts (ECMWF), Available online: http://www.ecmwf.int/ (accessed on 14 September 2012).
- Tanaka, M. The Role of Modulational Instability in the Formation of Wave Groups. In Breaking Waves; Banner, M.L., Grimshaw, R.H.J., Eds.; Springer-Verlag: Berlin, Germany, 1992; pp. 237–242. [Google Scholar]
- Onorato, M.; Osborne, A.R.; Serio, M.; Bertone, S. Freak waves in random oceanic sea states. Phys. Rev. Lett 2001, 86, 5831–5834. [Google Scholar]
- Trulsen, K.; Dysthe, K. Freak waves: A Three-dimensional Wave Simulation. In Proceedings of the 21st Symposium on Naval Hydrodynamics; National Academy Press: Washington, DC, USA, 1997; pp. 550–558. [Google Scholar]
- Ship-sinking Monster Waves Revealed by ESA Satellites, Available online: http://www.esa.int/esaEO/SEMOKQL26WD_index_0.html (accessed on 14 September 2012).
- Niedermeier, A.; Nieto Borge, J.C.; Lehner, S.; Schulz-Stellenfleth, J. A wavelet-based algorithm to estimate ocean wave group parameters from radar images. IEEE Trans. Geosci. Remote Sens 2005, 43, 327–336. [Google Scholar]
- Munk, W.H. Internal waves in the Gulf of California. J. Mar. Res 1941, 4, 81–91. [Google Scholar]
- Ewing, G. Slick, surface films and internal waves. J. Mar. Res 1950, 9, 161–187. [Google Scholar]
- Lafond, E.C. Internal Waves. In The Sea; Hill, M.L., Ed.; Interscience: New York, NY, USA, 1962; Volume 1, pp. 731–751. [Google Scholar]
- Davis, R.E.; Acrivos, A. Solitary internal waves in deep water. J. Fluid Mech 1967, 29, 593–607. [Google Scholar]
- Garrett, C.; Munk, W. Internal waves in the ocean. Ann. Rev. Fluid Mech 1979, 11, 339–369. [Google Scholar]
- Okazaki, M. Internal tidal waves and internal long period waves in the Sanriku coastal seas, eastern coast of northern Japan. La mer 1990, 28, 5–29. [Google Scholar]
- Leichter, J.J.; Shellenbarger, G.; Genovese, S.J.; Wing, S.R. Breaking internal waves on a Florida (USA) coral reef: A plankton pump at work? Mar. Ecol. Prog. Ser 1998, 166, 83–97. [Google Scholar]
- Ekman, V.W. On Dead Water. The Norwegian North Polar Expedition 1893–1896 : Science Results; Nansen, F., Ed.; Longmans Green and Co.: London, UK, 1906; V, Chapter XV. pp. 1–152. Available online: http://archive.org/stream/norwegiannorthpo05nans?page/n81/mode/2up (accessed on 20 December 2012). [Google Scholar]
- Mercier, M.J.; Vasseur, R.; Dauxiois, T. Resurrecting dead-water phenomenon. Nonlin. Processes Geophys 2011, 18, 193–208. [Google Scholar]
- Jackson, C.R.; Apel, J.R. An Atlas of Internal Solitary-Like Waves and their Properties, 2nd ed.; Global Ocean Associates: Rockville, MD, USA, 2004; Available online: http://www.internalwaveatlas.com/Atlas2_index.html (accessed on 14 September 2012). [Google Scholar]
- Alpers, W. Theory of radar imaging of internal waves. Nature 1985, 314, 245–247. [Google Scholar]
- Stefanick, T. The nonacoustic detection of submarines. Sci. Am 1988, 258, 25–31. [Google Scholar]
- Ermakov, S.A.; de Silva, J.C.B.; Robinson, I.S. Role of surface films in ERS SAR signatures of internal waves on the shelf, 2. Internal tidal waves. J. Geophys. Res 1998, 103, 8032–8043. [Google Scholar]
- De Silva, J.C.B.; Ermakov, S.A.; Robinson, I.S.; Jeans, D.R. G,; Kijashko, S.V. Role of surface films in ERS SAR signatures of internal waves on the shelf, 1. Short-period internal waves. J. Geophys. Res 1998, 103, 8009–8031. [Google Scholar]
- De Silva, J.C.B.; Ermakov, S.A.; Robinson, I.S. Role of surface films in ERS SAR signatures of internal waves on the shelf, 3. Mode transitions. J. Geophys. Res 2000, 105, 24089–24104. [Google Scholar]
- Korteweg, D.J.; de Vries, G. On the change if form of long waves advancing in a rectangular canal, and on a type of long stationary waves. Phil. Mag 1895, 39, 422–443. [Google Scholar]
- Miles, J.W. The Korteweg-De Vries equation: A historical essay. J. Fluid Mech 1981, 106, 131–147. [Google Scholar]
- Gardner, C.S.; Greene, J.M.; Kruskal, M.D.; Miura, R.M. Method for folving the Korteweg-deVries equation. Phys. Rev. Lett 1967, 19, 1095–1097. [Google Scholar]
- Osborne, A.R.; Burch, T.L. Internal solitons in the Andaman Sea. Science 1980, 208, 451–460. [Google Scholar]
- Grimshaw, R. Slowly varying solitary waves. I. Korteweg-de Vries equation. Proc. R. Soc. London Ser. A 1979, 368, 359–375. [Google Scholar]
- Ko, K.; Kuehl, H.H. Modified Korteweg-de Vries solitary wave in a slowly varying medium. Phys. Fluid 1980, 23, 31–33. [Google Scholar]
- Helai, M.A.; Molines, J.M. Non-linear internal waves in shallow water. A theoretical and expetimental study. Tellus 1981, 5, 488–504. [Google Scholar]
- Liu, A.K.; Apel, J.R.; Holbrook, J.R. Nonlinear internal wave evolution in the Sulu Sea. J. Phys. Ocean 1985, 15, 1613–1624. [Google Scholar]
- Helfrich, K.R.; Melville, W.K. On long nonlinear internal waves over slope-shelf topography. J. Fluid Mech 1986, 167, 285–308. [Google Scholar]
- Liu, A.K. Analysis of nonlinear internal waves in the New York Bight. J. Geophys. Res 1988, 93, 12317–12329. [Google Scholar]
- Liu, A.K.; Chang, Y.S.; Hsu, M.-K.; Liang, N.K. Evolution of nonlinear internal waves in the East and South China Seas. J. Geophy. Res 1998, 103, 7995–8008. [Google Scholar]
- Dejak, S.I.; Sigal, I.M. Long-time dynamics of KdV solitary waves over a variable bottom. Commun. Pure Appl. Math 2006, 59, 869–905. [Google Scholar]
- Bocharov, A.A.; Khabakhpashev, G.A.; Tsvelodub, O.Y. Numerical simulation of plane and spatial nonlinear stationary waves in a two-layer fluid of arbitrary depth. Fluid Dyn 2008, 43, 118–124. [Google Scholar]
- Gargett, A.E.; Hughes, B.A. On the interaction of surface and internal waves. J. Fluid Mech 1972, 52, 179–191. [Google Scholar]
- Hughes, B.A. The effect of internal waves on surface wind waves 2. Theoretical analysis. J. Geophys. Res 1978, 83, 455–465. [Google Scholar]
- Thopmson, D.R.; Gasparovic, R.F. Intensity modulation in SAR images of internal waves. Nature 1986, 320, 345–348. [Google Scholar]
- Thompson, D.R.; Gotwols, B.L.; Sterner, R.E., II. A comparison of measured surface wave spectral modulations with predictions from a wave-current interaction model. J. Geopyhs. Res 1988, 93, 12339–12343. [Google Scholar]
- Holliday, D.; St-Cyr, G.; Woods, N.E. A radar ocean imaging model for small to moderate incidence angles. Int. J. Remote Sens 1986, 7, 1809–1834. [Google Scholar]
- Lyzenga, D.R.; Bennett, J.R. Full-spectrum modeling of synthetic aperture radar internal wave signatures. J. Geophys. Res 1988, 93, 12345–12353. [Google Scholar]
- Thompson, D.R. Calculation od radar backscatter modulations from internal waves. J. Geophys. Res 1988, 93, 12371–12380. [Google Scholar]
- Shand, J.A. Internal waves in the Georgia Strait. Eos. Trans. AGU 1953, 34, 849–856. [Google Scholar]
- Apel, J.R.; Byrne, H.M.; Proni, J.R.; Charnell, R.L. Observation of oceanic internal waves from the Earth Resources Technology Satellite. J. Geophys. Res 1975, 80, 865–881. [Google Scholar]
- Elachi, C.; Apel, J.R. Internal wave observations made with an airborne synthetic aperture imaging radar. Geophy. Res. Lett 1976, 3, 647–650. [Google Scholar]
- Alpers, W.; Salusti, E. Scylla and Charybdis observed from space. J. Geophys. Res 1983, 88, 1800–1808. [Google Scholar]
- Apel, J.R.; Gonzalez, F.I. Nonlinear features of internal waves off Baja California as observed from the SEASAT imaging radar. J. Geophy. Res. 1983, 88, 4459–4466. [Google Scholar]
- Fu, L.-L.; Holt, B. Internal waves in the Gulf of California: Observations from a space borne radar. J. Geophy. Res 1984, 89, 2053–2060. [Google Scholar]
- Gasparovic, R.F.; Apel, J.R.; Kasischke, E.S. An overview of the SAR internal wave signature experiment. J. Geophys. Res 1988, 93, 12304–12316. [Google Scholar]
- Kasischke, E.S.; Lyzenga, D.R.; Shuchman, R.A.; Wakerman, C.C. Contrast ratios of internal waves in synthetic aperture radar imagery: A comparison of SAR Internal Wave Signature Experiment observations with theory. J. Geophys. Res 1988, 93, 12355–12369. [Google Scholar]
- Shuchman, A.; Lyzenga, D.R.; Lake, B.M.; Hughes, B.A.; Gasparovic, R.F.; Kasischke, E.S. Comparison of Joint Cadana-U.S. Ocean Wave Investigation Project synthetic aperture radar data with internal wave observations and modeling results. J. Geophys. Res 1988, 93, 12283–12291. [Google Scholar]
- Holliday, D.; St-Cyr, G.; Woods, N.E. Comparson of a new ocean imaging model with SARSEX internal wave image data. Int. J. Remote Sens 1988, 9, 1423–1430. [Google Scholar]
- Hsu, M.-K.; Liu, A.K. Nonlinear internal waves in the South China Sea. Can. J. Remote Sens 2000, 26, 72–81. [Google Scholar]
- Susanto, R.D.; Mitnik, L.; Zheng, Q. Ocean internal waves observed in the Lombok Strait. Oceanography 2005, 18, 80–87. [Google Scholar]
- Klemas, V. Remote sensing of ocean internal waves: An overview. J. Coast. Res 2012, 28, 540–546. [Google Scholar]
- Giant Internal Waves Caught Breaking, Available online: http://dsc.discovery.com/news/2008/01/22/tidal-waves.html (accessed on 14 September 2012).
- Internal Waves in the Tsushima Strait, Available online: http://earthobservatory.nasa.gov/IOTD/view.php-id=7230 (accessed on 14 September 2012).
- Internal Waves in the Indian Ocean, Available online: http://earthobservatory.nasa.gov/IOTD/view.php-id=44567 (accessed on 14 September 2012).
- Gasparovic, R.F.; Thompson, D.R.; Apel, J.R. Synthetic aperture radar imaging of ship-generated internal waves. Johns Hopkins APL Tech. Dig 1989, 10, 326–331. [Google Scholar]
- Watson, G.; Chapman, R.D.; Apel, J.R. Measurements of the internal wave wake of a ship in a highly stratified sea loch. J. Geophys. Res 1992, 97, 9689–9703. [Google Scholar]
- Thompson, D.R.; Jensen, J.R. Synthetic aperture radar interferometry applied to ship-generated internal waves in the 1989 Loch Linnhe Experiment. J. Geophys. Res 1993, 98, 10259–10269. [Google Scholar]
- Ouchi, K. Modulation of waveheight spectrum and radar cross section by varying surface currents. IEEE Trans. Geosci. Remote Sens. 1994, GE-32, 995–1003. [Google Scholar]
- Ouchi, K.; Stapleton, N.R.; Barber, B.C. Multi-Frequency SAR images of ship-generated internal waves. Int. J. Remote Sens 1997, 18, 3709–3718. [Google Scholar]
- Valenzuela, G.R.; Chen, D.T.; Garrett, W.D.; Kaiser, J.A.C. Shallow water bottom topography from radar imagery. Nature 1983, 303, 687–689. [Google Scholar]
- Alpers, W.; Hennings, I. A theory of the imaging mechanism of underwater bottom topography. J. Geophys. Res 1984, 89, 1029–10546. [Google Scholar]
- Shuchman, R.; Lyzenga, D.; Meadows, G. Synthetic aperture radar imaging of ocean-bottom topography via tidal-current interactions: Theory and observations. Int. J. Remote Sens 1985, 6, 1179–1200. [Google Scholar]
- Romeiser, R.; Alpers, W. An improved composite surface model for the radar backscattering cross section of the ocean surface, 2. Model response to surface roughness variations and the radar imaging of underwater bottom topography. J. Geophys. Res 1997, 102, 25251–25267. [Google Scholar]
- Li, X.; Li, C.; Xu, Q.; Pichel, W.G. Sea surface manifestation of along-tidal-channel underwater ridges imaged by SAR. IEEE Trans. Geosci. Remote Sens 2009, 47, 2467–2477. [Google Scholar]
- Calkoen, C.; Hasselmans, G.; Wensink, G.; Vogelzang, J. The bathymetry assessment system: Efficient depth mapping in shallow sea using radar images. Int. J. Remote Sens 2001, 22, 2973–2998. [Google Scholar]
- Weissmann, D.E.; Thompson, T.W.; Legeckis, R. Modulation of sea surface radar cross section by surface stress: Wind speed and temperature effects across the Gulf Stream. J. Geophys. Res 1980, 85, 5032–5042. [Google Scholar]
- Jenkins, A.D.; Johannessen, O.M.; Lyzenga, D. Intercomparison of SAR Imaging Models for Upper Ocean Current Boudaries. Proceedings of IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Seattle, WA, USA, 6– 10 July 1998; 3, pp. 1656–1658.
- Dohan, C.; Maximenko, N. Monitoring ocean currents with satellite sensors. Oceanography 2010, 23, 94–103. [Google Scholar]
- Xie, T.; Perrie, W.; Chen, W. Gulf Stream thermal fronts detected by synthetic aperture radar. J. Geophys. Lett. 2010. [Google Scholar] [CrossRef]
- Jones, C.T.; Sikora, T.D.; Vachon, P.W.; Wolfe, J. Toward automated identification of sea surface temperature front signatures in Radarsat-2 images. Atmos. Ocean. Tech 2012, 29, 89–102. [Google Scholar]
- Kuang, H.; Perrie, W.; Xie, T.; Zhang, B.; Chen, W. Retrievals of sea surface temperature fronts from SAR imagery. Geophy. Res. Lett. 2012. [Google Scholar] [CrossRef]
- Munk, W.H.; Scully-Power, P.; Zachariasen, F. Ships from space. Proc. R. Soc. London. A 1987, 412, 231–254. [Google Scholar]
- Eldhuset, K. An automatic ship and ship wake detection system for spaceborne SAR images in coastal regions. IEEE Trans. Geosci. Remote Sens 1996, 34, 1010–1019. [Google Scholar]
- Vachon, P.W.; Thomas, S.J.; Cranton, J.; Edel, H.; Henschel, M.D. Validation of ship detection by the RADARSAT synthetic aperture radar and the ocean monitoring workstation. Can. J. Remote Sen 2000, 26, 200–212. [Google Scholar]
- Greidanus, H.; Clayton, P.; Indregard, M.; Staples, G.; Suzuki, N.; Vachon, P.; Wackerman, C.; Tennvassas, T.; Mallorqu’i, J.; Kourti, N.; et al. Benchmarking Operational SAR Ship Detection. Proceedings of IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Anchorage, AK, USA, 20– 24 September 2004; pp. 4215–4218.
- Ouchi, K.; Tamaki, S.; Yaguchi, H.; Iehara, M. Ship detection based on coherence images derived from cross-correlation of multilook SAR images. IEEE Trans. Geosci. Remote Sens. Lett 2004, 1, 184–187. [Google Scholar]
- Touzi, R.; Charbonneau, F.J.; Hwakins, R.K.; Vachon, P.W. Ship detection and characterization using polarimetric SAR. Can. J. Remote Sens 2004, 30, 552–559. [Google Scholar]
- DECLIMS consortium, Sate of the Art and User Needs; Greidanus, H., Jackson, A.M., Eds.; JRC: Ispra, Italy, 2005.
- Liu, C.; Vachon, P.W.; Geling, G.W. Improved ship detection with airborne plarimetric SAR data. Can. J. Remote Sens 2005, 31, 122–131. [Google Scholar]
- Greidanus, H.; Kourti, N. Findings of the DECLIMS Project-Detection and Classification of Marine Traffic from Space, Available online: http://earth.esa.int/workshops/seasar2006/ (accessed on 14 November 2012).
- Greidanus, H.; Kourti, N. Finding of the DECLIMS Project-Detection and Classification of Marine Traffic Control. Electronic Proceedings of the 1st International Workshop on Advances in SAR Oceanography from ENVISAT and ERS Missions, ESA-ESRIN, Frascati, Italy, 23–26 January 2006.
- Budillon, A.; Pascazio, V.; Schirinzi, G. Multichannel along-track interferometric SAR systems: Moving targets detection and velocity estimation. Int. J. Navigat. Obs. 2008. [Google Scholar] [CrossRef]
- Liao, M.; Wang, C.; Wang, Y.; Jiang, L. Using SAR images to detect ships from sea clutter. IEEE Geosci. Remote Sens. Lett 2008, 5, 194–198. [Google Scholar]
- Chen, J.; Chen, Y.; Yang, J. Ship detection using polarization cross-entropy. IEEE Geosci. Remote Sens. Lett 2009, 6, 723–727. [Google Scholar]
- Li, H.; He, Y.; Wang, W. Improving ship detection with polarimetric SAR based on convolution between co-polarization channels. Sensors 2009, 9, 1221–1236. [Google Scholar]
- Hwang, S.-I.; Ouchi, K. On a novel approach using MLCC and CFAR for the improvement of ship detection by synthetic aperture radar. IEEE Geosci. Remote Sens. Lett 2010, 7, 391–395. [Google Scholar]
- Marino, A.; Walker, N. Ship Detection with SAR Data Using a Notch Filter Based on Perturbation Analysis. Proceedings of IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25– 30 July 2010; pp. 3704–3707.
- Suchandt, A.; Runge, H.; Steinbrecher, U. Ship Detection and Measurement Using the TerraSAR-X Dual-receive Antenna Mode. Proceedings of IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25– 30 July 2010; pp. 2860–2863.
- Marino, A.; Walker, N. Ship Detection with Quad Polarimetric Terrasar-X Data: An Adaptive Notch Filter. Proceedings of IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Vancouver, BC, Canada, 24– 29 July 2011; pp. 245–248.
- Yin, J.; Yang, J.; Zhang, X. On the Ship Detection Performance with Compact Polarimetry. Proceedings of IEEE Radar Conference, Kansas City, MO, USA, 23– 27 May 2011; pp. 675–680.
- Chaturvedi, S.K.; Yang, C.-S.; Ouchi, K.; Shanmugam, P. Ship recognition by integration of SAR and AIS. J. Navigat 2012, 65, 323–337. [Google Scholar]
- Migliaccio, M.; Nunziata, F.; Montuori, A.; Paes, R.L. Single-look complex COSMO-SkyMed SAR data to observe metallic targets at sea. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens 2012, 5, 893–901. [Google Scholar]
- Nunziata, F.; Migliaccio, M.; Brown, C.E. Reflection symmetry for polarimetric observation of man-made metallic targets at sea. IEEE J. Ocean. Eng 2012, 37, 384–394. [Google Scholar]
- Fingas, M.F.; Brown, C.E. Review of ship detection from airborne platforms. Can. J. Remote Sens 2001, 27, 379–385. [Google Scholar]
- Arnesen, T.N.; Olsen, R.B. Literature Review on Vessel Detection; FFI/RAPPORT-2004/02619; Forsvarets Forskningsinstitutt (Norwegian Defence Research Establishment): Kjeller, Norway, 2004. [Google Scholar]
- Crisp, D.J. The State-of-the-Art in Ship Detection in Synthetic Aperture Radar Imagery, Available online: http://www.dsto.defence.gov.au/publications/2660/DSTO-RR-0272.pdf (accessed on 14 November 2012).
- Vachon, P.W. Ship Detection in Synthetic Aperture Radar Imagery. Proceedings of OceanSAR 2006-Thrid Workshop on Coastal and Marine Applications of SAR, St. John’s, NL, Canada, 23–25 October 2006; pp. 1–10.
- Piracy and Armed Robbery Against Ships: Annual Report; ICC International Maritime Bureau: London, UK, 2010.
- AIS, Available online: http://www.orbcomm.com/services-ais.htm (accessed on 15 November 2012).
- Satellite AIS, Available online: http://www.exactearth.com/technology/satellite-ais/ (accessed on 15 November 2012).
- Vesseltracker–Ports, Available online: http://www.vesseltracker.com/en/CoveredAreas.html?sat=1 (accessed on 15 November 2012).
- Rohling, H. Radar CFAR thresholding in clutter and multiple target situations. IEEE Trans. Aerosp. Electron. Eng 1983, 19, 608–621. [Google Scholar]
- Sekine, M; Mao, Y. Weibull Radar Clutter; Peter Peregrinus: London, UK, 1990. [Google Scholar]
- Armstrong, B.C.; Griffiths, H.D. CFAR detection of fluctuating targets in spatially correlated K-distributed clutter. IEE Proc. F Rad. Sig. Proc 1991, 138, 139–152. [Google Scholar]
- Gagnon, L.; Klepko, R. Hierarchical classifier design for airborne SAR images of ships. Proc. SPIE 1998, 3371, 38–49. [Google Scholar]
- Valin, P.; Bosse, E.; Jouan, A. Airborne Application of Information Fusion Algorithms to Classification; Defence R & D Canada -Valcarier, Technical Report; DRDC Valcartier: Quebec, Canada, 2006. [Google Scholar]
- Margarit, G.; Tabasco, A. Ship classification in single-Pol SAR images based on fuzzy logic. IEEE Trans. Geosci. Remote Sens 2011, 49, 3129–3138. [Google Scholar]
- Gibbins, D.; Gray, D.A.; Dempsey, D. Classifying Ships Using Low Resolution Maritime Radar. Proceedings of 5th International Symposium on Signal Processing and Its Applications (ISSPA), Brisbane, Australia, 22–25 August 1999; 1, pp. 325–328.
- Touzi, R.; Raney, R.K.; Charbonneau, F. On the use of permanent symmetric scatterers for ship characterization. IEEE Trans. Geosci. Remote Sens 2004, 42, 2039–2045. [Google Scholar]
- Margarit, G.; Mallorquí, J.J.; Rius, J.M.; Sanz-Marcos, J. On the usage of GRECOSAR, an orbital polarimetric SAR simulator of complex targets, to vessel classification studies. IEEE Trans. Geosci. Remote Sens 2006, 44, 3517–3526. [Google Scholar]
- Margarit, G.; Mallorquí, J.J. Assessment of polarimetric SAR interferometry for improving ship classification based on simulated data. Sensors 2008, 8, 7715–7735. [Google Scholar]
- Margarit, G.; Mallorquí, J.J.; Fortuny-Guasch, J.; López-Martínez, C. Exploitation of ship scattering in polarimetric SAR for an improved classification under high clutter conditions. IEEE Trans. Geosci. Remote Sens 2009, 47, 1224–1235. [Google Scholar]
- Paladini, R.; Martorella, M.; Berizzi, F. Classification of man-made targets via invariant coherency-matrix eigenvector decomposition of polarimetric SAR/ISAR images. IEEE Trans. Geosci. Remote Sens 2011, 49, 3022–3034. [Google Scholar]
- Musman, S.; Bachmann, C. Automatic recognition of ISAR ship images. IEEE Trans. Aerosp. Electron. Syst 1996, 32, 1392–1404. [Google Scholar]
- ESA: MARISS Project, Available online: http://www.esa.int/Our_Activities/Observing_the_Earth/GMES/Security_services (accessed on 15 November 2012).
- MEOS SAR Ship Detection, Available online: http://www.spacetec.no/download_docs/doc_pdf/SAR-Ship.pdf/view (accessed on 15 November 2012).
- Margarit, G.; Milanés, J.A.B.; Tabasco, A. Operational ship monitoring system based on synthetic aperture radar processing. Remote Sens 2009, 1, 375–392. [Google Scholar]
- Liu, C.; Vachon, P.W.; English, R.A.; Sandirasegaram, N. Ship Detection Using RADARSAT-2 Fine Quad Mode and Simulated Compact Polarimetry Data, Available online: http://cradpdf.drdc-rddc.gc.ca/PDFS/unc93/p533016.pdf (accessed on 15 November 2012).
- Hains, K.A.; Hildebrand, B.P. Contour generation by wavefront reconstruction. Phys. Lett 1965, 19, 10–11. [Google Scholar]
- Hildebrand, B.P.; Hains, K.A. Multiple-wavelength and multiple-source holography applied to contour generation. J. Opt. Soc. Amer 1967, 67, 155–162. [Google Scholar]
- Hecht, E.; Zajac, A. Optics, 6th ed; Addison-Wesley: New York, NY, USA, 1980. [Google Scholar]
- Rogers, A.E.E.; Ingalls, R.P. Venus: Mapping the surface reflectivity by radar interferometry. Science 1969, 165, 797–799. [Google Scholar]
- Zisk, S.H. A new, Earth-based radar technique for the measurement of Lunar topography. The Moon 1972, 4, 2976–306. [Google Scholar]
- Shapiro, I.I.; Zisk, S.H.; Rogers, A.E.E.; Slade, M.A.; Thompson, T.W. Lunar topography: Global determination by radar. Science 1972, 178, 939–948. [Google Scholar]
- Zebker, H.A.; Goldstein, R.M. Topography mapping from interferometric SAR observations. J. Geophys. Res 1986, 91, 4993–4999. [Google Scholar]
- Gabriel, A.K.; Goldstein, R.M. Crossed orbit interferometry: Theory and experimental results from SIR-B. Int. J. Remote Sens 1988, 9, 857–872. [Google Scholar]
- Goldstein, R.M.; Zebker, H.A.; Werner, C.L. Satellite radar interferometry: Two-dimensional phase unwrapping. Radio Sci 1988, 23, 713–720. [Google Scholar]
- Li, F.; Goldstein, R.M. Studies of multibaseline spaceborne interferometric synthetic aperture radars. IEEE Trans. Geosci. Remote Sens 1990, 28, 88–97. [Google Scholar]
- Tribolet, J. A new phase unwrapping algorithm. IEEE Trans. Accus. Speech Signal Proc 1997, 25, 170–177. [Google Scholar]
- Takajo, H.; Takahashi, T. Noniterative method for obtaining the exact solution for the normal equation in least-squares phase estimation from the phase difference. J. Opt. Soc. Amer. A 1988, 5, 1818–1827. [Google Scholar]
- Huntley, J.M. Noise-immune phase unwrapping algorithm. Appl. Opt 1989, 28, 3268–3270. [Google Scholar]
- Takajo, H.; Takahashi, T. Suppression of the influence of noise in least-squares phase estimation from the phase difference. J. Opt. Soc. Amer. A 1990, 7, 1153–1162. [Google Scholar]
- Moon-Ho Song, S.; Napel, S.; Pelc, N.J.; Glover, G.H. Phase unwrapping of MR phase images using Poisson equation. IEEE Trans. Image Proc 1995, 4, 667–676. [Google Scholar]
- Liang, Z.-P. A model-based method for phase unwrapping. IEEE Trans. Med. Imaging 1996, 15, 893–897. [Google Scholar]
- Qianqian, F.; Meaney, P.M.; Paulsen, K.D. The multidimensional phase unwrapping integral and applications to microwave tomographical image reconstruction. IEEE Trans. Image Process 2006, 15, 3311–3324. [Google Scholar]
- Ghiglia, D.C.; Romero, L.A. Robust two-dimensional weighted and unweighted phase unwrapping that uses fast transforms and iterative methods. J. Opt. Soc. Amer. A 1994, 11, 107–117. [Google Scholar]
- Pritt, M.D.; Shipman, J.S. Least-squares two-dimensional phase unwrapping using FFT’s. IEEE Trans. Geosci. Remote Sens 1994, 32, 706–708. [Google Scholar]
- Fornaro, G.; Franceschetti, G.; Lanari, R. Interferometric SAR phase unwrapping using Green’s formulation. IEEE Trans. Geosci. Remote Sens 1996, 34, 720–727. [Google Scholar]
- Ghiglia, D.C.; Romero, L.A. Minimum Lp-norm two-dimensional phase unwrapping. J. Opt. Soc. Am. A 1996, 13, 1999–2013. [Google Scholar]
- Pritt, M.D. Phase unwrapping by means of multigrid techniques for interferometric SAR. IEEE Trans. Geosci. Remote Sens 1996, 34, 728–738. [Google Scholar]
- Ghiglia, D.C.; Pritt, M.D. Two-Dimensional Phase Unwrapping: Theory, Algorithm, and Software; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Fornaro, G.; Sansosti, E. A two-dimensional region growing least squares phase unwrapping algorithm for interferometric SAR processing. IEEE Trans. Geosci. Remote Sens 1999, 37, 2215–2226. [Google Scholar]
- Xu, W.; Cumming, I. A region-growing algorithm for InSAR phase unwrapping. IEEE Trans. Geosci. Remote Sens 1999, 37, 123–134. [Google Scholar]
- Carballo, G.F.; Fieguth, P.W. Probabilistic cost functions for network flow phase unwrapping. IEEE Trans. Geosci. Remote Sens 2000, 38, 2192–2201. [Google Scholar]
- Fornaro, G.; Pauciullo, A.; Sansosti, E. Phase difference-based multichannel phase unwrapping. IEEE Trans. Image Process 2005, 14, 960–972. [Google Scholar]
- Mao, Z.; Liao, G. Optimum data vector approach to multibaseline SAR interferometry phase unwrapping. IEEE Geosci. Remote Sens. Lett 2009, 6, 42–46. [Google Scholar]
- Fornaro, G.; Pauciullo, A.; Reale, D. A null-space method for the phase unwrapping of multitemporal SAR interferometric stacks. IEEE Trans. Geosci. Remote Sens 2011, 49, 2323–2334. [Google Scholar]
- Moreira, J.; Schwabisch, M; Fornaro, G.; Lanari, R.; Bamler, R.; Just, D.; Steinbrecher, U.; Breit, H.; Eineder, M.; Granceschetti, G.; et al. X-SAR interferometry: First results. IEEE Trans. Geosci. Remote Sens 1995, 33, 950–956. [Google Scholar]
- Coltelli, M.; Fornaro, G.; Franceschetti, G.; Lanari, R.; Migliaccio, M.; Moreira, J.R.; Papathanassiou, K.P.; Puglisi, G.; Riccio, D.; Schwabisch, M. SIR-C/X-SAR multifrequency multipass interferometry: A new tool for geological interpretation. J. Geophys. Res 1996, 101, 23127–23148. [Google Scholar]
- Brown, C.G.; Sarabandi, K.; Pierce, L.E. Validation of the Shuttle Radar Topography Mission height data. IEEE Trans. Geosci. Remote Sens 2005, 43, 1707–1715. [Google Scholar]
- SRTM Website, Available online: http://www2.jpl.nasa.gov/srtm/ (accessed on 15 November 2012).
- National Imagery and Mapping Agency (NIMA). Performance Specification Digital Terrain Elevation Data (DTED), MIL-PRF-89020B. 2000. Available online: http://earth-info.nga.mil/publications/specs/printed/89020B/89020B.pdf (accessed on 15 November 2012).
- High Resolution Terrain Information (HRTI): Performance Specification; MIL-PRF-89048; National Imagery and Mapping Agency (NIMA): Springfield, VA, USA, 2000.
- Moreira, A.; Krieger, G.; Hajnsek, I.; Hounam, D.; Werner, M.; Riegger, S.; Settelmeyer, E. TenDEM-X: A TerraSAR-X add-on Satellite for Single-pass SAR Interferometry. Proceedings of IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Anchorage, AK, USA, 24– 29 September 2004; pp. 215–4218.
- Huber, M.; Gruber, A.; Wessel, B.; Breunig, M.; Wendleder, A. Validation of Tie-point Concepts by the DEM Adjustment Approach of TanDEM-X. Proceedings of IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25– 30 July 2010; pp. 2644–2647.
- Gruber, A.; Wessel, B.; Huber, M.; Roth, A. Operational TanDEM-X DEM calibration and first validation results. ISPRS J. Photogramm 2012, 73, 39–49. [Google Scholar]
- Huber, M.; Gruber, A.; Wendleder, A.; Wessel, B.; Roth, A.; Schmitt, A. The global TanDEM-X DEM: Production status and first validation results. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, XXXIX-B7, 45–50. [Google Scholar]
- TanDEM-X Website, Available online: http://www.dlr.de/hr/desktopdefault.aspx/tabid-2317//3669_read-5488/ (accessed on 15 November 2012).
- Martone, M.; Bräutigam, B.; Rizzoli, P.; Gonzalez, C.; Bachmann, M.; Krieger, G. Coherence evaluation of TanDEM-X interferometric data. ISPRS J. Photogram 2012, 73, 21–29. [Google Scholar]
- Rizzoli, P.; Bräutigam, B.; Kraus, T.; Martone, M.; Krieger, G. Relative height error analysis of TanDEM-X elevation data. ISPRS J. Photogram 2012, 73, 30–38. [Google Scholar]
- Wyss, M.; Sobolev, G.; Clippard, J.D. Seismic equiescence precursors to two M7 earthquakes on Sakhalin Island, measured by two methods. Earth Planets Space 2004, 56, 752–740. [Google Scholar]
- Bechor, N.B.D.; Zebker, H.A. Measuring two-dimensional movements using a single InSAR pair. Geophys. Res. Lett. 2006. [Google Scholar] [CrossRef]
- Jung, H.-S.; Won, J.-S.; Kim, S.-W. An improvement of the performance of multiple aperture SAR interferometry (MAI). IEEE Trans. Geosci. Remote Sens 2009, 47, 2859–2869. [Google Scholar]
- Barbot, S.; Hamiel, Y.; Fialko, Y. Space geodetic investigation of the coseismic and postseismic deformation due to the 2003 Mw7.2 Altai earthquake: Implications for the local lithospheric rheology. J. Geophys. Res. 2008. [Google Scholar] [CrossRef]
- Biggs, J.; Amelung, F.; Gourmelen, N.; Dixon, T.H.; Kim, S.-W. InSAR observations of 2007 Tanzania rifting episode reveal mixed fault and dyke extension in an immature continental rift. Geophys. J. Int 2009, 179, 549–558. [Google Scholar]
- Lu, Z.; Dzurisin, D. Ground surface deformation patterns, magma supply, and magma storage at Okmok volcano, Alaska, from InSAR analysis: 2. Coeruptive deflation, July– August 2008. J. Geophys. Res. 2010. [Google Scholar] [CrossRef]
- Goldstein, R.M. Atmospheric limitations to repeat-track radar interferometry. Geophys. Res. Lett 1995, 22, 2517–2520. [Google Scholar]
- Tarayre, H.; Massonnet, D. Atmospheric propagation heterogeneities revealed by ERS-1. Geophys. Res. Lett 1996, 23, 989–992. [Google Scholar]
- Zebker, H.A.; Rosen, P.A.; Hensley, S. Atmospheric artifacts in interferometric synthetic aperture radar surface deformation and topographic maps. J. Geophys. Res 1997, 102, 7547–7564. [Google Scholar]
- Hanssen, R.F.; Weckworth, T.M.; Zebker, H.A.; Klees, R. High resolution water vapour mapping from interferometric radar measurements. Science 1999, 283, 1297–1299. [Google Scholar]
- Rocken, C.; Van Hove, T.; Johnson, J.; Solheim, F.; Ware, R.; Bevis, M.; Businger, S.; Chiswell, S. GPS/STORM-GPS sensing of atmospheric water vapor for meteorology. J. Atmos. Ocean. Tech 1995, 12, 468–478. [Google Scholar]
- Duan, J.; Bevis, M.; Fang, P.; Bock, Y.; Chiswell, S.; Businger, S.; Roken, C.; Solheim, F.; Von Hove, T.; Ware, R.; et al. GPS Meteorology: Direct estimation of the absolute value of precipitable water. J. Appl. Meteorol 1996, 35, 830–838. [Google Scholar]
- Li, Z.-W.; Ding, X.-L.; Liu, G.-X.; Huang, C. Atmospheric Effects on InSAR Measurements—A review. Geom. Res. Austr 2003, 79, 43–58. [Google Scholar]
- Ding, X.-L.; Li, Z.-W.; Zhu, J.-J.; Feng, G.-C.; Long, J.-P. Atmospheric effects on InSAR measurements and their mitigation. Sensors 2008, 8, 5426–5449. [Google Scholar]
- Schmidt, D.A.; Bürgmann, R. Time-dependent land uplift and subsidence in the Santa Clara valley, California, from a large interferometric synthetic aperture radar data set. J. Geophys. Res. Solid Earth 2003. [Google Scholar] [CrossRef]
- Chaabane, F.; Avallonio, A.A.; Tupin, F.; Briole, P.; Maître, H. A multitemporal method for correction of tropospheric effects in differential SAR inteferometry: Application to the Gulf of Corinth Earthquakes. IEEE Trans. Geosci. Remote Sens 2007, 45, 1605–1615. [Google Scholar]
- Pinel-Puysségur, B.; Michel, R.; Avouac, J.-P. Multi-link InSAR time series: Enhancement of a wrapped interferometric database. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens 2012, 5, 784–794. [Google Scholar]
- Beauducel, F.; Briole, P.; Froger, J.-L. Volcano-wide fringes in ERS synthetic aperture radar interferograms of Etna (1992–1998): Deformation or tropospheric effect? J. Geophys. Res. Sol. Es 2000, 105, 16391–16402. [Google Scholar]
- Wadge, G.; Webley, P.W.; James, I.N.; Bingley, R.; Dodson, A.; Waugh, S.; Veneboer, T.; Puglisi, G.; Mattia, M.; Baker, D.; et al. Atmospheric models, GPS and InSAR measurements of the tropospheric water vapour field over Mount Etna. In Geophys. Res. Lett.; 2002; Volume 29, pp. 11-1–11-4. [Google Scholar]
- Bonforte, A.; Ferretti, A.; Prati, C.; uglisi, G.; Rocca, F. Calibration of atmospheric effects on SAR interferograms by GPS and local atmosphere models: First results. J. Atmos. Sol. Terr. Phys 2001, 63, 1343–1357. [Google Scholar]
- Webley, P.W.; Bingley, R.M.; Dodson, A.H.; Wadge, G.; Waugh, S.J.; James, I.N. Atmospheric water vapour correction to InSAR surface motion measurements on mountains: Results from a dense GPS network on Mount Etna. Phys. Chem. Earth Parts A/B/C 2002, 27, 363–370. [Google Scholar]
- Onn, F.; Zebker, H. Correction for interferometric synthetic aperture radar atmospheric phase artifacts using time series of zenith wet delay observations from a GPS network. J. Geophys. Res. 2006. [Google Scholar] [CrossRef]
- Li, Z.; Fielding, E.; Cross, P. Integration of InSAR time series analysis and water vapour correction for mapping postseismic deformation after the 2003 Bam (Iran) Earthquake. IEEE Trans. Geosci. Remote Sens 2009, 47, 3220–3230. [Google Scholar]
- Li, Z.; Fielding, E.; Cross, P.; Preusker, R. Advanced InSAR atmospheric correction: MERIS/MODIS combination and stacked water vapour models. Int. J. Remote Sens 2009, 30, 3343–3363. [Google Scholar]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansoti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens 2002, 40, 2375–2383. [Google Scholar]
- Lauknes, T.R. InSAR tropospheric stratification delays: Correction using a small baseline approach. IEEE Geosci. Remote Sens. Lett 2011, 8, 1070–1074. [Google Scholar]
- Lin, Y.N.; Simons, M.; Hetland, E.A.; Muse, P.; DiCaprio, C. A multiscale approach to estimating topographically correlated propagation delays in radar interferograms. Geochem. Geophys. Geosyst. 2010. [Google Scholar] [CrossRef]
- Doin, M.-P.; Lasserre, C.; Peltzer, G.; Cavalié, O.; Doubre, C. Corrections of stratified tropospheric delays in SAR interferometry: Validation with global atmospheric models. J. Appl. Geophys 2009, 69, 35–50. [Google Scholar]
- Jolivet, R.; Grandin, R.; Lasserre, C.; Doin, M.-P.; Peltzer, G. Systematic InSAR tropospheric phase delay corrections from global meteorological reanalysis data. Geophys. Res. Lett. 2011. [Google Scholar] [CrossRef]
- Quegan, S.; Lamont, J. Ionospheric and tropospheric effects on synthetic aperture radar performance. Int. J. Remote Sens 1986, 7, 525–539. [Google Scholar]
- Ishimaru, A.; Kuga, Y.; Liu, J.; Kim, Y.; Freeman, A. Ionospheric effects on synthetic aperture radar at 100 MHz to 2 GHz. Radio Sci 1999, 34, 257–268. [Google Scholar]
- Xu, Z.-W.; Wu, J.; Wu, Z.-S. A survey of ionospheric effects on space-based radar. Waves Random Media 2004, 14, 189–272. [Google Scholar]
- Gray, A.L; Mattar, K.E.; Sofko, G. Influence of ionospheric electron density fluctuations on satellite radar interferometry. Geophys. Res. Lett 2000, 27, 1451–1454. [Google Scholar]
- Meyer, F.; Nicoll, J. Ionospheric Effects on SAR, InSAR, and SAR Polarimetry Theory and Experiences with ALOS/PALSAR. Proceedings of IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Boston, MA, USA, 7– 10 July 2008; II, pp. 391–394.
- Pi, X.; Freeman, A.; Chapman, B.; Rosen, P.; Li, Z. Imaging ionospheric inhomogeneities using spaceborne synthetic aperture radar. J. Geophys. Res. Space Phys 2011, 116, A04303. [Google Scholar]
- De Michele, M.; Raucoules, D.; Lasserre, C.; Pathier, E.; Klinger, Y.; van Der Woerd, J.; de Sigoyer, J.; Xu, X. The Mw 7.9, 12 May 2008 Sichuan earthquake rupture measured by sub-pixel correlation of ALOS PALSAR amplitude images. Earth Planets Space 2010, 62, 875–879. [Google Scholar]
- Raucoules, D.; de Michele, M. Assessing ionospheric influence on L-Band SAR data: Implications on coseismic displacement measurements of the 2008 Sichuan Earthquake. IEEE Geosci. Remote Sens. Lett 2010, 7, 286–290. [Google Scholar]
- Rosen, P.A.; Hensley, S.; Chen, C. Measurement and Mitigation of the Ionosphere in L-band Interferometric SAR Data. Proceedings of IEEE Radar Conference, Arlington, VA, USA, 10– 14 May 2010; pp. 1459–1463.
- Meyer, F. A Review of Ionospheric Effects in Low-Frequency SAR-Signals, Correction Methods, and Performance Requirements. Proceedings of IEEE International Geosience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25– 30 July 2010; pp. 29–30.
- Mattar, K.E.; Gray, A.L. Reducing ionospheric electron density errors in satellite radar interferometry applications. Can. J. Remote Sens 2002, 28, 593–600. [Google Scholar]
- Meyer, F.; Bamler, R.; Jakowski, N.; Fritz, T. Methods for Small Scale Ionospheric TEC Mapping from Broadband L-Band SAR Data. Proceedings of IEEE International Geosience and Remote Sensing Symposium (IGARSS), Denvor, CO, USA, 31 July– 4 August 2006; pp. 3735–3738.
- Meyer, F.; Bamler, R.; Jakowski, N.; Fritz, T. The Potential of low-frequency SAR systems for mapping ionospheric TEC distributions. IEEE Geosci. Remote Sens. Lett 2006, 2, 560–564. [Google Scholar]
- Bickel, S.H.; Bates, R.H.T. Effects of magneto-ionic propagation on the polarization scattering matrix. Proc. IEEE 1965, 53, 1089–1091. [Google Scholar]
- Freeman, A. Calibration of linearly polarized polarimetric SAR data subject to Faraday rotation. IEEE Trans. Geosci. Remote Sens 2004, 42, 1617–1624. [Google Scholar]
- Nicoll, J.; Meyer, F. Mapping the Ionosphere Using L-Band SAR Data. Proceedings of IEEE International Geosience and Remote Sensing Symposium (IGARSS), Boston, MA, USA, 7– 11 July 2008; II, pp. 537–540.
- Massonnet, D.; Rossi, M.; Carmona, C.; Adragna, F.; Peltzer, G.; Feigl, K.; Rabaute, T. The displacement field of the Landers earthquake mapped by radar interferometry. Nature 1993, 364, 138–142. [Google Scholar]
- Massonnet, D.; Feigl, K.; Rossi, M.; Adragna, F. Radar interferometric mapping of deformation in the year after the Landers earthquake. Nature 1994, 369, 337–230. [Google Scholar]
- Zebker, H.; Rosen, P.A.; Goldstein, R.M.; Gabriel, A.; Werner, C.L. On the derivation of coseismic displacement fields using differential radar interferometry: The Landers earthquake. J. Geophys. Res 1994, 99, 19617–19634. [Google Scholar]
- Goldstein, R.M.; Engelhardt, H.; Kamb, B.; Frolich, R.M. Satellite radar interferometry for monitoring ice sheet motion: Application to an Antarctic ice stream. Science 1993, 262, 1525–1530. [Google Scholar]
- Murakami, M.; Tobita, M.; Fujiwara, S.; Saito, T.; Masaharu, H. Coseismic crustal deformation of 1994 Northridge, California, earthquake detected by interferometric JERS 1 synthetic aperture radar. J. Geophys. Res 1996, 101, 8605–8614. [Google Scholar]
- Ohkura, H.; Jitsuchi, T.; Matsumoto, T.; Fujinawa, Y. Application of SAR data to monitoring of earthquake disaster. Adv. Space Res 1997, 19, 1429–1436. [Google Scholar]
- Chini, M.; Atzori, S.; Trasatti, E.; Bignami, C.; Kyriakopoulos, C.; Tolomei, C.; Stramondo, S. The May 12, 2008, (Mw 7.9) Sichuan Earthquake (China): Multiframe ALOS-PALSAR DInSAR analysis of coseismic deformation. IEEE Geosci. Remote Sens. Lett 2010, 7, 266–270. [Google Scholar]
- Atzori, S.; Hunstad, I.; Chini, M.; Salvi, S.; Tolomei, C.; Bignami, C.; Stramondo, S.; Trasatti, E.; Antonioli, A.; Boschi, E. Finite fault inversion of DInSAR coseismic displacement of the 2009 LAquila earthquake (central Italy). Geophys. Res. Lett 2009, 36, L17307. [Google Scholar]
- Feng, G.; Ding, X.; Li, Z.; Mi, J.; Zhang, L.; Omura, M. Callibration of an InSAR-derived coseismic deformation map associated with the 2011 Mw-9.0 Tohoku-Oki Earthquake. IEEE Geosci. Remote Sens. Lett 2012, 9, 302–306. [Google Scholar]
- ALOS/PALSAR Observation Results of the Magnitude-9.0 Earthquake off the Pacific Coast of Tohoku-Kanto District in Japan in 2011 (3), Available online: http://www.eorc.jaxa.jp/ALOS/en/img_up/dis_pal_tohokueq_110401-06.htm (accessed on 15 November 2012).
- Rosen, P.A.; Hensley, S.; Zebker, H.A.; Webb, F.H.; Fielding, E.J. Surface deformation and coherence measurements of Kilauea volcano, Hawaii, from SIR-C radar interferometry. J. Geophys. Res 1996, 101, 23109–23125. [Google Scholar]
- Pritchard, M.E.; Simons, M. A satellite geodetic survey of large-scale deformation of volcanic centres in the central Andes. Nature 2002, 418, 167–171. [Google Scholar]
- Strozzi, T.; Wegmuller, U.; Werner, C.L.; Wiesmann, A.; Spreckels, V. JERS SAR interferometry for land subsidence monitoring. IEEE Trans. Geosci. Remote Sens 2003, 41, 1702–1708. [Google Scholar]
- Löpez-Quiroz, P.; Doin, M.-P.; Tupin, F.; Briole, P.; Nicolas, J.-M. Time series analysis of Mexico City subsidence constrained by radar interferometry. J. Apply. Geophys 2009, 69, 1–15. [Google Scholar]
- Arjona, A.; Santoyo, M.A.; Fernández, J.; Monells, D.; Prieto, J.F.; Pallero, J.L.G.; Prieto, E.; Seco, A.; Luzón, F.; Mallorquí, J. On the Applicability of an Advanced DInSAR Technique Near Itoiz and Yesa Reservoirs, Navarra, Spain. Proceedings of the Workshop Fringe 2009, Frascati, Italy, 30 November–4 December 2009.
- Ge, L.; Chang, H.-C.; Rizos, C. Mine subsidence monitoring using multi-source satellite SAR images. Photogramm. Eng. Remote Sensing 2007, 73, 259–266. [Google Scholar]
- Herrera, G.; Tomás, R.; López-Sánchez, J.M.; Delgado, J.; Mallorquí, J.J.; Duque, S.; Mulas, J. Advanced DInSAR analysis on mining areas: La Union case study (Murcia, SE Spain). Eng. Geol 2007, 90, 148–159. [Google Scholar]
- Motagh, M.; Walter, T.R.; Shariff, M.A.; Fielding, E.; Schenk, A.; Anderssohn, A.; Zschau, J. Land subsidence in Iran caused by widespread water reservoir overextraction. Geophys. Res. Lett. 2008. [Google Scholar] [CrossRef]
- Akbari, V.; Motagh, M. Improved ground subsidence monitoring using small baseline SAR interferograms and a weighted least square inversion algorithm. IEEE Geosci. Remote Sens. Lett 2012, 9, 437–441. [Google Scholar]
- Geospatial Information Authority of Japan, Available online: http://vldb.gsi.go.jp/sokuchi/sar/index-e.html (accessed on 15 November 2012).
- Mattar, K.E.; Vachon, P.W.; Geudtner, D.; Gray, A.L.; Cumming, I.G.; Brugman, M. Validation of alpine glacier velocity measurements using ERS Tandem Mission SAR data. IEEE Trans. Geosci. Remote Sens 1998, 36, 974–984. [Google Scholar]
- F. Pattyn, F.; Derauw, D. Ice-dynamic conditions of Shirase Glacier, Antarctica, inferred from ERS SAR interferometry. J. Glaciol 2002, 48, 559–565. [Google Scholar]
- Yamanokuchi, T.; Doi, K.; Shibuya, K. Validation of grounding line of the East Antarctica Ice Sheet derived by ERS-1/2 interferometric SAR data. Polar Geosci 2005, 18, 1–14. [Google Scholar]
- Rignot, E.; Kanagaratnam, P. Changes in the velocity structure of the Greenland Ice Sheet. Science 2006, 311, 986–990. [Google Scholar]
- Mouginot, J.; Scheuchl, B.; Rignot, E. Mapping of ice motion in Antarctica by synthetic-aperture rada data. Remote Sens 2012, 4, 2753–2767. [Google Scholar]
- ESA Website. Advances in the Science and Applications of SAR Interferometry, ESA Fringe 2009 Workshop, Available online: http://earth.eo.esa.int/workshops/fringe09/ (accessed on 22 July 2012).
- Engdahl, M. Forward to the Fringe Special Issue, Available online: http://www.sciencedirect.com/science/journal/09269851/69/1 (accessed on 22 January 2013).
- Mei, S.; Poncos, V.; Froese, C. Mapping millimeter-scale ground deformation over the underground coal mines in the Frank Slide area, Alberta, Canada, using spaceborne InSAR technology. Can. J. Remote Sens 2008, 34, 113–134. [Google Scholar]
- Singhroy, V.; Alasser, P.-J.; Couture, R.; Froese, C. InSAR Monitoring of Landslides in Canada. Proceedings of IEEE International Geosience and Remote Sensing Symposium (IGARSS), Boston, MA, USA, 7– 11 July 2008; III, pp. 202–205.
- Osmanoğlu, B.; Dixon, T.H.; Wdowinski, S.; Cabral-Cano, E.; Jiang, Y. Mexico city subsidence observed with persistent scatterer InSAR. Int. J. Appl. Earth Obs. Geoinf 2010, 13, 1–12. [Google Scholar]
- Perissina, D.; Wang, Z.; Lin, H. Shanghai subway tunnels and highways monitoring through Cosmo-SkyMed persistent scatterers. ISPRS J. Photogram. 2012. in press. [Google Scholar]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A new algorithm for processing interferometric data-stacks: SqueeSAR. IEEE Trans. Geosci. Remote sens 2011, 49, 3460–3470. [Google Scholar]
- Hooper, A. A multi-temporal InSAR method incorporating both persestent scatterer and small baseline approaches. Geophys. Res. Lett. 2008. [Google Scholar] [CrossRef]
- Pieraccini, M.; Luzi, G.; Atzeni, C. Terrain mapping by ground-based interferometric radar. IEEE Trans. Geosci. Remote Sens 2001, 39, 2176–2181. [Google Scholar]
- Nico, G.; Leva, D.; Antonello, G.; Tarchi, D. Ground-based SAR interferometry for terrain mapping: Theory and sensitivity analysis. IEEE Trans. Geosci. Remote Sens 2004, 42, 1344–1350. [Google Scholar]
- Nico, G.; Leva, D.; Fortuny-Guasch, J.; Antonello, G.; Tarchi, D. Generation of digital terrain models with a ground-based SAR system. IEEE Trans. Geosci. Remote Sens 2005, 43, 45–49. [Google Scholar]
- Noferini, L.; Pieraccini, M.; Mecatti, D.; Macaluso, G.; Luzi, G.; Atzeni, C. DEM by ground based SAR interferometry. IEEE Geosci. Remote Sens. Lett 2007, 4, 659–663. [Google Scholar]
- Pieraccini, M.; Tarchi, D.; Rudolf, H.; Leva, D.; Luzi, G.; Atzeni, C. Interferometric radar for remote monitoring of building deformation. Electron. Lett 2000, 36, 569–570. [Google Scholar]
- Luzi, G.; Pieraccini, M.; Mecatti, D.; Noferini, L.; Guidi, G.; Moia, F.; Atzeni, C. Ground-based radar interferometry for landslides monitoring: Atmospheric and instrumental decorrelation sources on experimental data. IEEE Trans. Geosci. Remote Sens 2004, 42, 2454–2466. [Google Scholar]
- Noferini, L.; Takayama, T.; Pieraccini, M.; Mecatti, D.; Macaluso, G.; Luzi, G.; Atzeni, C. Analysis of ground-based SAR data with diverse temporal baselines. IEEE Trans. Geosci. Remote Sens 2008, 46, 1614–1623. [Google Scholar]
- Strozzi, T.; Werner, C.; Wiesmann, A.; Wegmüller, U. Topography mapping with a portable real-aperture radar interferometer. IEEE Geosci. Remote Sens. Lett 2012, 9, 277–281. [Google Scholar]
- O’Donnell, K.A.; Brames, B.J.; Dainty, J.C. Measurements of the spatial-temporal statistics of stellar speckle patterns at Mauna Kea, Hawai. Opt. Commun 1982, 41, 79–82. [Google Scholar]
- Roddier, F.; Gilli, J.M.; Lund, G. On the origin of speckle boiling and its effects in stellar speckle interferometry. J. Opt 1982, 13, 263–271. [Google Scholar]
- Yoshimura, T. Statistical properties of dynamic speckles. J. Opt. Soc. Amer. A 1986, 3, 1032–1054. [Google Scholar]
- Rabal, H.J.; Braga, R.A., Jr. Dynamic Laser Speckle and Applications; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Gray, L.; Short, N.; Mattar, K.; Jezek, K. Velocities and flux of the Filchner Ice Shelf and its tributaries determined from speckle tracking interferometry. Can. J. Remote Sens 2001, 27, 193–206. [Google Scholar]
- Joughin, I. Ice-sheet velocity mapping: A combined interferometric and speckle-tracking approach. Ann. Glaciol 2002, 34, 195–201. [Google Scholar]
- Strozzi, T.; Luckman, A.; Murray, T.; Wegmuller, U.; Werner, C.L. Glacier motion estimation using SAR offset-tracking procedures. IEEE Trans. Geosci. Remote Sens 2002, 40, 2384–2391. [Google Scholar]
- Liu, H.; Zhao, Z.; Jezek, K.C. Synergistic fusion of interferometric and speckle-tracking methods for deriving surface velocity from interferometric SAR data. IEEE Geosci. Remote Sens. Lett 2007, 4, 102–106. [Google Scholar]
- Kobayashi, T.; Takada, Y.; Furuya, M.; Murakami, M. Locations and types of ruptures involved in the 2008 Sichuan earthquake inferred from SAR image matching. Geophys. Res. Lett. 2009. [Google Scholar] [CrossRef]
- Yun, S.-H.; Zebker, H.; Segall, P.; Hooper, A.; Poland, M. Interferogram formation in the presence of complex and large deformation. Geophys. Res. Lett. 2007, 745. [Google Scholar] [CrossRef]
- Tucker, M.J. The decorrelation time of microwave radar echoes from the sea surface. Int. J. Remote Sens 1985, 6, 1075–1089. [Google Scholar]
- Alpers, W.R.; Brüning, C. On the relative importance of motion-related contributions to the SAR imaging mechanism of ocean surface waves. IEEE Trans. Geosci. Remote Sens 1986, 24, 873–885. [Google Scholar]
- Kasilingham, D.P.; Shemdin, O.H. Theory for synthetic aperture radar imaging of the ocean surface: With application to the tower ocean wave and radar dependence experiment of focus, resolution and wave height spectra. J. Geophys. Res 1988, 93, 13837–13848. [Google Scholar]
- Plant, W.J.; Keller, W.C. Evidence of Bragg scattering in microwave Doppler spectra of sea return. J. Geophys. Res 1990, 95, 16299–16310. [Google Scholar]
- Pottier, E. Recent Advances in the Development on the Open Source Toolbox for Polarimetric and Interferometric Polarimetric SAR Data Processing: The PolSARpro v4.1.5 Software. Proceedings of IEEE International Geosience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25– 30 July 2010; pp. 2527–2530.
- Ainsworth, T.L.; Ferro-Famil, L.; Lee, J.-S. Orientation angle preserving a posteriori polarimetric SAR calibration. IEEE Trans. Geosci. Remote Sens 2006, 44, 994–1003. [Google Scholar]
- Touzi, R.; Shimada, M. Polarimetric PALSAR calibration. IEEE Trans. Geosci. Remote Sens 2009, 48, 3951–3959. [Google Scholar]
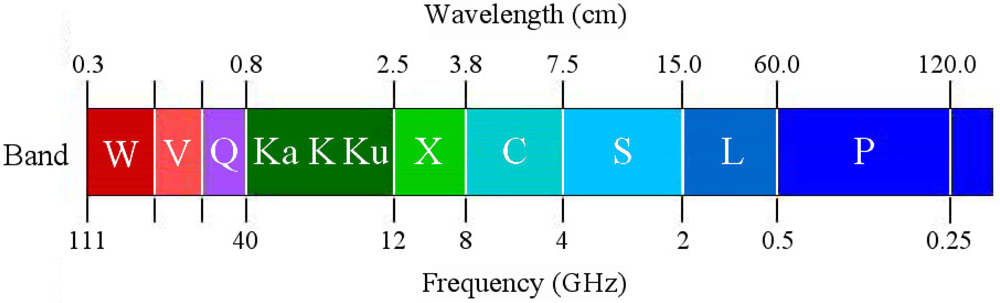
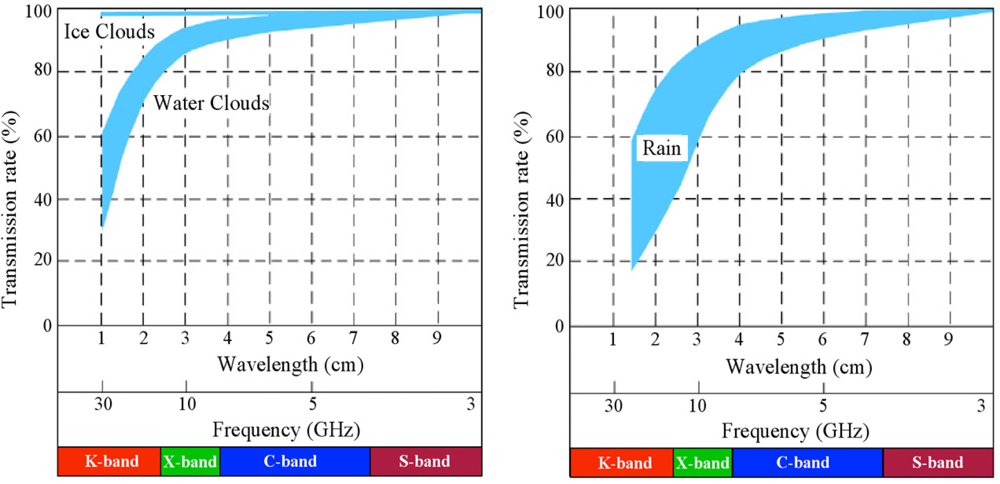


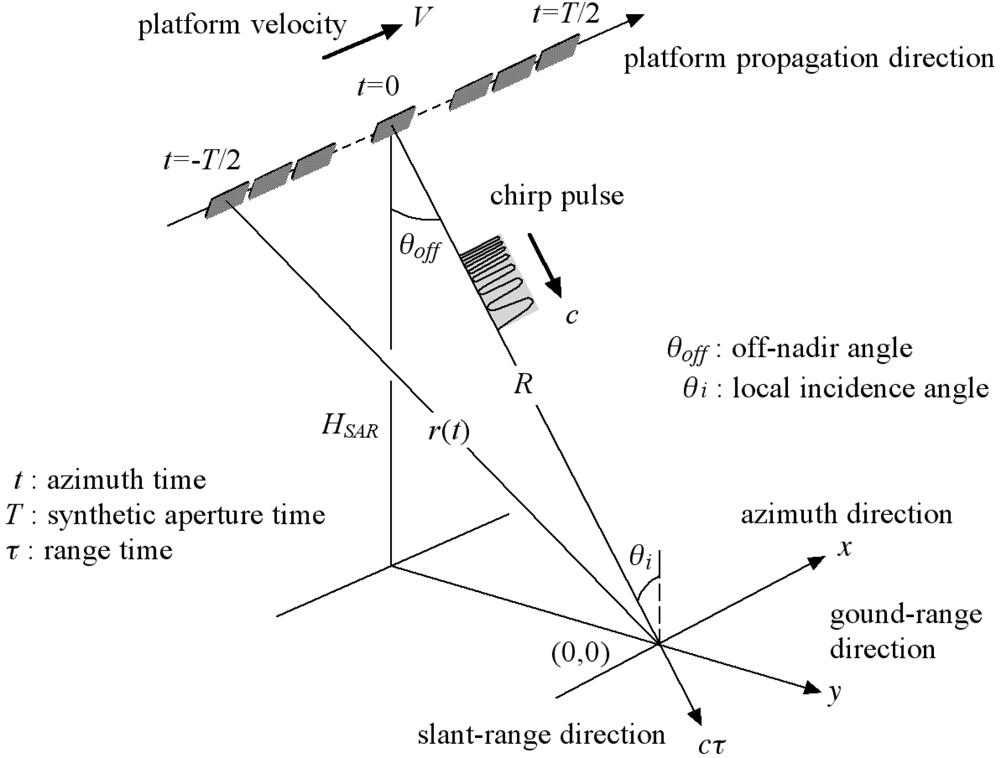
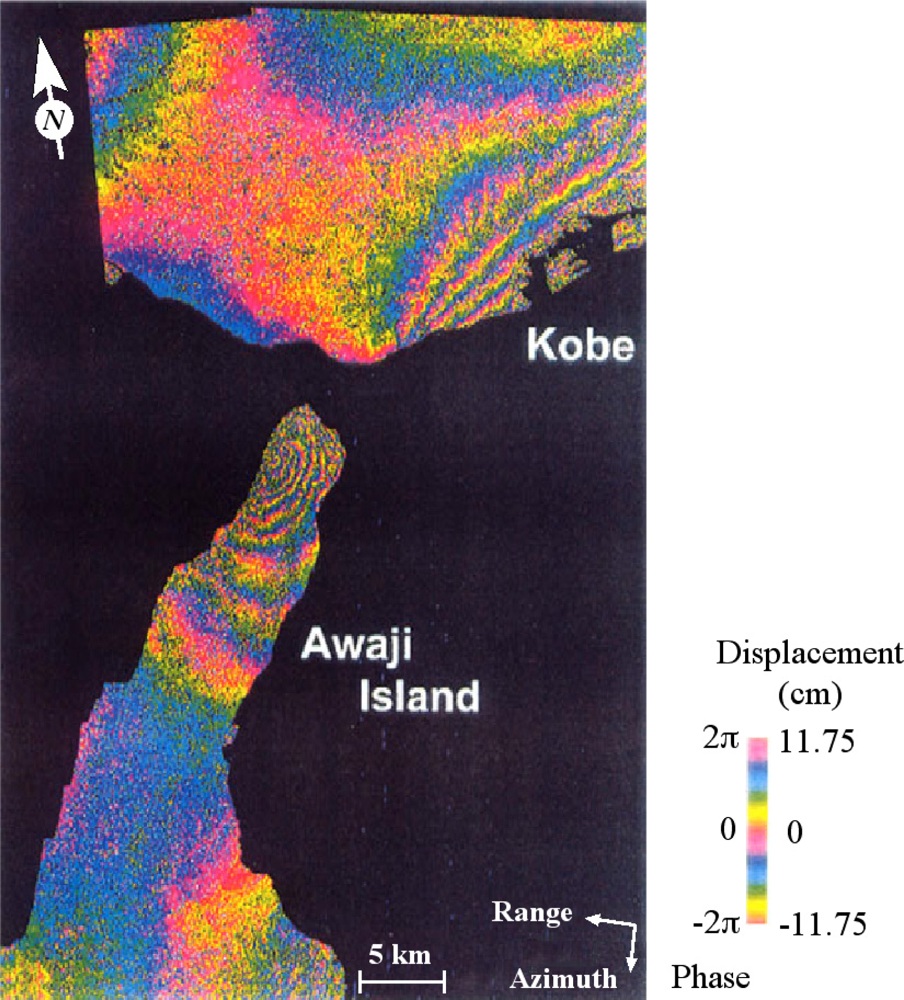
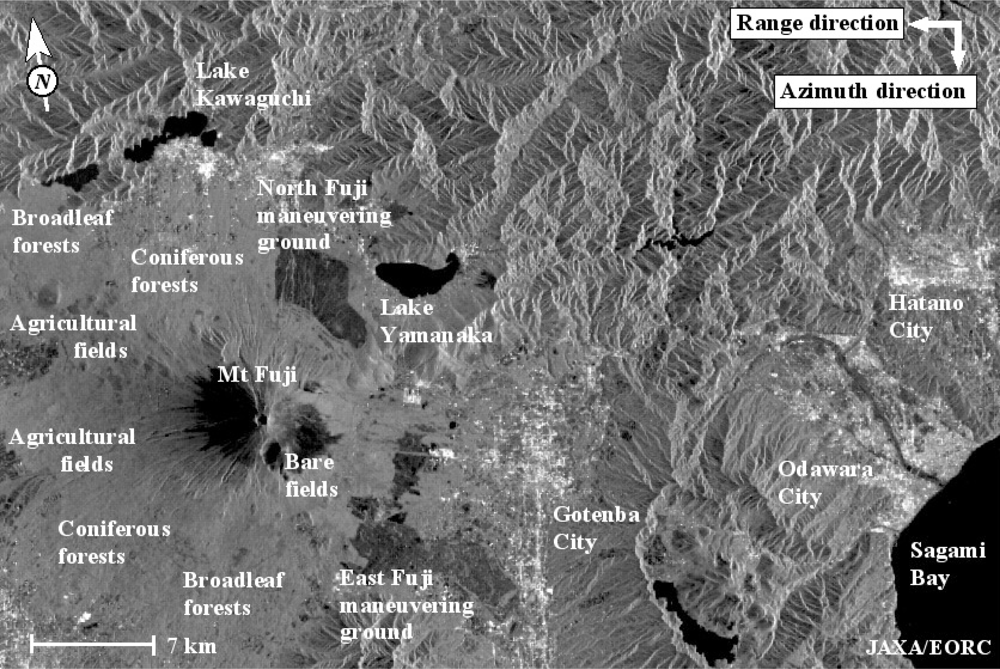

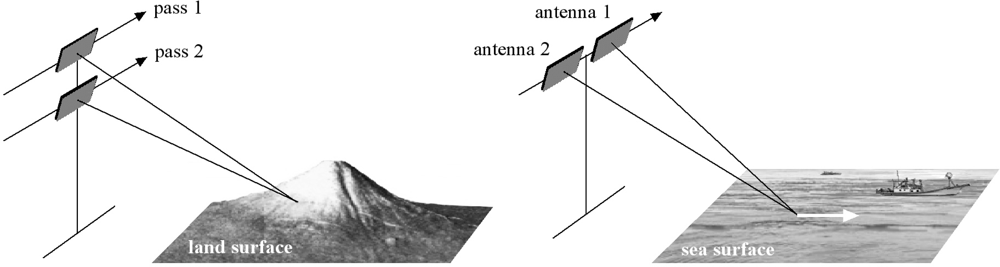
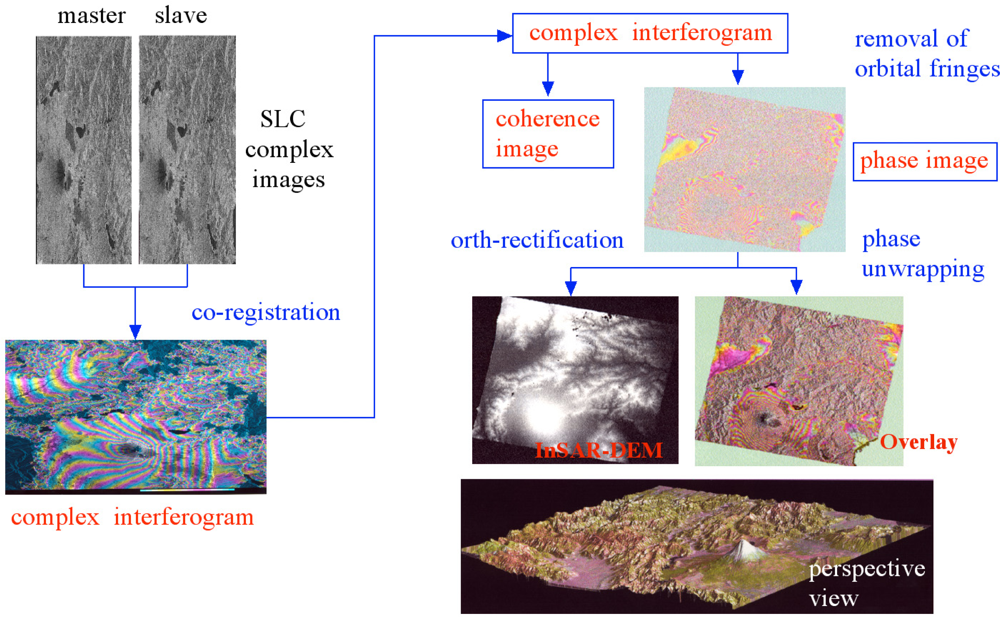
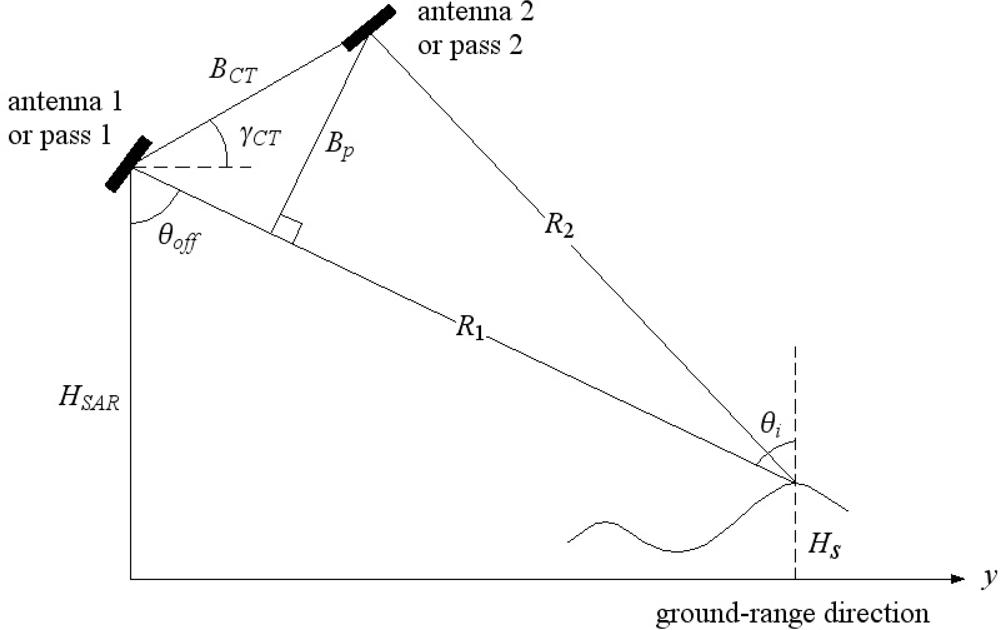
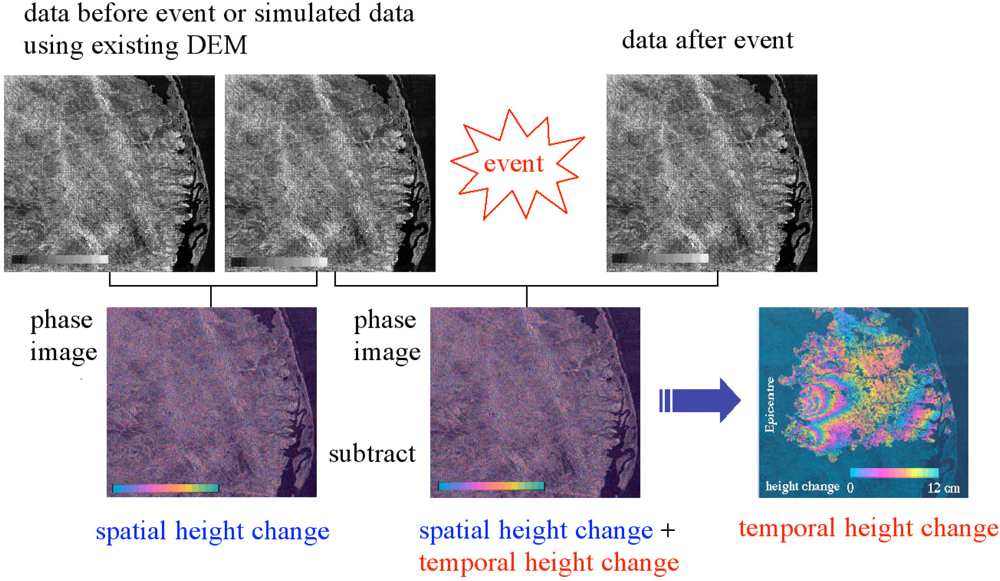

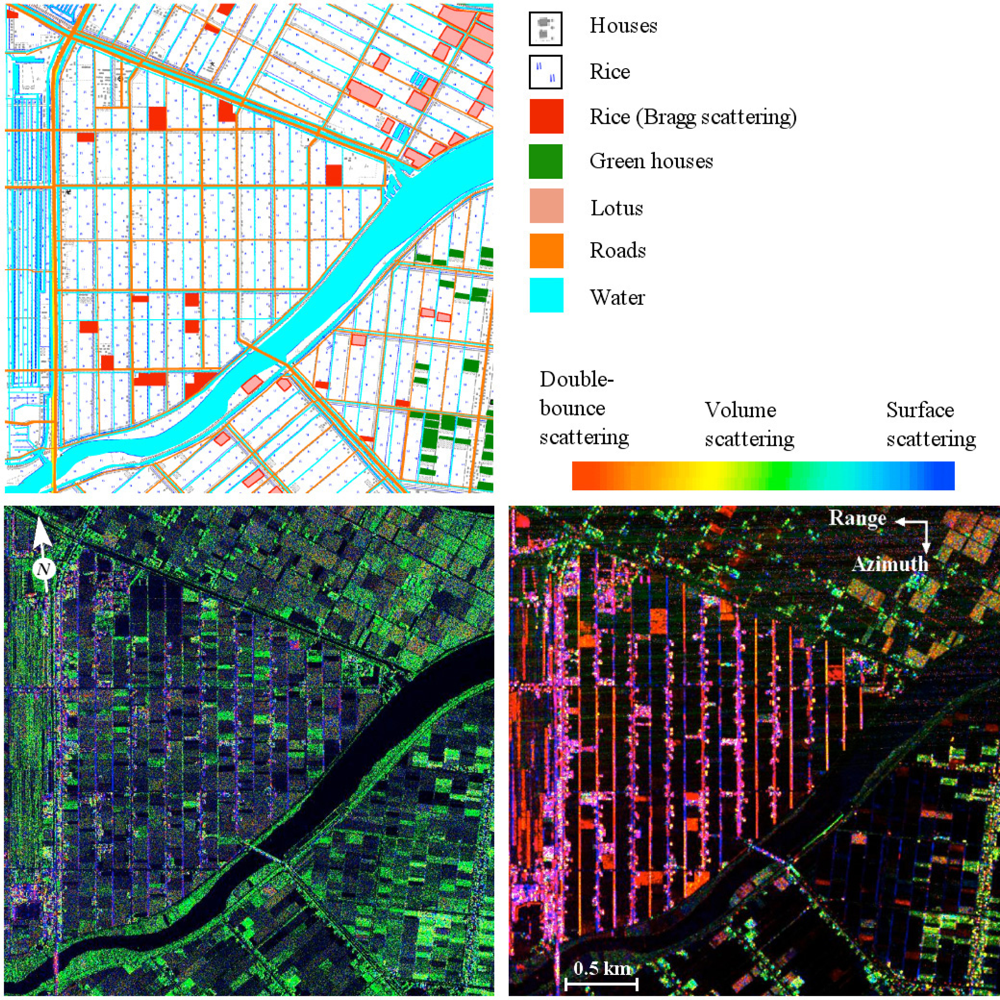


| Fields | Objects |
|---|---|
| Geology | topography, DEM & DSM production, crust movement, faults, GIS, soil structure, lithology, underground resources |
| Agriculture | crop classification, plantation acreage, growth, harvest & disaster, soil moisture |
| Forestry | tree biomass, height, species, plantation & deforestation, forest fire monitoring |
| Hydrology | soil moisture, wetland, drainage pattern, river flow, water equivalent snow & ice water cycle, water resources in desert |
| Urban | urban structure & density, change detection, subsidence, urbanization, skyscraper height estimation, traffic monitoring |
| Disaster | prediction, lifeline search, monitoring of damage & recovery, tsunami & high tide landslide & subsidence by earthquake, volcano & groundwater extraction |
| Oceanography | ocean waves, internal waves, wind, ship detection, identification & navigation, currents, front, circulation, oil slick, offshore oil field, bottom topography |
| Cryosphere | classification, distribution & changes of ice & snow on land, sea & lake, ice age, equivalent water, glacier flow, iceberg tracking, ship navigation in sea ice |
| Archeology | exploration of aboveground and underground remains, survey, management |
| Satellite | Agency/Country | Year | Band | Resolution | Polarization | Weight |
|---|---|---|---|---|---|---|
| SEASAT-SAR | NASA/USA | 1978 | L | 6, 25 | HH | 2,290 |
| SIR-A1 | NASA/USA | 1981 | L | 7, 25 | HH | |
| SIR-B1 | NASA/USA | 1984 | L | 6, 13 | HH | |
| ERS-1/2 | ESA | 1991/1995 | C | 5, 25 | VV | 2,400 |
| ALMAZ-1 | USSR | 1991 | S | 8, 15 | HH | 3,420 |
| HH | (payload) | |||||
| JERS-1 SAR | NASDA/Japan | 1992 | L | 6, 18 | HH | 1,400 |
| NASA/USA | C/L | 7.5, 13 | quad | 11,000 | ||
| SIR-C/X-SAR1 | DLR/Germany | 1994 | X | 6, 10 | VV | (approx.) |
| ASI/Italy | ||||||
| RADARSAT-1 | CSA/Canada | 1995 | C | 8, 8 | HH | 3,000 |
| SRTM1 | NASA/USA | 2000 | C | 15, 8 | dual | 13,600 |
| DLR/Germany | X | 8, 19 | VV | (payload) | ||
| ENVISAT-ASAR | ESA | 2002 | C | 10, 30 | dual | 8,211 |
| ALOS-PALSAR | JAXA/Japan | 2006 | L | 5, 10 | quad | 3,850 |
| SAR-Lupe (5) | Germany | 2006–2008 | X | 0.5, 0.5 | quad | 770 |
| RARDASAT-2 | CSA/Canada | 2007 | C | 3, 3 | quad | 2,200 |
| Cosmo-SkyMed (4) | ASI/Italy | 2007–2010 | X | 1, 1 | quad | 1,700 |
| TerraSAR-X | DLR/Germany | 2007 | X | 1, 1 | quad | 1,230 |
| TanDEM-X | DLR/Germany | 2009 | X | 1, 1 | quad | 1,230 |
| RISAT-1 | ISRO/India | 2012 | C | 3, 3 | dual | 1,858 |
| HJ-1-C | China | 2012 | S | 5, 20 | VV | N/A |
1Shuttle-borne SAR.
| Sensor | Agency/Counry | Band | Resolution |
|---|---|---|---|
| C/X-SAR | CCRS/Canada | X/C | 0.9, 6 |
| AIRSAR | NASA/USA | C/X/L | 0.6, 3 |
| E-SAR | DLR/Germany | X/C/S/L/P | 0.3, 1 |
| F-SAR | DLR/Germany | X/C/S/L/P | 0.3, 0.2 |
| Pi-SAR | NICT, JAXA/Japan | X/L | 0.37, 3 |
| EMISAR | DCRS/Denmark | C/L | 2, 2 |
| PHARUS | TNO-FEL/Netherland | C | 1, 3 |
| Ingara | DSTO/Australia | X | 0.15, 0.3 |
| RAMSES | ONERA/France | W/Ka/Ku/X/C/S/L/P | 0.12, 0.12 |
| CALABAS | FOA/Sewden | HF/VHF | 3, 3 |
| DBSAR | NASA/USA | L | 10, 10 |
| UAVSAR | NASA/USA | L | 1.0, 1.8 |
| Lynx | Sandia/USA | Ku | 0.1, 0.1 |
| Platform | Agency/Country | Band | Azimuth, Range Resolution (m) |
|---|---|---|---|
| Lynx on Predator | Sandia/USA | Ku | 0.1, 0.1 |
| Global Hawk | Northrop Grumman/USA | X | 1.8, 1.8 |
| MiniSAR | Sandia/USA | Ka, Ku, X | 0.1, 0.1 |
| LiMIT | MIT Lincoln Lab./USA | X | < 1, < 1 |
| CP-140 Spotlight SAR | Lockheed Martin/Canada | X | < 1, < 1 |
| I-MASTER | Thales-Astrium/UK | Ku | < 1, < 1 |
| Mini-SAR | Netherlands, TNO/The Netherland | X | 0.05. 0.05 |
| PAMIR | FHR-FGAN/Germany | X | 0.1, 0.1 |
| Requirement | Specification | DTED-2 | HRTI-3 |
|---|---|---|---|
| Relative vertical accuracy | 90% linear point-to-point | 12 m (slope < 20%) | 2 m (slope < 20%) |
| error over a 1° × 1° cell | 15 m (slope > 20%) | 4 m (slope > 20%) | |
| Absolute vertical accuracy | 90% linear error | 18 m | 10 m |
| Relative horizontal | 90% circular error | 15 m | 3 m |
| Horizontal accuracy | 90% circular error | 23 m | 10 m |
| Spatial resolution | independent pixels | 30 m (1 arc sec at equator) | 12 m (0.4 arc sec at equator) |
Share and Cite
Ouchi, K. Recent Trend and Advance of Synthetic Aperture Radar with Selected Topics. Remote Sens. 2013, 5, 716-807. https://doi.org/10.3390/rs5020716
Ouchi K. Recent Trend and Advance of Synthetic Aperture Radar with Selected Topics. Remote Sensing. 2013; 5(2):716-807. https://doi.org/10.3390/rs5020716
Chicago/Turabian StyleOuchi, Kazuo. 2013. "Recent Trend and Advance of Synthetic Aperture Radar with Selected Topics" Remote Sensing 5, no. 2: 716-807. https://doi.org/10.3390/rs5020716
APA StyleOuchi, K. (2013). Recent Trend and Advance of Synthetic Aperture Radar with Selected Topics. Remote Sensing, 5(2), 716-807. https://doi.org/10.3390/rs5020716




