Remote Sensing-Based Fractal Analysis and Scale Dependence Associated with Forest Fragmentation in an Amazon Tri‑National Frontier
Abstract
: In the Amazon, the development and paving of roads connects regions and peoples, and over time can form dense and recursive networks, which often serve as nodes for continued development. These developed areas exhibit robust fractal structures that could potentially link their spatial patterns with deforestation processes. Fractal dimension is commonly used to describe the growth trajectory of such fractal structures and their spatial-filling capacities. Focusing on a tri-national frontier region, we applied a box-counting method to calculate the fractal dimension of the developed areas in the Peruvian state of Madre de Dios, Acre in Brazil, and the department of Pando in Bolivia, from 1986 through 2010. The results indicate that development has expanded in all three regions with declining forest cover over time, but with different patterns and rates in each country. Such differences were summarized within a proposed framework to indicate deforestation progress/level, which can be used to understand and regulate deforestation and its evolution in time. In addition, the role and influence of scale was also assessed, and we found local fractal dimensions are not invariant at different spatial scales and thus concluded such scale-dependent features of fragmentation patterns are here mainly shaped by the road paving.1. Introduction
Land use and land cover changes are occurring globally and at increasingly unprecedented rates, impacting almost all major biomes worldwide [1,2]. Significant attention has been drawn to areas of tropical forest cover, and specifically the Amazon region across the past few decades due to the alarming rates of clearing which have been occurring in the Amazon region [3–13]. Such losses have profound impacts on biodiversity, global carbon storage, potential future and current climate changes, all of which have significant impacts on the resilience of social-ecological systems [14]. As such, understanding the process of deforestation and the pattern of development is key in this critical ecosystem.
This human-induced alteration may also signal an impending ecological meltdown [15], that is, for example, the loss of predator stimulates the disproportionate increase of prey and dramatic reduction of seedlings and saplings of canopy tree, and sometimes ends in biodiversity loss or even a biotic collapse [16–18]. Restoring such a deforested landscape may require drastic and rather expensive intervention [19] due to positive feedbacks that tend to stabilize the new situations [20]. For example, if the trees are removed, evapotranspiration of moisture from the canopy/vegetation back to the atmosphere is reduced; as such more solar energy goes into the heating of the land, less into evapotranspiration, resulting in a warmer and drier environment [21]. Thus, neglect of the possibility of shifts to alternative stable states in ecosystems may severely damage both social and ecological systems. To prevent such surprising or discontinuous shifts in disturbed systems, it is necessary to study system dynamics comprehensively, starting with the actual pattern and formation of the vegetation cover itself: Specifically, to address land cover conversion rates and patterns of such changes, in an attempt to better understand the underlying mechanisms and to prevent potentially disastrous conversions.
Concentrating on land cover changes and related problems, there is a large literature accumulated in the past several decades [22–25]. Land-cover changes often exhibit high degrees of spatial and temporal complexity, and the examination of land-cover change trajectories can be used to capture this complexity [26]. Landscape ecology emphasizes the interactions between spatial pattern and ecological process, that is, the spatial heterogeneity across a range of scales [27]. In the forest landscape, the same amount of forest cover area could exhibit different spatial arrangements [28,29] and forest patterns affect the spatial patterning of all components of the system [30]. Window analysis with designed convolution kernels has been widely applied to measure land cover pattern changes between time lags [31–35]. Alternatively, buffer analysis can be used to calculate land cover pattern changes but along multiple distance lags [12,36,37]. However, window analysis cannot capture the detailed information as the kernel operation blurs the images inevitably, and likewise, buffer analysis cannot characterize the spatial patterns within each buffer zone.
We propose fractal geometry as a powerful quantitative approach to describe such spatial patterns and their dynamics during the deforestation process. This is because most objects in the real world are not regular geometric shapes of the standard geometry derived from Euclid and thus fractal geometry is introduced complementarily to solve this exceptional characteristic of nature.
Fractal analysis has been used to study complex structures for years [38,39], and there have been many analyses using fractals to understand landscape problems [40], such as animal movement, urban development, and forest management [41–44]. Fractal structures have been observed in the patterns of surface growth [45], like forest fragmentation, hence we will apply fractal analysis in this research to study the deforestation patterns around a tri-national frontier in Brazil, Bolivia and Peru, where extensive road development and paving has been occurring. Specifically the three regions exhibit a pathway of development from most developed (Brazil) to developing (Peru) and currently much less developed (Bolivia). This therefore provides an ideal study area for an examination of the spatial mosaics of the deforestation-development process linked to the drivers of road development and paving, agricultural expansion and colonization and national versus regional policies. The research will address how these three regions, while spatially contiguous, have (i) had differing patterns of forest fragmentation across the past three decades; (ii) how time-series fractal dimensions can be used to link spatial patterns with deforestation processes related to patterns and rates of change across these regions; and (iii) the role of scale in the use of time-series fractal dimensions.
2. Data and Method
2.1. Study Area
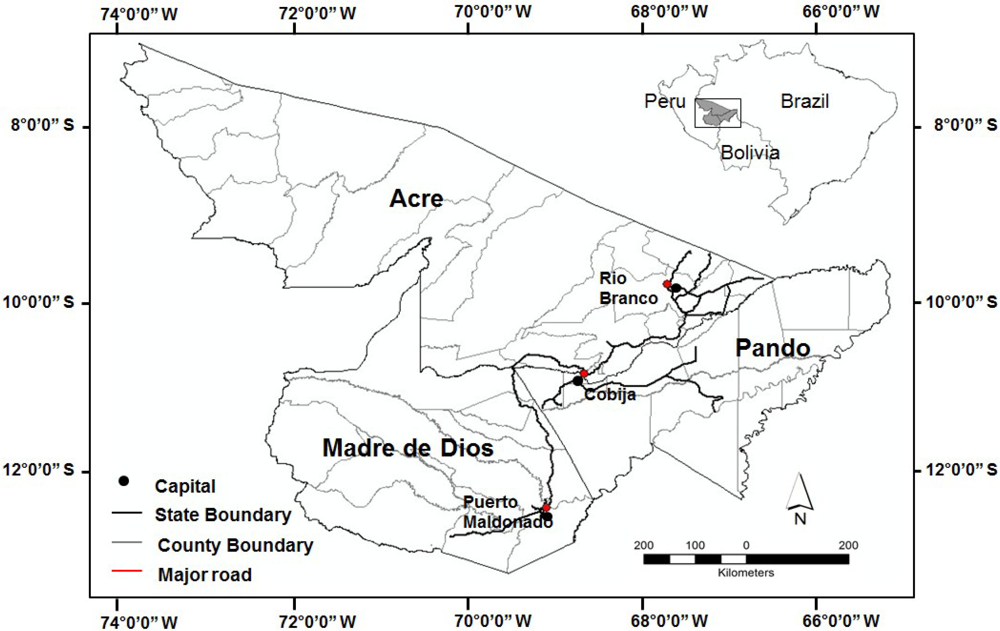
The study area is a tri-national frontier in the southwestern Amazon, where the Peruvian state Madre de Dios, Acre in Brazil, and the Bolivian department of Pando meet (termed the ‘MAP’ region, Figure 1).
This tri-national frontier was historically covered by humid tropical forest, and remains roughly 90% forested. MAP is a relatively remote area in all three countries, and is characterized by a combination of rich natural resources and low incomes. The construction of the Inter-Oceanic highway connects central Brazil with the Pacific ports in Peru and in many ways, symbols the end of the relative isolation of this part of the Amazon. Road paving is likely to bring rapid changes in land use and livelihoods, with the potential prospect of substantial forest and biodiversity loss, changes in land tenure, and unsustainable livelihoods. Specifically, forest fragmentation occurs along the road and will probably continue expanding, and as described previously fragmentation patterns can influence many processes that are ecologically important [46]. The paving in the MAP region is extensive and so took a number of years to be completed, even though it was undertaken in sections. The paving of the road in Acre was completed in 2002, and the paving in Madre de Dios began in the mid 2000’s and is now completed, while the road in Pando is not paved. As such the changes really flowed in sections across this landscape and as the plans were public there was a great deal of prospecting of land (clearing lots along the future paved route) ahead of the road paving. So that changes occurred in advance of the road in many places, not just post-paving [13].
2.2. Remote Sensing Analysis of Forest Cover Change
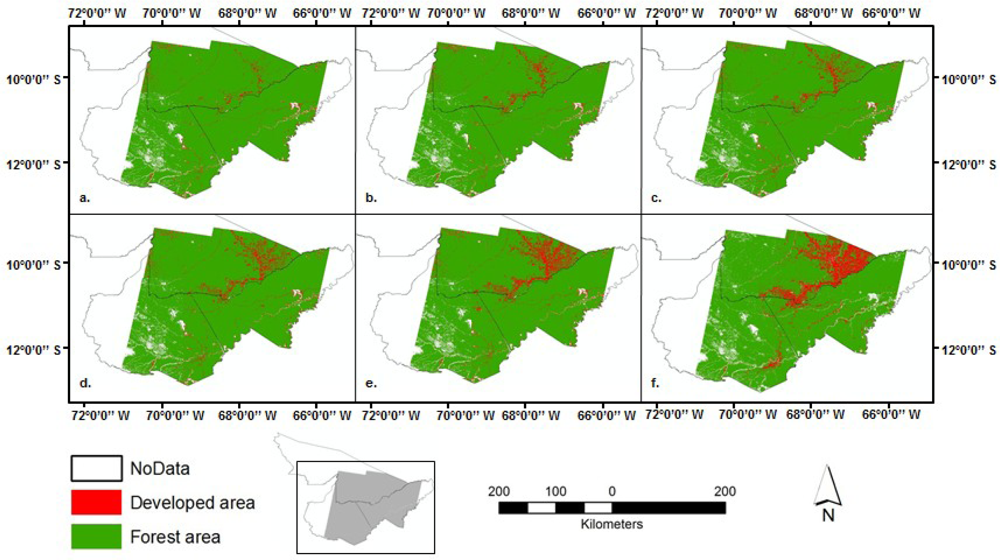
Time-series of classified satellite images can reflect the change trajectories of forest cover, forest area, and their associated fragmentation patterns [47]. In the MAP region, we generate forest/non-forest maps with 30 meter resolution from Landsat TM 4, 5 and ETM+ 7 images across six near-anniversary months, with less than 10% cloud cover (May to October 1986-1991-1996-2000-2005-2010, corresponding to the dry season that permits minimal cloud cover and lower aerosol concentrations). The forest class includes all dense vegetated covers, which by default would include secondary succession as a cover type once a dense canopy was achieved, and non-forest class includes agriculture, agro-forestry areas, cleared areas, major roads, urban fabrics, and shrub (Figure 2). For each image, we performed image registration, calibration, and atmospheric corrections, and undertook a decision tree supervised classification. To create the decision rules, the data mining software Compumine (Compumine AB, Uppsala, Sweden) predicts user specified classes based on recursive partitioning of the input data that result in a decision tree based on variable importance. A split sample validation was used for the training sample points whereby 85% were used to train or create the decision tree and 15% were used to test the tree. The rules, once developed and tested for accuracy (each year was analysed separately and percentage accuracy of the rules were 98%–99.8% accurate, see [12] for more detailed information) were then incorporated into the ERDAS Knowledge Engineer rule-based classifier to create each year’s land cover classifications. We assessed the classification accuracy using over 350 training samples collected during fieldwork from 2005 to 2006 and Kappa coefficient and overall percent accuracy for each class and for the overall classification, with resulting accuracies for 2005 exceeds 90%. We also checked the 2000 image data using ASTER images for the year 2000, and an overall accuracy of 96% was achieved across our products. For 2010 data, Google Earth is used to check the results, where the overall accuracy reached 95% for the entire MAP region.
Additionally, in this research the uncertainties are areas where there may be error, misinterpretations. So accuracy of remote sensed data across dates will bring in some uncertainties into this, for example, we created the classifications, each having different accuracy levels. Other uncertainties may occur with timing, as we used set dates at approximately 5-year intervals but perhaps this missed some key events which occurred between dates and we did not pick those up.
2.3. Fractal Dimension
A fractal structure is self-similar if it looks like itself at different scales [38,39] and can be described by a scaling law. Consider an object in Euclidean dimension D, if we reduce its linear size by 1/r in each spatial direction, its measure (length, area, or volume) would increase to N = rD times the original. Next, taking the log of both sides, log (N) = D log (r), and solving for D, we have Equation (1)
In a 2-dimensional plane, the fractal dimension has been characterized as a measure of the space-filling capacity of certain patterns. For instance, for an object residing in a 2-dimensional plane, the more it fills a plane, the closer it approaches the dimension 2. In addition, values of less than 1 are also possible, indicating very small and isolated objects occurring across the 2-dimensional plane. As the value increases the size of the objects increases and also their consolidation with each other such that as we approach the maximum values (2 would be an absolute maximum, but generally the range 1.8–2 approaches this maximum) we are often looking at very consolidated, compact regions [49].
2.4. Box-Counting Fractal Dimension
To characterize the fractals, a box counting method is used to calculate the capacity dimension, which is geometrically based on the recursive subdivision of space [50] and the cascade structure of hierarchies [51]. The procedure is simple: we cover the target object with square, non-overlapping boxes of size r2 and repeat the procedure using a range of r values. The target object here is the cleared area and as the value approaches 2, it is indicating larger clearings. The values of r could range from the minimal rm, corresponding to the image resolution, to the maximal value rM, corresponding to the entire image size. For each r ε (rm, rM), the number of boxes N containing at least one point of the target object will be counted. Based on Equation (1), we can calculate the fractal dimension D [52]. In practice, box-counting is modified to grid-counting with the same procedures, but squares are replaced by rectangles.
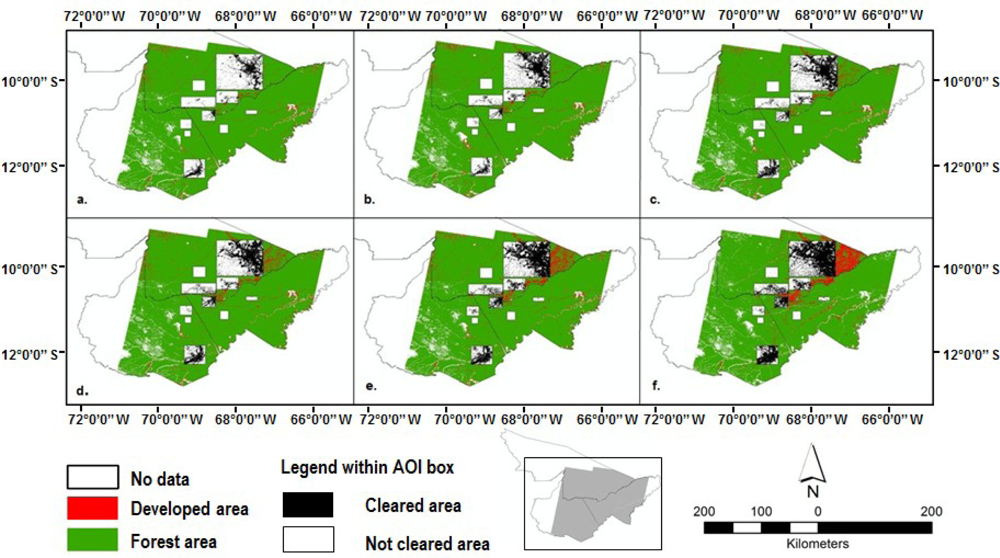
Not like other study objects, such as limnology, finding clear and applicable boundaries for many terrestrial problems are difficult. Neither political boundaries nor watersheds are absolutely proper. In the MAP region, Rio Branco (capital of Acre state, Brazil), Puerto Maldonado (capital of Madre de Dios, Peru), and Cobija (capital of Pando, Bolivia) are three regions with highly developed areas. Three ‘area of interest’ (AOI) boxes were drawn around them to encompass the core areas, on the land cover map of the year 2010 (see Figure 3 for box locations). Additional AOIs were also drawn in areas in-between these three major regions, along a continuum of development and also along the road features given these are considered to be the major conduits for development [8,9,53]. This resulted in an additional box each in Peru and Bolivia showing this intermediate development rate and 2 additional boxes in Brazil, where development has been occurring for longer and so is represented in a continuum of three boxes. In addition, for each country a final AOI was drawn that was as close to a control or undeveloped (forested) region as possible, i.e., it was in an area of the least land cover change possible. As such this would allow for a contrast in values in terms of the developed and forested landscapes, but also show change across time for all these regions—across the continuum of development, for each of the three countries. The sizes of AOI boxes are not the same, as the areas are different, but the relative dimension values along the time axis should be able to explain the evolutionary features of the development in each of the areas. Moreover, even though the box sizes are different, the fractal dimensions calculated can still provide reference to compare the deforestation processes underway in each of the areas. As such, this research will allow for a truly comparative analysis, using AOIs of varying locations, rates of development and also size.
2.5. Fractal Dimension Calculation of AOIs
Next, a series of grids are generated within each rectangle AOI box by recursive steps, and the size of grid is taken as r = 1/(2n), where n is an integer ranging from 1 to 9 and r = 1/(29) or 1/512 is set as the finest grid with the consideration that 1/512 of the AOI box is small enough to approximate the target feature and thus to make stable calculations. Then, developed areas for the years 1986, 1991, 1996, 2000, 2005, and 2010 are intersected with the generated grids to count non-empty grids N. Finally, the estimation of the linear regression of log (N) = D log (r) + A is implemented in R (the R foundation for Statistical Computing), where A is a constant and was forced to be zero in the calculation and the coefficient D, R-squared, and standard error δ are calculated.
In addition, to address the impact of AOI scale on fractal dimension results, we divide one AOI box around Rio Branco (A1 in Figure 3) into quarters and re-run the same procedure described to calculate the fractal dimension at lower levels within each quarter. The methodology applied is identical but on the new “quarters” and then the results can be compared.
3. Results
3.1. Forest Fragmentation and Spatial Patterns across the Larger Study Region
Over the past 25 years, we observed an increase in non-forest area for all three states (Acre, Madre de Dios, and Pando), at the expense of forest areas, while our results across all three regions reveal a landscape still dominated by forest cover up until 2010 with Acre at 80%, Madre de Dios at 97.4%, and Pando at 98%, forest cover remaining (where 1% represents approximately 620 km2 in Acre, 495 km2 in Madre de Dios, and 545 km2 in Pando; Table 1). Road building plays a determined role in this process [8,9,12,53], where forest fragmentation occurs along major roads and will probably continue expanding. Therefore, we focused the analysis at the local level and emphasized deforestation dynamics in the selected AOI boxes (Figure 4). Visually, the growth of the developed areas appears to be recursive patterns embedded at different scales, whose evolutionary features emerge to be fractal-like structures and thus among the landscape metrics, fractal dimension calculated by this box-counting method could be a useful measure to describe such patterns.
3.2. Area and Rates of Development within AOIs
The most intensive deforestation areas were highlighted in AOI boxes from 1986 to 2010 (Figure 4), in which the most developed areas (box 1 in each state), the three capital cities can be viewed first. Rio Branco expands rapidly from 4.8% in 1986 to 34.8% in 2010, while the growth of the developed area around Puerto Maldonado is much slower with a change from 4.5% in 1986 to 14% in 2010, Cobija falls between these two with a change from 3.8% in 1986 to 28% in 2010 (Table 1). Likewise, the developed areas in boxes 2 and 3 of Acre, box 2 of Madre de Dios, and box 2 of Pando all experience significant increases in clearing. For Acre, box 2 changes from 9.7% in 1986 to 34.2% in 2010 and box 3 changes from 3.6% in 1986 to 32.3% in 2010. Again Acre rates of change are the highest for the region under study. In comparison, Madre de Dios box 2 changes from 1.1% in 1986 to 9.6% in 2010, and Pando box 2 changes from 0.1% in 1986 to 8.7% in 2010. Due to policy changes [13] there were slightly more variable land cover changes in Madre de Dios box 2, and a brief respite from clearing with some reforestation occurring, during the time-series. This was quite unique to this region and is not seen in the other two regions, where those polices were not in place. Illustrating this trend is linked to roads and urban centre locations; each region also had a ‘control’ or an area where change in forest cover was minimal due to its location away from roads and towns. These controls all reveal similar patterns over time, although again, Acre does have the highest rates of change, although they are small in comparison with the changes in AOI boxes 1–3. Acre’s control box changes from 0.1% in 1986 to 1.5% which contrasts significantly with the previously discussed box regions in Acre, all of which over 30% are developed by 2010. The control areas in Pando and Madre de Dios have very little change, starting at 0.03% and 0.02% respectively in 1986 and changing to only 0.5% by 2010. It does appear that much of these landscapes at distance from roads and towns is indeed still dominated by forest cover. As such, it is not only the amount of change, but rather its spatial organization and pattern that become key. Hence, the use of fractal analysis can characterize these spatial patterns over time and relate these potential changes in spatial arrangements to important social-ecological change in the landscape.
3.3. Fractal Dimensions of Change in Each AOI
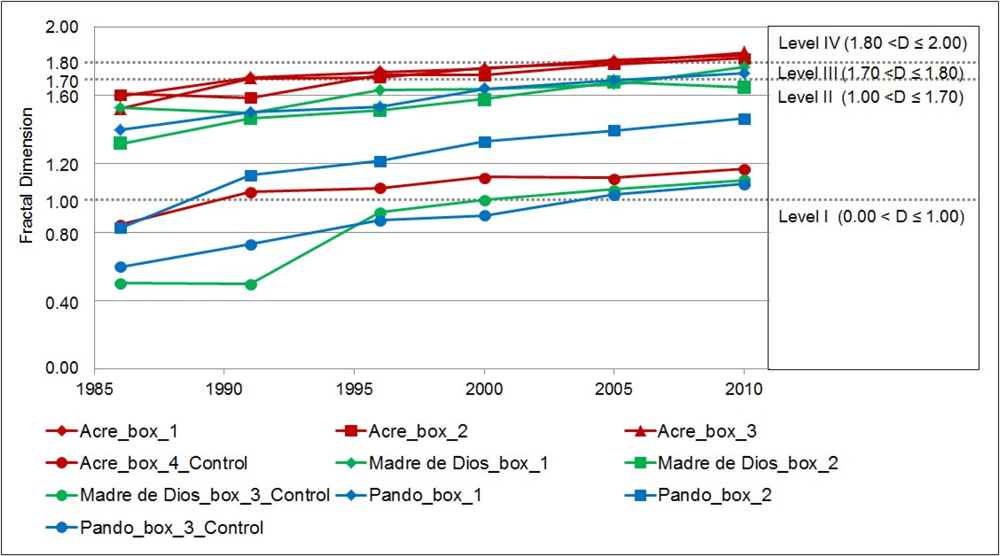
The fractal dimensions for the developed areas within each of the AOI boxes are calculated and summarized in Table 2 and Figure. 5. The estimated dimensions D are non-integer but fractional, which indicate that the developed areas exhibit fractal characteristic in a mathematical case, and the results of goodness-of-fit test: large R-square and small stand errors, also suggest a fractal property. Based on Encarnação et al.[49] we can interpret urbanization as a development process globally, using their baseline fractal dimensions such that different levels of development emerge (Figure 5). For our study region then, in an attempt to interpret deforestation as a development process, we propose four levels of development: level I (D ≤ 1), cleared areas are very small and dispersed and do not show any spatial structure, and from this point forward (D > 1) we found areas with linear spatial organization as for example some cleared areas that grow along roads; level II (1< D ≤ 1.70), clearings start to grow, from quite dispersed to clumped, where D = 1.70 is a worldwide average of urban build-up areas [51,54]. Particularly, Chen [55,56] gives additional theoretical support to this average value by employing the wave-spectrum analysis, where the closer the fractal dimension is to 1.70, the better estimated the results will be. Finally we arbitrarily choose D = 1.80 to divide level III (1.70 < D ≤ 1.80) and level IV (1.80 < D ≤ 2.00), as we observed clump consolidation takes place rapidly in level III and appears to be consolidated regions of clearings mostly in level IV. Using this framework of analysis, purported for all global studies we can thus compare our regions both with each other but also with a global model of urbanization form and development.
The fractal dimensions among the three states keep increasing monotonically from 1986 to 2010 (Figure 5). In Acre, the fractal dimensions of box 1 change from 1.59 in 1986 to 1.83 in 2010, box 2 changes from 1.61 in 1986 to 1.82 in 2010, and box 3 changes from 1.52 in 1986 to 1.85 in 2010. All boxes end above 1.80 by 2010, and this relatively high value, representing urbanization in level IV with very high levels of consolidation of clearings, is quite close to the maximum value of 2, and reveals that there is a strong spatial-filling capacity of the developed areas occurring within all three boxes. For Madre de Dios, the fractal dimensions of box 1 change from 1.53 in 1986 to 1.77 by 2010 and box 2 changes from 1.32 in 1986 to 1.64 by 2010. In Pando the fractal dimensions of box 1 change from 1.40 in 1986 to 1.73 by 2010 and box 2 changes from 0.82 in 1986 to 1.47 by 2010. While the fractal dimensions in Madre de Dios and Pando are lower than those of Acre, they are still exhibiting in-filling of developed areas with the most developed boxes entering level II of development by 2010, but the box 2’s still being located in level II. This does illustrate that these capital areas are developing at a faster rate in terms of urbanization and land clearing, and clump consolidation has occurred across all these box 1’s by 2010. Areas further from these regions, but still along the roads are also increasing their clearings but not yet at the higher levels of urbanization as representing by the four levels presented here.
In Figure 5, boxes 1, 2, and 3 in Acre all increase from level II in 1986 into level IV in 2010, while box 1 in Madre de Dios and box 1 in Pando both enter level III by 2010. Box 2 in Madre de Dios stays in level II over the study period, and box 3 in Pando increases from level I to level II. The differing urbanization rates really correspond well to the rates of forest clearing and development across these three countries and with increasing distance from urban centers. It is worth noting that similar values of the fractal dimension for the different AOI’s (as shown in Table 2 and Figure 5) correspond to quite different values of the developed area changes (as shown in Table 1). This is because if a small fraction of a pixel was occupied by developed areas, this pixel was counted as one non-empty pixel, that is, if there is any developed land within the AOI box then it is counted as a developed pixel. While if the entire pixel was occupied by the developed areas, this pixel was still counted as one non-empty pixel, so that the same fractal dimension could have different areas, and vice versa. Encarnação et al.[49] provide proof to support this process as fractal dimension is a measure of space-filling capacity, not a measure of area. In addition, to emphasize the scaling relations between the scale (linear size) and the corresponding measure (length, area, or volume) or the fractal properties of a system, the typical log-log plots (double logarithmic plots) of scaling relations of developed areas in AOI box 1 in Acre, Brazil from 1986 to 2010 were provided in Figure 6. The straight-line segment on the double logarithmic plot is what is called the ‘scaling range’. There is no significant difference between the trend line of the scaling range and that of all the point displayed in Figure 6.
The fractal dimensions of the three control boxes in each state were also calculated. Logically, due to little or very small, cleared areas, all the fractal dimensions of Acre (from 0.84 in 1986 to 1.17 in 2010), Madre de Dios (from 0.50 in 1986 to 1.11 in 2010), and Pando (from 0.60 in 1986 to 1.08 in 2010) started from values below level I and ended just barely into level II, indicating the initiation of development, even in these control regions. This highlights that these regions are still forest dominated landscapes but that even here, we see an increase in clearing and resultant fragmentation being initiated, but so far only at a small scale (Figure 5). This is of course, a precursor to likely continued change and further clearing and development processes.
3.4. Impact of Box Scale of AOIs on Fractal Calculations
This region emphasizes the relative fractal value along a time axis within each study box, not the exact value, and the size and location of the box will affect the fractal value. The distribution of the developed areas in each AOI box is however, not uniform, but rather developed outwards along the roads. To better understand the impact of box location and size on the results, a smaller study was undertaken on AOI Box 1 centered on Rio Branco in Acre, Brazil (Figure 6, Table 3) the most developed region within our study landscape with a fractal dimension increasing from 1.59 in 1986 to 1.83 in 2010. As roads have not stretched to the southwest quadrant of AOI box 1, the fractal object or developed area is still in the early stage of its growth process (fractal dimension is low in this SW quadrant of AOI box 1) as represented by a change in fractal dimension from 1.02 in 1986 to 1.49 in 2010. On the contrary, in Rio Branco, located in the southeast and northeast quadrants of AOI box 1, the road paving stimulated the expansion of the developed area, and therefore the fractal dimensions within the SE and NE quadrants of AOI box 1 are much larger, as illustrated by changes from 1.62 and 1.67 in 1986 to 1.88 and 1.89 in 2010, respectively. The northwest quadrant of AOI box 1 does include a small road segment and so the change over time as more development occurs along this region is significant, and is indicated by a fractal dimension of 1.32 in 1986 increasing to 1.80 in 2010 due to the infilling of urban development within this sector.
The results of this smaller calculation reveal that forest fragmentation is not evenly distributed, but occurs intensively in certain directions and along some features, such as roads. From Table 3, and due to the landscape heterogeneity, in the real world fractal dimensions are not invariant at different scales, and such scale-dependent features in the MAP region are mainly shaped by the road paving.
4. Discussion
Amazon deforestation has often been seen as the most prominent galvanizing image of environmental change during the last several decades, and thus it is not easy to position this research within the literature. Focusing on the MAP region, however, Peralta and Mather [60] interpreted multi-temporal forest/non-forest maps in Acre and then calculated landscape metrics to characterize the impacts of social and economic processes on the development of the forest landscape. Millington et al.[61] measured different spatial patterns of forest fragmentation in Bolivia, and explained these patterns with reference to specific government policies. Moreover, their results also indicated that most landscape metrics were highly dependent on pixel size. Similarly, Bradley and Millington [62] discussed the mismatch between the spatial scale of biomass burning and the satellite products in Bolivia and Peru and found that an entire component of the fire region in the study region is omitted, despite its importance in the farming systems.
The MAP region provides an ideal case for study because it contains high ecological and cultural diversity, while entering a period of rapid change triggered by the paving of the Inter-Oceanic highway. The road paving in Brazil has been completed to the Peruvian and Bolivian borders, which has greatly stimulated local economic development. New legislation for logging concessions in Peru and Bolivia has fostered increased logging, and consequently, land values have risen [57]. However, this tri-national frontier is still largely forested and has been designated a global biodiversity hotspot [58]. If we calculate the developed areas at the whole MAP region level, the fractal dimensions of such discretely developed areas will be extremely low and meaningless (like an amplified control box).
To access the natural resources, the paving of major roads stimulate the construction of secondary and tertiary level roads, as well as ‘unofficial’, often temporary logging roads which continue to be used well after initial creation and often become permanent landscape features [8,9]. These roads form dense and hierarchical networks where the land cover changes along them exhibit some recursive structures. On the other hand, the three sides of the MAP region share the same borders, but the deforestation processes are quite different. Again, the locations of the AOI boxes affect the absolute dimension values, but these relative values are able to reflect the fractal changes over time. With the support from long-term research conducted in the MAP region [13,59], the forest/non-forest datasets cover a 25-year time span with relatively uniform temporal intervals, and such consistent records of land surface events provide a very useful and consistent means for monitoring forest dynamics across improved spatial and temporal scales.
5. Conclusion
There is no single correct scale or level at which to describe a system, nor does that mean all scales serve equally well [63]. Depending on the research objects, there are many different interpretations of the term ‘scale’. For example, from a wildlife perspective, each organism scales the environment differently, and thus there is no absolute size for a landscape. Or, from an abiotic perspective, the disparity between political boundaries (ranging from basic communities to whole countries) and other physically existing boundaries (like watershed) makes it difficult to communicate, study, and even more difficult to establish consistent management policies.
The recently proposed global model of urbanization allows us to compare our stages of development to other more developed urban regions and to position our study boxes within this larger context [49] which provides and interesting comparative and contextual framework for analysis. Regarding the use of fractal analysis per se, it must be acknowledged that conventional measures use Euclid geometric parameters (e.g., area, perimeter, etc.) to characterize objects, while the dimension of most objects in the real world are not integer. As such the use of fractals better matches the objects under study. One of the exceptional characteristics of fractals is that they can be described by a non-integer dimension. As a standardized value (D: between 1 and 2 or 2 and 3), fractal dimension can be used to describe the geometry and morphology of the target objects, and importantly, to do comparisons both over time and space, as well as to be useful in developing more global models and comparisons [49]. In urban research, fractal dimension can be used to relate size, scale, shape, and density of urban growth including the developed areas in the MAP region and therefore, it has been widely applied in geography and urban planning [64] and based on all of these factors, models can be built (and calibrated) to simulate fractal structures, that can be used for future predictions based on simple rules of land development (e.g., iterated pattern, biotics growth). As such the use of fractal analyses provides a rigorous, comparative framework for better understanding our landscapes and their changes across space and time.
To fully appreciate the consequences of deforestation and to accumulate knowledge for conservation, it is necessary to develop a useful body of theories, methods, and applications to study the composition, configuration, and connectivity of such landscapes, and here fractal analyses provide an alternative way to understand landscape configuration. Deforestation processes exhibit complex spatial patterns, hence, understanding how such spatial patterns relate to these processes that generate such complex patterns is fundamental to landscape analysis. Fractal analysis along a time axis provides a link between the resultant spatial pattern and the underlying deforestation process, because adequately long observation periods can yield significant results to detect fundamental system changes and to support predictions.
The fractal analysis carried out in this paper, though very simple, provides an alternative perspective to the spatial methods devised to date, and given the proposed framework to indicate deforestation progress evolving from highly dispersed clearings occurring in a dominantly forested landscape (level I), to areas where clearing is initiated and forest fragmentation begins (level II), then to a process of increased forest clearings, and where fragmentation converts over to clumping of patches (level III) and then finally into clearing consolidation (level IV) or urbanization consolidation. As such, we were able to define the fragmentation/development level according to fractal dimension and this could be further utilized to provide useful context to conservation and management programs. Development of these ideals and models, such as is presented in Figure 5 and linked to the research of Encarnacao et al.[49] could be further developed and tested, as just one potential indicator of significant landscape changes. This could then serve as one potential precursor or warning to conservation or management groups of the types of changes already in progress, their rates of change and ideally an idea of future trajectories assuming no change in current patterns/trends. Such planning tools seem imperative in these fragile landscapes and biodiversity hotspots.
Acknowledgments
This research was funded as part of an NSF Human and Social Dynamics Program (FY2005) project, entitled “Agents of Change: Infrastructure Change, Human Agency, and Resilience in Social-Ecological Systems” #0527511 and also from NSF Coupled Natural Human Systems #1114924, “Global sensitivity and uncertainty analysis in the evaluation of social-ecological resilience: Theoretical debates over infrastructure impacts on livelihoods and forest change”.
References
- Lambin, E.F.; Geist, H.J. Land-Use and Land Cover Change: Local Processes and Global Impacts; Springer: Berlin, Germany, 2006. [Google Scholar]
- Gutman, G.; Janetos, A.; Justice, C.; Moran, E.; Mustard, J.; Rindfuss, R.; Skole, D.; Turner, B.L. Land Change Science: Observing, Monitoring, and Understanding Trajectories of Change on the Earth’s Surface; Kluwer Academic Publishers: New York, NY, USA, 2004. [Google Scholar]
- Nepstad, D.C.; Verssimo, A.; Alencar, A.; Nobre, C.; Lima, E.; Lefebvre, P.; Schlesinger, P.; Potter, C.; Moutinho, P.; Mendoza, E.; et al. Large-scale impoverishment of Amazonian forests by logging and fire. Nature 1999, 398, 505–508. [Google Scholar]
- Nepstad, D.; Carvalho, G.; Barros, C.A.; Alencar, A.; Capobianco, J.P.; Bishop, J.; Moutinho, P.; Lefebvre, P.; Silva, U.L.; Prins, E. Road paving, fire regime feedbacks, and the future of Amazon forests. Forest Ecol. Manage 2001, 154, 395–407. [Google Scholar]
- Laurance, W.F.; Albernaz, A.K.M.; Da Costa, C. Is deforestation accelerating in the Brazilian Amazon? Environ. Conserv 2001, 28, 305–311. [Google Scholar]
- Laurance, W.F.; Albernaz, A.; Schroth, G.; Fearnside, P.M.; Bergen, S.; Venticinque, E.M.; Costa, C.D. Predictors of deforestation in the Brazilian Amazon. J. Biogeogr 2002, 29, 737–748. [Google Scholar]
- Andersen, L.E.; Granger, C.W.J.; Reis, E.J.; Weinhold, D.; Wunder, S. The Dynamics of Deforestation and Economic Development in the Brazilian Amazon; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Perz, S.G.; Caldas, M.M.; Arima, E.; Walker, R.J. Socio-spatial process of unofficial road building in the Amazon: Socioeconomic and biophysical explanations. Dev. Change 2007, 38, 529–551. [Google Scholar]
- Perz, S.G.; Overdevest, C.; Arima, E.Y.; Caldas, M.M.; Walker, R.J. Unofficial road building in the Brazilian Amazon: dilemmas and models of road governance. Environ. Conserv 2007, 34, 112–121. [Google Scholar]
- Pfaff, A.; Kerr, S.; Lipper, L.; Cavatassi, R.; Davis, B.; Hendy, J.; Sanchez-Azofeifa, G.A. Will buying tropical forest carbon benefit the poor? Evidence from Costa Rica. Land Use Policy 2007, 24, 600–610. [Google Scholar]
- Giles, P.T.; Burgoyne, J.M.; Skole, D.L.; Tucker, C.J. 1993: Tropical deforestation and habitat fragmentation in the Amazon: satellite data from 1978 to 1988. Science, 260, 1905–1910. Progr. Phys. Geogr 2008, 32, 575–580. [Google Scholar]
- Marsik, M.; Stevens, F.; Southworth, J. Amazon deforestation: Rates and patterns of land cover change and fragmentation in Pando, northern Bolivia, 1986 to 2005. Progr. Phys. Geogr 2011, 35, 353–374. [Google Scholar]
- Southworth, J.; Marsik, M.; Qiu, Y.; Perz, S.; Cumming, G.; Stevens, F.; Rocha, K.; Duchelle, A.; Barnes, G. Roads as drivers of change: Trajectories across the Tri-National frontier in MAP, the southwestern Amazon. Remote Sens 2011, 3, 1047–1066. [Google Scholar]
- Cumming, G.S.; Southworth, J.; Rondon, X.J.; Marsik, M. Spatial complexity in fragmenting Amazonian rainforests: Do feedbacks from edge effects push forests towards an ecological threshold? Ecol. Complex 2012, 11, 67–74. [Google Scholar]
- Terborgh, J.; Lopez, L.; Nuñez, P.; Rao, M.; Shahabuddin, G.; Orihuela, G.; Riveros, M.; Ascanio, R.; Adler, G.H.; Lambert, T.D.; et al. Ecological meltdown in Predator-Free forest fragments. Science 2001, 294, 1923–1926. [Google Scholar]
- Wilcox, B.A.; Murphy, D.D. Conservation strategy: The effects of fragmentation on extinction. Am. Nat 1985, 125, 879–887. [Google Scholar]
- Steininger, M.C.; Tucker, C.J.; Townshend, J.R.G.; Killeen, T.J.; Desch, A.; Bell, V.; Ersts, P. Tropical deforestation in the Bolivian Amazon. Environ. Conserv 2001, 28, 127–134. [Google Scholar]
- Nobre, P.; Malagutti, M.; Urbano, D.F.; de Almeida, R.A.F.; Giarolla, E. Amazon deforestation and climate change in a coupled model simulation. J. Clim 2009, 22, 5686–5697. [Google Scholar]
- Mäler, K.G. Development, ecological resources and their management: A study of complex dynamic systems. Eur. Econ. Rev 2000, 44, 645–665. [Google Scholar]
- Scheffer, M.; Carpenter, S.; Foley, J.A.; Folke, C.; Walker, B. Catastrophic shifts in ecosystems. Nature 2001, 413, 591–596. [Google Scholar]
- Wilson, J.B.; Agnew, A.D.Q. Positive-feedback Switches in Plant Communities. Adv. Ecol. Res 1992, 23, 263–336. [Google Scholar]
- Foster, D.R. Land-use history (1730–1990) and vegetation dynamics in central New England, USA. J. Ecol 1992, 80, 753–771. [Google Scholar]
- Houghton, R.A. The worldwide extent of land-use change. BioScience 1994, 44, 305–313. [Google Scholar]
- Chomitz, K.M.; Gray, D.A. Roads, land use, and deforestation: A spatial model applied to Belize. World Bank Econ. Rev 1996, 10, 487–512. [Google Scholar]
- Ramankutty, N.; Foley, J.A. Characterizing patterns of global land use: An analysis of global croplands data. Global Biogeochem. Cy 1998, 12, 667–685. [Google Scholar]
- Mertens, B.; Lambin, E.F. Land-cover-change trajectories in Southern Cameroon. Ann. Assoc. Am. Geogr 2000, 90, 467–494. [Google Scholar]
- Turner, M.; Gardner, R.H.; O’Neill, R.V. Landscape Ecology in Theory and Practice: Pattern and Process; Springer: New York, NY, USA, 2001. [Google Scholar]
- Vogt, P.; Riitters, K.; Estreguil, C.; Kozak, J.; Wade, T.G.; Wickham, J.D. Mapping spatial patterns with morphological image processing. Lands. Ecol 2007, 22, 171–177. [Google Scholar]
- Vogt, P.; Riitters, K.; Iwanowski, M.; Christine, E.; Jacek, K.; Pierre, S. Mapping landscape corridors. Ecol. Indicat 2007, 7, 481–488. [Google Scholar]
- Peterson, G. Forest Dynamics in the Southeastern United States: Managing Multiple Stable States. In Resilience and the Behavior of Large-Scale Systems; Gunderson, L.H., Pritchard, L., Jr., Eds.; Island Press: Washington, DC, USA/Covelo, London, 2002. [Google Scholar]
- Riitters, H.; Wickham, J.D.; O’Neill, R.; Jones, B.; Smith, E. Global-scale patterns of forest fragmentation. Conserv. Ecol 2000, 4, 27–56. [Google Scholar]
- Riitters, H.; Wickham, J.D.; O’Neill, R.V.; Jones, B.K.; Smith, E.R.; Coulston, J.W.; Wade, T.G.; Smith, J.H. Fragmentation of continental United States forests. Ecosystems 2002, 5, 815–822. [Google Scholar]
- Southworth, J.; Cumming, G.S.; Marsik, M.; Binford, M.W. Linking spatial and temporal variation at multiple scales in a heterogeneous landscape. Prof. Geogr 2006, 58, 406–420. [Google Scholar]
- Zurlini, G.; Riitters, K.; Zaccarelli, N.; Petrosillo, I.; Jones, K.; Rossi, L. Disturbance patterns in a socioecological system at multiple scales. Ecol. Complex 2006, 3, 119–128. [Google Scholar]
- Zaccarelli, N.; Petrosillo, I.; Zurlini, G.; Riitters, K. Source/sink patterns of disturbance and cross-scale mismatches in a Panarchy of social-ecological landscapes. Ecol. Soc 2008, 13, 26. [Google Scholar]
- Naughton-Treves, L.; Holland, M.B.; Brandon, K. The role of protected areas in conserving biodiversity and sustaining local livelihoods. Annu. Rev. Environ. Resour 2005, 30, 219–252. [Google Scholar]
- Mehring, M.; Stoll-Kleemann, S. How effective is the buffer zone? Linking institutional processes with satellite images from a case study in the Lore Lindu Forest Biosphere Reserve, Indonesia. Ecol. Soc 2011, 16, 3. [Google Scholar]
- Mandelbrot, B.B. Fractals, Form, Chance and Dimension; W.H. Freeman and Company: San Francisco, CA, USA, 1977. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W.H. Freeman and Company: New York, NY, USA, 1983. [Google Scholar]
- Gardner, R.H. Neutral Models the Analysis of Landscape Structure Modelling Complex Ecological Dynamics. In Modelling Complex Ecological Dynamics; Jopp, F., Reuter, H., Breckling, B., Eds.; Springer Berlin-Heidelberg: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- With, K. Using fractal analysis to assess how species perceive landscape structure. Lands. Ecol 1994, 9, 25–36. [Google Scholar]
- Laidre, K.L.; Heide-Jørgensen, M.P.; Logsdon, M.L.; Hobbs, R.C.; Dietz, R.; VanBlaricom, G.R. Fractal analysis of narwhal space use patterns. Zoology (Jena) 2004, 107, 3–11. [Google Scholar]
- Alados, C.; Pueyo, Y.; Navas, D.; Cabezudo, B.; Gonazales, A.; Freeman, D. Fractal analysis of plant spatial patters: a monitoring tool for vegetation transition shift. Biodivers. Conserv 2005, 14, 1453–1468. [Google Scholar]
- Feng, J.; Chen, Y.G. Spatiotemporal evolution of urban form and land use structure in Hangzhou, China: evidence from fractals. Environ. Plann. B Plann. Des 2010, 37, 838–856. [Google Scholar]
- Barabasi, A.L.; Stanley, H.E. Fractal Concepts in Surface Growth, 1st ed; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Turner, M.G. Landscape ecology: The effect of pattern on process. Annu. Rev. Ecol. Syst 1989, 20, 171–197. [Google Scholar]
- Tole, L. Measurement and management of human-induced patterns of forest fragmentation: a case study. Environ. Manage 2006, 37, 788–801. [Google Scholar]
- Theiler, J. Estimating fractal dimension. J. Opt. Soc.Am. A 1990, 7, 1055–1073. [Google Scholar]
- Encarnação, S.; Gaudiano, M.; Santos, F.; Tenedório, J.; Jorge, M.P. Fractal cartography of urban areas. Scientific Reports 2012. [Google Scholar] [CrossRef]
- Goodchild, M.F.; Mark, D.M. The Fractal nature of geographic phenomena. Ann. Assoc. Am. Geogr 1978, 77, 265–278. [Google Scholar]
- Batty, M.; Longley, P. Fractal Cities; Academic Press: London, UK, 1994. [Google Scholar]
- Solé, R.V.; Bascompte, J. Self-Organization in Complex Ecosystems; Princeton University Press: Princeton, MA, USA, 2006. [Google Scholar]
- Perz, S.G.; Brilhante, S.; Brown, F.; Caldas, M.; Ikeda, S.; Mendoza, E.; Overdevest, C.; Reis, V.; Reyes, J.F.; Rojas, D.; et al. Road building, land use and climate change: Prospects for environmental governance in the Amazon. Phil. Trans. Biol. Sci 2008, 363, 1889–1895. [Google Scholar]
- Alfasi, N.; Portugali, J. Planning just-in-time versus Planning just-in-case. Cities 2004, 21, 29–39. [Google Scholar]
- Chen, Y. Exploring the fractal parameters of urban growth and form with wave-spectrum analysis. Discrete Dynam. Nat. Soc. 2010. [Google Scholar] [CrossRef]
- Chen, Y. Fractal dimension evolution and spatial replacement dynamics of urban growth. Chaos, Soliton. Fract 2012, 45, 115–124. [Google Scholar]
- Wadt, L.H.O.; Kainer, K.A.; Gomes-Silva, D.A.P. Population structure and nut yield of a bertholletia excelsa stand in southwestern Amazonia. Forest Ecol. Manage 2005, 211, 371–384. [Google Scholar]
- Myers, N.; Mittermeier, R.A.; Mittermeier, C.G.; Fonseca, G.A.B.; Kent, J. Biodiversity hotspots for conservation priorities. Nature 2000, 403, 853–858. [Google Scholar]
- Cumming, G.; Barnes, G.; Perz, S.; Schmink, M.; Sieving, K.; Southworth, J.; Binford, M.; Holt, R.; Stickler, C.; van Holt, T. An exploratory framework for the empirical measurement of resilience. Ecosystems 2005, 8, 975–987. [Google Scholar]
- Peralta, P.; Mather, P. An analysis of deforestation patterns in the extractive reserves of acre, Amazonia from satellite imagery: A landscape ecological approach. Int. J. Remote Sens 2000, 21, 2555–2570. [Google Scholar]
- Millington, A.C.; Velez-Liendo, X.M.; Bradley, A.V. Scale dependence in multitemporal mapping of forest fragmentation in Bolivia: implications for explaining temporal trends in landscape ecology and applications to biodiversity conservation. ISPRS J. Photogramm 2003, 57, 289–299. [Google Scholar]
- Bradley, A.V.; Millington, A.C. Spatial and temporal scale issues in determining biomass burning regimes in Bolivia and Peru. Int. J. Remote Sens 2006, 27, 2221–2253. [Google Scholar]
- Levin, S.A. Orchestrating environmental research assessment. Ecol. Appl 1992, 2, 103–106. [Google Scholar]
- Batty, M. The size, scale, and shape of cities. Science 2008, 319, 769–771. [Google Scholar]


| Region | Box | Box Size (km2) | 1986 (%) | 1991 (%) | 1996 (%) | 2000 (%) | 2005 (%) | 2010 (%) |
|---|---|---|---|---|---|---|---|---|
| Acre | 1 | 13,737 | 4.77 | 11.61 | 15.12 | 17.19 | 26.84 | 34.82 |
| 2 | 2,161 | 9.71 | 16.29 | 18.25 | 18.11 | 28.64 | 34.16 | |
| 3 | 2,993 | 3.61 | 9.59 | 10.14 | 15.14 | 20.67 | 32.26 | |
| 4 | 1,079 | 0.12 | 0.44 | 0.25 | 0.31 | 0.52 | 1.51 | |
| Madre de Dios | 1 | 3,304 | 4.49 | 2.94 | 7.94 | 7.87 | 8.35 | 14.00 |
| 2 | 929 | 1.11 | 3.96 | 3.14 | 4.78 | 12.77 | 9.58 | |
| 3 | 313 | 0.02 | 0.01 | 0.11 | 0.16 | 0.32 | 0.50 | |
| Pando | 1 | 1,153 | 3.79 | 6.74 | 7.39 | 13.28 | 17.60 | 28.06 |
| 2 | 343 | 0.13 | 0.87 | 1.36 | 2.45 | 4.10 | 8.73 | |
| 3 | 583 | 0.03 | 0.06 | 0.07 | 0.22 | 0.27 | 0.54 | |
*Where 1% in Acre represents 622.79 km2, 1% in Madre de Dios represents 493.48km2, and 1% in Pando represents 542.87 km2.
| State | Box | Parameter | 1986 | 1991 | 1996 | 2000 | 2005 | 2010 |
|---|---|---|---|---|---|---|---|---|
| Acre | 1 | D | 1.5920 | 1.7014 | 1.7355 | 1.7544 | 1.8043 | 1.8340 |
| δ | 0.0553 | 0.0470 | 0.0409 | 0.0376 | 0.0349 | 0.0341 | ||
| R2 | 0.9916 | 0.9947 | 0.9961 | 0.9968 | 0.9974 | 0.9976 | ||
| 2 | D | 1.6078 | 1.5863 | 1.7172 | 1.7172 | 1.7829 | 1.8152 | |
| δ | 0.0458 | 0.0760 | 0.0408 | 0.0391 | 0.0351 | 0.0351 | ||
| R2 | 0.9944 | 0.9842 | 0.9961 | 0.9964 | 0.9973 | 0.9974 | ||
| 3 | D | 1.5198 | 1.6987 | 1.7056 | 1.7597 | 1.7888 | 1.8481 | |
| δ | 0.0621 | 0.0521 | 0.0518 | 0.0424 | 0.0393 | 0.0360 | ||
| R2 | 0.9884 | 0.9935 | 0.9936 | 0.9960 | 0.9966 | 0.9973 | ||
| 4 | D | 0.8437 | 1.0380 | 1.0574 | 1.1216 | 1.1160 | 1.1687 | |
| δ | 0.0567 | 0.0894 | 0.0995 | 0.0897 | 0.0640 | 0.0956 | ||
| R2 | 0.9693 | 0.9648 | 0.9416 | 0.9571 | 0.9775 | 0.9712 | ||
| Madre de Dios | 1 | D | 1.5257 | 1.4974 | 1.6287 | 1.6343 | 1.6639 | 1.7657 |
| δ | 0.0450 | 0.0488 | 0.0432 | 0.0431 | 0.0436 | 0.0348 | ||
| R2 | 0.9940 | 0.9926 | 0.9951 | 0.9952 | 0.9952 | 0.9973 | ||
| 2 | D | 1.3168 | 1.4661 | 1.5106 | 1.5766 | 1.6779 | 1.6438 | |
| δ | 0.0568 | 0.0399 | 0.0702 | 0.0577 | 0.0424 | 0.0457 | ||
| R2 | 0.9871 | 0.9948 | 0.9851 | 0.9907 | 0.9955 | 0.9946 | ||
| 3 | D | 0.5010 | 0.4960 | 0.9148 | 0.9893 | 1.0503 | 1.1052 | |
| δ | 0.0651 | 0.0374 | 0.1023 | 0.1020 | 0.0614 | 0.0717 | ||
| R2 | 0.8942 | 0.9618 | 0.9195 | 0.9308 | 0.9766 | 0.9714 | ||
| Pando | 1 | D | 1.3979 | 1.5008 | 1.5305 | 1.6383 | 1.6864 | 1.7303 |
| δ | 0.0540 | 0.0482 | 0.0490 | 0.0422 | 0.0391 | 0.0362 | ||
| R2 | 0.9897 | 0.9928 | 0.9929 | 0.9954 | 0.9962 | 0.9970 | ||
| 2 | D | 0.8239 | 1.1345 | 1.2159 | 1.3323 | 1.3943 | 1.4669 | |
| δ | 0.0610 | 0.0539 | 0.0453 | 0.0476 | 0.0444 | 0.0575 | ||
| R2 | 0.9631 | 0.9844 | 0.9904 | 0.9911 | 0.9930 | 0.9907 | ||
| 3 | D | 0.5984 | 0.7321 | 0.8699 | 0.8964 | 1.0189 | 1.0820 | |
| δ | 0.0519 | 0.0498 | 0.0865 | 0.0641 | 0.0965 | 0.1000 | ||
| R2 | 0.9499 | 0.9687 | 0.9353 | 0.9654 | 0.9410 | 0.9592 | ||
| Parameter | 1986 | 1991 | 1996 | 2000 | 2005 | 2010 | |
|---|---|---|---|---|---|---|---|
| 1 | D | 1.5920 | 1.7014 | 1.7355 | 1.7544 | 1.8043 | 1.8340 |
| δ | 0.0553 | 0.0470 | 0.0409 | 0.0376 | 0.0349 | 0.0341 | |
| R2 | 0.9916 | 0.9947 | 0.9961 | 0.9968 | 0.9974 | 0.9976 | |
| NE | D | 1.6654 | 1.7876 | 1.8132 | 1.8313 | 1.8655 | 1.8947 |
| δ | 0.0434 | 0.0385 | 0.0349 | 0.0330 | 0.0321 | 0.0410 | |
| R2 | 0.9953 | 0.9968 | 0.9974 | 0.9977 | 0.9979 | 0.9972 | |
| NW | D | 1.3198 | 1.5980 | 1.6093 | 1.6531 | 1.7476 | 1.8043 |
| δ | 0.0646 | 0.0622 | 0.0517 | 0.0390 | 0.0348 | 0.0360 | |
| R2 | 0.9835 | 0.9895 | 0.9928 | 0.9961 | 0.9972 | 0.9972 | |
| SE | D | 1.6186 | 1.7406 | 1.7854 | 1.7971 | 1.8492 | 1.8826 |
| δ | 0.0477 | 0.0388 | 0.0360 | 0.0342 | 0.0323 | 0.0322 | |
| R2 | 0.9940 | 0.9965 | 0.9972 | 0.9975 | 0.9979 | 0.9980 | |
| SW | D | 1.0237 | 1.3450 | 1.2123 | 1.1932 | 1.3468 | 1.4852 |
| δ | 0.1035 | 0.0837 | 0.1003 | 0.0893 | 0.0759 | 0.0819 | |
| R2 | 0.9333 | 0.9736 | 0.9543 | 0.9623 | 0.9783 | 0.9792 | |
Share and Cite
Sun, J.; Southworth, J. Remote Sensing-Based Fractal Analysis and Scale Dependence Associated with Forest Fragmentation in an Amazon Tri‑National Frontier. Remote Sens. 2013, 5, 454-472. https://doi.org/10.3390/rs5020454
Sun J, Southworth J. Remote Sensing-Based Fractal Analysis and Scale Dependence Associated with Forest Fragmentation in an Amazon Tri‑National Frontier. Remote Sensing. 2013; 5(2):454-472. https://doi.org/10.3390/rs5020454
Chicago/Turabian StyleSun, Jing, and Jane Southworth. 2013. "Remote Sensing-Based Fractal Analysis and Scale Dependence Associated with Forest Fragmentation in an Amazon Tri‑National Frontier" Remote Sensing 5, no. 2: 454-472. https://doi.org/10.3390/rs5020454
APA StyleSun, J., & Southworth, J. (2013). Remote Sensing-Based Fractal Analysis and Scale Dependence Associated with Forest Fragmentation in an Amazon Tri‑National Frontier. Remote Sensing, 5(2), 454-472. https://doi.org/10.3390/rs5020454





