Openness as Visualization Technique for Interpretative Mapping of Airborne Lidar Derived Digital Terrain Models

Abstract

Openness is proposed as a visualization technique for the archaeological interpretation of digital terrain models derived from airborne laser scanning. In contrast to various shading techniques, openness is not subject to directional bias and relief features highlighted by openness do not contain any horizontal displacement. Additionally, it offers a clear distinction between relief features and the surrounding topography, while it highlights both the highest and lowest parts of features. This makes openness an ideal tool for mapping and outlining of archaeological features. A comparison with sky-view factor and local relief model visualizations helps to evaluate advantages and limits of the technique.

1. Introduction

In archaeological prospection, airborne laser scanning (ALS) is mainly used to obtain information about archaeological sites and environmental structures in relief. For this purpose, high quality digital terrain models (DTM) are derived from ALS data, and are subsequently interpreted. Until now, this has mainly been done based on 2D visualizations created from the respective DTM. Of these, simple shaded relief has long been used as a standard visualization technique. While it is easily perceived and “read”, its major drawback lies in the fact that it has reduced information content [1,2]. As a consequence, the number of publications dealing with the problem of displaying and interpreting archaeological ALS data is constantly growing. Published techniques include dense contour mapping [3], a simple combination of slope and hillshade ([4]; pp. 66–67), geostatistical filtering [5], local relief model (LRM, [6]), principal component analysis (PCA) based on several shaded reliefs with varying illumination angles [1], and sky-view factor (SVF, [7]).

Recently, a number of publications have attempted to compare these visualization methods. Kokalj et al. discuss various techniques, including hillshades and derivatives, techniques of elevation differentiations, LRM, SVF, PCA, and various composites [8]. Keith Challis et al. [9] published an assessment of visualization techniques and proposed a “toolbox” for low and high relief landscapes, which includes elevation shading, slope severity, solar insolation models and LRM. Another comparison of these techniques was made by Bennett et al. [10]. Testing slope, aspect, PCA, local relief model and sky-view factor, it became clear that no technique was able to visualize all of the known relief features. Therefore, a combination of these techniques is the only way to obtain a maximum amount of information on potential archaeological sites in relief.

This brief overview shows that there is abundant literature on visualizing ALS-derived DTMs. Although most of the abovementioned visualization techniques help the user to perceive archaeological and palaeoenvironmental features, not all of them are helpful when trying to delineate individual structures during interpretative mapping. Distinguishing the borderline between an archaeologically induced micro-topographic variation and its surrounding surface can be quite a challenge. This has already been observed by Rebecca Bennett et al. [10], who remarked that, with most of the available techniques, the outline of features will shift in a horizontal direction.

For mapping purposes, visualization techniques that “homogenize” archaeologically induced micro-topographic features and enable them to be clearly distinguished from the surrounding terrain become important. The most prominent methods are SVF (see especially ([8]; p. 110)) and LRM, which have been shown to be among the ‘strongest combination of techniques’ ([10]; p. 47). However, as will be demonstrated below, SVF delineates mainly concave features, while LRM does not provide correct outlines of features in certain situations. The aim of this paper is therefore to propose openness as an additional visualization technique for interpretation of archaeological DTMs. It is not subject to directional bias and is very useful for delineating both convex and concave features. In the following section the basic concept of the technique will be explained. Afterwards, openness will be applied to various case studies and the results discussed. Finally, a comparison with SVF and LRM will show the advantages and disadvantages of each method.

2. The Openness Algorithm

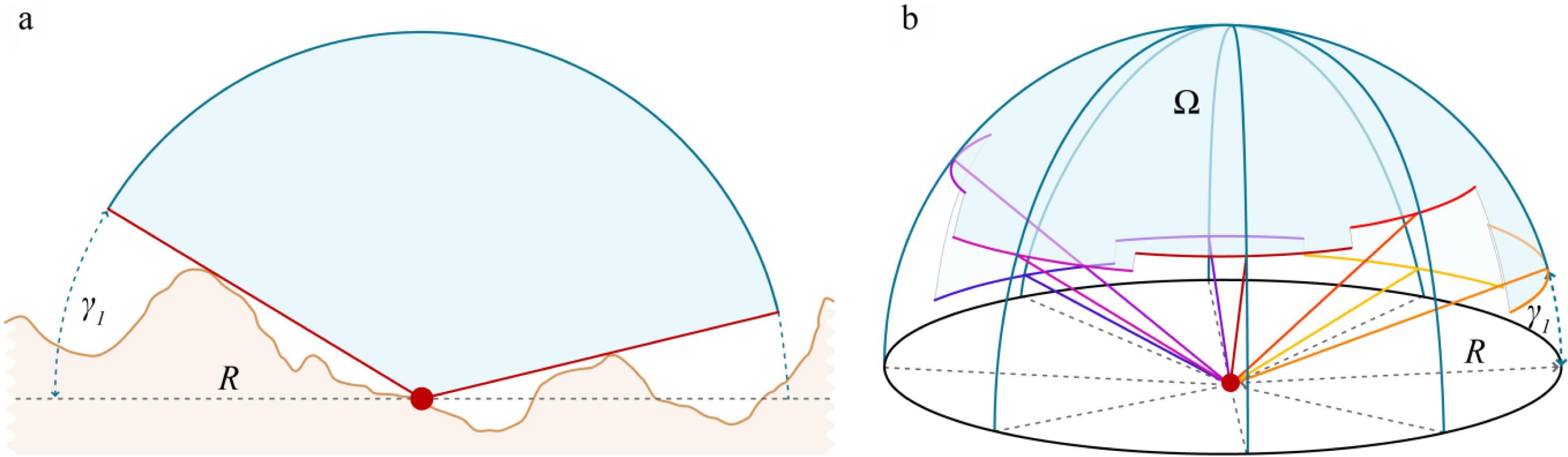
A decade ago, Ryuzo Yokoyama, Michio Shirasawa and Richard J. Pike published “openness” as a then novel way to express ‘the degree of dominance or enclosure of a location on an irregular surface’ ([11]; p. 257). To determine the openness value for a specific location, profiles along at least eight directions (N, NW, W, SW, S, SE, E, NE) are derived from a given digital elevation model within a defined radial distance. Starting from the raster element under consideration, the largest possible zenith (Figure 1, α) or nadir (Figure 1, β) angle along each profile is determined. The mean value of all zenith angles equals the positive openness, while the mean nadir value designates negative openness (Figure 1). The derived values can theoretically range from >0° to <180°, where smallest and largest possible values depend on the cell size of the DTM raster. Perfectly flat surfaces, regardless of whether they are horizontal or tilted, have openness values of 90°.

The chosen radial distance defines a circular kernel or moving window which is moved across the DTM to compute openness for all grid cells. Topographic features outside the kernel will be ignored during calculation of an openness value for the specific location. Therefore, deciding upon the length of the radial distance will have an impact on the calculation results and in consequence on the final visualization. Generally speaking, small distances (a few meters) will enhance local micro-topographic variations, while large values (a few hundred meters) will highlight river valleys and hilltops. Therefore, the size of the radial parameter is directly dependent on the spatial scale of the research question, and this will sometimes necessitate computing openness with different radial parameters.

To date, openness has only rarely been used in archaeology. Chiba and Yokoyama combined openness, shaded relief and graduated coloring to generate archaeological maps of artifacts, walls and sites [12]. The author has used positive openness with a radial distance of 1000 m in landscape archaeology to visualize an area of rolling hills and used it as component of a friction surface for least cost path analysis ([13]; p. 311). During this research, tests with different radial sizes were carried out and it was realized that when using small radial values between 5 and 30 m, similar-sized micro-topographic features could be enhanced in a very useful way ([14]; p. 39). Another short mention of openness, which will be discussed below, can be found from Zakšek et al. [7].

3. Sample Areas and Processing

In this section, the potential of openness will be demonstrated using various examples taken from two different archaeological ALS missions: (1) a scan of the Leithagebirge in the east of Austria in 2007 [15], and (2) the scan of the archaeological site of Birka-Hovgården, located west of Stockholm on the neighboring islands of Björkö and Adelsö, which is one of the case-study areas of the LBI ArchPro [16,17]. The parameters of both scans are listed in

Table 1. Parameters of the airborne laser scanning (ALS) data used in this paper.

ALS-Project	Leithagebirge	Birka
Purpose of Scan	Archaeology	Archaeology
Time of Data Acquisition	26 March–12 April 2007	28 and 29 November 2011
Mean Point-Density (last echoes per sq m)	7	11
Strip Overlap	70%	20%
Scanner Type	Riegl LMS-Q560 Full-Waveform	Riegl LMS-Q680i Full-Waveform
Scan Angle (whole FOV)	45°	60°
Flying Height above Ground	600 m	300 m
Speed of Aircraft (TAS)	36 m/s	54 m/s
Laser Pulse Rate	100 000 Hz	400 000 Hz
Scan Rate	66 000 Hz	266 000 Hz
Strip Adjustment	Yes	Yes
Filtering	Robust interpolation (SCOP++)	Robust interpolation (SCOP++)
DTM-Resolution	0.5 m	0.5 m

.

In all cases, openness was calculated using the software package OPALS (Orientation and Processing of Airborne Laser Scanning data), see [18,19]. After testing different kernel sizes, a radial distance with a radius of 15 grid cells (corresponding to 7.5 m) was used for processing. The resulting images display high values as bright and low values as dark tones. Because high positive openness has a different meaning than high negative openness, a simple greyscale coding of both versions would result in an inconsistent symbolization: bright areas denominate crests in positive and valleys in negative openness. To avoid this, the negative openness can be inverted resulting in easier comprehension of the displayed topographic micro-relief. As Kokalj et al. [8] have recently suggested for displaying SVF images, a histogram stretch was applied to all openness maps (see image captions for further detail). This resulted in clearly outlined homogenized areas within relief features. Currently, there are also two publicly available tools to calculate openness images, (1) “Relief Visualization Toolbox” from the Institute of Anthropological and Spatial Studies ZRC SAZU [20], and (2) “Lidar Visualization Toolbox” from the Landesamt für Denkmalpflege Baden-Württemberg [21,22].

SVF was calculated using the Relief Visualization Toolbox [20]. LRM models were produced in ArcGIS using a self-developed model, which follows the processing workflow outlined by Hesse [6]. In some cases, openness maps were combined in ArcGIS with other visualization images (e.g., positive and negative openness, positive openness and slope) by setting the top layer to a transparency value of 50%.

4. Result and Discussion

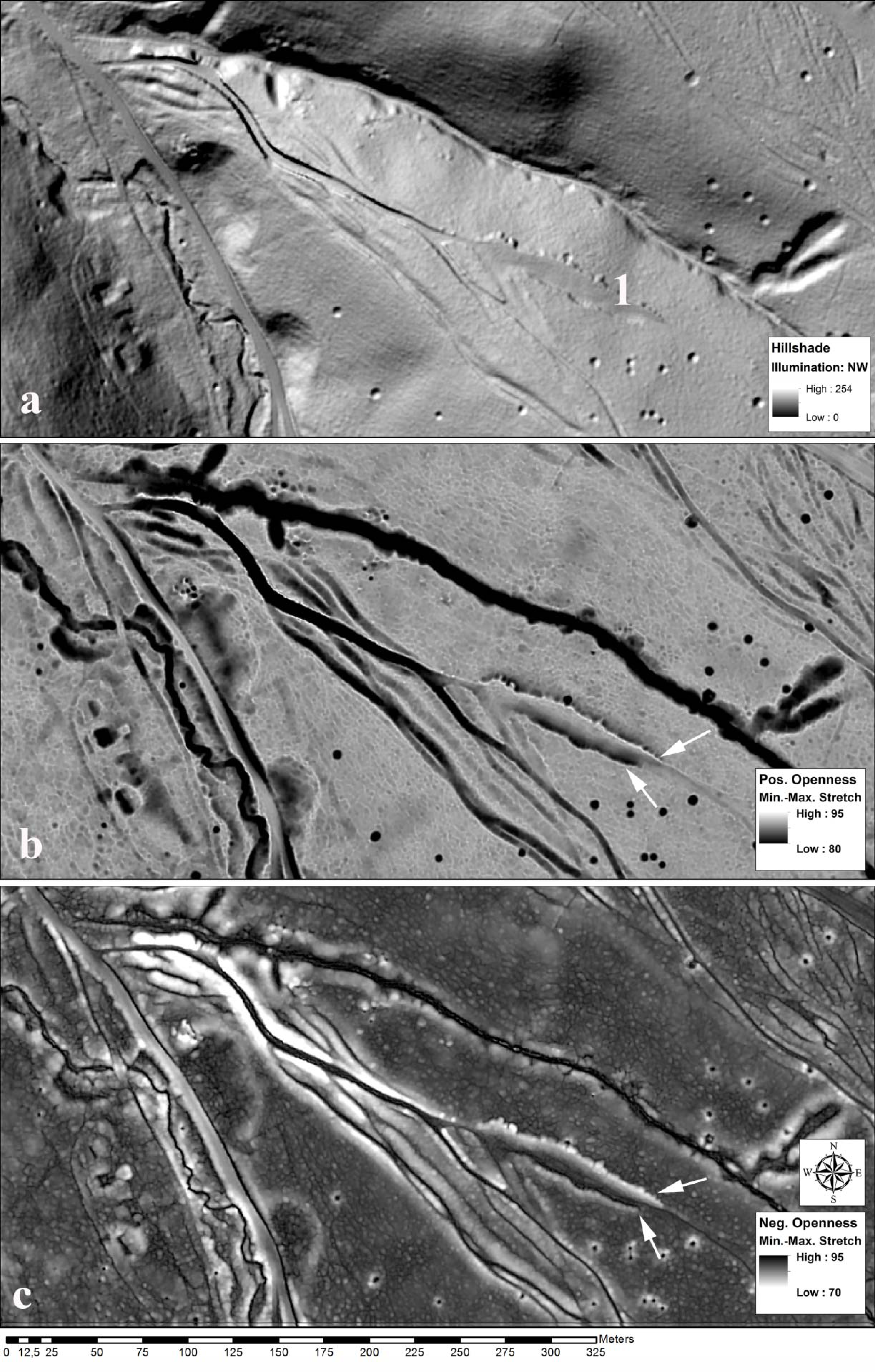
In the following, the effects of positive and negative openness on DTM representation will be demonstrated and discussed. The first example (Figure 2) contains abundant information on modern, archaeological, and natural features. For the sake of this paper, the focus will be set on the hollow-ways of various depths, a terrace (annotation 1 in Figure 2a) and a number of bomb craters from WW2. They are located in the Leithagebirge, east of St Anna in der Wüste (Austria).

While the shaded relief visualization (Figure 2a) provides a good impression of the general topography, some of those hollow-ways which run from NW to SE are not clearly visible as they are aligned with the illumination direction (a well-known problem; see [1,2]). In contrast, all linear features are clearly visible in both openness images (Figure 2b,c), which also exclude general topographic information. Neither slopes nor shading are indicated, although the height differences in the map measure 80 m between the upper left and lower right corner of the image. As will be explained below (Section 4.1), this can be regarded as an advantage. Positive openness (Figure 2b), displayed with an applied histogram stretch, depicts the sunken paths and the hollows of the bomb craters in distinct dark tones, which makes them easily identifiable. More importantly, abrupt changes in slope (i.e., at ridges, where up and down slopes intersect or at terraces, where steep slopes change to level surfaces) are outlined as bright lines and can therefore be easily mapped. This is the case at the narrow ridges between the partly intersecting hollow-ways. Also, the rims of the craters are clearly defined. In contrast, features initially seem to be less clear in (inverted) negative openness (Figure 2c). A more thorough investigation, however, reveals additional important information: while the rims are less pronounced at the bomb craters, their deepest parts are now clearly marked by dark spots. Also, the trench bottoms of the individual hollow-ways become distinct as dark lines, rendering the shallow ones clearly visible.

Terrace features also become clearly delineated (annotation 1 in Figure 2a) due to the abrupt change in slope. While the upper edges of terraces display higher (bright) values in positive openness (arrows in Figure 2b), negative openness will result in higher (dark) values only at lower terrace edges (see arrows in Figure 2c). Thus, both upper and lower terrace edges are outlined, while the width of the “lines” corresponds to the degree of sharpness of the edge. Rounded terrace edges will be represented as wider “lines”.

As can be seen at the hollow-ways in Figure 2, openness turned out to be informative where up and down slopes intersect or abruptly change. This is also the case in Birka, where hundreds of round barrows are in close proximity to each other. The heights of the tumuli depicted in Figure 3 range between 0.5 and 2 m. Positive openness (Figure 3b) shows low values (dark) from the base of the mounds to midway upslope, while the top exposes high values (bright). At some of the barrows, small depressions—probably from prior looting—become visible as small, dark, and roundish areas of lower openness values.

Conversely, inverted negative openness (Figure 3c) clearly delimits all of the barrows through high values at their base (dark), while the mounds themselves have low negative openness values (bright). This visualization is well suited for outlining barrows and similar features during interpretative mapping. The more or less homogenous low openness values (after application of histogram stretching) of the individual barrows also make this visualization suitable for automated classification [23].

Both examples clearly demonstrate the potential of positive and negative openness. In combination, they will both highlight the outlines as well as the highest and lowest parts of sunken and raised relief. What makes this technique so useful for visualization is the fact that openness enhances both local concavities and convexities ([11]; p. 257): Openness (in its positive version) quantifies the degree of unobstructedness of a location. Depending on the radial distance, hilltops, peaks and ridges generally will be assigned high values, while valley-bottoms are characterized by low values. Openness is therefore similar to other calculations such as visibility [24], topographic prominence [25], or sky-view-factor [7]. It is important to stress that as can be seen from Figure 1, negative openness (Figure 1, red lines and α) is not the inverse of positive openness (Figure 1, white lines and β). High negative openness values correspond to valley-bottoms and other low lying structures.

Despite this potential, openness has so far been largely neglected in archaeological literature. Zakšek et al. do mention it and compare it with the very similar technique of sky-view factor, but regard it as less ‘intuitive’, because it does not show the general topography ([7]; pp. 403–404). Therefore, openness and SVF need to be compared in order to evaluate their potential in greater detail.

4.1. Openness Compared to Sky-View Factor

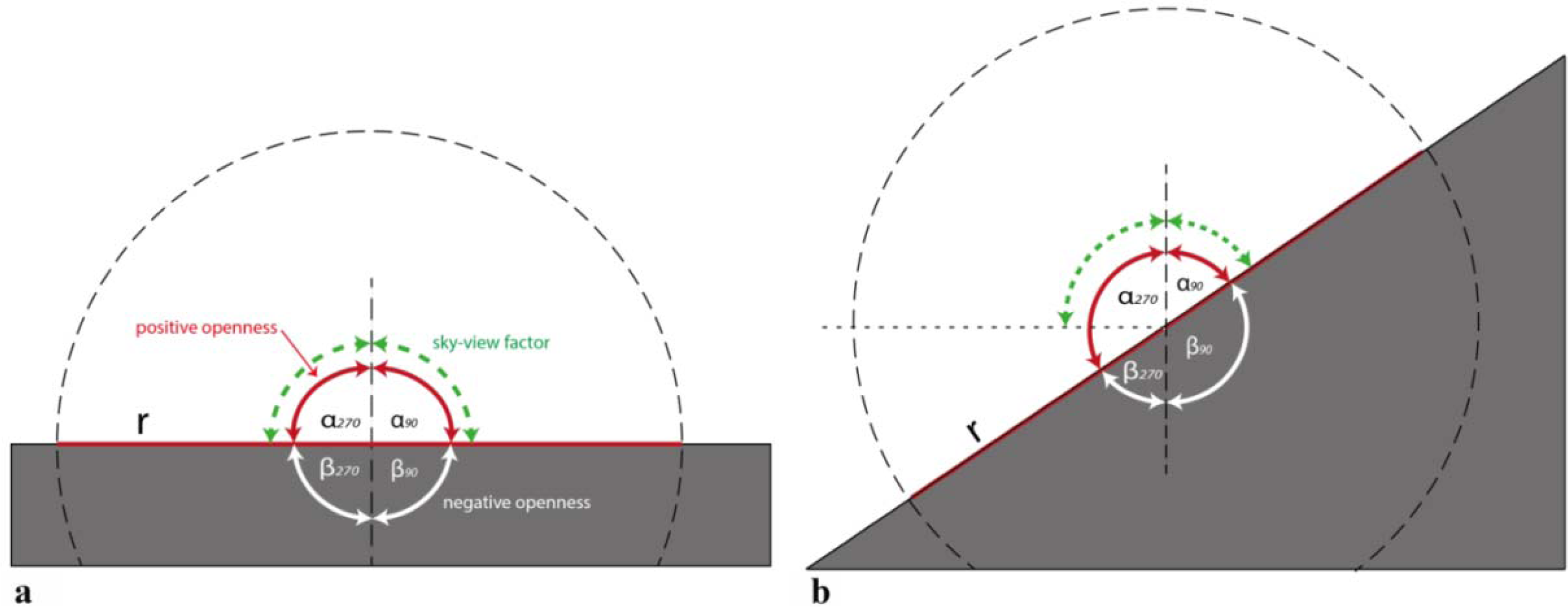
As mentioned above, openness is very similar to sky-view factor (Figure 4), which is regarded as highly efficient ([8]; p. 112; [10]; p. 47) and has become an often used visualization technique in archaeological ALS. As its name suggests, SVF quantifies ‘the portion of the sky visible from a certain point’ within a certain radius ([26]; p. 266). Locations with large SVF have a large portion of the sky visible. Similar to openness, the size of the observed area (i.e., the chosen radius) has an effect on the result. To highlight local, small-scale topography, small radii are necessary (e.g., 10–15 m).

Although openness is similar to SVF, there are three main differences:

(1)

Unlike openness, SVF is a physical quantity (the portion of the sky visible indicates also the amount of potential illumination) which can be used in energy balance studies ([7]; p. 403).

(2)

SVF uses only zenith angles above the horizontal plane. Therefore, the maximum angle derived during processing SVF can be a zenith of 90°. This means that the SVF (or in other words, the portion of the sky visible from a specific location) cannot be larger than the half-sphere, which would be the case on a perfectly planar, horizontal surface (Figure 4). In contrast, openness also includes angles which are larger. As a result, a location in an openness map will display the same value regardless if it was determined on a tilted or on a horizontal plane, while the sky-view factor of these two locations would differ (Figure 5, see also ([7]; pp. 403–404)). In practical terms, the slope of the general topography will be visible in a SVF image, while it is disregarded in openness. As demonstrated in Figure 6, while the SVF (Figure 6a) also visualizes slope, both positive (Figure 6b) and negative (Figure 6c) versions of openness disregard slope. Although this reduces the “readability” of the general topography ([7]; p. 404), it gives a purer view of the topographic structures, which are no longer masked by slope values. As a consequence, openness values characterizing local micro-topography (e.g., a barrow) will be similar, irrespective of whether the feature is located on a tilted or horizontal plane. This results in more homogeneous “signatures”, which is an advantage for automated classification approaches. If necessary (to enhance the general topographic context), positive openness can be combined with slope. The results of this are very similar to SVF (compare Figure 6a with 6d).

(3)

As mentioned above, SVF uses only zenith angles above the horizontal plane. As a result, it delineates mainly concave features ([8]; p. 110). In contrast, an openness process calculates an additional “negative” version using nadir angles (which theoretically could be also computed for SVF). While positive openness highlights ridges and crests, negative openness will mark the deepest parts. As already demonstrated above, this is very useful during manual mapping and can be also important for automated procedures. Figure 2 depicts hollow-ways and bomb craters. While positive openness outlines the ridges of each individual hollow-way and the rims of the bomb craters, negative openness outlines the lowest parts within each structure. In Birka, positive openness highlights topographic convexities and the tops of the burial mounds. Negative openness emphasizes topographic concavities: the bottoms are highlighted by dark lines and show the boundaries of the barrows in Birka quite clearly (Figure 3).

4.2. Openness Compared to Local Relief Model

As demonstrated, openness shows local micro-topography independent of the general topography. Again, this is similar to local relief model, a technique originally published by Hesse [6] which has proven extremely useful for interpretation of ALS-derived terrain models. The idea behind a LRM is to remove the general topography from a scene by subtracting the low-pass filtered terrain model from the original one in an iterative process. Based on the zero contour of the first subtraction (which marks those lines, where the original DTM and the low-pass filtered DTM intersect), a refined or “purged” general topography model is calculated, which is then subtracted from the original DTM [6]. In that way the terrain is flattened, leaving just the micro-topographical features which can then be enhanced by graduated coloring. The advantage of LRM is thus (1) to acquire a visualization which lets the interpreter immediately perceive and discern sunken from raised features, and (2) the possibility to measure height-differences between individual features and the surrounding area, as well as to calculate volumes of individual structures.

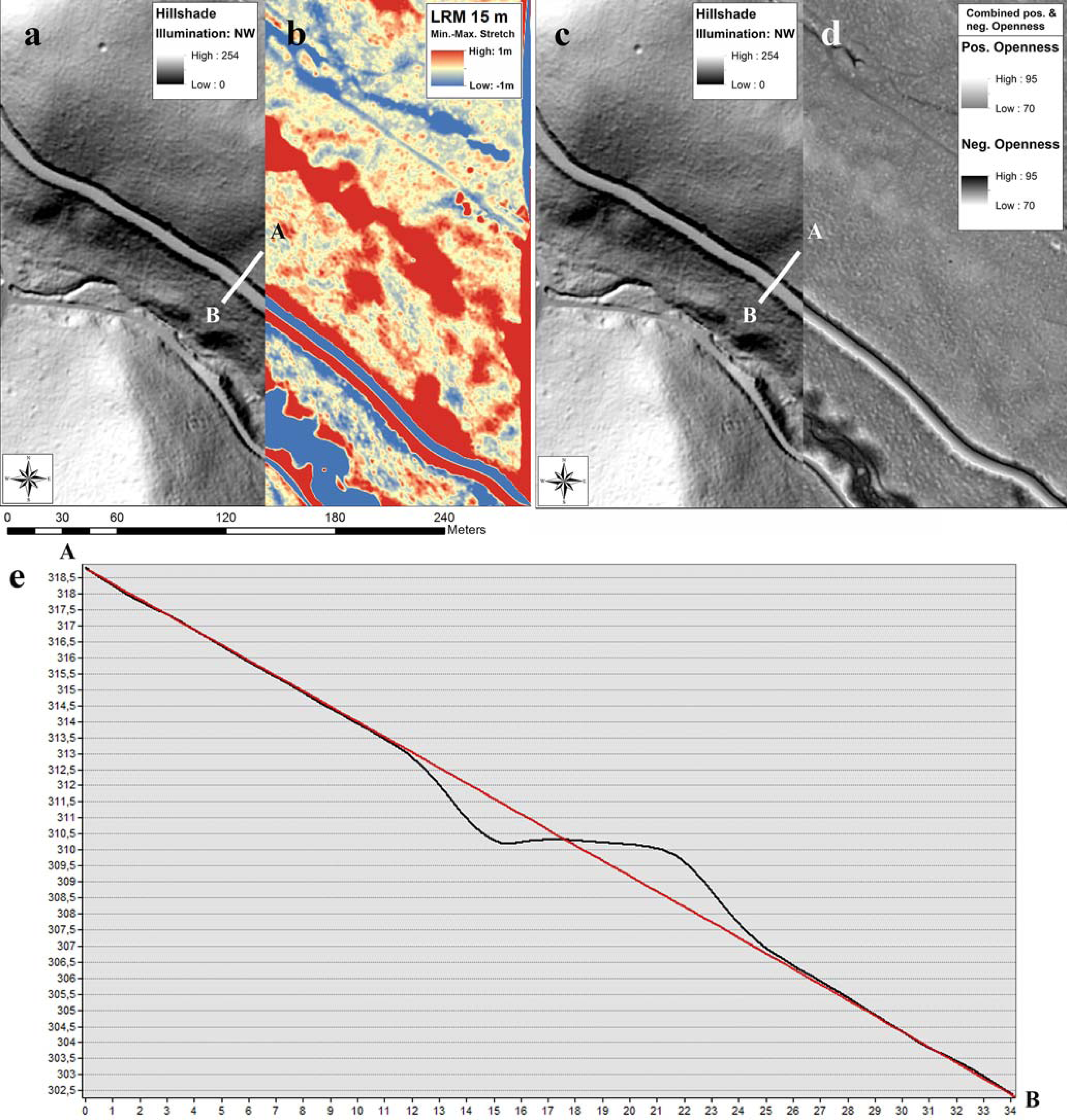
Computation of LRM is not straightforward. During calculation various processing steps have to be applied, where—as with openness—a kernel is used to derive statistical parameters from the original DTM. Depending on the kernel size, the resulting visualizations will differ. Therefore, different topographic settings (relief, size and structure of objects) will need different parameters to compute a LRM.

Additionally, LRM visualizations are not always immediately comprehensible. They can only be interpreted correctly when the computation process is understood and taken into consideration (see also [8]; p. 102). This becomes evident at the situation of a terrace or a road which is cut into a slope (Figure 7). The LRM will display a sequence of positive and negative relief, which could be also “read” as an earthwork showing as a ditch accompanied by two banks (Figure 7b) (see also the evaluation by [6]; p. 71). In this situation, a combination of positive and negative openness gives a more distinct image, where the areas of breaking terrain are displayed as dark and white linear areas (Figure 7d).

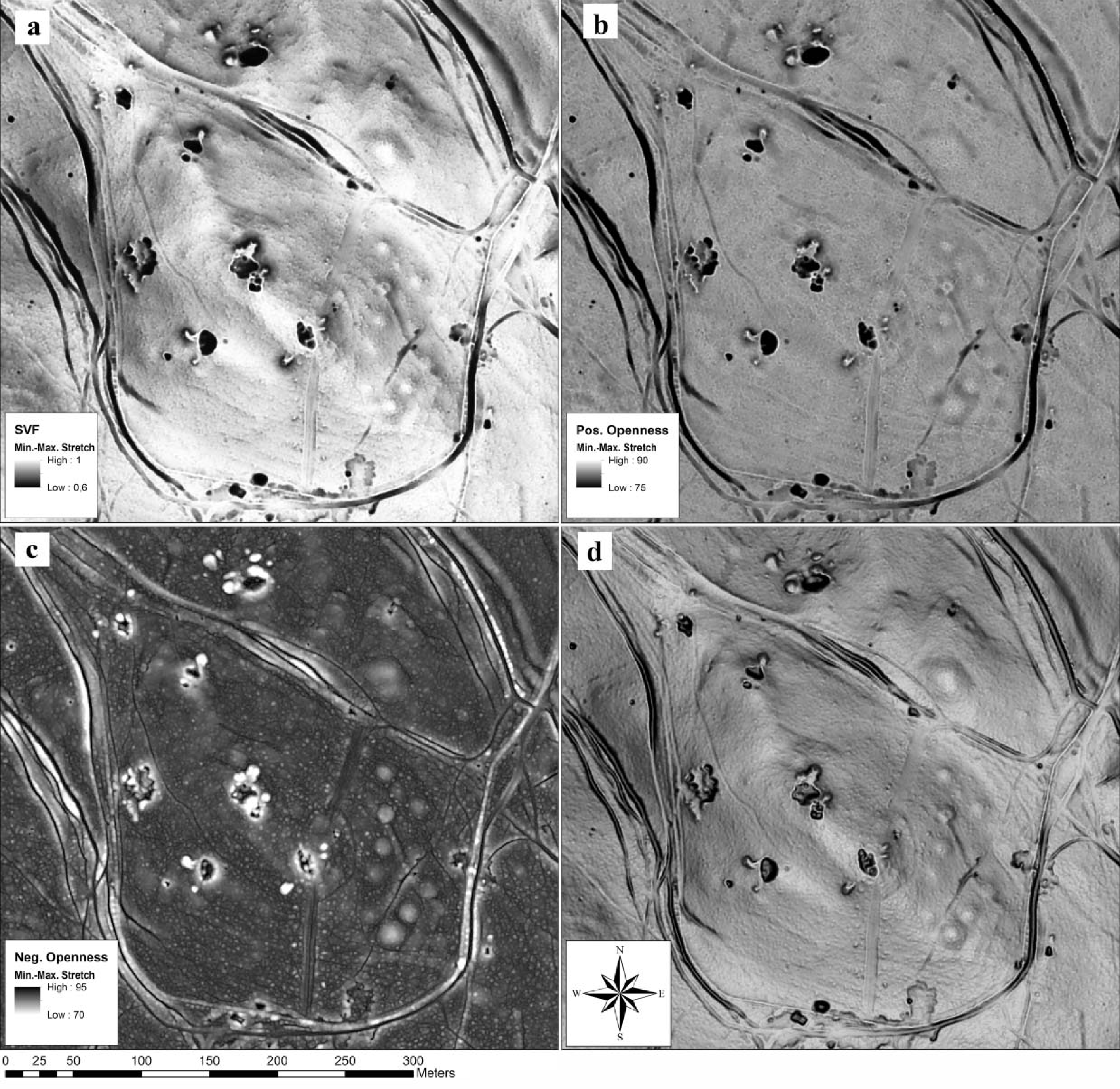
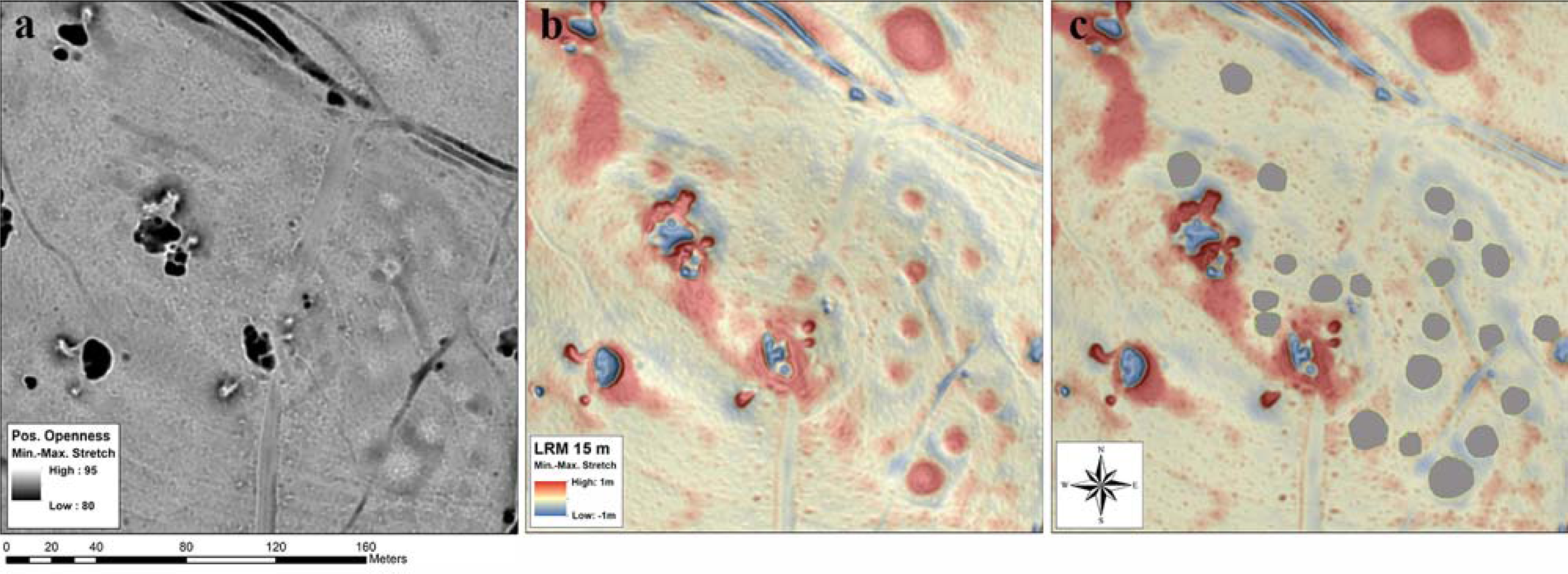
In areas of shallow relief, the application of LRM produces clear and distinct visualizations. Figure 8 shows the situation of highly eroded round barrows in the Leithagebirge. While in positive openness (Figure 8a) only nine barrows are visible, according to the interpretation of the LRM the area is covered by at least fifteen burials (Figure 8b,c). This is a clear advantage of LRM over any other known technique and demonstrates the importance of combining various visualizations, since all of them filter and display information content in a different way (see also [9] and [10]; p. 47).

LRM becomes, however, problematic in situations where archaeological topographic features are better preserved (i.e., displaying steeper slopes) and are extremely close to each other, as is the case in Birka. Here, both the low-pass filtered and purged DTM created during the LRM-workflow are slightly too high, resulting in a zero contour which is not at the bottom of the round barrows but cuts through the slope of the barrows (Figure 9b). Therefore, the red areas in the final LRM will not cover the whole barrow, but will be slightly smaller. In comparison, negative openness gives particularly good results in this case. The crests are highlighted by dark lines and show the boundaries of the barrows quite clearly (Figure 9c; see also Figure 3c).

5. Conclusion

This study has examined the use of positive and negative openness to visualize digital terrain models for interpretative mapping of topographic archaeological features. It is the first time that openness has been systematically investigated on a micro-topographic scale using data provided by airborne laser scanning. The examples and comparisons discussed in the paper demonstrate that this technique clearly distinguishes the highest as well as the lowest areas of features such as banks, ditches, and barrows. In contrast to many of the currently available techniques, the highlighted feature extents do not suffer from horizontal shift (as is also true for slope and sky-view factor), which is imperative for accurate interpretative mapping. Thus, openness can be viewed as an important supplementary technique for visualization of archaeological remains present in terrain models derived from airborne laser scanning.

A comparison with the most prominent current archaeological visualization techniques—sky-view factor and local relief model—revealed the advantages and limitations of openness. While local relief models perform better with very shallow relief features, they are problematic in areas with steep relief and large differences in slope, resulting in ambiguously illustrated and incorrectly outlined topographic features. In these situations, openness creates accurate and clear images. In contrast to sky-view factor, openness enhances both convex and concave structures and creates a visualization which is stripped of the general topography, displaying only differences in the micro-relief. Application of a histogram stretch hence results in clearly delineated archaeological features (e.g., bases of barrows, edges of bomb craters, terraces, and hollow-ways).

While openness has been shown to be a valuable technique for the visualization and manual interpretation of archaeological relief features, it could be of even greater use for image analysis applications. The way forward is therefore to investigate the applicability of openness images to function as a basis for (semi-)automatic classification based on pattern recognition and image classification algorithms. This further increases its value as a tool for rapid identification of archaeological features present in large area, high resolution datasets.