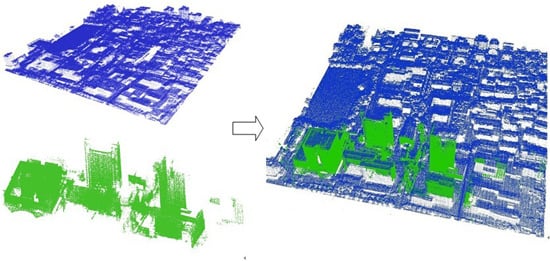
Semi-Automatic Registration of Airborne and Terrestrial Laser Scanning Data Using Building Corner Matching with Boundaries as Reliability Check
Abstract
:1. Introduction
2. Related Work
2.1. Review of Registration of Point Clouds from the Same Platform
2.2. Review of the Registration of ALS and TLS Data
2.3. Review of Building Extraction from Terrestrial Laser Scanning
3. Method
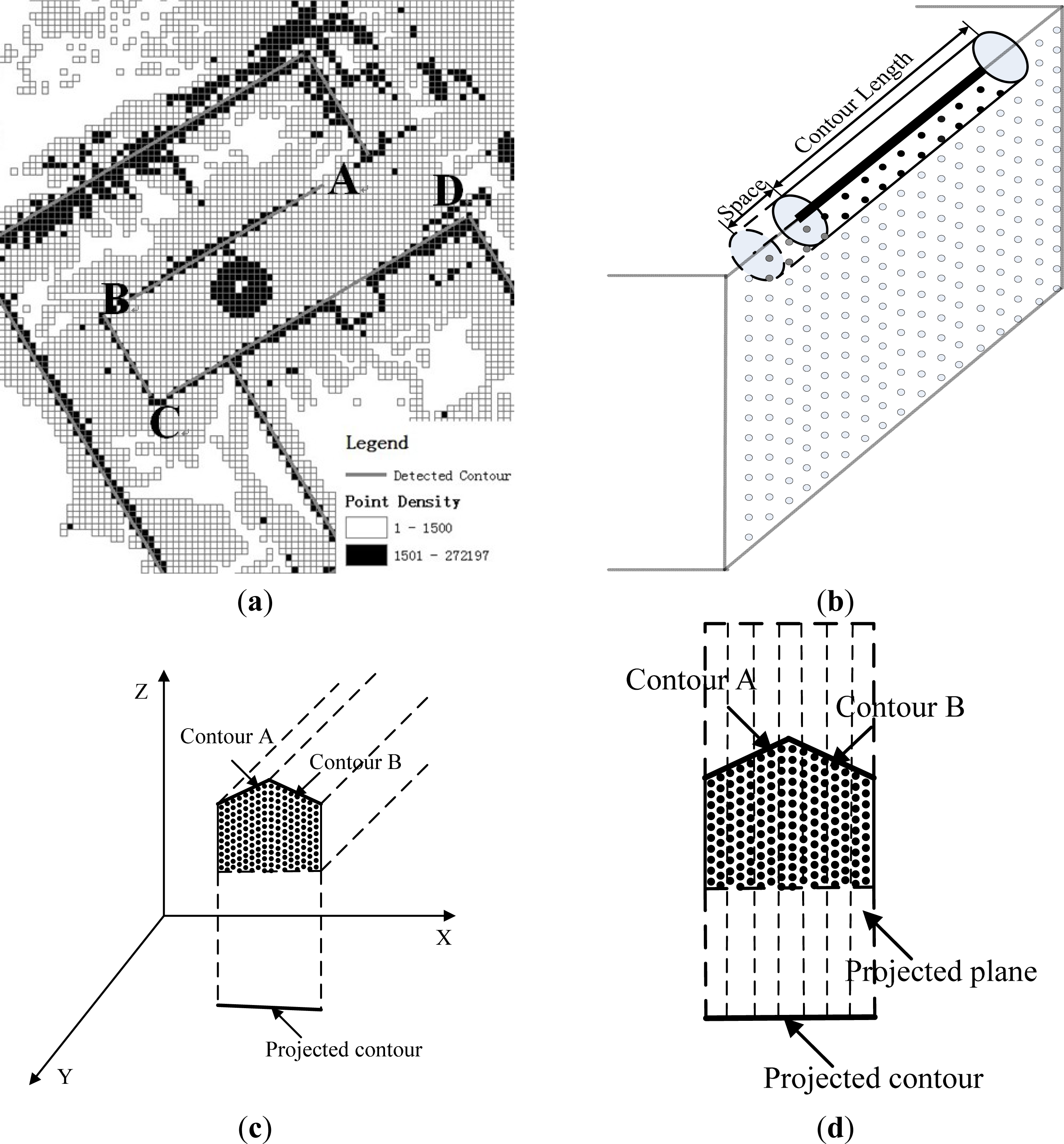
3.1. Building Boundary Segment Extraction
3.1.1. Boundary Segment Extraction from Terrestrial Laser Scanning Data
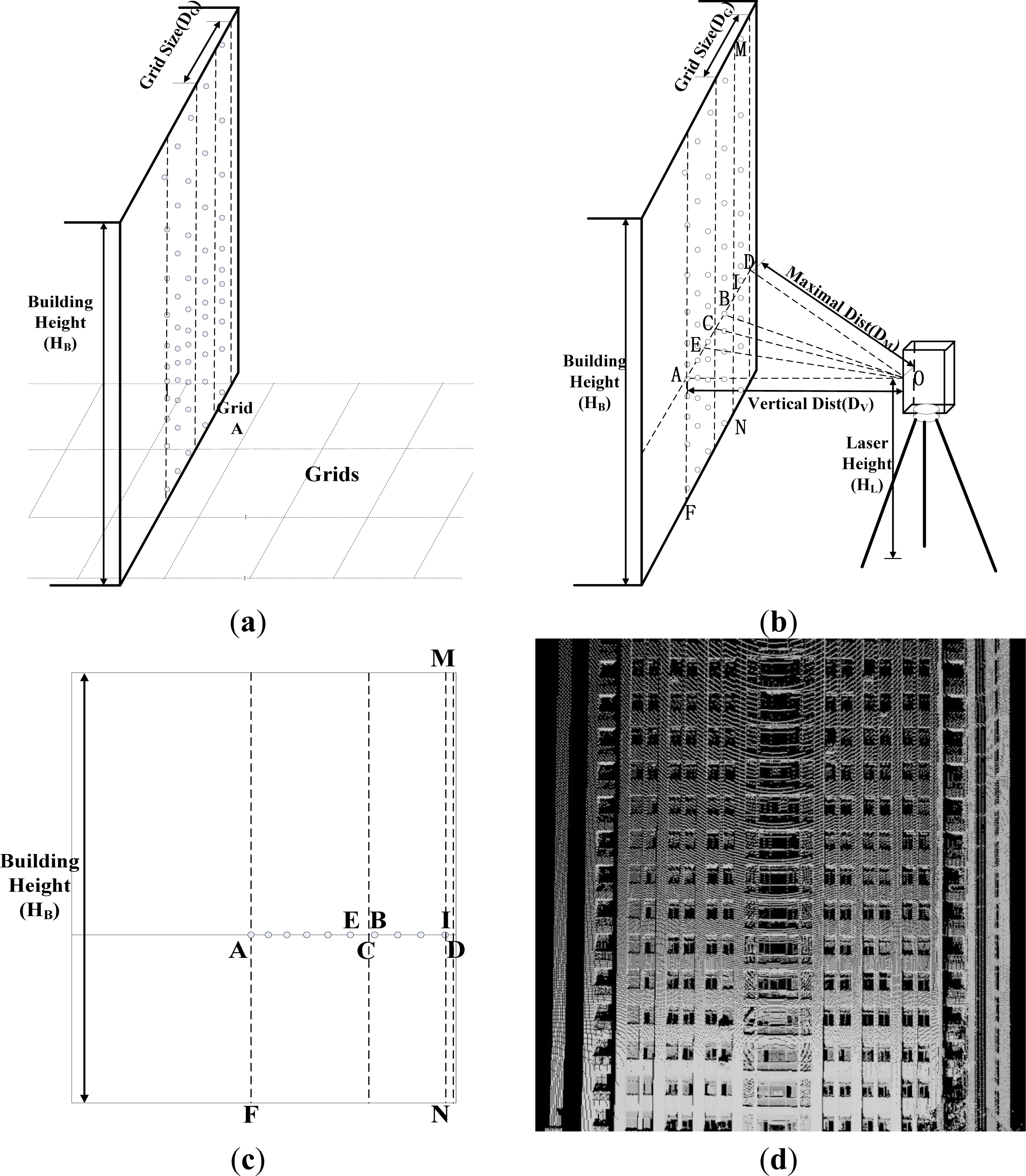
- Step 1: Large boundary grid selection. A grid with a relatively large size (1 m × 1 m in this study), named a large grid, is constructed in the XY plane. All terrestrial points are projected onto the XY plane. The point density of each grid is calculated by obtaining the number of points in each grid based on the point-grid spatial relationship. A point density threshold is estimated (as discussed later), and this is used to identify the grids belonging to the building walls. All rough grids are separated into two sets: wall grids (with point densities above the threshold) and non-wall grids (with point densities below the threshold).
- Step 2: Small boundary grid selection. The wall grids selected in Step 1 are used to construct grids of relatively small size (0.2 m × 0.2 m in this study), named small grids. The point density of each grid is recalculated according to the point-grid relationship. Similarly, based on a point density threshold, all grids are separated into two sets: wall grids and non-wall grids.
- Step 3: Boundary segment extraction. The Hough transform is used to convert the selected small boundary grids into vector boundary segments.
3.1.2. Boundary Segment Extraction from Airborne Laser Scanning Data
3.2. Building Corner Extraction
3.3. Point Cloud Registration Using Corner Matching with Boundaries as Reliability Check
4. Experiments and Analysis
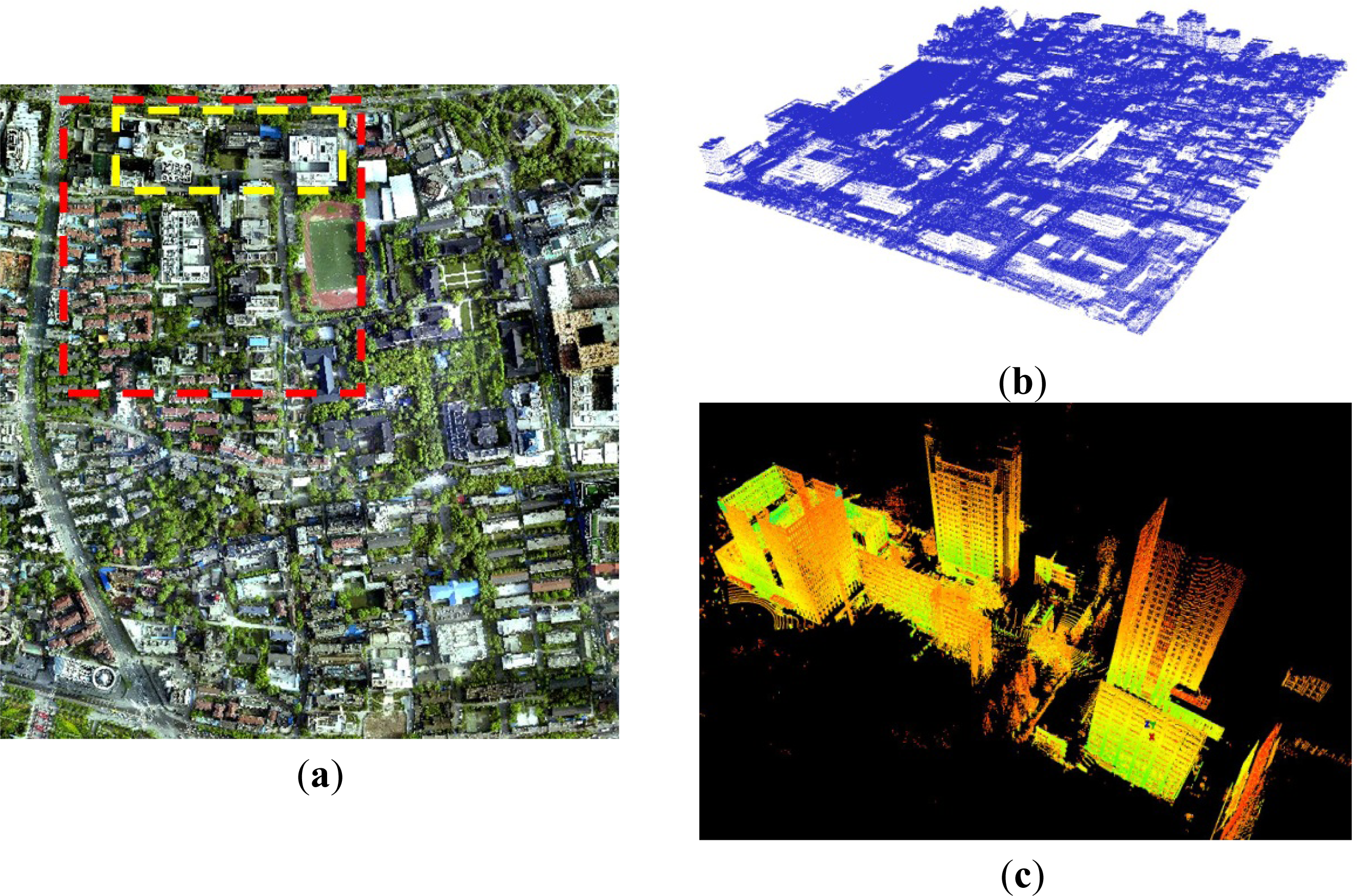
4.1. Experimental Data
4.2. Registration Results
4.2.1. Boundary Segment Extraction
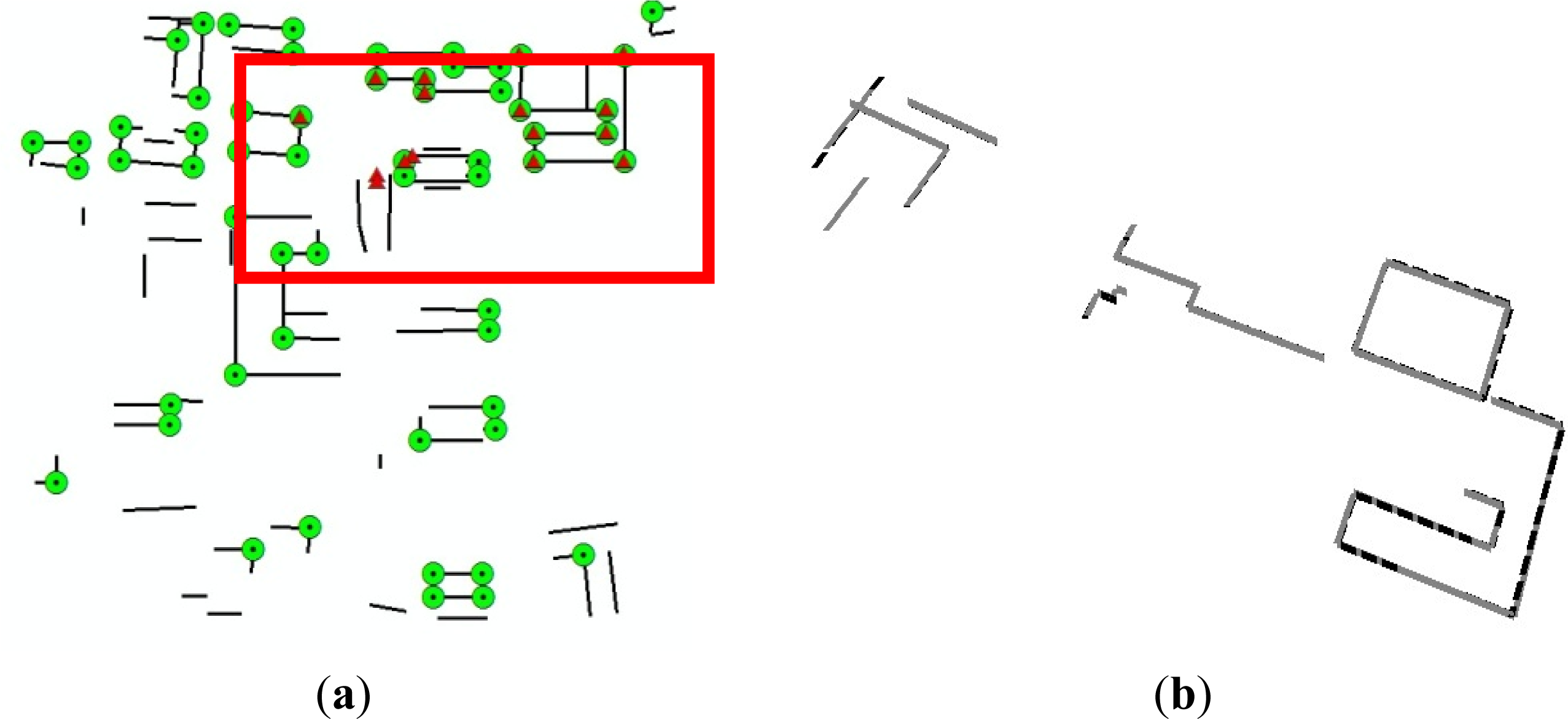
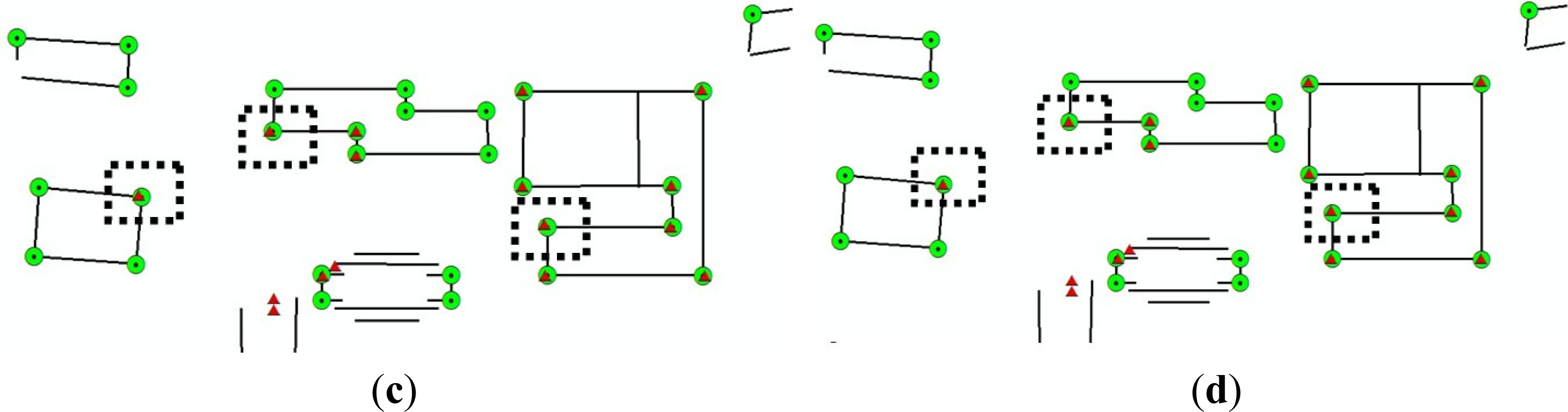
4.2.2. Building Corner Extraction
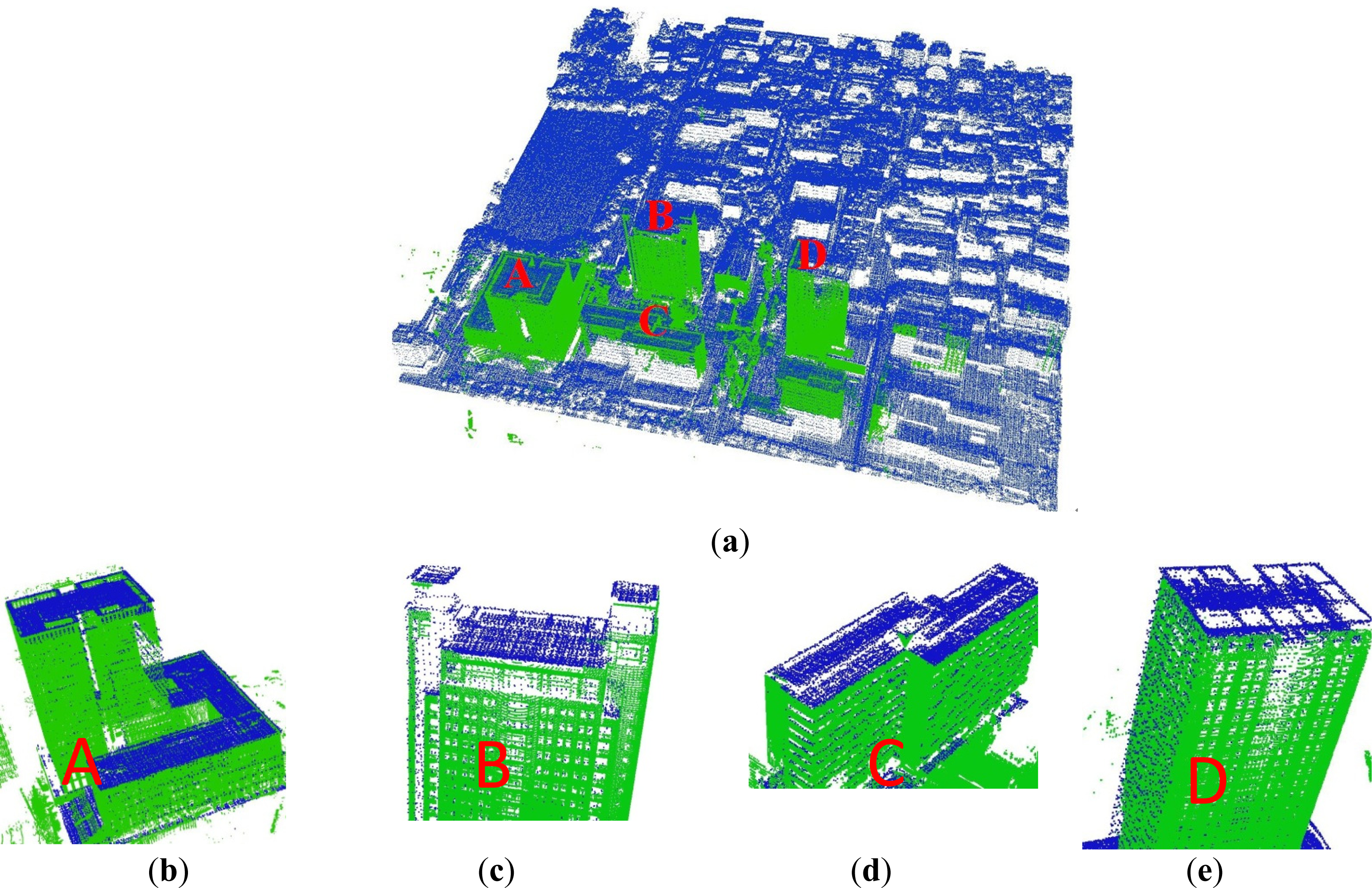
4.2.3. Registration Results of ALS and TLS Data
4.3. Reliability Analysis
4.4. Geometric Accuracy Analysis
5. Conclusion
- (1)
- The grid density method for boundary extraction from TLS data is feasible. The key to this method is the ability of the proposed theoretical estimation to determine an appropriate threshold.
- (2)
- Airborne corners and terrestrial corners can be reliably matched in a fully automatic way, and the reliability check strategy ensures the reliability of this automatic process. It is meaningful to combine points and lines for the fast generation of reliable matching relationships.
- (3)
- The proposed method can result in both high reliability and high geometric accuracy of the final registration of ALS and TLS data.
Acknowledgments
Conflicts of Interest
References
- Starek, M.J.; Mitasova, H.; Hardin, E.; Weaver, K.; Overton, M.; Harmon, R.S. Modeling and analysis of landscape evolution using airborne, terrestrial, and laboratory laser scanning. Geosphere 2011, 7, 1340–1356. [Google Scholar]
- Van Leeuwen, M.; Hilker, T.; Coops, N.C.; Frazer, G.; Wulder, M.A.; Newnham, G.J.; Culvenorc, D.S. Assessment of standing wood and fiber quality using ground and airborne laser scanning: A review. For. Ecol. Manag 2011, 261, 1467–1478. [Google Scholar]
- Large, A.R.G.; Heritage, G.L.; Charlton, M.E. Laser scanning: The future. Laser Scanning. Environ. Sci 2009, 262–271. [Google Scholar]
- Leberl, F.; Irschara, A.; Pock, T.; Meixner, P.; Gruber, M.; Scholz, S.; Wiechert, A. Point Clouds: Lidar versus 3D Vision. Photogramm. Eng. Remote Sens 2010, 76, 1123–1134. [Google Scholar]
- Bremer, M.; Sass, O. Combining airborne and terrestrial laser scanning for quantifying erosion and deposition by a debris flow event. Geomorphology 2012, 138, 49–60. [Google Scholar]
- Von Hansen, W.; Gross, H.; Thoennessen, U. Line-based registration of terrestrial and airborne LIDAR data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2008, 37, 161–166. [Google Scholar]
- Al-Durgham, M.; Habib, A. A framework for the registration and segmentation of heterogeneous lidar data. Photogramm. Eng. Remote Sens 2013, 79, 135–145. [Google Scholar]
- Ruiz, A.; Kornus, W.; Talaya, J.; Colomer, J.L. Terrain modeling in an extremely steep mountain: A combination of airborne and terrestrial lidar. Proceedings of 20th International Society for Photogrammetry and Remote Sensing (ISPRS) Congress on Geo-imagery Bridging Continents, Istanbul, Turkey, 12–23 July 2004; pp. 281–284.
- Ghuffar, S.; Szekely, B.; Roncat, Andreas; Pfeifer, N. Landslide displacement monitoring using 3D range flow on airborne and terrestrial LiDAR data. Remote Sens 2013, 5, 2720–2745. [Google Scholar]
- Heckmann, T.; Bimböse, M.; Krautblatter, M.; Haas, F.; Becht, M.; Morche, D. From geotechnical analysis to quantification and modelling using LiDAR data: A study on rockfall in the Reintal catchment, Bavarian Alps, Germany. Earth Surf. Process. Landforms 2012, 37, 119–133. [Google Scholar]
- Rentsch, M.; Krismann, A.; Krzystek, P. Extraction of Non-Forest Trees for Biomass Assessment Based on Airborne and Terrestrial LiDAR Data. Proceedings of the 2011 ISPRS conference on Photogrammetric image analysis, Munich, Germany, 5–7 October 2011; pp. 121–132.
- Sampson, C.C.; Fewtrell, T.J.; Duncan, A.; Shaad, K.; Horritt, M.S.; Bates, P.D. Use of terrestrial laser scanning data to drive decimetric resolution urban inundation models. Adv. Water Resour 2012, 41, 1–17. [Google Scholar]
- Hohenthal, J.; Alho, P.; Hyyppä, J.; Hyyppä, H. Laser scanning applications in fluvial studies. Prog. Phys. Geogr 2011, 35, 782–809. [Google Scholar]
- Andrews, J. Merging Surface Reconstructions of Terrestrial and Airborne LIDAR Range Data. Ph.D. Dissertation, University of California, Berkeley, CA, USA. 2009; 41. [Google Scholar]
- Cheng, L.; Gong, J.; Li, M.; Liu, Y. 3D building model reconstruction from multi-view aerial imagery and LiDAR data. Photogramm. Eng. Remote Sens 2011, 77, 125–139. [Google Scholar]
- Cheng, L.; Li, T.; Chen, Y.; Zhang, W.; Shan, J.; Liu, Y.; Li, M. Integration of LiDAR data and optical multi-view images for 3D reconstruction of building roofs. Opt. Lasers Eng 2013, 51, 493–502. [Google Scholar]
- Wu, H.; Li, Y.; Li, J.; Gong, J. A Two-step displacement correction algorithm for registration of lidar point clouds and aerial images without orientation parameters. Photogramm. Eng. Remote Sens 2010, 76, 1135–1145. [Google Scholar]
- Han, J.Y.; Perng, N.H.; Chen, H.J. LiDAR point cloud registration by image detection technique. IEEE Geosci. Remote Sens. Lett 2013, 10, 746–750. [Google Scholar]
- Al Manasir, K.; Fraser, C.S. Registration of terrestrial laser scanner data using imagery. Photogramm. Rec 2006, 21, 255–268. [Google Scholar]
- Akca, D. Matching of 3D surfaces and their intensities. ISPRS J. Photogramm. Remote Sens 2007, 62, 112–121. [Google Scholar]
- Kang, Z.; Li, J.; Zhang, L.; Zhao, Q.; Zlatanova, S. Automatic registration of terrestrial laser scanning point clouds using panoramic reflectance images. Sensors 2009, 9, 2621–2646. [Google Scholar]
- Eo, Y.D.; Pyeon, M.W.; Kim, S.W.; Kim, J.R.; Han, D.Y. Coregistration of terrestrial lidar points by adaptive scale-invariant feature transformation with constrained geometry. Autom. Constr 2012, 25, 49–58. [Google Scholar]
- Besl, P.J.; McKay, N.D. A method for registration of 3-D shapes. IEEE Trans. Pattern Anal. Mach. Intell 1992, 14, 239–256. [Google Scholar]
- He, B.; Lin, Z.; Li, Y.F. An automatic registration algorithm for the scattered point clouds based on the curvature feature. Opt. Laser Technol 2013, 46, 56–60. [Google Scholar]
- Chen, H.; Bhanu, B. 3D free-form object recognition in range images using local surface patches. Pattern Recognit. Lett 2007, 28, 1252–1262. [Google Scholar]
- Makadia, A.; Patterson, A.I.; Daniilidis, K. Fully automatic registration of 3D point clouds. Proceedings of 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New York, NY, USA, 17–22 June 2006; pp. 1297–1304.
- Stamos, I.; Leordeanu, M. Automated feature-based range registration of urban scenes of large scale. Proceedings of 2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New York, NY, USA, 16–22 June 2003; pp. 555–561.
- Jaw, J.J.; Chuang, T.Y. Registration of ground-based LiDAR point clouds by means of 3D line features. J. Chin. Inst. Eng 2008, 31, 1031–1045. [Google Scholar]
- Lee, J.; Yu, K.; Kim, Y.; Habib, A.F. Adjustment of discrepancies between LIDAR data strips using linear features. IEEE Geosci. Remote Sens. Lett 2007, 4, 475–479. [Google Scholar]
- Bucksch, A.; Khoshelham, K. Localized registration of point clouds of botanic trees. IEEE Geosci. Remote Sens. Lett 2013, 10, 631–635. [Google Scholar]
- Von Hansen, W. Robust automatic marker-free registration of terrestrial scan data. Proc. Photogramm. Comput. Vis 2006, 36, 105–110. [Google Scholar]
- Zhang, D.; Huang, T.; Li, G.; Jiang, M. Robust algorithm for registration of building point clouds using planar patches. J. Surv. Eng 2011, 138, 31–36. [Google Scholar]
- Brenner, C.; Dold, C.; Ripperda, N. Coarse orientation of terrestrial laser scans in urban environments. ISPRS J. Photogramm. Remote Sens 2008, 63, 4–18. [Google Scholar]
- Tinkham, W.; Huang, H.; Smith, A.; Shrestha, R.; Falkowski, M.; Hudak, A.; Link, T.; Glenn, N.; Marks, D. A comparison of two open source LiDAR surface classification algorithms. Remote Sens 2011, 3, 638–649. [Google Scholar]
- Yang, C.; Medioni, G. Object modelling by registration of multiple range images. Image Vis. Comput 1992, 10, 145–155. [Google Scholar]
- Rusinkiewicz, S.; Levoy, M. Efficient Variants of the ICP Algorithm. Proceedings of Third International Conference on 3-D Digital Imaging and Modeling, Quebec City, Canada, 28 May–1 June 2001; pp. 145–152.
- Huang, T.; Zhang, D.; Li, G.; Jiang, M. Registration method for terrestrial LiDAR point clouds using geometric features. Opt. Eng 2012, 51, 21111–21114. [Google Scholar]
- Fruh, C.; Zakhor, A. Constructing 3D city models by merging aerial and ground views. IEEE Comput. Graph. Appl 2003, 23, 52–61. [Google Scholar]
- Jaw, J.J.; Chuang, T.Y. Feature-Based Registration of Terrestrial and Aerial LIDAR Point Clouds Towards Complete 3D Scene. Proceedings of the 29th Asian Conference on Remote Sensing, Colombo, Sri Lanka, 10–14 November 2008; pp. 1295–1300.
- Bang, K.I.; Habib, A.F.; Kusevic, K.; Mrstik, P. Integration of terrestrial and airborne LiDAR data for system calibration. Proceedings of The International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Beijing, China, 3–11 July 2008; pp. 391–398.
- Hermosilla, T.; Ruiz, L.; Recio, J.; Estornell, J. Evaluation of automatic building detection approaches combining high resolution images and LiDAR data. Remote Sens 2011, 3, 1188–1210. [Google Scholar]
- Awrangjeb, M.; Zhang, C.; Fraser, C. Building detection in complex scenes thorough effective separation of buildings from trees. Photogramm. Eng. Remote Sens 2012, 78, 729–745. [Google Scholar]
- Meng, X.; Currit, N.; Wang, L.; Yang, X. Detect residential buildings from Lidar and aerial photographs through object-oriented land-use classification. Photogramm. Eng. Remote Sens 2012, 78, 35–44. [Google Scholar]
- Vosselman, G.; Gorte, B.G.H.; Sithole, G.; Rabbani, T. Recognising structure in laser scanner point clouds. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2004, 46, 33–38. [Google Scholar]
- Rabbani, T.; van den Heuvel, F.A.; Vosselmann, G. Segmentation of point clouds using smoothness constraint. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2006, 36, 248–253. [Google Scholar]
- Belton, D.; Lichti, D.D. Classification and segmentation of terrestrial laser scanner point clouds using local variance information. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2006, 36, 44–49. [Google Scholar]
- Schmitt, A.; Vogtle, T. An advanced approach for automatic extraction of planar surfaces and their topology from point clouds. Photogrammetrie Fernerkundung Geoinf 2009, 1, 43–52. [Google Scholar]
- Pu, S.; Vosselman, G. Knowledge based reconstruction of building models from terrestrial laser scanning data. ISPRS J. Photogramm. Remote Sens 2009, 64, 575–584. [Google Scholar]
- Manandhar, D.; Shibasaki, R. Auto-extraction of urban features from vehicle-borne laser data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2002, 34, 650–655. [Google Scholar]
- Tong, L.; Cheng, L.; Li, M.; Chen, Y.; Wang, Y.; Zhang, W. Extraction of building contours and corners from terrestrial LiDAR data. J. Image Graph 2013, 18, 1–10. [Google Scholar]
- Li, B.; Li, Q.; Shi, W.; Wu, F. Feature extraction and modeling of urban building from vehicle-borne laser scanning data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2004, 35, 934–939. [Google Scholar]
- Hammoudi, K.; Dornaika, F.; Paparoditis, N. Extracting building footprints from 3D point clouds using terrestrial laser scanning at street level. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci 2009, 38, 65–70. [Google Scholar]




| Horizontal Error (m) | Vertical Error (m) | Total Error (m) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Average | Max | RMSE | Average | Max | RMSE | Average | Max | RMSE | |
| Airborne corner | 0.66 | 1.22 | 0.73 | 0.20 | 0.29 | 0.21 | 0.70 | 1.24 | 0.77 |
| Terrestrial corner | 0.25 | 0.38 | 0.26 | 0.11 | 0.21 | 0.11 | 0.27 | 0.39 | 0.29 |
| Horizontal Error (m) | Vertical Error (m) | Total Error (m) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Average | Max | RMSE | Average | Max | RMSE | Average | Max | RMSE | |
| Proposed method | 0.44 | 0.77 | 0.49 | 0.15 | 0.34 | 0.18 | 0.50 | 0.79 | 0.53 |
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Cheng, L.; Tong, L.; Li, M.; Liu, Y. Semi-Automatic Registration of Airborne and Terrestrial Laser Scanning Data Using Building Corner Matching with Boundaries as Reliability Check. Remote Sens. 2013, 5, 6260-6283. https://doi.org/10.3390/rs5126260
Cheng L, Tong L, Li M, Liu Y. Semi-Automatic Registration of Airborne and Terrestrial Laser Scanning Data Using Building Corner Matching with Boundaries as Reliability Check. Remote Sensing. 2013; 5(12):6260-6283. https://doi.org/10.3390/rs5126260
Chicago/Turabian StyleCheng, Liang, Lihua Tong, Manchun Li, and Yongxue Liu. 2013. "Semi-Automatic Registration of Airborne and Terrestrial Laser Scanning Data Using Building Corner Matching with Boundaries as Reliability Check" Remote Sensing 5, no. 12: 6260-6283. https://doi.org/10.3390/rs5126260