A Novel Integrated Algorithm for Wind Vector Retrieval from Conically Scanning Scatterometers
Abstract
:1. Introduction
2. Algorithm Description
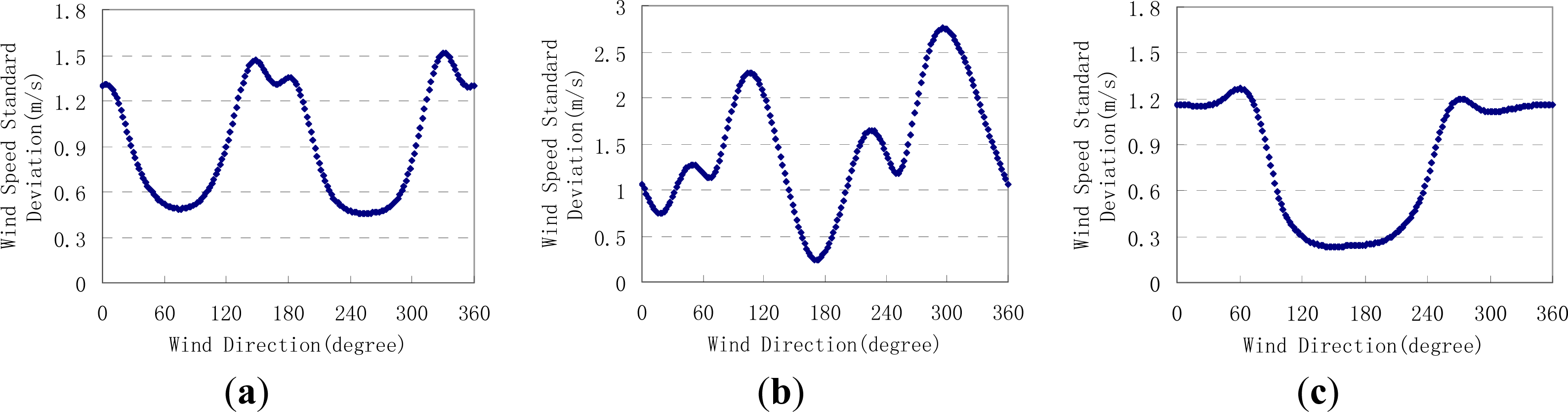
2.1. Wind Speed Standard Deviation Algorithm
- (1)
- Set the wind direction intervals for the coarse search and fine search steps. Let the wind direction be 0 degrees.
- (2)
- Determine the wind speed for each σ0 observation by Geophysical Model Function, and calculate the average and the standard deviation of all the wind speeds at this given wind direction by Equation (1).
- (3)
- Move to the next wind direction by a coarse direction interval, repeat step (2) until all the average and standard deviation values of wind speeds are calculated for each wind direction position within the range between 0 and 360 degree.
- (4)
- Search and rank the local minima of Equation (1) along wind direction. Record the local minima and their corresponding wind speed average values and wind directions as ambiguities.
- (5)
- For each wind vector solution identified by step (4), take its neighboring left (or right) wind direction as the current wind direction and calculate the average and standard deviation of wind speed by Equation (1). A smaller wind direction interval is used in updating the current wind direction. Here, left wind direction refers to the one with smaller value, and right wind direction corresponds to the larger one with respect to the current wind direction.
- (6)
- Compare the wind speed standard deviation value of the left (or right) wind direction with that of the current wind direction, if the former is smaller, then continue to move the current position to the left (or right) direction, else move the current position to the right (or left) direction.
- (7)
- Continue to search along the wind direction until the wind speed standard deviation value of the current wind direction is smaller than that of the left (or right) wind direction, or it exceeds the effective range of [0,360]. Take the wind speed standard deviation of the current wind direction as a local minimum.
- (8)
- Repeat steps (5) to (7) for all the other coarse ambiguities.
- (9)
- Rank and save up to four precise local minima as the final possible ambiguities.
2.2. New Integrated Wind Vector Retrieval Algorithm
- (1)
- Take the wind direction of the ambiguity solution as the right wind direction dr, and calculate the current wind direction dc by the following equation:
- (2)
- Calculate the wind speed standard deviation Sc at the current wind direction using Equation (1).
- (3)
- Similarly, calculate the left wind direction dl using the following equation:
- (4)
- Calculate the wind speed standard deviation Sl at the left wind direction.
- (5)
- Calculate the change rate of wind speed standard deviation for the current wind direction using Equation (2).
- (6)
- Update the right and current direction with the current and left direction respectively and repeat steps (2) to (6) until the change rate k is larger than the given threshold k0.
2.3. Modified Ambiguity Removal Algorithm
- Step 1: Initialize the wind field by selecting an ambiguity whose direction is closest to that of the NWP wind at each wind vector cell. This procedure is called nudging. It should be noted that the behavior of selecting the closest solution in nudging inevitably assimilates some information of the NWP wind field into the retrieval system. Therefore the quality of the retrieved wind field will partly depend on the quality of the NWP wind field.
- Step 2: Perform the circle median filter over the entire swath until no wind direction is changed in a pass or a maximum iterative time is reached. For the detailed description of the circle median filter, see [15].
- Step 3: Nudge the filtered wind field by the NWP wind direction once again. However, this time, it is a conditional nudging in which only if the difference between the current wind direction and the NWP wind direction is larger than the threshold value, would the operation of nudging be conducted at this wind vector cell. Statistical analysis found that about 95 percent of the co-located buoy and NWP data pairs have a wind direction difference less than 60°. Hence, if a wind direction deviates from the co-located NWP more than 60°, then it can be regarded as a small probability event. Based on this consideration, the threshold value was set to be 60° in this paper.
2.4. Wind Speed Refinement
3. Data Preparation
3.1. Data Reading and Screening
3.2. Temporal and Spatial Matching
- (1)
- Spatial precise matching
- (2)
- Temporal precise matching
3.3. Data Preprocessing
- (1)
- Atmospheric correction of σ0
- (2)
- Conversion of wind speed to 10 m height
- (3)
- Removal of exceptional data points
4. Retrieval Experiments
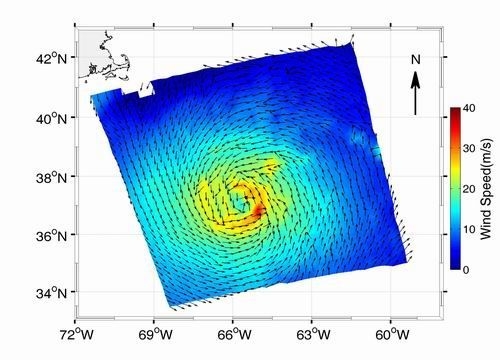
4.1. Experiment Data and Parameters
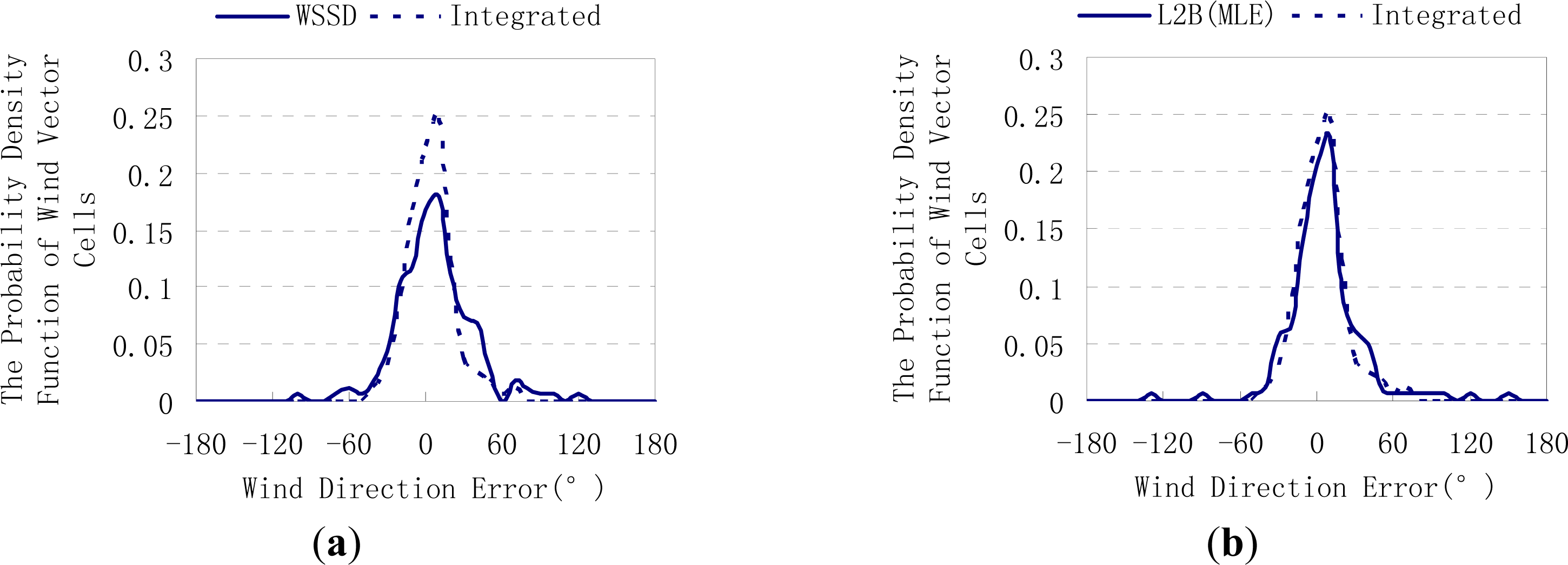
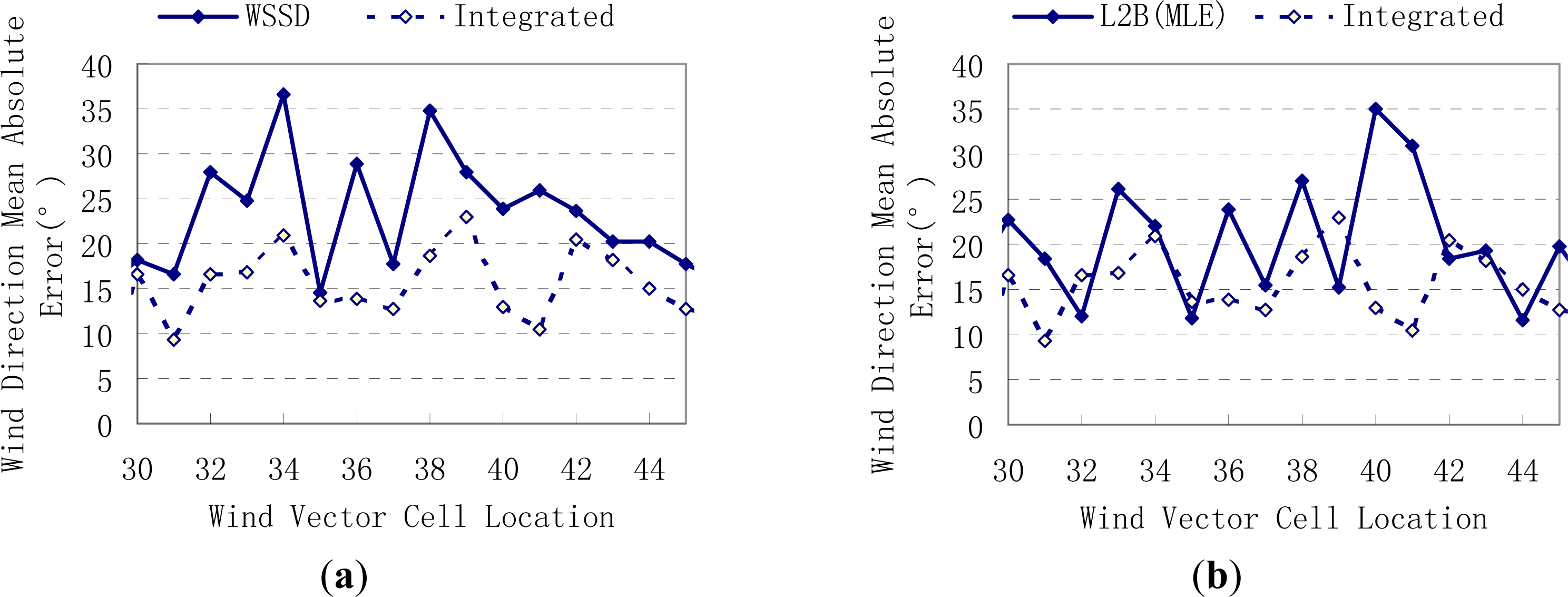
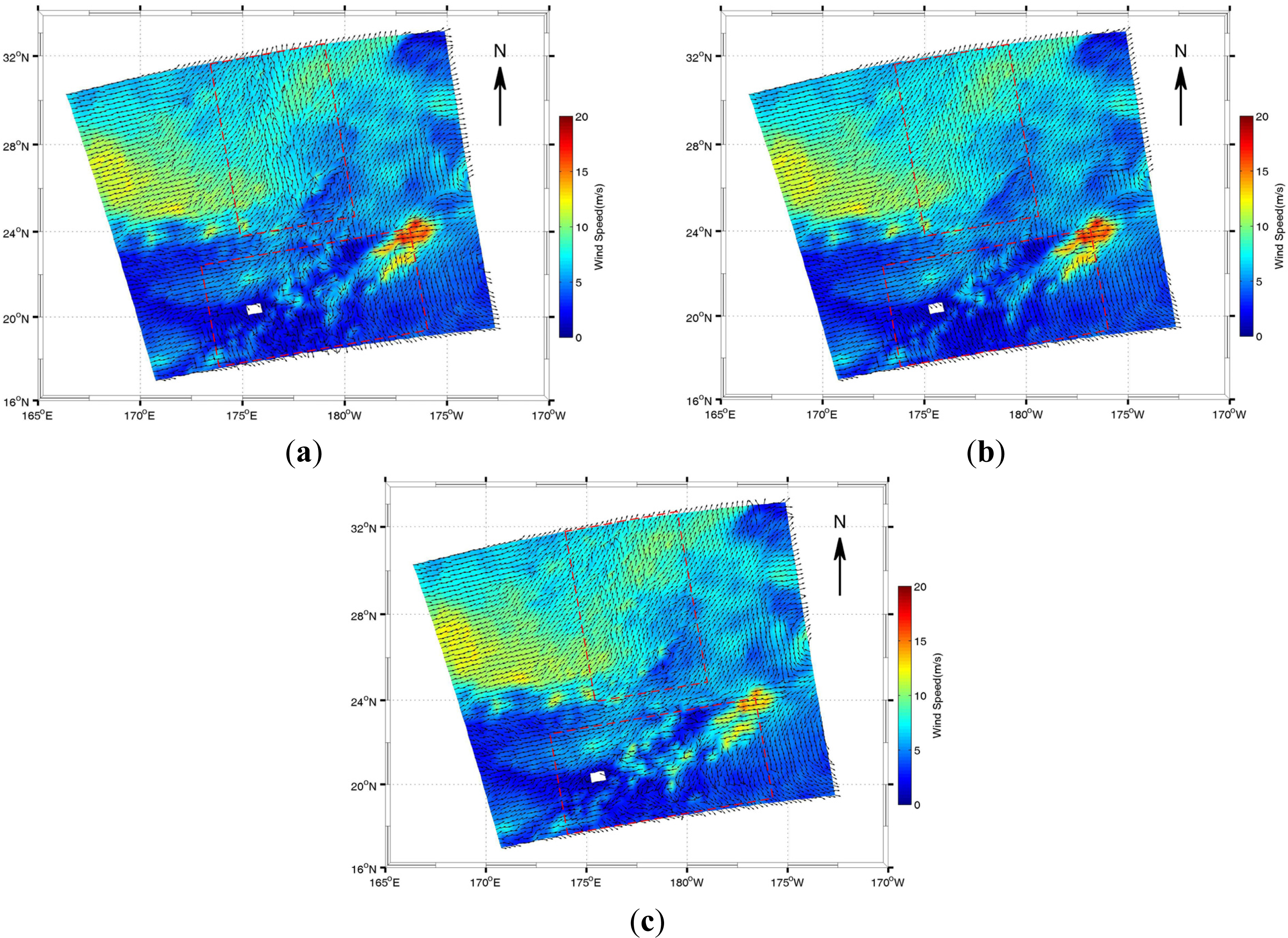
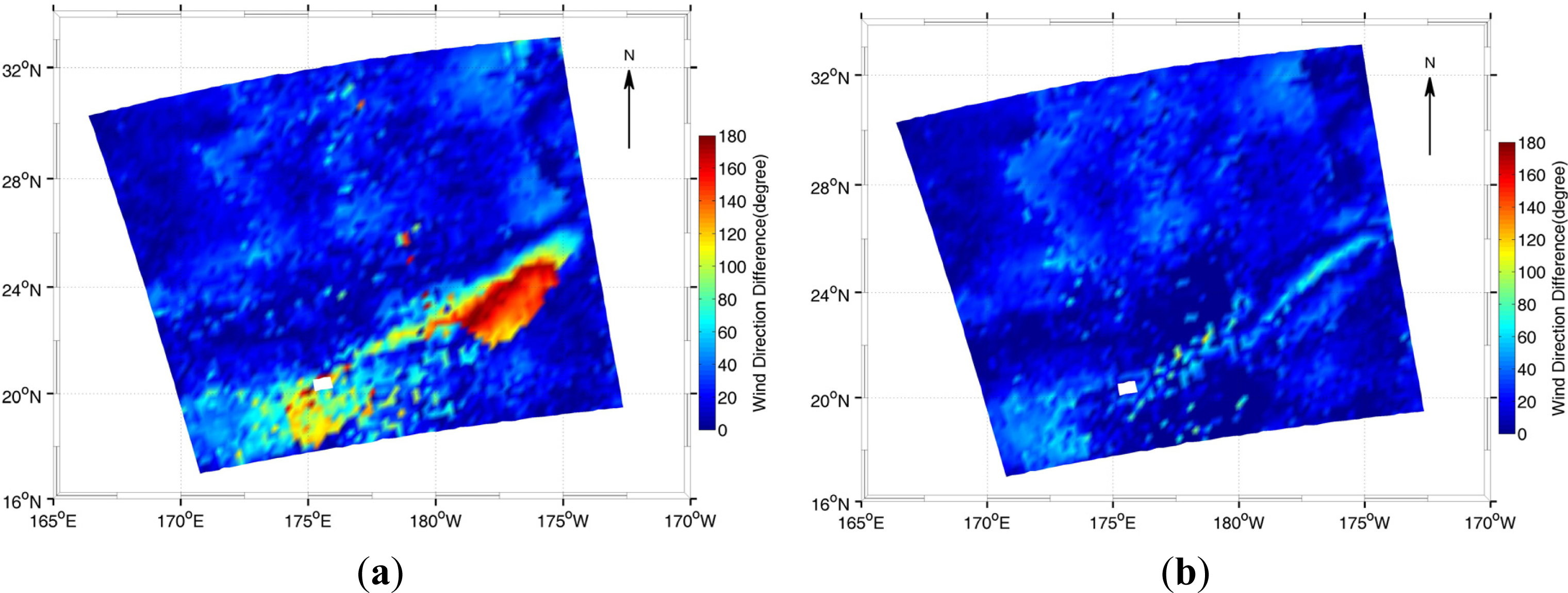
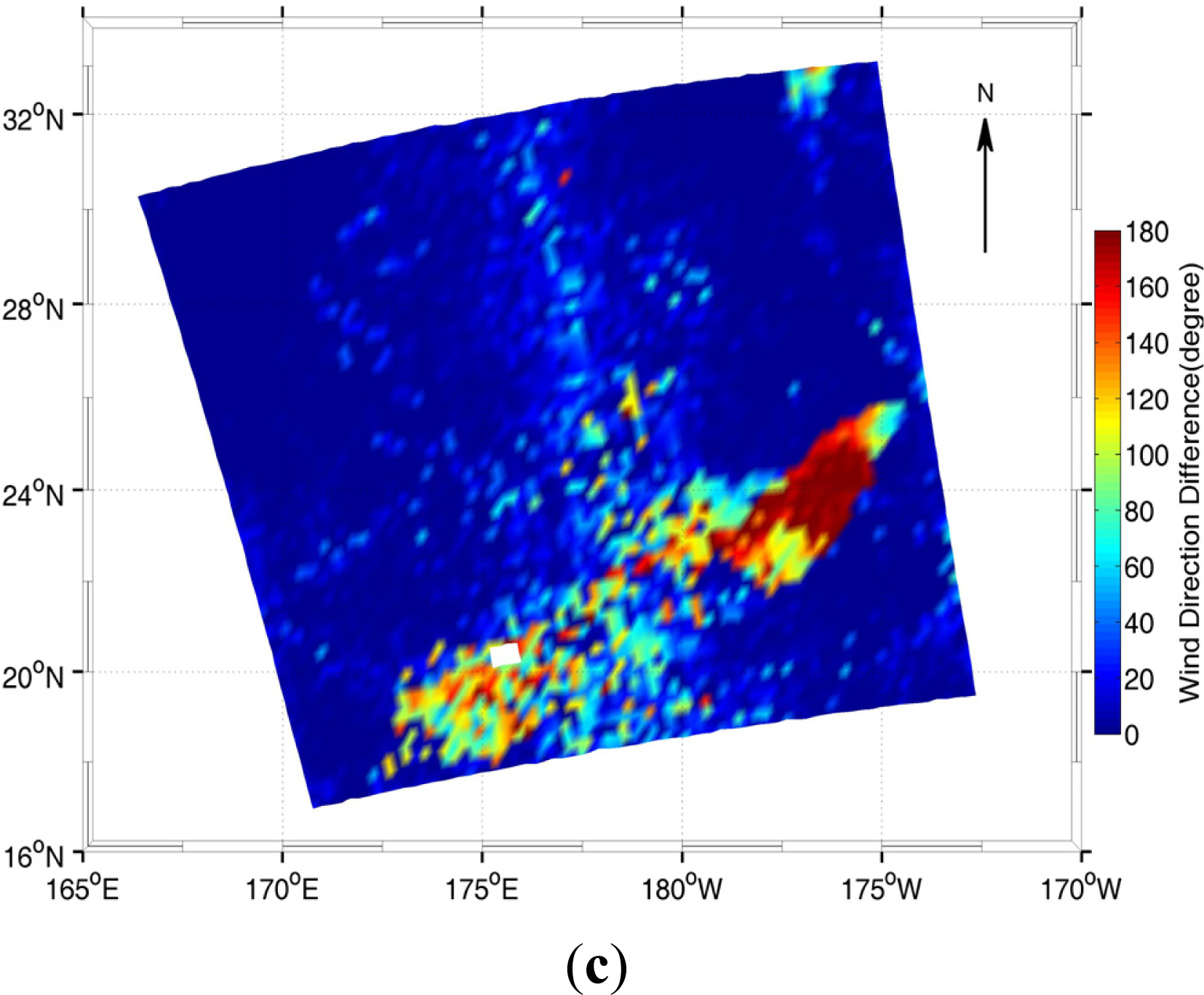
4.2. Experiment Results
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Schroeder, L.C.; Boggs, D.H.; Dome, G.J.; Halberstam, I.M.; Jones, W.L.; Pierson, W.J.; Wentz, F.J. The relationship between wind vector and normalized radar cross section used to derive SEASAT-A satellite scatterometer winds. J. Geophys. Res 1982, 87, 3318–3336. [Google Scholar]
- Jones, W.L.; Schroeder, L.C.; Boggs, D.H.; Bracalente, E.M.; Brown, R.A.; Dome, G.J.; Pierson, W.J.; Wentz, F.J. The SEASAT-A satellite scatterometer: The geophysical evaluation of remote sensed wind vectors over the ocean. J. Geophys. Res 1982, 87, 3297–3317. [Google Scholar]
- Wentz, F.J.; Peteherych, S.; Thomas, L.A. A model function for ocean radar cross sections at 14.6 GHz. J. Geophys. Res 1984, 89, 3689–3740. [Google Scholar]
- Wentz, F.J.; Mattox, L.A. New algorithms for microwave measurements of ocean winds: Application to seasat and the special sensor microwave imager. J. Geophys. Res 1986, 91, 2289–2307. [Google Scholar]
- Nghiem, S.V.; Li, F.K.; Neumann, G. Ku-Band Ocean Backscatter Functions for Surface Wind Retrieval. Proceedings of the IEEE Geosicence and Remote Sensing Symposium, Lincoln Nebraska, NE, USA, 27–31 May 1996; 3, pp. 1469–1471.
- Wentz, F.J.; Smith, D.K. A model function for ocean radar cross sections at 14 GHz derived from NSCAT observations. J. Geophys. Res 1999, 104, 11499–11514. [Google Scholar]
- Chi, C.Y.; Li, F.K. A comparative study of several wind estimation algorithms for spaceborne scatterometers. IEEE Trans. Geosci. Remote Sens 1988, 26, 115–121. [Google Scholar]
- Stoffelen, A.; Anderson, D. Scatterometer data interpretation: Measurement space and inversion. J. Atmos. Ocean. Technol 1997, 14, 1298–1313. [Google Scholar]
- Stoffelen, A.; Portabella, M. On Bayesian scatterometer wind inversion. IEEE Trans. Geosci. Remote Sens 2006, 44, 1523–1533. [Google Scholar]
- Freilich, M.H. SeaWinds Algorithm Theoretical Basis Document. Available online: http://podaac.jpl.nasa.gov/quikscat/qscat-doc/html (accessed on 18 March 2002).
- Xie, X.T.; Fang, Y.; Chen, X.X.; Chen, K.H. A New Fast Wind Vector Retrieval Algorithm for SeaWinds Scatterometer. Proceedings of the 2005 IEEE Geoscience and Remote Sensing Symposium, Seoul, Korea, 25–29 July 2005; V, pp. 3298–3301.
- Stiles, B.W.; Pollard, B.D.; Dunbar, R.S. Direction interval retrieval with thresholded nudging: A method for improving the accuracy of QuikSCAT winds. IEEE Trans. Geosci. Remote Sens 2002, 40, 79–89. [Google Scholar]
- Xie, X.T.; Lin, M.S.; Huang, Z.; Zou, J.H.; Tian, D.X.; Liu, L.X.; Wang, X.N.; Dong, S.W. A Modified Wind Vector Retrieval Algorithm for Polarimetric Scatterometer. Proceedings of the IEEE Geosicence and Remote Sensing Symposium, Hawaii, HI, USA, 25–30 July 2010; pp. 52–55.
- Xie, X.T.; Lin, M.S.; Chen, K.H.; Huang, Z.; Liu, L.X.; Tian, D.X.; Wang, X.N.; Chen, W.X.; He, R.R.; Zou, J.H. A Wind Direction Extension Based Algorithm for Scatterometer Wind Vector Retrieval. Proceedings of the IEEE Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 2821–2824.
- Shaffer, S.J.; Dunbar, R.S.; Hsaio, S.V.; Long, D.G. A median-filter-based ambiguity removal algorithm for NSCAT. IEEE Trans. Geosci. Remote Sens 1991, 29, 167–173. [Google Scholar]
- Weiss, B. L2A Data Software Interface Specification (SIS-2). Available online: ftp://ftp.scp.byu.edu/data/qscat/docs/PD686-644-2.pdf (accessed on 15 May 2013).
- Elfouhaily, T.; Chapron, B.; Katsaros, K. A unified directional spectrum for long and short wind-driven waves. J. Geophys. Res 1997, 102, 15781–15796. [Google Scholar]
- Fung, A.K.; Lee, K.K. A semi-empirical sea spectrum model for scattering coefficient estimation. IEEE J. Ocean. Eng 1982, (OE-7), 166–176. [Google Scholar]



| Error | Region | SeaWinds L2B Data | Traditional WSSD Algorithm | Integrated Algorithm |
|---|---|---|---|---|
| wind speed mean absolute error (m/s) | nadir | 0.764 | 0.762 | 0.710 |
| middle | 0.760 | 0.695 | 0.696 | |
| outer | 0.753 | 0.684 | 0.667 | |
| wind direction mean absolute error (°) | nadir | 20.912 | 23.881 | 15.783 |
| middle | 14.601 | 13.979 | 12.994 | |
| outer | 13.162 | 13.474 | 12.095 | |
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Xie, X.; Huang, Z.; Lin, M.; Chen, K.; Lan, Y.; Yuan, X.; Ye, X.; Zou, J. A Novel Integrated Algorithm for Wind Vector Retrieval from Conically Scanning Scatterometers. Remote Sens. 2013, 5, 6180-6197. https://doi.org/10.3390/rs5126180
Xie X, Huang Z, Lin M, Chen K, Lan Y, Yuan X, Ye X, Zou J. A Novel Integrated Algorithm for Wind Vector Retrieval from Conically Scanning Scatterometers. Remote Sensing. 2013; 5(12):6180-6197. https://doi.org/10.3390/rs5126180
Chicago/Turabian StyleXie, Xuetong, Zhou Huang, Mingsen Lin, Kehai Chen, Youguo Lan, Xinzhe Yuan, Xiaomin Ye, and Juhong Zou. 2013. "A Novel Integrated Algorithm for Wind Vector Retrieval from Conically Scanning Scatterometers" Remote Sensing 5, no. 12: 6180-6197. https://doi.org/10.3390/rs5126180