A Production Efficiency Model-Based Method for Satellite Estimates of Corn and Soybean Yields in the Midwestern US
Abstract
:1. Introduction
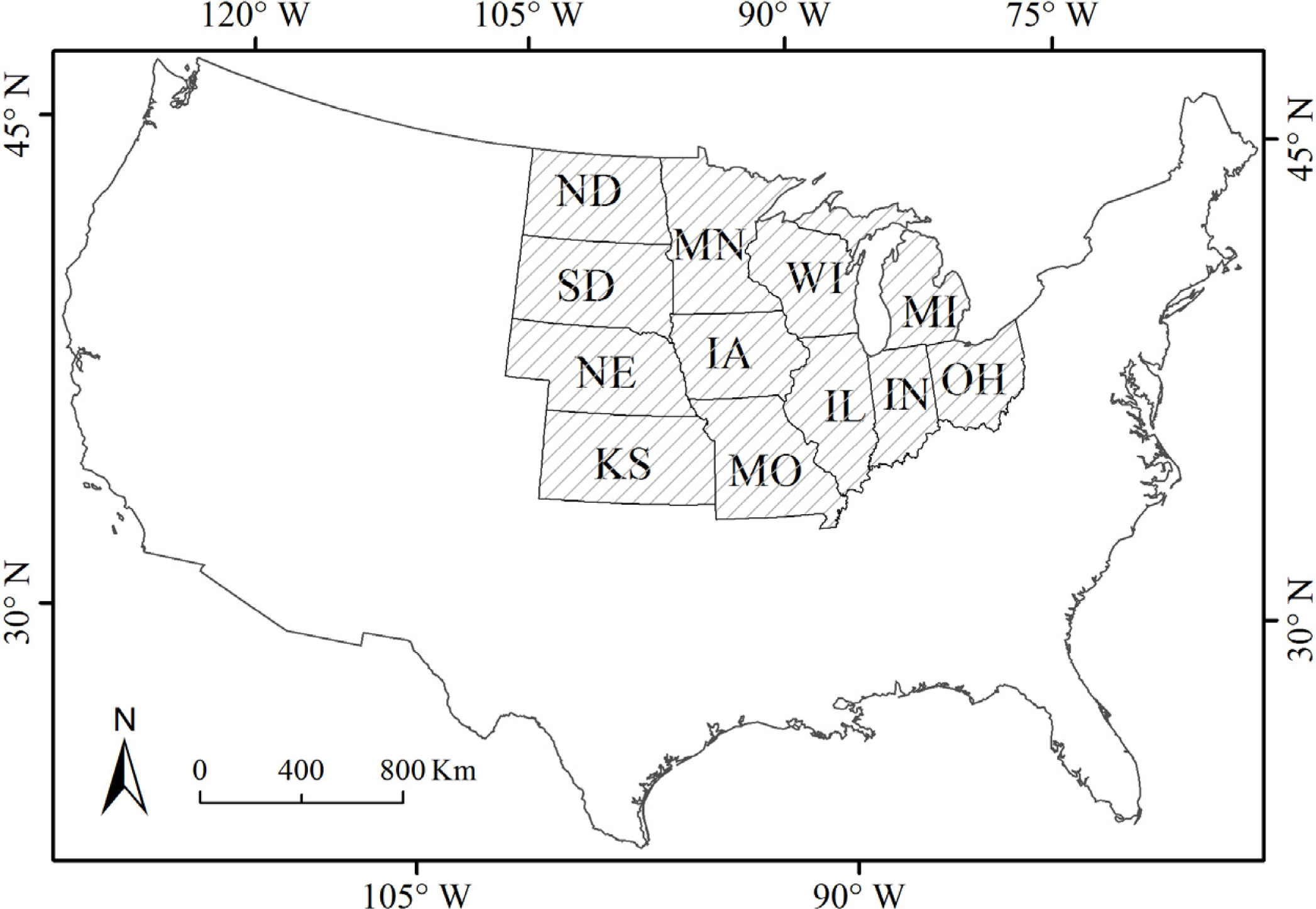
2. Study Area and Materials
3. Theoretical Background and Improvements
3.1. A Brief Description of the MOD17 Algorithm
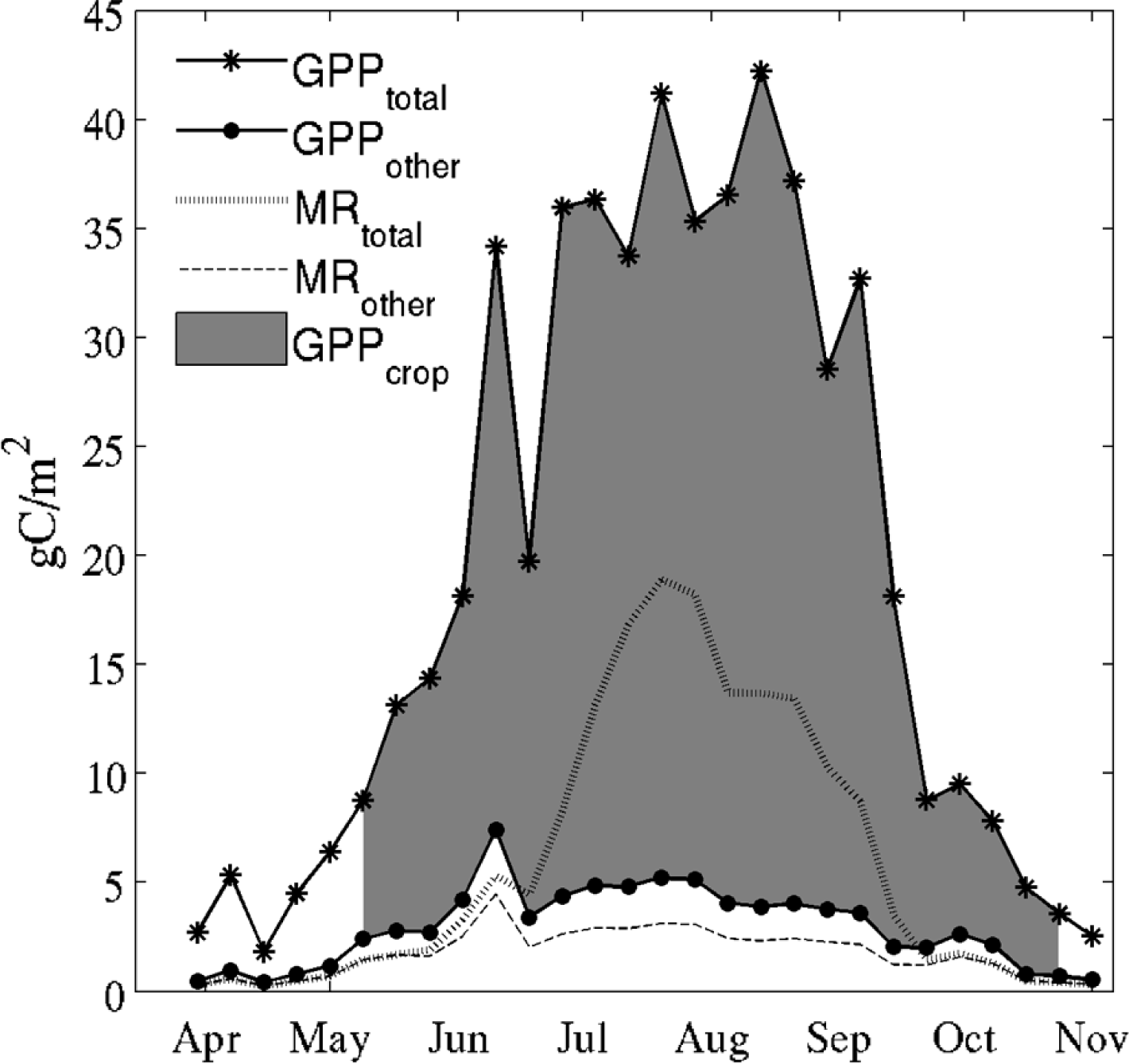
3.2. Improvements to Estimate Crop Productivity
3.3. Converting MODIS GPP Estimates to Crop Yields
4. Results
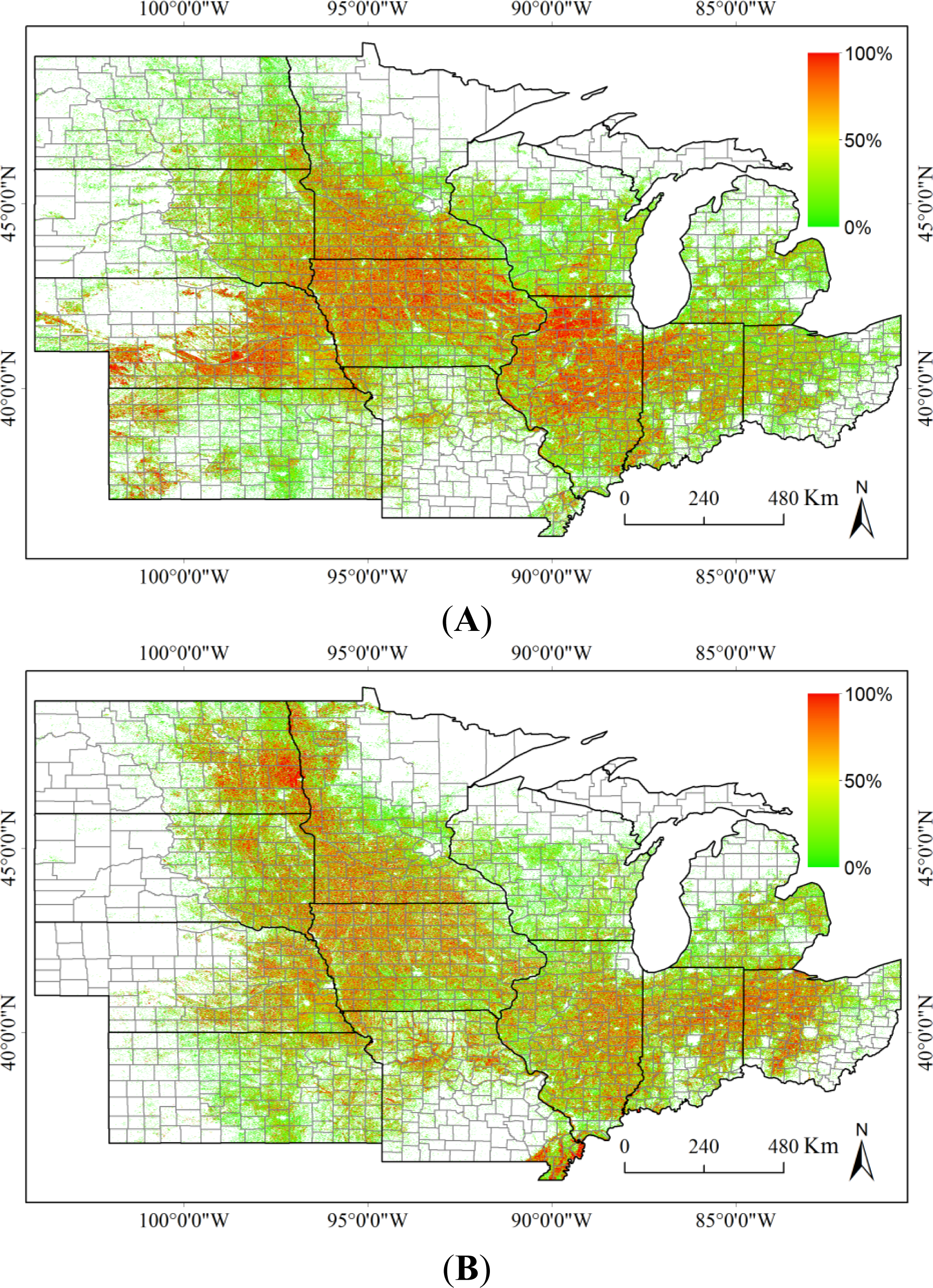
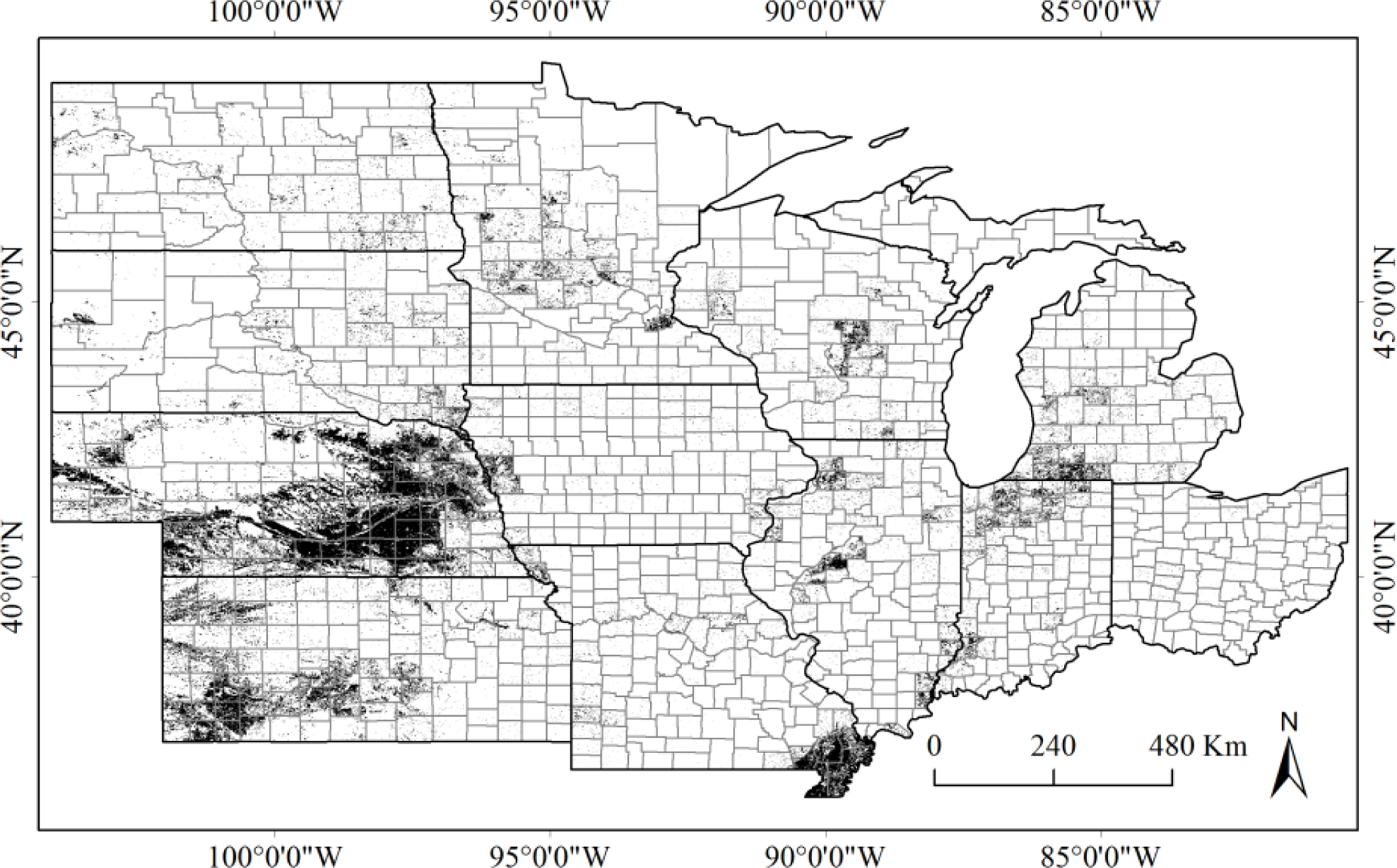
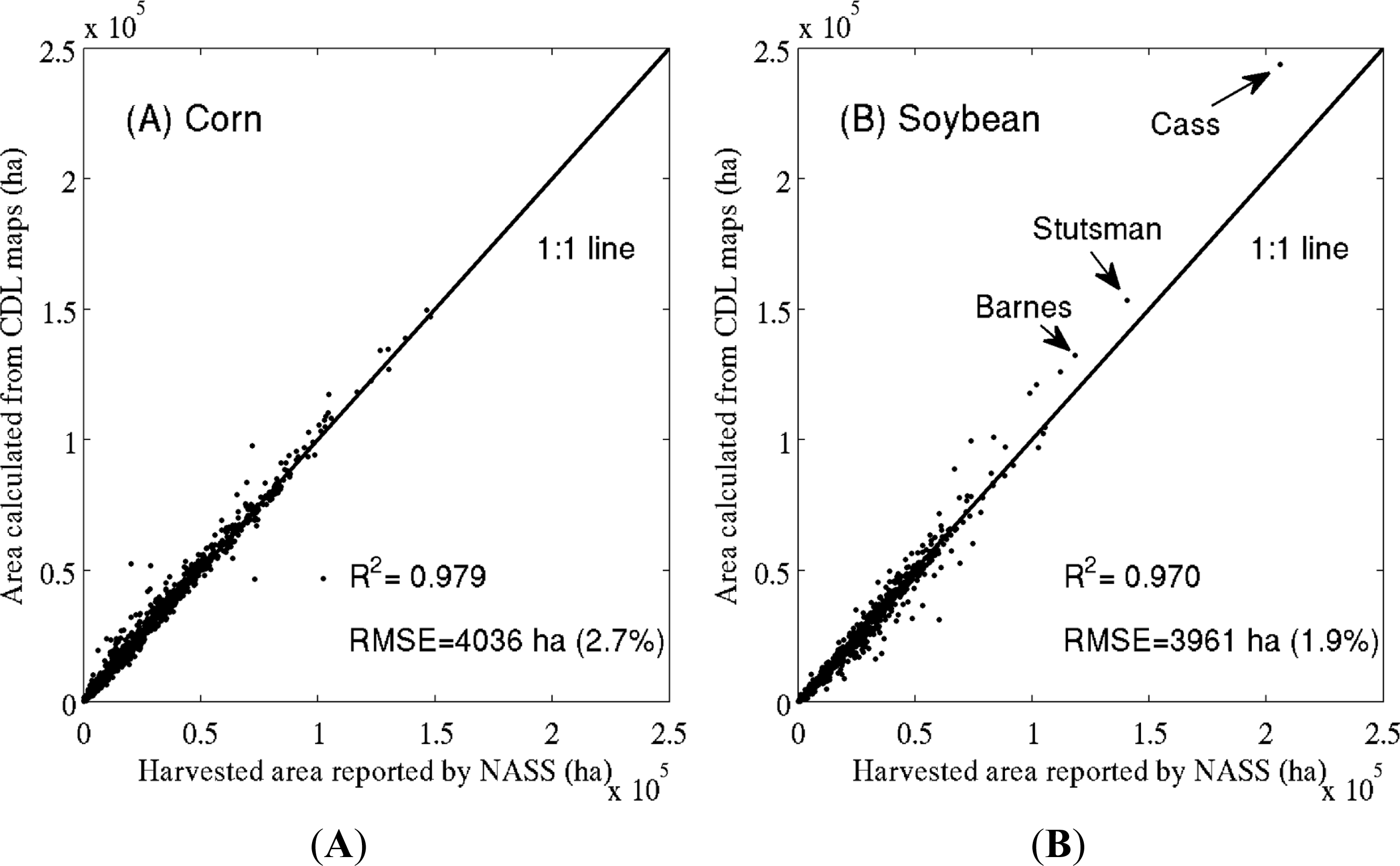
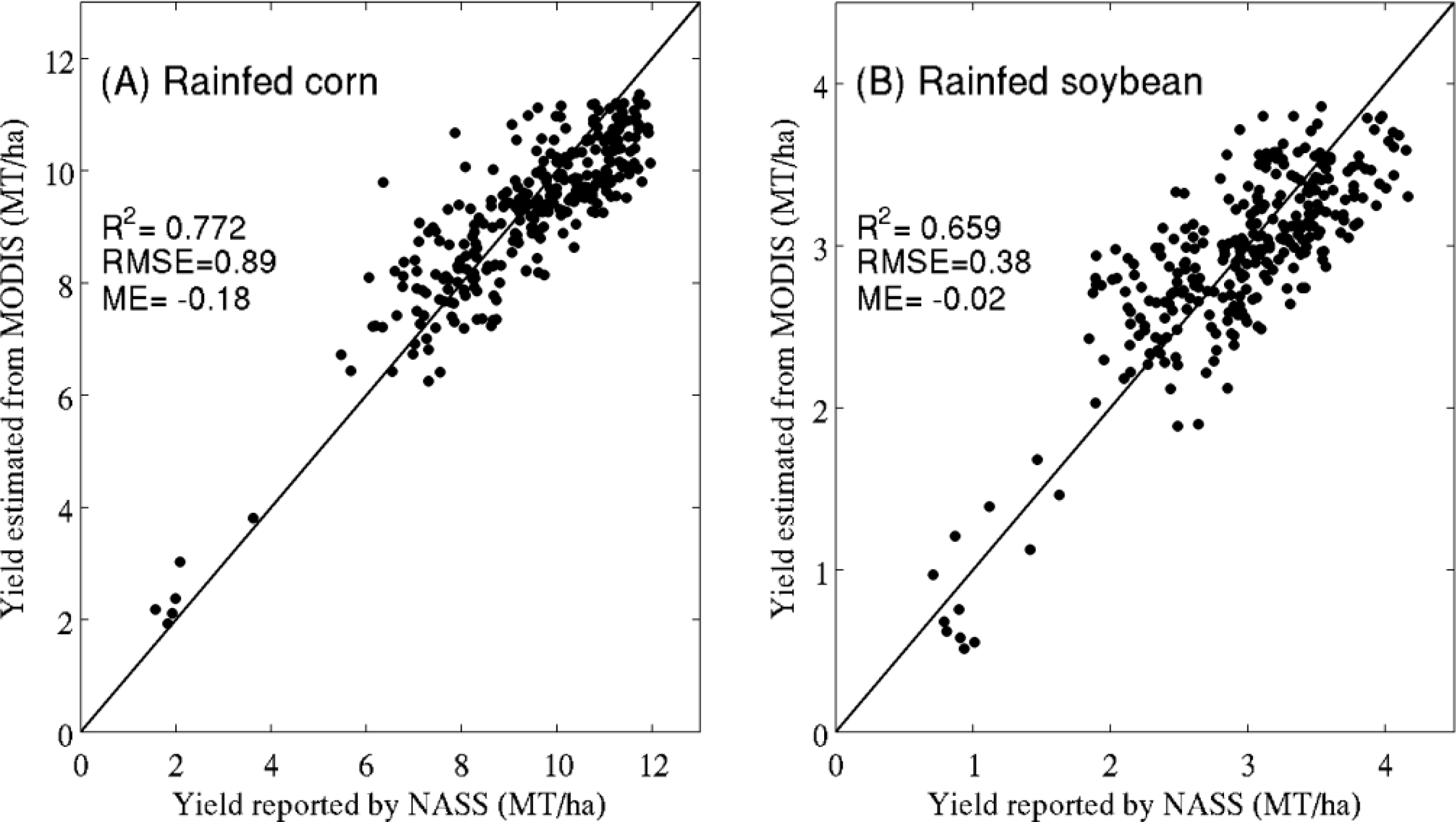
4.1. Analysis at the County Level
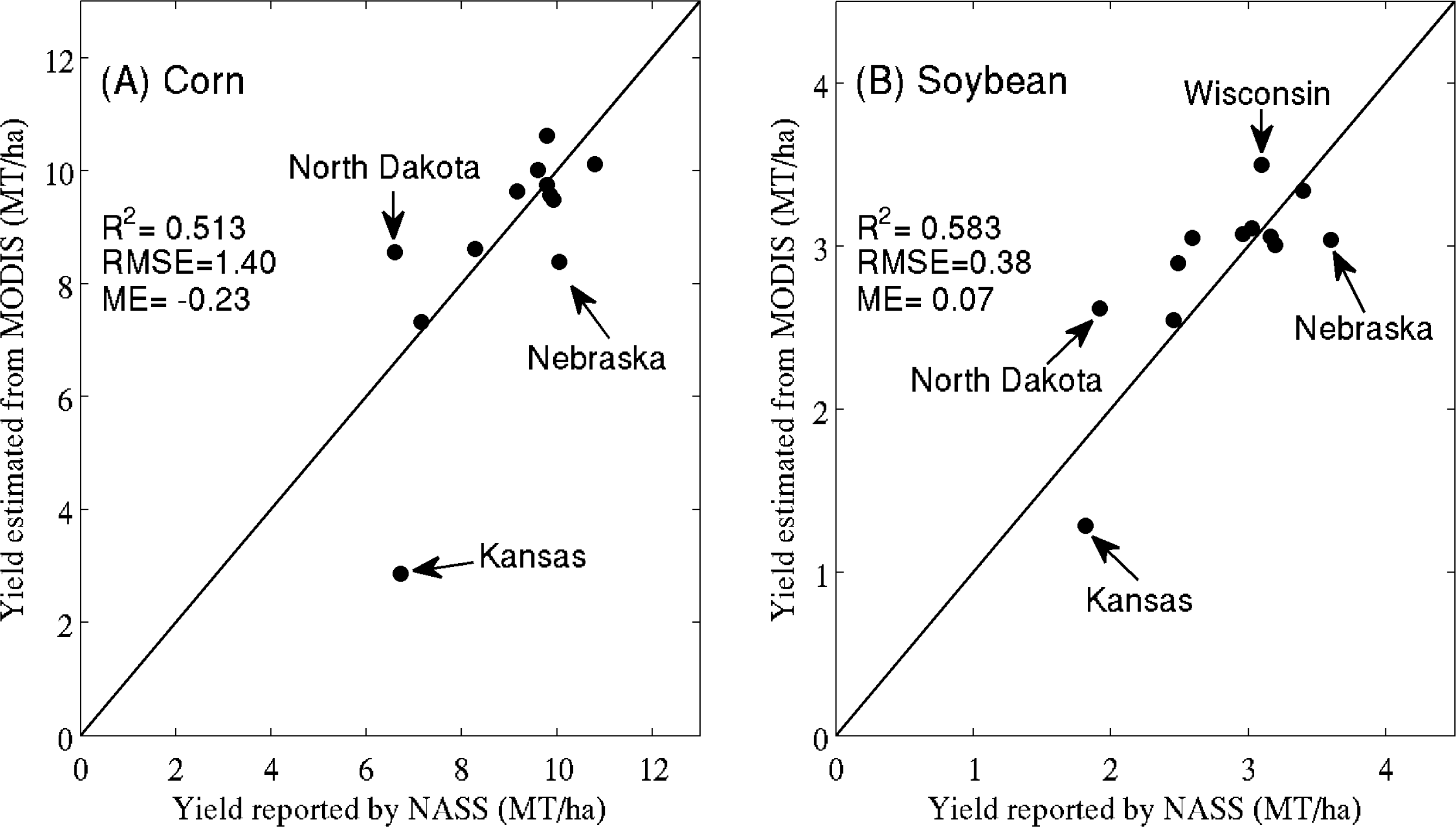
4.2. Analysis at the State Level
5. Discussions
5.1. Major Findings
5.2. Limitations and Future Improvements
6. Conclusions
Acknowledgments
Conflict of Interest
References
- Hertel, T.W.; Burke, M.B.; Lobell, D.B. The poverty implications of climate-induced crop yield changes by 2030. Glob. Environ. Chang 2010, 20, 577–585. [Google Scholar]
- Lobell, D.B.; Schlenker, W.; Costa-Roberts, J. Climate trends and global crop production since 1980. Science 2011, 333, 616–620. [Google Scholar]
- Doraiswamy, P.C.; Moulin, S.; Cook, P.W.; Stern, A. Crop yield assessment from remote sensing. Photogramm. Eng. Remote Sens. 2003, 69, 665–674. [Google Scholar]
- Friedl, M.A.; McIver, D.K.; Hodges, J.C.F.; Zhang, X.Y.; Muchoney, D.; Strahler, A.H.; Woodcock, C.E.; Gopal, S.; Schneider, A.; Cooper, A.; et al. Global land cover mapping from MODIS: Algorithms and early results. Remote Sens.Environ 2002, 83, 287–302. [Google Scholar]
- Gong, P.; Wang, J.; Yu, L.; Zhao, Y.; Zhao, Y.; Liang, L.; Niu, Z.; Huang, X.; Fu, H.; Liu, S. Finer resolution observation and monitoring of global land cover: First mapping results with Landsat TM and ETM+ data. Int. J. Remote Sens. 2013, 34, 2607–2654. [Google Scholar]
- Thenkabail, P.S.; Wu, Z. An automated cropland classification algorithm (ACCA) for Tajikistan by combining Landsat, MODIS, and secondary data. Remote Sens. 2012, 4, 2890–2918. [Google Scholar]
- Pan, Y.; Li, L.; Zhang, J.; Liang, S.; Zhu, X.; Sulla-Menashe, D. Winter wheat area estimation from MODIS-EVI time series data using the crop proportion phenology index. Remote Sens.Environ 2012, 119, 232–242. [Google Scholar]
- Vancutsem, C.; Marinho, E.; Kayitakire, F.; See, L.; Fritz, S. Harmonizing and combining existing land cover/land use datasets for cropland area monitoring at the African continental scale. Remote Sens. 2012, 5, 19–41. [Google Scholar]
- Myneni, R.B.; Hall, F.G.; Sellers, P.J.; Marshak, A.L. The interpretation of spectral vegetation indexes. IEEE Trans. Geosci. Remote Sens. 1995, 33, 481–486. [Google Scholar]
- Myneni, R.B.; Nemani, R.R.; Running, S.W. Estimation of global leaf area index and absorbed par using radiative transfer models. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1380–1393. [Google Scholar]
- Veroustraete, F.; Patyn, J.; Myneni, R.B. Estimating net ecosystem exchange of carbon using the normalized difference vegetation index and an ecosystem model. Remote Sens.Environ 1996, 58, 115–130. [Google Scholar]
- Thenkabail, P.S.; Smith, R.B.; de Pauw, E. Hyperspectral vegetation indices and their relationships with agricultural crop characteristics. Remote Sens.Environ 2000, 71, 158–182. [Google Scholar]
- Atzberger, C. Advances in remote sensing of agriculture: Context description, existing operational monitoring systems and major information needs. Remote Sens. 2013, 5, 949–981. [Google Scholar]
- Moulin, S.; Bondeau, A.; Delecolle, R. Combining agricultural crop models and satellite observations: From field to regional scales. Int. J. Remote Sens. 1998, 19, 1021–1036. [Google Scholar]
- Becker-Reshef, I.; Vermote, E.; Lindeman, M.; Justice, C. A generalized regression-based model for forecasting winter wheat yields in Kansas and Ukraine using MODIS data. Remote Sens.Environ 2010, 114, 1312–1323. [Google Scholar]
- Mulianga, B.; Bégué, A.; Simoes, M.; Todoroff, P. Forecasting regional sugarcane yield based on time integral and spatial aggregation of MODIS NDVI. Remote Sens. 2013, 5, 2184–2199. [Google Scholar]
- Panda, S.S.; Ames, D.P.; Panigrahi, S. Application of vegetation indices for agricultural crop yield prediction using neural network techniques. Remote Sens. 2010, 2, 673–696. [Google Scholar]
- Reeves, M.C.; Zhao, M.; Running, S.W. Usefulness and limits of MODIS GPP for estimating wheat yield. Int. J. Remote Sens. 2005, 26, 1403–1421. [Google Scholar]
- Claverie, M.; Demarez, V.; Duchemin, B.; Hagolle, O.; Ducrot, D.; Marais-Sicre, C.; Dejoux, J.-F.; Huc, M.; Keravec, P.; Béziat, P. Maize and sunflower biomass estimation in southwest France using high spatial and temporal resolution remote sensing data. Remote Sens.Environ 2012, 124, 844–857. [Google Scholar] [Green Version]
- Launay, M.; Guerif, M. Assimilating remote sensing data into a crop model to improve predictive performance for spatial applications. Agric. Ecosyst. Environ 2005, 111, 321–339. [Google Scholar]
- Mishra, V.; Cruise, J.F.; Mecikalski, J.R.; Hain, C.R.; Anderson, M.C. A remote-sensing driven tool for estimating crop stress and yields. Remote Sens. 2013, 5, 3331–3356. [Google Scholar]
- Fumoto, T.; Kobayashi, K.; Li, C.; Yagi, K.; Hasegawa, T. Revising a process-based biogeochemistry model (DNDC) to simulate methane emission from rice paddy fields under various residue management and fertilizer regimes. Glob. Chang. Biol 2008, 14, 382–402. [Google Scholar]
- Jones, J.W.; Hoogenboom, G.; Porter, C.H.; Boote, K.J.; Batchelor, W.D.; Hunt, L.A.; Wilkens, P.W.; Singh, U.; Gijsman, A.J.; Ritchie, J.T. The DSSAT cropping system model. Eur. J. Agron 2003, 18, 235–265. [Google Scholar]
- Keating, B.A.; Carberry, P.S.; Hammer, G.L.; Probert, M.E.; Robertson, M.J.; Holzworth, D.; Huth, N.I.; Hargreaves, J.N.G.; Meinke, H.; Hochman, Z.; et al. An overview of APSIM, a model designed for farming systems simulation. Eur. J. Agron 2003, 18, 267–288. [Google Scholar]
- Krobel, R.; Smith, W.N.; Grant, B.B.; Desjardins, R.L.; Campbell, C.A.; Tremblay, N.; Li, C.S.; Zentner, R.P.; McConkey, B.G. Development and evaluation of a new Canadian spring wheat sub-model for DNDC. Can. J. Soil. Sci 2011, 91, 503–520. [Google Scholar]
- Tonitto, C.; David, M.B.; Drinkwater, L.E.; Li, C.S. Application of the DNDC model to tile-drained Illinois agroecosystems: model calibration, validation, and uncertainty analysis. Nutr. Cycl. Agroecosyst 2007, 78, 51–63. [Google Scholar]
- Monteith, J.L. Solar-radiation and productivity in tropical ecosystems. J. Appl. Ecol 1972, 9, 747–766. [Google Scholar]
- Monteith, J.L. Climate and efficiency of crop production in Britain. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci 1977, 281, 277–294. [Google Scholar]
- Potter, C.S.; Randerson, J.T.; Field, C.B.; Matson, P.A.; Vitousek, P.M.; Mooney, H.A.; Klooster, S.A. Terrestrial ecosystem production—A process model-based on global satellite and surface data. Glob. Biogeochem. Cy 1993, 7, 811–841. [Google Scholar]
- Ruimy, A.; Saugier, B.; Dedieu, G. Methodology for the estimation of terrestrial net primary production from remotely sensed data. J. Geophys. Res.: Atmos 1994, 99, 5263–5283. [Google Scholar]
- Running, S.W.; Coughlan, J.C. A general-model of forest ecosystem processes for regional applications. 1. Hydrologic balance, canopy gas-exchange and primary production processes. Ecol. Model 1988, 42, 125–154. [Google Scholar]
- Running, S.W.; Justice, C.O.; Salomonson, V.; Hall, D.; Barker, J.; Kaufmann, Y.J.; Strahler, A.H.; Huete, A.R.; Muller, J.P.; Vanderbilt, V.; et al. Terrestrial remote-sensing science and algorithms planned for EOS MODIS. Int. J. Remote Sens. 1994, 15, 3587–3620. [Google Scholar]
- Liu, J.; Pattey, E.; Miller, J.R.; McNairn, H.; Smith, A.; Hu, B. Estimating crop stresses, aboveground dry biomass and yield of corn using multi-temporal optical data combined with a radiation use efficiency model. Remote Sens.Environ 2010, 114, 1167–1177. [Google Scholar]
- Lobell, D.B.; Asner, G.P.; Ortiz-Monasterio, J.I.; Benning, T.L. Remote sensing of regional crop production in the Yaqui Valley, Mexico: Estimates and uncertainties. Agric. Ecosyst. Environ 2003, 94, 205–220. [Google Scholar]
- Lobell, D.B.; Hicke, J.A.; Asner, G.P.; Field, C.B.; Tucker, C.J.; Los, S.O. Satellite estimates of productivity and light use efficiency in United States agriculture, 1982–98. Glob. Chang. Biol 2002, 8, 722–735. [Google Scholar]
- Heinsch, F.A.; Reeves, M.; Votava, P.; Kang, S.; Milesi, C.; Zhao, M.; Glassy, J.; Jolly, W.M.; Loehman, R.; Bowker, C.F. User’s Guide GPP and NPP (MOD17A2/A3) Products NASA MODIS Land Algorithm; MODIS Land Team: Washington, DC, USA, 2003; pp. 1–57. [Google Scholar]
- Zhao, M.; Heinsch, F.A.; Nemani, R.R.; Running, S.W. Improvements of the MODIS terrestrial gross and net primary production global data set. Remote Sens.Environ 2005, 95, 164–176. [Google Scholar]
- Turner, D.P.; Urbanski, S.; Bremer, D.; Wofsy, S.C.; Meyers, T.; Gower, S.T.; Gregory, M. A cross-biome comparison of daily light use efficiency for gross primary production. Glob. Chang. Biol 2003, 9, 383–395. [Google Scholar]
- Rembold, F.; Atzberger, C.; Savin, I.; Rojas, O. Using low resolution satellite imagery for yield prediction and yield anomaly detection. Remote Sens. 2013, 5, 1704–1733. [Google Scholar]
- Turner, D.P.; Gower, S.T.; Cohen, W.B.; Gregory, M.; Maiersperger, T.K. Effects of spatial variability in light use efficiency on satellite-based NPP monitoring. Remote Sens. Environ 2002, 80, 397–405. [Google Scholar]
- Li, A.N.; Liang, S.L.; Wang, A.S.; Qin, J. Estimating crop yield from multi-temporal satellite data using multivariate regression and neural network techniques. Photogramm. Eng. Remote Sens. 2007, 73, 1149–1157. [Google Scholar]
- Myneni, R.B.; Hoffman, S.; Knyazikhin, Y.; Privette, J.L.; Glassy, J.; Tian, Y.; Wang, Y.; Song, X.; Zhang, Y.; Smith, G.R.; et al. Global products of vegetation leaf area and fraction absorbed PAR from year one of MODIS data. Remote Sens.Environ 2002, 83, 214–231. [Google Scholar]
- USGS Earth Resources Observation and Science (EROS) Center. Available online: http://eros.usgs.gov/ (accessed on 1 November 2013).
- USGS Land Processes Distributed Active Archive Center (LP DAAC). Available online: https://lpdaac.usgs.gov/ (accessed on 1 November 2013).
- National Agricultural Statistics Service (NASS). Quick Stats Database. Available online: http://www.nass.usda.gov/Quick_Stats/ (accessed on 1 November 2013).
- Han, W.G.; Yang, Z.W.; Di, L.P.; Mueller, R. CropScape: A web service based application for exploring and disseminating US conterminous geospatial cropland data products for decision support. Comput. Electron. Agric 2012, 84, 111–123. [Google Scholar]
- Pervez, M.S.; Brown, J.F. Mapping irrigated lands at 250-m scale by merging MODIS data and national agricultural statistics. Remote Sens. 2010, 2, 2388–2412. [Google Scholar]
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.S.; Reeves, M.; Hashimoto, H. A continuous satellite-derived measure of global terrestrial primary production. Bioscience 2004, 54, 547–560. [Google Scholar]
- Running, S.W.; Thornton, P.E.; Nemani, R.; Glassy, J.M. Global terrestrial gross and net primary productivity from the earth observing system. Method. Ecosyst. Sci 2000, 5, 44–57. [Google Scholar]
- de Wit, A.; Duveiller, G.; Defourny, P. Estimating regional winter wheat yield with WOFOST through the assimilation of green area index retrieved from MODIS observations. Agric. For. Meteorol 2012, 164, 39–52. [Google Scholar]
- Lindquist, J.L.; Arkebauer, T.J.; Walters, D.T.; Cassman, K.G.; Dobermann, A. Maize radiation use efficiency under optimal growth conditions. Agron. J 2005, 97, 72–78. [Google Scholar]
- Sinclair, T.R.; Muchow, R.C. Radiation use efficiency. Adv. Agron 1999, 65, 215–265. [Google Scholar]
- Singer, J.W.; Meek, D.W.; Sauer, T.J.; Prueger, J.H.; Hatfield, J.L. Variability of light interception and radiation use efficiency in maize and soybean. Field Crop. Res 2011, 121, 147–152. [Google Scholar]
- DeLucia, E.; Drake, J.E.; Thomas, R.B.; Gonzalez-Meler, M. Forest carbon use efficiency: Is respiration a constant fraction of gross primary production? Glob. Chang. Biol 2007, 13, 1157–1167. [Google Scholar]
- Liang, S.; Zheng, T.; Liu, R.; Fang, H.; Tsay, S.-C.; Running, S. Estimation of incident photosynthetically active radiation from Moderate resolution imaging spectrometer data. J. Geophys. Res.: Atmos 2006, 111, 1–13. [Google Scholar]
- Prince, S.D.; Haskett, J.; Steininger, M.; Strand, H.; Wright, R. Net primary production of US Midwest croplands from agricultural harvest yield data. Ecol. Appl 2001, 11, 1194–1205. [Google Scholar]
- Kiniry, J.R.; Williams, J.R.; Vanderlip, R.L.; Atwood, J.D.; Reicosky, D.C.; Mulliken, J.; Cox, W.J.; Mascagni, H.J.; Hollinger, S.E.; Wiebold, W.J. Evaluation of two maize models for nine US locations. Agron. J 1997, 89, 421–426. [Google Scholar]
- Schapaugh, W.T.; Wilcox, J.R. Relationships between harvest indexes and other plant characteristics in soybeans. Crop. Sci 1980, 20, 529–533. [Google Scholar]
- Bolton, D.K.; Friedl, M.A. Forecasting crop yield using remotely sensed vegetation indices and crop phenology metrics. Agric. For. Meteorol 2013, 173, 74–84. [Google Scholar]
- Suyker, A.E.; Verma, S.B.; Burba, G.G.; Arkebauer, T.J. Gross primary production and ecosystem respiration of irrigated maize and irrigated soybean during a growing season. Agric. For. Meteorol 2005, 131, 180–190. [Google Scholar]
| Data Type | Data Source | Description |
|---|---|---|
| satellite data | USGS EROS center | MODIS LAI/FPAR data (MOD15A2) |
| USGS EROS center | MODIS vegetation productivity data (MOD17A2) | |
| classification maps | NASS Cropland Data Layer | crop-type specific classification maps at 30 or 56 m |
| USGS early warning program | a classification map of irrigated areas at 250 m | |
| national survey | NASS Quick Stats | statistics of crop yields and harvested areas |
| Parameter | Description | Corn | Soybean | Units |
|---|---|---|---|---|
| ε | the radiation use efficiency | 3.35 | 1.44 | g·MJ−1 PAR |
| RS | the root: shoot ratio | 0.18 | 0.15 | dimensionless |
| HI | the harvest index | 0.53 | 0.42 | dimensionless |
| MC | the moisture content of the grain | 0.11 | 0.10 | dimensionless |
| Year | Corn | Soybean | ||||
|---|---|---|---|---|---|---|
| R2 | RMSE (MT/ha) | ME (MT/ha) | R2 | RMSE (MT/ha) | ME (MT/ha) | |
| 2009 | 0.55 (0.15) | 1.21 (5.52) | −0.60 (−5.39) | 0.50 (0.35) | 0.38 (0.86) | −0.07 (0.77) |
| 2010 | 0.54 (0.22) | 1.17 (4.65) | −0.14 (−4.38) | 0.73 (0.53) | 0.30 (0.97) | −0.09 (0.89) |
| 2011 | 0.77 (0.46) | 0.89 (4.56) | −0.18 (−4.28) | 0.66 (0.53) | 0.38 (1.06) | −0.02 (0.95) |
| Year | Corn Production | Soybean Production | ||||
|---|---|---|---|---|---|---|
| Estimated (Tg) | Reported (Tg) | Error | Estimated (Tg) | Reported (Tg) | Error | |
| 2009 | 253.6 | 291.7 | −13.04% | 68.2 | 75.6 | −9.74% |
| 2010 | 268.1 | 276.3 | −2.95% | 73.9 | 77.7 | −4.79% |
| 2011 | 273.0 | 277.1 | −1.49% | 69.8 | 70.2 | −0.56% |
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Xin, Q.; Gong, P.; Yu, C.; Yu, L.; Broich, M.; Suyker, A.E.; Myneni, R.B. A Production Efficiency Model-Based Method for Satellite Estimates of Corn and Soybean Yields in the Midwestern US. Remote Sens. 2013, 5, 5926-5943. https://doi.org/10.3390/rs5115926
Xin Q, Gong P, Yu C, Yu L, Broich M, Suyker AE, Myneni RB. A Production Efficiency Model-Based Method for Satellite Estimates of Corn and Soybean Yields in the Midwestern US. Remote Sensing. 2013; 5(11):5926-5943. https://doi.org/10.3390/rs5115926
Chicago/Turabian StyleXin, Qinchuan, Peng Gong, Chaoqing Yu, Le Yu, Mark Broich, Andrew E. Suyker, and Ranga B. Myneni. 2013. "A Production Efficiency Model-Based Method for Satellite Estimates of Corn and Soybean Yields in the Midwestern US" Remote Sensing 5, no. 11: 5926-5943. https://doi.org/10.3390/rs5115926







