Using Visible Spectral Information to Predict Long-Wave Infrared Spectral Emissivity: A Case Study over the Sokolov Area of the Czech Republic with an Airborne Hyperspectral Scanner Sensor
Abstract
:1. Introduction
1.1. Approaches to Handling the Missing Data Problem
1.2. Importance of LWIR Sensors and Their Relation to Reflectance
1.3. Missing Data Scenarios in This Study
1.4. Paper Outline
2. Materials and Methods
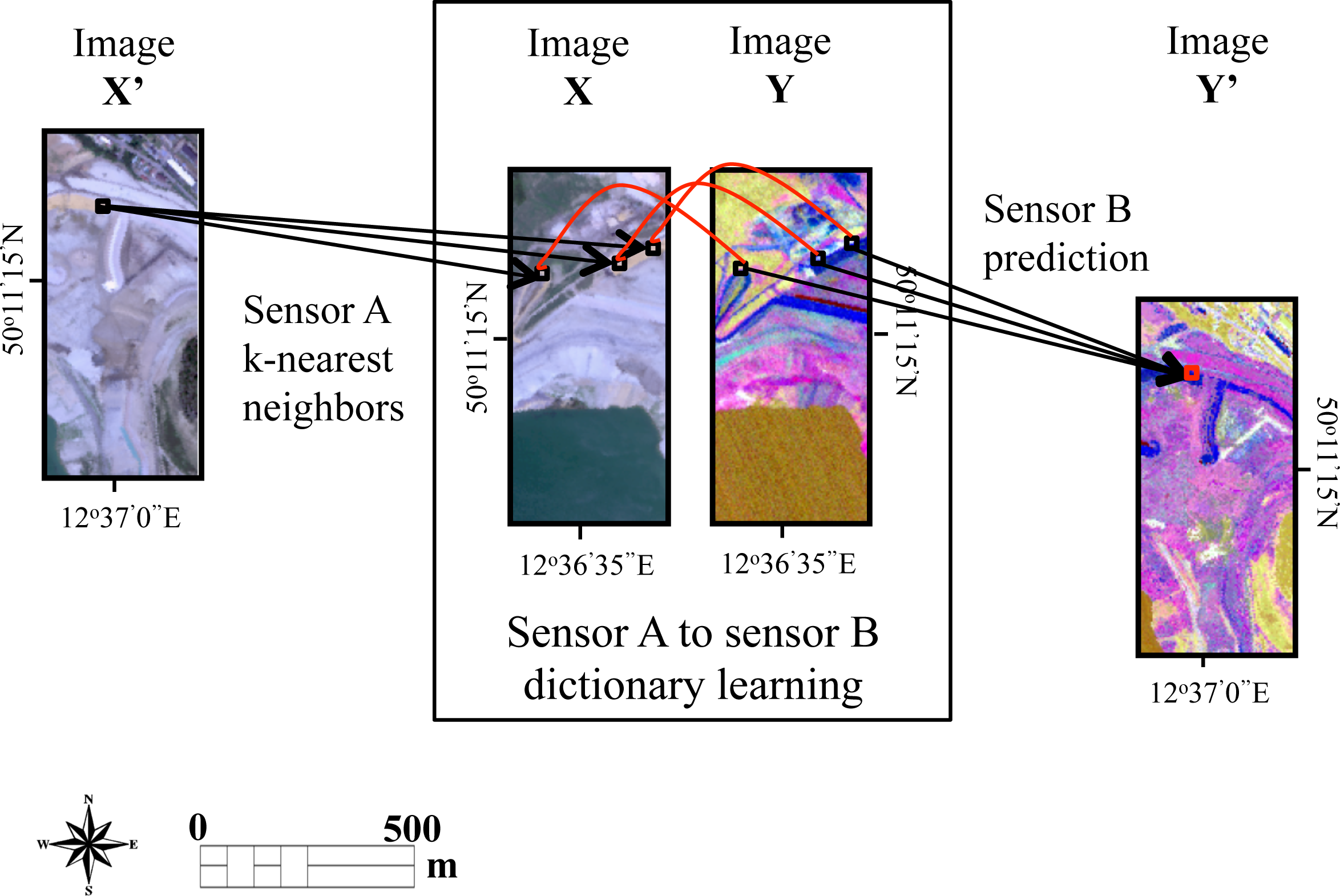
2.1. Sensor-to-Sensor Prediction (SENTOS) Method

2.2. Study Area
2.2.1. Flight Acquisition, Sensor Description, Band Selection and Preprocessing
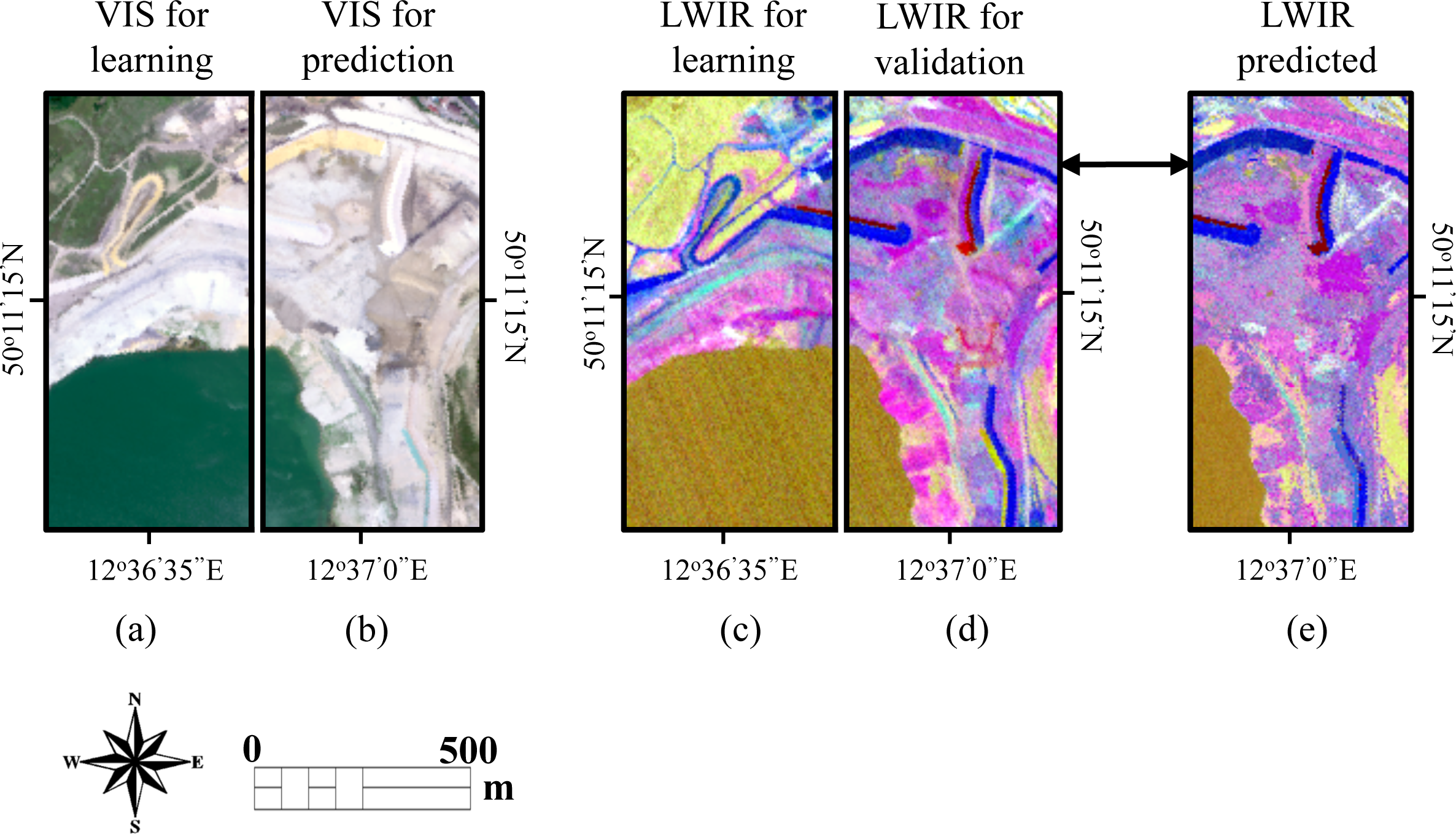
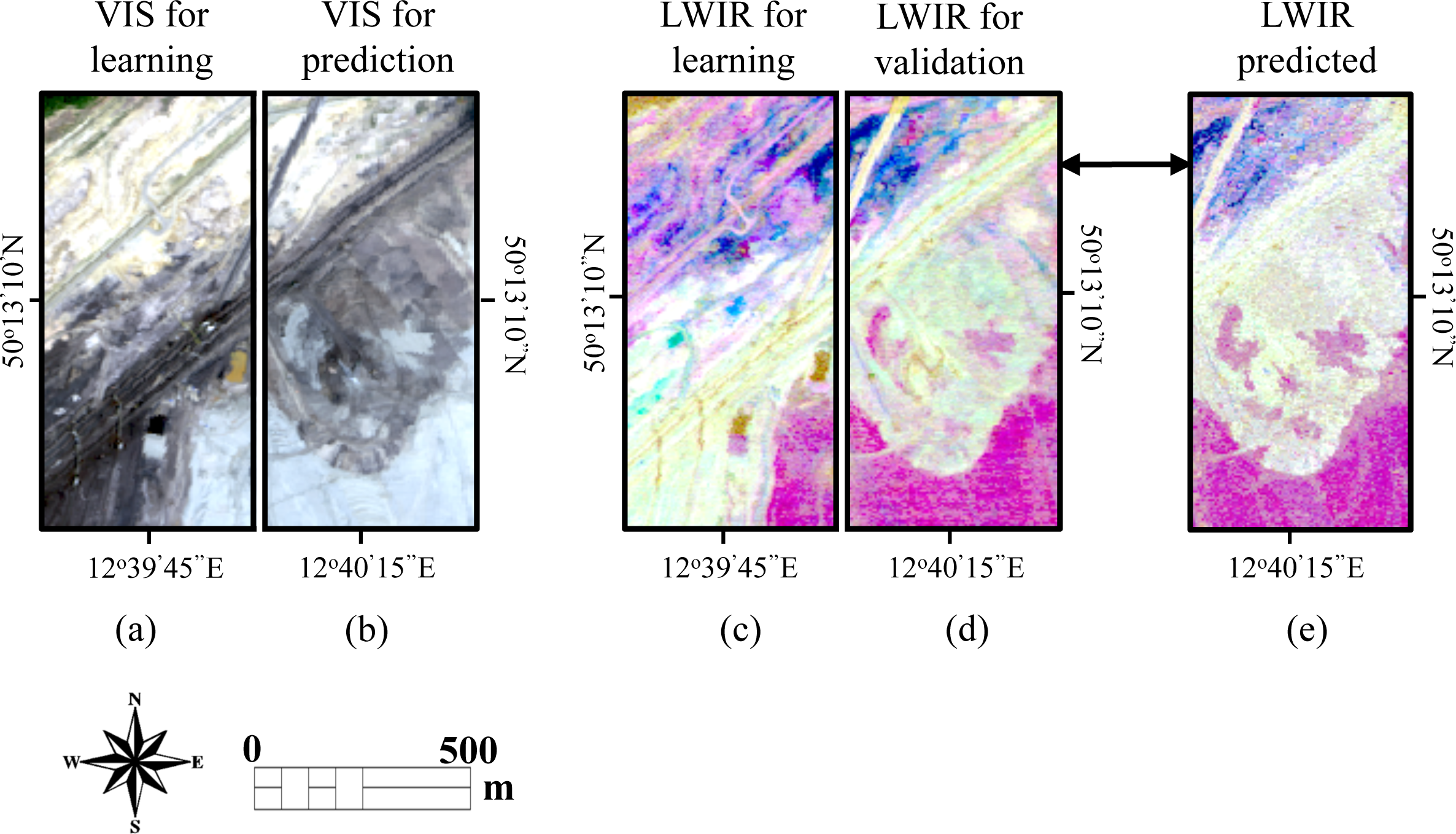
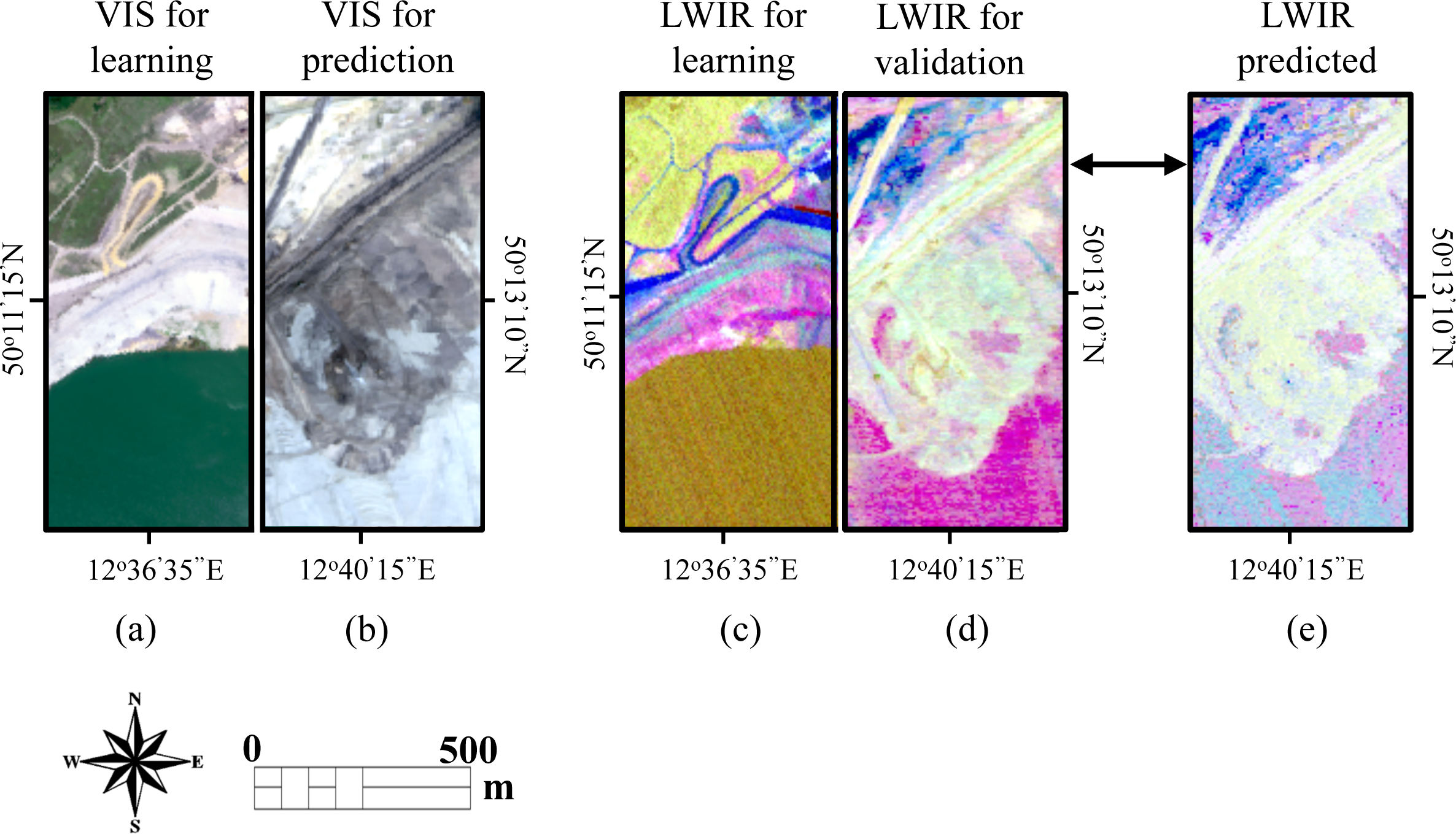
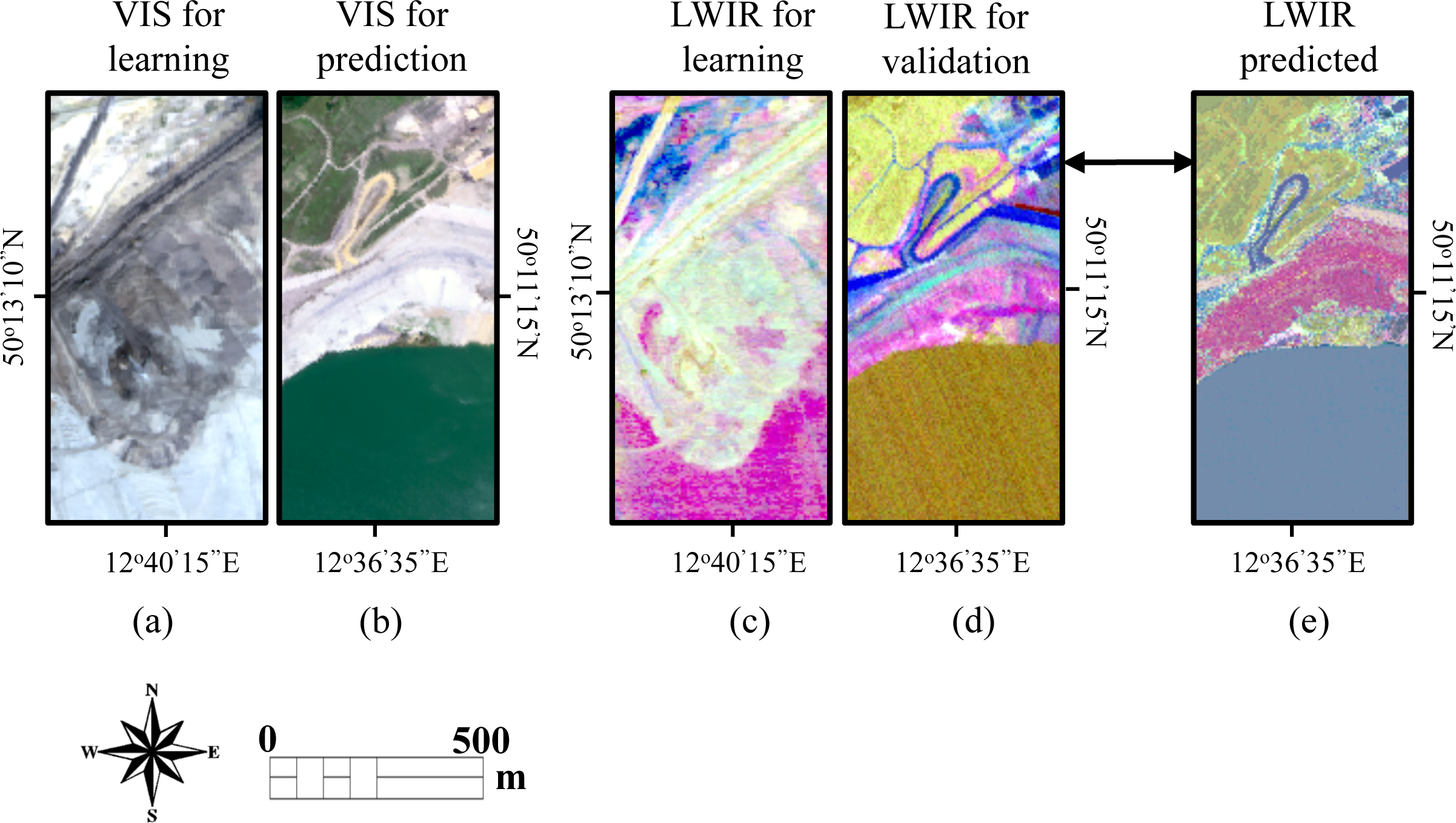
2.2.2. LWIR Prediction Schemes
3. Experimental Results
3.1. LWIR Spectral Image Prediction Error
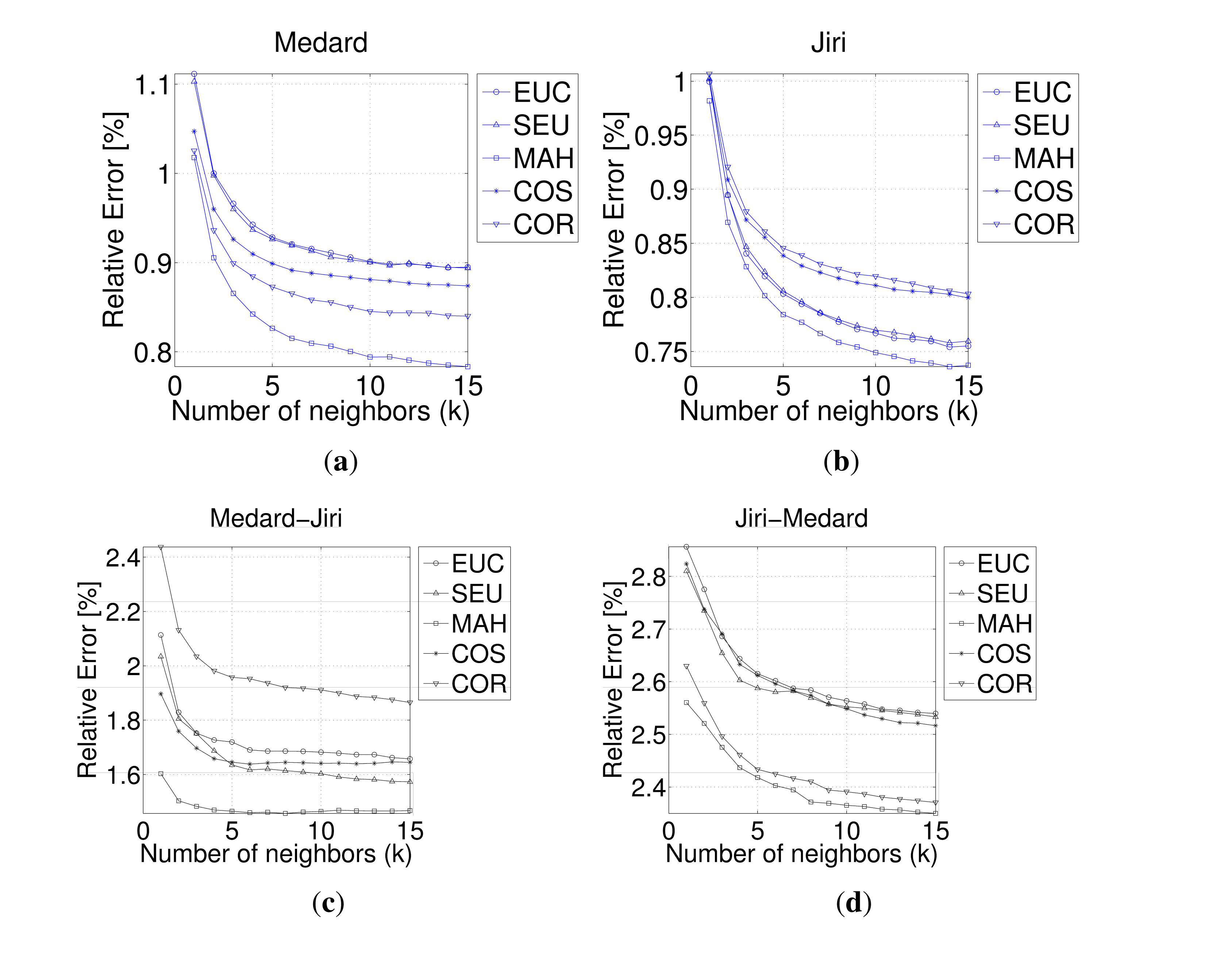
3.1.1. Tuning the kNN Algorithm
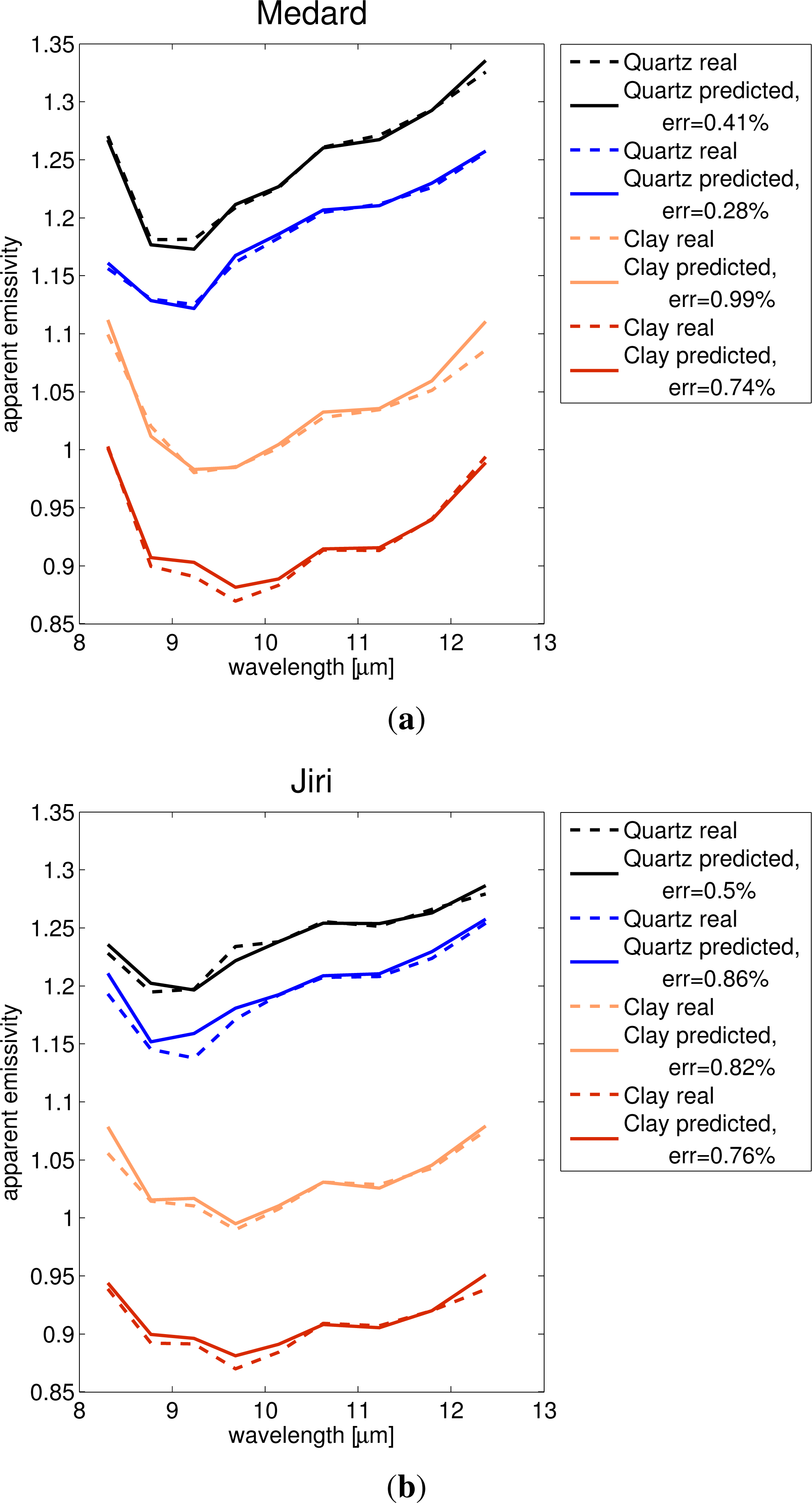
3.1.2. Examples of Predicted LWIR Spectra
3.1.3. LWIR Prediction Error across the Different Datasets
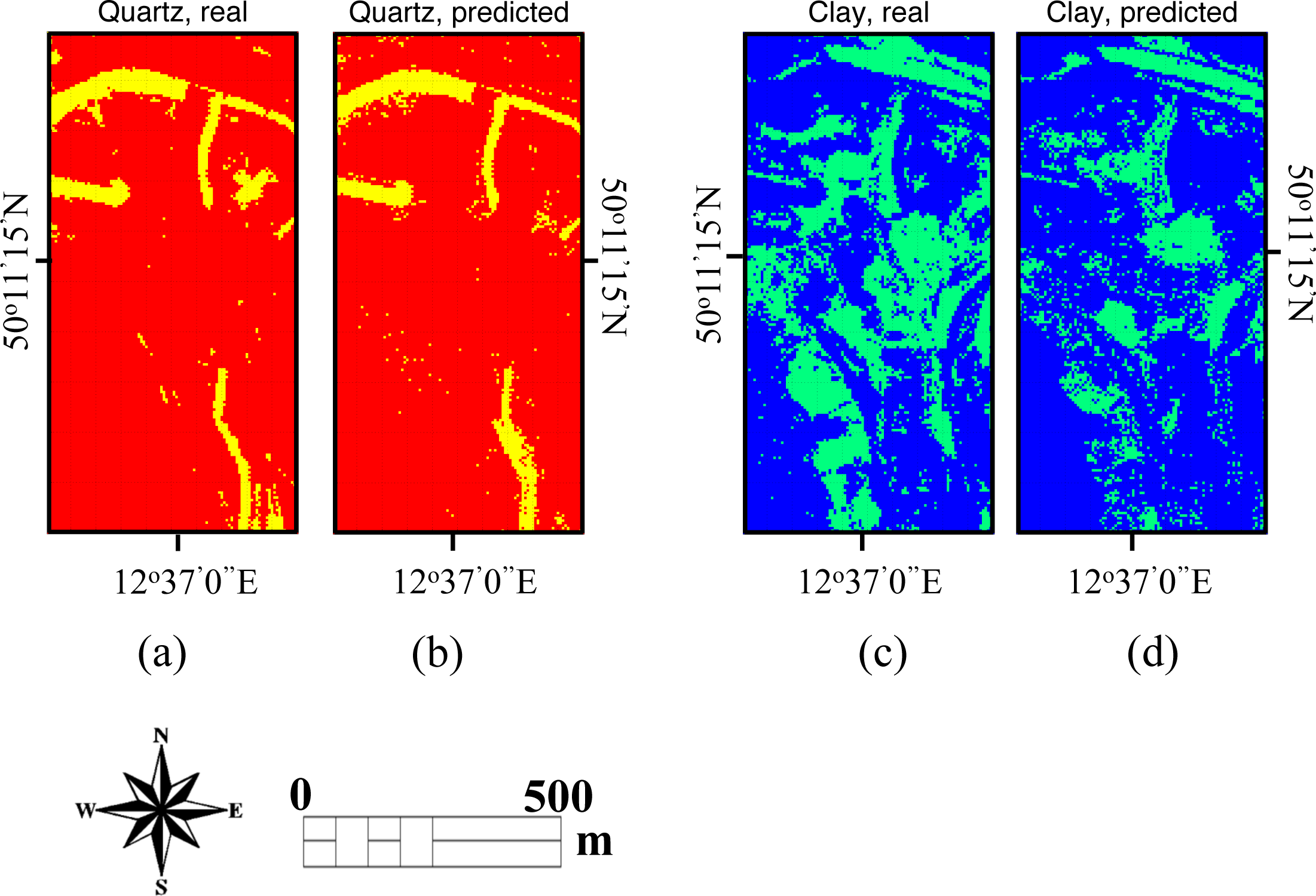
3.2. Predicting Quartz and Clay Mapping
3.3. Uncertainties, Errors and Accuracies
4. Summary and Conclusions
Acknowledgments
Conflicts of Interest
References
- Cihlar, J.; Ly, H.; Li, Z.; Chen, J.; Pokrant, H.; Huang, F. Multitemporal, multichannel AVHRR data sets for land biosphere studies—Artifacts and corrections. Remote Sens. Environ 1997, 60, 35–57. [Google Scholar]
- Roy, D.; Lewis, P.; Justice, C. Burned area mapping using multi-temporal moderate spatial resolution data-a bi-directional reflectance model-based expectation approach. Remote Sens. Environ 2002, 83, 263–286. [Google Scholar]
- Jonsson, P.; Eklundh, L. Seasonality extraction by function fitting to time-series of satellite sensor data. IEEE Trans. Geosci. Remote Sens 2002, 40, 1824–1832. [Google Scholar]
- Lunetta, R.S.; Knight, J.F.; Ediriwickrema, J.; Lyon, J.G.; Worthy, L.D. Land-cover change detection using multi-temporal MODIS NDVI data. Remote Sens. Environ 2006, 105, 142–154. [Google Scholar]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote Sens 2006, 44, 2207–2218. [Google Scholar]
- Baladrón, C.; Aguiar, J.M.; Calavia, L.; Carro, B.; Sánchez-Esguevillas, A.; Hernández, L. Performance study of the application of artificial neural networks to the completion and prediction of data retrieved by underwater sensors. Sensors 2012, 12, 1468–1481. [Google Scholar]
- Karnieli, A.; Ben-Dor, E.; Bayarjargal, Y.; Lugasi, R. Radiometric saturation of Landsat-7 ETM+ data over the Negev Desert (Israel): Problems and solutions. Int. Appl. Earth Obs. Geoinf 2004, 5, 219–237. [Google Scholar]
- Shen, H.; Zhang, L. A MAP-based algorithm for destriping and inpainting of remotely sensed images. IEEE Trans. Geosci. Remote Sens 2009, 47, 1492–1502. [Google Scholar]
- Little, R.J.; Rubin, D.B. Statistical Analysis with Missing Data; Wiley: New York, NY, USA, 1987; Volume 539. [Google Scholar]
- Bertalmio, M.; Sapiro, G.; Caselles, V.; Ballester, C. Image Inpainting. Proceedings of the 27th Annual Conference on Computer Graphics and Interactive Techniques (SIGGRAPH’00), New Orleans, LA, USA, 23–28 July 2000; pp. 417–424.
- García-Laencina, P.J.; Sancho-Gómez, J.L.; Figueiras-Vidal, A.R. Pattern classification with missing data: A review. Neural Comput. Appl 2010, 19, 263–282. [Google Scholar]
- Roy, D.P.; Ju, J.; Lewis, P.; Schaaf, C.; Gao, F.; Hansen, M.; Lindquist, E. Multi-temporal MODIS–Landsat data fusion for relative radiometric normalization, gap filling, and prediction of Landsat data. Remote Sens. Environ 2008, 112, 3112–3130. [Google Scholar]
- Gao, F.; Masek, J.G.; Huang, C.; Wolfe, R.E. Building a consistent medium resolution satellite data set using moderate resolution imaging spectroradiometer products as reference. J. Appl. Remote Sens 2010, 4, 043526:1–043526:22. [Google Scholar]
- Walker, J.; de Beurs, K.; Wynne, R.; Gao, F. Evaluation of Landsat and MODIS data fusion products for analysis of dryland forest phenology. Remote Sens. Environ 2012, 117, 381–393. [Google Scholar]
- Shen, H.; Wu, P.; Liu, Y.; Ai, T.; Wang, Y.; Liu, X. A spatial and temporal reflectance fusion model considering sensor observation differences. Int. J. Remote Sens 2013, 34, 4367–4383. [Google Scholar]
- Ramsey, M.S.; Christensen, P.R.; Lancaster, N.; Howard, D.A. Identification of sand sources and transport pathways at the Kelso Dunes, California, using thermal infrared remote sensing. Geol. Soc. Am. Bull 1999, 111, 646–662. [Google Scholar]
- Vaughan, R.; Calvin, W.M.; Taranik, J.V. SEBASS hyperspectral thermal infrared data: Surface emissivity measurement and mineral mapping. Remote Sens. Environ 2003, 85, 48–63. [Google Scholar]
- Eisele, A.; Lau, I.; Hewson, R.; Carter, D.; Wheaton, B.; Ong, C.; Cudahy, T.J.; Chabrillat, S.; Kaufmann, H. Applicability of the thermal infrared spectral region for the prediction of soil properties across semi-arid agricultural landscapes. Remote Sens 2012, 4, 3265–3286. [Google Scholar]
- Liang, S. Quantitative Remote Sensing of Land Surfaces; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Zhou, L.; Dickinson, R.E.; Ogawa, K.; Tian, Y.; Jin, M.; Schmugge, T.; Tsvetsinskaya, E. Relations between albedos and emissivities from MODIS and ASTER data over North African Desert. Geophys. Res. Lett. 2003. [Google Scholar] [CrossRef]
- Stathopoulou, M.; Cartalis, C.; Petrakis, M. Integrating corine land cover data and landsat TM for surface emissivity definition: Application to the urban area of Athens, Greece. Int. J. Remote Sens 2007, 28, 3291–3304. [Google Scholar]
- Roerink, G.; Su, Z.; Menenti, M. S-SEBI: A simple remote sensing algorithm to estimate the surface energy balance. Phys. Chem. Earth B 2000, 25, 147–157. [Google Scholar]
- Courault, D.; Seguin, B.; Olioso, A. Review on estimation of evapotranspiration from remote sensing data: From empirical to numerical modeling approaches. Irrig. Drain. Syst 2005, 19, 223–249. [Google Scholar]
- Specim AISA Airborne Hyperspectral Imaging Systems—Spectral Cameras. Available online: http://www.specim.fi/index.php/products/airborne (1 March 2013).
- Cover, T.; Hart, P. Nearest neighbor pattern classification. IEEE Trans. Inf. Theory 1967, 13, 21–27. [Google Scholar]
- García-Laencina, P.J.; Sancho-Gómez, J.-L.; Figueiras-Vidal, A.R. K nearest neighbors with mutual information for simultaneous classification and missing data imputation. Neurocomputing 2009, 72, 1483–1493. [Google Scholar]
- Franco-Lopez, H.; Ek, A.R.; Bauer, M.E. Estimation and mapping of forest stand density, volume, and cover type using the k-nearest neighbors method. Remote Sens. Environ 2001, 77, 251–274. [Google Scholar]
- Ohmann, J.L.; Gregory, M.J. Predictive mapping of forest composition and structure with direct gradient analysis and nearest-neighbor imputation in coastal Oregon, U.S.A. Can. J. For. Res 2002, 32, 725–741. [Google Scholar]
- Haapanen, R.; Ek, A.R.; Bauer, M.E.; Finley, A.O. Delineation of forest/nonforest land use classes using nearest neighbor methods. Remote Sens. Environ 2004, 89, 265–271. [Google Scholar]
- Hudak, A.T.; Crookston, N.L.; Evans, J.S.; Hall, D.E.; Falkowski, M.J. Nearest neighbor imputation of species-level, plot-scale forest structure attributes from LiDAR data. Remote Sens. Environ 2008, 112, 2232–2245. [Google Scholar]
- Muinonen, E.; Parikka, H.; Pokharel, Y.; Shrestha, S.; Eerikäinen, K. Utilizing a multi-source forest inventory technique, MODIS data and Landsat TM images in the production of forest cover and volume maps for the Terai physiographic zone in Nepal. Remote Sens 2012, 4, 3920–3947. [Google Scholar]
- Holopainen, M.; Haapanen, R.; Karjalainen, M.; Vastaranta, M.; Hyyppä, J.; Yu, X.; Tuominen, S.; Hyyppä, H. Comparing accuracy of airborne laser scanning and TerraSAR-X radar images in the estimation of plot-level forest variables. Remote Sens 2010, 2, 432–445. [Google Scholar]
- Kankare, V.; Vastaranta, M.; Holopainen, M.; Räty, M.; Yu, X.; Hyyppä, J.; Hyyppä, H.; Alho, P.; Viitala, R. Retrieval of forest aboveground biomass and stem volume with airborne scanning LiDAR. Remote Sens 2013, 5, 2257–2274. [Google Scholar]
- Lindberg, E.; Holmgren, J.; Olofsson, K.; Wallerman, J.; Olsson, H. Estimation of tree lists from airborne laser scanning using tree model clustering and k-MSN imputation. Remote Sens 2013, 5, 1932–1955. [Google Scholar]
- Friedman, J.H.; Bentley, J.L.; Finkel, R.A. An algorithm for finding best matches in logarithmic expected time. ACM Trans. Math. Softw 1977, 3, 209–226. [Google Scholar]
- Jones, P.W.; Osipov, A.; Rokhlin, V. A randomized approximate nearest neighbors algorithm. Appl. Computat. Harmon. A 2013, 34, 415–444. [Google Scholar]
- Rojik, P. New stratigraphic subdivision of the Tertiary in the Sokolov Basin in Northwestern Bohemia. J. GEOsci 2004, 49, 173–185. [Google Scholar]
- Murad, E.; Rojik, P. Iron mineralogy of mine-drainage precipitates as environmental indicators: Review of current concepts and a case study from the Sokolov Basin, Czech Republic. Clay Miner 2005, 40, 427–440. [Google Scholar]
- Kopackova, V.; Chevrel, S.; Bourguignon, A.; Rojík, P. Application of high altitude and ground-based spectroradiometry to mapping hazardous low-pH material derived from the Sokolov open-pit mine. J. Map 2012, 8, 220–230. [Google Scholar]
- Casal, G.; Sánchez-Carnero, N.; Domínguez-Gómez, J.A.; Kutser, T.; Freire, J. Assessment of AHS (Airborne Hyperspectral Scanner) sensor to map macroalgal communities on the Ría de vigo and Ría de Aldán coast (NW Spain). Mar. Biol 2012, 159, 1997–2013. [Google Scholar]
- Green, R.O. Atmospheric Correction Now (ACORN); ImSpec LLC: Palmdale, CA, USA, 2001. [Google Scholar]
- Gillespie, A.; Rokugawa, S.; Matsunaga, T.; Cothern, J.; Hook, S.; Kahle, A. A temperature and emissivity separation algorithm for Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) images. IEEE Trans. Geosci. Remote Sens 1998, 36, 1113–1126. [Google Scholar]
- Schlapfer, D.; Schaepman, M.; Itten, K. PARGE: Parametric geocoding based on GCP-calibrated auxiliary data. Proc. SPIE 1998. [Google Scholar] [CrossRef]
- Hapke, B. Theory of Reflectance and Emittance Spectroscopy; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Tokola, T.; Pitkanen, J.; Partinen, S.; Muinonen, E. Point accuracy of a non-parametric method in estimation of forest characteristics with different satellite materials. Int. J. Remote Sens 1996, 17, 2333–2351. [Google Scholar]
- Nilsson, M. Estimation of Forest Variables Using Satellite Image Data and Airborne Lidar. 1997. [Google Scholar]
- McGill, R.; Tukey, J.W.; Larsen, W.A. Variations of box plots. Am. Stat 1978, 32, 12–16. [Google Scholar]
- Metz, C.E. Basic principles of ROC analysis. Semin. Nucl. Med 1978, 8, 283–298. [Google Scholar]
- De Maesschalck, R.; Jouan-Rimbaud, D.; Massart, D. The Mahalanobis distance. Chemometr. Intell. Lab 2000, 50, 1–18. [Google Scholar]
- Blitzer, J.; Weinberger, K.Q.; Saul, L.K. Distance metric learning for large margin nearest neighbor classification. Adv. Neural Inf. Process Syst 2005, 1473–1480. [Google Scholar]
- Inamdar, A.K.; French, A.; Hook, S.; Vaughan, G.; Luckett, W. Land surface temperature retrieval at high spatial and temporal resolutions over the southwestern United States. J. Geophys. Res.:Atmos 2008, 113, 7–16. [Google Scholar]
- Wu, P.; Shen, H.; Ai, T.; Liu, Y. Land-surface temperature retrieval at high spatial and temporal resolutions based on multi-sensor fusion. Int. J. Digital Earth 2013, 6, 1–21. [Google Scholar]
Appendix
A. Metric Distances







| Sensor | Band No. | Units | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| VIS | WL FWHM | [μm] [μm] | 0.500 0.028 | 0.530 0.029 | 0.560 0.029 | 0.591 0.029 | 0.620 0.028 | 0.650 0.028 | 0.679 0.028 | 0.709 0.028 | 0.738 0.028 | 0.767 0.029 | 0.796 0.028 |
| LWIR | WL FWHM | [μm] [μm] | 8.310 0.458 | 8.770 0.421 | 9.237 0.424 | 9.680 0.455 | 10.143 0.412 | 10.624 0.556 | 11.230 0.552 | 11.796 0.566 | 12.371 0.543 |
| Experiment Dataset No. | Medard Left | Medard Right | Jiri Left | Jiri Right |
|---|---|---|---|---|
| 1 | Learning | Predicted | ||
| 2 | Learning | Predicted | ||
| 3 | Learning | Predicted | ||
| 4 | Predicted | Learning |
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Adar, S.; Shkolnisky, Y.; Notesco, G.; Ben-Dor, E. Using Visible Spectral Information to Predict Long-Wave Infrared Spectral Emissivity: A Case Study over the Sokolov Area of the Czech Republic with an Airborne Hyperspectral Scanner Sensor. Remote Sens. 2013, 5, 5757-5782. https://doi.org/10.3390/rs5115757
Adar S, Shkolnisky Y, Notesco G, Ben-Dor E. Using Visible Spectral Information to Predict Long-Wave Infrared Spectral Emissivity: A Case Study over the Sokolov Area of the Czech Republic with an Airborne Hyperspectral Scanner Sensor. Remote Sensing. 2013; 5(11):5757-5782. https://doi.org/10.3390/rs5115757
Chicago/Turabian StyleAdar, Simon, Yoel Shkolnisky, Gila Notesco, and Eyal Ben-Dor. 2013. "Using Visible Spectral Information to Predict Long-Wave Infrared Spectral Emissivity: A Case Study over the Sokolov Area of the Czech Republic with an Airborne Hyperspectral Scanner Sensor" Remote Sensing 5, no. 11: 5757-5782. https://doi.org/10.3390/rs5115757





