An Enhanced Spatial and Temporal Data Fusion Model for Fusing Landsat and MODIS Surface Reflectance to Generate High Temporal Landsat-Like Data
Abstract
:1. Introduction
2. Algorithms
2.1. Theoretical Basis
2.2. The STDFM Algorithm
2.3. Improvements in the ESTDFM Algorithm
2.3.1. Patch-Based ISODATA Classification
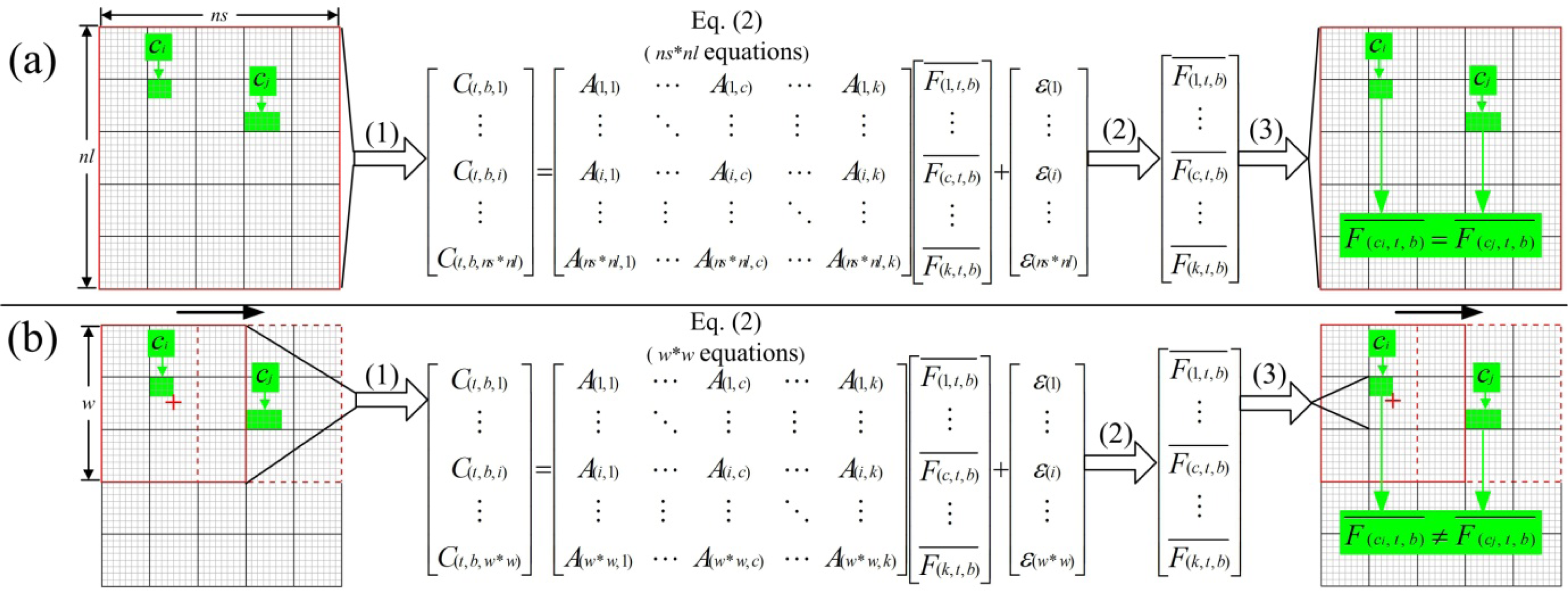
2.3.2. Sliding Window
2.3.3. Temporal Weights
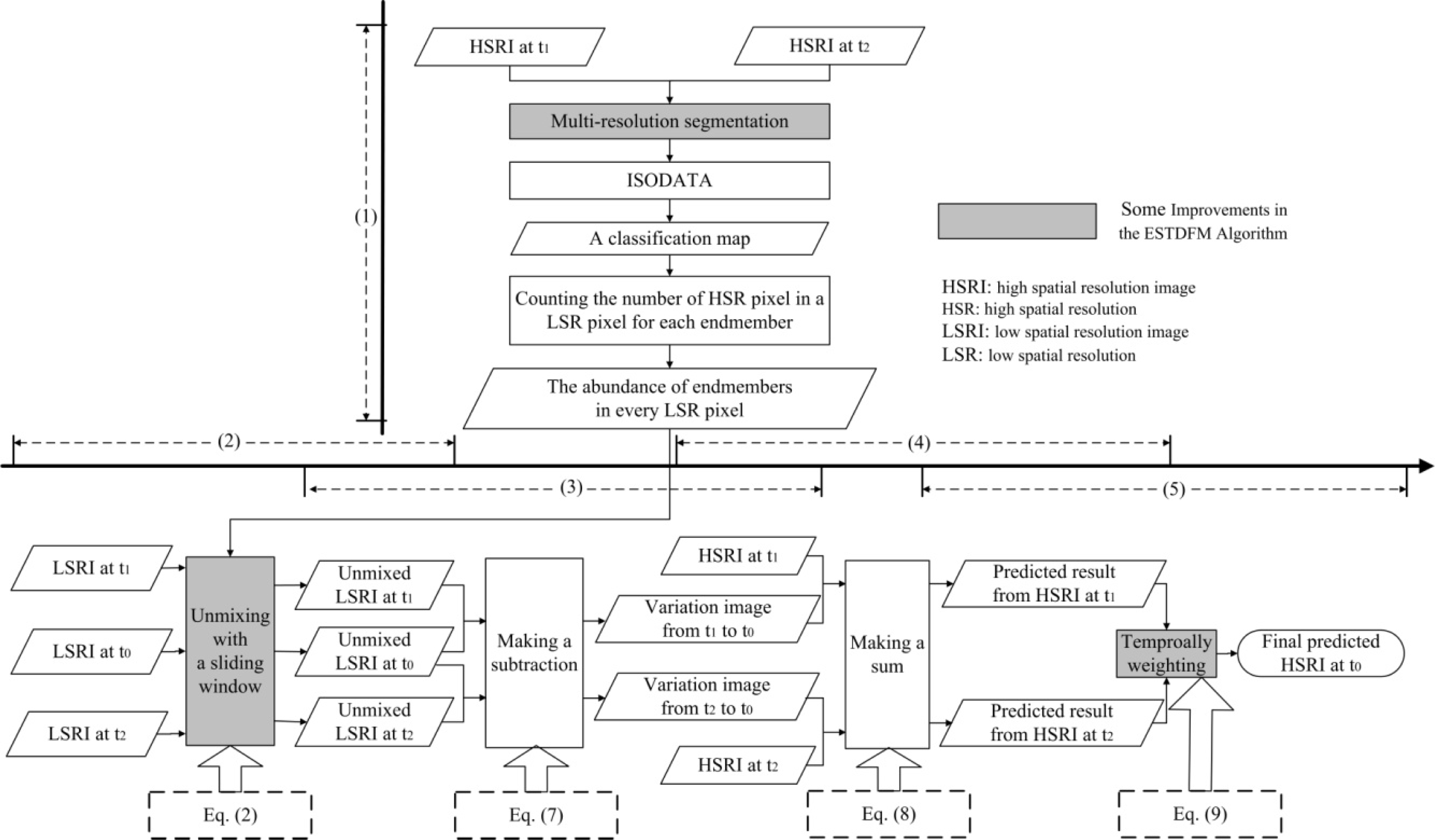
2.4. Process of the ESTDFM Algorithm Implementation
3. Algorithm Test
3.1. Test Data and Preprocessing
3.2. Implementation Considerations
3.2.1. Patch-Based ISODATA Classification Map
3.2.2. Calculation of the Abundance of Endmembers
3.2.3. Unmixing of the MOD09GA Images
3.3. Evaluation Methods
4. Test Results of Algorithm
4.1. Visual Evaluation
4.2. Scatter Plots
4.3. AAD and AD
5. Discussions
5.1. Point Spread Function
5.2. Suitability of the New Classification Method
5.3. Definition of Optimal Parameter Combination
5.4. Drawbacks in the ESTDFM Algorithm
5.4.1. “Patch Effect”
5.4.2. Time Consumption
5.4.3. Constraints
6. Conclusions and Summary
- (1)
- The most important improvement in the ESTDFM algorithm is to apply a sliding widow for unmixing a low spatial resolution image (LSRI). Only one reflectance value for each endmember can be obtained in the unmixing of an LSRI in the original STDFM algorithm, as all low spatial resolution (LSR) pixels are unmixed at once. Obviously, such an algorithm rejects all the within-endmember variability. By introducing the sliding widow technology, the ESTDFM algorithm unmixes the adjacent pixels in a window to get the mean reflectance of different endmembers, and assigns them to the HSR pixels corresponding to the central target LSR pixel with reference to a classification map; subsequently unmixes all LSR pixels by a sliding window, moved with the step of one LSR-pixel size. The spatial heterogeneity of the mean reflectance of endmembers has been fully considered, which would be more consistent with the variation of real ground objects.
- (2)
- The temporal-weight concept is introduced in the ESTDFM algorithm. One predicted high spatial resolution image (HSRI) can be acquired, by making a sum of one base HSRI and its corresponding variation image calculated by solving a difference between the unmixed LSRI at base date and the unmixed one at prediction date. Therefore, two different predicted HSRIs can be obtained, as two high- and low-spatial resolution image pairs at base date, and one LSRI at prediction date, are available in the ESTDFM algorithm. Thus, making full use of the information of the known HSRIs, a more reasonable scheme to obtain the final predicted HSRI is temporally weighting the two predicted results.
- (3)
- A patch-based ISODATA classification method is also introduced in the ESTDFM algorithm. Two main procedures are included in the method: A single-pixel HSRI is firstly converted into a homogeneous-patch image base on multi-resolution segmentation. A patch-based ISODATA classification map then can be acquired by applying the ISODATA classification rule to the “patches image”. Test results show that the new classification method is more suitable for unmixing an LSRI than some conventional unsupervised classification methods, since an unmixed LSRI based on a patch-based ISODATA classification map not only has low “salt and pepper noise” but is more consistent with the real object.
Acknowledgments
Conflict of Interest
References
- Price, J.C. How unique are spectral signatures? Remote Sens. Environ 1994, 49, 181–186. [Google Scholar]
- Sakamoto, T.; van Nguyen, N.; Ohno, H.; Ishitsuka, N.; Yokozawa, M. Spatio-temporal distribution of rice phenology and cropping systems in the Mekong Delta with special reference to the seasonal water flow of the Mekong and Bassac rivers. Remote Sens. Environ 2006, 100, 1–16. [Google Scholar]
- Notarnicola, C.; Duguay, M.; Moelg, N.; Schellenberger, T.; Tetzlaff, A.; Monsorno, R.; Costa, A.; Steurer, C.; Zebisch, M. Snow cover maps from MODIS images at 250 m resolution, Part 1: Algorithm description. Remote Sens 2013, 5, 110–126. [Google Scholar]
- Zhou, H.; Aizen, E.; Aizen, V. Deriving long term snow cover extent dataset from AVHRR and MODIS data: Central Asia case study. Remote Sens. Environ 2013, 136, 146–162. [Google Scholar]
- Rees, W.; Williams, M.; Vitebsky, P. Mapping land cover change in a reindeer herding area of the Russian Arctic using Landsat TM and ETM+ imagery and indigenous knowledge. Remote Sens. Environ 2003, 85, 441–452. [Google Scholar]
- Lier, O.R.V.; Luther, J.E.; Leckie, D.G.; Bowers, W.W. Development of large-area land cover and forest change indicators using multi-sensor Landsat imagery: Application to the Humber River Basin, Canada. Int. J. Appl. Earth Obs. Geoinf 2011, 13, 819–829. [Google Scholar]
- Santillan, J.; Makinano, M.; Paringit, E. Integrated Landsat image analysis and hydrologic modeling to detect impacts of 25-year classification change on surface runoff in a Philippine watershed. Remote Sens 2011, 3, 1067–1087. [Google Scholar]
- Marfai, M.A.; Almohammad, H.; Dey, S.; Susanto, B.; King, L. Coastal dynamic and shoreline mapping: Multi-sources spatial data analysis in Semarang Indonesia. Environ. Monit. Assess 2008, 142, 297–308. [Google Scholar]
- Hilker, T.; Wulder, M.A.; Coops, N.C.; Linke, J.; McDermid, G.; Masek, J.G.; Gao, F.; White, J.C. A new data fusion model for high spatial-and temporal-resolution mapping of forest disturbance based on Landsat and MODIS. Remote Sens. Environ 2009, 113, 1613–1627. [Google Scholar]
- Arai, E.; Shimabukuro, Y.E.; Pereira, G.; Vijaykumar, N.L. A multi-resolution multi-temporal technique for detecting and mapping deforestation in the Brazilian Amazon rainforest. Remote Sens 2011, 3, 1943–1956. [Google Scholar]
- Gao, F.; Masek, J.; Schwaller, M.; Hall, F. On the blending of the Landsat and MODIS surface reflectance: Predicting daily Landsat surface reflectance. IEEE Trans. Geosci. Remote Sens 2006, 44, 2207–2218. [Google Scholar]
- Hilker, T.; Wulder, M.A.; Coops, N.C.; Seitz, N.; White, J.C.; Gao, F.; Masek, J.G.; Stenhouse, G. Generation of dense time series synthetic Landsat data through data blending with MODIS using a spatial and temporal adaptive reflectance fusion model. Remote Sens. Environ 2009, 113, 1988–1999. [Google Scholar]
- Zhu, X.; Chen, J.; Gao, F.; Chen, X.; Masek, J.G. An enhanced spatial and temporal adaptive reflectance fusion model for complex heterogeneous regions. Remote Sens. Environ 2010, 114, 2610–2623. [Google Scholar]
- Zurita-Milla, R.; Kaiser, G.; Clevers, J.; Schneider, W.; Schaepman, M. Downscaling time series of MERIS full resolution data to monitor vegetation seasonal dynamics. Remote Sens. Environ 2009, 113, 1874–1885. [Google Scholar]
- Zurita-Milla, R.; Clevers, J.; van Gijsel, J.; Schaepman, M. Using MERIS fused images for classification mapping and vegetation status assessment in heterogeneous landscapes. Int. J. Remote Sens 2011, 32, 973–991. [Google Scholar]
- Wu, M.; Wang, J.; Niu, Z.; Zhao, Y.; Wang, C. A model for spatial and temporal data fusion (In Chinese). J. Infrared Millim. Waves 2012, 31, 80–84. [Google Scholar]
- Maselli, F. Definition of spatially variable spectral endmembers by locally calibrated multivariate regression analyses. Remote Sens. Environ 2001, 75, 29–38. [Google Scholar]
- Busetto, L.; Meroni, M.; Colombo, R. Combining medium and coarse spatial resolution satellite data to improve the estimation of sub-pixel NDVI time series. Remote Sens. Environ 2008, 112, 118–131. [Google Scholar]
- Minghelli-Roman, A.; Polidori, L.; Mathieu-Blanc, S.; Loubersac, L.; Cauneau, F. Spatial resolution improvement by merging MERIS-ETM images for coastal water monitoring. IEEE Geosci. Remote Sens. Lett 2006, 3, 227–231. [Google Scholar]
- Zhukov, B.; Oertel, D.; Lanzl, F.; Reinhackel, G. Unmixing-based multisensor multiresolution image fusion. IEEE Trans. Geosci. Remote Sens 1999, 37, 1212–1226. [Google Scholar]
- Settle, J.; Drake, N. Linear mixing and the estimation of ground cover proportions. Int. J. Remote Sens 1993, 14, 1159–1177. [Google Scholar]
- Oleson, K.; Sarlin, S.; Garrison, J.; Smith, S.; Privette, J.; Emery, W. Unmixing multiple classification type reflectances from coarse spatial resolution satellite data. Remote Sens. Environ 1995, 54, 98–112. [Google Scholar]
- Zurita-Milla, R.; Clevers, J.; Schaepman, M.E. Unmixing-based Landsat TM and MERIS FR data fusion. IEEE Geosci. Remote Sens. Lett 2008, 5, 453–457. [Google Scholar]
- Baatz, M.; Schape, A. Multiresolution Segmentation—An Optimization Approach for High Quality Multi-Scale Image Segmentation. In Angewandte Geographische Informations-Verarbeitung XII; Strobl, J., Blaschke, T., Griesebner, G., Eds.; Wichmann Verlag: Karlsruhe, Germany, 2000; pp. 12–23. [Google Scholar]
- Benz, U.C.; Hofmann, P.; Willhauck, G.; Lingenfelder, I.; Heynen, M. Multi-resolution, object-oriented fuzzy analysis of remote sensing data for GIS-ready information. ISPRS J. Photogramm. Remote Sens 2004, 58, 239–258. [Google Scholar]
- Masek, J.G.; Vermote, E.F.; Saleous, N.E.; Wolfe, R.; Hall, F.G.; Huemmrich, K.F.; Gao, F.; Kutler, J.; Lim, T.-K. A Landsat surface reflectance dataset for North America, 1990–2000. IEEE Geosci. Remote Sens. Lett 2006, 3, 68–72. [Google Scholar]
- Wolfe, R.E.; Nishihama, M.; Fleig, A.J.; Kuyper, J.A.; Roy, D.P.; Storey, J.C.; Patt, F.S. Achieving sub-pixel geolocation accuracy in support of MODIS land science. Remote Sens. Environ 2002, 83, 31–49. [Google Scholar]
- Wald, L. Quality of High Resolution Synthesized Images: Is There a Simple Criterion? Proceedings of the International Conference Fusion of Earth Data, Sophia Antipolis, France, 26–28 January 2000; pp. 99–103.
- Townshend, J.; Huang, C.; Kalluri, S.; Defries, R.; Liang, S.; Yang, K. Beware of per-pixel characterization of land cover. Int. J. Remote Sens 2000, 21, 839–843. [Google Scholar]
- Huang, C.; Townshend, J.R.; Liang, S.; Kalluri, S.N.; DeFries, R.S. Impact of sensor’s point spread function on land cover characterization: Assessment and deconvolution. Remote Sens. Environ 2002, 80, 203–212. [Google Scholar]
- Tan, B.; Woodcock, C.; Hu, J.; Zhang, P.; Ozdogan, M.; Huang, D.; Yang, W.; Knyazikhin, Y.; Myneni, R. The impact of gridding artifacts on the local spatial properties of MODIS data: Implications for validation, compositing, and band-to-band registration across resolutions. Remote Sens. Environ 2006, 105, 98–114. [Google Scholar]
- Ranchin, T.; Aiazzi, B.; Alparone, L.; Baronti, S.; Wald, L. Image fusion—The ARSIS concept and some successful implementation schemes. ISPRS J. Photogramm. Remote Sens 2003, 58, 4–18. [Google Scholar]
- Kohonen, T. Self-Organizing Maps, 3rd ed.; Springer-Verlag: New York, NY, USA, 2001. [Google Scholar]
- Amorós-López, J.; Gomez-Chova, L.; Alonso, L.; Guanter, L.; Zurita-Milla, R.; Moreno, J.; Camps-Valls, G. Multitemporal fusion of Landsat/TM and ENVISAT/MERIS for crop monitoring. Int. J. Appl. Earth Obs. Geoinf 2013, 23, 132–141. [Google Scholar]
- Amorós-López, J.; Gomez-Chova, L.; Alonso, L.; Guanter, L.; Moreno, J.; Camps-Valls, G. Regularized multiresolution spatial unmixing for ENVISAT/MERIS and Landsat/TM image fusion. IEEE Geosci. Remote Sens. Lett 2011, 8, 844–848. [Google Scholar]
- Somers, B.; Asner, G.P.; Tits, L.; Coppin, P. Endmember variability in spectral mixture analysis: A review. Remote Sens. Environ 2011, 115, 1603–1616. [Google Scholar]







| Landsat ETM+ | MOD09GA | ||||
|---|---|---|---|---|---|
| Acquisition Date | Path/Row | Main Usage | Acquisition Date | Path/Row | Main Usage |
| 10/08/02 | 120/38 | Classification and validation | 10/08/02 | 28/05 | Unmixing |
| 10/24/02 | 120/38 | Validation | 10/24/02 | 28/05 | Unmixing |
| 11/09/02 | 120/38 | Classification | 11/09/02 | 28/05 | Unmixing |
| ETM+ Band | Bandwidth (nm) | Spatial Resolution (m) | MODIS Land Band | Bandwidth (nm) | Spatial Resolution (m) |
|---|---|---|---|---|---|
| 1 | 450–520 | 30 | 3 | 459–479 | 500 |
| 2 | 520–600 | 30 | 4 | 545–565 | 500 |
| 3 | 630–690 | 30 | 1 | 620–670 | 250a |
| 4 | 760–900 | 30 | 2 | 841–876 | 250a |
| 5 | 1,550–1,750 | 30 | 6 | 1,628–1,652 | 500 |
| 7 | 2,080–2,350 | 30 | 7 | 2,105–2,155 | 500 |
| ETM+ | AAD | AD | ||||||
|---|---|---|---|---|---|---|---|---|
| Band | Base Date1 | Base Date2 | Prediction | Base Date1 | Base Date2 | Prediction | ||
| 10/08/02 | 11/09/02 | ESTDFM | STDFM | 10/08/02 | 11/09/02 | ESTDFM | STDFM | |
| Green | 0.0081 | 0.0110 | 0.0073 | 0.0078 | 0.0014 | 0.0089 | 0.0006 | 0.0010 |
| Red | 0.0111 | 0.0212 | 0.0090 | 0.0102 | 0.0001 | 0.0202 | 0.0012 | 0.0013 |
| NIR | 0.0475 | 0.0191 | 0.0167 | 0.0265 | 0.0474 | −0.0112 | 0.0130 | 0.0243 |
| w | 11 | 21 | 31 | 41 | 51 | 61 | |
|---|---|---|---|---|---|---|---|
| Method | |||||||
| patch-based ISODATA classification | 1.89 | 1.46 | 1.33 | 1.29 | 1.26 | 1.24 | |
| Majority Analysis1 (3 × 3) a | 2.18 | 1.60 | 1.41 | 1.33 | 1.29 | 1.27 | |
| Majority Analysis2 (5 × 5) b | 1.87 | 1.49 | 1.39 | 1.36 | 1.34 | 1.33 | |
| No Post Classification c | 5.12 | 2.48 | 2.15 | 2.03 | 1.97 | 1.96 | |
© 2013 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Zhang, W.; Li, A.; Jin, H.; Bian, J.; Zhang, Z.; Lei, G.; Qin, Z.; Huang, C. An Enhanced Spatial and Temporal Data Fusion Model for Fusing Landsat and MODIS Surface Reflectance to Generate High Temporal Landsat-Like Data. Remote Sens. 2013, 5, 5346-5368. https://doi.org/10.3390/rs5105346
Zhang W, Li A, Jin H, Bian J, Zhang Z, Lei G, Qin Z, Huang C. An Enhanced Spatial and Temporal Data Fusion Model for Fusing Landsat and MODIS Surface Reflectance to Generate High Temporal Landsat-Like Data. Remote Sensing. 2013; 5(10):5346-5368. https://doi.org/10.3390/rs5105346
Chicago/Turabian StyleZhang, Wei, Ainong Li, Huaan Jin, Jinhu Bian, Zhengjian Zhang, Guangbin Lei, Zhihao Qin, and Chengquan Huang. 2013. "An Enhanced Spatial and Temporal Data Fusion Model for Fusing Landsat and MODIS Surface Reflectance to Generate High Temporal Landsat-Like Data" Remote Sensing 5, no. 10: 5346-5368. https://doi.org/10.3390/rs5105346







