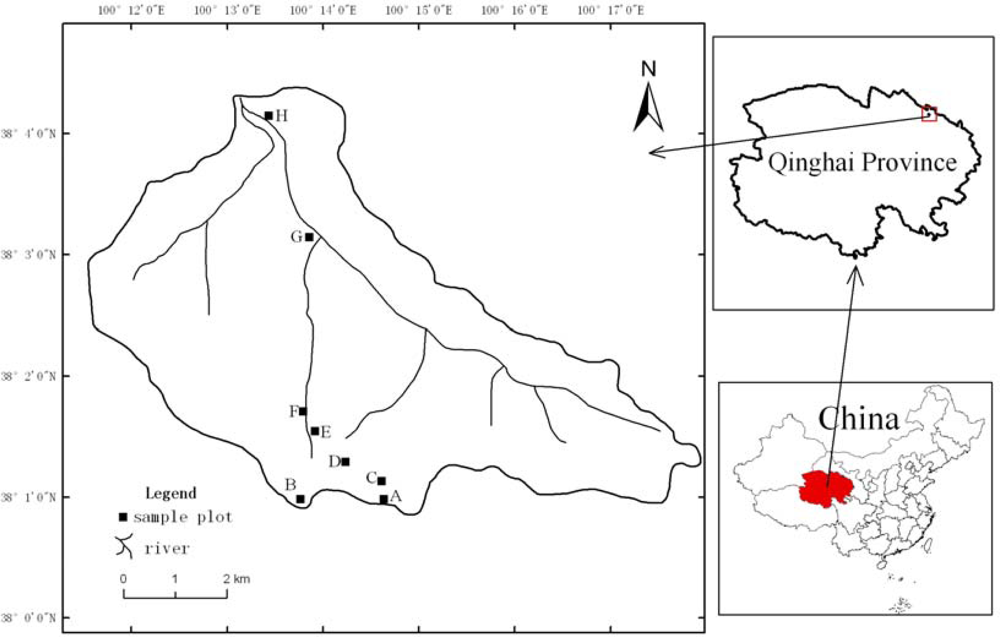
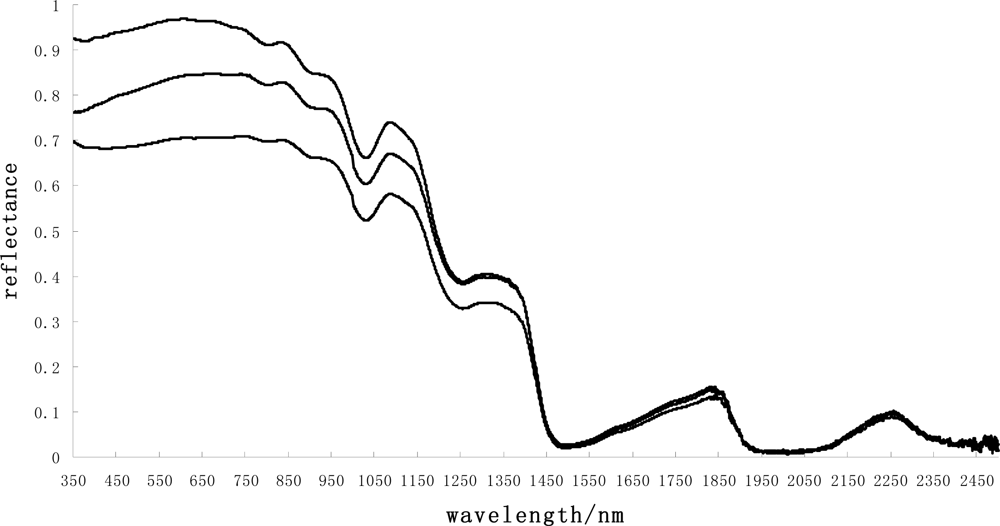
1. Introduction
Snow is an important subject of cryosphere-environment science and is a useful environmental indicator of global changes in terms of long-term monitoring [
1]. The temporal and spatial distribution of snow cover is an important indicator of the climate [
2]. As one of the optical characteristics of snow, snow grain size is an important factor causing albedo changes and thus is also one of the factors affecting the global radiation balance.
Assuming snow grains to be granular spheres and ignoring the scattering effect between grains in the “near-field,” the “delta-Eddington” approximation for multiple scattering together with Mie theory for single scattering could be used to calculate the scattering of individual snow grains. Wiscombe and Warren found effects of grain size on reflectance spectra [
3]. The researchers noted that (1) when the snow grain size becomes larger, the absorption and forward scattering of snow increases, and (2) the snow surface reflectance declines with increasing grain size, and, as the grain size grows, the absorption intensity in near-infrared bands is larger than in the visible bands. Dozier
et al. used the theoretical model of Wiscombe and Warren and NOAA-6 AVHRR data to highlight that using remote sensing tools to measure the snow grain size was a potentially effective method [
4], but their result was difficult to interpret because the authors did not address near-infrared bands, which were sensitive to grain size in the NOAA-6 AVHRR data.
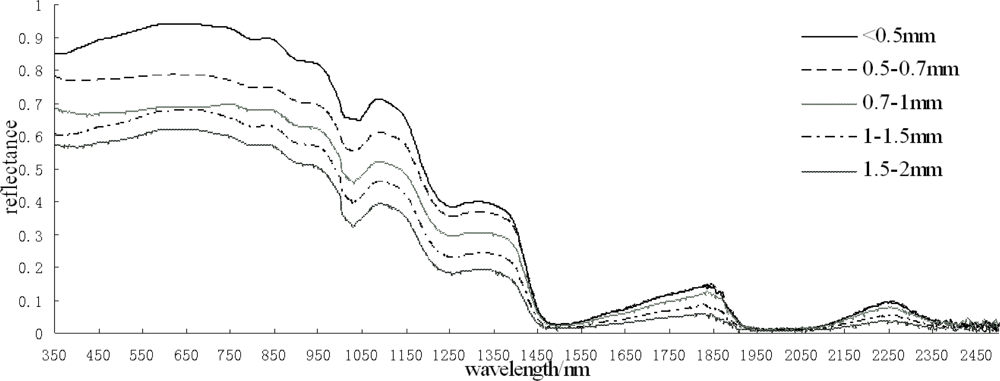
According to Landsat TM images, snow types have been classified as: clean new snow, older metamorphosed snow, and snow mixed with vegetation [
5], but the results were not verified with measured data at the time of the satellite transit. The contaminant content of the snow mainly affected the reflectivity in the visible range; however, the near-infrared reflectance depended on the snow grain size. The estimated results based on the TM band 4 in the near-infrared range were close to the measured data, although no atmospheric correction of the Landsat TM images was completed [
6].
Nolin and Dozier used an airborne visible/infrared imaging spectrometer (AVIRIS) and discrete-ordinate model to calculate directional reflectance as a function of snow grain size [
7]. Their inversion method was validated using measured data and had a higher accuracy for solar incidence angles between 0° and 30°. The authors improved their model by using a radiative transfer model based on the near-infrared reflectance characteristics of snow to obtain a quantitative retrieval of snow grain size [
8]. This method had a higher accuracy and fewer errors caused by topography.
Hemisphere-directed reflections of snow cover at the wavelengths of 1.8 μm and 2.2 μm have been used to estimate snow grain size based on MODIS/ASTER data [
9]. However, this approach caused large errors when the grain size was large, and the method was greatly impacted by the atmosphere and solar radiation. The normalized index or relative reflectivity of the MODIS band may estimate the snow grain size more accurately and robustly [
10–
12].
Several snow grain size inversion models and algorithms have been established, including models based on optical scattering theory, single-channel inversion algorithms, and ratios of multichannel algorithms. Previous images for inversion are, generally, multispectral images with low or medium spatial resolution, e.g., AVHRR or MODIS, and high resolution multispectral images, such as Landsat TM, or airborne hyperspectral images, such as AVIRIS. However, the number of studies estimating snow grain size using hyperspectral aerospace images is limited, especially combining both synchronized hyperspectral spectrometer data and snow grain size data. In this study, we used the Earth Observing-1 (EO-1) Hyperion hyperspectral imagery, which also has a high resolution, to establish the relationship between the bands and the snow grain size based on the spectral analysis of ground-synchronized measurement data. The study aimed to estimate the snow grain-size distribution of the Heihe River Basin region in the Binggou watershed and evaluate the estimates using ground-measured data.
3. Results and Discussion
3.1. Expression of the Grain-Size Estimation Model
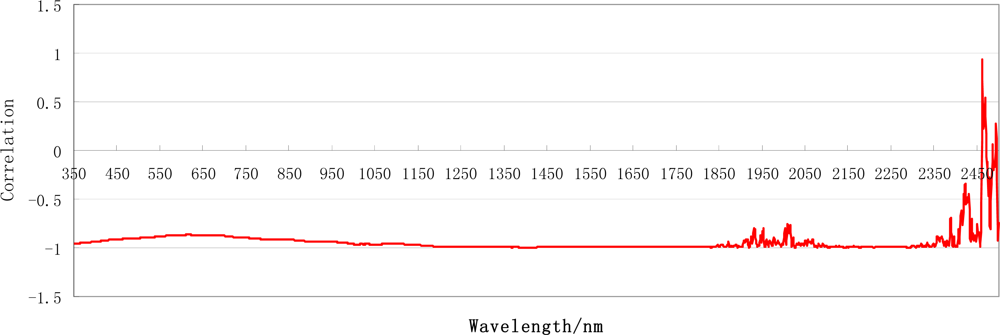
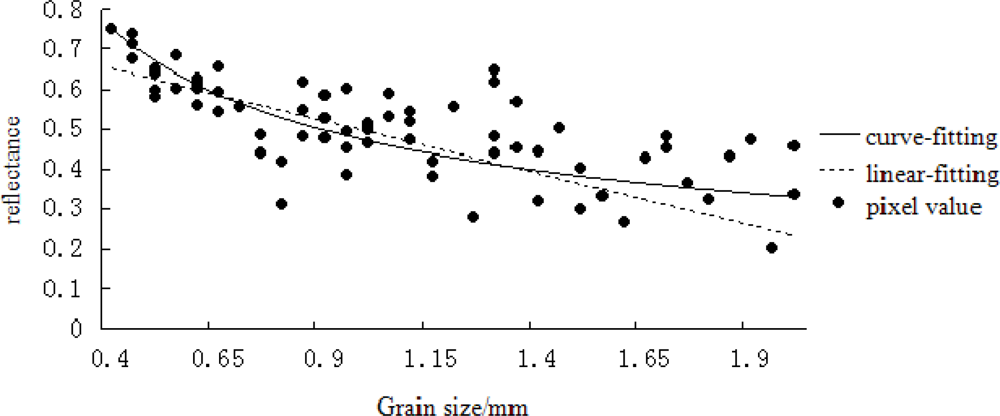
Figure 11 indicates the relationship between the pixel value of the Hyperion band 89 after atmospheric correction and the snow grain size. Linear fitting and curve fitting of the pixel value and grain size led to the following relationships, respectively:
ρ = −0.26
R + 0.67, where
ρ is the reflectance,
R is the snow grain size. The correlation coefficient
r of the fitting line was 0.81.
ρ = 0.47
R−0.51, the correlation coefficient
r was 0.84. The root mean square error (RMSE) was 0.24 mm and 0.21 mm for the linear fitting and curve fitting, respectively. These results indicate that the pixel value had an index function and a linear relation with the grain size.
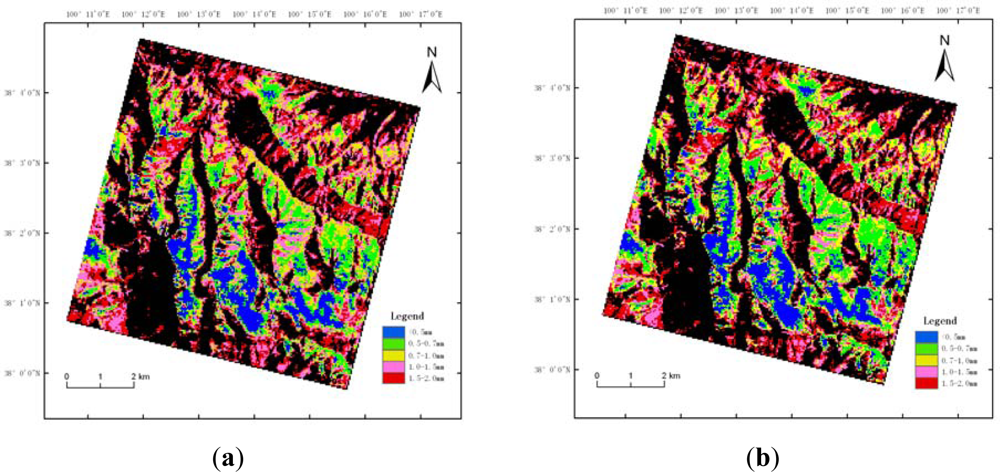
3.2. Mapping the Snow Grain Size Using the Hyperion Imagery
According to the linear and exponential models, we classified the snow into five categories based on the grain size, as shown in
Figure 12.
Figure 12 indicates that the estimation results of the snow grain size using the linear model and exponential model were almost the same. A total of 11.7% of the snow had a grain size less than 0.5 mm; 16.2% was between 0.5 mm and 0.7 mm; 20.7% was between 0.7 mm and 1 mm; 26.2% was between 1 mm and 1.5 mm; and, 25.5% was between 1.5 mm and 2 mm. Similar estimates resulted due to the similar function curves of the two models in the grain-size range of 0.5–1.5 mm. There were differences only in the grain-size ranges of less than 0.5 mm and greater than 1.5 mm.
3.3. Improvement of the Snow Grain-Size Estimation Model
In this study, we selected a dry snowy surface as test plot to facilitate the reading of the snow grain size. However, the water content of the Binggou watershed is inconsistent, and water has a strong absorption band in the near-infrared bands near 980 nm. Because the contaminant content of the snow mainly affected the reflectivity in the visible range and almost no effect on snow albedo beyond 900 nm wavelength [
15], the snow’s water content maybe the main reason of causing the spectrum-absorption valley in the near-infrared bands to shift in a short-wave direction.
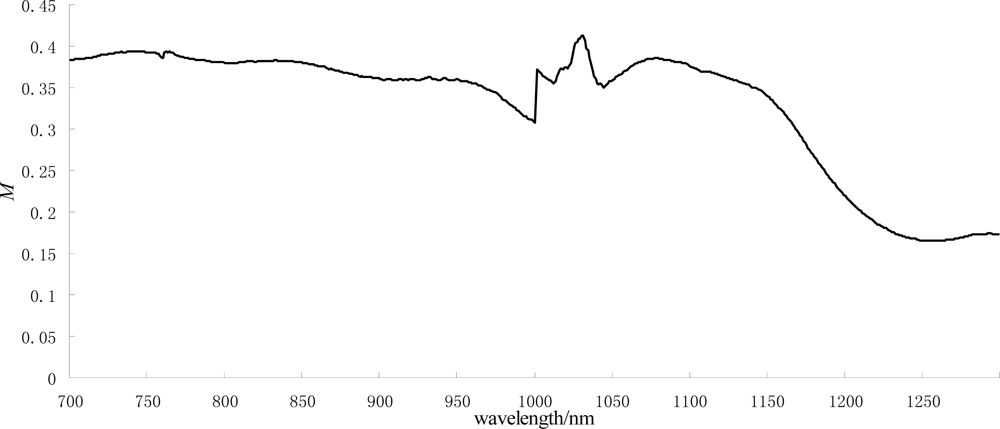
For the Hyperion imagery, the snow absorption valley of the near-infrared bands was not necessarily in band 89, which led to a high snow reflectance error of a single band. In the study, we explored the location of snow spectrum-absorption valleys in the near-infrared bands. There were 36,747 pixels in the normal absorption position, which is band 89. There were 2,329 pixels whose absorption-valley location moved to band 88, 110 pixels moved to band 87, 108 pixels moved to band 86, and 7 pixels moved to band 85, as shown in
Figure 13.
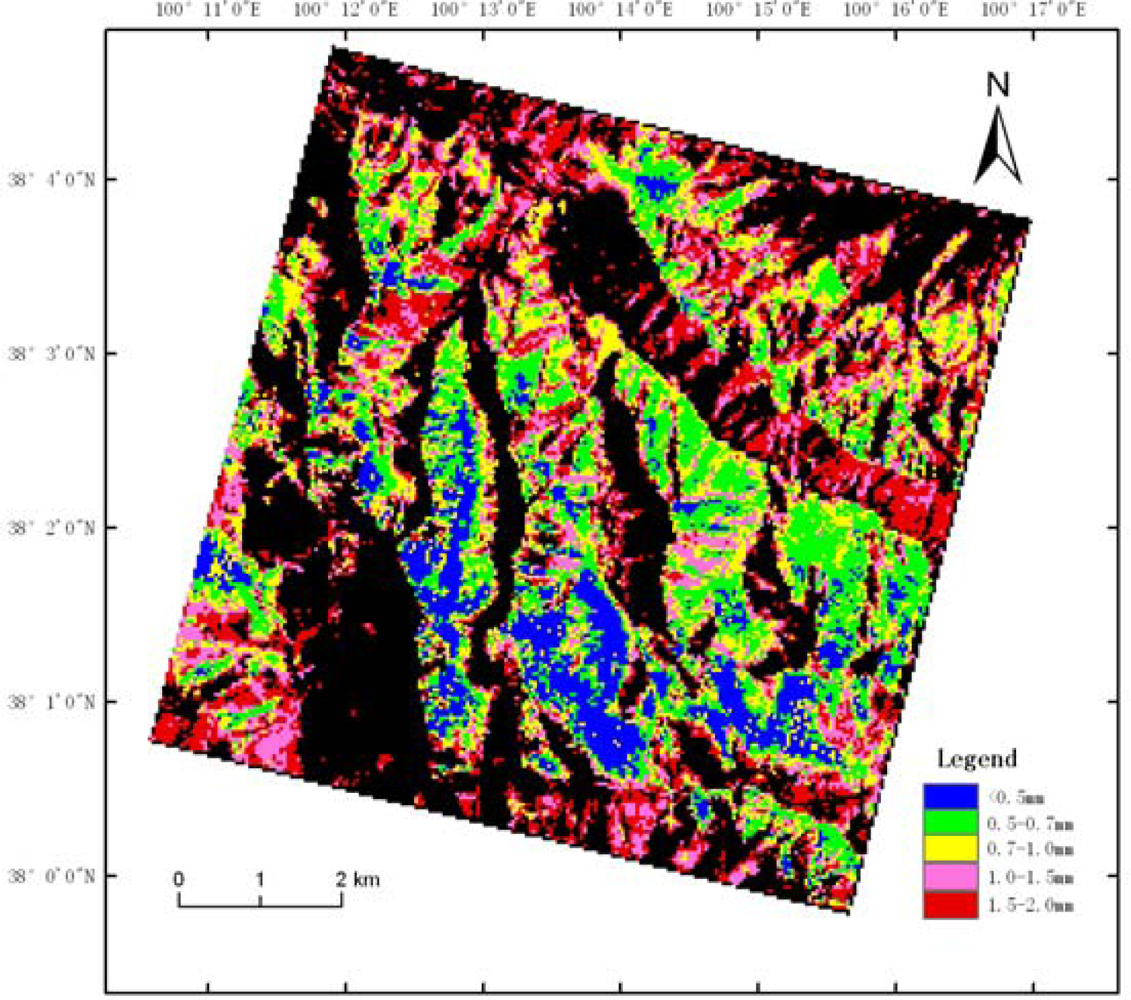
We assumed that the snow’s water content was proportional to the movement of the spectrum absorption valley and that the location reflected the water content of the snow. Using models of the snow reflectance and snow grain size in band 89 will result in large errors. For the 2,554 pixels that had spectrum absorption-valley movement, we could replace the assumed snow-reflectance wavelength with the new one.
Figure 14 shows the new distribution of the snow grain size. These abnormal pixels were affected by both the snow humidity and grain size. The relationship between the reflectance and snow characteristics was not a simple linear or exponential relationship, and there were no measured data. The estimation accuracy of the method requires further study.
3.4. Assessment of Snow Grain-Size Estimation Results
It can be seen from the distribution of the snow grain-size inversion that the snow grain size is relatively small in places with less sunlight, such as valleys and shady slopes, and vice versa, which is consistent with the actual situation. Snow in valleys and on shady slopes can easily maintain the characteristics of new snow. Snow on sunny slopes is often affected by sunlight and wind, which lead to significant deterioration.
Remote-sensing inversion data can be validated using directly measured snow grain sizes [
6,
12,
16,
17]. The remaining 163 measured snow grain-size data in Section 2.3, corresponding to 163 pixels of the Hyperion imagery, were synchronized with the transit time of the hyperspectral remote-sensing satellite. The
RMSE were calculated for both the linear and exponential models as follows:
where
yi is the measured value,
ŷ is an estimated value, and
n is the number of samples. The
RMSE were 0.14 mm and 0.12 mm for the linear model and the exponential model, respectively. The linear relationship between the estimated and measured snow grain sizes was calculated and shown in
Figure 15. The linear relationship coefficient
r2 is 0.86. The kappa coefficient of the estimate accuracy was calculated (
Table 1).
3.6. Uncertainties
First, the error of the measured spectral data could be caused during the field measurement. The standard reference versions of the spectral resolution, central wavelength position, signal-to-noise ratio, and diffuse reflectance are less precise. The staff and the surrounding environment will also have an impact the measured spectra. The low signal-to-noise ratio of the SWIR bands is lower than that of the VNIR bands for the Hyperion data. The low signal-to-noise ratio of the Hyperion data may impact the estimation accuracy. This problem may be addressed by using multiple bands near 1,030 nm, which can average one single-band noise.
The change in snow reflectance caused by the sun’s elevation angle is not a simple linear relationship, and the changes caused by different wavelengths of snow reflectance with solar elevation angle are also different. We cannot obtain reflectance data with the same snow-surface conditions but with different solar elevation angles, and therefore, it is difficult to correct for the solar altitude angle. The analysis results can also be affected.
Secondly, measurement error of snow grain size. Currently, the best measurement method of grain size is to extract a snow sample for observation using three-dimensional measurement techniques at a low-temperature laboratory [
4,
18,
19]. This technology can be used to observe not only the snow grain size but also the snow volume and surface area. However, with limited conditions, we used a hand-held 40-times-magnified calibrated microscope to measure the grain size and record the long axis diameter and shape of the snow particles. Measurements of the spectrum and grain size cannot be fully synchronized in exactly the same environment, which means that there will be subtle changes in the measurement process. Operating personnel may introduce reading errors due to different snow particle shapes. Different particle shapes also affect the optical properties of snow [
20,
21]. Forward-reflected radiances and backscattering radiances may be overestimated or underestimated, regardless of the particle shapes.
The topography can affect the snow reflectance, especially if there is shaded area. The normalized reflectance, like the absorption band depth or area [
8], may reduce the topographic effect to a certain extent. Considering that the topography of the study area was mainly aligned from north to south and the satellite-transit time was close to noon, we used a single-band model. In further work, we may combine the images with DEM data to remove the topography influence.
Different wavelengths have different snow penetration depths, and a single wavelength also has different penetration depths with different grain sizes. The penetration depth of a snow layer was normally within 10 cm near the wavelength of 1,030 nm. The estimated results only represent the snow grain size within 10 cm depth. The estimation of the grain size at different depths is a problem worth further exploration.
4. Conclusions
The wavelength near 1,030 nm is most sensitive to snow grain size, which was found by implementing the variogram algorithm based on the analysis of field spectral and snow grain size measurements in the paper. This wavelength corresponding to band 89 of Hyperion imagery, whereby the waveband center is 1,033.5 nm and band width is 10 nm. We built linear and exponential models using band 89 to estimate snow grain size in the Heihe River Basin, China, and found that the exponential relationship performed slightly better than the linear correlation. The square of the correlation coefficient between estimated and measured snow grain sizes is 0.86 and the Kappa coefficient of the estimate accuracy is 0.611.
Furthermore, water had a strong absorption band in the near-infrared region at approximately 980 nm (band 63 on Hyperion imagery). Thus, the water content in snow may cause the near-infrared snow-spectrum absorption to shift to shorter wavelengths. We calculated the location of the absorption and showed the influence of water content on some pixels, in which the wavelength of the absorption shifted 1–4 bands from band 89.
The current model can be run operationally and has a robust performance over the study area of the paper. However the model needs some further development. Therefore, future endeavors should focus on multibands and radar imaging to develop a method for estimating snow grain size at different depths, while considering the influence of the more irregular snow grain shapes.