Radiometric and Geometric Analysis of Hyperspectral Imagery Acquired from an Unmanned Aerial Vehicle
Abstract
:1. Introduction
2. System Overview
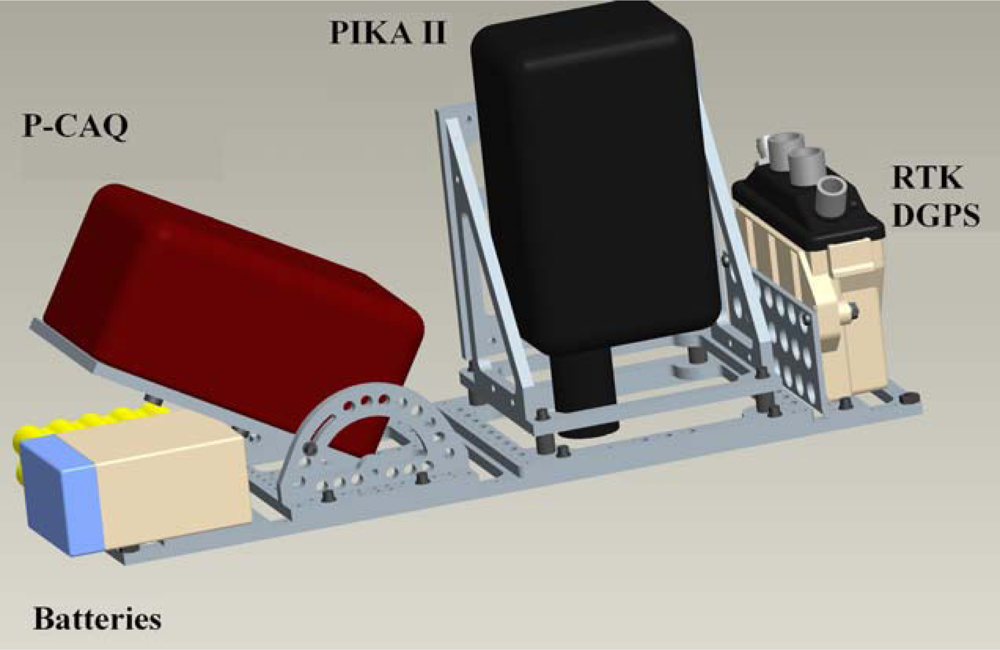
2.1. Sensor System
2.2. Platform
2.3. System Integration
3. Methods
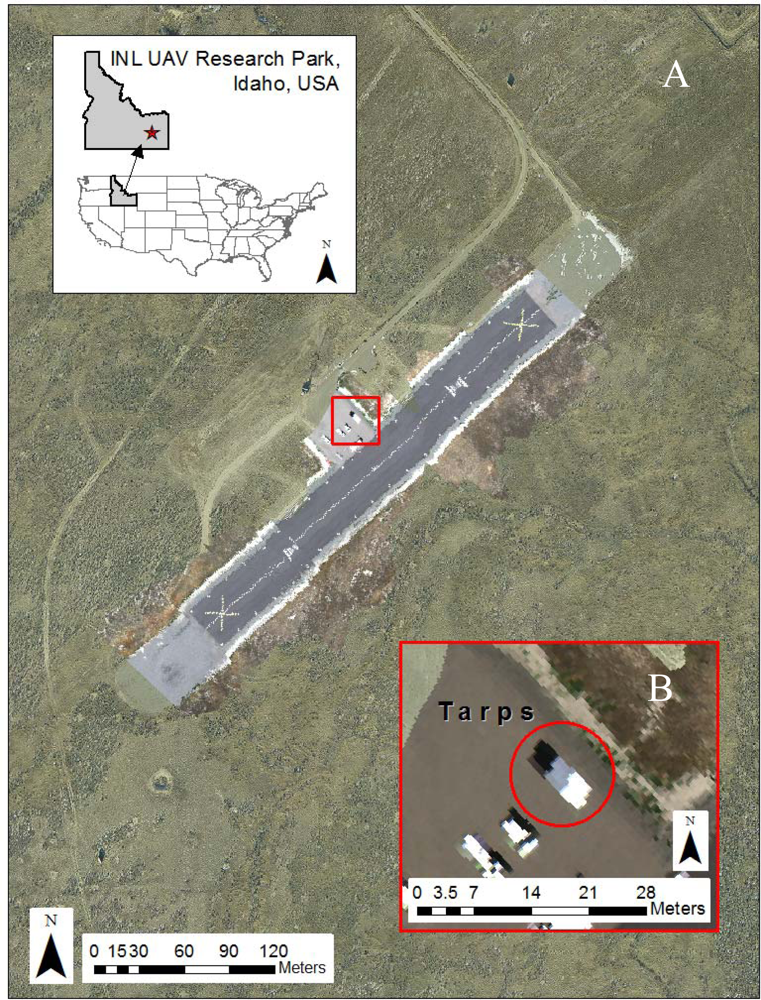
3.1. Data Collection
3.2. Image Pre-Processing
3.3. Geometric Analysis
3.4. Radiometric Analysis
3.4.1. In situ Spectral Measurements
3.4.2. Radiative Transfer Modeling
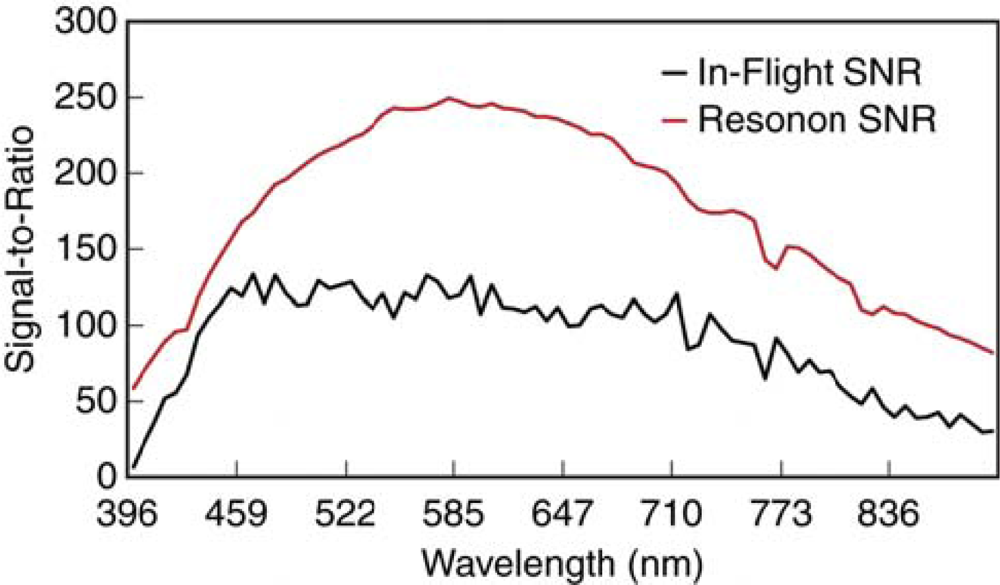
3.4.3. PIKA II Radiometric Evaluation
4. Results and Discussions
4.1. Geometric Correction
4.2. Radiometric Analysis
5. Conclusions
Acknowledgments
References
- Vane, G.; Green, R.O.; Chrien, T.G.; Enmark, H.T.; Hansen, E.G.; Porter, W.M. The airborne visible/infrared imaging spectrometer (AVIRIS). Remote Sens. Environ 1993, 44, 27–143. [Google Scholar]
- Cocks, T.; Jenssen, R.; Stewart, A.; Wilson, I.; Shields, T. The HYMAP Airborne Hyperspectral Sensor: The System, Calibration, and Performance. Proceedings of the 1st EARSEL Workshop on Imaging Spectroscopy, Zurich, Switzerland, 6–8 October 1998; pp. 37–42.
- Mitchell, J.; Glenn, N. Leafy spurge (Euphorbia esula L.) classification performance using hyperspectral and multispectral sensors. Rangeland Ecol. Manag 2009, 62, 16–27. [Google Scholar]
- Zhang, Y.; Slaughter, D.C.; Staab, E.S. Robust hyperspectral vision-based classification for multi-season weed mapping. ISPRS J. Photogramm 2012, 69, 65–73. [Google Scholar]
- Hestir, E.L.; Khanna, S.; Andrew, M.E.; Santos, M.J.; Viers, J.H.; Greenberg, J.A.; Rajapakse, S.S.; Ustin, S.L. Identification of invasive vegetation using hyperspectral remote sensing in the California Delta ecosystem. Remote Sens. Environ 2008, 112, 4034–4047. [Google Scholar]
- Yang, C.; Everitt, J. Using spectral distance, spectral angle and plant abundance derived from hyperspectral imagery to characterize crop yield variation. Precis. Agric 2012, 13, 62–75. [Google Scholar]
- Corp, L.A.; Middleton, E.M.; Campbell, P.E.; Huemmrich, K.F.; Daughtry, C.S.T.; Russ, A.; Cheng, Y.B. Spectral indices to monitor nitrogen-driven carbon uptake in field corn. J. Appl. Remote Sens 2010, 4, 043555–043555. [Google Scholar]
- Ye, X.; Sakai, K.; Sasao, A; Shin-Ichi, A. Estimation of citrus yield from canopy spectral features determined by airborne hyperspectral imagery. Int. J. Remote Sens 2009, 30, 4621–4642. [Google Scholar]
- Haboudane, D.; Tremblay, N; Miller, J.R.; Vigneault, P. Remote estimation of crop chlorophyll content using spectral indices derived from hyperspectral data. IEEE Trans. Geosci. Remote Sens 2008, 46, 423–437. [Google Scholar]
- Zhang, Q.; Middleton, E.M.; Gao, B.; Cheng, Y. Using E0-1 hyperion to simulate products for a coniferous forest: The fraction of PAR absorbed by chlorophyll (fAPARchl) and Leaf Water Content (LWC). IEEE Trans. Geosci. Remote Sens 2012, 50, 1844–1852. [Google Scholar]
- Mitchell, J.; Glenn, N.; Sankey, T.; Derryberry, D.; Germino, M. Hyperspectral remote sensing of sagebrush canopy nitrogen. Remote Sens. Environ 2012, 124, 217–223. [Google Scholar]
- Kokaly, R.F.; Asner, G.P.; Ollinger, S.V.; Martin, M.E.; Wessman, C.A. Characterizing canopy biochemistry from imaging spectroscopy and its application to ecosystem studies. Remote Sens. Environ 2009, 113, S78–S91. [Google Scholar]
- Kaufman, H.; Segl, K.; Itzerott, H.; Bach, A.; Wagner, J.; Hill, B.; Heim, K.; Oppermann, K.; Heldens, W.; Stein, E.; et al. Hyperspectral Algorithms: Report in the Frame of EnMAP Preparation Activities; Scientific Technical Report STR 10/08. Deutsches GeoForschungsZentrum GFZ: Potsdam, Germany, 2010.
- Jacquemond, S.; Verhouf, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S. PROSPECT + SAIL models: A review of use for vegetation characterization. Remote Sens. Environ 2009, 113, S56–S66. [Google Scholar]
- Acevo-Herrera, R.; Aguasca, A.; Bosch-Lluis, X.; Camps, A.; Martínez-Fernández, J.; Sánchez-Martín, N.; Pérez-Gutiérrez, C. Design and first results of an UAV-borne L-band radiometer for multiple monitoring purposes. Remote Sens 2010, 2, 1662–1679. [Google Scholar]
- Rango, A.; Havstad, K.; Estell, R. The utilization of historical data and geospatial technology advances at the jornada experimental range to support western America ranching culture. Remote Sens 2011, 3, 2089–2109. [Google Scholar]
- Green, R.O. Spectral calibration requirement for earth-looking imaging spectrometers in the solar-reflected spectrum. Appl. Opt 1998, 37, 683–690. [Google Scholar]
- Schaepman-Strub, G.; Schaepman, M.E.; Painter, T.H.; Dangel, S.; Martonchik, J.V. Reflectance quantities in optical remote sensing—Definitions and case studies. Remote Sens. Environ 2006, 103, 27–42. [Google Scholar]
- Hunt, E.R.; Everitt, J.H.; Ritchie, J.C.; Moran, M.S.; Booth, D.T.; Anderson, G.L. Applications and research using remote sensing for rangeland management. Photogramm. Eng. Remote Sensing 2003, 69, 675–693. [Google Scholar]
- Hardin, P.J.; Jackson, M.W. An unmanned aerial vehicle for rangeland photography. Rangeland Ecol. Manag 2005, 58, 439–442. [Google Scholar]
- Laliberte, A.S.; Rango, A. Texture and scale in object-based analysis of subdecimeter resolution unmanned aerial vehicle (UAV) imagery. IEEE Trans. Geosci. Remote Sens 2009, 47, 761–770. [Google Scholar]
- Berni, J.A.J.; Zarco-Tejada, P.J.; Suarez, L.; Fereres, E. Thermal and narrowband multispectral remote sensing for vegetation monitoring from an unmanned aerial vehicle. IEEE Trans. Geosci. Remote Sens 2009, 47, 722–738. [Google Scholar]
- Nagai, M.; Chen, T.; Shibasaki, R.; Kumagai, H.; Ahmed, A. UAV-Borne 3-D mapping system by multisensor integration. IEEE Trans. Geosci. Remote Sens 2009, 47, 701–708. [Google Scholar]
- Laliberte, S.A.; Goforth, M.A.; Steele, C.M.; Rango, A. Multispectral remote sensing from unmanned aircraft: Image processing workflow and application for rangeland environments. Remote Sens 2011, 3, 2529–2551. [Google Scholar]
- Kelcey, J.; Lucieer, A. Sensor correction of a 6-band multispectral imaging sensor for UAV remote sensing. Remote Sens 2012, 4, 1462–1493. [Google Scholar]
- Lin, Y.; Hyyppä, A. Mini-UAV-borne LIDAR for fine-scale mapping. IEEE Geosci. Remote Sens. Lett 2011, 8, 426–430. [Google Scholar]
- Koo, V.C.; Chan, Y.K.; Gobi, V.; Chua, M.Y.; Lim, C.H.; Lim, C.-S.; Thum, C.C.; Lim, T.S.; Ahmad, Z.; Mahmood, K.A.; et al. A new unmanned aerial vehicle synthetic aperture radar for environmental monitoring. Prog. Electromagn. Res 2012, 122, 245–268. [Google Scholar]
- Watts, A.C.; Ambrosia, V.G.; Hinkley, E.A. Unmanned aircraft systems in remote sensing and scientific research: Classification and considerations of use. Remote Sens 2012, 4, 1671–1692. [Google Scholar]
- Zarco-Tejada, P.J.; Gonzalez-Dugo, V.; Berni, J.A.J. Fluorescence, temperature and narrow-band indices acquired from a UAV platform for water stress using a micro-hyperspectral images and a thermal camera. Remote Sens. Environ 2012, 117, 322–337. [Google Scholar]
- Skaloud, J. Problems in Direct-Georeferencing by INS/DGPS in the Airborne Environment. Proceedings of the ISPRS Workshop WG III/1, Barcelona, Spain, 25–26 November 1999; pp. 25–26.
- Federal Geographic Data Committee, Geospatial Positioning Accuracy Standards, Part 3: National Standards for Spatial Data Accuracy. Subcommittee for Base Cartographic Data; Standard FGDC-STD-007.3-1998; Federal Geographic Data Committee: Reston, WV, USA, 1998.
- Green, R.; Pavri, B.; AVIRIS in-flight Calibration Experiment, Sensitivity Analysis, and Intraflight Stability. Proceedings of the 9th JPL Airborne Earth Science Workshop, Pasadena, CA, USA, 23–25 February 2000; pp. 207–221.
- Anderson, K.; Milton, E.J.; Rollin, E.M. Sources of Uncertainty in Vicarious Calibration: Understanding Calibration Target Reflectance. Proceedings of the 2003 IEEE International Geoscience and Remote Sensing Symposium, Toulouse, France, 21–25 July 2003; pp. 2072–2074.
- Berk, A.; Bernstein, L.S.; Anderson, G.P.; Acharya, P.K.; Robertson, D.C.; Chetwynd, J.H.; Adler-Golden, S.M. MODTRAN cloud and multiple scattering upgrades with application to AVIRIS. Remote Sens. Environ 1998, 65, 367–375. [Google Scholar]
- Fujimoto, N.; Takahashi, Y.; Moriyama, T.; Shimada, M.; Wakabayashi, H.; Nakatani, Y.; Obayani, S. Evaluation of SPOT HRV Image Data Received in Japan. Proceedings of the International Geoscience and Remote Sensing Symposium, Vancouver, BC, Canada, 10–14 July 1989; pp. 463–466.
- Lee, C.; Bethel, J. Georegistration of airborne hyperspectral image data. IEEE Trans. Geosci. Remote Sens 2001, 39, 1347–1351. [Google Scholar]
- Gurtner, A.; Greer, D.G.; Glassock, R.; Mejias, L.; Walker, R.A.; Boles, W.W. Investigation of fish-eye lenses for small-UAV aerial photography. IEEE Trans. Geosci. Remote Sens 2009, 47, 709–721. [Google Scholar]
- McKeown, D.M., Jr.; Cochran, S.D.; Ford, S.J.; McClone, J.C.; Shufelt, J.A.; Yocum, D.A. Fusion of HYDICE hyperspectral data with panchromatic imagery for cartographic feature extraction. IEEE Trans. Geosci. Remote Sens 1999, 37, 1261–1277. [Google Scholar]
- Cariou, C.; Chehdi, K. Automatic Georeferencing of airborne pushbroom scanner images with missing ancillary data using mutual information. IEEE Trans. Geosci. Remote Sens 2008, 46, 1290–1306. [Google Scholar]
- Gao, B. An operational method for estimating signal to noise ratios from data acquired with imaging spectrometers. Remote Sens. Environ 1993, 43, 23–33. [Google Scholar]
- Smith, G.M.; Curran, P.J. The Effects of Signal Noise on the Remote Sensing of Foliar Biochemical Concentration. Proceedings of the JPL AVIRIS Airborne Geoscience Workshop, Pasadena, CA, USA, 25–29 October 1993; pp. 161–164.





| Parameter | PIKA II/P-CAQ |
|---|---|
| Volume (mm) | |
| PIKA II | 102 × 165 × 70 |
| P-CAQ | 102 × 165 × 82 |
| Weight (kg) | |
| PIKA II | 1.043 |
| P-CAQ | 1.16 |
| Average power (W) | 15W nominal, 30W max |
| Aperture (F/#) | f/3 |
| IFOV(mrad) | 0.65 |
| Crosstrack FOV (deg) | 12.0 |
| Crosstrack pixels | 640 max |
| Wavelength range (nm) | 400–900 |
| Spectral resolution (nm) | 2.1 max |
| Number of spectral bands | 240 max |
| Bit depth | 12 bits |
| Frame rate (Hz) | 135 fps max in-flight |
| Smile | <1 Pixel |
| Keystone | <1 Pixel |
| Parameter | Flight Configuration |
|---|---|
| Elevation-AGL (m) | 344 |
| Nominal ground speed (m/s) | 28 |
| Swath width (m) | 80 |
| GSD (cm) | 28 |
| Wavelength range (nm) | 396.3–892.1 |
| Spectral resolution (nm) | 6.2 |
| Cross track pixels | 320 |
| Number of spectral bands | 80 |
| Gain (db) | 0 |
| Frame rate (Hz) | 107 fps |
| Parameter | Flight Configuration |
|---|---|
| Date | 2010-07-27 |
| GMT | 17:30:00 |
| Latitude | 43.599° |
| Longitude | −112.905° |
| Sensor altitude | 1.782 km AGL |
| Atmospheric model | Mid-latitude summer |
| Aerosol model | Continental (rural) |
| Solar zenith angle | 24.57° |
| Solar azimuth angle | 175.46° |
| Terrain elevation | 1.483 km AGL |
| Water vapor content | 1 g/cm2 |
| Ozone column | Default |
| CO2 mixing ratio | 365 ppm |
| Visibility | 50 km |
| Parameter | ΔX(m) | ΔY(m) |
|---|---|---|
| Image 20 | −31.04 | −7.80 |
| Image 27 | −33.22 | −4.41 |
| Image 29 | −31.23 | −4.88 |
| Image 42 | −36.22 | −10.48 |
| Image 66 | −34.41 | −6.36 |
| Average Δ | −33.19 | −6.69 |
| Estimated roll bias | 2.8° | |
| Estimated pitch bias | 4.3° | |
| Parameter | RMSEX | RMSEY | RMSER | AccuracyR |
|---|---|---|---|---|
| Image 20 | 2.99 | 4.48 | 5.39 | 9.15 |
| Image 27 | 2.58 | 1.89 | 3.20 | 5.48 |
| Image 29 | 4.23 | 2.59 | 4.96 | 8.34 |
| Image 42 | 3.53 | 5.81 | 6.80 | 11.43 |
| Image 66 | 1.79 | 2.17 | 2.81 | 4.85 |
| Average | 4.63 | 7.85 |
Share and Cite
Hruska, R.; Mitchell, J.; Anderson, M.; Glenn, N.F. Radiometric and Geometric Analysis of Hyperspectral Imagery Acquired from an Unmanned Aerial Vehicle. Remote Sens. 2012, 4, 2736-2752. https://doi.org/10.3390/rs4092736
Hruska R, Mitchell J, Anderson M, Glenn NF. Radiometric and Geometric Analysis of Hyperspectral Imagery Acquired from an Unmanned Aerial Vehicle. Remote Sensing. 2012; 4(9):2736-2752. https://doi.org/10.3390/rs4092736
Chicago/Turabian StyleHruska, Ryan, Jessica Mitchell, Matthew Anderson, and Nancy F. Glenn. 2012. "Radiometric and Geometric Analysis of Hyperspectral Imagery Acquired from an Unmanned Aerial Vehicle" Remote Sensing 4, no. 9: 2736-2752. https://doi.org/10.3390/rs4092736




