Flux Measurements in Cairo. Part 2: On the Determination of the Spatial Radiation and Energy Balance Using ASTER Satellite Data

Abstract

This study highlights the possibilities and constraints of determining instantaneous spatial surface radiation and land heat fluxes from satellite images in a heterogeneous urban area and its agricultural and natural surroundings. Net radiation was determined using ASTER satellite data and MODTRAN radiative transfer calculations. The soil heat flux was estimated with two empirical methods using radiative terms and vegetation indices. The turbulent heat fluxes finally were determined with the LUMPS (Local-Scale Urban Meteorological Parameterization Scheme) and the ARM (Aerodynamic Resistance Method) method. Results were compared to in situ measured ground data. The performance of the atmospheric correction was found to be crucial for the estimation of the radiation balance and thereafter the heat fluxes. The soil heat flux could be modeled satisfactorily by both of the applied approaches. The LUMPS method, for the turbulent fluxes, appeals by its simplicity. However, a correct spatial estimation of associated parameters could not always be achieved. The ARM method showed the better spatial results for the turbulent heat fluxes. In comparison with the in situ measurements however, the LUMPS approach rendered the better results than the ARM method.

1. Introduction

The surface energy budget is an important term in the climatological system. It determines how the energy received from solar irradiation is distributed to other climatological terms. For example, areas with a high albedo reflect back a high amount of the solar irradiation, following that, the available energy for heating the soil and the near-surface air layers or evaporating water from the surface is low. Despite this, a change of the surface albedo has a direct impact on the radiative forcing and therefore on the microclimate. Such changes can arise by natural processes or through human impact. The construction of cities is an example of such a human interference. Besides the albedo, other surface properties like the heat storage capacity or the soil water storage capacity are also altered in cities, leading to different magnitudes and ratios of surface fluxes. In particular, megacities came to the notice of recent national and international political and social attention. More than half of the world’s population lives now in urban regions and megacities are a consequence of this migration process. Through the increased spatial extent of such urban regions, megacities become relevant for the local and even regional climate [1,2].

In the last decade, many studies have tried to estimate land surface fluxes from remote sensing images, e.g., [3–12]. A successful methodology would be extremely helpful, for example, for the determination of surface energy fluxes from remote areas, where it is difficult or even impossible to set up in situ measurements because of geographical, political, infrastructural, or social reasons.

The goal of this study is to show the possibilities to determine the whole instantaneous energy budget from ASTER satellite images for single dates of a remote area featuring very contrasting surface covers, using as few in situ measurements as possible. For this purpose, a megacity was selected, consisting of many different quarters and located in a natural environment with a variety of different landscapes. This study is the second publication from the CAPAC (Climate and Air Pollution Analysis of Cairo) project, following the first part dealing with in situ measurements [13].

From literature, there are three distinct groups of methods for the estimation of instantaneous turbulent heat fluxes. They can be summarized as (a) Bulk transfer approaches, (b) the Local-Scale Urban Meteorological Parameterization Scheme (LUMPS) scheme, and (c) extreme pixel approaches. These three groups, which all need a measurement channel in the thermal infrared, will be touched on in the following.

The bulk transfer approach uses remotely-sensed surface temperatures, together with an estimation of air temperature, net radiation, and ground heat flux to derive turbulent heat fluxes. The approach focuses on the determination of the resistance to heat transfer r_h. The estimation of the single terms is sometimes problematic. For example, the term r_h is a function of surface roughness, wind speed, and stability [4,14]. It inherently shows a high variability over heterogeneous surfaces. Several approaches using morphometric methods have been presented to account for this problem [15,16]. Also, the estimation of net radiation can be tricky, due to shading effects and multiple scattering of radiation by surface roughness elements. Nonetheless, several studies have used this method to derive urban sensible heat fluxes or the whole energy budget. In some cases, fairly good results were achieved, however other studies reported larger uncertainties and errors in the results [9,17,18]. In this paper, a bulk transfer approach is used, similar to the one described in [18], henceforward referred to as Aerodynamic Resistance Method (ARM).

The LUMPS approach, introduced by [19], is a linked set of equations using the method presented in [20] and [21]. LUMPS requires only standard meteorological observations and basic knowledge of the surface cover. Similar to the bulk transfer approach, it is driven by net radiation. Although the LUMPS approach was originally developed for surface station data, it was also used recently in combination with remote sensing data [18,22,23]. Central to the LUMPS approach is the determination of surface dependent parameters, which also show a high variability over heterogeneous surfaces. In this paper, the LUMPS approach was applied additionally to the ARM approach.

The third group of methods, the extreme pixel approaches, uses extreme wet and dry pixels rendered either by manual setting or by the relation of surface temperature and surface albedo to find the partition of turbulent heat fluxes for each pixel. These methods originate in the SEBI (Surface Energy Balance Index) formulation proposed by [24]. SEBI was developed further by many researchers. For example, Su [10] introduced the SEBS (Surface Energy Balance System) scheme incorporating the aerodynamic roughness length for heat in the model. S-SEBI (Simplified Surface Energy Balance Index, [8,25]) was derived from SEBS for use with remote sensing data. Although the S-SEBI approach appeals by its simplicity, it was found to be unusable for the area of interest in this study.

Please refer to [26] for a more comprehensive review on energy balance methods with special focus on the determination of evapotranspiration.

To compare the results of the LUMPS and ARM methods against field values, a measurement campaign was conducted from October 2007 to February 2008 in Greater Cairo. All relevant variables were continuously measured at three stations, each representing a major land cover class: ‘urban’, ‘suburban agricultural’ and ‘suburban desert’. Further details and results from this campaign are described in [13]. For simplicity, the last two stations will be named ‘agricultural’ and ‘desert’ in this paper.

2. Study Area

The study area is Greater Cairo, the largest city in Egypt and on the African continent. Greater Cairo is a megacity, which administratively belongs to three different units: the governorates of Cairo, Giza and Qalyubiyya. For this historical division of the contiguous agglomeration of the megacity, and due to many unregistered residents, cited inhabitant numbers may differ considerably. As a whole, the population can be estimated to about 20 million inhabitants [27]. Next to the study area of the urban agglomeration, there are neighboring agricultural and natural desert landscapes, resulting in a high diversity of surface characteristics dominating the scene (see Figure 1). Landscape features range from small-scale, irrigated farming spots, to the labyrinthine of the wadi systems in the Eastern desert, to diverse urban settlements (extremely dense housing to spacious villa quarters). This high diversity, manifesting itself in large amplitudes of surface albedo, emissivity, irradiation, soil humidity, and roughness, requires extremely robust procedures for the processing of the remote sensing data and quickly exposes potential weaknesses of each of the methodologies. Additional information about the study area can be found in [13].

3. Data

3.1. Satellite Data

The main remote sensing data source was ASTER (Advanced Spaceborne Thermal Emission and Reflection Radiometer), an optical imager on the TERRA satellite of NASA. It crosses the equator at about 10:30 local time. The spectral resolution ranges from the very visible to the thermal infrared with a spatial resolution from 15 m in the visible to 90 m in the thermal infrared. ASTER has a swath width of 60 km and its revisit time is 16 days. These features make ASTER an optimal candidate for medium-scale landscape analyses. A key question of this paper is how this ASTER data can be used for energy balance studies in urban regions.

Atmospheric correction of the ASTER data was performed using the radiative transfer model MODTRAN with midday radiosonde ascents from Helwan, south of Cairo, as input atmosphere. After [13], evidence is given that the aerosol load is not equally distributed over the images. To account for this, the path radiance and transmissivity used for the atmospheric correction were modeled in dependence on the aerosol optical depth (AOD), taken from the operational aerosol product from MISR (Multi-angle Imaging SpectroRadiometer), also onboard TERRA [28]. Path radiance is not only dependent on the AOD, but also on the surface reflectance. An additional interpolation was introduced to scale the estimated path radiance to the apparent reflectance. As the reflectance is available only after the atmospheric correction, a first rough guess of reflectances was used for this step.

Two versions of atmospheric correction are used in this study: a ‘best guess’ version, using the MODTRAN aerosol setting ‘urban, visibility 5 km’, and a ‘best fit’ version, using the aerosol setting ‘rural, visibility 23 km’. The second version produced the better matching of the broadband albedo with in situ measured values. However, the first one was considered to be the logical one to take, having no comparison values at hand. The use of these two versions of atmospheric correction shed light on the impact of atmospheric correction on the accuracy of flux determination. However, the versioning only affected the short wave bands. The ‘best guess’ correction of long wave bands was considered to be very good, so no ‘best fit’ was introduced for these bands.

Unfortunately, the ASTER SWIR instrument suffers from thermal anomalies from December 2008. Therefore, the SWIR data from 24 December and 2 January could not be used in this study. It mainly affected the estimation of the broadband albedo. All scenes had more or less cloud contaminations. Cloud areas were first detected using an automated cloud-detection algorithm. As the algorithm was not able to detect all areas where strong haze occurred, additional manual edition was necessary. The cloudy areas were not used in any of the following analyses.

Additionally, a scene of ASAR (Advanced Synthetic Aperture Radar), an imaging microwave radar operating at C-band, was used in this study. The scene was acquired in the ASAR image mode, where only one of seven predetermined swaths is sensed. A geolocated level 1B product with polarization set to ‘VV’ was chosen. Spatial resolution of the delivered product was 12.5 m. Further, the SRTM (Shuttle Radar Topography Mission) digital elevation model of the region was downloaded. Both the ASAR and the SRTM were georeferenced to the VNIR ASTER images using manual chosen pass points. Through this process, the spatial resolution was also adjusted to the VNIR ASTER resolution (15 m).

3.2. In situ Data

In situ data from the CAPAC campaign [13] were used in additional to the satellite data. Besides standard meteorological parameters like air temperature, humidity and wind speed/direction, the long and short wave up- and down-welling radiation, the ground heat flux and the turbulent heat fluxes were also measured continuously from 20 October 2007 to 20 February 2008 at three locations. The first station was on the roof of a building inside the campus of the Cairo University in Giza, west of the River Nile. At this station the ground heat flux was not measured, but indirectly derived from the other terms. The second station was on the northern rim of Cairo in the Bahteem district on an agricultural field inside a meteorological station of EMA (Egyptian Meteorological Authority). The third station was also part of a meteorological station of EMA outside the agglomeration of Cairo in the desert, next to the satellite town, 10th Ramadan. Further details of the campaign and a description of the data can be found in [13].

Flux measurements using the eddy covariance technique frequently suffer from a closure gap in the energy balance (e.g., [29]). The sum of the measured turbulent fluxes is sometimes lower than the available energy (the difference between net radiation and the ground heat flux). This residual is subject to current research and was attributed, amongst other reasons, to the influence of advection, lacking homogeneity of the surface, weak turbulence, and the exclusion of large eddies through a probably too short sampling time [30]. In the data of CAPAC, a considerable residual was found too, [13]. Most probably, it is reasonable to partition the residual among the turbulent heat fluxes to close the gap. However, it is unclear to which percentages this distribution must take place. Twine et al. [31] proposed a simple distribution proportional to the Bowen ratio. This approach was applied here, despite the supposition that the ratio might be different for large eddies [30].

Another constraint of the eddy covariance technique is that fluxes are average values of a certain time period (30 min in the CAPAC campaign), while satellite data are instantaneous measurements. Therefore, during the averaging period, considerable changes in the radiation situation might occur, probably influencing the derivation of these fluxes. Such changes are not incorporated in the satellite measurement, surely leading to a certain mismatch when comparing products from the two approaches.

Finally, it should be mentioned that the anthropogenic heat flux cannot be measured separately and is included in the sensible and the ground heat flux.

Not all stations (‘Cairo University’, ‘Bahteem’, and ‘10^th Ramadan’) were covered by all scenes. The following dates of ASTER data were available during the campaign in Cairo. An X in

Table 1. Dates of ASTER acquisitions during the CAPAC campaign.

Date	Number of Scenes	Urban: ‘Cairo University’	Agricultural: ‘Bahteem’	Desert: ‘10th Ramadan’
22nd November 2007	2(a + b)	X	X	X
1st December 2007	2(a + b)	X	X	X
24th December 2007	2(a + b)	X	X	X
2nd January 2008				X

indicates that the station is covered by at least one scene during this day. Scenes (a) are usually depicting the northern part of the agglomeration; scenes (b) show the southern part.

4. Methods: Radiation Balance

4.1. Modeling of Net Radiation

The net radiation Q^* [W·m⁻²] is given as

$${\text{Q}}^{*}=(1-\alpha )\cdot {\text{K}}_{\downarrow }+{\text{L}}_{\downarrow }-L_{\uparrow },$$

(1)

with α denoting the broadband surface albedo, K↓ the broadband irradiation [W·m⁻²], L↓ incoming long wave radiation [W·m⁻²], and L↑ outgoing long wave emission [W·m⁻²]. In the following, all terms will be explained separately.

4.1.1. Broadband Albedo α

To convert the spectral reflectances ρ of ASTER obtained from the atmospheric correction algorithm to broadband albedos, an empirical equation was used, which was gained from a multiple regression approach similar to [32]. The equation, using 86 samples of different surface materials of the ASTER spectral library Version 1.2 of JPL Laboratories.

In case of the ASTER scenes from 24 December 2007 and 01 February 2008, only the VNIR bands were available due to a temperature anomaly in the detector. Therefore, another equation was obtained for these dates. The resulting empirical regression equations are listed in the annex.

4.1.2. Outgoing Long Wave Emission L_↑

For the outgoing long wave emission L_↑, the atmospheric corrected TOA (Top Of the Atmosphere) radiances using the ‘best guess’ option for the atmospheric correction were converted to brightness temperatures using the Planck-function. As the Planck-function is only valid for a single band wave number, the correction of the least-square-fit method described in [32] was used. Using assumed synthetic emissivities, surface temperatures were then calculated for band 14. The assumed emissivities were 0.98 (water and pure vegetation) and 0.90 (urban and desert). In urban and agricultural areas of the ASTER scenes, where mixed pixels often occur, the formulas of [33] were used, incorporating the above-mentioned emissivities for pure pixels. The emissivities of the other bands were obtained by comparing their surface temperatures with the surface temperatures of the emissivity-corrected band 14. The resulting band emissivities (ε_bi) were then converted to broadband emissivities (ε), using empirical regression equations for each land use, similar to the albedo approach. The equations for the different land use classes are also in the annex.

4.1.3. Incoming Broadband Irradiation K_↓ and Incoming Long Wave Radiation L_↓

Incoming broadband irradiation K_↓ was estimated using MODTRAN runs over the short wave range from 0.25 to 4 μm. For the option ‘best guess’, the same MODTRAN settings were used, as for the atmospheric correction of the band radiances in the ‘best guess’ mode. For the option ‘best fit’ however, the in situ measured K_↓ values from the CAPAC campaign [13] were used to iteratively find the optimal AOD values for the three available stations by minimizing the differences between the measured and the modeled K_↓ values. The spatial solar irradiation K_↓ is given as the sum of beam irradiation, diffuse irradiation, and irradiation reflected from the environment and is calculated in dependence on the sky view factor which was derived from the SRTM DEM [34].

Incoming long wave radiation L_↓ was also estimated using the ‘best guess’ option in MODTRAN. Yet, no ‘best fit’ option was introduced to the long wave fluxes.

5. Methods: Heat Fluxes

5.1. Modeling of the Ground Heat Flux Q_s

The ground heat flux Q_s [W·m⁻²] is a function of the available energy on the surface and the layers beneath and the thermal properties of the soil. Thermal properties are dependent on soil moisture and porosity and therefore only constant at sealed surfaces. Whilst the estimated Q* stands for the available energy, it is more difficult to describe the thermal properties of the ground. Common approaches found in literature are using different vegetation indices for this purpose [3,5,7,35–37]. In this work the approach found in [38] and a new approach are presented. According to [38] the ground heat flux in urban areas is

$$Q_{\mathit{urban}}=(0.3673-0.3914\cdot \mathit{NDVI})\cdot Q^{*}$$

(2)

Apart from this approach, a new formula was derived using linear regression with a set of in situ data from the CAPAC campaign. Due to extremely high fluctuations in the storage term of the ground heat flux [13], it was decided only to work with 30 min averages. Daytime Q* and Q_s (07:00–16:00) from the period from 20 November 2007 to 20 February 2008 were used. The data were filtered for sunny hours by comparing actual net radiation to an adapted sine wave. The daily curve of Q_s features a time offset towards the curve of Q* of about one hour (see Figure 8 in [13]). The reason for this offset is probably found in the measurement technique of in situ Q_s, measuring the flux a few centimeters underground. Therefore, the whole time series of the latter parameter was shifted backwards one hour for the regression calculations (Q*_h−1). The NDVI then explains the differences between the stations, similar to the ‘Parlow/urban’ approach. The first term in equation 9 explains the variation of the land use and was derived specifically for the late morning hours. The second term describes the relation between Q* and Q_s and is valid for the whole day.

$${\text{Q}}_{\text{s}}=(-0.529\cdot \text{NDVI}+0.37)\cdot (1.155\cdot {\text{Q}}_{\text{h}-1}^{*}-17.542)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\text{r}}^2=0.6$$

(3)

Q_s was not measured at the urban station. Therefore, it had to be deduced from the balance of Q* and the turbulent heat fluxes. However, for surfaces which were not perfectly homogeneous, the energy balance is not closed and a considerable unexplained residual remains. This residual was roughly estimated for the urban station using the residuals from the agricultural and the desert station. Then Q_s was derived as balance from Q*, the turbulent heat fluxes and the estimated residual.

Besides Q*, other variables like α or ε were tested for their feasibility in describing Q_s. However, none of these variables was able to improve the regression coefficients.

5.2. LUMPS

LUMPS stands for the Local-Scale Urban Meteorological Parameterization Scheme and was developed to calculate turbulent fluxes using standard meteorological measurements and two semi-empirical parameters describing the surface cover. Its origin is a simplified Penman-Monteith approach, incorporating the Priestley–Taylor coefficient for extensive wet surfaces and extending it to non-saturated surfaces [19]. While the α parameter should account for the strong correlation between the heat fluxes (Q_H, Q_LE) and the available energy (Q* − Q_s), β stands for the uncorrelated part [21]. In this study, both parameters were derived empirically from the in situ data of the CAPAC campaign. The values are derived for each station for a vegetated and a non-vegetated wind sector. Further, a comparison with a set of selected values from literature from [19] is given. Thereby the values from Mexico City are taken for the urban station.

Table 2. α and β parameter derived from the in situ data of the CAPAC campaign.

	Urban: ‘Cairo University’		Agricultural: ‘Bahteem’		Desert: ‘10th Ramadan’
	α	β	α	β	α	β
Non-vegetated sector	1.46	3.43	1.52	43.99	0.78	0.78
Vegetated sector	1.64	7.2	3.17	33.16	0.71	9.70
Values from literature (Grimmond & Oke 2002)	0.19	−0.3	1.2	20	0.2	20

gives the α and β values. The values were applied to the ASTER images according to the land uses: ‘urban’, ‘vegetation’ and ‘desert’. The LUMPS equations for the turbulent heat fluxes are as follows:

$${\text{Q}}_{\text{LE}}=\alpha \cdot \left[\frac{1}{1+\frac{\gamma }{s}}\right]\cdot \left(Q^{*}-Q_s\right)+\beta$$

(4)

and

$${\text{Q}}_{\text{H}}=\alpha \cdot \left[\frac{1-\alpha +\frac{\gamma }{s}}{1+\frac{\gamma }{s}}\right]\cdot \left(Q^{*}-Q_s\right)-\beta$$

(5)

5.3. ARM (Aerodynamic Resistance Method)

An alternative method to estimate the sensible heat flux is the bulk transfer equation,

$${\text{Q}}_{\text{H}}={\rho }_{\mathit{air}}\cdot C_p\cdot \frac{T_s-T_a}{r_h},$$

(6)

where ρ_air is the density of air [kg·m⁻³], C_p the specific heat of air at constant pressure [J·kg⁻¹·K⁻¹], T_s is the surface temperature [°K] calculated from the ASTER TIR data and T_a is the air temperature [°K]. r_h is the aerodynamic resistance for heat [s·m⁻¹] [14]. Q_LE is then the residual of the available energy and Q_H. Spatial T_a had to be estimated and was deduced using empirical regression equations with T_s and wind speed obtained from the CAPAC campaign data. The equations are given in the appendix.

The aerodynamic resistance r_h can be determined with an approach using the roughness length, stability correction functions for momentum and heat, and the friction velocity [9]. The estimation of these parameters needs a detailed surface scheme, including a digital surface model of the urban area. However, no such detailed model was available for Cairo in sufficient accuracy; therefore, another empirical approach using radar data was pursued. Several studies have shown that aerodynamic roughness length can be represented by radar data [39–41]. Using the measurement data from the CAPAC campaign, an empirical relation was found between r_h and the radar backscattering coefficient σ⁰ of the ASAR image from 2 January 2008.

The radar image was smoothed with a 13 × 13 filter to remove speckle and other disturbing effects before serving as input in the regression calculation, together with the wind speed wnd_spd [m·s⁻¹]. The resulting equation is

$${\text{r}}_{\text{h}}=-1.051\cdot {\sigma }^0-5.64\cdot \mathit{wnd}\_\mathit{spd}+134.82.$$

(7)

5.4. Source Footprint Models

Eddy flux towers measure fluxes originating from an extended upwind source area of the tower. The spatial extent of the source area depends on the measuring height, the roughness of the surface, and the stability of the boundary layer. In the CAPAC campaign, considerable directionality was found in the turbulent flux data, especially at the agricultural station ‘Bahteem’ [13]. To be able to compare these in situ measurements with the remote sensing data, it was decided to use a source footprint model. Analytical approaches describing the source area have their origin in the works of [42] and [43]. In this work, a simple analytical model, the KM (Korman & Meixner) model [44], was used. In parallel, two other models [45], as used in [46] and [47], were investigated. However, even though the calculated footprints were not identical, the resulting fluxes were nearly the same. Figure 2 shows the footprints for the three stations on 24 December 2007. Footprints were used for the evaluation of the LUMPS and the ARM results.

6. Results

The presentation of the results follows two strategies. First, the calculated parameters from the ASTER data are compared to the in situ measurements. The comparison is executed by the analysis of mean absolute differences (MAD), which are the mean values of the absolute differences between associated values from each of the in situ measurements and the remote sensing approaches. The MAD is given by

$$\mathit{MAD}=\frac{1}{n}{\sum }_{i=1}^n\left|{\mathit{Value}}_{\text{Re}{\mathit{mSens}}_i}-{\mathit{Value}}_{{\mathit{InSitu}}_i}\right|$$

(8)

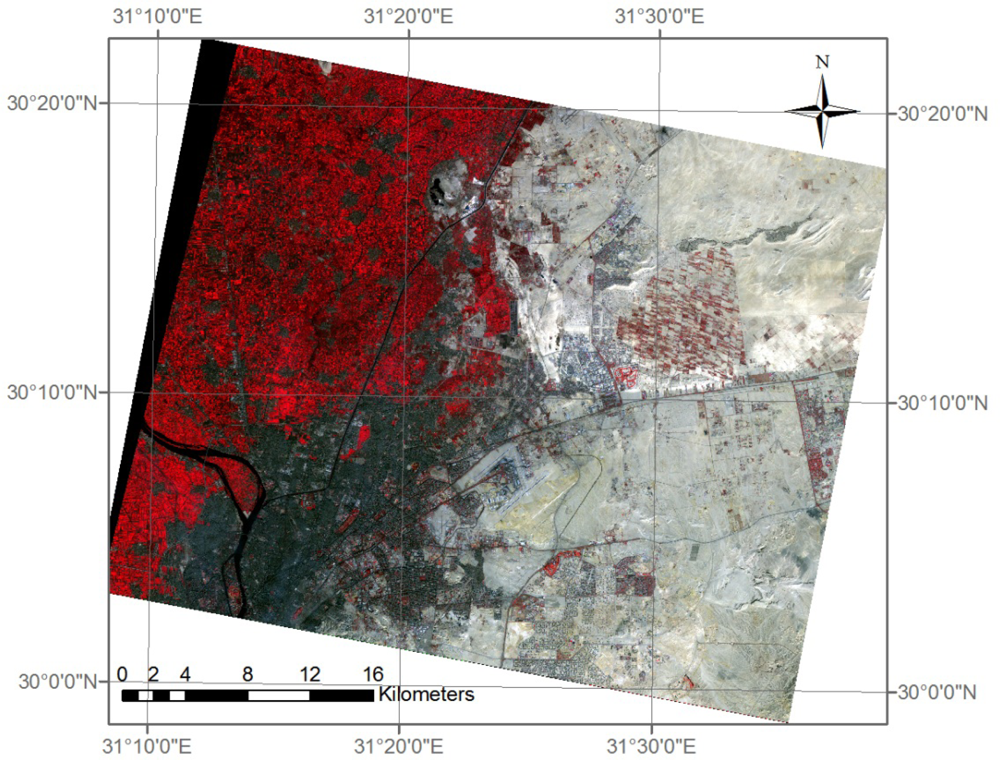
In a second step, the spatial variations in the image are discussed on the basis of what is expected and realistic. The basis for this discussion are the general land use classes ‘urban’, ‘agriculture’ and ‘desert’.

6.1. Radiation Fluxes

The calculated radiation fluxes from the ‘best guess‘ and the ‘best fit‘ option were compared to the in situ measured fluxes (original 1 min averages) using the values of the pixel directly associated with the station. Assuming a purely cosine dependent sensor response of the in situ radiation measurement instrument, reflected radiation for the agricultural and the desert station comes from a circular area within a radius of 11 m. In the case of the urban station however, the radius is much larger. Though, using only the height difference between the sensor and the roof, about 90% of the flux would come from a circle within a radius of 45 m.

For the urban and the agricultural station, three overflights could be used; the desert station had four scenes available for comparison. The MADs of these 10 value pairs were calculated and are listed in

Table 3. Mean absolute difference (MAD) of the four terms of the radiation balance. The values in brackets indicate the percentage of the MAD on the mean of the in situ measured values.

	MAD ‘Best Guess’	MAD ‘Best Fit’
Albedo [%]	3.5 (14.8 %)	2.3 (9.7 %)
Irradiation [W·m−2]	43.0 (7.4 %)	10.1 (1.7 %)
Long wave emission [W·m−2]	8.4 (2.0 %)	Na
Incoming long wave radiation [W·m−2]	20.4 (6.5 %)	Na
Net radiation [W·m−2]	37.6 (11.6 %)	22.3 (6.9 %)

. The critical term is the albedo, which has a MAD of 2.3% in the ‘best fit’ option. All differences of the albedo were of such magnitude, independent on the station. The high MAD of the ‘best guess’ irradiation of 43.0 W·m⁻² could be improved significantly by using the ‘best fit’ option, reducing the MAD to only 10.1 W·m⁻². The two long wave terms both showed good agreement in the ‘best guess’ case, therefore no ‘best fit’ option was introduced. Finally, the net radiation could be determined with 11.6% accuracy in the ‘best guess’ option, and with 6.9% in the ‘best fit’ option. As the ‘best fit’ option is fitted to the measurement values, this comparison is of course not independent. Anyhow, the ‘best guess’ version can be interpreted as an error measure for other pixels not included in this comparison.

The in situ radiation values were measured using CNR1 from Kipp & Zonen. The specification sheet lists the expected accuracy for the daily totals to be ±10%. A calibration of the instruments at the end of the campaign improved the accuracy to about 5–10% for single measurements. Having this in mind, the achieved 11.6% accuracy for the net radiation using the ‘best guess’ option is good.

A main constraint in the modeling of the irradiation was the limited accuracy of the used DEM. The DEM had a spatial resolution of 3 arcsecond (≈90 m), but could not resolve exactly the geomorphologic features occurring in the desert, such as wadi systems. Further, the modeling of the irradiance reflected from opposed slopes is simply parameterized using the neighboring pixel’s reflectance and therefore might be underestimated. Hence, areas of massive over- and underestimation of the incoming spectral irradiance were present in some areas of the desert, finally resulting in wrong albedo values. Also, radar data exhibit increased scattering over rough surfaces. Therefore, the SRTM data over urban areas showed some irregularities. To account for this, the slope was set to zero over urban areas. A further constraint is given by the fact that solar irradiation was modeled assuming the urban surface to be flat; for example, no enhanced reflections from sun-facing walls and sloped roofs or diminishing effects of shadows were considered. In urban areas, this assumption can lead to considerable errors, as was shown in [34]. For the ASTER scenes used, a maximum error of 2% is estimated for this geometry effect.

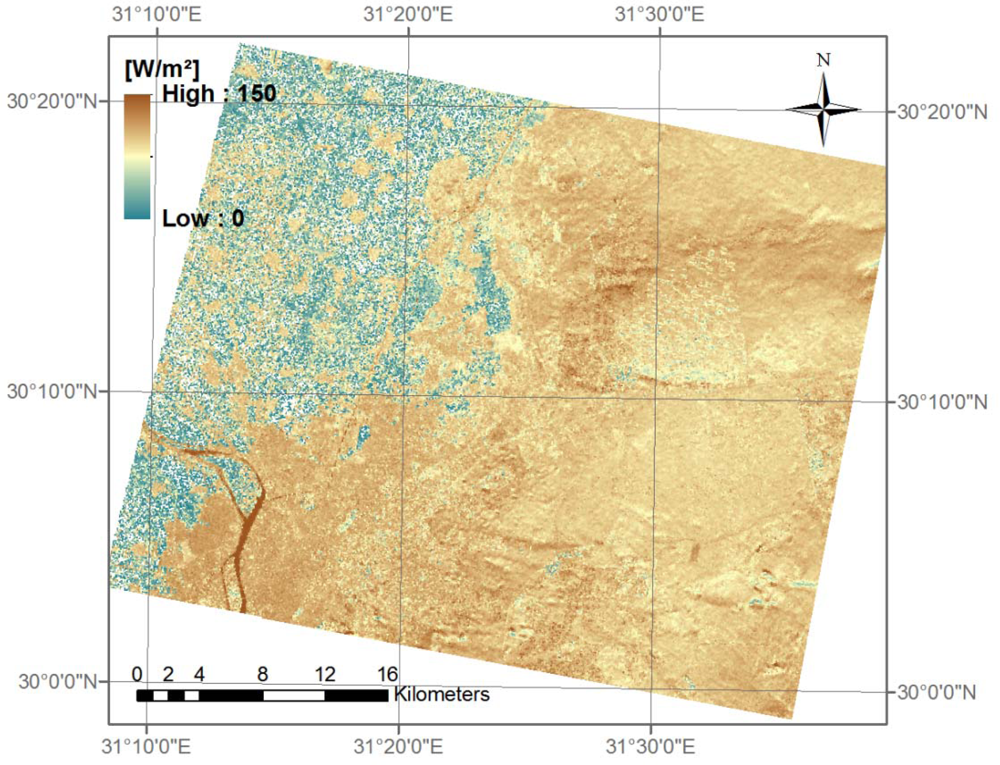
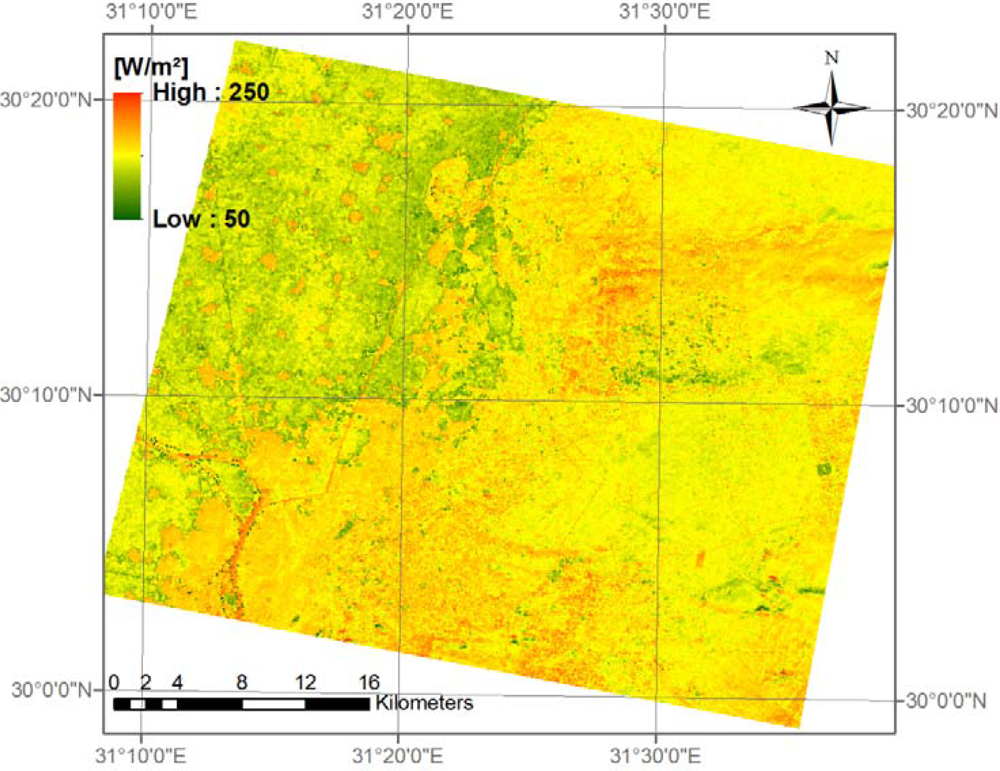
Figure 3 shows the ‘best fit’ net radiation from scene (b) of 24 December 2007 for a part of Greater Cairo. The three main landscape features can be easily recognized: the desert areas in the right part of the image with low net radiation values, the agricultural fields in the upper left part with high net radiation values and the urban parts with medium net radiation values. The River Nile is also clearly visible with very high values.

A similar distribution is found in all scenes; however, in some scenes, the net radiation of the urban areas almost equaled the net radiation of the agricultural areas. The main reason for this difference is the albedo. For example, the difference between the mean urban and mean agricultural albedo of the scene (b) from 01 December 2007 is only 0.7%, while in the scene (b) from 24 December 2007, which covers a very similar sector, it is 4.1%. Even though the difference between the mean values seems to be small, there is a resultant effect on the spatial pattern. The urban net radiation of the scene (b) from 01 December 2007 is only 9.1 W·m⁻² lower than the agricultural net radiation. In the case of the scene (b) from 24 December 2007, it is 30.3 W·m⁻² lower.

6.2. Ground Heat Flux

Q_s was derived using the ‘Parlow/urban’ and the new ‘Frey/NDVI’ approaches. It was compared to half hour averages of Q_s from the measurement campaign. The option ‘best guess’ and the option ‘best fit’ were used as input in the comparison through the net radiation. Generally, the option ‘best fit’ performed slightly better than the option ‘best guess’, although the MAD of ‘best fit’ was only few percent higher than ‘best guess’. The best agreement showed the ‘Parlow/urban’ approach. There the MAD for the option ‘best fit’ was 18.9 % of mean Q_s. The new approach performed similarly well.

Table 4. MAD of the ground heat flux, option ‘best fit’. The values in the third row indicate the percentage of the MAD on the mean of the in situ measured values.

	MAD [W·m−2]	MAD [%]	MAD [W·m−2] Single Stations
			Urban	Agriculture	Desert
‘Parlow/urban’	15.47	18.90	27.42	8.44	10.02
‘Frey/NDVI’	17.53	21.42	24.07	13.69	14.54

shows the MADs of Q_s.

Spatial analysis showed that both approaches were in agreement with the general assumed spatial pattern with agricultural pixels having the lowest Q_s and urban pixels featuring the highest values. The desert pixels ranged somewhere in between. However, the ‘Parlow/urban’ approach showed another pattern in 3 scenes: here the means of the urban and the means of the desert pixels were almost similar. Figures 4 and 5 show a sample from the scene (b) on 24 December 2007. The values of the River Nile are probably not realistic, as no special algorithm for water was used.

6.3. LUMPS

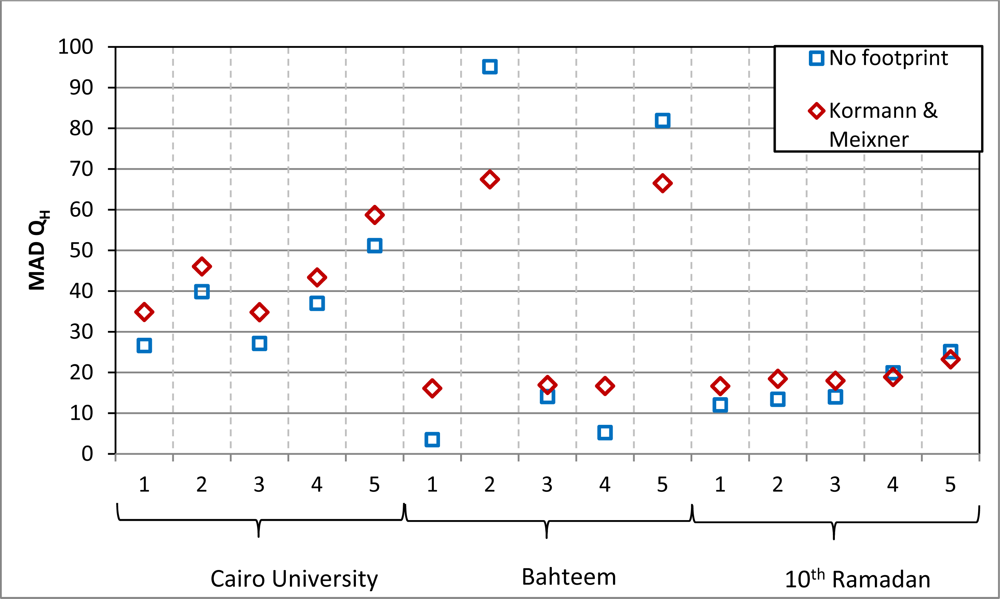
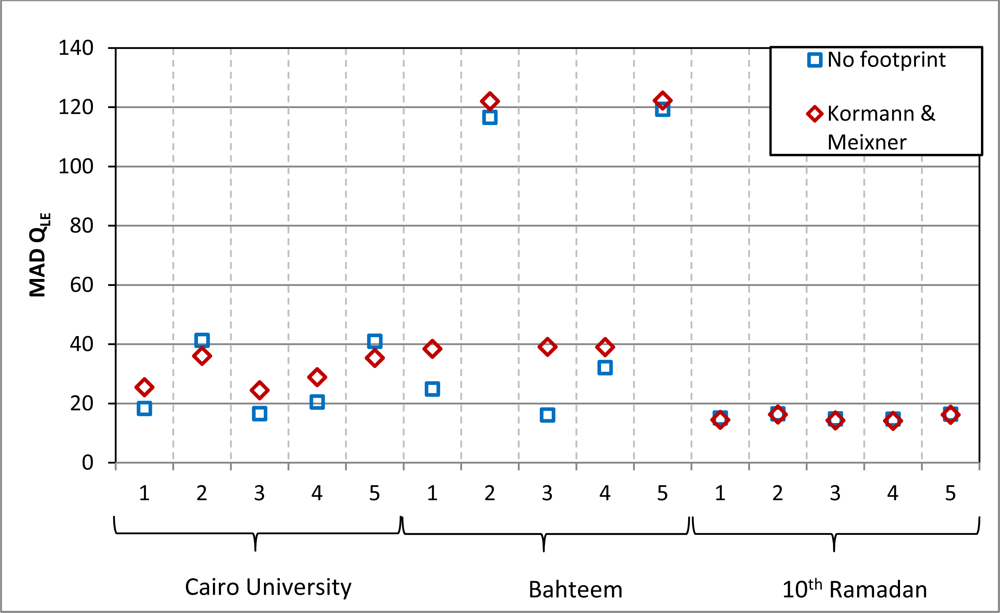
Q_H and Q_LE estimated with the LUMPS scheme were calculated using both the ‘Parlow/urban’ and the ‘Frey/NDVI’ approaches for Q_s. At the urban station, three value pairs (a pair consists of one in situ and one remote sensing value) of each turbulent heat flux were available for comparison; the agricultural station had only one pair, and the desert station also had three pairs. For simplicity, the agricultural pair is also addressed as MAD in the further analysis. The comparison was firstly conducted simply matching the value of the pixel of the mast’s location to the corresponding in situ value. In a second step, the footprint model was used for the retrieval of the remote sensing values.

The parameters from [19] produced fairly good Q_H and Q_LE at the desert station. Taking the ‘Parlow/urban’ method for Q_s and using the ‘best fit’ option for Q*, the MAD of Q_H and Q_LE was 13.4 W·m⁻², and 16.2 W·m⁻² respectively, in case no footprint model was used. The parameters retrieved from the campaign in Cairo produced similar good results for this station. This good fit is mainly due to the simple environment at the desert station, facilitating the model development. At the urban and the agricultural stations, higher MADs of 40.0 W·m⁻² and 95.2 W·m⁻² for Q_H and 41.3 W·m⁻² and 116.6 W·m⁻² for Q_LE were observed for the same setting taking the parameters from [19]. The deviation of the agricultural station is extreme, even though the best fitting value for α proposed by [19] (α =1.2) was taken.

Of course, the LUMPS parameters derived from the measurement data performed better for both the urban and the agricultural station. MAD of Q_H of the urban station was 26.6 W·m⁻², of the agricultural station 3.5 W·m⁻² and of the desert station 12.0 W·m⁻² in case no footprint model was used. The respective values of Q_LE are 18.3 W·m⁻², 24.9 W·m⁻², and 15.1 W·m⁻² (compare Figures 6 and 7).

The MAD mostly increased, not when using the ‘best fit’ option, but rather the ‘best guess’ option for the net radiation input in the calculations. The appropriate MADs for the urban, the agricultural and the desert station also using the ‘Parlow/urban’ Q_s were then 37.0 W·m⁻², 5.2 W·m⁻² and 20.0 W·m⁻² for Q_H and 20.5 W·m⁻², 32.1 W·m⁻², and 14.8 W·m⁻² for Q_LE. The MAD also increased in almost all cases, taking the parameters from [19] and using the ‘best guess’ option.

MADs for Q_H and Q_LE change only at the agricultural station, when using the ‘Frey/NDVI’ approach for Q_s. There, the MAD of Q_LE decreases to 16.2 W·m⁻², and MAD of Q_H increases to 14.1 W·m⁻², both for the ‘best fit’ option. At the two other stations, the MADs remained almost the same.

From the results of the LUMPS method, we can see that it is fairly reasonable to model turbulent heat fluxes in desert-like environments from values in the literature, but it is more critical to do so in urban or agricultural environments.

To evaluate the performance of the LUMPS approach further, the KM footprint model was applied to the results of the approach. Due to cloudiness, not all values could be used in the footprint analyses. There was a limitation in the calculation that at least 70% of the accumulated flux footprint must be cloud free, otherwise the result was invalid. Unfortunately, the pixel of the desert station of the first ASTER scene was set to invalid due to cloud cover. The use of the footprint model only partly improved the results. In most cases, the results were even worse. The Q_H MAD values only improved significantly at the agricultural station, and in some cases, the LUMPS parameters from literature were used. Q_LE sometimes improved, other times not. Overall, the effect of the footprint models was ambiguous. Figures 6 and 7 show the MAD of Q_H and Q_LE for all calculated combinations.

Spatial analysis of the LUMPS heat fluxes showed that the different approaches produced fairly different patterns. Following [13], it was assumed that the sensible heat flux should be highest in desert areas, closely followed by urban areas and lowest over agricultural fields. However, the latent heat flux should be highest over the agricultural fields, followed by the urban areas, and be lowest in the desert areas. This pattern was partly fulfilled by the LUMPS approaches. The latent heat flux was modeled fairly in accordance with this pattern in almost all cases. Only the approaches using the parameters of [19] rendered urban Q_LE which were lower than the desert Q_LE. 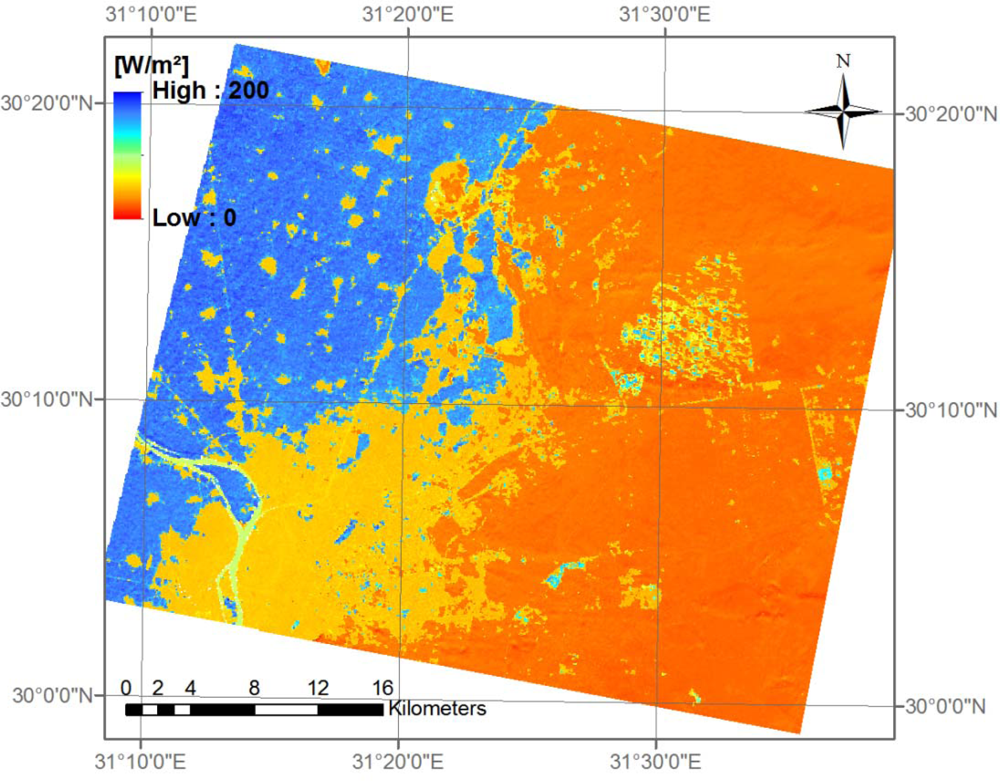Figure 9 shows Q_LE modeled using the ‘Parlow/urban’ Q_s and the newly-retrieved parameters for the LUMPS parameters.

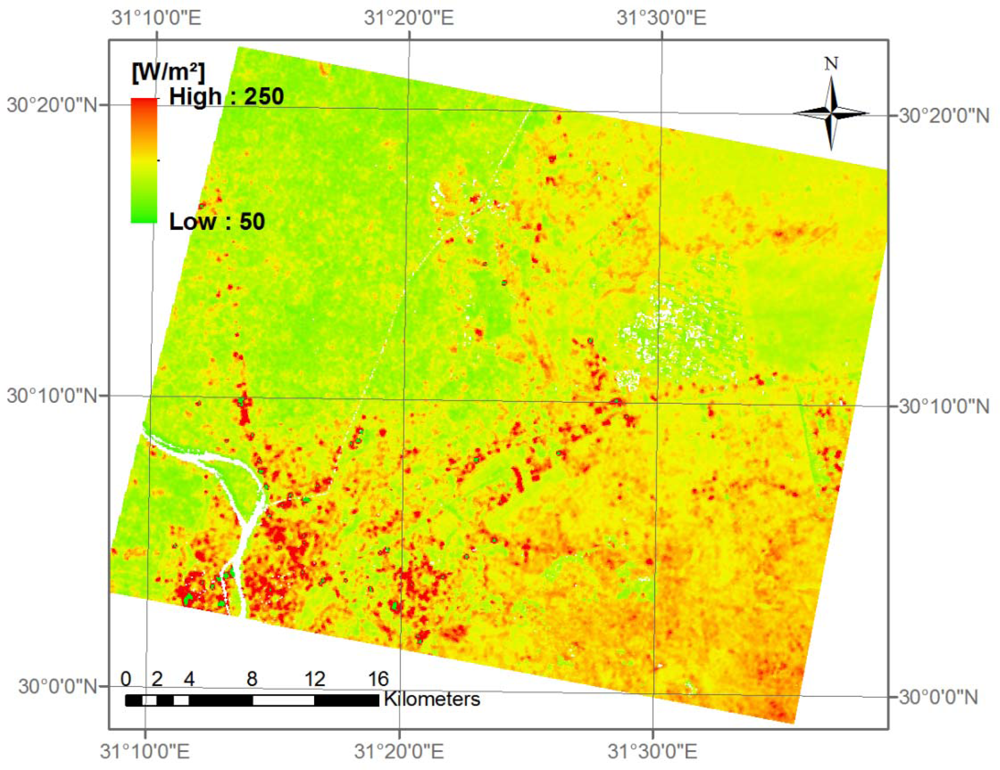
Q_H however, did not always follow this order. On one day for example, 22 November 2007, mean agricultural Q_H was higher than mean urban or mean desert Q_H. In Figure 8, the agricultural areas show clearly the lowest values, but the urban and the desert areas are almost similar. As mentioned before, Q_LE was modeled quite well. This is attributed to the fact that the LUMPS parameters α and β deducted from the in situ measured values were retrieved for Equation (4), which estimates Q_LE. Q_H in Equation (5) then uses the same parameters. Due to the structure of the formula, it is not possible to retrieve α and β for Equation (5).

Looking at the Bowen ratio β (=Q_H/Q_LE), the desert showed the highest β values, the urban areas slightly lower values and the agricultural areas the lowest β. The MAD of the desert β thereby was found to be 5 < β < 7, agricultural areas featured 0.5 < β < 3 and urban areas 1 < β < 3. However, using the parameters from the literature, they rendered extremely high urban β (10 < β < 28) and also very high agricultural values (β ≈ 3).

6.4. ARM

Q_LE estimated with the ARM method was calculated with the ‘Parlow/urban’ Q_s only, as no significant influence was found from taking either the ‘Parlow/urban’ or the ‘Frey/NDVI’ Q_S in the analysis of the LUMPS results. Generally, MAD of Q_H and Q_LE from the ARM method were higher than the MAD of the LUMPS approach. Especially at the desert station, the agreement worsened. Only the agricultural value matched better with the ARM method. MAD of Q_H for the urban, the agricultural and the desert station were 49.1 W·m⁻², 1.4 W·m⁻² and 25.0 W·m⁻² for the ‘best⁻fit’ option. The MAD of Q_LE for the same stations was 74.8 W·m⁻², 27.7 W·m⁻² and 25.4 W·m⁻². At the urban, station the ‘best guess’ option of Q_LE performed better than the ‘best fit’ option (65.3 W·m⁻²). However, at the agricultural and the desert station, the ‘best fit’ approach performed better.

Spatial analysis of the ARM heat fluxes followed the same rules as in the LUMPS analysis. Q_LE was modeled correctly, with the agricultural Q_LE the highest, the desert Q_LE the lowest and the urban Q_LE somewhere in between. Also, Q_H showed a reasonable distribution. Figures 10 and 11 show Q_H and Q_LE for the ‘best fit’ option and the ‘Parlow/urban’ Q_s.

The analysis of the Bowen ratios β also showed that most methods assigned the desert β highest values, the urban areas slightly lower β and the agricultural areas the lowest. However, in some cases the desert had a negative latent heat flux, resulting in negative β values.

7. Discussion

The findings of this study highlight the possibilities and difficulties of instantaneous flux determination from remote sensing images. ASTER images are well suited for this task concerning their spatial and spectral resolution. The temporal resolution, however, is insufficient for a regular flux determination from space.

This study showed that it is possible to determine turbulent heat fluxes from space within a good accuracy range. The differences found between remote sensing and in situ measured fluxes compare well to other values found in the literature, e.g., [48–50], or [12]. However, differences are higher than the ones found in [51], which compare remote sensing and in situ measured fluxes at relatively simple homogeneous sites on the Tibetan Plateau. Also [52] found a better agreement, yet they had only one scene to compare. Nevertheless, there is still room for improvement. Mainly, there are two concerns:

• There is the error propagation from input variables, which was mentioned by [49]. Inaccuracies from input variables can result from various sources like BRDF effects, thermal anisotropy or an imprecise atmospheric correction. For example, in a single case at the desert station, the solar irradiation was underestimated about 99.6 W·m⁻² (scene (a) of 22 November 2007, ‘best guess’) due to an inappropriate value of a MISR AOD product pixel. Q* then was underestimated 111.2 W·m⁻². In the LUMPS approach this produced a difference to the ‘best fit’ option in Q_H of 31.1 W·m⁻² taking the campaign retrieved parameters and the Q_s of ‘Parlow/urban’. The difference in Q_LE with the same input is only 4.7 W·m⁻². Using the ARM approach, the difference between this ‘best guess’ option and the ‘best fit’ option is 35.7 W·m⁻² for Q_LE. Dealing with such magnitudes, it is difficult to decide whether a spatial pattern is mainly governed by land use or due to incorrect atmospheric correction.
  The ground heat flux is an important input variable and also determines the accuracy of the subsequently calculated heat fluxes. Differences found between the remote sensing and the in situ ground heat flux are in the range of values found in [38]. It can be noted that differences are higher at the urban station compared to the agricultural and the desert station. This is probably due to the inability to measure directly the ground heat flux of an urban surface. So, the in situ data of the urban station are less accurate. The remote sensing ground heat flux was compared to 30-minute averages of in situ measurements. Direct comparison to one-minute averages would render extreme differences. This is because the storage heat flux as part of the ground heat flux showed extreme deviations due to short-time fluctuations of the surface temperature. Such high fluctuations can never be explained by instantaneous net radiation and vegetation indices only.
• The second concern in determining turbulent heat fluxes is the model uncertainty itself. Especially in heterogeneous environments, the development of a good model is important. For instance, the LUMPS method is using two empirical parameters which are dependent on the environment. It is a great challenge to find the right values for each pixel in such a fast changing landscape, especially as in situ measurements are scarce. This study has shown that adapting values from literature can lead to high mismatches.
  In the ARM method, both concerns can be found in the determination of the aerodynamic resistance for heat, which is dependent on surface roughness and on the conditions of convection and winds. An improper estimation of this variable will lead to a weak determination of heat fluxes. Additionally, the spatially distributed air temperature has to be estimated in the ARM method—A step which is crucial for flux determination accuracy.
  Bare soil and plant foliage temperatures contribute both to radiometric surface temperatures and contribute to the turbulent transport of sensible heat [6]. This problem, which applies only at the agricultural station, is not addressed by either the ARM or the LUMPS methods, and probably leads to higher differences at the agricultural station compared to the urban and the desert station.
  The discussion so far about flux determination accuracy neglects the problem of the imprecise determination of the turbulent fluxes by eddy covariance measurements. In inhomogeneous areas especially, the onsite flux determination is difficult, but also at our desert station, the measured energy balance had to be closed by force. Before closing, midday ensemble average of the residual term from the desert station was nearly 60 W·m⁻²; at the agricultural station, it almost reached 150 W·m⁻². Similar residuals were found by [51] or [29]. Having these magnitudes of closure gaps in mind, the results of the remote sensing fluxes do actually compare quite well.

7. Conclusions

The estimation of the radiation and energy balance from satellite images strongly depends on a successful atmospheric correction. Especially in areas where the aerosol content of the troposphere is not constant (for example due to air pollution as in our research area), the atmospheric correction is a crucial task. In this research, two versions of atmospheric correction were used: ‘best guess’ and ‘best fit’, with ‘best fit’ being the version that produced albedos that fit the ground measurements better than the ‘best guess’ version. The albedo is estimated with a 14.8% accuracy in the ‘best guess’ scenario. Short wave irradiation was estimated with 7.4%, long wave emission with 2.0%, incoming long wave radiation with 6.5%, and finally the net radiation with 11.6% accuracy. The ‘best fit’ case improved these values considerably, e.g., the net radiation was estimated in the ‘best fit’ case with 6.9% accuracy. Considering the accuracy of the in situ measurements to be 5–10%, achieved percentages are good.

The ground heat flux could be modeled satisfactorily using two different approaches when comparing the values to 30-minute averages of in situ measurements. Single differences were lower than 30 W·m⁻² in all cases. The MAD (mean absolute difference) is 15.5 W·m⁻² for the ‘Parlow/urban’ method and 17.5 W·m⁻² for the ‘Frey/NDVI’ method using the ‘best fit’ option. Looking at the spatial distribution, both approaches rendered proper values.

All in all, five possible methodological combinations were used to calculate Q_H and Q_LE with the LUMPS approach. Combinations included the ‘best guess’ and the ‘best fit’ option of Q*, different approaches for α and β, and two sources for the ground heat flux. Overall, MAD (including all combinations) of Q_H of the urban station was 36 W·m⁻², which is 19% of the mean in situ measured flux. At the agricultural station, the overall MAD was 40 W·m⁻² (34%), and at the desert station, it was 17 W·m⁻² (17%). The respective values for Q_LE were 28 W·m⁻² (57%), 62 W·m⁻² (34%) and 16 W·m⁻²⁻(61%). The best combination consisted of the 'best fit' case for the atmospheric correction, the ‘Parlow/urban’ approach for the ground heat flux and the newly-derived LUMPS parameters. In this case, the MADs for Q_H were 27 W·m⁻² (14%), 4 W·m⁻² (3%), and 12 W·m⁻² (8%) and the MADs for Q_LE were 18 W·m⁻² (38%), 25 W·m⁻² (14%), and 15 W·m⁻² (60%).

The desert station showed the best absolute results due to its simple and homogeneous environment and general very low latent heat fluxes. The agricultural station, on the contrary, showed the highest deviations, which probably resulted from the high fragmentation of the landscape. The urban station was somewhere in between. Considering the uncertainty of the in situ measurements, these results are good. Single combinations showed differing results, with generally the ‘best fit’ option improving the MAD and the empirical estimated α and β delivering better results than the values from literature. The choice of the ground heat flux did not influence the results significantly.

The analysis of the spatial distribution of the LUMPS fluxes revealed that Q_LE was modeled according to our expectations; however, Q_H showed some irregularities. Summarizing the LUMPS results, we conclude that the estimation of the turbulent heat fluxes with literature values is only applicable when the environment is fairly simple, like our desert example. As soon as the environment becomes more complex, the determination is more difficult.

The ARM approach was calculated with the two combinations for the atmospheric correction - ‘best guess’ and ‘best fit’ options of Q*. MAD of Q_H of the urban station was 49 W·m⁻², which is 26% of the mean in situ measured flux. At the agricultural station, the MAD was 1 W·m⁻² (1%) and at the desert station, it was 25 W·m⁻² (16%). The respective values for Q_LE were 70 W·m⁻² (145%), 37 W·m⁻² (20%) and 35 W·m⁻² (211%). Generally, similar results to the LUMPS analysis were found. ‘Best fit’ worked better than the ‘best guess’ option. The spatial analysis showed that the ARM approaches were able to reproduce meaningful spatially-distributed fluxes in contrary to the LUMPS approach.

The application of the footprint model increased the MAD in most cases for both the LUMPS and the ARM method. It is therefore not encouraged to use such models when working with high uncertainties.

This study showed that it is reasonable to calculate the energy balance using spaceborne data when sufficient in situ data for model adjustments are available. Without such ground truth data, results are most probably disputable. The remaining differences between in situ measured and the remote sensing energy balance in this study suggests further efforts in conducting research on this topic. Besides the definition of robust parameters for different land uses, the methods of comparison, e.g., using footprint models, should be evaluated more in detail.