Influence of Surface Topography on ICESat/GLAS Forest Height Estimation and Waveform Shape
Abstract
:1. Introduction
- How precise are ICESat/GLAS measurements of terrain elevation and tree height in mountainous terrain?
- How does surface topography affect the accuracy of the GLAS tree height estimates?
- How does surface topography influence GLAS waveform structure?
2. Study Area and Data
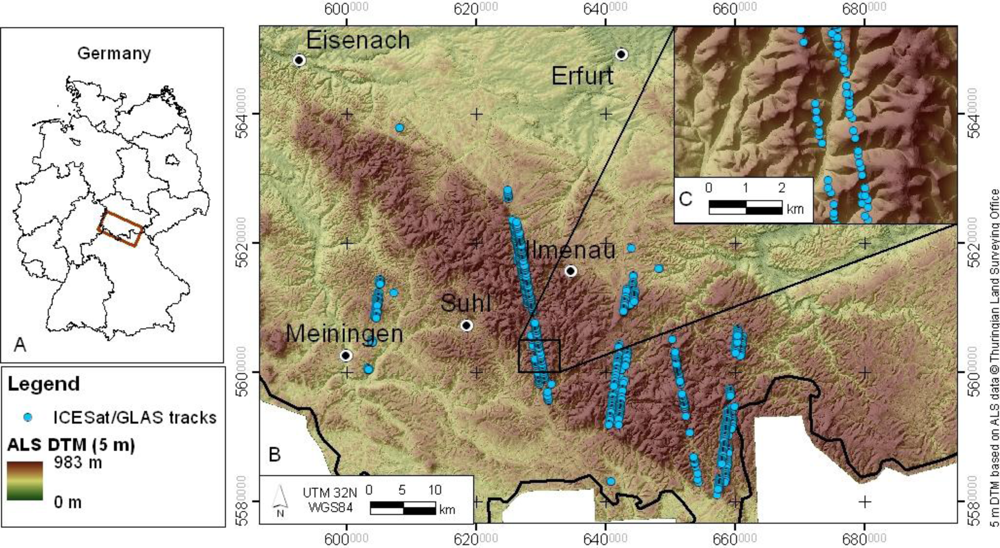
2.1. Thuringian Forest
2.2. ICESat/GLAS Data
2.3. Additional Data Sets
3. Methodology
3.1. ICESat/GLAS Pre-Processing
3.2. Calculation of Waveform Parameters
3.3. Definition of Waveform Types
3.4. Calculation of ALS DTM Measures
4. Results and Discussion
4.1. Comparison of ICESat/GLAS and ALS Terrain Elevation
4.2. Comparison of ICESat/GLAS and Reference Tree Heights
4.3. Influence of Terrain Characteristics on the GLAS Waveform Structure
5. Discussion
6. Conclusions
- - The approach based on the GLA01 data product performed better than the approach using the GLA14 Gaussian decomposition parameters regarding both, terrain elevation and tree height.
- - GLAS and reference terrain elevations exhibited a very good agreement with a mean elevation difference of −2.09 m (SD = 6.17 m) for GLA14 elevation and 0.29 m (SD = 5.01 m) for GLA01 elevation. The accuracy slightly decreases with increasing slope.
- - The mean tree height difference between field based inventory and GLAS tree height is 3.58 m (SD = 7.84 m) for GLA14 height and 1.13 m (SD = 6.39 m) for GLA01 height regarding all species and slope classes. The accuracy clearly decreases with increasing slope. GLAS waveforms are most useful to retrieve tree height for areas up to a 10° slope. Slopes between 10–15° are a critical limit and tree height retrieval is very challenging for steep areas above 15°.
- - Waveform shape and deduced metrics like leading and trailing edge are not only affected by surface topography, but rather by the complex interaction of the three-dimensional footprint structure. The probability of broadened and fuzzy waveforms with mixed ground and vegetation signals increases with steeper and rougher terrain. Further factors influencing waveform shape are tree height, canopy density or gappiness and forest types as they develop species-specific vertical canopy structure and crown shapes.
Acknowledgments
References and Notes
- Hese, S.; Lucht, W.; Schmullius, C.; Barnsley, M.; Dubayah, R.; Knorr, D.; Neumann, K.; Riedel, T.; Schröter, K. Global biomass mapping for an improved understanding of the CO2 balance—The Earth observation mission Carbon-3D. Remote Sens. Environ 2005, 94, 94–104. [Google Scholar]
- West, P.W. Tree and Forest Measurement; Springer: Berlin, Germany, 2004. [Google Scholar]
- Næsset, E.; Gobakken, T.; Holmgren, J.; Hyyppä, H.; Hyyppä, J.; Maltamo, M.; Nilsson, M.; Olsson, H.; Persson, A.; Soederman, U. Laser scanning of forest resources: The Nordic experience. Scand. J. For. Res 2004, 19, 482–499. [Google Scholar]
- van Leeuwen, M.; Nieuwenhuis, M. Retrieval of forest structural parameters using LiDAR remote sensing. Eur. J. For. Res 2010, 129, 749–770. [Google Scholar]
- Koch, B. Status and future of laser scanning, synthetic aperture radar and hyperspectral remote sensing data for forest biomass assessment. ISPRS J. Photogramm 2010, 65, 581–590. [Google Scholar]
- Breidenbach, J.; Næsset, E.; Lien, V.; Gobakken, T.; Solberg, S. Prediction of species specific forest inventory attributes using a nonparametric semi-individual tree crown approach based on fused airborne laser scanning and multispectral data. Remote Sens. Environ 2010, 114, 911–924. [Google Scholar]
- Hollaus, M.; Wagner, W.; Eberhöfer, C.; Karel, W. Accuracy of large-scale canopy heights derived from LiDAR data under operational constraints in a complex alpine environment. ISPRS J. Photogramm 2006, 60, 323–338. [Google Scholar]
- Zhao, K.; Popescu, S.; Nelson, R. Lidar remote sensing of forest biomass: A scale-invariant estimation approach using airborne lasers. Remote Sens. Environ 2009, 113, 182–196. [Google Scholar]
- Zwally, H.J.; Schutz, B.; Abdalati, W.; Abshire, J.; Bentley, C.; Brenner, A.; Bufton, J.; Dezio, J.; Hancock, D.; Harding, D.; et al. ICESat’s laser measurements of polar ice, atmosphere, ocean, and land. J. Geodyn 2002, 34, 405–445. [Google Scholar]
- Schutz, B.E.; Zwally, H.J.; Shuman, C.A.; Hancock, D.; DiMarzio, J.P. Overview of the ICESat mission. Geophys. Res. Lett 2005, 32, L21S01. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Harding, D.J.; Keller, M.; Cohen, W.B.; Carabajal, C.C.; Espirito-Santo, F.D.B.; Hunter, M.O.; de Oliveira, R. Estimates of forest canopy height and aboveground biomass using ICESat. Geophy. Res. Lett 2005, 32, L22S02. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Keller, M.; Pang, Y.; De Camargo, P.B.; Hunter, M.O. Revised method for forest canopy height estimation from Geoscience Laser Altimeter System waveforms. J. Appl. Remote Sens 2007, 1, 013537. [Google Scholar]
- Rosette, J.A.B.; North, P.R.J.; Suárez, J.C. Vegetation height estimates for a mixed temperate forest using satellite laser altimetry. Int. J. Remote Sens 2008, 29, 1475–1493. [Google Scholar]
- Sun, G.; Ranson, K.; Kimes, D.; Blair, J.; Kovacs, K. Forest vertical structure from GLAS: An evaluation using LVIS and SRTM data. Remote Sens. Environ 2008, 112, 107–117. [Google Scholar]
- Ballhorn, U.; Jubanski, J.; Siegert, F. ICESat/GLAS data as a measurement tool for peatland topography and peat swamp forest biomass in Kalimantan, Indonesia. Remote Sens 2011, 3, 1957–1982. [Google Scholar]
- Yang, W.; Ni-Meister, W.; Lee, S. Assessment of the impacts of surface topography, off-nadir pointing and vegetation structure on vegetation lidar waveforms using an extended geometric optical and radiative transfer model. Remote Sens. Environ 2011, 115, 2810–2822. [Google Scholar]
- Pang, Y.; Lefsky, M.; Sun, G.; Ranson, J. Impact of footprint diameter and off-nadir pointing on the precision of canopy height estimates from spaceborne lidar. Remote Sens. Environ 2011, 115, 2798–2809. [Google Scholar]
- Hancock, S. Understanding the Measurements of Forests with Waveform Lidar, Ph.D. Dissertation, University College London, London, UK. 2010.
- Chen, Q. Retrieving vegetation height of forests and woodlands over mountainous areas in the Pacific Coast region using satellite laser altimetry. Remote Sens. Environ 2010, 114, 1610–1627. [Google Scholar]
- Xing, Y.; de Gier, A.; Zhang, J.; Wang, L. An improved method for estimating forest canopy height using ICESat-GLAS full waveform data over sloping terrain: A case study in Changbai mountains, China. Int. J. Appl. Earth Obs 2010, 12, 385–392. [Google Scholar]
- Allouis, T.; Durrieu, S.; Couteron, P. A new method for incorporating hillslope effects to improve canopy-height estimates from large-footprint lidar waveforms. IEEE Geosci. Remote Sens. Lett 2012, 9, 730–734. [Google Scholar]
- Hiekel, W.; Fritzlar, F.; Nöllert, A.; Westhus, W. Die Naturräume Thüringens; Thüringer Landesanstalt für Umwelt und Geologie: Jena, Germany, 2004. [Google Scholar]
- Nieuwenhuis, M. Terminology of Forest Management: Terms and Definitions in English; IUFRO: Vienna, Austria, 2010; Volume 2. [Google Scholar]
- NSIDC. Attributes for ICESat Laser Operations Periods. Available online: http://nsidc.org/data/icesat/laser_op_periods.html (accessed on 28 November 2011).
- Brenner, A.C.; Zwally, J.; Bentley, C.R.; Csathó, B.M.; Harding, D.J.; Hofton, M.A.; Minster, J.-B.; Roberts, L.; Saba, J.L.; Thomas, R.H.; et al. Derivation of Range and Range Distributions From Laser Pulse Waveform Analysis for Surface Elevations, Roughness, Slope, and Vegetation Heights, Algorithm Theoretical Basis Document, Version 4.1; Goddard Space Flight Center: Greenbelt, MD, USA, 2003; p. 92. [Google Scholar]
- Harding, D.J. Personal Communication. 2011.
- Neuenschwander, A.L. Evaluation of waveform deconvolution and decomposition retrieval algorithms for ICESat/GLAS data. Can. J. Rem. Sens 2008, 34, S240–S246. [Google Scholar]
- Hoechstetter, S. Enhanced Methods for Analysing Landscape Structure—Landscape Metrics for Characterizing Three-Dimensional Patterns and Ecological Gradients; Rhombos: Berlin, Germany, 2009. [Google Scholar]
- Sappington, J.M.; Longshore, K.M.; Thompson, D.B. Quantifying Landscape Ruggedness for Animal Habitat Analysis: A Case Study Using Bighorn Sheep in the Mojave Desert. J. Wildlife Manage 2007, 71, 1419–1426. [Google Scholar]
- Weiss, A. Topographic Position and Landforms Analysis. Proceedings of ESRI User Conference, San Diego, CA, USA, 9–13 July 2001.
- Jenness, J. Topographic Position Index (tpi_jen.avx) Extension for ArcView 3.x; v. 1.3a;. Jenness Enterprises: Flagstaff, AZ, USA, 2006. Available online: http://www.jennessent.com/arcview/tpi.htm (accessed on 25 July 2011).
- Chen, Q. Assessment of terrain elevation derived from satellite laser altimetry over mountainous forest areas using airborne lidar data. ISPRS J. Photogramm 2010, 65, 111–122. [Google Scholar]
- Heurich, M.; Thoma, F. Estimation of forestry stand parameters using laser scanning data in temperate, structurally rich natural European beech (Fagus sylvatica) and Norway spruce (Picea abies) forests. Forestry 2008, 81, 645–661. [Google Scholar]
- Næsset, E. Determination of mean tree height of forest stands using airborne laser scanner data. ISPRS J. Photogramm 1997, 52, 49–56. [Google Scholar]
- Zimble, D.A.; Evans, D.L.; Carlson, G.C.; Parker, R.C.; Grado, S.C.; Gerard, P.D. Characterizing vertical forest structure using small-footprint airborne LiDAR. Remote Sens. Environ 2003, 87, 171–182. [Google Scholar]
- Pflugmacher, D.; Cohen, W.B.; Kennedy, R.; Levsky, M. Regional Applicability of forest height and aboveground biomass models for the geoscience laser altimeter system. For. Sci. 2008, 54, 647–657. [Google Scholar]
- Harding, D.J. ICESat waveform measurements of within-footprint topographic relief and vegetation vertical structure. Geophys. Res. Lett 2005, 32, L21S10. [Google Scholar] [CrossRef]
- Rosette, J.A.B.; North, P.R.J.; Suárez, J.C.; Los, S.O. Uncertainty within satellite LiDAR estimations of vegetation and topography. Int. J. Remote Sens 2010, 31, 1325–1342. [Google Scholar]
- Nicke, A. Wachstum und Ertrag von Waldbeständen; Lecture Report; University of Applied Sciences Erfurt: Erfurt, Germany, 2009. [Google Scholar]
- Miller, M.E.; Lefsky, M.; Pang, Y. Optimization of Geoscience Laser Altimeter System waveform metrics to support vegetation measurements. Remote Sens. Environ 2011, 115, 298–305. [Google Scholar]
- Hancock, S.; Disney, M.; Muller, J.-P.; Lewis, P.; Foster, M. A threshold insensitive method for locating the forest canopy top with waveform lidar. Remote Sens. Environ 2011, 115, 3286–3297. [Google Scholar]
- Duncanson, L.I.; Niemann, K.O.; Wulder, M.A. Estimating forest canopy height and terrain relief from GLAS waveform metrics. Remote Sens. Environ 2010, 114, 138–154. [Google Scholar]
- Hilbert, C.; Knuth, R.; Schmullius, C. Ableitung von Waldstrukturparametern mittels TerraSAR-X und ICESat/GLAS-Daten im Thüringer Wald. Proceedings of Jahrestagung der Deutschen Gesellschaft für Photogrammetrie, Fernerkundung und Geoinformation (DGPF) 2012, Potsdam, Germany, 14–17 March 2012; 21, pp. 391–399.









| Slope (deg) | Height (m) | Age (years) | Stocking Volume (m3/ha) | ||
|---|---|---|---|---|---|
| Spruce | mean | 12.14 | 27.13 | 77.78 | 365.08 |
| No. of shots 345 | SD | 7.26 | 5.16 | 31.55 | 120.58 |
| Beech | mean | 21.01 | 29.47 | 109.42 | 340.4 |
| No. of shots 65 | SD | 6.38 | 4.59 | 35.97 | 95.87 |
| Pine | mean | 8.63 | 23.43 | 88.03 | 252.53 |
| No. of shots 32 | SD | 5.52 | 5.12 | 36.96 | 87.96 |
| Laser Period | Season | Original (*) | After Processing and Filtering | Percent of Remaining Shots |
|---|---|---|---|---|
| L1 | Spring 2003 | 525 | 91 | 17 |
| L2A | Autumn 2003 | 148 | 68 | 46 |
| L2C | Summer 2004 | 154 | 18 | 12 |
| L3A | Autumn 2004 | 193 | 91 | 47 |
| L3B | Spring 2005 | 65 | 15 | 23 |
| L3C | Summer 2005 | 2 | 1 | 50 |
| L3D | Autumn 2005 | 102 | 21 | 21 |
| L3E | Spring 2006 | 2 | 0 | 0 |
| L3F | Summer 2006 | 146 | 58 | 40 |
| L3G | Autumn 2006 | 14 | 0 | 0 |
| L3H | Spring 2007 | 138 | 71 | 51 |
| L3I | Autumn 2007 | 27 | 10 | 37 |
| L3J | Spring 2008 | 22 | 1 | 5 |
| L3K | October 2008 | 14 | 8 | 57 |
| L2D | Nov/Dec 2008 | 4 | 0 | 0 |
| All | 1577 | 453 | 29 |
| Landscape Structure Category | |||||||
| OSF | OSS | ORF | ORS | CRF | CRS | All | |
| Landform | Open Slope | Open Slope | Open Slope | Open Slope | Complex | Complex | All |
| Roughness | Smooth | Smooth | Rough | Rough | Rough | Rough | All |
| Slope | Flat | Steep | Flat | Steep | Flat | Steep | All |
| Number of Available Shots | |||||||
| Spruce | 59 | 73 | 1 | 10 | 0 | 13 | 156 |
| Beech | 6 | 24 | 1 | 4 | 3 | 19 | 47 |
| GLA14 | GLA01 | |||||||
|---|---|---|---|---|---|---|---|---|
| Spruce | Beech | Pine | All | Spruce | Beech | Pine | All | |
| Mean difference | −2.11 | −1.99 | −1.98 | −2.09 | 0.31 | −0.26 | −0.1 | 0.19 |
| SD | 6.08 | 7.69 | 3.10 | 6.17 | 5.09 | 5.49 | 2.52 | 5.01 |
| RMSE | 6.43 | 7.89 | 3.64 | 6.51 | 5.10 | 5.46 | 2.48 | 5.01 |
| Correlation coefficient | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 |
| GLA14 | GLA01 | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Spruce | Beech | Pine | All | Spruce | Beech | Pine | All | ||
| ALS CHM | Mean difference | 9.93 | 12.70 | 7.18 | 10.14 | 7.22 | 11.51 | 4.97 | 7.69 |
| SD | 7.16 | 8.83 | 5.36 | 7.41 | 5.66 | 8.01 | 4.11 | 6.19 | |
| RMSE | 12.24 | 15.43 | 8.91 | 12.56 | 9.17 | 13.99 | 6.41 | 9.87 | |
| Correlation coefficient | 0.58 | 0.41 | 0.52 | 0.56 | 0.67 | 0.39 | 0.62 | 0.63 | |
| Inventory | Mean difference | 3.27 | 5.59 | 2.82 | 3.58 | 0.56 | 4.39 | 0.62 | 1.13 |
| SD | 7.56 | 9.34 | 7.00 | 7.84 | 5.96 | 7.78 | 5.97 | 6.39 | |
| RMSE | 8.23 | 10.82 | 7.44 | 8.61 | 5.98 | 8.88 | 5.91 | 6.48 | |
| Correlation coefficient | 0.51 | 0.24 | 0.24 | 0.49 | 0.63 | 0.32 | 0.31 | 0.59 | |
| Slope Mean | TPI Mean | VRM Mean | ALS DTM Elevation Range | |||||
|---|---|---|---|---|---|---|---|---|
| Spruce | Beech | Spruce | Beech | Spruce | Beech | Spruce | Beech | |
| GLA14 – ALS CHM | 0.36 | 0.21 | −0.23 | −0.29 | 0.17 | 0.34 | 0.49 | 0.17 |
| GLA14 – inventory | 0.37 | 0.39 | −0.18 | −0.27 | 0.16 | 0.14 | 0.49 | 0.35 |
| GLA01 – ALS CHM | 0.37 | 0.07 | −0.34 | −0.37 | 0.27 | 0.36 | 0.32 | 0.01 |
| GLA01 – inventory | 0.38 | 0.31 | −0.29 | −0.39 | 0.26 | 0.15 | 0.35 | 0.24 |
Share and Cite
Hilbert, C.; Schmullius, C. Influence of Surface Topography on ICESat/GLAS Forest Height Estimation and Waveform Shape. Remote Sens. 2012, 4, 2210-2235. https://doi.org/10.3390/rs4082210
Hilbert C, Schmullius C. Influence of Surface Topography on ICESat/GLAS Forest Height Estimation and Waveform Shape. Remote Sensing. 2012; 4(8):2210-2235. https://doi.org/10.3390/rs4082210
Chicago/Turabian StyleHilbert, Claudia, and Christiane Schmullius. 2012. "Influence of Surface Topography on ICESat/GLAS Forest Height Estimation and Waveform Shape" Remote Sensing 4, no. 8: 2210-2235. https://doi.org/10.3390/rs4082210
APA StyleHilbert, C., & Schmullius, C. (2012). Influence of Surface Topography on ICESat/GLAS Forest Height Estimation and Waveform Shape. Remote Sensing, 4(8), 2210-2235. https://doi.org/10.3390/rs4082210




