Combined Use of Airborne Lidar and DBInSAR Data to Estimate LAI in Temperate Mixed Forests
Abstract
:1. Introduction
2. Methods
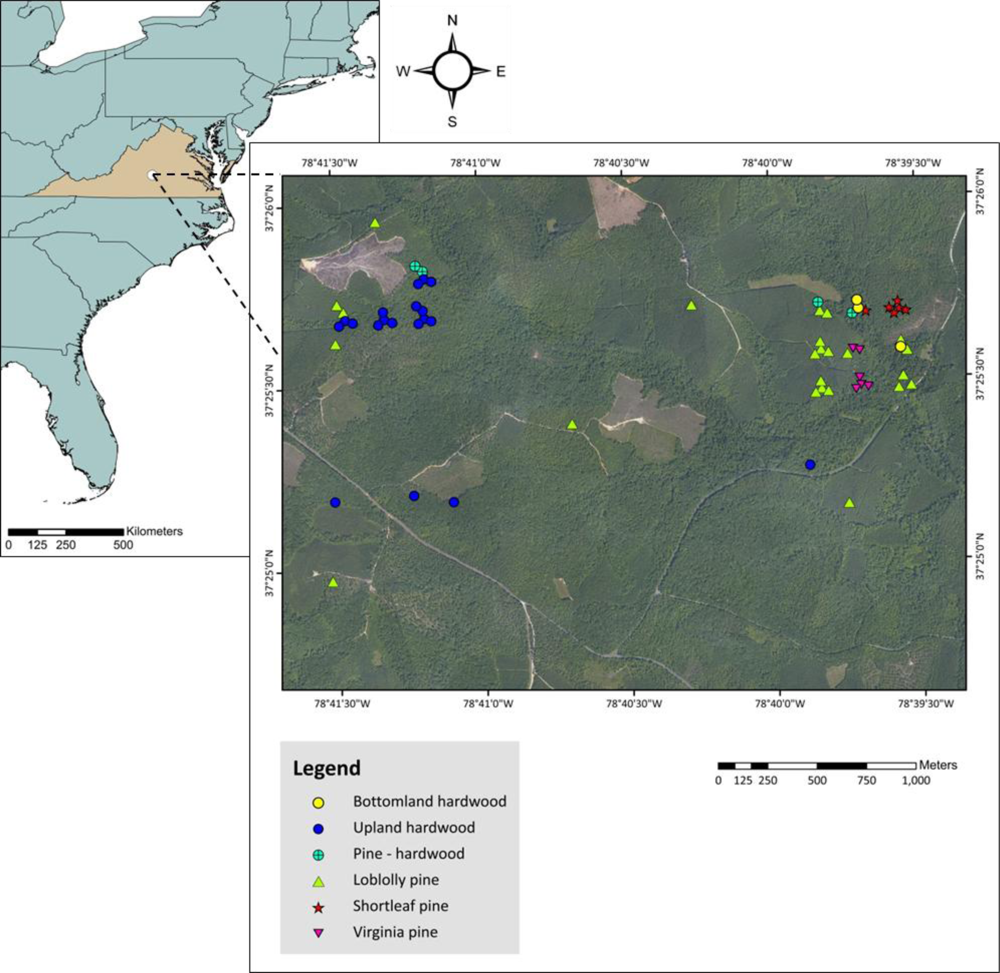
2.1. Study Site
2.2. Field Data Collection and Analysis
2.2.1. Leaf Area Measured with an Optical Sensor
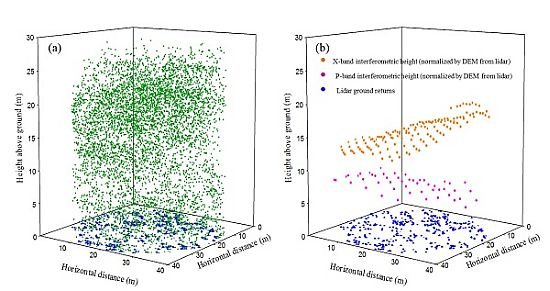
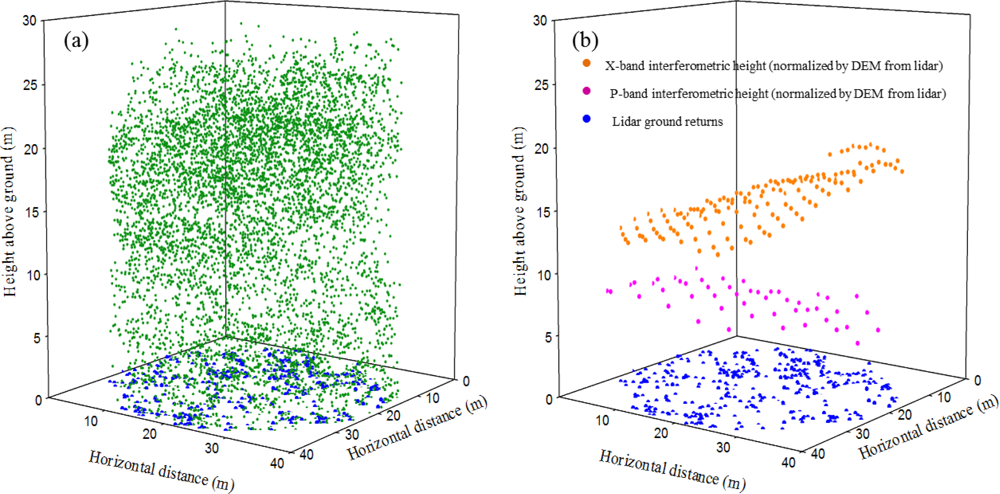
2.2.2. Lidar Data
2.2.3. GeoSAR Data
- In order to evaluate the vegetation height, the difference between X-band (mostly backscattered from the vegetation/canopy surface) and P-band (mostly from the ground and lower tree branches) interferometric heights was calculated. In addition, the X-band was divided by the P-band with the purpose of evaluating any other relationship between the two bands.
- The high resolution DEM created from the lidar data was used to generate the heights above ground for the X and P bands.
- No changes were made to the magnitude or the σ0 bands.
- The cell values from all the rasters created (10 in total) were extracted and the frequency, mean, standard deviation, coefficient of variation, minimum, maximum, and percentiles (10th to 90th) were calculated for all plots.
2.2.4. Statistical Analysis
- High coefficient of determination (R2) value.
- Low residual mean square (RMSE).
- Similarity between the adjusted coefficients of determination R2adj’ and R2 values. The R2adj’ is a rescaling of R2 by degrees of freedom, hence involves the ratio of mean squares instead of sum of squares.
- Mallows’ Cp statistic values [41]. When the model is correct, the Cp is close to the number of variables in the model.
- Low values from two information criteria, the [42] Information Criterion (AIC) and [43] Bayesian Criterion (SBC). The AIC is known for its tendency to select larger subset sizes than the true model; hence the SBC was used for comparison, since it penalizes models with larger number of explanatory variables more heavily than AIC.
3. Results
3.1. Summary Statistics from Ground Measurements and Lidar Metrics
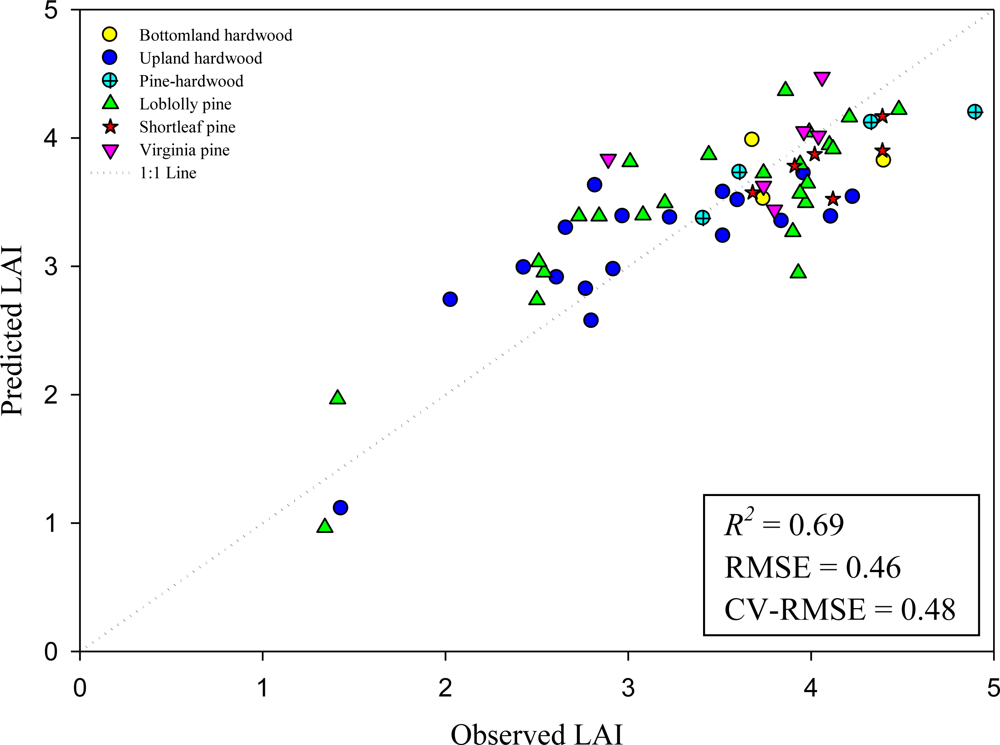
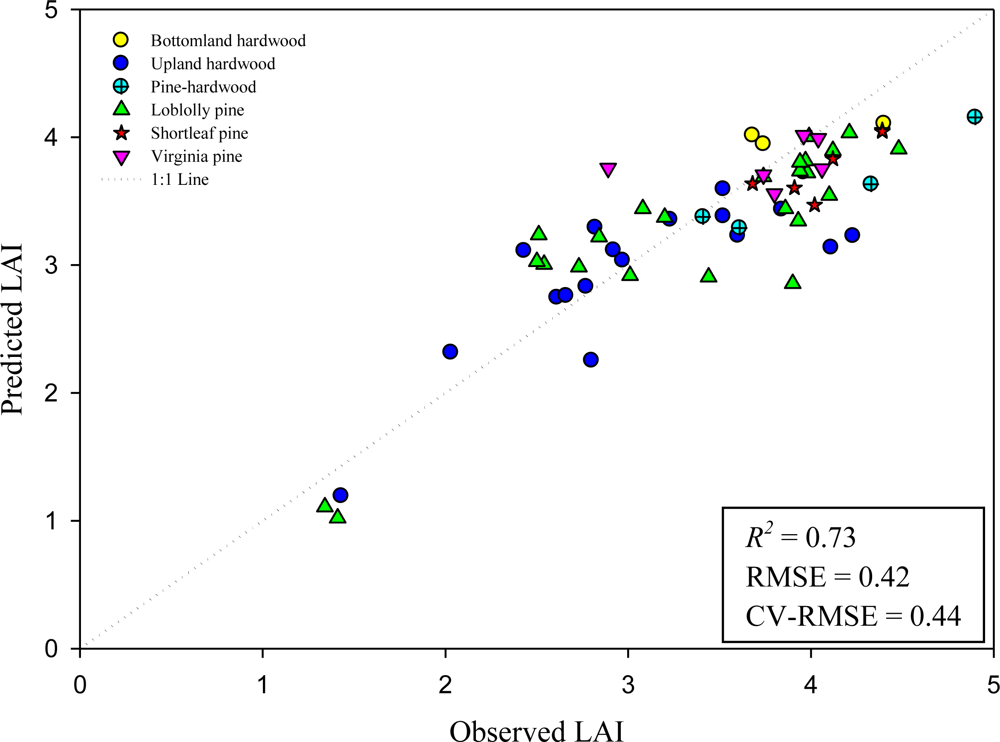
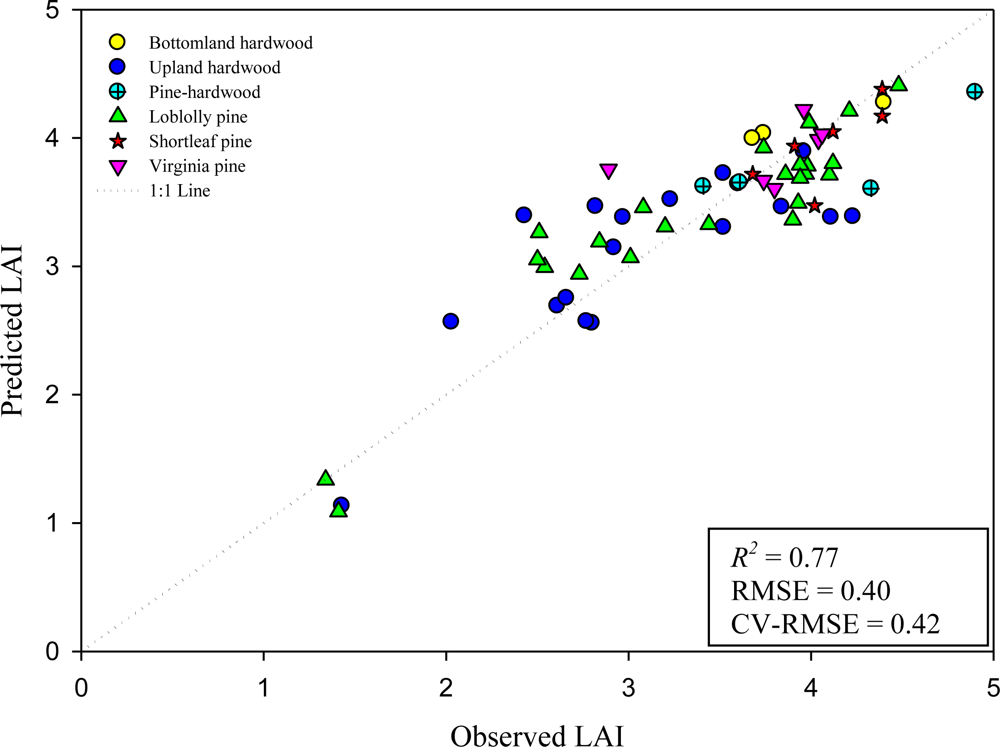
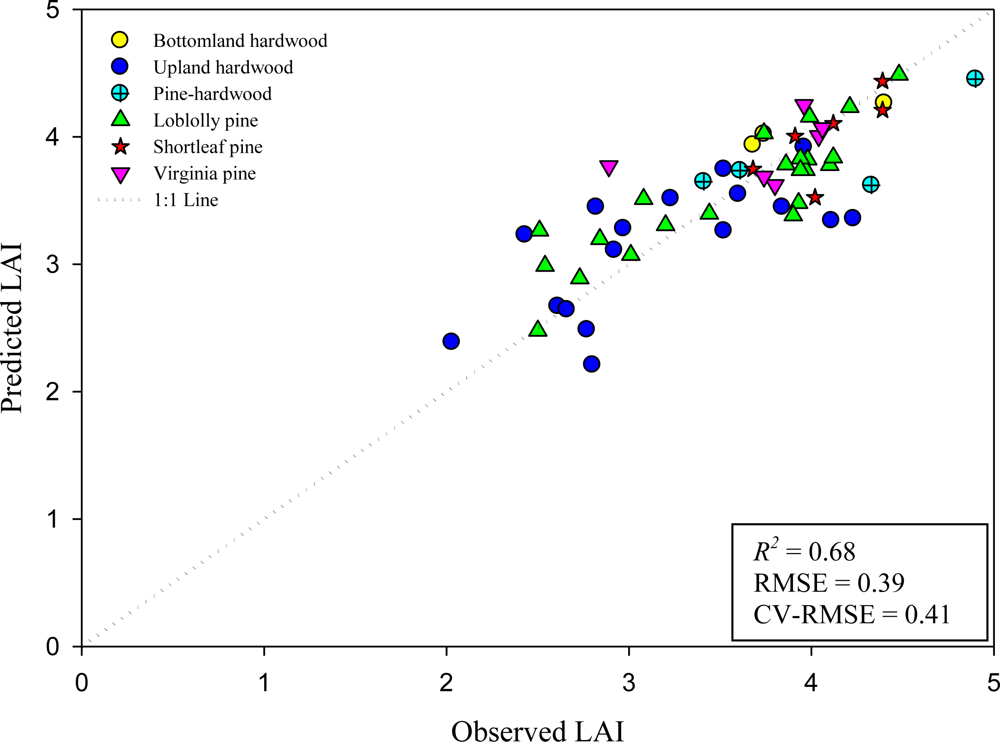
3.2. Variable Selection and Modeling
4. Discussion
5. Conclusions
Acknowledgments
References
- Watson, D.J. Comparative physiological studies in the growth of field crops. I. Variation in net assimilation rate and leaf area between species and varieties, and within and between years. Ann. Bot 1947, 41–76. [Google Scholar]
- Spanner, M.A.; Pierce, L.L.; Running, S.W.; Peterson, D.L. The seasonality of AVHRR data of temperate coniferous forests: Relationship with leaf area index. Remote Sens. Environ 1990, 33, 97–112. [Google Scholar]
- Turner, D.P.; Cohen, W.B.; Kennedy, R.E.; Fassnacht, K.S.; Briggs, J.M. Relationships between leaf area index and Landsat TM spectral vegetation indices across three temperate zone sites. Remote Sens. Environ 1999, 70, 52–68. [Google Scholar]
- Anderson, M.C.; Neale, C.M.U.; Li, F.; Norman, J.M.; Kustas, W.P.; Jayanthi, H.; Chavez, J. Upscaling ground observations of vegetation water content, canopy height, and leaf area index during SMEX02 using aircraft and Landsat imagery. Remote Sens. Environ 2004, 92, 447–464. [Google Scholar]
- Vose, J.M.; Sullivan, N.H.; Clinton, B.D.; Bolstad, P.V. Vertical leaf area distribution, light transmittance, and application of the Beer-Lambert law in four mature hardwood stands in the southern Appalachians. Can. J. For. Res 1995, 25, 1036–1043. [Google Scholar]
- Sampson, D.A.; Vose, J.M.; Allen, H.L. A Conceptual Approach to Stand Management Using Leaf Area Index as the Integral of Site Structure, Physiological Function, and Resource Supply. Proceedings of Ninth Biennial Southern Silvicultural Research Conference, Clemson, SC, USA, 25–27 February 1997; pp. 447–451.
- Barilotti, A.; Turco, S.; Alberti, G. LAI Determination in Forestry Ecosystem by Lidar Data Analysis. Proceedings of International Workshop 3D Remote Sensing in Forestry, Vienna, Austria, 14–15 February 2006; pp. 248–252.
- Kwak, D.-A.; Lee, W.-K.; Cho, H.-K. Estimation of LAI Using Lidar Remote Sensing in Forest. Proceedings of ISPRS Workshop on Laser Scanning and SilviLaser, Espoo, Finland; 2007; pp. 248–252. [Google Scholar]
- Sasaki, T.; Imanishi, J.; Ioki, K.; Morimoto, Y.; Kitada, K. Estimation of leaf area index and canopy openness in broad leaved forest using an airborne laser scanner in comparison with high-resolution near-infrared digital photography. Landscape Ecol. Eng 2008, 4, 47–55. [Google Scholar]
- Solberg, S.; Brunner, A.; Hanssen, K.H.; Lange, H.; Næsset, E.; Rautiainen, M.; Stenberg, P. Mapping LAI in a Norway spruce forest using airborne laser scanning. Remote Sens. Environ 2009, 113, 2317–2327. [Google Scholar]
- Hopkinson, C.; Chasmer, L. Testing LiDAR models of fractional cover across multiple forest ecozones. Remote Sens. Environ 2009, 113, 275–288. [Google Scholar]
- Zhao, K.; Popescu, S. Lidar-based mapping of leaf area index and its use for validating GLOBCARBON satellite LAI product in a temperate forest of the southern USA. Remote Sens. Environ 2009, 113, 1628–1645. [Google Scholar]
- Richardson, J.J.; Moskal, L.M.; Kim, S.-H. Modeling approaches to estimate effective leaf area index from aerial discrete-return LIDAR. Agr. For. Meteorol 2009, 149, 1152–1160. [Google Scholar]
- Jensen, J.L.R.; Humes, K.S.; Vierling, L.A.; Hudak, A.T. Discrete return lidar-based prediction of leaf area index in two conifer forests. Remote Sens. Environ 2008, 112, 3947–3957. [Google Scholar]
- Solberg, S. Mapping gap fraction, LAI and defoliation using various ALS penetration variables. Int. J. Remote Sens 2010, 31, 1227–1244. [Google Scholar]
- Riaño, D.; Valladares, F.; Condes, S.; Chuvieco, E. Estimation of leaf area index and covered ground from airborne laser scanner (lidar) in two contrasting forests. Agr. For. Meteorol 2004, 124, 269–275. [Google Scholar]
- Korhonen, L.; Korpela, I.; Heiskanen, J.; Maltamo, M. Airborne discrete-return LIDAR data in the estimation of vertical canopy cover, angular canopy closure and leaf area index. Remote Sens. Environ 2011, 115, 1065–1080. [Google Scholar]
- Thomas, V.; Noland, T.; Treitz, P.; McCaughey, J.H. Leaf area and clumping indices for a boreal mixed-wood forest: lidar, hyperspectral, and Landsat models. Int. J. Remote Sens 2011, 32, 8271–8297. [Google Scholar]
- Cerrillo, R.M.N.; de la Orden, M.S.; Bonilla, J.G.; Garcia-Ferrer, A.; Clemente, R.H.; Lanjeri, S. LIDAR-based estimation of leaf area index on Holm oak Quercus ilex L. subsp ballota (Desf.) Samp. trees. For. Syst 2010, 19, 61–69. [Google Scholar]
- Williams, M.L.; Milne, T.; Tapley, I.; Reis, J.J.; Sanford, M.; Kofman, B.; Hensley, S. Tropical Forest Biomass Recovery Using GeoSAR Observations. Proceedings of 2009 IEEE International Geoscience and Remote Sensing Symposium, Capte Town, South Africa, 12–17 July 2009; pp. IV-173–IV-176.
- Sexton, J.O.; Bax, T.; Siqueira, P.; Swenson, J.J.; Hensley, S. A comparison of lidar, radar, and field measurements of canopy height in pine and hardwood forests of southeastern North America. For. Ecol. Manage 2009, 257, 1136–1147. [Google Scholar]
- Williams, M.L.; Silman, M.; Saatchi, S.; Hensley, S.; Sanford, M.; Yohannan, A.; Kofman, B.; Reis, J.; Kampes, B. Analysis of GeoSAR Dual-Band InSAR Data for Peruvian Forest. Proceedings of 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 1398–1401.
- Carson, T.M. Topographic mapping in the equatorial belt using dual-frequency airborne IFSAR (GeoSAR). Photogramm. Eng Reote Sensing 2008, 74, 939–944. [Google Scholar]
- Williams, M.L.; Jenkins, L.G. GeoSAR and DBInSAR: Combining “X” With “P” for Tropical Forest “C”. Photogramm. Eng. Reote Sensing 2009, 75, 738–743. [Google Scholar]
- Svoray, T.; Shoshany, M.; Curran, P.J.; Foody, G.M.; Perevolotsky, A. Relationship between green leaf biomass volumetric density and ERS-2 SAR backscatter of four vegetation formations in the semi-arid zone of Israel. Int. J. Remote Sens 2001, 22, 1601–1607. [Google Scholar]
- Sun, G.Q.; Ranson, K.J.; Guo, Z.; Zhang, Z.; Montesano, P.; Kimes, D. Forest biomass mapping from lidar and radar synergies. Remote Sens. Environ 2011, 115, 2906–2916. [Google Scholar]
- Solberg, S.; Weydahl, D.J.; Naesset, E. Simulating X-Band Interferometric Height in a Spruce Forest From Airborne Laser Scanning. IEEE Trans. Geosci. Remote Sens 2010, 48, 3369–3378. [Google Scholar]
- Durden, S.L.; Morrissey, L.A.; Livingston, G.P. Microwave backscatter and attenuation dependence on leaf area index for flooded rice fields. IEEE Trans. Geosci. Remote Sens 1995, 33, 807–810. [Google Scholar]
- Paloscia, S. An empirical approach to estimating leaf area index from multifrequency SAR data. Int. J. Remote Sens 1998, 19, 361–366. [Google Scholar]
- Manninen, T.; Stenberg, P.; Rautiainen, M.; Voipio, P.; Smolander, H. Leaf area index estimation of boreal forest using ENVISAT ASAR. IEEE Trans. Geosci. Remote Sens 2005, 43, 2627–2635. [Google Scholar]
- Jenkins, J.C.; Chojnacky, D.C.; Heath, L.S.; Birdsey, R.A. National-scale biomass estimators for United States tree species. For. Sci 2003, 49, 12–35. [Google Scholar]
- Means, J.E.; Acker, S.A.; Harding, D.J.; Blair, J.B.; Lefsky, M.A.; Cohen, W.B.; Harmon, M.E.; McKee, W.A. Use of large-footprint scanning airborne lidar to estimate forest stand characteristics in the Western Cascades of Oregon. Remote Sens. Environ 1999, 67, 298–308. [Google Scholar]
- van Aardt, J.; Wynne, R.H.; Oderwald, R.G. Forest volume and biomass estimation using small-footprint lidar-distributional parameters on a per-segment basis. For. Sci 2006, 52, 636–649. [Google Scholar]
- Popescu, S.C.; Wynne, R.H.; Nelson, R. Estimating plot-level tree heights with lidar: Local filtering with a canopy-height based variable window size. Comput. Electron. Agr 2002, 37, 71–95. [Google Scholar]
- LI-COR, FV2000 the LAI-2000 Data File Viewer; LI-COR Biosciences: Lincoln, NE USA, 2010; p. 73.
- Welles, J.M.; Norman, J.M. Instrument for indirect measurement of canopy architecture. Agron. J 1991, 83, 818–825. [Google Scholar]
- Holmgren, J. Prediction of tree height, basal area and stem volume in forest stands using airborne laser scanning. Scand. J. Forest Res 2004, 19, 543–553. [Google Scholar]
- Barilotti, A.; Turco, S.; Napolitano, R.; Bressan, E. La Tecnologia LiDAR per lo Studio Della Biomassa Negli Ecosistemi Forestali. Proceedings of 15th Meeting of the Italian Society of Ecology, Torino, Italy, 12–14 September 2005.
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ 2002, 80, 88–99. [Google Scholar]
- SAS, The SAS System for Windows Release 9.1.3; SAS Institute Inc: Cary, NC, USA, 2010.
- Hocking, R. The analysis and selection of variables in linear regression. Biometrics 1976, 32, 1–49. [Google Scholar]
- Akaike, H. Fitting autoregressive models for prediction. Ann. Inst. Stat. Math 1969, 21, 243–247. [Google Scholar]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat 1978, 6, 461–464. [Google Scholar]
- Belsley, D.A. Demeaning conditioning diagnostics through centering (with discussion). Amer. Statistician 1984, 38, 73–77. [Google Scholar]
- Marquart, D.W. Comment: you should standarize the predictor variables in your regression models. J. Amer. Stat. Assoc 1980, 75, 87–91. [Google Scholar]
- Rawlings, J.O.; Pantula, S.G.; Dickey, D.A. Applied Regression Analysis: A Research Tool, 2nd ed.; Springer: Ann Arbor, MI, USA, 2001; p. 657. [Google Scholar]
- Allen, D. The Prediction Sum of Squares as a Criterion for Selection of Predictor Variables; Tech. Report 23. Department of Statistics, University of Kentucky: Lexington, KY, USA, 1971.
- Solberg, S.; Næsset, E.; Hanssen, K.H.; Christiansen, E. Mapping defoliation during a severe insect attack on Scots pine using airborne laser scanning. Remote Sens. Environ 2006, 102, 364–376. [Google Scholar]
- Nasahara, K.N.; Muraoka, H.; Nagai, S.; Mikami, H. Vertical integration of leaf area index in a Japanese deciduous broad-leaved forest. Agr. Forest Meteorol 2008, 148, 1136–1146. [Google Scholar] [Green Version]
- Gower, S.T.; Norman, J.M. Rapid Estimation of Leaf Area Index in Conifer and Broad-Leaf Plantations. Ecology 1991, 72, 1896–1900. [Google Scholar]
- Sampson, D.A.; Allen, H.L. Direct and indirect estimates of leaf-area index (LAI) for lodgepole and loblolly-pine stands. Trees-Struct. Funct 1995, 9, 119–122. [Google Scholar]


| Lidar Metrics | Symbol |
|---|---|
| Total number of ground returns | Grtotal |
| All returns (return hag > 0.2 m) | Alltotal, Allmean, Allstdv, Allcv, Allmin, Allmax, All10th,…, All90th |
| Units are meters for all metrics except for Alltotal and Allcv. | |
| Vegetation returns (return hag > 1 m) | Vegtotal, Vegmean, Vegmode, Vegstdv, Vegcv, Vegmin, Vegmax, Veg10th,...,Veg90th |
| Units are meters for all metrics except for Vegtotal and Vegcv. | |
| Pulses (number of lidar pulses per return class) | Grreturns, Allpulses |
| Laser penetration index (LPI) | LPI = Grreturns/(Grreturns + Allpulses) |
| Intensity values (returns hag > 1 m) | Imean, Imin, Imax, Istdv, Icv |
| Units are watts for all metrics except for Icv. | |
| Proportion of 1st, 2nd, 3rd and 4th returns | Ri = total number of i returns/ Vegtotal |
| Ri is a proportion of returns | i = 1st, 2nd, 3rd, and 4th |
| Density | di = [x + (Vegmax − Vegmin)/10]/Vegtotal |
| di is a proportion of returns | x = Vegmin,1,..,10 |
| i= 1, 2,…,10 | |
| Crown density slices around Vegmode | Cdi, Cdimean, Cdistdv, Cdicv |
| Refer to Figure 2 for a graphic explanation of the slices | Cdi = [number of returns in i / (Alltotal + Grtotal)] |
| Units are meters for Cdimean, Cdistdv, and Cdicv. | (i=+1,+ 2,+3,+4,+5, 0, −1, −2, −3, −4, and −5) |
| Cdi is a proportion of returns | i=+1,…,+ 5 at i meters above Vegmode |
| i = 0 at Vegmode | |
| i = −1,…, −5 at i meters below Vegmode | |
| GeoSAR Metrics | −Symbol |
| Values from all cells per plot | itotal, imean, istdv, icv, imin, imax, i10th, i20th, i25th, i40th, i50th, i60th, i75th, i80th, and i90th |
| Units are meters for all metrics (except for itotal and icv) obtained from the interferometric height bands. | i = P (P-band interferometric heights), X (X-band interferometric heights), X-P (X minus P), Pmag (P-band magnitude), Xmag (X-band magnitude), sn01xl (σ0 for flight line 1), sn02xl (σ0 for flight line 2), sn03xl (σ0 for flight line 3), sn04xl (σ0 for flight line 4) |
| Units from magnitude bands are | |
| Units for σ0 are dB/m2 (dB=decibels) |
| Forest Type | n | Stand Age | ht (m) | dbh (cm) | LAI | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Stdv | Range | Mean | Stdv | Range | Mean | Stdv | Range | ||||||
| Bottomland hardwood | 3 | 89 | 14.0 | 6.4 | 0.4 | 26.8 | 18.7 | 11.2 | 3.1 | 43.7 | 3.94 | 0.40 | 3.68 | 4.40 |
| Upland hardwood | 18 | 12–164 | 16.3 | 6.3 | 2.7 | 41.2 | 23.7 | 11.9 | 2.5 | 55.1 | 3.08 | 0.74 | 1.43 | 4.23 |
| Pine-hardwood | 4 | 45–118 | 14.9 | 5.9 | 2.4 | 35.4 | 17.0 | 9.0 | 2.5 | 50.0 | 4.06 | 0.68 | 3.41 | 4.90 |
| Loblolly pine | 24 | 10–63 | 13.3 | 3.8 | 0.9 | 33.8 | 16.3 | 6.9 | 2.5 | 86.1 | 3.37 | 0.86 | 1.34 | 4.48 |
| Shortleaf pine | 6 | 30–38 | 12.9 | 3.8 | 4.0 | 24.1 | 14.1 | 7.4 | 2.5 | 42.7 | 4.09 | 0.28 | 3.68 | 4.39 |
| Virginia pine | 6 | 60 | 14.1 | 3.6 | 4.3 | 33.5 | 12.4 | 8.0 | 2.8 | 73.7 | 3.75 | 0.44 | 2.89 | 4.06 |
| Total | 61 | 10–164 | 14.2 | 3.2 | 0.4 | 41.2 | 17.0 | 5.9 | 2.5 | 86.1 | 3.71 | 0.57 | 1.34 | 4.90 |
| Forest Type | n | Grtotal (Mean) | Alltotal (Mean) | Return Heights (m) | Intensity (W) | LPI | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Stdv | Max | Mean | Stdv | Max | |||||
| Bottomland hardwood | 3 | 222 | 4,343 | 12.7 | 6.8 | 36.6 | 51 | 29 | 136 | 0.019 |
| Upland hardwood | 18 | 537 | 5,278 | 13.2 | 6.8 | 31.0 | 44 | 28 | 150 | 0.039 |
| Pine-hardwood | 4 | 264 | 5,009 | 12.7 | 5.9 | 34.9 | 49 | 28 | 126 | 0.003 |
| Loblolly pine | 24 | 534 | 4,436 | 10.2 | 4.8 | 32.7 | 41 | 24 | 149 | 0.034 |
| Shortleaf pine | 6 | 353 | 5,165 | 9.9 | 4.5 | 25.3 | 43 | 27 | 137 | 0.003 |
| Virginia pine | 6 | 555 | 4,617 | 13.2 | 5.1 | 37.6 | 37 | 22 | 125 | 0.005 |
| Total | 61 | 411 | 4,808 | 12.0 | 5.7 | 37.6 | 44 | 26 | 150 | 0.017 |
| Forest Type | n | P-Band Heights (m) | X-Band Heights (m) | (X − P) Heights (m) | Pmag (W/m2) | Xmag (W/m2) | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Stdv | Max | Mean | Stdv | Max | Mean | Stdv | Max | Mean | Stdv | Max | Mean | Stdv | Max | ||
| Bottomland hardwood | 3 | 10.48 | 1.70 | 14.71 | 16.06 | 2.35 | 25.30 | 5.57 | 1.85 | 11.78 | 0.24 | 0.05 | 0.45 | 0.13 | 0.04 | 0.31 |
| Upland hardwood | 18 | 6.65 | 1.35 | 13.53 | 11.96 | 1.81 | 20.91 | 5.20 | 1.99 | 13.40 | 0.26 | 0.05 | 0.62 | 0.11 | 0.03 | 0.25 |
| Pine-hardwood | 4 | 8.03 | 1.52 | 16.27 | 13.72 | 1.66 | 24.77 | 5.47 | 1.71 | 11.74 | 0.23 | 0.05 | 0.48 | 0.12 | 0.04 | 0.41 |
| Loblolly pine | 24 | 5.46 | 1.30 | 13.26 | 10.84 | 1.22 | 22.55 | 5.46 | 1.70 | 15.40 | 0.36 | 0.08 | 0.99 | 0.07 | 0.02 | 0.27 |
| Shortleaf pine | 6 | 6.89 | 1.45 | 11.77 | 11.78 | 1.44 | 18.83 | 4.98 | 1.55 | 12.95 | 0.30 | 0.06 | 0.55 | 0.09 | 0.03 | 0.21 |
| Virginia pine | 6 | 6.83 | 1.94 | 18.38 | 15.04 | 1.71 | 30.02 | 8.15 | 1.86 | 15.46 | 0.41 | 0.09 | 0.88 | 0.08 | 0.03 | 0.25 |
| Total | 61 | 7.39 | 1.54 | 18.38 | 13.23 | 1.70 | 30.02 | 5.80 | 1.78 | 15.46 | 0.30 | 0.06 | 0.99 | 0.10 | 0.03 | 0.41 |
| LAI | LPI | All10th | All50th | d2 | d10 | Cd-1 | Cd-3 | Cd-3stdv | Xcv | X50th | Xmagstdv | Pmagstdv | Pmagmax | sn01xlcv | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| LAI | 1 | −0.698 | 0.638 | −0.116 | 0.085 | −0.347 | 0.030 | −0.084 | 0.223 | −0.485 | 0.609 | 0.241 | −0.013 | −0.092 | −0.124 |
| LPI | 1 | −0.546 | 0.063 | −0.054 | 0.160 | −0.237 | −0.242 | −0.262 | 0.693 | −0.520 | −0.065 | 0.181 | 0.187 | 0.071 | |
| All10th | 1 | 0.163 | −0.091 | −0.148 | 0.106 | −0.031 | 0.168 | −0.451 | 0.685 | 0.269 | 0.072 | 0.054 | −0.075 | ||
| All50th | 1 | −0.292 | 0.508 | −0.438 | −0.168 | 0.013 | 0.087 | 0.550 | 0.168 | −0.116 | −0.112 | 0.252 | |||
| d2 | 1 | −0.083 | −0.286 | −0.290 | 0.085 | 0.050 | 0.086 | 0.331 | 0.078 | 0.031 | 0.105 | ||||
| d10 | 1 | −0.242 | −0.181 | 0.199 | 0.039 | 0.080 | −0.041 | −0.190 | −0.146 | 0.286 | |||||
| Cd-1 | 1 | 0.562 | −0.269 | −0.429 | −0.285 | −0.421 | 0.136 | 0.216 | −0.251 | ||||||
| Cd-3 | 1 | −0.062 | −0.326 | −0.176 | −0.413 | 0.024 | 0.131 | −0.083 | |||||||
| Cd-3stdv | 1 | −0.127 | 0.316 | 0.176 | −0.408 | −0.430 | 0.105 | ||||||||
| Xcv | 1 | −0.363 | 0.222 | −0.074 | −0.109 | 0.044 | |||||||||
| X50th | 1 | 0.345 | −0.096 | −0.111 | 0.159 | ||||||||||
| Xmagstdv | 1 | −0.225 | −0.358 | 0.210 | |||||||||||
| Pmagstdv | 1 | 0.931 | −0.196 | ||||||||||||
| Pmagmax | 1 | −0.185 | |||||||||||||
| sn01xlcv | 1 |
| Sensor | # var. | R2 | R2adj’ | RMSE | CV-RMSE | Variable | Coefficient | SSCC | VIF | CI |
|---|---|---|---|---|---|---|---|---|---|---|
| Lidar | 2 | 0.58 | 0.57 | 0.52 | 0.53 | Intercept | 3.363 | ---- | ---- | ---- |
| LPI | −6.602 | 0.17 | 1.43 | 1.28 | ||||||
| All10th | 0.173 | 0.09 | 1.43 | 1.94 | ||||||
| 4 | 0.69 | 0.67 | 0.46 | 0.48 | Intercept | 3.405 | ---- | ---- | ---- | |
| LPI | −7.480 | 0.20 | 1.58 | 1.24 | ||||||
| All10th | 0.134 | 0.05 | 1.50 | 1.28 | ||||||
| d10 | −12.498 | 0.06 | 1.06 | 1.56 | ||||||
| Cd-3 | −15.113 | 0.06 | 1.14 | 2.16 | ||||||
| GeoSAR | 4 | 0.52 | 0.49 | 0.56 | 0.58 | Intercept | 3.407 | ---- | ---- | ---- |
| Xcv | −0.032 | 0.10 | 1.37 | 1.08 | ||||||
| X50th | 0.104 | 0.13 | 1.49 | 1.20 | ||||||
| Xmagstdv | 16.887 | 0.04 | 1.37 | 1.38 | ||||||
| sn01xlcv | −0.002 | 0.05 | 1.06 | 2.00 |
| # var. | R2 | R2adj’ | RMSE | CV-RMSE | Variable | Coefficient | SSCC | VIF | CI |
|---|---|---|---|---|---|---|---|---|---|
| 2 | 0.66 | 0.65 | 0.47 | 0.47 | Intercept | 3.439 | ---- | ---- | ---- |
| All50th | −0.153 | 0.29 | 1.43 | 1.27 | |||||
| X50th | 0.229 | 0.65 | 1.43 | 1.88 | |||||
| 3 | 0.71 | 0.69 | 0.44 | 0.45 | Intercept | 3.393 | ---- | ---- | ---- |
| LPI | −3.732 | 0.04 | 1.80 | 1.27 | |||||
| All50th | −0.120 | 0.14 | 1.88 | 1.43 | |||||
| X50th | 0.176 | 0.21 | 2.57 | 2.97 | |||||
| 4 | 0.73 | 0.71 | 0.42 | 0.44 | Intercept | 3.391 | ---- | ---- | ---- |
| LPI | −3.044 | 0.03 | 1.91 | 1.20 | |||||
| All50th | −0.147 | 0.16 | 2.39 | 1.33 | |||||
| d2 | −3.027 | 0.03 | 1.28 | 1.58 | |||||
| X50th | 0.201 | 0.24 | 3.00 | 3.34 | |||||
| 5 | 0.76 | 0.74 | 0.40 | 0.42 | Intercept | 3.401 | ---- | ---- | ---- |
| LPI | −4.253 | 0.05 | 2.19 | 1.11 | |||||
| All50th | −0.148 | 0.16 | 2.39 | 1.20 | |||||
| d2 | −3.996 | 0.04 | 1.39 | 1.46 | |||||
| X50th | 0.183 | 0.18 | 3.20 | 2.00 | |||||
| Cd-3 | −11.703 | 0.03 | 1.36 | 3.41 | |||||
| 6 | 0.77 | 0.75 | 0.40 | 0.42 | Intercept | 3.475 | ---- | ---- | ---- |
| LPI | −4.246 | 0.05 | 2.13 | 1.19 | |||||
| All50th | −0.185 | 0.20 | 3.00 | 1.33 | |||||
| d2 | −4.979 | 0.05 | 1.65 | 1.41 | |||||
| X50th | 0.208 | 0.24 | 3.22 | 2.31 | |||||
| Cd-3stdv | −14.977 | 0.02 | 1.34 | 2.98 | |||||
| Cd-1 | −7.805 | 0.04 | 2.07 | 3.92 |
| # var. | R2 | R2adj’ | RMSE | CV-RMSE | Variable | Coefficient | SSCC | VIF | CI |
|---|---|---|---|---|---|---|---|---|---|
| 5 | 0.74 | 0.72 | 0.42 | 0.44 | Intercept | 3.442 | ---- | ---- | ---- |
| All50th | −0.180 | 0.34 | 1.72 | 1.16 | |||||
| d2 | −4.187 | 0.05 | 1.23 | 1.38 | |||||
| X50th | 0.247 | 0.68 | 1.59 | 1.47 | |||||
| Pmagstdv | 16.079 | 0.04 | 7.63 | 2.47 | |||||
| Pmagmax | −2.731 | 0.04 | 7.61 | 5.50 | |||||
| 6 | 0.77 | 0.74 | 0.40 | 0.42 | Intercept | 3.406 | ---- | ---- | ---- |
| LPI | −3.110 | 0.03 | 2.00 | 1.17 | |||||
| All50th | −0.147 | 0.16 | 2.45 | 1.31 | |||||
| d2 | −3.455 | 0.03 | 1.30 | 1.45 | |||||
| X50th | 0.199 | 0.23 | 3.04 | 1.75 | |||||
| Pmagstdv | 16.643 | 0.04 | 7.64 | 3.71 | |||||
| Pmagmax | −2.632 | 0.04 | 7.63 | 0.07 |
Share and Cite
Peduzzi, A.; Wynne, R.H.; Thomas, V.A.; Nelson, R.F.; Reis, J.J.; Sanford, M. Combined Use of Airborne Lidar and DBInSAR Data to Estimate LAI in Temperate Mixed Forests. Remote Sens. 2012, 4, 1758-1780. https://doi.org/10.3390/rs4061758
Peduzzi A, Wynne RH, Thomas VA, Nelson RF, Reis JJ, Sanford M. Combined Use of Airborne Lidar and DBInSAR Data to Estimate LAI in Temperate Mixed Forests. Remote Sensing. 2012; 4(6):1758-1780. https://doi.org/10.3390/rs4061758
Chicago/Turabian StylePeduzzi, Alicia, Randolph H. Wynne, Valerie A. Thomas, Ross F. Nelson, James J. Reis, and Mark Sanford. 2012. "Combined Use of Airborne Lidar and DBInSAR Data to Estimate LAI in Temperate Mixed Forests" Remote Sensing 4, no. 6: 1758-1780. https://doi.org/10.3390/rs4061758