Advances in Forest Inventory Using Airborne Laser Scanning
Abstract
:1. Introduction
2. Material and Methods
2.1. Test Site and Field Data
2.2. Airborne Laser Data Collection
2.3. Laser Data Pre-Processing
2.4. Improved Tree Detection
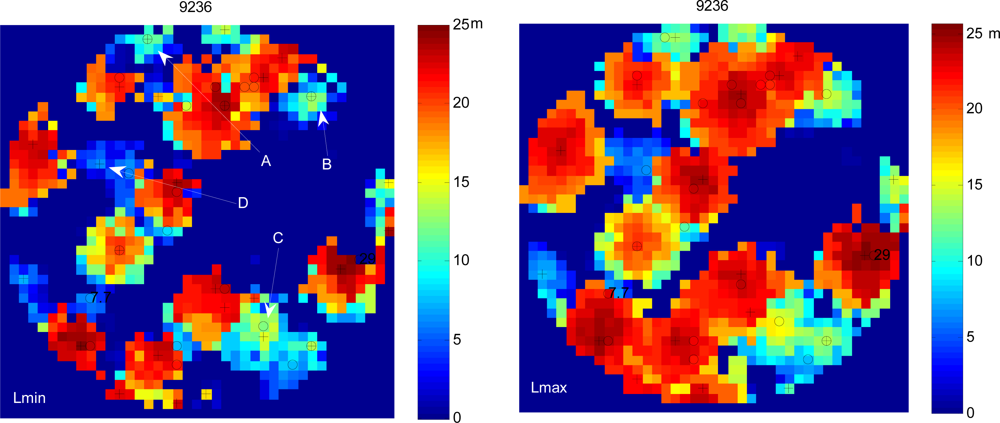
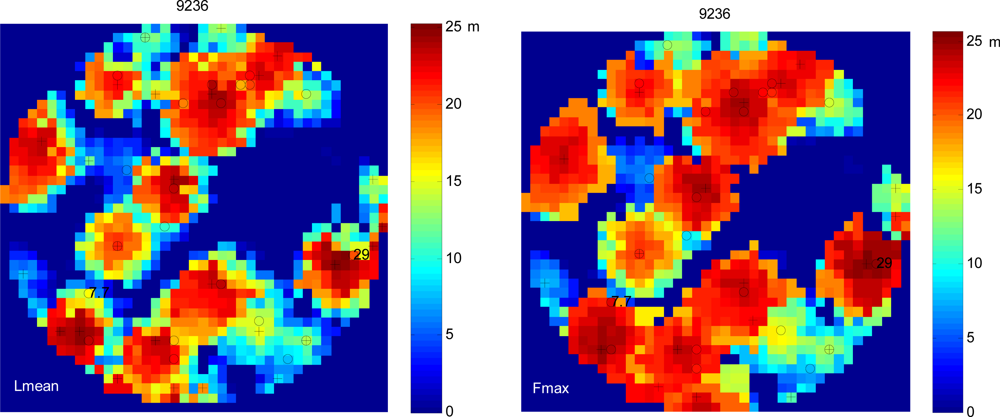
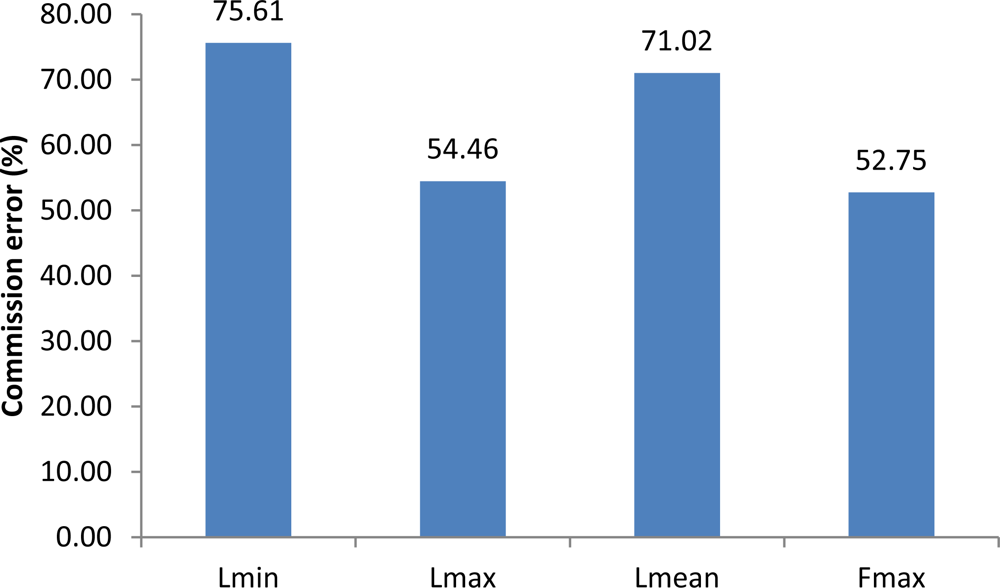
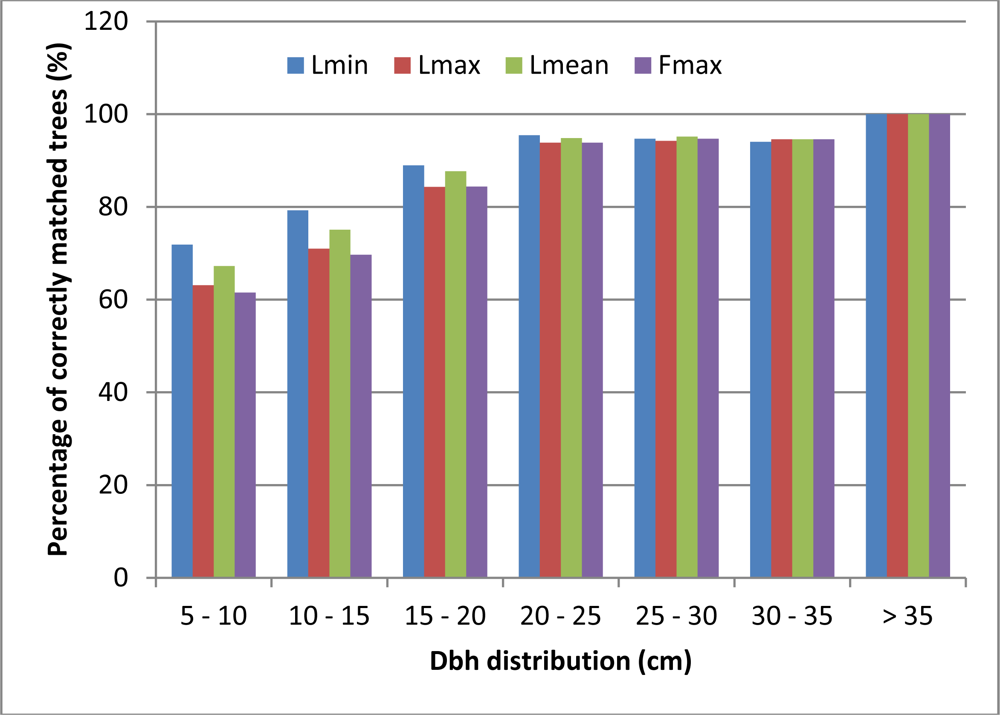
- Different raster models with 0.5 m × 0.5 m pixel size were created for tree location. The created models were as follows: minimum of last returns (Lmin), maximum of last returns (Lmax), mean of last returns (Lmean), and first returns maximum (Fmax).
- The raster models were smoothed by means of a Gaussian filter. A 3 m × 3 m window size was selected in order to eliminate minor tree level fluctuations and to avoid the merging of overlapping trees. Given Finland’s forest conditions, larger window sizes lead to the merging of overlapping trees, especially when trying to locate trees from within the suppressed tree storey.
- Local maxima were sought from the smoothed surface model in a 3 m × 3 m window, and trees were considered to have been detected if the local maxima were greater than 2 m above the ground.
2.5. Using Point Height Metrics and Individual Tree-Based Features in Area-Based Predictions
3. Results and Discussion
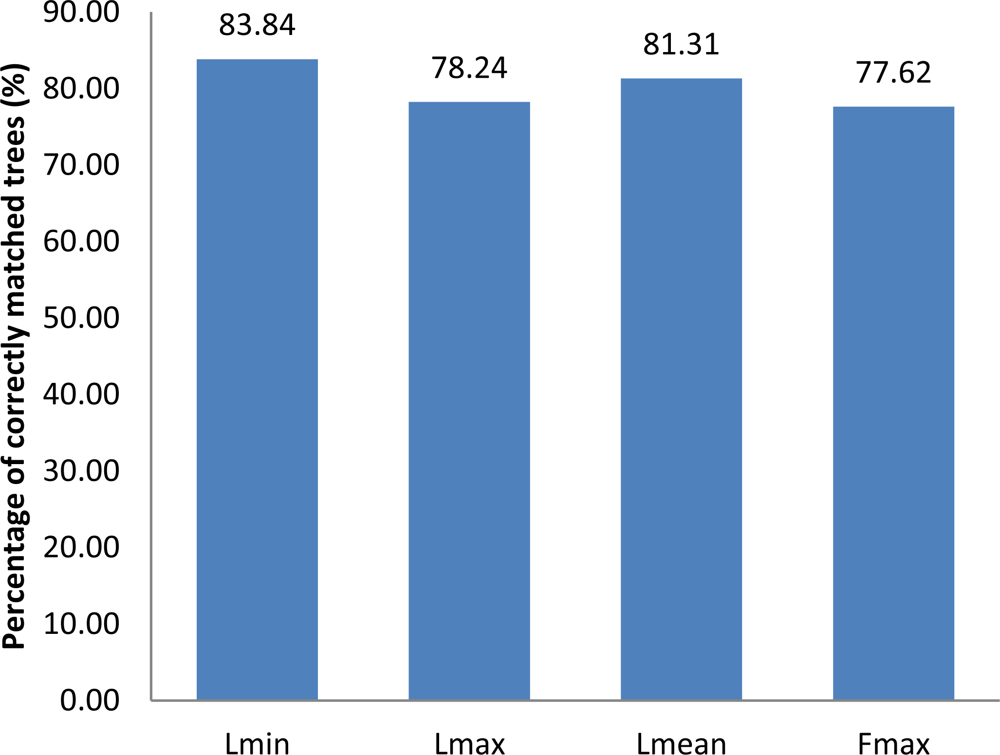
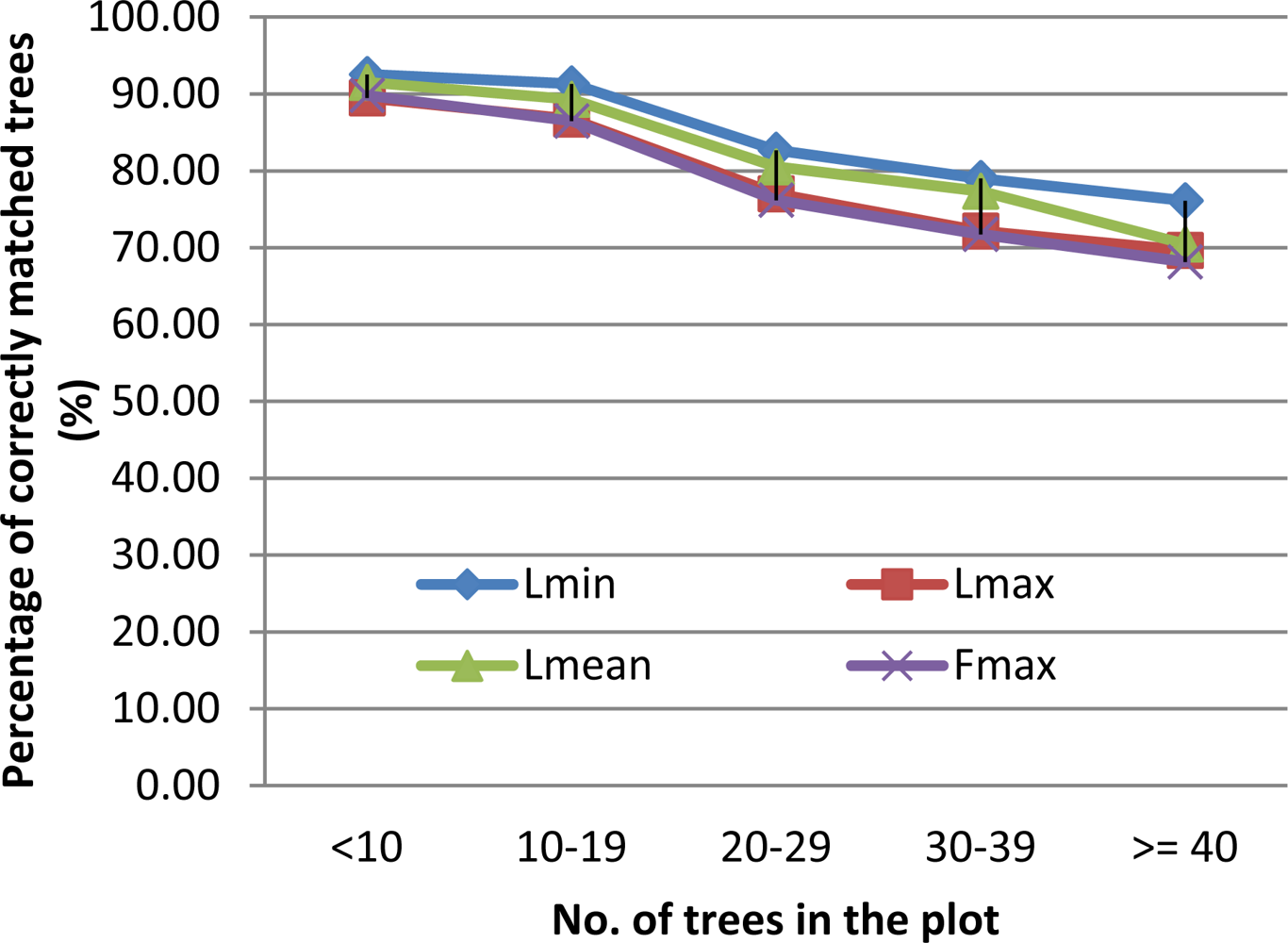
3.1. Tree Detection Accuracy
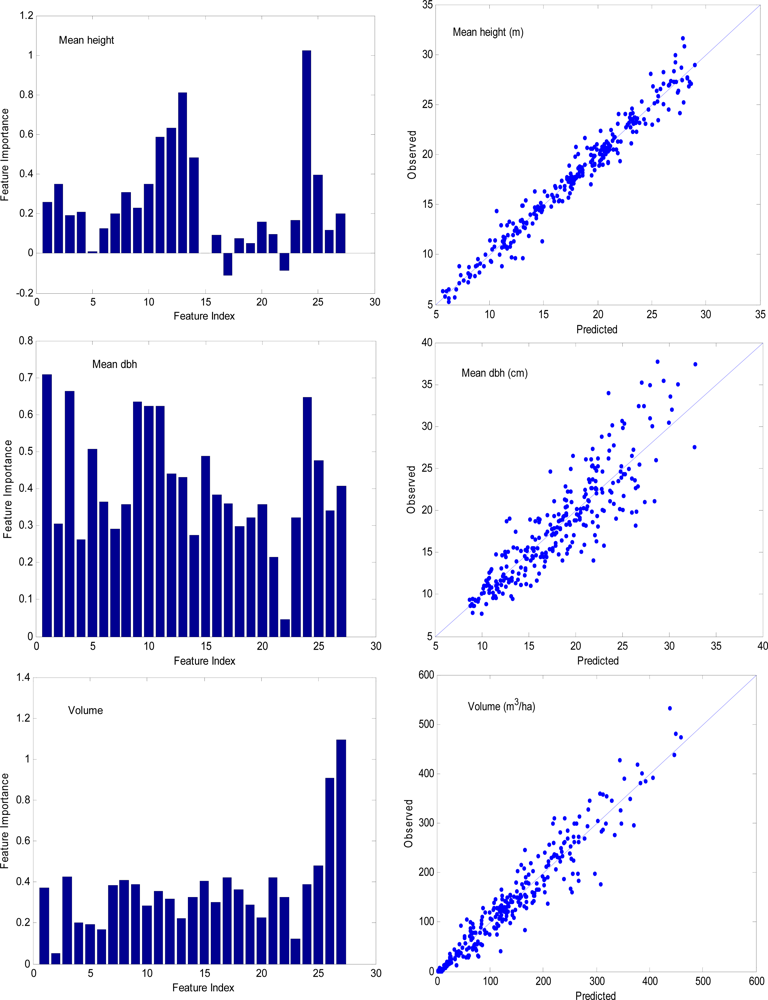
3.2. The Accuracy of Area-Based Prediction of Forest Variables
4. Conclusions
Acknowledgments
References
- Sexton, J.O.; Bax, T.; Siqueira, P.; Swenson, J.J.; Hensley, S. A comparison of lidar, radar, and field measurements of canopy height in pine and hardwood forests of south-eastern North America. For. Ecol. Manage 2009, 257, 1136–1147. [Google Scholar]
- Houghton, R.A.; Hall, F.; Goetz, S.J. Importance of biomass in the global carbon cycle. J. Geophys. Res 2009, 114. [Google Scholar] [CrossRef]
- Hyyppä, J.; Hyyppä, H.; Leckie, D.; Gougeon, F.; Yu, X.; Maltamo, M. Review of methods of small-footprint airborne laser scanning for extracting forest inventory data in boreal forests. Int. J. Remote Sens 2008, 29, 1339–1366. [Google Scholar]
- Maclean, G.; Krabill, W. Gross-merchantable timber volume estimation using and airborne LiDAR system. Can. J. Remote Sens 1986, 12, 7–18. [Google Scholar]
- Nelson, R.; Krabill, W.; Maclean, G. Determining forest canopy characteristics using airborne laser data. Remote Sens. Environ 1984, 15, 201–212. [Google Scholar]
- Nelson, R.; Krabill, W.; Tonelli, J. Estimating forest biomass and volume using airborne laser data. Remote Sens. Environ 1988, 24, 247–267. [Google Scholar]
- Næsset, E. Determination of mean tree height of forest stands using airborne laser scanner data. ISPRS J. Photogramm 1997, 52, 49–56. [Google Scholar]
- Means, J.; Acker, S.; Harding, D.; Blair, J.; Lefsky, M.; Cohen, W.; Harmon, W.; McKee, A. Use of large-footprint scanning airborne lidar to estimate forest stand characteristics in the western cascades of oregon. Remote Sens. Environ 1999, 67, 298–308. [Google Scholar]
- Lim, K.; Treitz, P.; Baldwin, K.; Morrison, I.; Green, J. Lidar remote sensing of biophysical properties of northern tolerant hardwood forests. Can. J. Remote Sens 2002, 29, 658–678. [Google Scholar]
- Lim, K.; Treitz, P.; Wulder, M.; St.-Onge, B.; Flood, M. LIDAR remote sensing of forest structure. Prog. Phys. Geogr 2003, 27, 88–106. [Google Scholar]
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ 2002, 80, 88–99. [Google Scholar]
- Maltamo, M.; Eerikäinen, K.; Packalen, P.; Hyyppä, J. Estimation of stem volume using laser scanning-based canopy height metrics. Forestry 2006, 79, 217–229. [Google Scholar]
- Hyyppä, J.; Inkinen, M. Detecting and estimating attributes for single trees using laser scanner. Photogramm. J. Fin 1999, 16, 27–42. [Google Scholar]
- Brandtberg, T. Automatic individual tree-based analysis of high spatial resolution remotely sensed data. Acta Univ. Agric. Sueciae Silvestria 1999, 118, 47. [Google Scholar]
- Ziegler, M.; Konrad, H.; Hofrichter, J.; Wimmer, A.; Ruppert, G.; Schardt, M.; Hyyppä, J. Assessment of forest attributes and single-tree segmentation by means of laser scanning. Laser Radar Technol. Appl. V 2000, 4035, 73–84. [Google Scholar]
- Hyyppä, J.; Kelle, O.; Lehikoinen, M.; Inkinen, M. A segmentation-based method to retrieve stem volume estimates from 3-dimensional tree height models produced by laser scanner. IEEE Trans. Geosci. Remote Sens 2001, 39, 969–975. [Google Scholar]
- Hyyppä, J.; Schardt, M.; Haggrén, H.; Koch, B.; Lohr, U.; Scherrer, H.U.; Paananen, R.; Luukkonen, H.; Ziegler, M.; Hyyppä, H.; et al. HIGH-SCAN: The first European-wide attempt to derive single-tree information from laserscanner data. Photogramm. J. Fin 2001, 17, 58–68. [Google Scholar]
- Hyyppä, J. Method for Determination of Stand Attributes and a Computer Program to. Perform the Method. US Patent 6792684 B1 2004. [Google Scholar]
- Persson, Å.; Holmgren, J.; Söderman, U. Detecting and measuring individual trees using an airborne laser scanner. Photogramm. Eng. Remote Sensing 2002, 68, 925–932. [Google Scholar]
- Gougeon, F.; Moore, T. Classification Individuelle des Arbres à Partir d’Images à Haute Résolution Spatiale. Proceedings of 6e Congrès de L'association Québécoise de Télédétection, Sherbrooke, QC, Canada, 4–6 May 1988; VI, pp. 185–196.
- Erikson, M.; Olofsson, K. Comparison of three individual tree crown detection methods. Mach. Vis. Appl 2005, 16, 258–265. [Google Scholar]
- Pitkänen, J.; Maltamo, M.; Hyyppä, J.; Yu, X. Adaptive Methods for Individual Tree Detection on Airborne Laser Based Canopy Height Model. Proceedings of ISPRS WG VIII/2 Laser-Scanners for Forest and Landscape Assessment, Freiburg, Germany, 3–6 October 2004; 36, pp. 187–191.
- Bortolot, Z.; Wynne, R. Estimating forest biomass using small footprint LiDAR data: An individual tree-based approach that incorporates training data. ISPRS J. Photogramm 2005, 59, 342–360. [Google Scholar]
- Hyyppä, J.; Mielonen, T.; Hyyppä, H.; Maltamo, M.; Yu, X.; Honkavaara, E.; Kaartinen, H. Using Individual Tree Crown Approach for Forest Volume Extraction with Aerial Images and Laser Point Clouds. Proceedings of ISPRS WG III/3, III/4, V/3 Workshop “Laser scanning 2005”, Enschede, The Netherlands, 12–14 September 2005; 36, pp. 144–149.
- Suarez, J.C.; Ontiveros, C.; Smith, S.; Snape, S. Use of airborne LiDAR and aerial photography in the estimation of individual tree heights in forestry. Comput. Geosci 2005, 31, 253–262. [Google Scholar]
- Hyyppä, J.; Yu, X.; Hyyppä, H.; Maltamo, M. Methods of Airborne Laser Scanning for Forest Information Extraction. Proceedings of the Workshop on 3D Remote Sensing in Forestry, Vienna, Austria, 14–15 February 2006; p. 16.
- Koch, B.; Heyder, U.; Weinacker, H. Detection of individual tree crowns in airborne lidar data. Photogramm. Eng. Remote Sensing 2006, 72, 357–363. [Google Scholar]
- Korpela, I.; Tokola, T. Potential of aerial image-based monoscopic and multiview single-tree forest inventory: A simulation approach. For. Sci 2006, 52, 136–147. [Google Scholar]
- Barilotti, A.; Sepic, F.; Abramo, E.; Crosilla, F. Assessing the 3D Structure of the Single Crowns in Mixed Alpine Forests. Proceedings of Photogrammetric Image Analysis PIA’07, Munich, Germany, 19–21 September 2007; XXXVI, pp. 129–134.
- Hirschmugl, M.; Ofner, M.; Raggam, J.; Schardt, M. Single tree detection in very high resolution remote sensing data. Remote Sens. Environ 2007, 110, 533–544. [Google Scholar]
- Popescu, S.C. Estimating biomass of individual pine trees using airborne lidar. Biomass Bioenergy 2007, 31, 646–655. [Google Scholar]
- Kwak, D.-A.; Lee, W.-K.; Lee, J.-H.; Biging, G.S.; Gong, P. Detection of individual trees and estimation of tree height using LiDAR data. J. For. Res 2007, 12, 425–434. [Google Scholar]
- Heurich, M. Automatic recognition and measurement of single trees based on data from airborne laser scanning over the richly structured natural forests of the Bavarian Forest National Park. For. Ecol. Manage 2008, 255, 2416–2433. [Google Scholar]
- Kaartinen, H.; Hyyppä, J. EuroSDR/ISPRS Project, Commission II, “Tree Extraction”, Final Report; European Spatial Data Research Official Publication: Amsterdam, The Netherlands, 2008; No. 53. [Google Scholar]
- Villikka, M.; Maltamo, M.; Packalén, P.; Vehmas, M.; Hyyppä, J. Alternatives for predicting tree-stem volume of Norway Spruce using airborne laser scanning. Photogramm. J. Fin 2008, 20, 33–42. [Google Scholar]
- Wang, Y.; Weinacker, H.; Koch, B. A lidar point cloud based procedure for vertical canopy structure analysis and 3D single tree modelling in forest. Sensors 2008, 8, 3938–3951. [Google Scholar]
- Balic, N.; Koch, B. Canscan—An algorithm for automatic extraction of canyons. Remote Sens 2009, 1, 197–209. [Google Scholar]
- Forzieri, G.; Guarnieri, L.; Vivoni, E.R.; Castelli, F.; Preti, F. Multiple attribute decision making for individual tree detection using high-resolution laser scanning. For. Ecol. Manage 2009, 258, 2501–2510. [Google Scholar]
- Hudak, A.; Evans, J.; Smith, A. LiDAR utility for natural resource managers. Remote Sens 2009, 1, 934–951. [Google Scholar]
- Kato, A.; Moskal, L.M.; Schiess, P.; Swanson, M.E.; Calhoun, D.; Stuetzle, W. Capturing tree crown formation through implicit surface reconstruction using airborne lidar data. Remote Sens. Environ 2009, 113, 1148–1162. [Google Scholar]
- Maltamo, M.; Peuhkurinen, J.; Malinen, J.; Vauhkonen, J.; Packalén, P.; Tokola, T. Predicting tree attributes and quality characteristics of scots pine using airborne laser scanning data. Silva Fenn 2009, 43, 507–521. [Google Scholar]
- Reitberger, J.; Schnörr, C.; Krzystek, P.; Stilla, U. 3D segmentation of single trees exploiting full waveform LIDAR data. ISPRS J. Photogramm 2009, 64, 561–574. [Google Scholar]
- Angelo, J.; Duncan, B.; Weishampel, J. Using lidar-derived vegetation profiles to predict time since fire in an Oak scrub landscape in East-Central Florida. Remote Sens 2010, 2, 514–525. [Google Scholar]
- Breidenbach, J.; Næsset, E.; Lien, V.; Gobakken, T.; Solberg, S. Prediction of species specific forest inventory attributes using a nonparametric semi-individual tree crown approach based on fused airborne laser scanning and multispectral data. Remote Sens. Environ 2010, 114, 911–924. [Google Scholar]
- Holopainen, M.; Mäkinen, A.; Rasinmäki, J.; Hyyppä, J.; Hyyppä, H.; Kaartinen, H.; Viitala, R.; Vastaranta, M.; Kangas, A. Effect of tree level airborne laser scanning accuracy on the timing and expected value of harvest decisions. Eur. J. For. Res 2010, 129, 899–910. [Google Scholar]
- Holopainen, M.; Vastaranta, M.; Rasinmäki, J.; Kalliovirta, J.; Mäkinen, A.; Haapanen, R.; Melkas, T.; Yu, X.; Hyyppä, J. Uncertainty in timber assortment estimates predicted from forest inventory data. Eur. J. For. Res 2010, 129, 1131–1142. [Google Scholar]
- Holopainen, M.; Vastaranta, M.; Haapanen, R.; Yu, X.; Hyyppä, J.; Kaartinen, H.; Viitala, R.; Hyyppä, H. Site-type estimation using airborne laser scanning and stand register data. Photogramm. J. Fin 2010, 22, 16–32. [Google Scholar]
- Gupta, S.; Weinacker, H.; Koch, B. Comparative analysis of clustering based approaches for 3-D single tree detection using airborne fullwave lidar data. Remote Sens 2010, 2, 968–989. [Google Scholar]
- Kantola, T.; Vastaranta, M.; Yu, X.; Lyytikäinen-Saarenmaa, P.; Holopainen, M.; Talvitie, M.; Kaasalainen, S.; Solberg, S.; Hyyppä, J. Classification of defoliated trees using tree-level airborne laser scanning data combined with aerial images. Remote Sens 2010, 2, 2665–2679. [Google Scholar]
- Koch, B. Status and future of laser scanning, synthetic aperture radar and hyperspectral remote sensing data for forest biomass assessment. ISPRS J. Photogramm 2010, 65, 581–590. [Google Scholar]
- Korpela, I.; Orka, H.; Hyyppa, J.; Heikkinen, V.; Tokola, T. Range and AGC normalization in airborne discrete-return LiDAR intensity data for forest canopies. ISPRS J. Photogramm 2010, 65, 369–379. [Google Scholar]
- Korpela, I.; Orka, H.; Maltamo, M.; Tokola, T.; Hyyppä, J. Tree species classification using airborne lidar-effects of stand and tree parameters, downsizing of training set, intensity normalization, and sensor type. Silva Fenn 2010, 44, 319–339. [Google Scholar]
- Kwak, D.-A.; Lee, W.-K.; Cho, H.-K.; Lee, S.-H.; Kafatos, M.; Kim, S.-R. Estimating stem volume and biomass of Pinus koraiensis using LiDAR data. J. Plant Res 2010, 123, 421–432. [Google Scholar]
- Puttonen, E.; Litkey, P.; Hyyppä, J. Individual tree species classification by illuminated—Shaded area separation. Remote Sens 2010, 2, 19–35. [Google Scholar]
- Vauhkonen, J.; Korpela, I.; Maltamo, M.; Tokola, T. Imputation of single-tree attributes using airborne laser scanning-based height, intensity, and alpha shape metrics. Remote Sens. Environ 2010, 114, 1263–1276. [Google Scholar]
- Yu, X.; Hyyppä, J.; Holopainen, M.; Vastaranta, M. Comparison of area-based and individual tree-based methods for predicting plot-level forest attributes. Remote Sens 2010, 2, 1481–1495. [Google Scholar]
- Edson, C.; Wing, M. Airborne light detection and ranging (LiDAR) for individual tree stem location, height, and biomass measurements. Remote Sens 2011, 3, 2494–2528. [Google Scholar]
- Heinzel, J.; Weinacker, H.; Koch, B. Prior-knowledge-based single-tree extraction. Int. J. Remote Sens 2011, 32, 4999–5020. [Google Scholar]
- Jung, S.-E.; Kwak, D.-A.; Park, T.; Lee, W.-K.; Yoo, S. Estimating crown variables of individual trees using airborne and terrestrial laser scanners. Remote Sens 2011, 3, 2346–2363. [Google Scholar]
- Listopad, C.; Drake, J.; Masters, R.; Weishampel, J. Portable and airborne small footprint LiDAR: Forest canopy structure estimation of fire managed plots. Remote Sens 2011, 3, 1284–1307. [Google Scholar]
- Tuominen, S.; Haapanen, R. Comparison of grid-based and segment-based estimation of forest attributes using airborne laser scanning and digital aerial imagery. Remote Sens 2011, 3, 945–961. [Google Scholar]
- Ussyshkin, V.; Theriault, L. Airborne lidar: Advances in discrete return technology for 3D vegetation mapping. Remote Sens 2011, 3, 416–434. [Google Scholar]
- Vauhkonen, J.; Ene, L.; Gupta, S.; Heinzel, J.; Holmgren, J.; Pitkänen, J.; Solberg, S.; Wang, Y.; Weinacker, H.; Hauglin, K.; et al. Comparative testing of single-tree detection algorithms under different types of forest. Forestry 2011. [Google Scholar] [CrossRef]
- Vastaranta, M.; Holopainen, M.; Yu, X.; Hyyppä, J.; Mäkinen, A.; Rasinmäki, J.; Melkas, T.; Kaartinen, H.; Hyyppä, H. Effects of individual tree detection error sources on forest management planning calculations. Remote Sens 2011, 3, 1614–1626. [Google Scholar]
- Vehmas, M.; Eerikäinen, K.; Peuhkurinen, J.; Packalén, P.; Maltamo, M. Airborne laser scanning for the site type identification of mature boreal forest stands. Remote Sens 2011, 3, 100–116. [Google Scholar]
- Yu, X.; Hyyppä, J.; Vastaranta, M.; Holopainen, M.; Viitala, R. Predicting individual tree attributes from airborne laser point clouds based on the random forests technique. ISPRS J. Photogramm 2011, 66, 28–37. [Google Scholar]
- Vastaranta, M.; Kankare, V.; Holopainen, M.; Yu, X.; Hyyppä, J.; Hyyppä, H. Combination of individual tree detection and area-based approach in imputation of forest variables using airborne laser data. ISPRS J. Photogramm 2012, 67, 73–79. [Google Scholar]
- Kaartinen, H.; Hyyppä, J.; Yu, X.; Vastaranta, M.; Hyyppä, H.; Kukko, A.; Holopainen, M.; Heipke, C.; Hirschmugl, M.; Morsdorf, F.; et al. An international comparison of individual tree detection and extraction using airborne laser scanning. Remote Sens 2012, 4, 950–974. [Google Scholar]
- Wang, Y.; Weinacker, H.; Koch, B.; Sterenczak, K. Lidar Point Cloud Based Fully Automatic 3D Single Tree Modelling in Forest and Evaluations of the Procedure. Proceedings of the 21st ISPRS Congress, Beijing, China, 3–11 July 2008; 37, pp. 45–51.
- Gupta, S.; Koch, B.; Weinacker, H. Tree Species Detection Using Full Waveform Lidar Data in a Complex Forest. In Technical Commission VII Symposium—100 Years of ISPRS; Wagner, W., Székely, B., Eds.; Vienna University of Technology: Vienna, Austria, 2010; pp. 249–254. [Google Scholar]
- Holmgren, J.; Wallerman, J. Estimation of Tree Size Distributions by Combining Vertical and Horizontal Distribution of Laser Measurements with Extraction of Individual Trees. Proceedings of the Workshop on 3D Remote Sensing in Forestry, Vienna, Austria, 14–15 February 2006; pp. 168–173.
- Axelsson, P. DEM Generation From Laser Scanner Data Using Adaptive TIN Models. Proceedings of XIXth ISPRS Congress, Amsterdam, The Netherlands, 16–22 July 2000; 33, pp. 110–117.
- Yu, X.; Hyyppä, J.; Kukko, A.; Maltamo, M.; Kaartinen, H. Change detection techniques for canopy height growth measurements using airborne laser scanning data. Photogramm. Eng. Remote Sensing 2006, 72, 1339–1348. [Google Scholar]
- Laasasenaho, J. Taper Curve and Volume Functions for Pine, Spruce and Birch; The Finnish Forest Research Institute: Helsinki, Finland, 1982; Volume 108, pp. 1–74. [Google Scholar]
- Kalliovirta, J.; Tokola, T. Functions for estimating stem diameter and tree age using tree height, crown width and existing stand database information. Silva Fenn 2005, 39, 227–248. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn 2001, 45, 5–32. [Google Scholar]
- Liang, X.; Hyyppä, J.; Matikainen, L. Deciduous-Coniferous Tree Classification Using Difference between First and Last Pulse Laser Signatures. ISPRS Workshop on Laser Scanning 2007 and SilviLaser 2007, Espoo, Finland, 12–14 September 2007; XXXVI, pp. 253–257.
- Matikainen, L.; Hyyppä, J.; Kaartinen, K. Comparison between first pulse and last pulse laser scanner data in the automatic detection of buildings. Photogramm. Eng. Remote Sensing 2009, 75, 133–146. [Google Scholar]
- Olofsson, K.; Lindberg, E.; Holmgren, J. A Method for Linking Field-Surveyed and Aerial-Detected Single Trees Using Cross Correlation of Position Images and the Optimization of Weighted Tree List Graphs. Proceedings of the SilviLaser 2008: 8th International Conference on LiDAR Applications in Forest Assessment and Inventory, Edinburgh, UK, 17–19 September 2008; pp. 95–104.
- Hyyppä, J.; Pulliainen, J.; Hallikainen, M.; Saatsi, A. Radar-derived standwise forest inventory. IEEE Trans. Geosci. Remote Sens 1997, 35, 392–404. [Google Scholar]
- Hyyppä, J.; Hallikainen, M. Applicability of airborne profiling radar to forest inventory. Remote Sens. Environ 1996, 57, 39–57. [Google Scholar]
- Ahokas, E.; Hyyppä, J.; Yu, X.; Holopainen, M. Transmittance of airborne laser scanning pulses for boreal forest elevation modeling. Remote Sens 2011, 3, 1365–1379. [Google Scholar]
- Holopainen, M.; Haapanen, R.; Tuominen, S.; Viitala, R. Performance of Airborne Laser Scanning- and Aerial Photograph-Based Statistical and Textural Features in Forest Variable Estimation. Proceedings of the SilviLaser 2008: 8th International Conference on LiDAR Applications in Forest Assessment and Inventory, Edinburgh, UK, 17–19 September 2008; pp. 105–112.
- Hollaus, M. Large Scale Applications of Airborne Laser Scanning for a Complex Mountainous Environment. 2006; p. 111. [Google Scholar]
| Mean Height (m) | Mean Diameter (cm) | Stem Volume m3/ha | |
|---|---|---|---|
| Minimum | 3.9 | 7.6 | 0.4 |
| Maximum | 31.7 | 50.8 | 586.2 |
| Mean | 18.0 | 18.3 | 148.2 |
| Standard deviation | 6.1 | 6.9 | 110.7 |
| No. | Feature | Explanation |
|---|---|---|
| Point Height Metrics | ||
| 1 | meanH | Mean canopy height calculated as the arithmetic mean of the heights from the point cloud |
| 2 | stdH | Standard deviations of heights from the point cloud |
| 3 | P | Penetration calculated as a proportion of ground returns to total returns |
| 4 | COV | Coefficient of variation |
| 5 | H10 | 10th percentile of canopy height distribution |
| 6 | H20 | 20th percentile of canopy height distribution |
| 7 | H30 | 30th percentile of canopy height distribution |
| 8 | H40 | 40th percentile of canopy height distribution |
| 9 | H50 | 50th percentile of canopy height distribution |
| 10 | H60 | 60th percentile of canopy height distribution |
| 11 | H70 | 70th percentile of canopy height distribution |
| 12 | H80 | 80th percentile of canopy height distribution |
| 13 | H90 | 90th percentile of canopy height distribution |
| 14 | maxH | Maximum height |
| 15 | D10 | 10th canopy cover percentile computed as the proportion of returns below 10% of the total height |
| 16 | D20 | 20th canopy cover percentile computed as the proportion of returns below 20% of the total height |
| 17 | D30 | 30th canopy cover percentile computed as the proportion of returns below 30% of the total height |
| 18 | D40 | 40th canopy cover percentile computed as the proportion of returns below 40% of the total height |
| 19 | D50 | 50th canopy cover percentile computed as the proportion of returns below 50% of the total height |
| 20 | D60 | 60th canopy cover percentile computed as the proportion of returns below 60% of the total height |
| 21 | D70 | 70th canopy cover percentile computed as the proportion of returns below 70% of the total height |
| 22 | D80 | 80th canopy cover percentile computed as the proportion of returns below 80% of the total height |
| 23 | D90 | 90th canopy cover percentile computed as the proportion of returns below 90% of the total height |
| Individual Tree Based Features | ||
| 24 | LH | Mean height of all extracted trees |
| 25 | LD | Mean DBH of all detected trees, derived from the extracted heights and crown areas |
| 26 | LB | Basal area of the plot, derived from the extracted DBH |
| 27 | LV | Volume of the plot, derived from the extracted DBH and height |
| Bias | RMSE | RMSE (%) | R | |
|---|---|---|---|---|
| With all features | ||||
| Mean height (m) | −0.00 | 1.10 | 6.15 | 0.98 |
| Mean DBH (cm) | 0.00 | 2.91 | 16.07 | 0.89 |
| Volume (m3/ha) | 0.24 | 30.05 | 20.32 | 0.96 |
| With point height metrics | ||||
| Mean height (m) | −0.03 | 1.25 | 6.99 | 0.98 |
| Mean DBH (cm) | 0.02 | 3.02 | 16.65 | 0.88 |
| Volume (m3/ha) | 0.13 | 37.56 | 25.41 | 0.93 |
| Individual tree-based features | ||||
| Mean height (m) | −0.00 | 1.24 | 6.97 | 0.98 |
| Mean DBH (cm) | −0.06 | 3. 54 | 19.54 | 0.83 |
| Volume (m3/ha) | −1.06 | 30.16 | 20.40 | 0.96 |
Share and Cite
Hyyppä, J.; Yu, X.; Hyyppä, H.; Vastaranta, M.; Holopainen, M.; Kukko, A.; Kaartinen, H.; Jaakkola, A.; Vaaja, M.; Koskinen, J.; et al. Advances in Forest Inventory Using Airborne Laser Scanning. Remote Sens. 2012, 4, 1190-1207. https://doi.org/10.3390/rs4051190
Hyyppä J, Yu X, Hyyppä H, Vastaranta M, Holopainen M, Kukko A, Kaartinen H, Jaakkola A, Vaaja M, Koskinen J, et al. Advances in Forest Inventory Using Airborne Laser Scanning. Remote Sensing. 2012; 4(5):1190-1207. https://doi.org/10.3390/rs4051190
Chicago/Turabian StyleHyyppä, Juha, Xiaowei Yu, Hannu Hyyppä, Mikko Vastaranta, Markus Holopainen, Antero Kukko, Harri Kaartinen, Anttoni Jaakkola, Matti Vaaja, Jarkko Koskinen, and et al. 2012. "Advances in Forest Inventory Using Airborne Laser Scanning" Remote Sensing 4, no. 5: 1190-1207. https://doi.org/10.3390/rs4051190







