An International Comparison of Individual Tree Detection and Extraction Using Airborne Laser Scanning
Abstract
:1. Introduction
2. Material
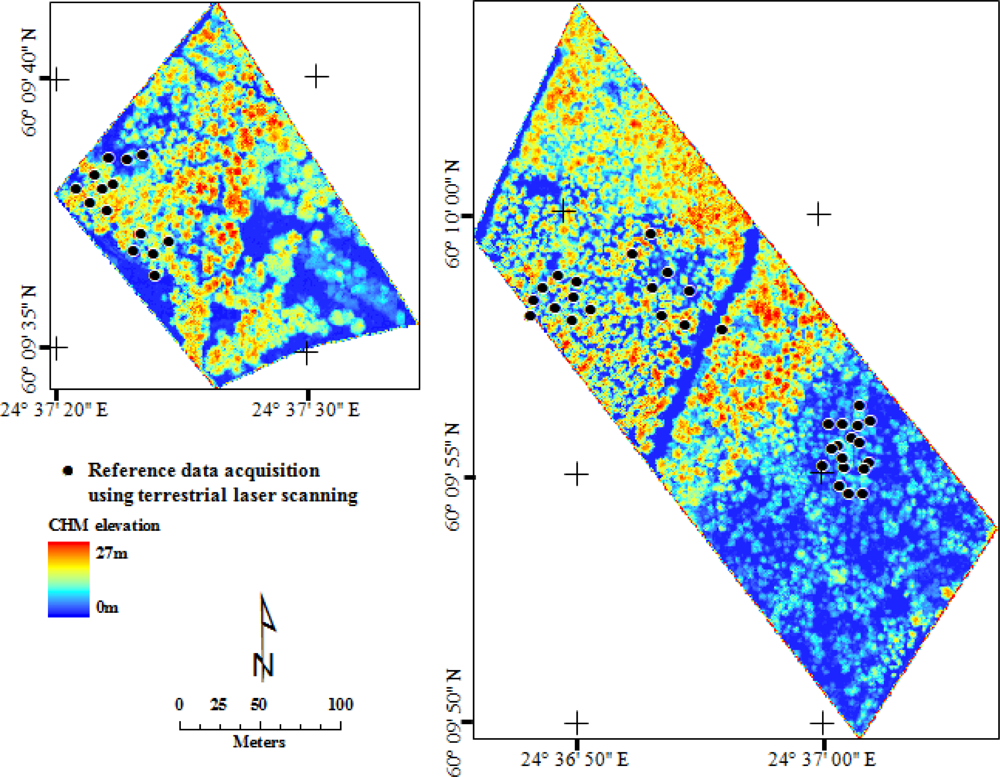
2.1. Study Area
2.2. Data Provided for Tree Extraction
2.3. Reference Data
2.4. Produced Tree Extraction Results
3. Methods
3.1. Methods Used by the Partners
3.1.1. Method Definiens
3.1.2. Method FOI
3.1.3. Method Hannover
3.1.4. Method Metla
3.1.5. Method Norway
3.1.6. Method Ilan
3.1.7. Method Texas
3.1.8. Method Udine
3.1.9. Method Zürich
- Position (x, y) was derived as the centre of gravity of the echo positions belonging to the cluster.
- Tree height was computed as the maximum height of the cluster’s echoes.
- Crown diameter was estimated using the convex hull of the cluster by transferring the circum-distance of the convex hull to a radius assuming circular shape.
3.1.10. Manually Extracted Trees (Manual)
3.2. Methods Added to the Test
3.2.1. Local Maxima Finding (FGI_LOCM)
3.2.2. Multi-scale Laplacian of Gaussian (FGI_MLOG)
3.2.3. Minimum Curvature-Based Tree Detection (FGI_MCV)
3.2.4. Local Maxima Finding with Varying Window Size (FGI_VWS)
3.3. Methods Used for Evaluation
3.3.1. Automated Matching Between Reference Models and Provided Models
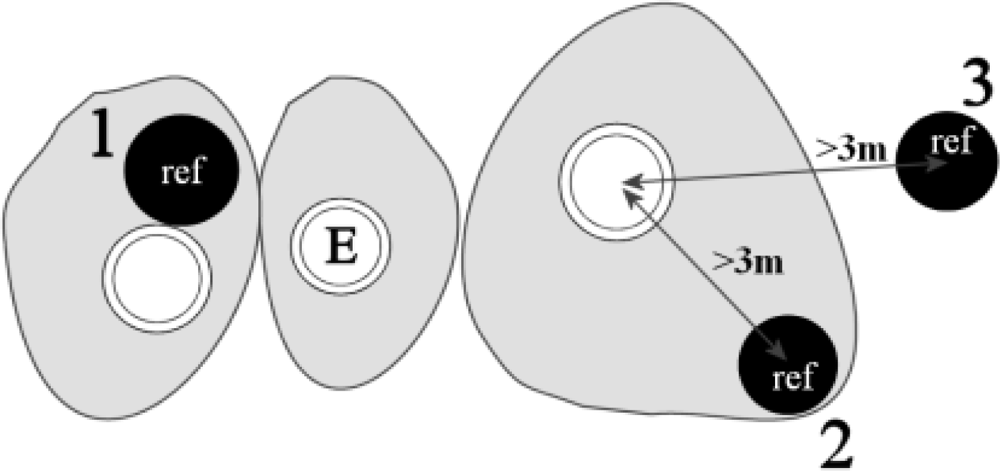
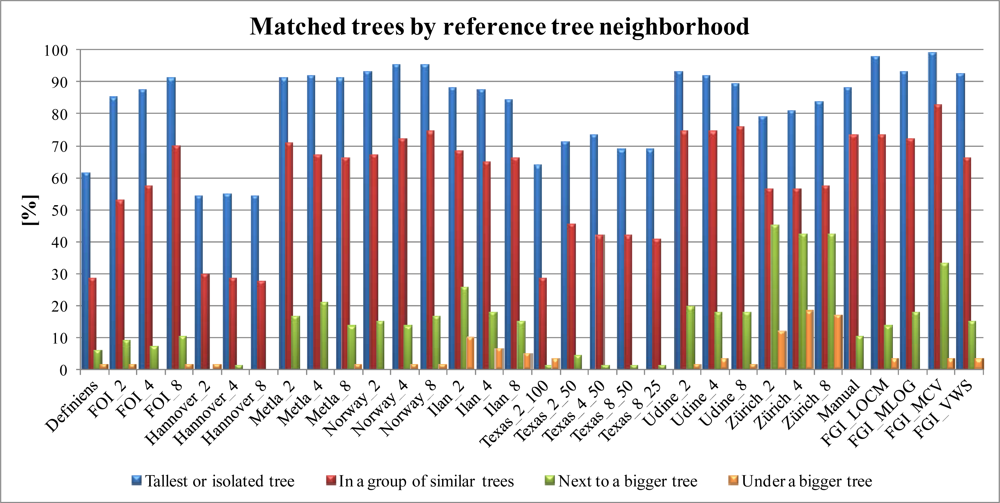
3.3.2. Impact of the Neighborhood
- Tallest tree in the neighborhood or isolated tree (neighbor distance in 2D over 3 m).
- Tree in a group of similar trees (neighbor within 3 m).
- Tree located next to a bigger tree.
- Tree under a bigger tree.
3.3.3. Matching Correctness and Commission and Omission Errors
- A matching tree was found in the model (within a distance of 3 m and the height difference less than 5 m, depending on the tree height and surroundings).
- Matching tree was not found (according to the criteria above), but a reference tree was within the model crown area.
- Matching tree was not found (according to the criteria above) and a reference tree was outside the model crown area (omission error).
3.3.4. Treatment of Outliers
4. Results and Discussion
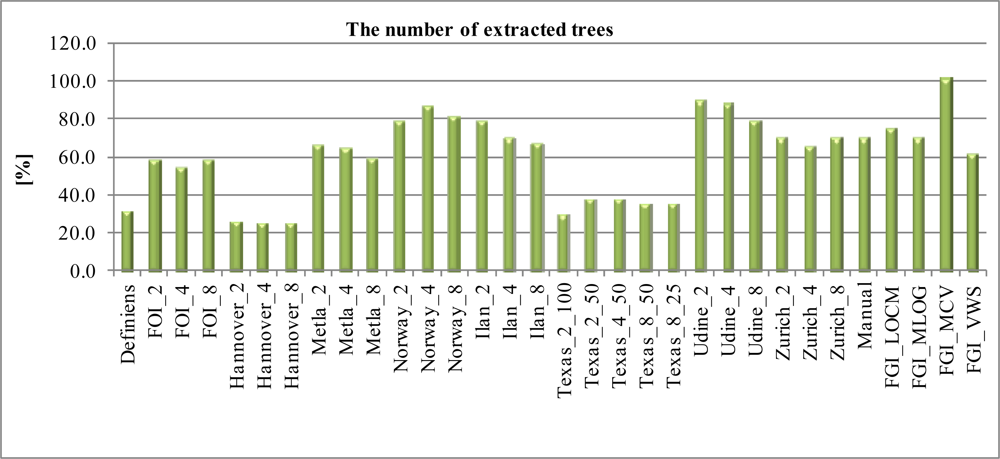
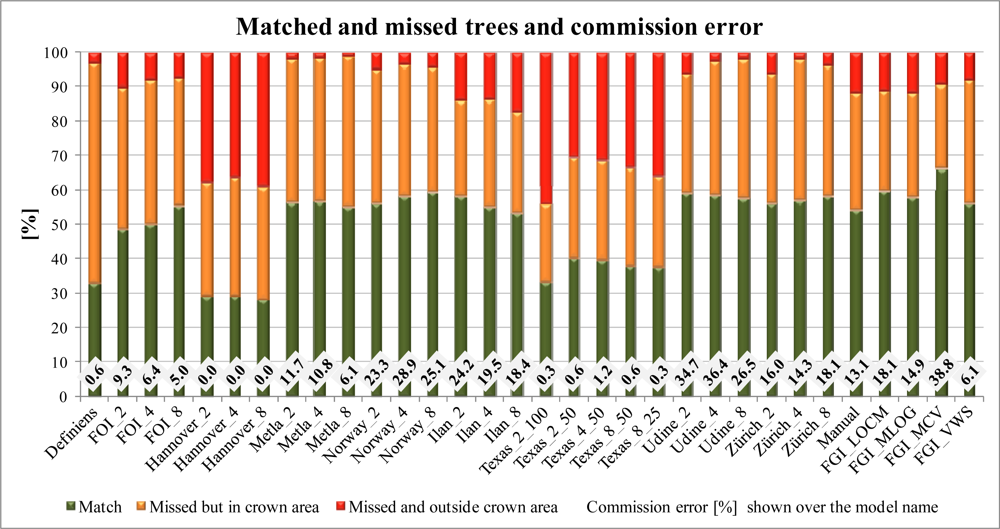
4.1. The Number of Extracted Trees
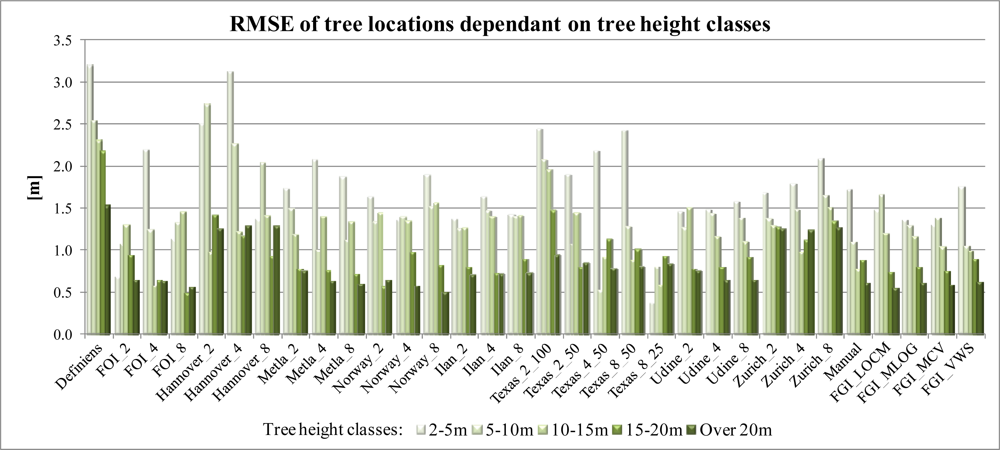
4.2. Accuracy of Determining Tree Location
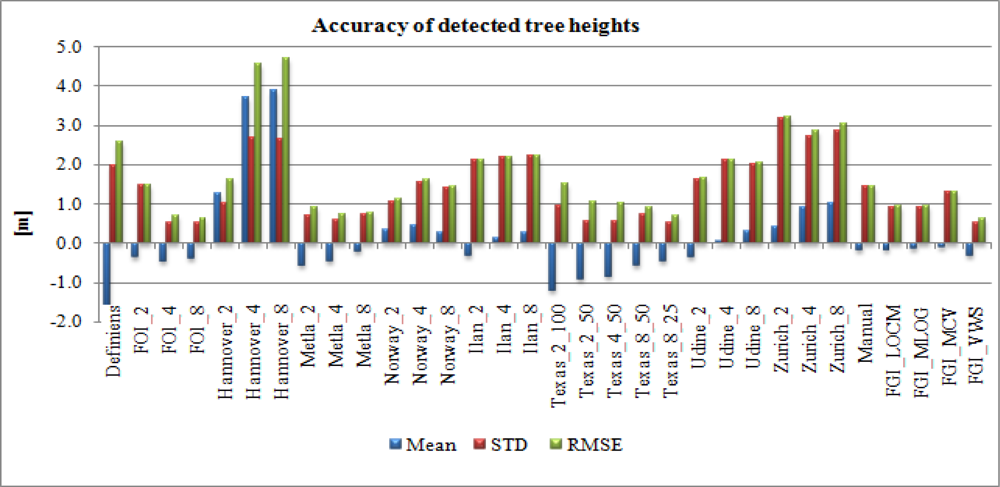
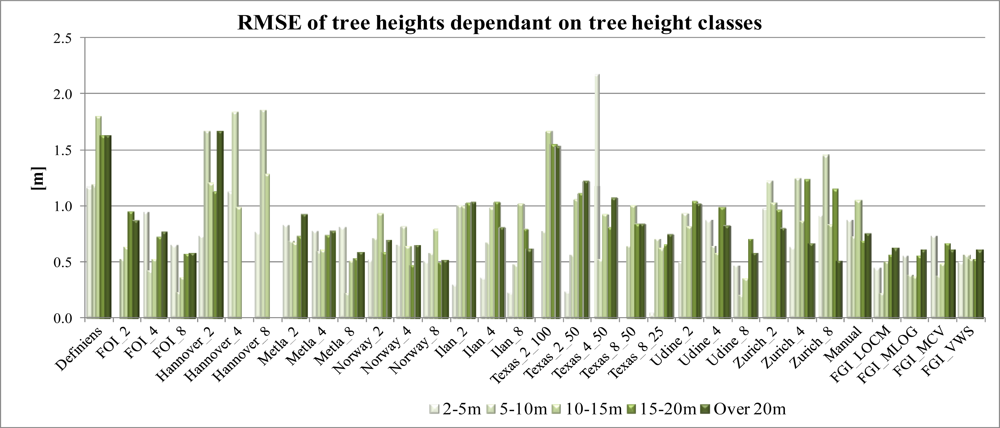
4.3. Accuracy of Tree Height
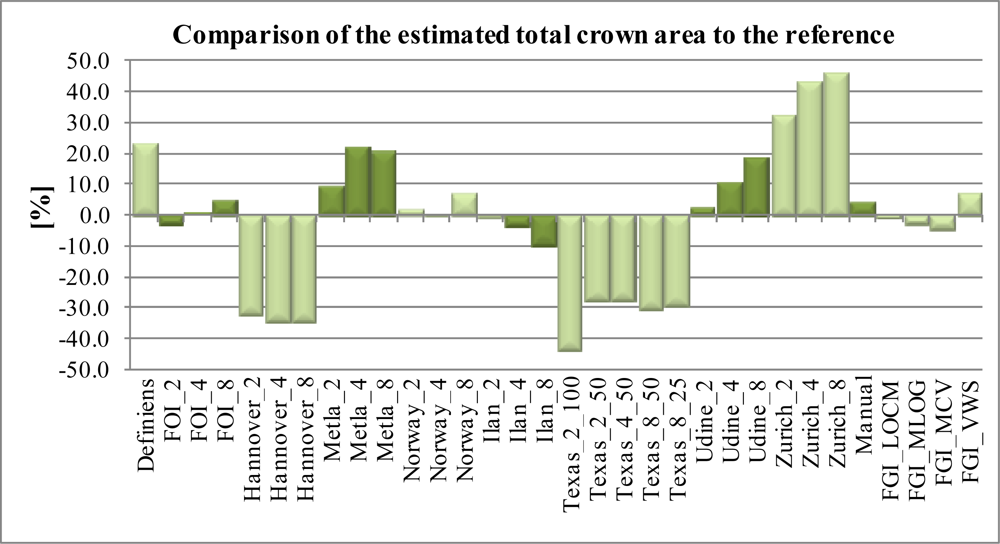
4.4. Crown Delineation Accuracy
5. Conclusions
Acknowledgments
References
- Solodukhin, V.I.; Zukov, A.J.; Mazugin, I.N. Laser aerial profiling of a forest. Lew. NIILKh. Leningrad. Lesnoe Khozyaistvo 1977, 10, 53–58. (in Russian). [Google Scholar]
- Nelson, R.; Krabill, W.; Maclean, G. Determining forest canopy characteristics using airborne laser data. Remote Sens. Environ 1984, 15, 201–212. [Google Scholar]
- Schreier, H.; Lougheed, J.; Tucker, C.; Leckie, D. Automated measurements of terrain reflection and height variations using airborne infrared laser system. Int. J. Remote Sens 1985, 6, 101–113. [Google Scholar]
- Nelson, R.; Krabill, W.; Tonelli, J. Estimating forest biomass and volume using airborne laser data. Remote Sens. Environ 1988, 24, 247–267. [Google Scholar]
- Maclean, G.A.; Krabill, W.B. Gross-merchantable timber volume estimation using an airborne lidar system. Can. J. Remote Sens 1986, 12, 7–18. [Google Scholar]
- Currie, D.; Shaw, V.; Bercha, F. Integration of Laser Rangefinder and Multispectral Video Data for Forest Measurements. Proceedings of IGARSS’89, Vancouver, BC, Canada, 10–14 July 1989; 4, pp. 2382–2384.
- Bernard, R.; Vidal-Madjar, D.; Baudin, F.; Laurent, G. Nadir looking airborne radar and possible applications to forestry. IEEE Trans. Geosci. Remote Sens 1987, 21, 297–309. [Google Scholar]
- Hallikainen, M.; Hyyppä, J.; Somersalo, E. Classification of Forest Types by Microwave Remote Sensing. Proceedings of EARSeL 9th General Assembly and Symposium, Espoo, Finland, 27 June–1 July 1989; pp. 293–298.
- Hyyppä, J.; Hallikainen, M.; Pulliainen, J. Accuracy of Forest Inventory Based on Radar-Derived Stand Profile. Proceedings of IGARSS’93, Tokyo, Japan, 18–21 August 1993; pp. 391–393.
- Hyyppä, J.; Hallikainen, M.; Hyyppä, H. A Scanning Ranging Radar for Forest Inventory. Proceedings of URSI/IEEE/IRC XXI National Convention on Radio Science 1996, Espoo, Finland, 2–3 October 1996; Report S 222. pp. 255–256.
- Hyyppä, J.; Hyyppä, H.; Inkinen, M. Capabilities of Multi-Source Remote Sensing for Forest Inventory. Proceedings of 3rd International Airborne Remote Sensing Conference and Exhibition, Copenhagen, Denmark, 7–10 July 1997.
- Kraus, K.; Pfeifer, N. Determination of terrain models in wooded areas with airborne laser scanner data. ISPRS J. Photogramm 1998, 53, 193–203. [Google Scholar]
- Vosselman, G. Slope Based Filtering of Laser Altimetry Data. Proceedings of XIXth ISPRS Congress Technical Commission III: Systems for Data Processing, Analysis and Representation, Amsterdam, The Netherlands, 16–23 July 2000. In International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences; ISPRS: Vienna, Austria, 2000; Volume 33, No. B3/2, pp. 935–942..
- Næsset, E. Determination of mean tree height of forest stands using airborne laser scanner data. ISPRS J. Photogramm 1997, 52, 49–56. [Google Scholar]
- Næsset, E. Estimating timber volume of forest stands using airborne laser scanner data. Remote Sens. Environ 1997, 61, 246–253. [Google Scholar]
- Hyyppä, H.; Hyyppä, J. Comparing the accuracy of laser scanner with other optical remote sensing data sources for stand attributes retrieval. Photogramm. J. Fin 1999, 16, 5–15. [Google Scholar]
- Hyyppä, J.; Inkinen, M. Detecting and estimating attributes for single trees using laser scanner. Photogramm. J. Fin 1999, 16, 27–42. [Google Scholar]
- Brandtberg, T. Automatic Individual Tree-Based Analysis of High Spatial Resolution Remotely Sensed Data. Ph.D. Thesis, Acta Universitatis Agriculturae Sueciae, Silvestria 118, Swedish University of Agricultural Sciences, Uppsala, Sweden, 1999.
- Ziegler, M.; Konrad, H.; Hofrichter, J.; Wimmer, A.; Ruppert, G.; Schardt, M.; Hyyppä, J. Assessment of forest attributes and single-tree segmentation by means of laser scanning. Proc. SPIE 2000, 4035, 73–84. [Google Scholar]
- Hyyppä, J.; Schardt, M.; Haggrén, H.; Koch, B.; Lohr, U.; Scherrer, H.U.; Paananen, R.; Luukkonen, H.; Ziegler, M.; Hyyppä, H.; et al. HIGH-SCAN: The first European-wide attempt to derive single-tree information from laserscanner data. Photogramm. J. Fin 2001, 17, 58–68. [Google Scholar]
- Brandtberg, T.; Warner, T.; Landenberger, R.; McGraw, J. Detection and analysis of individual leaf-off tree crowns in small footprint, high sampling density lidar data from the eastern deciduous forest in North America. Remote Sens. Environ 2003, 85, 290–303. [Google Scholar]
- Holmgren, J.; Persson, Å. Identifying species of individual trees using airborne laser scanning. Remote Sens. Environ 2004, 90, 415–423. [Google Scholar]
- Yu, X.; Hyyppä, J.; Kaartinen, H.; Maltamo, M. Automatic detection of harvested trees and determination of forest growth using airborne laser scanning. Remote Sens. Environ 2004, 90, 451–462. [Google Scholar]
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ 2002, 80, 88–99. [Google Scholar]
- Holopainen, M.; Vastaranta, M.; Rasinmäki, J.; Kalliovirta, J.; Mäkinen, A.; Haapanen, R.; Melkas, T.; Yu, X.; Hyyppä, J. Uncertainty in timber assortment estimates predicted from forest inventory data. Eur. J. For. Res 2010, 129, 1131–1142. [Google Scholar]
- Falkowski, M.; Smith, A.; Gessler, P.; Hudak, A.; Vierling, L.; Evans, J. The influence of the conifer forest canopy cover on the accuracy of two individual tree detection algorithms using lidar data. Can. J. Remote Sens 2008, 34, 1–13. [Google Scholar]
- Kaartinen, H.; Hyyppä, J. EuroSDR/ISPRS Project, Commission II “Tree Extraction”; Final Report; Official Publication no 53; EuroSDR (European Spatial Data Research): Dublin, Ireland, 2008. [Google Scholar]
- Vastaranta, M.; Holopainen, M.; Yu, X.; Hyyppä, J.; Mäkinen, A.; Rasinmäki, J.; Melkas, T.; Kaartinen, H.; Hyyppä, H. Effects of ALS individual tree detection error sources on forest management planning calculations. Remote Sens 2011, 3, 1614–1626. [Google Scholar]
- Holopainen, M.; Mäkinen, A.; Rasinmäki, J.; Hyyppä, J.; Hyyppä, H.; Kaartinen, H.; Viitala, R.; Vastaranta, M.; Kangas, A. Effect of tree level airborne laser scanning accuracy on the timing and expected value of harvest decisions. Eur. J. For. Res 2010, 29, 899–910. [Google Scholar]
- Persson, Å.; Holmgren, J.; Söderman, U. Detecting and measuring individual trees using an airborne laser scanner. Photogramm. Eng. Remote Sensing 2002, 68, 925–932. [Google Scholar]
- Leckie, D.; Gougeon, F.; Hill, D.; Quinn, R.; Armstrong, L.; Shreenan, R. Combined high-density lidar and multispectral imagery for individual tree crown analysis. Can. J. Remote Sens 2003, 29, 633–649. [Google Scholar]
- Straub, B. A Top-Down Operator for the Automatic Extraction of Trees: Concept and Performance Evaluation. Proceedings of the ISPRS Working Group III/3 Workshop ‘3-D Reconstruction from Airborne Laserscanner and InSAR Data’, Dresden, Germany, 8–10 October 2003; pp. 34–39.
- Popescu, S.; Wynne, R.; Nelson, R. Measuring individual tree crown diameter with lidar and assessing its influence on estimating forest volume and biomass. Can. J. Remote Sens 2003, 29, 564–577. [Google Scholar]
- Andersen, H-E.; Reutebuch, S.; Schreuder, G. Bayesian Object Recognition for the Analysis of Complex Forest Scenes in Airborne Laser Scanner Data. Proceedings of ISPRS Commission III, Symposium 2002 Photogrammetric Computer Vision, Graz, Austria, 9–13 September 2002. In International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences; ISPRS: Vienna, Austria, 2002; Volume 34, part 3A, pp. 35–41..
- Morsdorf, F.; Meier, E.; Kötz, B.; Itten, K. I.; Dobbertin, M.; Allgöwer, B. LIDAR-based geometric reconstruction of boreal type forest stands at single tree level for forest and wildland fire management. Remote Sens. Environ 2004, 3, 353–362. [Google Scholar]
- Wack, R.; Schardt, M.; Lohr, U.; Barrucho, L.; Oliveira, T. Forest Inventory for Eucalyptus Plantations Based on Airborne Laser Scanner Data. Proceedings of ISPRS Workshop 3-D Reconstruction from Airborne Laserscanner and InSAR Data, Dresden, Germany, 8–10 October 2003. In International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences; ISPRS: Vienna, Austria, 2003; Volume 34, Part 3/W13, pp. 40–46.
- Pitkänen, J.; Maltamo, M.; Hyyppä, J.; Yu, X. Adaptive Methods for Individual Tree Detection on Airborne Laser Based Canopy Height Model. Proceedings of ISPRS Workshop Laser-Scanners for Forest and Landscape Assessment, Freiburg, Germany, 3–6 October 2004. In International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences; ISPRS: Vienna, Austria, 2004; Volume 36, Part 8/W2, pp. 187–191..
- Yu, X.; Hyyppä, J.; Vastaranta, M.; Holopainen, M.; Viitala, R. Predicting individual tree attributes from airborne laser point clouds based on random forests technique. ISPRS J. Photogramm 2011, 66, 28–37. [Google Scholar]
- Heinzel, J.N.; Weinacker, H.; Koch, B. Prior-knowledge-based single-tree extraction. Int. J. Remote Sens 2011, 32, 4999–5020. [Google Scholar]
- Vauhkonen, J.; Ene, L.; Gupta, S.; Heinzel, J.; Holmgren, J.; Pitkänen, J.; Solberg, S.; Wang, Y.; Weinacker, H.; Hauglin, K.M.; et al. Comparative testing of single-tree detection algorithms under different types of forest. Forestry 2011. [Google Scholar] [CrossRef]
- Peuhkurinen, J.; Maltamo, M.; Malinen, J.; Pitkänen, J.; Packalén, P. Preharvest measurement of marked stands using airborne laser scanning. Forest Sci 2007, 53, 653–661. [Google Scholar]
- Falkowski, M.J.; Smith, A.M.S.; Gessler, P.E.; Hudak, A.T.; Vierling, L.A.; Evans, J.S. The influence of conifer forest canopy cover on the accuracy of two individual tree measurement algorithms using lidar data. Can. J. Remote Sens 2008, 34, 338–350. [Google Scholar]
- Vastaranta, M.; Kankare, V.; Holopainen, M.; Yu, X.; Hyyppä, J.; Hyyppä, H. Combination of individual tree detection and area-based approach in imputation of forest variables using airborne laser data. ISPRS J. Photogramm 2012, 67, 73–79. [Google Scholar]
- Axelsson, P. Ground Estimation of Laser Data Using Adaptive TIN Models. Proceedings of OEEPE Workshop on Airborne Laserscanning and Interferometric SAR for Detailed Digital Elevation Models, Stockholm, Sweden, 1–3 March 2001; Publication No. 40. pp. 185–208.
- Bilker, M.; Kaartinen, H. The Quality of Real-Time Kinematic (RTK) GPS Positioning; Reports of the Finnish Geodetic Institute; FGI: Masala, Finland, 2001; pp. 1–25. [Google Scholar]
- Wolf (né Straub), B.-M.; Heipke, C. Automatic extraction and delineation of single trees from remote sensing data. Machine Vis. Appl 2007, 18, 317–330. [Google Scholar]
- Solberg, S.; Næsset, E.; Bollandsås, O.M. Single-tree segmentation using airborne laser scanner data in a structurally heterogeneous spruce forest. Photogramm. Eng. Rem. Sensing 2006, 72, 1369–1378. [Google Scholar]
- Serra, J. Image Analysis and Mathematical Morphology; Academic Press: London, UK, 1982; Volume 1. [Google Scholar]
- Serra, J. Image Analysis and Mathematical Morphology: Theoretical Advances; Academic Press: London, UK, 1988; Volume 2. [Google Scholar]
- Maltamo, M.; Peuhkurinen, J.; Malinen, J.; Vauhkonen, J.; Packalén, P.; Tokola, T. Predicting tree attributes and quality characteristics of Scots pine using airborne laser scanning data. Silva Fennica 2009, 43, 507–521. [Google Scholar]
- Vauhkonen, J.; Korpela, I.; Maltamo, M.; Tokola, T. Imputation of single-tree attributes using airborne laser scanning-based height, intensity, and alpha shape metrics. Remote Sens. Environ 2010, 114, 1263–1276. [Google Scholar]
- Hyyppä, J.; Yu, X.; Hyyppä, H.; Vastaranta, M.; Holopainen, M.; Kukko, A.; Kaartinen, H.; Jaakkola, A.; Vaaja, M.; Koskinen, J.; Alho, A. Improved forest inventory using penetrated Hits and data fusion at feature level. Remote Sens 2012. submitted. [Google Scholar]
- Hyyppä, J.; Mielonen, T.; Hyyppä, H.; Maltamo, M.; Honkavaara, E.; Yu, X.; Kaartinen, H. Using Individual Tree Crown Approach for Forest Volume Extraction with Aerial Images and Laser Point Clouds. Proceedings of The ISPRS Workshop Laser Scanning 2005, Enschede, The Netherlands, 12–14 September 2005. In International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, ISPRS: Vienna, Austria, 2005; Volume 36, Part 3/W19, pp. 144–149..
- Hyyppä, J.; Yu, X.; Hyyppä, H.; Maltamo, M. Methods of Airborne Laser Scanning for Forest Information Extraction. Presented at Workshop on 3D Remote Sensing in Forestry, Vienna, Austria, 14–15 February 2006; CD-ROM. p. 16.
- Lindberg, E.; Holmgren, J.; Olofsson, K.; Wallerman, J.; Olsson, H. Estimation of tree lists from airborne laser scanning by combining single-tree and area-based methods. Int. J. Remote Sens 2010, 31, 1175–1192. [Google Scholar]
- Breidenbach, J.; Næsset, E.; Lien, V.; Gobakken, T.; Solberg, S. Prediction of species specific forest inventory attributes using a nonparametric semi-individual tree crown approach based on fused airborne laser scanning and multispectral data. Remote Sens. Environ 2010, 114, 911–924. [Google Scholar]
- Vastaranta, M.; Holopainen, M.; Yu, X.; Haapanen, R.; Melkas, T.; Hyyppä, J.; Hyyppä, H. Individual tree detection and area-based approach in retrieval of forest inventory characteristics from low-pulse airborne laser scanning data. Photogramm. J. Fin 2011, 22, 1–13. [Google Scholar]


| Acquisition | 29 June 2004 |
| Instrument | Optech ALTM 2033 |
| Flight altitude | 600 m |
| Pulse frequency | 33,000 Hz |
| Field of View | ±9 degrees |
| Measurement density | 2 points per m2 per echo per strip |
| Swath width | 185 m |
| Mode | First and last pulse |
| Species | % | Tree Height (m) | ||
|---|---|---|---|---|
| Mean | Max. | Std. | ||
| Scots pine | 20 | 11.2 | 22.9 | 7.3 |
| Norway spruce | 46 | 14.2 | 25.5 | 6.7 |
| Birch | 15 | 20.3 | 27.2 | 5.3 |
| Other deciduous | 19 | 10.2 | 25.6 | 7.1 |
| Method | Partner | Country |
|---|---|---|
| Definiens | Definiens AG | Germany |
| FOI | Swedish Defense Research Agency | Sweden |
| Hannover | Leibniz Universität Hannover | Germany |
| Metla | Finnish Forest Research Institute | Finland |
| Norway | Norwegian Forest and Landscape Institute and Norwegian University of Life Sciences | Norway |
| Ilan | National I-Lan University | Taiwan |
| Texas | Texas A&M University | USA |
| Udine | University of Udine | Italy |
| Zürich | University of Zürich | Switzerland |
Share and Cite
Kaartinen, H.; Hyyppä, J.; Yu, X.; Vastaranta, M.; Hyyppä, H.; Kukko, A.; Holopainen, M.; Heipke, C.; Hirschmugl, M.; Morsdorf, F.; et al. An International Comparison of Individual Tree Detection and Extraction Using Airborne Laser Scanning. Remote Sens. 2012, 4, 950-974. https://doi.org/10.3390/rs4040950
Kaartinen H, Hyyppä J, Yu X, Vastaranta M, Hyyppä H, Kukko A, Holopainen M, Heipke C, Hirschmugl M, Morsdorf F, et al. An International Comparison of Individual Tree Detection and Extraction Using Airborne Laser Scanning. Remote Sensing. 2012; 4(4):950-974. https://doi.org/10.3390/rs4040950
Chicago/Turabian StyleKaartinen, Harri, Juha Hyyppä, Xiaowei Yu, Mikko Vastaranta, Hannu Hyyppä, Antero Kukko, Markus Holopainen, Christian Heipke, Manuela Hirschmugl, Felix Morsdorf, and et al. 2012. "An International Comparison of Individual Tree Detection and Extraction Using Airborne Laser Scanning" Remote Sensing 4, no. 4: 950-974. https://doi.org/10.3390/rs4040950
APA StyleKaartinen, H., Hyyppä, J., Yu, X., Vastaranta, M., Hyyppä, H., Kukko, A., Holopainen, M., Heipke, C., Hirschmugl, M., Morsdorf, F., Næsset, E., Pitkänen, J., Popescu, S., Solberg, S., Wolf, B. M., & Wu, J.-C. (2012). An International Comparison of Individual Tree Detection and Extraction Using Airborne Laser Scanning. Remote Sensing, 4(4), 950-974. https://doi.org/10.3390/rs4040950









