1. Introduction
Satellite observations play an important role for global monitoring and characterization of the atmosphere and terrestrial environment in relation with Earth system science. In these studies, multi-year to multi-decadal observation records are often required to detect changes that have occurred or are occurring, and to identify trends and causes of those changes. In order to continue long-term satellite observations effectively, an interdisciplinary approach in the framework of interagency and international cooperation is indispensable.
In the field of ocean studies, a NASA program, Sensor Intercomparison and Merger for Biological and Interdisciplinary Oceanic Studies (SIMBIOS) [
1], has been operating for the integration of information from multiple satellite ocean color sensors. SIMBIOS involves extensive efforts of collection, processing, archival, and documentation of calibration datasets from multiple sensors to ultimately eliminate incompatibilities among sensor data across multiple missions [
2]. For land studies, numerous efforts have been made to continue and extend the long-term dataset acquired by the Advanced Very High Resolution Radiometer (AVHRR) sensor series with current and future sensors such as Moderate Resolution Imaging Spectroradiometer (MODIS), Vegetation (VGT), Medium Resolution Imaging Spectrometer (MERIS), and Visible Infrared Imaging Radiometer Suite (VIIRS) onboard the National Polar-orbiting Operational Environmental Satellite System Preparatory Project (NPP) platform and planned for the Joint Polar Satellite System (JPSS).
Generation of such long-term observation records by merging multiple sensor data requires a considerable amount of scientific investigations on data continuity and compatibility due to differences in both hardware and software configurations, e.g., sensor/platform characteristics and processing algorithms [
3–
9]. Systematic differences in VI products among sensors [
10] are one such problem to be resolved. Instrument spectral band-pass filters (BPFs) are one of the factors that induce systematic differences in reflectance and VIs across sensors where this paper is aimed to contribute.
Sensor calibration, including both pre- and post-launch absolute calibration and sensor cross calibrations, has been a major issue and intensively studied by numerous researchers [
11–
19]. In recent years, several studies were conducted to simulate broad AVHRR bands using a weighted sum of several narrow bands of new sensors for continuity and compatibility, especially, of the NDVI [
20]. Gitelson and Kaufman [
21] introduced a MODIS NDVI optimization method where the MODIS red-channel was adjusted by adding the MODIS green-channel with the weight optimized to fit the broader AVHRR visible channel. Gao [
22] proposed a practical technique of simulating AVHRR NIR reflectance from MODIS by combining the MODIS NIR channel with the water vapor-sensitive MODIS 0.941
μm channel. A similar approach can also be seen in their earlier work [
23] for the purpose of water-vapor correction in Hyperspectral data from AVIRIS known as the atmospheric removal (ATREM) program. Gunther and Maier [
24] used multiple MERIS bands to simulate AVHRR red and NIR channels with the goal of deriving an AVHRR-compatible NDVI. An assumption underlaying those approaches is that one sensor’s output can be modeled by a weighted sum of several channels.
More recently, a modeling study was reported by Trinshchenko
et al. [
10] to evaluate the effects of BPFs on surface reflectance and NDVI measured with AVHRR, MODIS, Global Imager, and Vegetation. They showed that surface reflectance and NDVI were both sensitive to the sensor’s BPF across various surface types and atmospheric conditions and concluded that the differences in surface reflectance and NDVI caused by the differences in BPFs are too large to neglect and, thus, need to be adjusted in particular for the purpose of consistent long-term monitoring of the Earth’s environment by multiple satellite sensors. In their study, relationships of two NDVI values measured with different sensors were modeled by a second order polynomial.
One common aspect in the studies by Gitelson and Kaufman [
21], Gao [
22], and Trinshchenko
et al. [
10] is that outputs from one sensor can be modeled by another with a certain functional form,
i.e., polynomials and weighted sums. Validity of using such functional forms which describe the relationships needs to be investigated solely from a theoretical point of view. This should also serve for better understanding of the fundamentals of multi-sensor VI continuity/compatibility.
This study is aimed at analytically providing a theoretical justification on and a functional form of inter-sensor VI relationship. In order to ensure the integrity of the derivation steps, a part of this work is devoted to provide comprehensive overview of our preliminary results [
25–
28]. Our approach is to use vegetation isoline equations which describe the relationships between two reflectances measured at different wavelengths for both the top-of-canopy reflectances [
29,
30] and the top-of-atmosphere reflectances [
31]. Its applications has been reported for several purposes [
32–
34].
In the reminder of this paper, we first introduce our basis of VI-to-VI relationships along with a brief review of the vegetation isoline equations in Section 2. We then introduce a derivation process of a relationship between two-band VIs in a general form in Section 3. The generalized process is then extended to the case of three-band VIs in the same section. The next three sections are devoted to explain its applicability by considering actual VI models. The first case is the relationship of two NDVIs computed from two pairs of reflectance measured at different pairs of wavelength and present the derived functional form in Section 4. The derivation is further applied to the soil adjusted VI [
35] and two-band enhanced VI [
36] in Section 5, and finally, EVI-like model [
37] as a representative of three-band VI in Section 6. Discussions and conclusions are provided in Sections 7 and 8, respectively.
2. Approach Based on Vegetation Isolines
Numerous kinds of VIs have been proposed by many researchers and routinely used for various purposes. Although those indices vary in form to some extent, the ultimate goal is to design an index sensitive only to vegetation biophysical and biochemical attributes [
38] such as biomass, leaf area index (LAI), fraction of green coverage, leaf angle distribution function, fraction of absorbed photosynthetically active radiation, and leaf chemical contents. Therefore, in nature, a VI should show a strong correlation to, at least, one of these attributes. Our approach of relating two VIs also assumes such implicit, strong correlations between VIs and biophysical parameters.
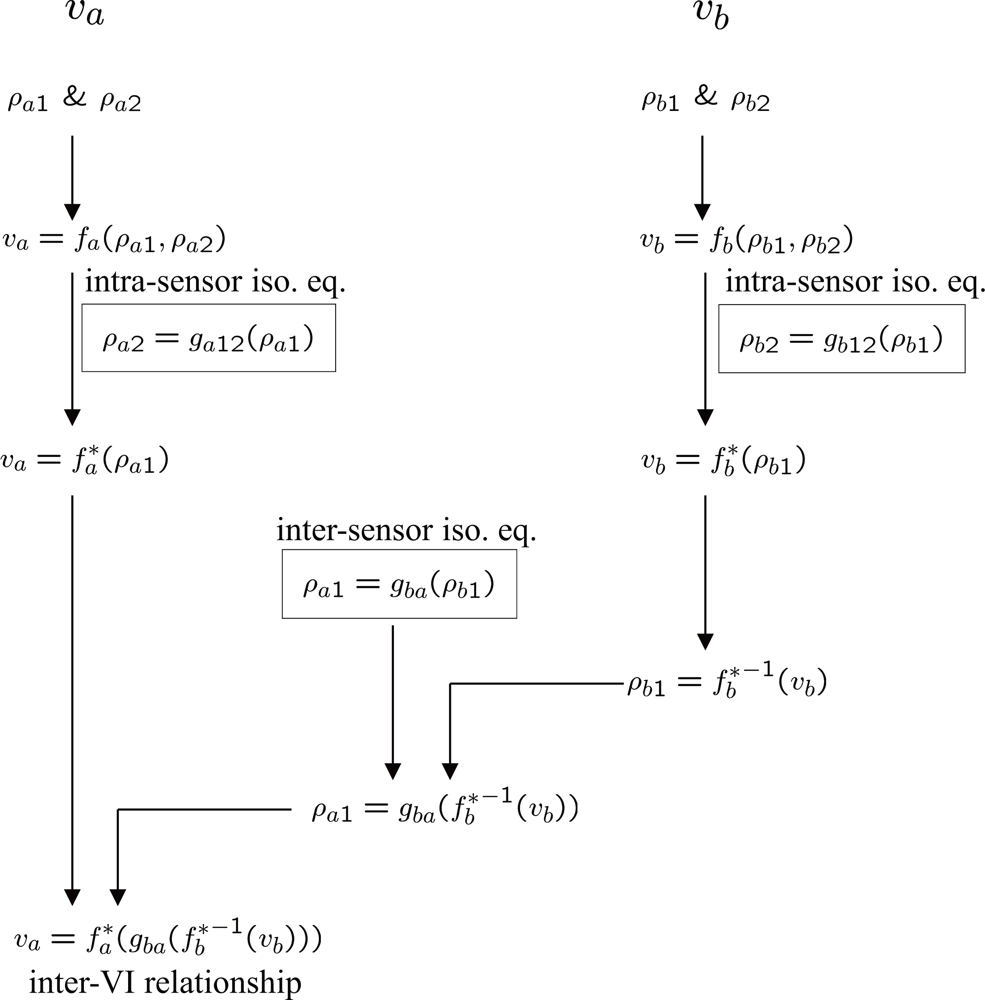
From the data continuity point of view, finding NDVI-to-NDVI relationships across multiple sensors is the issue to be addressed, especially for continuation of AVHRR broader bands observations with narrower bands of new sensors. Hence, in this study, we assume the conditions that either of two VIs, for which to derive an VI-to-VI relationship, do not have a derived explicit relationship with any biophysical parameters and that the spectral band passes used to compute VIs are not identical among sensors (e.g., AVHRR channel 1 vs. MODIS band 1).
In order to derive a relationship between two VIs of different sensors under such conditions, we need to relate any two variables used in the VI model equations either implicitly (i.e., about biophysical parameters) or explicitly (e.g., about reflectances). The latter approach is taken here: We relate two VIs based on the analytical relationships of two reflectances used in VI model equation. The relationships of two reflectances at different wavelengths are represented by vegetation isoline equations derived in our previous work.
The isoline equation is written by [
31]
Since details of the isoline equation and its derivation were already provided in [
31], here we explain the equation briefly. The reflectances
ρ at two wavelengths,
λ1 and
λ2, are related by the above equation as a function of biophysical parameters represented by
Cv, atmospheric conditions,
Ca, and soil conditions,
Cs.
A(
λ1,
λ2,
Cv, Ca) and
D(
λ1,
λ2,
Cv, Ca) represent slope and offset of the isoline, respectively. Note that these isoline parameters are independent of the soil status,
Cs, but functions of a soil line slope and offset. Thus, they are independent of the soil brightness. The last term in the isoline equation (
O2) represents the contributions of the higher order interactions between the two boundary layers, namely, the atmospheric and canopy layer, and the canopy and soil layer. As was discussed in [
31], the contributions of those higher order terms are up to 5%, depending on the soil brightness and the optical thickness of the canopy layer. In this paper, for the purpose of brevity, the higher order interaction term will be implicitly included in the offset,
D. The isoline equations are the key information that connects two VIs of different sensors and allows us to derive such a relationship analytically. The next section illustrates our approach in a general form. The generalized derivation is then applied to the case of NDVI-to-NDVI relationship and two other cases later in this work.
4. Inter-Sensor NDVI Relationship
In this section we introduce an application of the above derivation to the case of inter-sensor NDVI relationship [
25,
26]. Note that, since we focus on the NDVI relationship, we assume that the reflectances of channel-1 and -2 are employed for both sensors, which is reflected in the subscripts of the reflectances for sensor-b.
The NDVI for sensor-a,
va, is written by
The first isoline equation, which relates
ρa1 and
ρa2 is then denoted by,
where
Aa,12 and
Da,12 are the isoline slope and offset, respectively, for the two channels of sensor-a.
Equation (19) is an analytical expression of intra-sensor vegetation isolines that can be observed in the red-NIR reflectance space.
Similarly, the NDVI observed by sensor-b,
vb, is written by
ρb1 and
ρb2 as
By repeating the same procedure described above,
ρb2 is eliminated from the equation by using the second isoline equation, or the intra-sensor isoline equation between
ρb1 and
ρb2,
and
where
From the relationship between
ρb1 and
vb, we write
ρb1 in terms of
vb,
The third isoline equation that relates
ρa1 and
ρb1, represented by
gba,1, is
Substituting
Equation (26) into
(27), we have
From
Equations (20) and
(28), we obtain a relationship between
va and
vb as
and
where
Equation (29) is an isoline-based NDVI translation equation with the four coefficients which are actually a function of the vegetation isoline parameters in similar form. The derived translation equation indicates an important fact: its coefficients may vary with optical properties of the atmosphere and vegetation layers. Note that the derivation has been performed on the first-order approximated form of vegetation isoline (
Equation (1)); a more accurate translation equation could be a ratio of higher order polynomials.
5. Inter-Sensor Relationship of SAVI/EVI2-Like Two-Band Model
In this section we extend one of our early work [
26] (about the case of SAVI [
35]) to the case of EVI2-like model [
36]. Their VI model equations can be written in a common form as the following
where
ki’s are the coefficients unique to each index. The derivation is proceeded on the following scaled form, instead of
va for brevity
Using the first isoline equation (
Equation (19)),
v′a becomes
with the new definitions of
and
D′a,12and
Note that
and
Da,12 remain the same (see
Equations (21) and
(19), respectively).
Similarly, using the second isoline equation, the rescaled VI value observed by sensor-b,
v′b, is written by
with the definitions of
and
D′b,12,
and
The inter-sensor VI relationship for SAVI/EVI2-like indices is obtained from
Equations (37) and
(40), and the third isoline equation (
Equation (27)) symbolically as
and the final form becomes
or
where
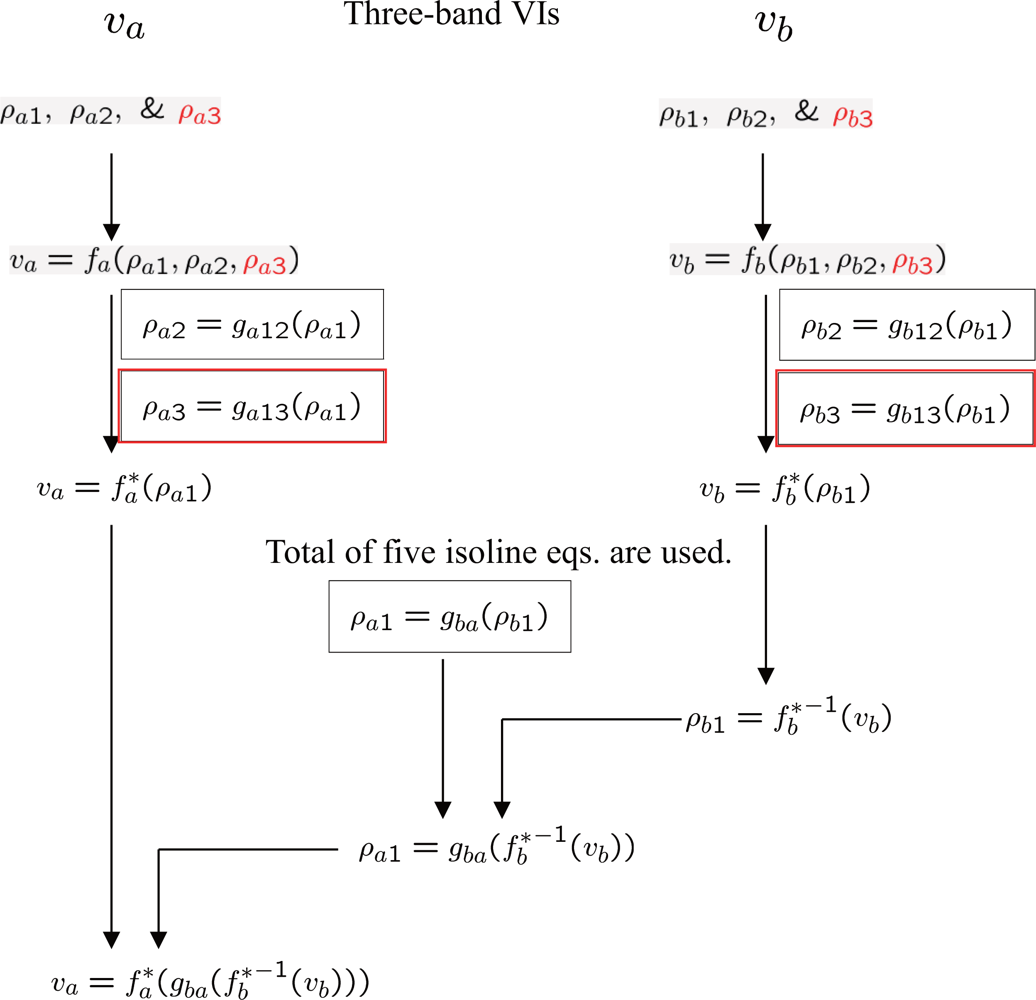
6. Inter-Sensor Relationship of EVI-Like Three-Band Model
In this section we further extend the derivation steps to the case of three-band VI, specifically to relate EVI-like indices from two sensors. The general form of EVI-like model can be written by
where
ki’s are the coefficients unique to each EVI-like model. By following the similar steps explained in the previous section, the derivation is proceeded using the scaled form, instead of
va for brevity,
The two intra-sensor isoline equations for sensor-a are
Equations (19) and a newly defined relationship
Using the two isoline equations,
v′a becomes
with the new definitions of
and
D′a,123,
and
Note that
and
Da,12 remain the same (see
Equations (21) and
(19), respectively).
Similarly, using the two intra-sensor isoline equations for sensor-b, namely
Equations (23) and the following newly defined isoline
the rescaled VI value observed by sensor-b,
v′b, is written by
with the definitions of
and
D′b,123,
and
The inter-sensor VI relationship for EVI-like indices is obtained from
Equations (53) and
(57), and the inter-sensor isoline equation (
Equation (27)). The final form becomes
or
where
7. Discussion
In general, there are three factors to consider for monitoring of vegetation status with optical sensors. One factor is the sensor spatial and temporal resolutions to meet specific monitoring requirements. However, a particular choice of the spatial and temporal resolutions comes with a particular sensor with its specific spectral bandpasses. For example, MODIS is one choice for high temporal resolution monitoring while ASTER is a choice of sensor for high resolution monitoring; however, these sensors’ red and NIR spectral bandpasses are different. Another factor is the index formulation (NDVI, SAVI, etc.), whether to meet required accuracy in capturing biophysical parameters of interest. The last factor is the band selection. While red and NIR spectral bands have been the most widely used combination, a green channel for example may be an alternative to the red as reported in [
21].
If we limit our discussions to the spectral aspect, it is the combination of bandpasses and VI equations that characterize VI-to-VI relationships. The derivation and derived equations relating two VIs presented in this study should be applicable to many possible combinations of various bandpasses and VI equations. The reason is that the general form of relationships,
Equation (11), does not assume any particular choices in the three factors (
i.e., sensors, VI equations, and spectral bands).
The NDVI translation equation,
Equation (29), was derived as an example application of
Equation (11).
Equation (29) tells the relationship between two NDVIs at some constant biophysical and atmospheric condition,
i.e., a constant LAI value and a constant atmospheric optical thickness. This is because the
h functions in the NDVI translation equation are a function of LAI and atmospheric optical thickness. If the NDVI shows a one-to-one relationship with LAI, or in other words if NDVI is free from soil influences, the
h functions become a function of the NDVI and atmospheric optical thickness. If the atmosphere is constant in addition, the translation equation further reduces to be a function only of NDVI. In this case, the final form of the translation equation can be approximated as a ratio of two polynomials with NDVI (of sensor-b). However, since NDVI is influenced by the soil brightness to some extent, any translation equation that uses NDVI as the only parameter cannot eliminate variations caused by the soil brightness. From practical point of view, if one can correlate soil brightness-induced variations, the ratio of two polynomials may be one choice of the form of translation equation. The orders of these polynomials and their coefficients should be determined using actual datasets.
Our results that the h functions which determine the actual form of the translation of two VIs depend on LAI (and atmospheric conditions as well) have several important implications. First, VI-to-VI relationships change with soil brightness, biophysical, and atmospheric conditions. Even after the accurate and precise atmospheric correction, the other two parameters remain undetermined. It should be noted that the relationship derived in this work as a VI translation equation eliminates the soil brightness effect by utilizing the vegetation isoline equation. However, we still need to determine at least one more parameter, such as LAI, to minimize the variations in VI relationships. Although it is desirable to have an estimation of LAI, such an estimation is often done by using the VI itself. Moreover, the purpose of computing VI is mainly to estimate such a biophysical parameter. Therefore, it is quite reasonable to assume that LAI estimation is not available before the VI computation. As a consequence, it sounds impossible to eliminate the variance by the soil brightness. Nevertheless, there is a possibility to do so by using an independent parameter alternative to LAI. One requirement for such a parameter is using another vegetation index than the target VI which shows stronger correlation with LAI. For example, utilizing one additional VI, the h functions could be approximated by the index. This possibility should be investigated solely.
8. Conclusions
An analytical form of relationship between spectral vegetation indices (VI) has been derived by using three of the vegetation isoline equations for the two-band case, and five isoline equations for the three-band case. The derivation steps were first introduced and explained conceptually by assuming a general functional form of VI model equation. This universal technique of the derivation with the isoline equations was then applied to the case of inter-NDVI relationship to identify functional form that is suitable to approximating the relationship. It was found that a rational function with two linear polynomials is appropriate, from analytical point of view, to approximate the relationship between the NDVIs from two sensors of different BPFs. The derivation technique was also applied to the SAVI/EVI2-like form and EVI-like three-band form of VI model equation. The derived expressions also indicate that the same functional form as the case of NDVI is relevant to model the relationships of such VIs.
Since this study clearly indicates the fact that the inter-VI relationships can be written by a rational function, one can chose such a functional form as a good candidate to model or determine the relationships, in practice, between the VIs from actual satellite data of two different sensors. In this connection, the derived expressions are useful from practical point of view. Further investigations are definitely needed to numerically demonstrate the validity of the derived expressions prior to practical applications of cross calibration of actual satellite data in the framework of continuity and compatibility studies.