1. Introduction
Information about individual tree species can be extremely beneficial when estimating many forest resource values, such as timber value, habitat quality, or susceptibility to loss. Unfortunately, detection of individual tree species using remote sensing (RS) data has proven to be a difficult task to accomplish. The species of a tree is only one of several factors that affect the realized shape and color of an individual tree crown. Other factors such as terrain, environment, competition, and genetic variation have large influences as well. As a result, for most variables that one can measure from RS data, there is significant distributional overlap between species, for instance (Figure 4 in [
1]) and (Figure 3 in [
2]). Due to the difficulty of obtaining sufficient classification accuracy, species information is commonly disregarded or alternative methods are found [
3]. One such alternative is to impute species information from the ground data observations best matching each identified crown segment [
4,
5]. This technique is a step forward, but further improvement should be possible.
Knowledge of the probable species of individual crown regions identified in the data would enable us to stratify model estimates by species. This will most likely increase precision in any stand-level estimates of interest. With this goal in mind, researchers have continuously tested new forms of RS data seeking improvements in detecting stand- and individual tree-level species information. As RS technology and computer algorithms have improved, so have the classification results achieved.
With the advent of scanning Lidar, many aspects of a forest inventory can now be accomplished using the aerial form of this data [
6,
7]. Even more recently, the abilities of terrestrial Lidar scanners for forest inventory are also being investigated [
8,
9]. While multi-spectral [
10] and hyperspatial [
11] imagery products have traditionally enabled the identification of individual tree species, the cost of additional datasets is likely to challenge budget constraints. Ideally, the use of a Lidar dataset alone would be sufficient to achieve the necessary species identification accuracy.
Many authors have investigated the potential of Lidar data for species classification. Sometimes Lidar is mixed with additional data sources, such as color or multi-spectral imagery [
12–
17]. Because each individual situation presents a unique arrangement of challenges, the overall results have been mixed. While the number of variables one can compute from discrete point Lidar data is infinite, there are only a few concepts that can be represented by these variables. These concepts are: crown density, crown shape, crown surface texture, and received energy from individual peaks. Most authors have incorporated variables from more than one of these concepts.
Crown density describes the leaf and branch size and arrangement and is typically measured using the proportions of the returns hitting vegetation versus those hitting the ground [
2,
18]. Crown shape information is often compared using parameters of surface models fit over the top of the Lidar point cloud [
19–
21]. The distribution of return heights, often described using select percentiles of the return heights [
1,
22], includes information about both crown density and crown shape. Crown surface texture refers to the roughness of a tree crown, and has been measured using a canopy height model [
19]. The instantaneous light energy received by the sensor when each peak is detected is typically referred to as intensity. The measured intensity is affected by several physical traits such as leaf size, chemistry, and incident angle, which are all affected by species. While most authors incorporate this intensity information, both Ørka
et al. [
23] and Kim
et al. [
24] found that intensity alone could be a reasonable predictor of species.
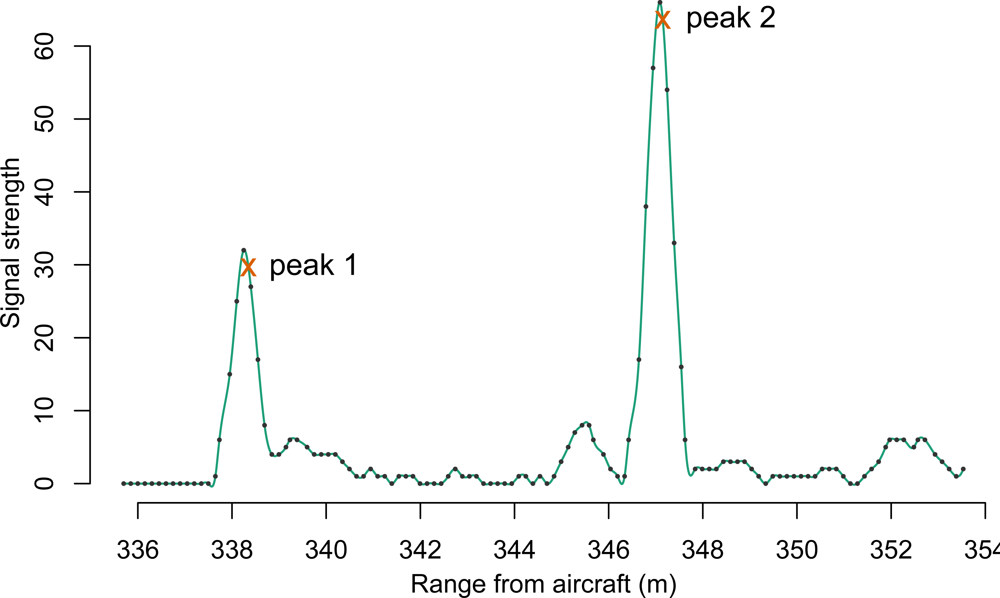
In the last half-decade, a newer format of Lidar information, commonly referred to as “waveform” or “fullwave” Lidar, has slowly increased in availability. In contrast to the more common discrete point Lidar systems, this newer Lidar system takes advantage of increased processor speeds and data storage capacity by digitally sampling at a high rate the return signal received at the sensor. The result mimics the appearance of a wave, and an example of such a waveform can be seen in
Figure 1. For comparison, if the waveform shown in
Figure 1 were to be passed through an onboard peak detector, the result might resemble the two exes immediately following the peak crests.
While a few authors have looked to waveform data for improving classification accuracy the first step has always been to decompose the waveforms into discrete peaks. One advantage of this technique is that information about peak shape can be preserved. The shapes of these peaks have successfully been used in distinguishing vegetation from other surfaces [
25] and in distinguishing the roughness of surfaces [
26]. Additionally, pulse width or cross section information has been helpful in classifying deciduous from coniferous species [
20,
27]. Little work has been done, however, to see if patterns within the original waveform data, prior to peak decomposition, provide information for species classification.
In a previous paper [
28], we showed that Fourier transformation of the waveforms crossing each crown led to moderate accuracy while classifying three hardwood species. In this work, no two-or three-dimensional information about crown structure computed from a discrete point array was included. However, the amplitude of a rather high frequency component of the Fourier transforms played an important role in distinguishing two of the species. This frequency was high enough that even high-density discrete point Lidar data could not contain such information. The purpose of this paper is to validate the results of the original paper as well as further test the importance of waveform Lidar in determining tree species. The latter is done by testing classification performance both before and after the addition of waveform information to a full suite of crown density, crown shape, crown surface texture and intensity metrics.
2. Methods
2.2. Crown Segmentation and Field Data Collection
Our field data were collected in a slightly different manner as one would collect information if an inventory was required. We segmented tree crowns from the Lidar data prior to visiting the field so that we could verify that each tree matches its associated data segment. Several trees of five species were collected in this manner to ensure that our data were as clean as possible. This segmentation and field data collection took part in three steps:
All waveforms were deconvolved and then decomposed into individual peaks using a simple peak-detection algorithm. This point information was indexed into a voxel array structure.
A segmentation algorithm was used on the voxel array data to map the volume of space occupied by individual tree crowns into clusters of voxels.
Outlines of these clusters were used to locate the trees on the ground and identify the species.
2.2.2. Peak Detection and Creation of the Voxel Array
A simple peak finding algorithm was performed on the waveform data after deconvolution with the Richardson–Lucy algorithm. The range at maximum for each peak found within the waveforms was used to compute an x, y, z position. Two additional pieces of information were kept for each peak. First was the total energy of the peak, or the sum of the intensity values for all waveform samples occurring during the defined peak. Second, we recorded the total range duration of the peak. The peak-finding algorithm had the following steps:
Decide on Mmin, the minimum size of a peak that will be recorded
Set D0 =0
d = ψ2 − ψ1. If d2 > 0.01 then D1 = d, otherwise D1 =0.
Set M = 0, P = FALSE
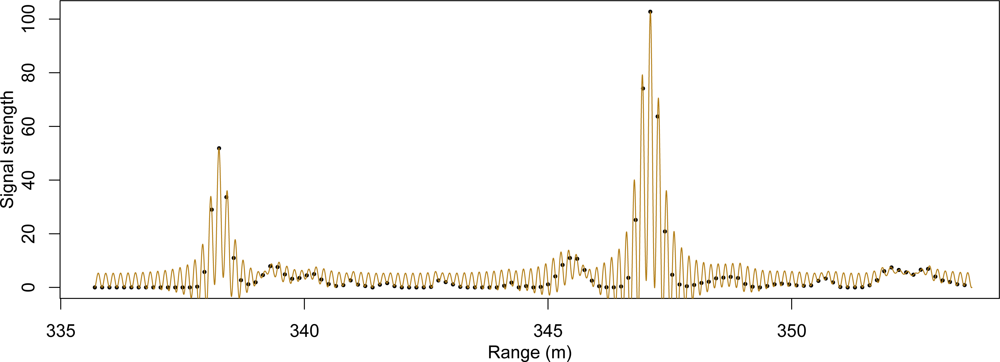
This process resulted in a fairly heavy discrete point dataset, with an average of 104 points per square meter within tree vegetation. An visual example of this data is presented in
Figure 3. We used a three-dimensional (voxel) grid overlaid on the volume of interest with horizontal dimensions set at one meter each and vertical dimension set at 0.75 m. A single file was created to contain the grid location of all peaks occurring within this grid. The file header also stored information about which voxels, referenced by layer, row and column, contain points. The voxels with one or more points were used to segment out the individual tree crowns as well as to compute statistics for species classification.
2.2.3. Crown Segmentation
In order to obtain three-dimensional crown information about each tree crown, we created a voxel-based segmentation algorithm. Under this three-dimensional region growing algorithm, individual layers of the voxel array are read one at a time starting with the topmost layer. Individual voxels from each layer are added to new or existing voxel-clusters depending on their distance from these existing clusters. The ability of a cluster to incorporate a new voxel depends on current number of member voxels, vertical center of mass of these member voxels, as well as distance from the new voxel.
Table 1 lists the default values for parameters that control search window size, cluster competition for new voxels, and cluster size limits. The algorithm, and the meaning of these parameters are given below.
Create an empty list of clusters.
Create an array, C⃗, with one element for each row and column combination of the voxel structure. This will represent the current owner cluster of a given vertical column in the voxel structure. Element (r, c) in this array will be set to NULL whenever a voxel (l, r, c) in the current layer l contains no points. Thus, a vertical voxel column above a given row and column combination can change ownership if a vertical gap exists in the voxel structure.
Create a second array, P⃗, which will function in a similar manner as C⃗. The difference will be that, once ownership of cell (r, c) is established, cell (r, c) will never be set to NULL again. This way, a search for neighboring clusters can be conducted for each (l, r, c) voxel investigated.
If any layers of interest remain, read in the next layer, l, of voxel cells from the voxel file. For each voxel cell of interest in layer l do:
Check if cell (l, r, c) contains points. If not, set element (r, c) in array C⃗ to NULL and proceed to next voxel.
Check grid C⃗ to determine if the current cell (r,c) is already owned. If yes, add the voxel (l, r, c) as a member to the indicated owner cluster and proceed to the next voxel. If no, do the following:
Check for neighboring clusters on grid P⃗ within a the square region described by the intersection of rows r − N to r + N and columns c − N to c + N. For each neighboring cluster found do the following:
Compute the cluster’s radius as
which is the minimum of: (1) the radius of a circle of equivalent area as the average number of cells per layer in the given cluster; and (2) a constant
radmin, multiplied by a correction factor,
FLi.
rx and
ry are the voxel dimensions in the
x and
y direction,
ni is the number of member voxels in cluster
i, and
li is the current number of layers in cluster
i. The value of
FL is determined by a function of the vertical length of the cluster:
Here,
FLmax,
FLmin,
A, and
BL are user-defined constants specified ahead of time, and
δz is the vertical length in map units of the cluster
i. This combination makes the search radius for taller trees greater, while
radmin makes sure newer clusters with few voxel members can still incorporate more voxels. The function
modlog (
x, A, B) is the two parameter logistic function, re-parametrized so that
A defines the change in
x necessary for the output to change from 0.01 to 0.99 (assuming a positive slope parameter in the original logistic function), and
B defines the value of
x for which an output of 0.5 occurs.
Here,
AW is a constant value that is computed as
Using the radius derived with
Equation (6) for each neighboring cluster, compute the “mass”,
Mi, of crown over the given cell using the formula:
where
Oi is the two-dimensional area of overlap between: (1) a circle of radius
radi centered around the cluster centroid; and (2) a circle around the cell center with radius
W, which is a user-defined constant.
FHi is a correction factor for horizontal distance
distH between the cell center and cluster centroid.
and
FVi is computed as a sum of individual corrections for each layer in the cluster.
If any of the Mi for the neighboring clusters exceed the minimum set by massmin, then select the neighboring cluster with the largest mass and add the voxel to this cluster. If no neighboring clusters meet the minimum mass requirement, begin a new cluster with the voxel (l, r, c) as the first member. Set element (r, c) in both C⃗ and P⃗ to the label of the new cluster.
Go through the preliminary clusters and merge a cluster into one of its neighboring clusters if it and the neighbor meet the following conditions:
The cluster is not too big (radi for the given cluster is less than 7 m).
The distance from cluster top to cluster centroid is less than 5 m, cluster is not nearly vertical (unit direction vector from top to centroid has z-component less than 0.94), or cluster bottom is below 2 m.
The cluster is smaller than the neighbor (has more total voxels than the neighboring cluster).
The cluster and the neighbor have a large enough interface (at least 60 percent of the horizontal rectangle envelope containing the cluster is shared with the envelope of the neighbor).
If the cluster has more than 3 layers and is larger than 50 voxels, the direction vector passing from cluster top through cluster centroid crosses through at least 4 voxels of neighbor (voxels must be within 2 mo f vector).
Go through the remaining clusters and delete any cluster that meets any of the following conditions:
The cluster is too small (contains less than 50 voxels).
The cluster is too flat (ratio of cluster height to the average of cluster width in rows and cluster width in columns is less than 0.8).
The cluster is too short (cluster top is less than 5 meters high).
We investigated the feasibility of the alternative voxel-based segmentation algorithm proposed in [
31] as well as those investigated in [
32]. Our decision to use the algorithms listed above is not based on their merit, but more simply on the speed and simplicity of implementation and refinement. Additionally, it was simpler to perfect an algorithm in one office than with multiple correspondences with another party. This algorithm was just a means to achieve one step towards the final goal, and it was not the focus of the study. Accordingly, only a visual evaluation of this algorithm was performed. All parameter settings were optimized for the given data using trial and error.
2.2.4. Collection of Tree Species
Using the voxel clusters produced in the last step, we created a GIS layer containing the two-dimensional outlines of each crown. The crown outline data were placed on a field computer with a built-in GPS receiver. Current position in the field was used to match voxel cluster outlines to the specimens of individual trees of five native species: Douglas-fir (Pseudotsuga menziesii (Mirb.) Franco) (DF), western redcedar (Thuja plicata Donn ex D. Don) (RC), black cottonwood (Populus balsamifera L. ssp. trichocarpa (Torr. & A. Gray ex Hook.) Brayshaw) (BC), bigleaf maple (Acer macrophyllum Pursh) (BM), and red alder (Alnus rubra Bong.) (RA). The first two of these are coniferous (CO) species, and the last three are deciduous hardwood (HW) species.
Clusters which contained parts of multiple trees, as well as those that contained only part of a single tree, could be identified in the field. These clusters were split along vertical planes or combined as necessary back at the office. This work was done in March of 2011, during which hardwoods were still in a leaf-off condition. To avoid scan angles too far from nadir, we stayed within 60 m of the flight line. In doing so, we were able to identify 22 to 29 individuals of each species, totaling 130 trees. Most conifers were large enough that crown segmentation was clear. However, we had some difficulty separating crowns of hardwood species growing in close proximity. Because we desired certainty that only a single tree crown is represented by a cluster, we skipped a small number of trees which could not be accurately deciphered.
Table 2 lists statistics describing the height distribution by species of the trees in the final training data set.
2.3. Waveform and Point Extraction
Using the voxel cluster representing each of the trees identified in the field data, we were able to extract the waveforms that cross each tree from indexed waveform data. First, we found the set of voxels, Vtop, that represent the highest layer in each row and column combination. To ensure that the collected waveforms represent only the tree of interest, we first discarded all waveforms that do not start within 3.0 m Euclidean distance from a voxel center in Vtop. Additionally, we also removed waveforms from this set that do not actually cross through a voxel in Vtop. Doing so should omit waveforms that cross through other objects prior to hitting the cluster of interest, which could introduce errors into our classification.
Additionally, using the voxel-array indexing, all peaks from the decomposed waveforms falling within the voxels of a cluster could be very quickly identified. We retained all information about all peaks contained within the voxel cluster of interest.
2.4. Classification Variables
2.4.2. Point and Voxel Cluster Characteristics
The peaks extracted from the waveforms are equivalent to three-dimensional points, such as those in a discrete point Lidar dataset. Several variables were computed from the collective properties of these points. In the past, many such variables have been proposed, and these can be classified into one of two categories: point arrangement statistics and intensity statistics. The former will yield information about crown shape, while the latter gives information about the ability of a tree’s foliage to reflect near-infrared light.
In order to obtain information about both crown shape and reflective properties, we used both the point representation and the voxel cluster representation of each tree. Most of the variables were chosen to mimic those presented in previous studies. A few were created in the hope of obtaining information similar to that provided by the Fourier transformation of waveform data. All of these point-derived variables can be theoretically computed from a modern discrete point Lidar dataset with at least three returns per pulse as well as recorded intensity data. For each tree in the dataset we computed the following variables for use as predictors in the test classifications:
| h25,h50,h75,h90 | These four variables are estimates of the 25th, 50th, 75th and 90th percentiles of the relative height (point height relative to maximum point height) distribution. |
| i1,i2,i3 | These three variables are the mean intensities of the first, second, and third peaks recorded for each pulse. |
| d12,d13,d23 | These three variables are the mean Euclidean distances from first to second, first to third, and second to third returns, respectively, across all pulses. |
| λ̂ | We collected all distances between two consecutive peaks, regardless of position in the waveform. This variable is the estimated rate parameter of an exponential distribution, with form f(x)= λe−λx, fit to these distances, across all pulses for each tree. |
| ptop | For each tree, we reserved the set of member voxels which contain the highest recorded peaks in the vertical region projected above their respective row and column. This set, T, was also limited to contain only voxels positioned above 6 m from ground level. Peaks falling within voxels in set T, represent those occurring near the surface of the tree, and the proportion of such peaks within the total number of peaks might represent canopy surface penetrability. The proportion of all peaks falling in the same row and column as a voxel in T, and positioned less than 1.5 m vertical distance this voxel was computed to create this variable. |
| rarea | We also reserved the set, U, of all member voxels positioned within the top eight voxel layers of each tree. The flattened projection of U gives a two-dimensional representation of the shape of the crown top. A convex hull can be drawn around the row and column centers of this projection. For illustration, both the projection and the convex hull are depicted in Figure 5(a). The area of the convex hull and the area of the projection may differ in cases where a tree is more branchy and less smooth along the outline. To measure this difference, we computed this variable which is the area of the projection divided by the area of the convex hull. Branchy trees should give lower values of this variable. |
| pn1,pnt,pnb | Using only the layer, row, and column address of member voxels of a tree, one can easily compute which neighbors a given voxel has. These three variables are the proportions of voxel members of the voxel cluster containing only one neighbor voxel, only a bottom neighbor, and only a top neighbor, respectively. Re-indexing the points to a 0.5 m × 0.5 m × 0.5 m voxel array improved the power of these variables. |
| sa,sb | A function, given in Equation (5), was fit in polar coordinates to only the centers of the voxel cells in set T described above
Here, dZ is the vertical difference between the given cell and the maximum layer within the voxel cluster; R and Θ are the horizontal polar coordinates of the given cell center from the cluster centroid in the horizontal plane; and a, b and c are parameters estimated by the R function
nls. An example model is plotted in Figure 5(b). Parameters a and b were kept to form these two variables, while parameter c was discarded. |
Many of the above variables describe crown shape and should be almost entirely unrelated to the information available from the Fourier transforms of the original waveforms. These include the height percentiles (h25,h50,h75,h90), the voxel neighbor statistics (pn1,pnt,pnb), the surface model parameters (sa,sb), as well as rarea.
Conversely, the remaining variables not mentioned above may be correlated with the Fourier transform variables. The Fourier transform statistics indirectly provide quantifications of both the propensity of samples at different distances apart to be part of peaks and the scale differences of these peaks. If variables exist that can alternatively describe these traits, they might act as surrogates for the information available in the Fourier transform variables.
The remainder of the listed point-based variables were intended to provide this surrogate information. A high value of ptop may be correlated to waveform shape as a highly reflective crown surface would produce a large first peak and fewer trailing peaks. The ordered intensity statistics (i1,i2,i3) and the distance statistics (d12,d13,d23 and λ̂) describe in several dimensions the average distances between peaks and the average intensities of those peaks. Any further detail about the relationships among the individual peaks in the waveforms would most likely require waveform data to compute, as the only description of each peak in discrete point Lidar datasets is maximum intensity.
2.5. Correlations and Data Reduction
2.5.1. Principal Components of Fourier Variables
The Fourier variables computed from the waveforms have very high dimension. Because of the high correlation among the amplitudes for all frequencies, it is very likely that the majority of this information could be described in fewer dimensions. Therefore, we ran separate principal component analyses on both the median and the IQR statistics for frequencies 1 though 31. This was done with the
prcomp function in the R programming language. Due to the large difference in scale among the 30 frequencies, the options to both center and scale the variables to have mean of 0 and a standard deviation of 1.0 were set prior to computing the singular value decomposition. The first five components of the rotation of the frequency medians (cm1 to cm5) as well as the first five components of the IQRs (cq1 to cq5) were then used as predictor variables in the classifications. As mentioned previously, the amplitude for frequency 0 on an individual waveform is the mean waveform sample intensity. The median and the IQR of this amplitude value were believed to be especially beneficial, and were therefore kept as predictors and not included in the principal component reductions. This procedure reduced the dimensionality of the Fourier transform variables from 62 to 12.
2.5.2. Canonical Correlations
We used the R function
cancor to investigate the inherent correlation between two sets of variables. The first set, X, contains those variables computed from the waveforms directly (cm1,...,cm5, cq1,...,cq5, m0, and q0) and the second set, Y, consists of those variables, computed from the extracted discrete point data, that may contain some of the same information provided by the Fourier transforms of the waveforms (i1,i2,i3, d12,d13,d23,λ̂, and ptop). The procedure yields eight pairs of canonical variates (Ui,Vi), such that each Ui is a linear combination of the columns in X and each Vi is a linear combination of the columns of Y. All variates are orthogonal to each other except the Ui and Vi within each pair, which are as highly correlated as possible. Examining these correlations, as well as the influence of the original variables in the canonical variates, gives insight into the nature of the relationships between the two sets of variables.
2.6. Classification
We were not only interested in the overall performance of the variable groups, but also for which species comparisons of the individual variable groups performed best. After comparing the predictions from several routines, including linear discriminant analysis, classification trees, and the neural-network approach, support vector machine (SVM) classification performed the best overall. SVM is typically used as a kernel-based algorithm, in which a linear algorithm is applied to a non-linear mapping
ϕ(
x) of the original data onto a higher-dimensional space. This allows for curvature in the surface dividing two groups in the original space. The SVM algorithm uses only the dot products of vectors in the higher-dimensional space, and a kernel function allows computation of these higher-dimensional dot products directly from the original data vectors. We chose the “radial basis” kernel function, given in
Equation (19), because it performed the best during initial testing.
We used the
svm function, part of the R library
e1071 [
34], to perform support vector machine classification. The default setting for the
γ parameter, 1 divided by the number of columns in the predictor matrix, was used because any adjustments resulted in reduced accuracy. Unable to find any improvements, we left all other parameters of the svm function at their default settings.
We tested several predictor groups, individually and in combination, for the classifications. These groupings were: (a) h25,h50,h75, and h90; (b) i1,i2, and i3; (c) d12,d13,d23, and λ̂; (d) ptop and rarea; (e) pn1,pnt, and pnb; (f) sa and sb; (g) “Point”: all variables in groups a to f; (h) cm1,...,cm5; (i) cq1,...,cq5; (j) m0 and q0; (k) “Fourier”: all variables in groups h to j; and (l) “All”: all variables combined. This breakdown was performed to understand the utility of each group for species classification as compared to the other groups. In particular we were concerned with the improvement in prediction accuracy that might come with incorporating information from waveform Lidar over using discrete point Lidar alone. Of course, the actual degree of improvement is dependent on our choices of variables from each dataset. However, the large number of variables were particularly chosen in order to span the full range of information available from the discrete point data.
We also applied the SVM on seven different classifications for each predictor group. This was to examine the species differences that were most sensitive to each predictor group. This information can help to better understand how the Fourier information either does or does not improve classification. The seven classifications were: (1) all species; (2) only hardwood species; (3) all species remapped to either CO or HW; (4) BC and BM only; (5) BC and RA only; (6) BM and RA only; and (7) DF and RC only.
For each classification, five-fold cross validation was used to test the performance of each predictor group. The trees in each species (or each growth form) were randomly split into five groups of similar size, and these species groups were combined into five data groupings. The species predictions for each grouping were performed by a decision rule based on the other four groupings combined. In this way no trees fall in a training set and validation set at the same time. Overall accuracy for each predictor group and classification was computed as the number of correctly predicted trees divided by the total number of trees.
For the classification of all five species, we performed the exact test by Liddell [
35] to ascertain whether the addition of the Fourier transformation variables significantly improved prediction accuracy in classification of all five species. Liddell’s test is designed to compare two proportions, measured on the same subjects. In this case, we used the proportion of correctly predicted trees using the variables in group
g (point-derived variables) and the proportion of correctly predicted trees using the variables in group
l (all variables).
4. Discussion
For five species the overall accuracy of just over 85 percent achieved by the combination of point-derived and Fourier transformation variables compared favorably to similar research on several species [
2,
12,
36,
37]. Most Lidar research focuses on two to three species, and as expected, increasing this number is generally associated with a loss in overall accuracy. As shown in
Table 5, we consistently achieved over 90 percent accuracy when the number of species is reduced to two or three. While it does little good to compare different study areas directly by this measure, we were comforted that the observed accuracies were in the same neighborhood as some of the higher accuracies in previous publications [
1,
16,
19,
22].
Because of the large number of predictor variables, dimensionality was a possible reason for concern. The SVM function is a good choice for this study because it is able to handle a large number of dimensions in the predictor set. However, one negative aspect of the SVM function is that it can require some fine-tuning for maximal performance for a given data set. Performing such a customization for several predictor groups and several species comparisons would have both allowed too much bias and taken far too much time. This lack of tuning likely results in strange predictive behavior. One example of such behavior is the reduction in accuracy from 96.4 to 91.1 percent comparing the classifications of the two conifers using variables in group g versus those of group b alone. While such a difference was disturbing to see, we were not as concerned with individual classification results as we were with general patterns across predictor groups and species combinations.
We reduced the dimensionality of the two sets of Fourier transformation variables, medians and IQR, to six variables each using principal component analysis. Despite the heavy reduction, the 72 percent accuracy achieved by all twelve of the Fourier transformation variables in the classification of the three hardwoods nearly matched the 75 percent accuracy reported previously in Vaughn
et al. [
28]. This is a significant result because many of the amplitudes for individual frequencies are correlated, and we can extract the important information contained in these amplitudes using a much smaller number of orthogonal predictors.
The strongest individual predictor group for the five species classification was group h, which is the combination of principal components for the Fourier transform medians. This group was not strongest for any of the other classifications, but it does perform nearly the best for differentiating cottonwood (BC) and alder (RA) and for differentiating the two conifers, Douglas-fir (DF) and cedar (RC). This indicates that these variables are actually quite strong as predictors. If other structural information was not available due to difficulty in segmenting out individual crowns, these variables might still be useful for at least classifying pixel-sized areas of the canopy.
The group containing all waveform information,
k, was better than the group containing all point-derived variables,
g, for only one pairing of species, DF and RC. This was a surprise because conifers were left out of the previous work in Vaughn
et al. [
28] due to the poor performance of the Fourier transform variables on the same two species. For this study, we limited the scan angle to less than 12 degrees off nadir. This might explain the observed reversal, as one could imagine scan angle having a large effect on the amount of conifer crown intercepting the laser pulse.
The point-derived variable group,
g, or components of this group performed very well on all species comparisons. Several of these variables are based on other publications, as will be described below, and similar results have been found before. The intensity information worked best for the classification of all five species as well as for differentiating the two conifers. Previous results have been mixed on the utility of intensity information. Ørka
et al. [
23] used only intensity, while Holmgren and Persson [
21] found only the standard deviation of intensity to be important. Moffiet
et al. [
2] found that intensity varied too highly to be used as a predictor.
The point height distribution statistics in group
a, which appear in similar form in many species classification studies [
1,
19–
21], were generally unimpressive as an individual predictor group. The main exception is for the classification of BC and RA, where a classification accuracy of over 80 percent is achieved with just these four height distribution percentiles. As with intensity, results have been mixed in the past with this group of variables. Vauhkonen
et al. [
19] achieved fairly good classification with just the relative height distribution percentiles before improving on these results with other variables. Holmgren and Persson [
21] found that the weakest individual variable was the 90th percentile of relative height. Ørka
et al. [
1] also find little value to relative height statistics in species classification.
In
Tables 5 and
6, we can see that the inter-peak distance variables in group
c performed very well distinguishing maple (BM) from the two other hardwood species. The means of three of the four variables in this group, i.e.,
d12,
d13, and
d13, are smaller for BM than for all other species. As the name suggests, bigleaf maple has very large leaves that may be larger than even the pulse footprint. Each leaf hit is then very likely to record a noticeable peak in the return signal. This might result in more detectable peaks close to the crown surface. The crown surface model parameters in group
f are also quite strong at differentiating BM from cottonwood (BC). More open-grown maples tend to present a more dome-like form, which is represented in our crown surface model by smaller values of the
sa parameter.
The voxel-based neighbor statistics in group
e were strong predictors for distinguishing conifers from hardwoods, but this group of texture variables underperformed as an individual group in all other classifications. The realizations of these variables varied greatly for the BC and BM trees, but were much more stable for the other species. The reason for this difference is unclear, though there seems to be some association between larger heights and larger values of
pn1 for these two species. Perhaps larger cottonwoods and maples are more prone to lone branches that would lead to a larger number of one-neighbor cells. Including height as a predictor might account for this difference. Ørka
et al. [
1] also found that many of their predictors were dependent on height.
Few authors have investigated Lidar-derived crown texture directly as a predictor variable. Vauhkonen
et al. [
19] looked at textural features of the Lidar-derived canopy height model. While analysis of changes in intensity characteristics of the returns can be seen as texture analysis [
18], this neglects the three-dimensional texture that is evident in many tree crowns. In high spatial resolution raster imagery analysis, texture has been considered important for species identification [
38,
39]. It is interesting that this idea did not transfer over to point cloud analysis. One explanation might be that three-dimensional texture is difficult to quantify. We determined that canopy texture, or “roughness”, could be measured more easily in the voxel representation of the data. As with two-dimensional raster data, it was very simple to identify the neighbors of a voxel using the row, column, and layer indices.
Our intentional attempt to create variables from the discrete point data that aliased the information available in the Fourier transformations was not successful. These variables, such as those in groups b and c, should contain information about intensity relationships among the peaks and inter-peak distances. According to the canonical correlation analysis, only two of the eight canonical pairs had high correlations. This indicates that we did indeed capture some of the same information available from the Fourier transformations. However, the remaining information was influential enough to improve the classification accuracy in most of the species comparisons. We expect that a noticeable part of these results may stem from our choice of variables, and a different choice of variables could lead to a different conclusion. However, much detail is lost in the conversion of wave signal to discrete point data, and we suspect that some information important to species detection will always be part of this loss.
The trees measured in this study, most notably the conifers, are mostly open grown. The results as they stand would not directly translate to a high density commercial forest. With the increased density a smaller portion of each tree’s crown would be uniquely identifiable. Because the waveform information used in this study only contains one-dimensional information about position from wave start, the density should not greatly affect the results reported here. However, many of the spatial variables we used, such as those in groups d, e and f would likely be affected by this reduced crown visibility. The effects would probably be largest in hardwood stands due to the additional difficulty of differentiating adjacent hardwood trees with intermingling branches and no distinct tops. In such a case, the result would most likely be an increase in the power of waveform information over crown shape information for species classification.
5. Conclusions
The prevalence of aerial Lidar for forest inventory information has increased over the last decade, and discrete point Lidar data has already shown much promise in distinguishing individual tree species [
19,
21]. In this study, we were able to provide one more example of high tree species classification accuracy from discrete point airborne Lidar data. Using only variables available from very dense discrete point Lidar data, an overall classification accuracy of 79.2 percent (kappa = 0.740) was found for five native commercially viable species. Multiple comparisons of two or three species resulted in even greater accuracy, achieving as high as 97.8 percent (kappa = 0.956).
For classification with discrete point data only, we introduced several new variables. In the five species classification, two groups of these new variables performed second and third best of all the groups. In each of the small classifications of two or three species or species groups, one of the groups of new variables performs at least second best. Note that the computation of each of these variables was very simple using a voxel representation of each tree. To provide such a representation, we introduced a new segmentation algorithm that can be easily adapted to local crown properties.
Perhaps of most interest, we discovered that summary information derived from entire waveforms provided predictive power above and beyond that of the discrete point data alone. This addition raised the overall accuracy to 85.4 percent (kappa = 0.817). The waveform information was important for separating Douglas-fir from western hemlock, increasing accuracy 3.5 percent (kappa increase = 0.072), and bigleaf maple from red alder, increasing accuracy 4.0 percent (kappa increase = 0.082). For other species comparisons, waveform information provided no gain in accuracy.
Other researchers have found that decomposing airborne waveform Lidar data into discrete points is useful for classification purposes [
20,
27,
40], using peak characteristics derived while decomposing the waveforms into discrete peaks. However, to our knowledge, this was the first study to directly compare waveform to discrete Lidar data for species classification performance. One should note that no such test can be entirely conclusive due to the immense number of options for variables and classification techniques. Regardless, our results, along with positive waveform results in the other studies, show that any additional cost of waveform data may very likely be sensible if optimal accuracy is a primary goal. Further investigation into the potential of this data format may lead to a complete species-level remote sensing-based inventory from Lidar data alone that can consistently provide all the information needed.