4.1. LAI Estimation
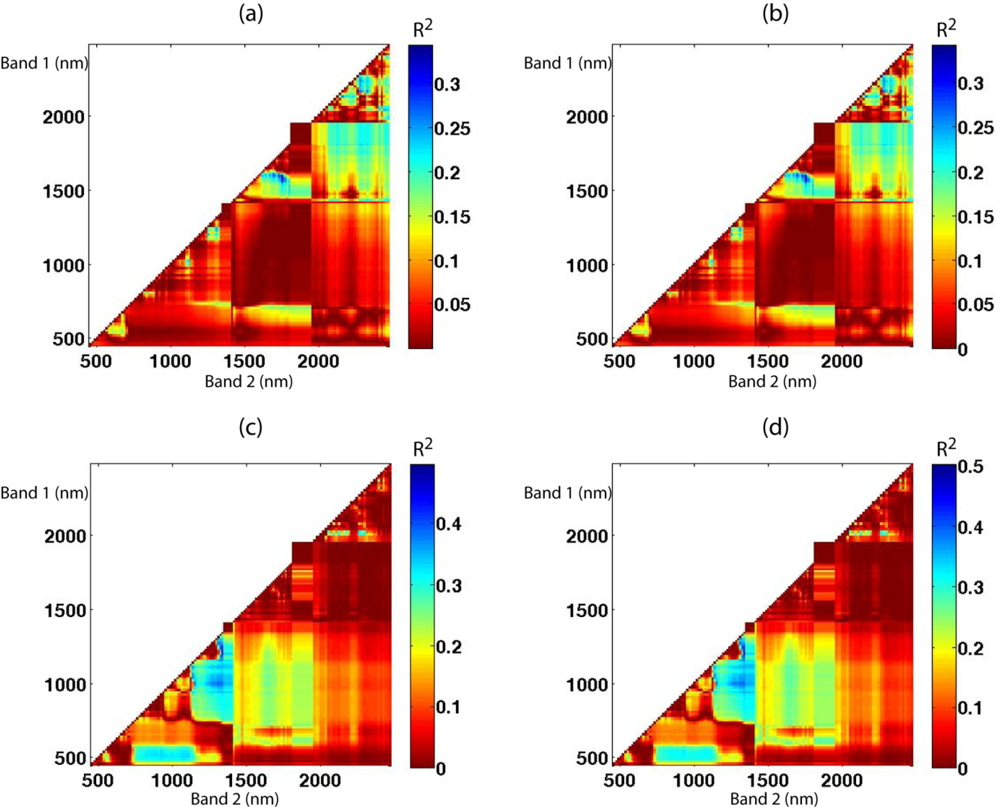
The results of the correlation matrices produced between the vegetation indices and LAI for all possible band combinations are shown in
Figure 3. The greater the correlation of the ground reference LAI value with the two bands used to compute the vegetation index, the more blue the pixel in the diagram. Both VI1 and VI2 exhibited very similar patterns for each site. While relatively high correlations between the vegetation indices and LAI were found in the region between 1,500 and 1,800 nm for the Monticello site, they were found in the region between 900 and 1,400 nm for the Monument Valley site (
Figure 3). Interestingly, the bands in the red and near-infrared regions, which are assumed to have more information regarding vegetation health, did not produce higher correlations than the bands in the middle-infrared region. This might be because the study sites are located in semi-arid/arid areas and thus the spectral response of each vegetation type may be distinguishable in the middle-infrared region, where the spectral response of vegetation to water is more sensitive.
Table 3 summarizes the best band combination and associated statistics (
i.e.,
R2,
RMSEs from calibration and cross-validation) of the two vegetation indices for each site. It was not surprising that one of the two best bands was found in the water absorption region (∼1,200 nm) [
67] for the Monument Valley site because some of the sample locations were irrigated while the others were not at this site. The vegetation index approach resulted in better performance for the Monument Valley site than the Monticello site (e.g.,
R2 = 0.501 accounting for 50% of the variance with
r = 0.7). This might be because the vegetation distribution and structure were more dynamic in the Monticello site than in the Monument Valley site. In particular, the grass and shrub species were highly mixed in the Monticello site, and this made it difficult to calibrate the
in situ LAI data with the HyMap data at the 2.3 × 2.3 m resolution. Slight difference between the field and the pixel location might have also introduced errors in LAI estimation. While the non-linear regression models did not result in better fit than the linear regression for the Monticello site, the logarithmic regression model yielded slightly higher
R2 and lower
RMSE values for the Monument Valley site (
Table 3). The best band combination for each site was consistent regardless of the regression method and the vegetation index used.
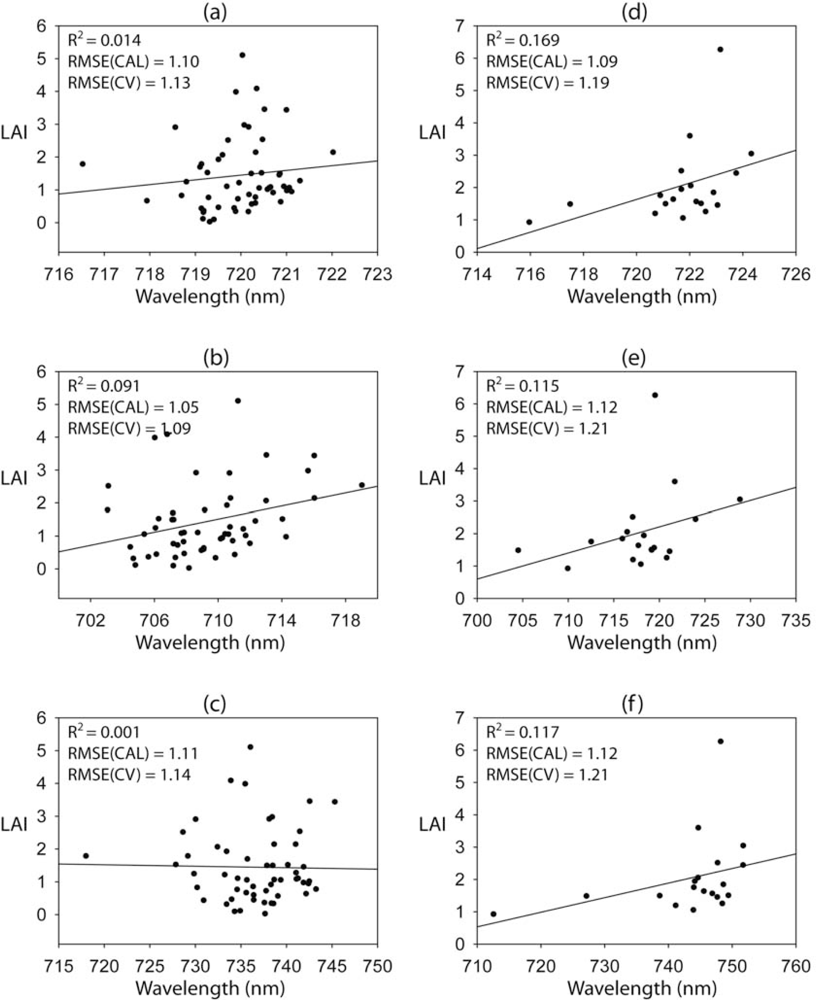
The scatterplots between each of the three REP approaches and LAI are shown in
Figure 4. The REP approach did not predict LAI well, resulting in low correlations (<0.2). Similar to the vegetation index approach, REP methods resulted in better performance for the Monument Valley site than the Monticello site. While the LG_REP resulted in the best performance for the Monticello site, the LI_REP produced the highest accuracy in LAI estimation for the Monument Valley site. However, there was no significant relationship between any of the REPs and LAI (
p > 0.05). One of the reasons for the poor performance of the REP approach might be background soil spectral influence within pixels. The REP approach typically works well for vegetation with full canopies [
68,
69]. Many of the sample pixels had vegetation cover between 70% and 90%, and thus the background soil could have influenced the spectral response associated with the red-edge. That most of the sample pixels contained multiple vegetation species may have also caused the REP approach fail to estimate LAI because each species typically has a unique REP characteristic.
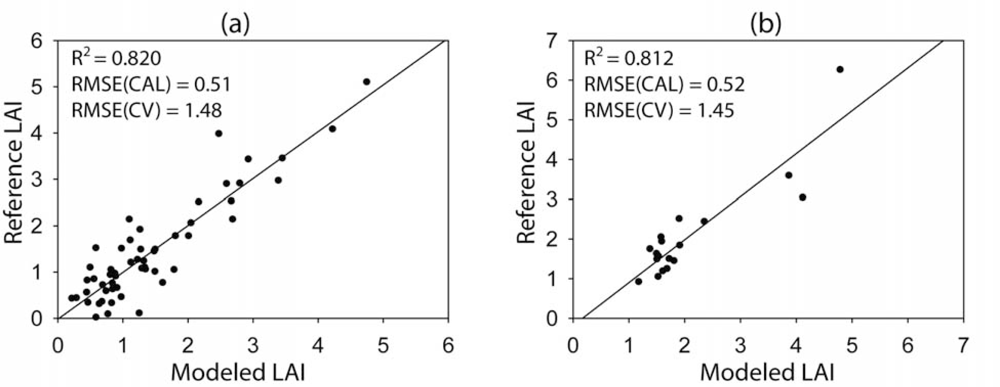
Unlike the results of the VI- and REP-based LAI estimation, the regression trees resulted in very good LAI estimation performance (
R2 > 0.8) (
Figure 5). The regression trees generated three rules for the Monticello, UT Site and two rules for the Monument Valley, AZ Site. Interestingly, one of the three rules for the Monticello site was associated mainly with the grass species samples (
i.e., wheatgrass and litter) while the other two rules were applied to most of shrub species samples (
i.e., sagebrush and rabbitbrush). Eight bands were used to generate the multivariate equations for the Monticello site, which was not efficient and resulted in inflation of the fitness of the models. Conversely, only two bands (709 and 754 nm) in the red-edge region were used to generate the multivariate equations in the regression trees for the Monument Valley site. One rule was applied to relatively high LAI (>2) samples for the Monument Valley site, while the other was applied to the lower LAI samples. The red-edge bands effectively divided the samples into the two groups.
Although the calibration using the regression trees outperformed those using the vegetation index and REP data, the cross-validation did not correspond to the calibration results. The RMSEs through cross-validation using the regression trees were higher than those using the other approaches. While most of the folds for cross-validation generally resulted in low errors, some of the folds (∼25%) resulted in high LAI estimation errors (e.g., >2), which consequently increased the total RMSE. The overfitting problem of the regression trees, especially when a small number of samples is used, often occurs [
27]. This is also related to the well known problem of decision/regression trees, which are sensitive to the training data configuration [
70]. Glenn
et al. [
71] investigated black greasewood and fourwing saltbush over the Monument Valley site using 2007 MODIS data. They measured LAI using the traditional direct method and found a good agreement with the scaled Enhanced Vegetation Index (EVI) from MODIS data based on a simple linear regression (
R2 = 0.77;
n = 55;
p < 0.001).
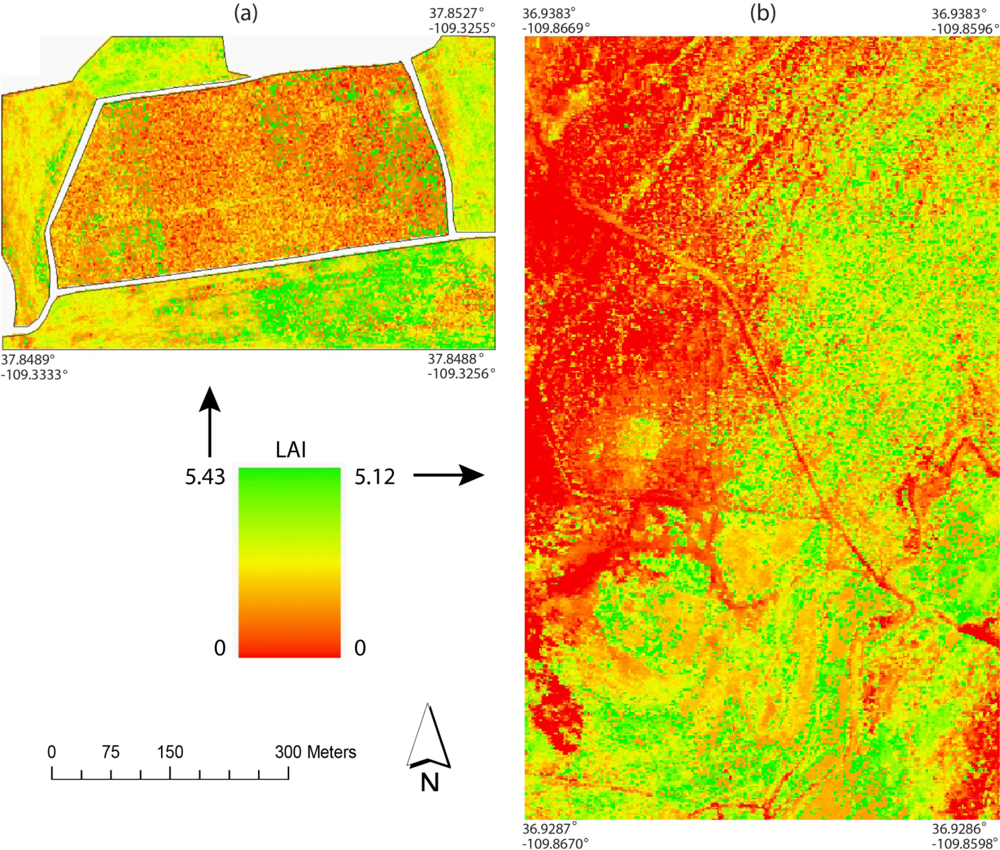
Figure 6 shows the LAI distribution maps estimated using the regression trees for the Monticello and Monument Valley sites.
Although all possible two-band combinations were tested for the VI1 and VI2 in this study, the most valuable VI might consist of more than two narrow hyperspectral bands. We tested a few narrow band-derived VIs such as the Vogelmann Red Edge Index 2 [
72], which uses spectral data at more than two wavelengths. However, the additionally tested indices did not outperform the VIs used in this study. Optimization of multiple wavelengths associated with such narrow band-derived VIs might further improve the performance of LAI estimation.
4.2. Vegetation Mapping
Figures 7 and
8 show the relationship between the percent cover and the matched filter scores for the Monticello, UT and Monument Valley, AZ Sites, respectively. The percent covers of wheatgrass and litter were correlated with the matched filter scores at the 90% and 95% confident levels, respectively. However, the percent covers of sagebrush and rabbitbrush failed to be significantly correlated with the corresponding matched filter scores. There might be two reasons for this: the spectral separability of sagebrush and rabbitbrush from other species was not strong. In addition, most of the sagebrush and rabbitbrush samples were dominated by the corresponding species (
i.e., percent cover > 70%), while a few of them were mixed with other species (
i.e., percent cover < 60%). MTMF is known to be sensitive to the amount of green vegetation present within a pixel [
38,
55]. Litter (dead plant materials) for the Monticello site and soil for the Monument Valley site could affect the determination of the matched filter scores of the healthy vegetation species. Locational errors could also influence the relatively lower correlation between the percent covers and the matched filter scores. Interestingly, the percent covers of saltbush were well correlated with the matched filter scores (
Figure 8(b)). Excluding one outlier, the percent covers of greasewood were also well correlated with the scores. The MTMF approach has been successfully applied to map single vegetation species resulting in good relationships between percent cover and matched filter scores [
73], but it typically results in more variation and confusion between species when multiple species are considered [
74]. In this study, while several vegetation species were mixed at each sampling location in the Monticello site, one species was dominant at each sampling location in the Monument Valley Site. Consequently, there was less influence from other species in the relationship between the percent cover and the matched filter scores for the Monument Valley site than for the Monticello site. However, because the matched filter scores were not sufficient for separating each species from the others, the use of a suite of vegetation indices was expected to improve classification accuracy using decision tree logic.
Figure 9 shows the performance variations of the multiple (
i.e., 20) decision trees using different sets of training samples for each site. Since the size of the reference data was small (
i.e., 53 samples of four classes for the Monticello site and 43 samples of three classes for the Monument Valley Site), the performance variation of the multiple decision trees for training and testing was slightly large. For both sites, the MTMF-derived metrics and the vegetation indices (labeled MV in
Figure 9) resulted in better performance (for both training and testing) than the original scaled reflectance (labeled REF in
Figure 9) in decision tree classification.
Table 4 lists the key input variables to the decision trees classifications for each site. The PRI and NDNI among the vegetation indices were very useful in the decision tree classification for the Monticello site. The MF scores of sagebrush and rabbitbrush also contributed to the decision tree generation for the Monticello site. When the original scaled reflectance data were used in the decision tree classification for the Monticello site, the red (663.4 nm) and red-edge bands (709 nm) contributed most to the classification, followed by the blue (443.3 nm) and middle-infrared band (2,477.5 nm). A different pattern of contributing variables was found for the Monument Valley site: The WBI, NDLI, and NDWI contributed most to the MTMF and vegetation index-based decision tree classification. The infeasibility of greasewood was also very useful. When the reflectance data were used, the bands near the water absorption features (
i.e., around 1,400 and 1,940 nm) contributed most to the classification. This may be because the Monument Valley site is located in an arid area and some of the sampling locations were irrigated while others were not. That is why the water-related vegetation indices and reflectance were very useful in vegetation mapping for the Monument Valley Site. The chlorophyll absorption features and related vegetation indices contributed moderately to the decision trees for both sites.
A majority rule was applied to produce the final species distribution map based on the multiple decision trees. Because some pixels had multiple maximum votes, additional processing was necessary. A three-step approach was used: a majority rule was first applied using all of the 20 decision trees, and then another majority rule was applied to the undecided pixels using the top 10 decision trees based on their testing performance. Finally, the best decision tree was used to determine the classes for the still undecided pixels and the final vegetation maps were created for each site.
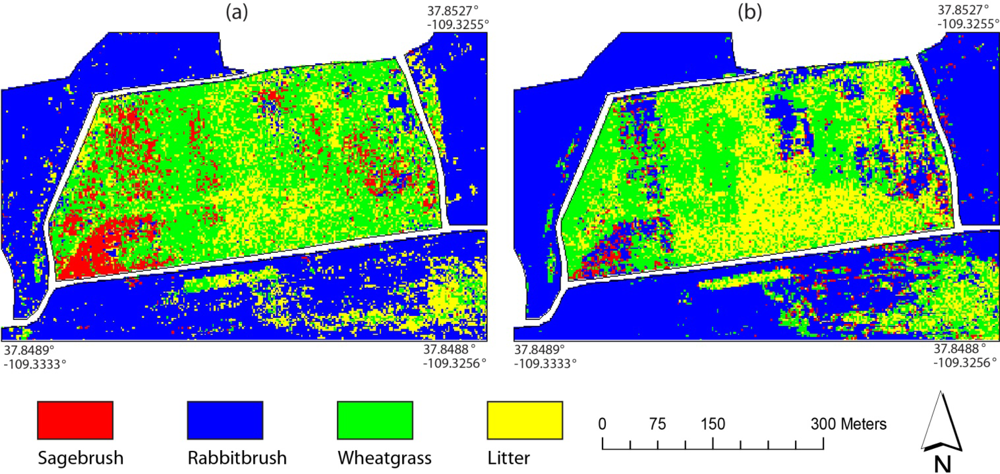
Figure 10 shows the vegetation maps over the Monticello site using the two sets of decision trees (
i.e., one set using the MTMF variables and vegetation indices and the other using the scaled reflectance). Sagebrush appeared to be somewhat overestimated through visual inspection when the MTMF variables and vegetation indices were used (
Figure 10(a)). On the other hand, rabbitbrush and litter were generally overestimated when the scaled reflectance data were used for decision tree classification (
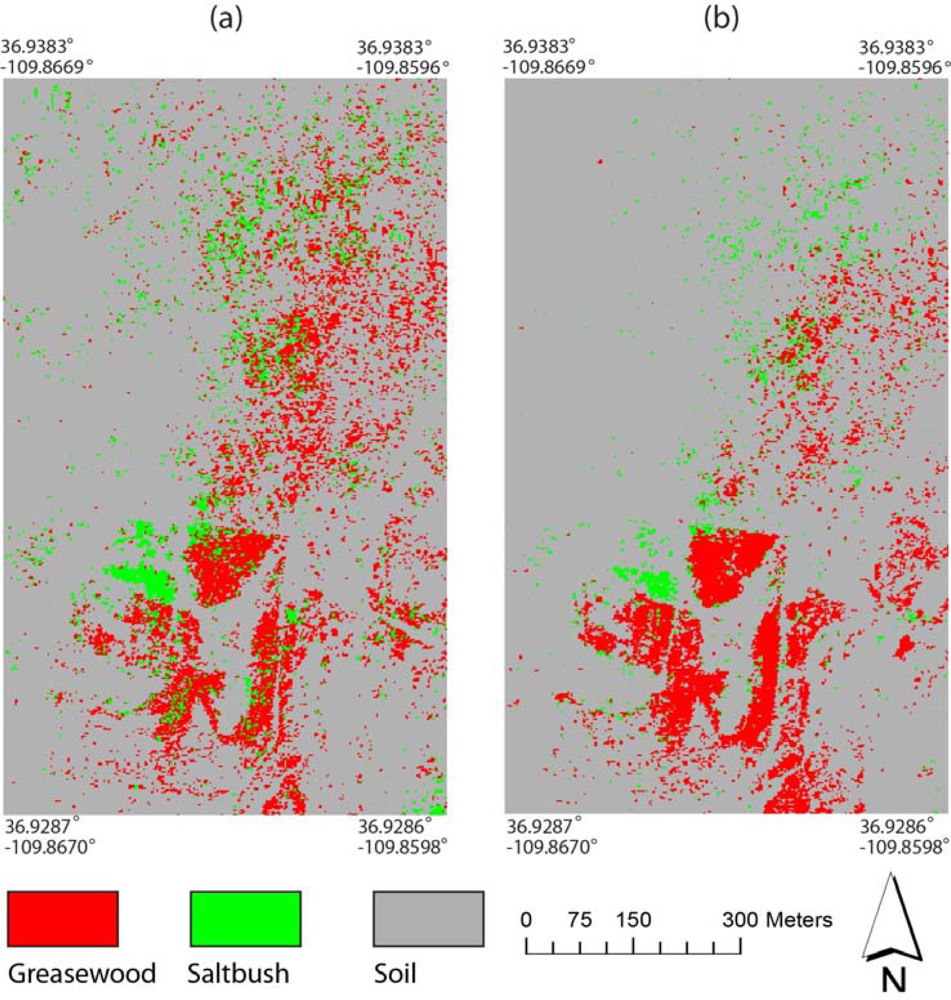
Figure 10(b)). The vegetation maps of the Monument Valley site using the two sets of the decision trees are shown in
Figure 11. The classes were more clumped in the map using the scaled reflectance than using the MTMF variables and vegetation indices. Soil appeared to be overestimated when the reflectance data were used. These classification maps exhibited some discrepancies with the actual field conditions. For example, while the disposal cell cover (central region) in
Figure 10 appears close to the field conditions, a monoculture of rabbitbrush on the side slopes does not agree with the field conditions. At the Monument Valley site, greasewood appears to be over classified. The limited quantity and quality of the field reference data might account for the discrepancies, including: (1) the small sample size resulted in variations in performance for multiple decision tree classifications; and (2) each ground reference sample was measured using a circular plot with a diameter of 1 m, which is smaller than the hyperspectral image pixel size (2.3 × 2.3 m). Given the small shrub and grass patches in the sites, this could result in significant confusion in classification.
Since all of the reference data might have been used to train decision trees (50% on average), the classification accuracy based on the assessment using the reference data might be slightly inflated. The classification accuracy assessment for the Monticello site is presented in
Table 5. Interestingly, although the MTMF variables and the vegetation indices outperformed the original scaled reflectance, based on the individual decision trees for both training and testing (refer to
Figure 9), the accuracy assessment results were similar between the two maps, resulting in the overall accuracy of around 87% and Kappa of around 0.82. Similar to the visual inspection of the classification maps, the commission error of sagebrush when using the MTMF variables and vegetation indices was large (∼36.4%), while the omission error of sagebrush when using the reflectance data was large (∼37.5%). Due to the small size of the reference data, the overestimation of rabbitbrush and litter when using the scaled reflectance was not clearly indicated by the error matrix. Wheatgrass was confused with sagebrush and litter in the classification using the reflectance data. There was no significant difference between the two Kappa values (
Table 5(c)).
Table 6 presents the accuracy assessment results of the classification maps for the Monument Valley site. Saltbush was confused with soil for both maps. This might be because some of the saltbush sample locations were grazed and not irrigated, causing their spectral response to be similar to soil. Saltbush was also confused with greasewood when the reflectance data were used in the decision tree classification. However, the confusion was much improved when the MTMF variables and vegetation indices were used in the decision tree classification. There was no significant Kappa difference between the two classifications due to the relatively large asymptotic standard errors (ASE), a measurement of uncertainty, even though there was a 10% difference between the two Kappa values (
Table 6(c)).
For vegetation mapping over hazardous waste sites, the omission errors of shrub could be more serious than the commission errors. The commission errors could be false alarms for biointrusion on the capped materials, but the omission errors might indicate undetected biointrusion, which requires quick response and treatment. From this point of view, the use of the MTMF-derived metrics and vegetation indices was better than the use of the scaled reflectance for vegetation mapping. The omission errors of rabbitbrush and saltbush (both shrub species) were relatively large when the scaled reflectance data were used.
At the Monticello site, rabbitbrush is an early successional shrub adapted to disturbed, unstructured soils. Sagebrush is a later successional shrub that appears to be increasing in abundance as soil structure develops in the engineered soil cover, creating preferential flow pathways for water to move deeper in the profile and, hence, gradually creating a more favorable habitat for sagebrush. The phytoremediation study at the Monument Valley site was designed, in part, to compare the two dominant native desert phreatophytes: the obligate black greasewood and facultative four-wing saltbush. Consequently, for long-term monitoring of these sites, differentiating rabbitbrush and sagebrush at the Monticello site, and greasewood and saltbush at the Monument Valley site are critical.
When considering the small shrub and grass patches (∼1 m and sometimes <1 m in size) found in the study sites, the spatial resolution of the HyMap imagery (2.3 × 2.3 m) appears to be a bit coarse. Although there is a concern that higher spatial resolution data may actually reduce classification accuracy by increasing within-class spectral variability [
75], the Monticello and Monument Valley sites should benefit from higher spatial resolution data (e.g., ∼1 × 1 m) for vegetation mapping, because small grass and shrub patches (not tall vegetation) are dominant and their cover is relatively dense (percent cover > 70%).