Calibration of a Species-Specific Spectral Vegetation Index for Leaf Area Index (LAI) Monitoring: Example with MODIS Reflectance Time-Series on Eucalyptus Plantations
Abstract
:1. Introduction
- The use of the reflectance of some specific spectral bands (e.g., NIR, red wavebands),
- The combination of these reflectance bands in a given mathematical formula, with the possibility of weighting these reflectances, which gives the SVI value,
- The use of a linear or nonlinear model between SVI and LAI to retrieve LAI from SVI. This relationship may or may not use additional external information.
2. Material and Methods
2.1. Study Site and LAI Measurements
2.2. Satellite Images: Stand-Scale MODIS Reflectance Time Series
2.3. Calibration of a Species-Specific Spectral Vegetation Index
2.4. Including a Third Variable in the Spectral Vegetation Index
2.5. Statistical Analysis
3. Results
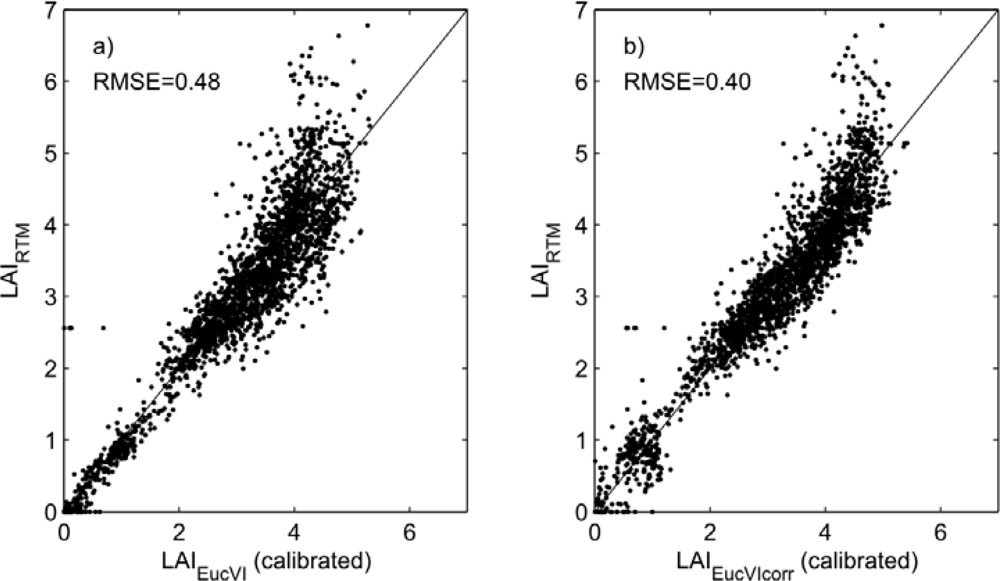
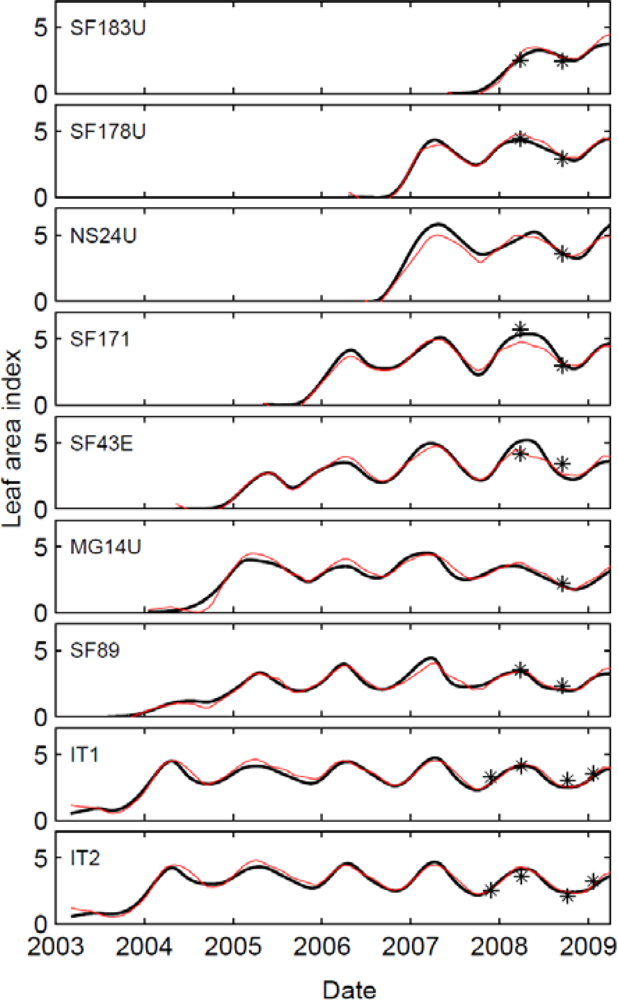
3.1. New Spectral Vegetation Index Calibration
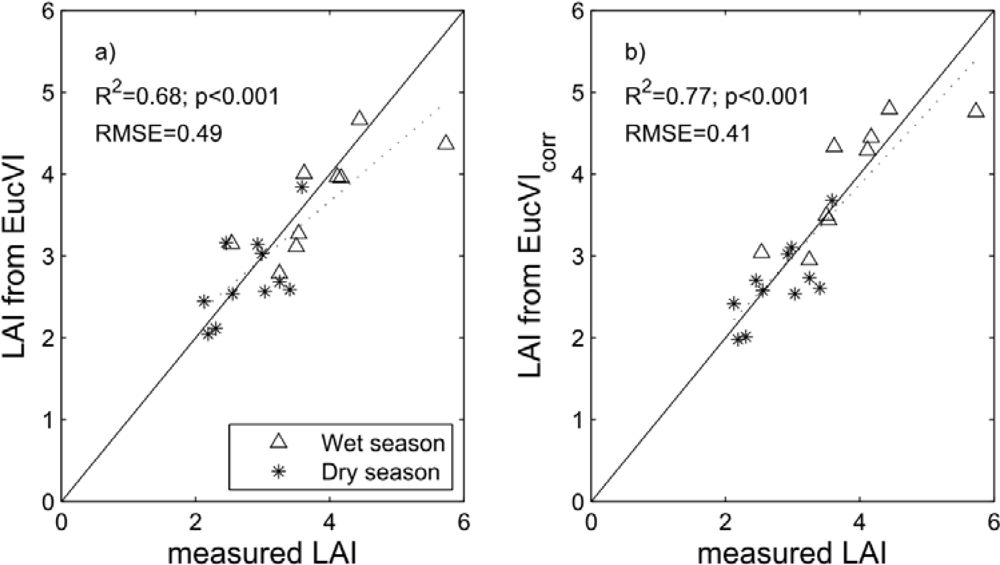
3.2. Comparison with LAI from Destructive Measurements
4. Discussion
5. Conclusion
Acknowledgments
References
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the great plains with ERTS. In Third ERTS Symposium, SP-351; Griswold, N., Ed.; NASA: Washington, WA, USA, 1973; Volume 1, pp. 309–317. [Google Scholar]
- Jordan, C.F. Derivation of leaf area index from quality of light on the forest floor. Ecology 1969, 50, 663–666. [Google Scholar]
- Baret, F.; Clevers, J.G.P.W.; Steven, M.D. The robustness of canopy gap fraction estimates from red and near-infrared reflectances: A comparison of approaches. Remote Sens. Environ 1995, 54, 141–151. [Google Scholar]
- Huete, A.R. A Soil-Adjusted Vegetation Index (SAVI). Remote Sens. Environ 1988, 25, 295–309. [Google Scholar]
- Justice, C.O.; Vermote, E.; Townshend, J.R.G.; Defries, R.; Roy, D.P.; Hall, D.K.; Salomonson, V.V.; Privette, J.L.; Riggs, G.; Strahler, A.; et al. The Moderate Resolution Imaging Spectroradiometer (MODIS): Land remote sensing for global change research. IEEE Trans. Geosci. Remote Sens 1998, 36, 1228–1249. [Google Scholar]
- Huete, A.R.; Liu, H.Q.; Batchily, K.; van Leeuwen, W. A comparison of vegetation indices over a global set of TM images for EOS-MODIS. Remote Sens. Environ 1997, 59, 440–451. [Google Scholar]
- Brown, L.; Chen, J.M.; Leblanc, S.G.; Cihlar, J. A shortwave infrared modification to the simple ratio for LAI retrieval in boreal forests: An image and model analysis. Remote Sens. Environ 2000, 71, 16–25. [Google Scholar]
- Fassnacht, K.S.; Gower, S.T.; MacKenzie, M.D.; Nordheim, E.V.; Lillesand, T.M. Estimating the leaf area index of North Central Wisconsin forests using the landsat thematic mapper. Remote Sens. Environ 1997, 61, 229–245. [Google Scholar]
- Qi, J.; Kerr, Y.H.; Moran, M.S.; Weltz, M.; Huete, A.R.; Sorooshian, S.; Bryant, R. Leaf area index estimates using remotely sensed data and BRDF models in a semiarid region. Remote Sens. Environ 2000, 73, 18–30. [Google Scholar]
- Propastin, P.A. Spatial non-stationarity and scale-dependency of prediction accuracy in the remote estimation of LAI over a tropical rainforest in Sulawesi, Indonesia. Remote Sens. Environ 2009, 113, 2234–2242. [Google Scholar]
- Yoshioka, H.; Miura, T.; Obata, K. Derivation of relationships between spectral vegetation indices from multiple sensors based on vegetation isolines. Remote Sens 2012, 4, 583–597. [Google Scholar]
- Soudani, K.; Francois, C.; le Maire, G.; Le Dantec, V.; Dufrene, E. Comparative analysis of IKONOS, SPOT, and ETM+ data for leaf area index estimation in temperate coniferous and deciduous forest stands. Remote Sens. Environ 2006, 102, 161–175. [Google Scholar] [Green Version]
- Jackson, R.D.; Huete, A.R. Interpreting vegetation indices. Prev. Vet. Med 1991, 11, 185–200. [Google Scholar]
- le Maire, G.; Marsden, C.; Verhoef, W.; Ponzoni, F.J.; Lo Seen, D.; Bégué, A.; Stape, J.-L.; Nouvellon, Y. Leaf area index estimation with MODIS reflectance time series and model inversion during full rotations of Eucalyptus plantations. Remote Sens. Environ 2011, 115, 586–599. [Google Scholar]
- Verrelst, J.; Romijn, E.; Kooistra, L. Mapping vegetation density in a heterogeneous river floodplain ecosystem using pointable CHRIS/PROBA data. Remote Sens 2012, 4, 2866–2889. [Google Scholar]
- Gilabert, M.A.; Gonzalez-Piqueras, J.; Garcia-Haro, F.J.; Melia, J. A generalized soil-adjusted vegetation index. Remote Sens. Environ 2002, 82, 303–310. [Google Scholar]
- Campoe, O.C.; Stape, J.L.; Nouvellon, Y.; Laclau, J.-P.; Bauerle, W.; Binkley, D.; le Maire, G. Stem production, light absorption and light use efficiency between dominant and non-dominant trees of Eucalyptus grandis across a productivity gradient in Brazil. For. Ecol. Manage 2012, 288, 14–20. [Google Scholar]
- Nouvellon, Y.; Laclau, J.-P.; Epron, D.; Kinana, A.; Mabiala, A.; Roupsard, O.; Bonnefond, J.-M.; le Maire, G.; Marsden, C.; Bontemps, J.-D.; et al. Within-stand and seasonal variations of specific leaf area in a clonal Eucalyptus plantation in the Republic of Congo. For. Ecol. Manage 2010, 259, 1796–1807. [Google Scholar]
- Gower, S.T.; Kucharik, C.J.; Norman, J.M. Direct and indirect estimation of leaf area index, fAPAR, and net primary production of terrestrial ecosystems. Remote Sens. Environ 1999, 70, 29–51. [Google Scholar]
- MacFarlane, C.; Arndt, S.K.; Livesley, S.J.; Edgar, A.C.; White, D.A.; Adams, M.A.; Eamus, D. Estimation of leaf area index in eucalypt forest with vertical foliage, using cover and fullframe fisheye photography. For. Ecol. Manage 2007, 242, 756–763. [Google Scholar]
- Wolfe, R. MODIS Geolocation. In Earth Science Satellite Remote Sensing; Springer: Berlin/Heidelberg, Germany, 2006; Volume 1, pp. 50–73. [Google Scholar]
- Feret, J.-B.; François, C.; Asner, G.P.; Gitelson, A.A.; Martin, R.E.; Bidel, L.P.R.; Ustin, S.L.; le Maire, G.; Jacquemoud, S. PROSPECT-4 and 5: Advances in the leaf optical properties model separating photosynthetic pigments. Remote Sens. Environ 2008, 112, 3030–3043. [Google Scholar]
- Jacquemoud, S.; Baret, F.; Hanocq, J.F. Modeling spectral and bidirectional soil reflectance. Remote Sens. Environ 1992, 41, 123–132. [Google Scholar]
- Verhoef, W.; Bach, H. Coupled soil-leaf-canopy and atmosphere radiative transfer modeling to simulate hyperspectral multi-angular surface reflectance and TOA radiance data. Remote Sens. Environ 2007, 109, 166–182. [Google Scholar]
- Baret, F.; Guyot, G. Potentials and limits of vegetation indices for LAI and APAR assesment. Remote Sens. Environ 1991, 35, 161–173. [Google Scholar]
- Clevers, J.G.P.W.; Verhoef, W. LAI estimation by means of the WDVI: A sensitivity analysis with a combined PROSPECT-SAIL model. Remote Sens. Rev 1993, 7, 43–64. [Google Scholar]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ 1996, 55, 95–107. [Google Scholar]
- Jiang, Z.; Huete, A.R.; Didan, K.; Miura, T. Development of a two-band enhanced vegetation index without a blue band. Remote Sens. Environ 2008, 112, 3833–3845. [Google Scholar]
- Peterson, D.L.; Spanner, M.A.; Running, S.W.; Teuber, K.B. Relationship of thematic mapper simulator data to leaf area index of temperate coniferous forests. Remote Sens. Environ 1987, 22, 323–341. [Google Scholar]
- Turner, D.P.; Cohen, W.B.; Kennedy, R.E.; Fassnacht, K.S.; Briggs, J.M. Relationships between leaf area index and Landsat TM spectral vegetation indices across three temperate zone sites. Remote Sens. Environ 1999, 70, 52–68. [Google Scholar]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ 1979, 8, 127–150. [Google Scholar]
- Crippen, R.E. Calculating the vegetation index faster. Remote Sens. Environ 1990, 34, 71–73. [Google Scholar]
- Clevers, J.G.P.W. Application of a weighted infrared-red vegetation index for estimating leaf area index by correcting for soil moisture. Remote Sens. Environ 1989, 29, 25–37. [Google Scholar]
- Richardson, A.J.; Wiegand, C.L. Distinguishing vegetation from soil background information. Photogramm. Eng. Remote Sensing 1977, 43, 1541–1552. [Google Scholar]
- le Maire, G.; François, C.; Soudani, K.; Berveiller, D.; Pontailler, J.-Y.; Bréda, N.; Genet, H.; Davi, H.; Dufrêne, E. Calibration and validation of hyperspectral indices for the estimation of broadleaved forest leaf chlorophyll content, leaf mass per area, leaf area index and leaf canopy biomass. Remote Sens. Environ 2008, 112, 3846–3864. [Google Scholar]
- le Maire, G.; Francois, C.; Dufrene, E. Towards universal broad leaf chlorophyll indices using PROSPECT simulated database and hyperspectral reflectance measurements. Remote Sens. Environ 2004, 89, 1–28. [Google Scholar]
- Press, W.; Teukolsky, S.; Vetterling, W.; Flannery, B. Numerical Recipes in Fortran 77, 2nd ed.; Cambridge University Press: New York, NY, USA, 1996. [Google Scholar]
- le Maire, G.; Marsden, C.; Nouvellon, Y.; Grinand, C.; Hakamada, R.; Stape, J.-L.; Laclau, J.-P. MODIS NDVI time-series allow the monitoring of Eucalyptus plantation biomass. Remote Sens. Environ 2011, 115, 2613–2625. [Google Scholar]
- Wang, Q.; Adiku, S.; Tenhunen, J.; Granier, A. On the relationship of NDVI with leaf area index in a deciduous forest site. Remote Sens. Environ 2005, 94, 244–255. [Google Scholar]
- Atzberger, C.; Darvishzadeh, R.; Schlerf, M.; le Maire, G. Suitability and adaptation of PROSAIL radiative transfer model for hyperspectral grassland studies. Remote Sens. Lett 2013, 4, 55–64. [Google Scholar]
- Brazilian Association of Forest Plantation Producers. Chapter 1 Planted forests in Brazil. Statistical Yearbook. 2012. Available online: http://www.abraflor.org.br/estatisticas/ABRAF12/ABRAF12-EN.pdf (accessed on 20 September 2012).
- Almeida, A.C.; Landsberg, J.J.; Sands, P.J.; Ambrogi, M.S.; Fonseca, S.; Barddal, S.M.; Bertolucci, F.L. Needs and opportunities for using a process-based productivity model as a practical tool in Eucalyptus plantations. For. Ecol. Manage 2004, 193, 167–177. [Google Scholar]
- le Maire, G.; Marsden, C.; Laclau, J.-P.; Stape, J.-L.; Corbeels, M.; Nouvellon, Y. Spatial and Temporal Variability of the Carbon Budget of Tropical Eucalyptus Plantations Assessed Using Ecosystem Modelling and Remote Sensing. Proceedings of Landmod 2010: International Conference on Integrative Landscape Modelling, Montpellier, France, 3–5 February 2010; pp. 1–8.
| Stand Name | Area (ha) | Plantation Date | Age on 1 April 2009 (yr) | Date of LAI Measurements (DOY) | LAI (m2·m−2) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| D.S. 2007 | W.S. 2008 | D.S. 2008 | W.S. 2009 | D.S. 2007 | W.S. 2008 | D.S. 2008 | W.S. 2009 | ||||
| SF183U | 108.27 | 03/04/2007 | 2 | 94 | 260 | 3.5 | 2.3 | ||||
| SF178U | 93.12 | 29/03/2006 | 3.01 | 93 | 262 | 4.4 | 2.9 | ||||
| NS24U | 108.53 | 04/04/2006 | 3 | 255 | 3.6 | ||||||
| SF171 | 48.7 | 05/05/2005 | 3.91 | 93 | 260 | 5.7 | 3.0 | ||||
| SF43E | 65.52 | 06/05/2004 | 4.91 | 91 | 263 | 4.2 | 3.4 | ||||
| MG14U | 37.13 | 26/03/2004 | 5.02 | 254 | 2.2 | ||||||
| SF89 | 40.31 | 11/06/2003 | 5.81 | 95 | 260 | 3.5 | 2.3 | ||||
| IT1 | 40 | 06/03/2003 | 6.08 | 332 | 93 | 282 | 21 | 3.2 | 4.1 | 3.0 | 3.5 |
| IT2 | 160 | 06/03/2003 | 6.08 | 332 | 93 | 282 | 21 | 2.6 | 3.6 | 2.1 | 3.2 |
| SVI | Reference | a | b | c | d | e | f |
|---|---|---|---|---|---|---|---|
| DVI | [31] | 1 | −1 | 0 | 0 | 0 | 1 |
| NDVI | [1] | 1 | −1 | 0 | 1 | 1 | 0 |
| IPVI | [32] | 1 | 0 | 0 | 1 | 1 | 0 |
| RVI | [2] | 1 | 0 | 0 | 0 | 1 | 0 |
| WDVI(1) | [33] | 1 | −A | 0 | 0 | 0 | 1 |
| PVI(1) | [34] | 1 | −A | −B | 0 | 0 | |
| SAVI(2) | [4] | (1 + L) | −(1 + L) | 0 | 1 | 1 | L |
| TSAVI(1,3) | [25] | A | −A2 | −A × B | A | 1 | −A × B + X(1 + A2) |
| OSAVI(4) | [27] | 1 | −1 | 0 | 1 | 1 | Y |
| EVI2(5) | [28] | G | −G | 0 | 1 | 6 – 7.5/C | 1 |
| GESAVI(1,6) | [16] | 1 | −A | −B | 0 | 1 | Z |
| GESAVI(7) | [14] | 1 | −1.505 | −0.034 | 0 | 1 | 0.0383 |
| EucVI(8) | This study | 1 | −1.881 | 0.001 | 0.094 | 1.407 | 0.018 |
Share and Cite
Le Maire, G.; Marsden, C.; Nouvellon, Y.; Stape, J.-L.; Ponzoni, F.J. Calibration of a Species-Specific Spectral Vegetation Index for Leaf Area Index (LAI) Monitoring: Example with MODIS Reflectance Time-Series on Eucalyptus Plantations. Remote Sens. 2012, 4, 3766-3780. https://doi.org/10.3390/rs4123766
Le Maire G, Marsden C, Nouvellon Y, Stape J-L, Ponzoni FJ. Calibration of a Species-Specific Spectral Vegetation Index for Leaf Area Index (LAI) Monitoring: Example with MODIS Reflectance Time-Series on Eucalyptus Plantations. Remote Sensing. 2012; 4(12):3766-3780. https://doi.org/10.3390/rs4123766
Chicago/Turabian StyleLe Maire, Guerric, Claire Marsden, Yann Nouvellon, José-Luiz Stape, and Flávio Jorge Ponzoni. 2012. "Calibration of a Species-Specific Spectral Vegetation Index for Leaf Area Index (LAI) Monitoring: Example with MODIS Reflectance Time-Series on Eucalyptus Plantations" Remote Sensing 4, no. 12: 3766-3780. https://doi.org/10.3390/rs4123766
APA StyleLe Maire, G., Marsden, C., Nouvellon, Y., Stape, J.-L., & Ponzoni, F. J. (2012). Calibration of a Species-Specific Spectral Vegetation Index for Leaf Area Index (LAI) Monitoring: Example with MODIS Reflectance Time-Series on Eucalyptus Plantations. Remote Sensing, 4(12), 3766-3780. https://doi.org/10.3390/rs4123766





