Mapping Savanna Tree Species at Ecosystem Scales Using Support Vector Machine Classification and BRDF Correction on Airborne Hyperspectral and LiDAR Data
Abstract
:1. Introduction
2. Methods
2.1. Overview
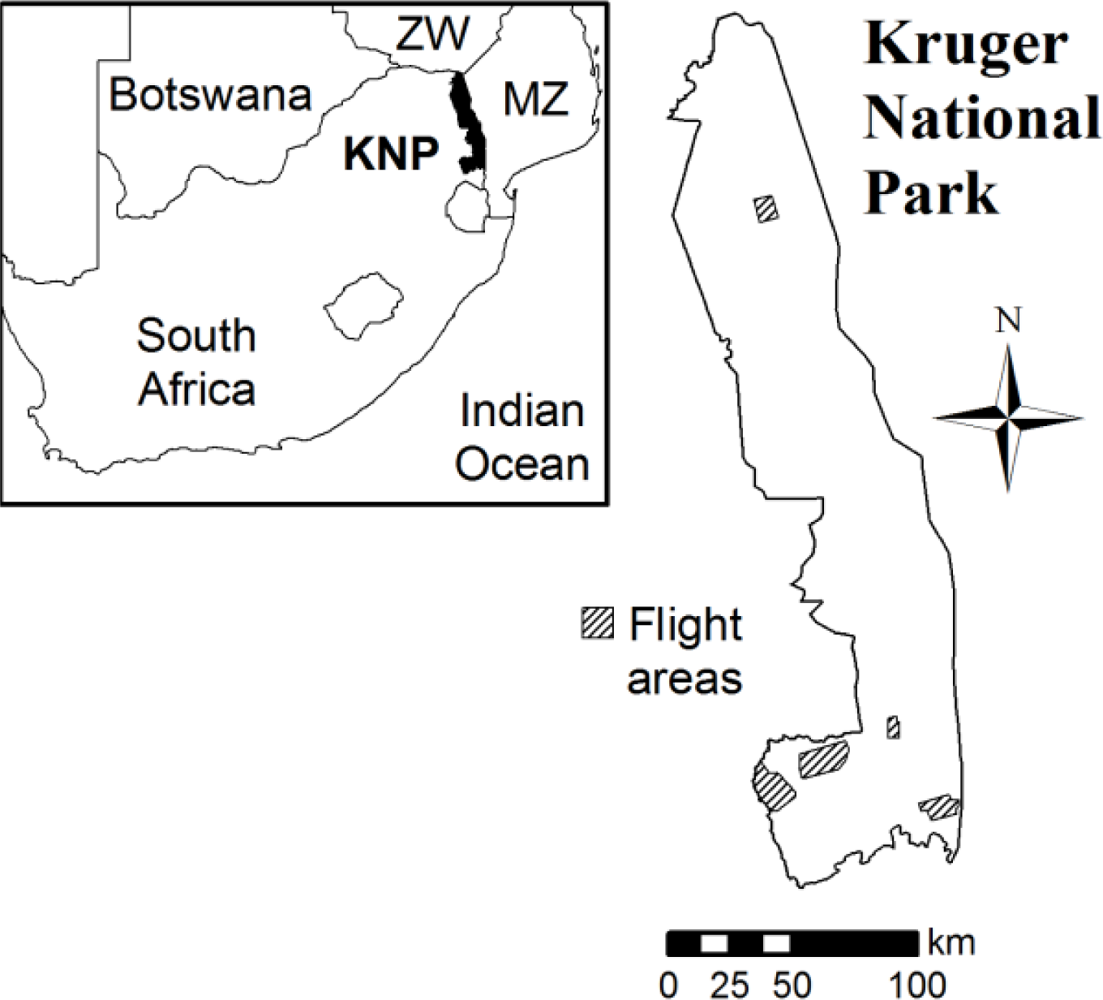
2.2. Study Site
2.3. Airborne Data Collection
2.4. Field Data Collection
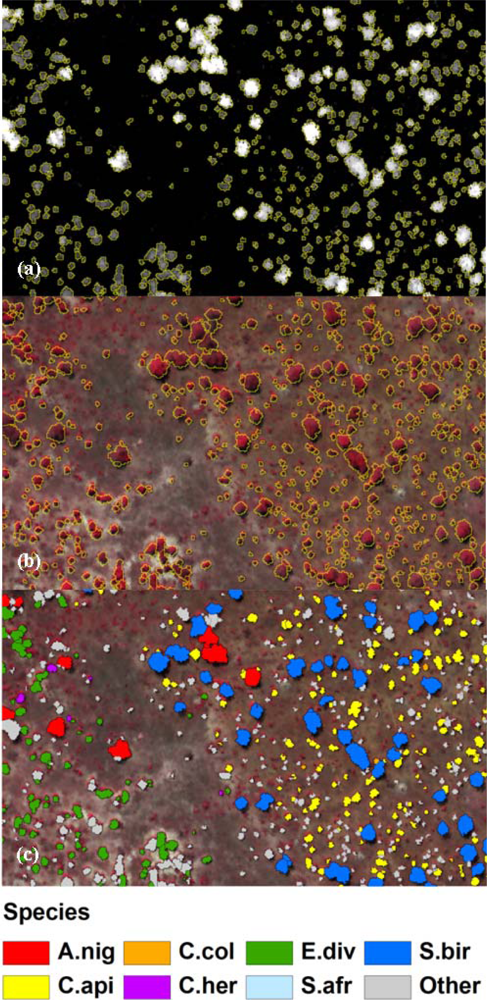
2.5. Crown Segmentation
2.6. BRDF Correction Model
2.7. SVM Model Testing, Calibration, and Validation
- S: An SVM was performed on image pixels using spectral data only. Each pixel was assigned a probability of belonging to each of the classes. Crown identities were predicted by averaging class probabilities over all pixels in a crown and taking the class with the highest probability (n = 14,998 pixels and 72 spectral bands as input variables).
- S + H: An SVM was performed on image pixels using spectral and LiDAR height data. This is the same as Model 1, but with the additional variable of pixel height. Crown identities were predicted in the same way as in Model 1.
- S: An SVM was first performed on image pixels using only spectral data, as in Model 1. The average probabilities of all pixels in a crown were then used as the input variables to a second SVM (n = 729 crowns and 15 class probabilities as input variables to the second SVM).
- S + MH: The same procedure as in Model 3, with the additional variable of maximum crown height added to the crown-level SVM.
- S + MH + A (final model): The same procedure as in Model 4 with the additional variable of crown area in the crown-level SVM. Crown area was defined as the number of pixels belonging to a tree crown, before filtering based on NDVI and mean NIR reflectance.
3. Results
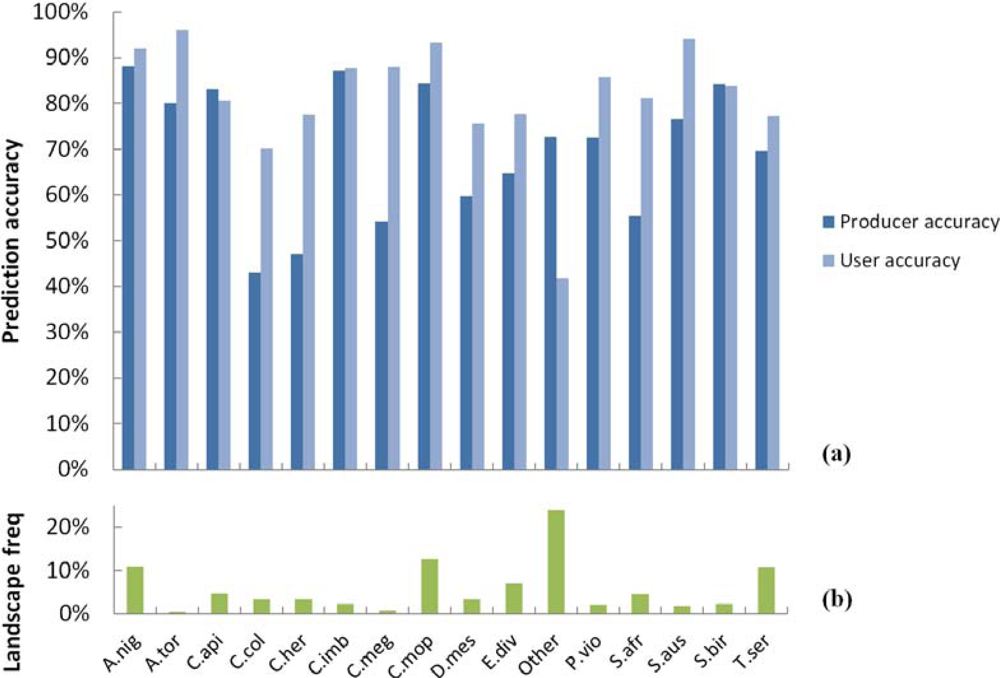
3.1. SVM Classification of Woody Plant Species
3.2. Spatial Performance of Automated Crown Segmentation and Species Predictions
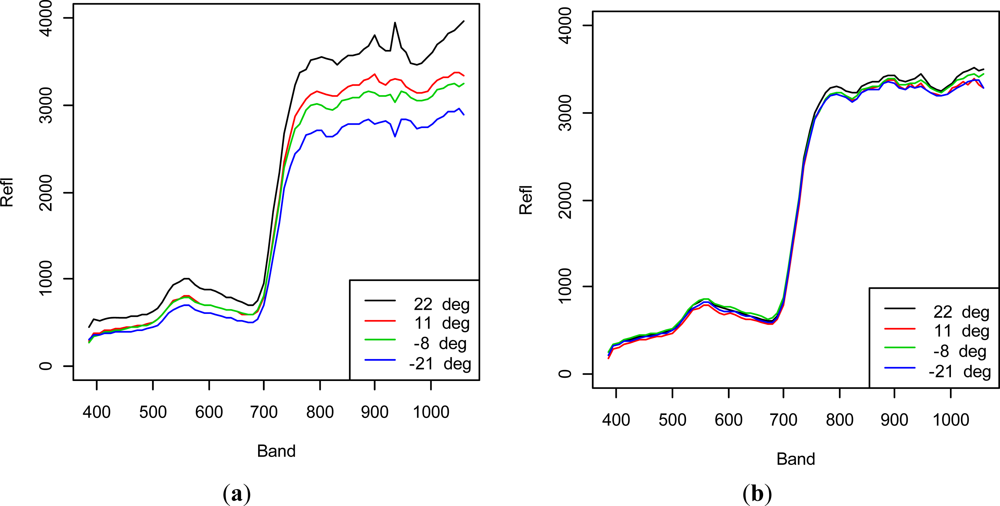
3.3. Spectral Performance of BRDF Correction
3.4. Effects of BRDF Correction on Species Prediction
4. Discussion
5. Conclusions
Acknowledgments
References
- Scholes, R.J.; Walker, B.H. An African Savanna: Synthesis of the Nylsvley Study; Cambridge University Press: New York, NY, USA, 1993. [Google Scholar]
- Du Toit, J.T.; Rogers, K.H.; Biggs, H.C. The Kruger Experience: Ecology and Management of Savanna Heterogeneity; Island Press: Washington, DC, USA, 2003. [Google Scholar]
- Scholes, R.J.; Archer, S.R. Tree-grass interactions in savannas. Annu. Rev. Ecol. Syst 1997, 28, 517–544. [Google Scholar]
- Archer, S.; Scifres, C.; Bassham, C.R. Autogenic succession in a subtropical savanna: Conversion of grassland to thorn woodland. Ecol. Monogr 1988, 58, 111–127. [Google Scholar]
- Carlson, K.M.; Asner, G.P.; Hughes, F.R.; Ostertag, R.; Martin, R.E. Hyperspectral remote sensing of canopy biodiversity in Hawaiian lowland rainforests. Ecosystems 2007, 10, 536–549. [Google Scholar]
- Cho, M.A.; Debba, P.; Mathieu, R.; Naidoo, L.; van Aardt, J.; Asner, G.P. Improving discrimination of savanna tree species through a multiple-endmember spectral angle mapper approach: Canopy-level analysis. IEEE Trans. Geosci. Remote Sens 2010, 48, 4133–4142. [Google Scholar]
- Dalponte, M.; Bruzzone, L.; Gianelle, D. Fusion of hyperspectral and LiDAR remote sensing data for classification of complex forest areas. IEEE Trans. Geosci. Remote Sens 2008, 46, 1416–1427. [Google Scholar]
- Hill, R.A.; Thomson, A.G. Mapping woodland species composition and structure using airborne spectral and LiDAR data. Int. J. Remote Sens 2005, 26, 3763–3779. [Google Scholar]
- Clark, M.L.; Roberts, D.A.; Clark, D.B. Hyperspectral discrimination of tropical rain forest tree species at leaf to crown scales. Remote Sen. Environ 2005, 96, 375–398. [Google Scholar]
- Naidoo, L.; Cho, M.A.; Mathieu, R.; Asner, G. Classification of savanna tree species, in the Greater Kruger National Park region, by integrating hyperspectral and LiDAR data in a Random Forest data mining environment. ISPRS J. Photogramm 2012, 69, 167–179. [Google Scholar]
- Féret, J.-B.; Asner, G.P. Tree species discrimination in tropical forests using airborne imaging spectroscopy. IEEE Trans. Geosci. Remote Sens 2012, PP,. 1–12. [Google Scholar]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens 2004, 42, 1778–1790. [Google Scholar]
- Mercier, G.; Lennon, M. Support Vector Machines for Hyperspectral Image Classification with Spectral-Based Kernels. Proceedings of 2003 IEEE International Geoscience and Remote Sensing Symposium, IGARSS ’03, Toulouse, France, 21–25 July 2003.
- Camps-Valls, G.; Gomez-Chova, L.; Calpe-Maravilla, J.; Martin-Guerrero, J.D.; Soria-Olivas, E.; Alonso-Chorda, L.; Moreno, J. Robust support vector method for hyperspectral data classification and knowledge discovery. IEEE Trans. Geosci. Remote Sens 2004, 42, 1530–1542. [Google Scholar]
- Bazi, Y.; Melgani, F. Toward an optimal SVM classification system for hyperspectral remote sensing images. IEEE Trans. Geosci. Remote Sens 2006, 44, 3374–3385. [Google Scholar]
- Ross, J. The Radiation Regime and Architecture of Plant Stands; Springer: The Hague, The Netherlands, 1981. [Google Scholar]
- Strahler, A.H.; Jupp, D.L.B. Modeling bidirectional reflectance of forests and woodlands using boolean models and geometric optics. Remote Sens. Environ 1990, 34, 153–166. [Google Scholar]
- Liang, S.; Strahler, A.H. Retrieval of surface BRDF from multangle remotely sensed data. Remote Sens. Environ 1994, 50, 18–30. [Google Scholar]
- Deering, D.W.; Eck, T.F.; Grier, T. Shinnery oak bidirectional reflectance properties and canopy model inversion. IEEE Trans. Geosci. Remote Sens 1992, 30, 339–348. [Google Scholar]
- Deering, D.W.; Middleton, E.M.; Irons, J.R.; Blad, B.L.; Walter-Shea, E.A.; Hays, C.J.; Walthall, C.; Eck, T.F.; Ahmad, S.P.; Banerjee, B.P. Prairie grassland bidirectional reflectance measured by different instruments at the FIFE site. J. Geophys. Res 1992. [Google Scholar] [CrossRef]
- Asner, G.P.; Wessman, C.A.; Privette, J.L. Unmixing the directional reflectances of AVHRR sub-pixel landcovers. IEEE Trans. Geosci. Remote Sens 1997, 35, 868–878. [Google Scholar]
- Asner, G.P.; Braswell, B.H.; Schimel, D.S.; Wessman, C.A. Ecological research needs from multiangle remote sensing data. Remote Sens. Environ 1998, 63, 155–165. [Google Scholar]
- Asner, G.P. Contributions of multi-view angle remote sensing to land-surface and biogeochemical research. Remote Sens. Rev 2000, 18, 137–162. [Google Scholar]
- Wanner, W.; Li, X.; Strahler, A.H. On the derivation of kernels for kernel-driven models of bidirectional reflectance. J. Geophys. Res 1995, 100, 21077–21089. [Google Scholar]
- Strahler, A.H.; Muller, J.-P. MODIS Science Team Members. In MODIS BRDF/Albedo Product: Algorithm Theoretical Basis Document Version 5.0. MODIS Documentation; Boston University: Boston, MA, USA, 1999. [Google Scholar]
- Beisl, U. A new method for correction of bidirectional effects in hyperspectral imagery. Proc. SPIE 2002, 45, 304–311. [Google Scholar]
- Chen, J.M.; Leblanc, S.G.; Miller, J.R.; Freemantle, J.; Loechel, S.E.; Walthall, C.L.; Innanen, K.A.; White, H.P. Compact Airborne Spectrographic Imager (CASI) used for mapping biophysical parameters of boreal forests. J. Geophys. Res 1999, 104, 27945–27958. [Google Scholar]
- Pisek, J.; Chen, J.M.; Miller, J.R.; Freemantle, J.R.; Peltoniemi, J.I.; Simic, A. Mapping forest background reflectance in a boreal region using multiangle compact airborne spectrographic imager data. IEEE Trans. Geosci. Remote Sens 2010, 48, 499–510. [Google Scholar]
- Lucas, R.; Bunting, P.; Paterson, M.; Chisholm, L. Classification of Australian forest communities using aerial photography, CASI and HyMap data. Remote Sens. Environ 2008, 112, 2088–2103. [Google Scholar]
- Asner, G.P.; Wessman, C.A.; Schimel, D.S. Heterogeneity of savanna canopy structure and function from imaging spectrometry and inverse modeling. Ecol. Appl 1998, 8, 1022–1036. [Google Scholar]
- Hoffmann, W.A.; da Silva, E.R.; Machado, G.C.; Bucci, S.J.; Scholz, F.G.; Goldstein, G.; Meinzer, F.C. Seasonal leaf dynamics across a tree density gradient in a Brazilian savanna. Oecologia 2005, 145, 306–315. [Google Scholar]
- Geerling, G.; Labrador-Garcia, M.; Clevers, J.; Ragas, A.; Smits, A. Classification of floodplain vegetation by data fusion of spectral (CASI) and LiDAR data. Int. J. Remote Sens 2007, 28, 4263–4284. [Google Scholar]
- Venter, F.J.; Scholes, R.J. The Abiotic Template and Its Associated Vegetation Pattem. In The Kruger Experience: Ecology and Management of Savanna Heterogeneity; Biggs, H.C., du Toit, J.T., Rogers, K.H., Eds.; Island Press: Washington, DC, USA, 2003; pp. 83–129. [Google Scholar]
- Asner, G.P.; Knapp, D.E.; Kennedy-Bowdoin, T.; Jones, M.O.; Martin, R.E.; Boardman, J.; Field, C.B. Carnegie airborne observatory: In-flight fusion of hyperspectral imaging and waveform light detection and ranging for three-dimensional studies of ecosystems. J. Appl. Remote Sens 2007, 1. [Google Scholar] [CrossRef]
- Asner, G.P.; Levick, S.R.; Kennedy-Bowdoin, T.; Knapp, D.E.; Emerson, R.; Jacobson, J.; Colgan, M.S.; Martin, R.E. Large-scale impacts of herbivores on the structural diversity of African savannas. Proc. Natl. Acad. Sci. USA 2009, 106, 4947–4952. [Google Scholar]
- Lucht, W.; Schaaf, C.B.; Strahler, A.H. An algorithm for the retrieval of albedo from space using semiempirical BRDF models. IEEE Trans. Geosci. Remote Sens 2000, 38, 977–998. [Google Scholar]
- Maignan, F.; Breon, F.M.; Lacaze, R. Bidirectional reflectance of earth targets: Evaluation of analytical models using a large set of spaceborne measurements with emphasis on the Hot Spot. Remote Sens. Environ 2004, 90, 210–220. [Google Scholar]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm 2011, 66, 247–259. [Google Scholar]
- Licciardi, G.; Pacifici, F.; Tuia, D.; Prasad, S.; West, T.; Giacco, F.; Thiel, C.; Inglada, J.; Christophe, E.; Chanussot, J. Decision fusion for the classification of hyperspectral data: Outcome of the 2008 GRS-S data fusion contest. IEEE Trans. Geosci. Remote Sens 2009, 47, 3857–3865. [Google Scholar]
- Cortes, C.; Vapnik, V. Support-Vector networks. Mach. Learn 1995, 20, 273–297. [Google Scholar]
- Dimitriadou, E.; Hornik, K.; Leisch, F.; Meyer, D.; Weingessel, A. e1071: Misc Functions of the Department of Statistics (e1071), TU Wien. Available online: http://CRAN.R-project.org/package=e1071 (accessed on 8 August 2012).
- R Development Core Team. R: The R Project for Statistical Computing. Available online: http://www.R-project.org/ (accessed on 7 July 2012).
- Wolpert, D.H. Stacked generalization. Neural Networks 1992, 5, 241–259. [Google Scholar]
- Harsanyi, J.C.; Chang, C.I. Hyperspectral image classification and dimensionality reduction: An orthogonal subspace projection approach. IEEE Trans. Geosci. Remote Sens 1994, 32, 779–785. [Google Scholar]
- Roberts, G. A review of the application of BRDF models to infer land cover parameters at regional and global scales. Prog. Phys. Geog 2001, 25, 483–511. [Google Scholar]
- Walthall, C.L.; Norman, J.M.; Welles, J.M.; Campbell, G.; Blad, B.L. Simple equation to approximate the bi-directional reflectance from vegetation canopies and bare soil surfaces. Appl. Opt 1985, 24, 383–87. [Google Scholar]



| Species | Family | Tree Crowns | Pixels | Basal D (cm) | Crown D (m) | H (m) |
|---|---|---|---|---|---|---|
| Acacia nigrescens | Fabaceae | 45 | 806 | 8–72 | 2–17 | 3–34 |
| Acacia tortilis | Fabaceae | 38 | 564 | 5–57 | 3–17 | 2–13 |
| Combretum apiculatum | Combretaceae | 60 | 365 | 2–49 | 2–11 | 2–9 |
| Combretum collinum | Combretaceae | 29 | 174 | 2–24 | 2–8 | 1–6 |
| Combretum hereoense | Combretaceae | 36 | 346 | 2–32 | 1–7 | 1–8 |
| Combretum imberbe | Combretaceae | 65 | 3,693 | 7–135 | 3–28 | 5–22 |
| Colophospermum mopane | Fabaceae | 44 | 542 | 5–96 | 1–13 | 2–18 |
| Croton megalobotrys | Euphorbiaceae | 12 | 114 | 7–90 | 2–9 | 2–6 |
| Diospyros mespiliformis | Ebenaceae | 31 | 1,425 | 16–182 | 4–28 | 4–26 |
| Euclea divinorum | Ebenaceae | 50 | 587 | 1–37 | 2–9 | 1–6 |
| Philenoptera violacea | Fabaceae | 44 | 1,397 | 6–109 | 2–18 | 0–19 |
| Spirostachys africana | Euphorbiaceae | 26 | 618 | 5–53 | 4–15 | 2–12 |
| Salvadora australis | Salvadoraceae | 26 | 298 | 3–45 | 2–14 | 1–7 |
| Sclerocarya birrea | Anacardiaceae | 73 | 1,469 | 4–87 | 4–20 | 6–15 |
| Terminalia sericea | Combretaceae | 48 | 408 | 1–43 | 2–13 | 2–11 |
| Other | 106 | 1,306 | ||||
| Total | 729 | 13,998 |
Share and Cite
Colgan, M.S.; Baldeck, C.A.; Féret, J.-B.; Asner, G.P. Mapping Savanna Tree Species at Ecosystem Scales Using Support Vector Machine Classification and BRDF Correction on Airborne Hyperspectral and LiDAR Data. Remote Sens. 2012, 4, 3462-3480. https://doi.org/10.3390/rs4113462
Colgan MS, Baldeck CA, Féret J-B, Asner GP. Mapping Savanna Tree Species at Ecosystem Scales Using Support Vector Machine Classification and BRDF Correction on Airborne Hyperspectral and LiDAR Data. Remote Sensing. 2012; 4(11):3462-3480. https://doi.org/10.3390/rs4113462
Chicago/Turabian StyleColgan, Matthew S., Claire A. Baldeck, Jean-Baptiste Féret, and Gregory P. Asner. 2012. "Mapping Savanna Tree Species at Ecosystem Scales Using Support Vector Machine Classification and BRDF Correction on Airborne Hyperspectral and LiDAR Data" Remote Sensing 4, no. 11: 3462-3480. https://doi.org/10.3390/rs4113462
APA StyleColgan, M. S., Baldeck, C. A., Féret, J.-B., & Asner, G. P. (2012). Mapping Savanna Tree Species at Ecosystem Scales Using Support Vector Machine Classification and BRDF Correction on Airborne Hyperspectral and LiDAR Data. Remote Sensing, 4(11), 3462-3480. https://doi.org/10.3390/rs4113462





