Evaluation of Four Supervised Learning Methods for Benthic Habitat Mapping Using Backscatter from Multi-Beam Sonar
Abstract
:1. Introduction
2. Methods
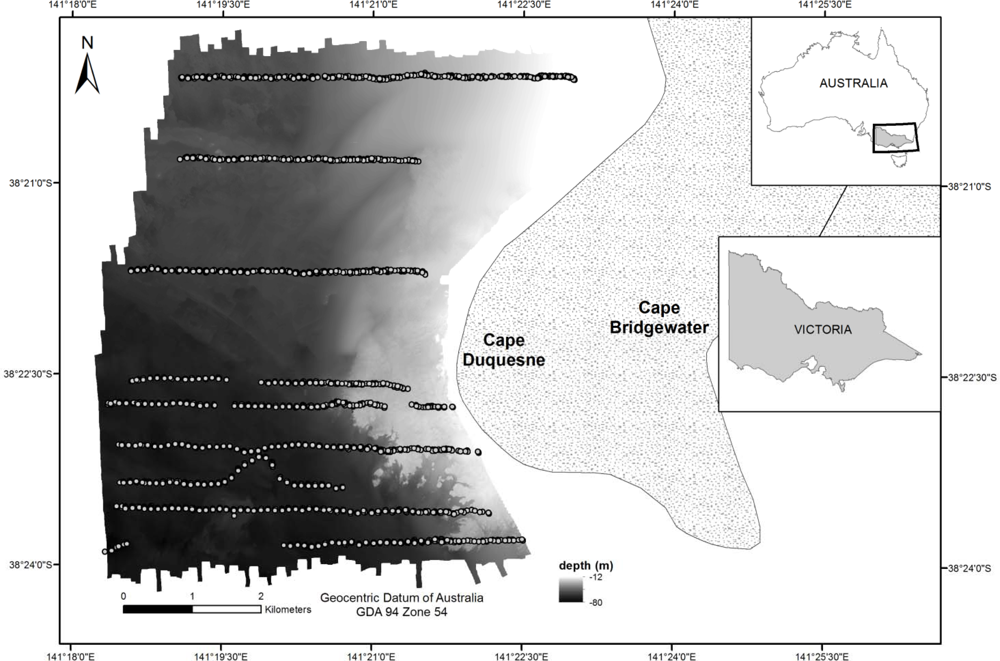
2.1. Study Site
2.2. Acoustic Data
2.3. Ground Truth Data
2.4. Supervised Learning
2.5. Spatial Segmentation and Class Assignment
2.6. Accuracy Assessment and Habitat Map Comparison
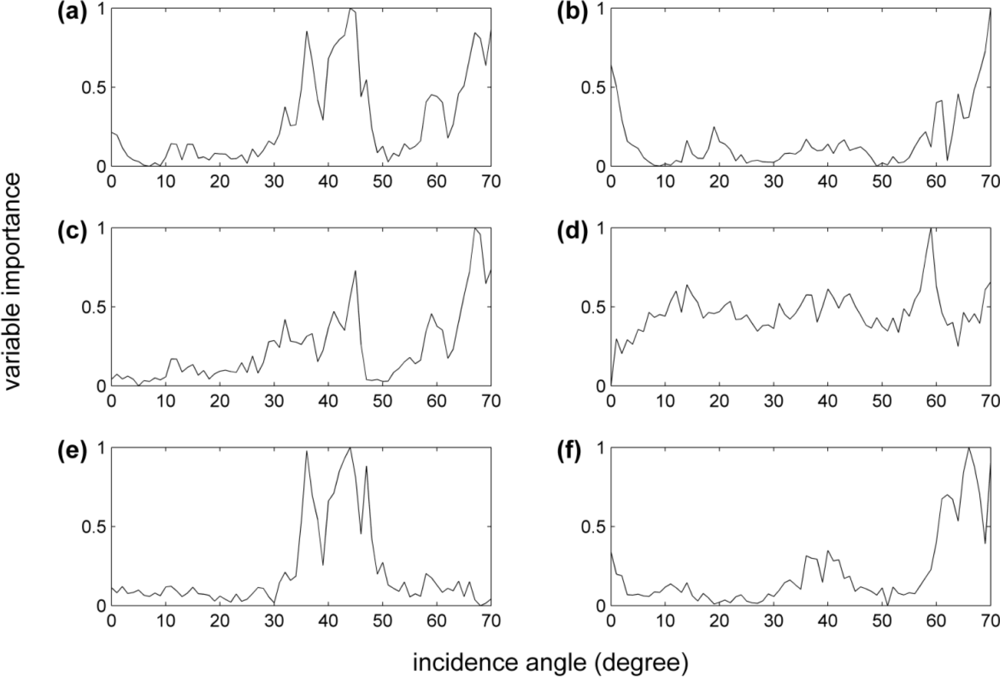
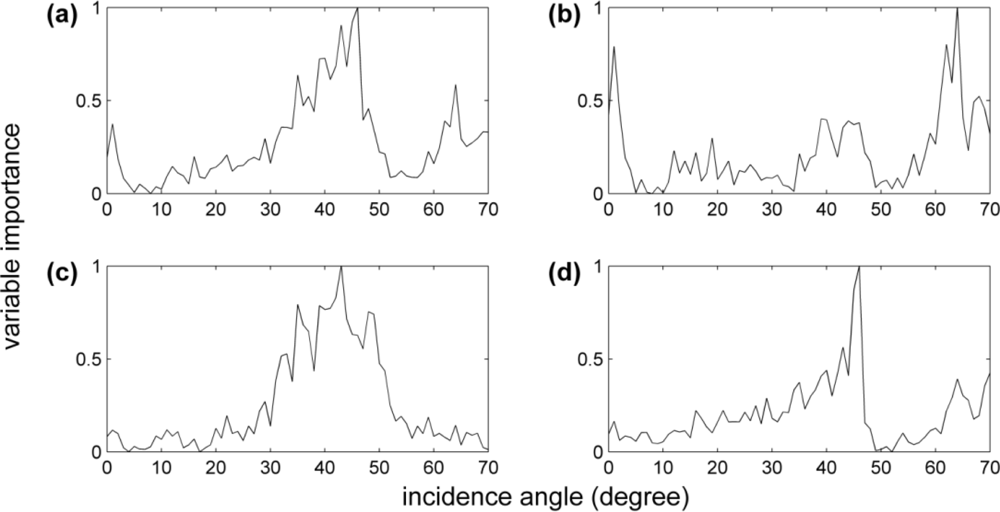
2.7. Variable Importance Measure
3. Results
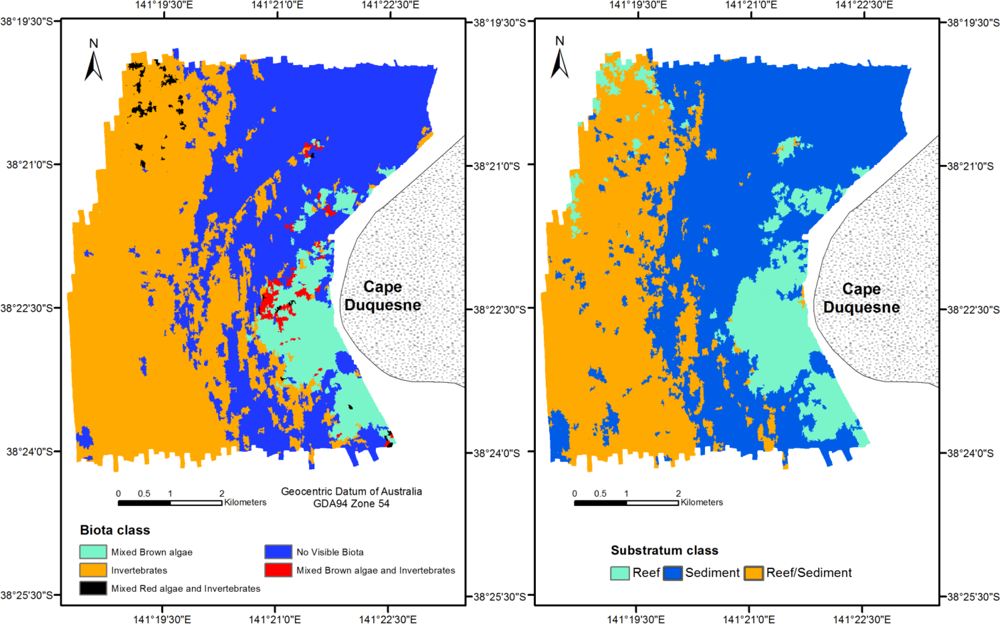
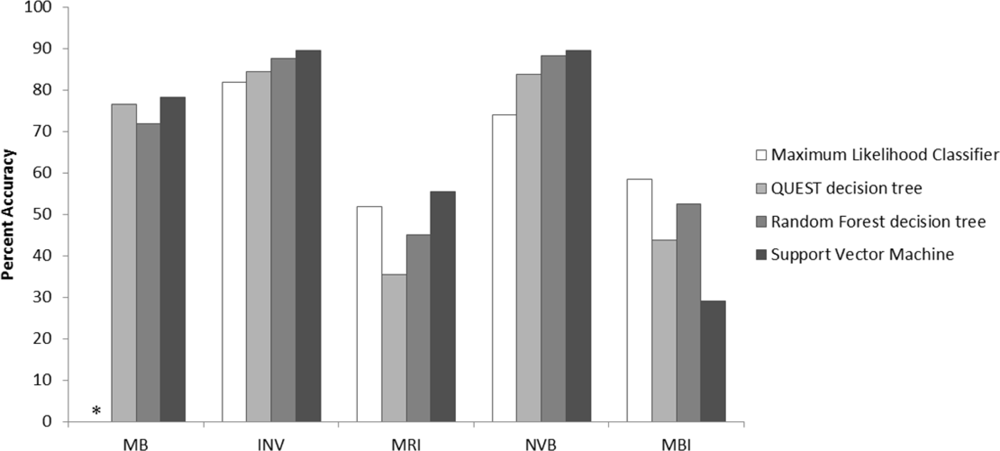
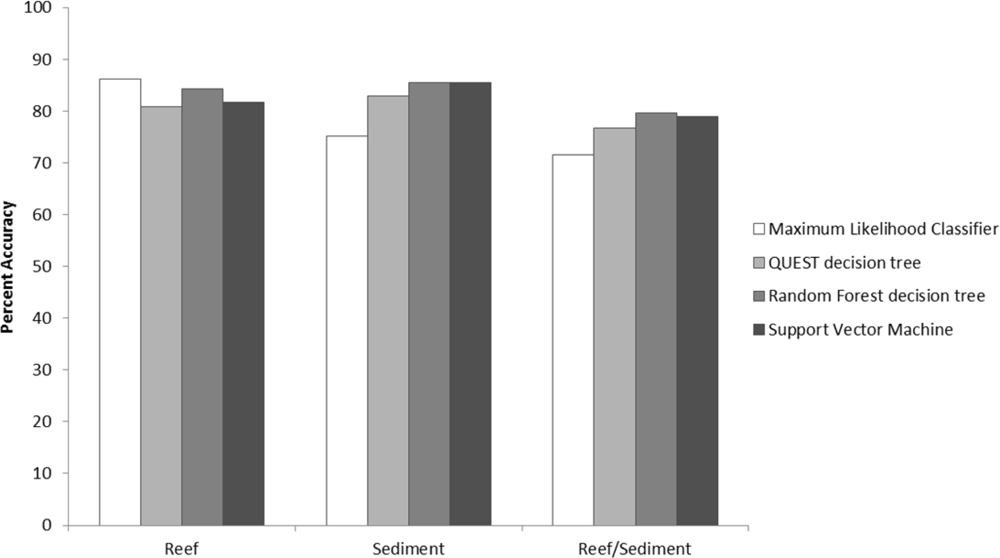
3.1. Habitat Map Accuracy
3.2. Habitat Map Comparison
3.3. Variable Importance
4. Discussion
5. Conclusions
Acknowledgments
References
- Fonseca, L.; Mayer, L. Remote estimation of surficial seafloor properties through the application Angular Range Analysis to multibeam sonar data. Mar. Geophys. Res 2007, 28, 119–126. [Google Scholar]
- Hughes-Clarke, J.E.; Danforth, B.W.; Valentine, P. Areal Seabed Classification using Backscatter Angular Response at 95 kHz. High Frequency Acoustics in Shallow Water (NATO SACLANTCEN Conference Proceedings), Series CP-45; Pace, N.G., Pouliquen, E., Bergem, O., Lyons, A.P., Eds.; Office of Naval Research, United States National Liaison Officer to the SACLANTCEN: Arlington, VA, USA, 1997; pp. 243–250. [Google Scholar]
- Lamarche, G.; Lurton, X.; Verdier, A.-L.; Augustin, J.-M. Quantitative characterization of seafloor substrate and bedforms using advanced processing of multibeam backscatter—Application to Cook Strait, New Zealand. Cont. Shelf Res 2010, 31, S93–S109. [Google Scholar]
- Simons, D.G.; Snellen, M. A Bayesian approach to seafloor classification using multi-beam echo-sounder backscatter data. Appl. Acoust 2009, 70, 1258–1268. [Google Scholar]
- Che-Hasan, R.; Ierodiaconou, D.; Laurenson, L. Combining angular response classification and backscatter imagery segmentation for benthic biological habitat mapping. Estuar. Coast. Shelf Sci 2012, 97, 1–9. [Google Scholar] [Green Version]
- De Falco, G.; Tonielli, R.; Di Martino, G.; Innangi, S.; Simeone, S.; Parnum, I.M. Relationships between multibeam backscatter, sediment grain size and Posidonia oceanica seagrass distribution. Cont. Shelf Res 2010, 30, 1941–1950. [Google Scholar]
- Kloser, R.J.; Penrose, J.D.; Butler, A.J. Multi-beam backscatter measurements used to infer seabed habitats. Cont. Shelf Res 2010, 30, 1772–1782. [Google Scholar]
- Hamilton, L.J.; Parnum, I. Acoustic seabed segmentation from direct statistical clustering of entire multibeam sonar backscatter curves. Cont. Shelf Res 2011, 31, 138–148. [Google Scholar]
- Parnum, I.M.; Gavrilov, A.N. High-frequency multibeam echo-sounder measurements of seafloor backscatter in shallow water: Part 2 Mosaic production, analysis and classification. Underwater Technology 2011, 30, 13–26. [Google Scholar]
- Parnum, I.M. Benthic Habitat Mapping Using Multibeam Sonar Systems. Curtin University of Technology, Bentley, WA, Australia, 2007. [Google Scholar]
- Jackson, D.R.; Winebrenner, D.P.; Ishimaru, A. Application of the composite roughness model to high-frequency bottom backscattering. J. Acoust. Soc. Am 1986, 79, 1410–1422. [Google Scholar]
- Augustin, J.M.; Suave, R.; Lurton, X.; Voisset, M.; Dugelay, S.; Satra, C. Contribution of the multibeam acoustic imagery to the exploration of the sea-bottom. Mar. Geophys. Res 1996, 18, 459–486. [Google Scholar]
- Fonseca, L.; Brown, C.; Calder, B.; Mayer, L.; Rzhanov, Y. Angular range analysis of acoustic themes from Stanton Banks Ireland: A link between visual interpretation and multibeam echosounder angular signatures. Appl. Acoust 2009, 70, 1298–1304. [Google Scholar]
- Rzhanov, Y.; Fonseca, L.; Mayer, L. Construction of seafloor thematic maps from multibeam acoustic backscatter angular response data. Comput. Geosci 2012, 41, 181–187. [Google Scholar]
- Ierodiaconou, D.; Rattray, A.; Laurenson, L.; Monk, J.; Lind, P. Victorian Marine Habitat Mapping Project; Deakin University: Geelong, VIC, Australia, 2007. [Google Scholar]
- The Interim Marine and Coastal Regionalisation for Australia: An Ecosystem-Based Classification for Marine and Coastal Environments (Version 3.3); Environment Australia-Commonwealth Department of the Environment: Canberra, ACT, Australia, 1998.
- Manandhar, R.; Odeh, I.; Ancev, T. Improving the accuracy of land use and land cover classification of Landsat data using post-classification enhancement. Remote Sens 2009, 1, 330–344. [Google Scholar]
- Dean, A.M.; Smith, G.M. An evaluation of per-parcel land cover mapping using maximum likelihood class probabilities. Int. J. Remote Sens 2003, 24, 2905–2920. [Google Scholar]
- Theodoridis, S.; Koutroumbas, K. Classifiers Based on Bayes Decision Theory. In Pattern Recognition, 4th ed; Academic Press: Boston, MA, USA, 2009. [Google Scholar]
- Friedl, M.A.; Brodley, C.E. Decision tree classification of land cover from remotely sensed data. Remote Sens. Environ 1997, 61, 399–409. [Google Scholar]
- Gray, J.B.; Fan, G. Classification tree analysis using TARGET. Comput. Stat. Data Anal 2008, 52, 1362–1372. [Google Scholar]
- Loh, W.Y.; Shih, Y.S. Split selection methods for classification trees. Stat. Sin 1997, 7, 815–840. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn 2001, 45, 5–32. [Google Scholar]
- Jaiantilal, A. Classification and Regression by Randomforest-Matlab. 2009. Available online: http://code.google.com/p/randomforest-matlab (accessed on 12 December 2010).
- Vapnik, V.N. An overview of statistical learning theory. IEEE Trans. Neural Netw 1999, 10, 988–999. [Google Scholar]
- Kavzoglu, T.; Colkesen, I. A kernel functions analysis for support vector machines for land cover classification. Int. J. Appl. Earth Obs. Geoinf 2009, 11, 352–359. [Google Scholar]
- Chang, C.-C.; Lin, C.-J. LIBSVM: A library for support vector machines. ACM TIST 2011, 2, 2:27:21–27:27. [Google Scholar]
- Lucieer, V.; Lamarche, G. Unsupervised fuzzy classification and object-based image analysis of multibeam data to map deep water substrates, Cook Strait, New Zealand. Cont. Shelf Res 2011, 31, 1236–1247. [Google Scholar]
- Comaniciu, D.; Meer, P. Mean Shift Analysis and Applications. Proceedings of the 7th IEEE International Conference on Computer vision, Kerkyra, Greece, 20–27 September 1999; 2, pp. 1197–1203.
- Congalton, R.G. A review of assessing the accuracy of classifications of remotely sensed data. Remote Sens. Environ 1991, 37, 35–46. [Google Scholar]
- Cohen, J. A Coefficient of agreement for nominal scales. Educ. Psychol. Meas 1960, 20, 37–46. [Google Scholar]
- Jensen, J.R. Introductory Digital Image Processing: A Remote Sensing Perspective, 3rd ed; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2005. [Google Scholar]
- Hagen, A. Multi-method Assessment of Map Similarity. Proceedings of the 5th AGILE Conference on Geographic Information Science, Palma de Mallorca, Spain, 25–27 April 2002; 2003; pp. 171–182. [Google Scholar]
- Cutler, D.R.; Edwards, T.C.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random forests for classification in ecology. Ecology 2007, 88, 2783–2792. [Google Scholar]
- Siwabessy, P.J.W.; Gavrilov, A.N.; Duncan, A.J.; Parnum, I.M. Statistical Analysis of High-Frequency Multibeam Backscatter Data in Shallow Water. Proceedings of ACOUSTICS 2006, Christchurch, New Zealand, 20–22 November 2006.
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices, 2nd ed; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm 2011, 66, 247–259. [Google Scholar]
- Schimel, A.C.G.; Healy, T.R.; Johnson, D.; Immenga, D. Quantitative experimental comparison of single-beam, sidescan, and multibeam benthic habitat maps. ICES J. Mar. Sci 2010, 67, 1766–1779. [Google Scholar]
- McGonigle, C.; Grabowski, J.H.; Brown, C.J.; Weber, T.C.; Quinn, R. Detection of deep water benthic macroalgae using image-based classification techniques on multibeam backscatter at Cashes Ledge, Gulf of Maine, USA. Estuar. Coast. Shelf Sci 2011, 91, 87–101. [Google Scholar]
- McGonigle, C.; Brown, C.J.; Quinn, R. Insonification orientation and its relevance for image-based classification of multibeam backscatter. ICES J. Mar. Sci 2010, 67, 1010–1023. [Google Scholar]
- Galway, R.S. Comparision of Target Detection Capabilities of the Reson Seabat 8101 and Reson Seabat 9001 Multibeam Sonars; Department of Geodesy and Geomatics Engineering, University of New Brunswick: Fredericton, NB, Canada, 2000. [Google Scholar]
- Ierodiaconou, D.; Burq, S.; Reston, M.; Laurenson, L. Marine benthic habitat mapping using multibeam data, georeferenced video and image classification techniques in Victoria, Australia. J. Spat. Sci 2007, 52, 93–104. [Google Scholar]
- Rattray, A.; Ierodiaconou, D.; Laurenson, L.; Burq, S.; Reston, M. Hydro-acoustic remote sensing of benthic biological communities on the shallow South East Australian continental shelf. Estuar. Coast. Shelf Sci 2009, 84, 237–245. [Google Scholar]
- Blondel, P.; Gómez Sichi, O. Textural analyses of multibeam sonar imagery from Stanton Banks, Northern Ireland continental shelf. Appl. Acoust 2009, 70, 1288–1297. [Google Scholar]
- Galparsoro, I.; Borja, Á.; Bald, J.; Liria, P.; Chust, G. Predicting suitable habitat for the European lobster (Homarus gammarus), on the Basque continental shelf (Bay of Biscay), using Ecological-Niche Factor Analysis. Ecol. Model 2009, 220, 556–567. [Google Scholar]
| Biota | Substratum | |||
|---|---|---|---|---|
| Classifiers | Overall Accuracy (%) | Kappa Coefficient | Overall Accuracy (%) | Kappa Coefficient |
| Maximum Likelihood Classifier | 69.9 | 0.51 | 74.5 | 0.59 |
| QUEST decision tree | 79.6 | 0.66 | 80.2 | 0.67 |
| Random Forest decision tree | 83.8 | 0.73 | 83.0 | 0.72 |
| Support Vector Machine | 84.8 | 0.75 | 82.6 | 0.71 |
| Comparison | Z Statistic | |
|---|---|---|
| Biota | Substratum | |
| MLC vs. QUEST | 3.6* | 2.0* |
| MLC vs. RF | 5.6* | 3.1* |
| MLC vs. SVM | 6.0* | 2.8* |
| QUEST vs. RF | 1.8 | 1.1 |
| QUEST vs. SVM | 2.2* | 0.8 |
| RF vs. SVM | 0.4 | 0.3 |
| Map Comparison | Biota | Substratum | ||
|---|---|---|---|---|
| KLoc | KHisto | KLoc | KHisto | |
| MLC vs. QUEST | 0.76 | 0.75 | 0.69 | 0.95 |
| MLC vs. RF | 0.70 | 0.81 | 0.70 | 0.95 |
| MLC vs. SVM | 0.70 | 0.76 | 0.70 | 0.88 |
| QUEST vs. RF | 0.88 | 0.91 | 0.87 | 0.97 |
| QUEST vs. SVM | 0.79 | 0.98 | 0.87 | 0.83 |
| RF vs. SVM | 0.90 | 0.90 | 0.94 | 0.84 |
Share and Cite
Hasan, R.C.; Ierodiaconou, D.; Monk, J. Evaluation of Four Supervised Learning Methods for Benthic Habitat Mapping Using Backscatter from Multi-Beam Sonar. Remote Sens. 2012, 4, 3427-3443. https://doi.org/10.3390/rs4113427
Hasan RC, Ierodiaconou D, Monk J. Evaluation of Four Supervised Learning Methods for Benthic Habitat Mapping Using Backscatter from Multi-Beam Sonar. Remote Sensing. 2012; 4(11):3427-3443. https://doi.org/10.3390/rs4113427
Chicago/Turabian StyleHasan, Rozaimi Che, Daniel Ierodiaconou, and Jacquomo Monk. 2012. "Evaluation of Four Supervised Learning Methods for Benthic Habitat Mapping Using Backscatter from Multi-Beam Sonar" Remote Sensing 4, no. 11: 3427-3443. https://doi.org/10.3390/rs4113427
APA StyleHasan, R. C., Ierodiaconou, D., & Monk, J. (2012). Evaluation of Four Supervised Learning Methods for Benthic Habitat Mapping Using Backscatter from Multi-Beam Sonar. Remote Sensing, 4(11), 3427-3443. https://doi.org/10.3390/rs4113427





