Downscaling Land Surface Temperature in an Urban Area: A Case Study for Hamburg, Germany
Abstract
:1. Introduction
2. Data and Methodology
2.1. LST Downscaling
2.2. Case Study Area
2.3. Data
2.3.1. Predictors
2.3.2 LST Data
2.4. Used Methods
2.4.1. Spatial Aggregation of Predictors to the SEVIRI Grid
2.4.2. Selection of Suitable Predictors
2.4.3. Downscaling
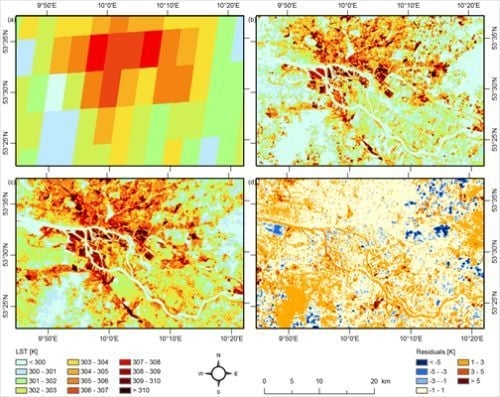
- a predictor, in the example MAST Figure 1(a) and the first TIR PC Figure 1(b) are used, is correlated to LST in both LR (red) and HR (blue) domain.
- the variance in the LR domain is much lower for both predictors and dependent variable (which is plausible since the upscaling is essentially a low pass filtering operation), and
- the linear relation is similar for both domains.
3. Results
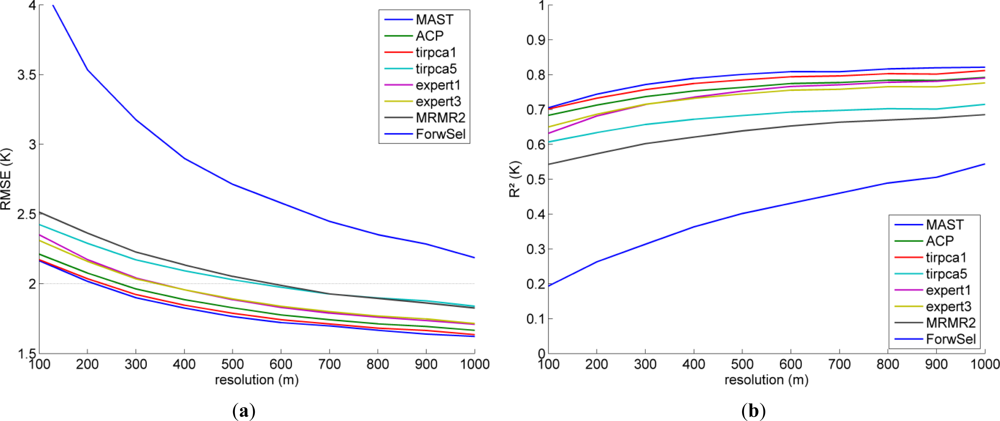
3.1. Linear Regression with Different Predictor Sets
3.2. Downscaling to Different Resolutions
4. Discussion
5. Conclusions
Acknowledgments
References
- Jin, M.S.; Kessomkiat, W.; Pereira, G. Satellite-observed urbanization characters in Shanghai, China: Aerosols, urban heat island effect, and land-atmosphere interactions. Remote Sens 2011, 3, 83–99. [Google Scholar]
- Xiong, Y.; Huang, S.; Chen, F.; Ye, H.; Wang, C.; Zhu, C. The impacts of rapid urbanization on the thermal environment: A remote sensing study of Guangzhou, South China. Remote Sens 2012, 4, 2033–2056. [Google Scholar]
- Frey, C.M.; Parlow, E. Flux measurements in Cairo. Part 2: On the determination of the spatial radiation and energy balance using aster satellite data. Remote Sens 2012, 4, 2635–2660. [Google Scholar]
- Kim, Y.-H.; Baik, J.-J. Spatial and temporal structure of the urban heat island in Seoul. J. Appl. Meteor 2005, 44, 591–605. [Google Scholar]
- Oke, T.R. City size and the urban heat island. Atmos. Environ 1973, 7, 769–779. [Google Scholar]
- Yow, D.M. Urban heat islands: Observations, impacts, and adaptation. Geogr. Compass 2007, 1, 1227–1251. [Google Scholar]
- Weng, Q. Thermal infrared remote sensing for urban climate and environmental studies: Methods, applications, and trends. ISPRS J. Photogramm 2009, 64, 335–344. [Google Scholar]
- Hamdi, R. Estimating urban heat island effects on the temperature series of uccle (Brussels, Belgium) using remote sensing data and a land surface scheme. Remote Sens 2010, 2, 2773–2784. [Google Scholar]
- Liu, L.; Zhang, Y. Urban heat island analysis using the landsat tm data and aster data: A case study in Hong Kong. Remote Sens 2011, 3, 1535–1552. [Google Scholar]
- Rinner, C.; Hussain, M. Toronto’s urban heat island—Exploring the relationship between land use and surface temperature. Remote Sens 2011, 3, 1251–1265. [Google Scholar]
- Zhou, J.; Chen, Y.; Wang, J.; Zhan, W. Maximum nighttime urban heat island (UHI) intensity simulation by integrating remotely sensed data and meteorological observations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens 2011, 4, 138–146. [Google Scholar]
- Weng, Q.; Rajasekar, U.; Hu, X. Modeling urban heat islands and their relationship with impervious surface and vegetation abundance by using aster images. IEEE Trans. Geosci. Remote Sens 2011, 49, 4080–4089. [Google Scholar]
- Fabrizi, R.; Bonafoni, S.; Biondi, R. Satellite and ground-based sensors for the urban heat island analysis in the city of Rome. Remote Sens 2010, 2, 1400–1415. [Google Scholar]
- Roth, M.; Oke, T.R.; Emery, W.J. Satellite-derived urban heat islands from three coastal cities and the utilization of such data in urban climatology. Int. J. Remote Sens 1989, 10, 1699–1720. [Google Scholar]
- Voogt, J.A.; Oke, T.R. Thermal remote sensing of urban climates. Remote Sens. Environ 2003, 86, 370–384. [Google Scholar]
- Tomlinson, C.J.; Chapman, L.; Thornes, J.E.; Baker, C. Remote sensing land surface temperature for meteorology and climatology: A review. Meteorol. Appl 2011, 18, 296–306. [Google Scholar]
- Li, J.; Song, C.; Cao, L.; Zhu, F.; Meng, X.; Wu, J. Impacts of landscape structure on surface urban heat islands: A case study of Shanghai, China. Remote Sens. Environ 2011, 115, 3249–3263. [Google Scholar]
- Schott, J.; Gerace, A.; Brown, S.; Gartley, M.; Montanaro, M.; Reuter, D.C. Simulation of image performance characteristics of the landsat data continuity mission (LDCM) thermal infrared sensor (TIRS). Remote Sens 2012, 4, 2477–2491. [Google Scholar]
- Price, J.C. Combining multispectral data of differing spatial resolution. IEEE Trans. Geosci. Remote Sens 1999, 37, 1199–1203. [Google Scholar]
- Švab, A.; Oštir, K. High-resolution image fusion: Methods to preserve spectral and spatial resolution. Photogramm. Eng. Remote Sensing 2006, 72, 565–572. [Google Scholar]
- Zhukov, B.; Oertel, D.; Lanzl, F.; Reinhackel, G. Unmixing-based multisensor multiresolution image fusion. IEEE Trans. Geosci. Remote Sens 1999, 37, 1212–1226. [Google Scholar]
- Kaheil, Y.H.; Creed, I.F. Detecting and downscaling wet areas on boreal landscapes. IEEE Geosci. Remote Sens. Lett 2009, 6, 179–183. [Google Scholar]
- Zurita-Milla, R.; Kaiser, G.; Clevers, J.G.P.W.; Schneider, W.; Schaepman, M.E. Downscaling time series of MERIS full resolution data to monitor vegetation seasonal dynamics. Remote Sens. Environ 2009, 113, 1874–1885. [Google Scholar]
- Denis, B.; Laprise, R.; Caya, D.; Côté, J. Downscaling ability of one-way nested regional climate models: The big-brother experiment. Clim. Dynam 2002, 18, 627–646. [Google Scholar]
- Gangopadhyay, S.; Clark, M.; Rajagopalan, B. Statistical downscaling using K-nearest neighbors. Water Resour. Res 2005, 41, W02024. [Google Scholar]
- Dozier, J. A method for satellite identification of surface temperature fields of subpixel resolution. Remote Sens. Environ 1981, 11, 221–229. [Google Scholar]
- Liu, D.; Pu, R. Downscaling thermal infrared radiance for subpixel land surface temperature retrieval. Sensors 2008, 8, 2695–2706. [Google Scholar]
- Inamdar, A.K.; French, A. Disaggregation of GOES land surface temperatures using surface emissivity. Geophys. Res. Lett 2009, 36, L02408. [Google Scholar]
- Inamdar, A.K.; French, A.; Hook, S.; Vaughan, G.; Luckett, W. Land surface temperature retrieval at high spatial and temporal resolutions over the southwestern United States. J. Geophys. Res 2008, 113, D07107. [Google Scholar]
- Kustas, W.P.; Norman, J.M.; Anderson, M.C.; French, A.N. Estimating subpixel surface temperatures and energy fluxes from the vegetation index-radiometric temperature relationship. Remote Sens. Environ 2003, 85, 429–440. [Google Scholar]
- Dominguez, A.; Kleissl, J.; Luvall, J.C.; Rickman, D.L. High-resolution urban thermal sharpener (HUTS). Remote Sens. Environ 2011, 115, 1772–1780. [Google Scholar]
- Zakšek, K.; Oštir, K. Downscaling land surface temperature for urban heat island diurnal cycle analysis. Remote Sens. Environ 2012, 117, 114–124. [Google Scholar]
- Prihodko, L.; Goward, S.N. Estimation of air temperature from remotely sensed surface observations. Remote Sens. Environ 1997, 60, 335–346. [Google Scholar]
- Czajkowski, K.P.; Goward, S.N.; Stadler, S.J.; Walz, A. Thermal remote sensing of near surface environmental variables: Application over the Oklahoma mesonet. Prof. Geogr 2000, 52, 345–357. [Google Scholar]
- Agam, N.; Kustas, W. P.; Anderson, M.C.; Li, F.; Neale, C.M.U. A vegetation index based technique for spatial sharpening of thermal imagery. Remote Sens. Environ 2007, 107, 545–558. [Google Scholar]
- Stisen, S.; Sandholt, I.; Nørgaard, A.; Fensholt, R.; Eklundh, L. Estimation of diurnal air temperature using MSG SEVIRI data in West Africa. Remote Sens. Environ 2007, 110, 262–274. [Google Scholar]
- Zakšek, K.; Schroedter-Homscheidt, M. Parameterization of air temperature in high temporal and spatial resolution from a combination of the SEVIRI and MODIS instruments. ISPRS J. Photogramm 2009, 64, 414–421. [Google Scholar]
- Merlin, O.; Duchemin, B.; Hagolle, O.; Jacob, F.; Coudert, B.; Chehbouni, G.; Dedieu, G.; Garatuza, J.; Kerr, Y. Disaggregation of MODIS surface temperature over an agricultural area using a time series of Formosat-2 images. Remote Sens. Environ 2010, 114, 2500–2512. [Google Scholar] [Green Version]
- Weng, Q.; Lu, D.; Schubring, J. Estimation of land surface temperature-vegetation abundance relationship for urban heat island studies. Remote Sens. Environ 2004, 89, 467–483. [Google Scholar]
- Yuan, F.; Bauer, M.E. Comparison of impervious surface area and normalized difference vegetation index as indicators of surface urban heat island effects in Landsat imagery. Remote Sens. Environ 2007, 106, 375–386. [Google Scholar]
- Stathopoulou, M.; Cartalis, C. Downscaling AVHRR land surface temperatures for improved surface urban heat island intensity estimation. Remote Sens. Environ 2009, 113, 2592–2605. [Google Scholar]
- Bechtel, B. Robustness of annual cycle parameters to characterize the urban thermal landscapes. IEEE Geosci. Remote Sens. Lett 2012, 9, 876–880. [Google Scholar]
- Bechtel, B.; Langkamp, T.; Ament, F.; Bohner, J.; Daneke, C.; Gunzkofer, R.E.N.; Leitl, B.; Ossenbrugge, J.; Ringeler, A. Towards an urban roughness parameterisation using interferometric SAR data taking the metropolitan region of Hamburg as an example. Meteorol. Z 2011, 20, 29–37. [Google Scholar]
- Benediktsson, J.A.; Palmason, J.A.; Sveinsson, J.R. Classification of hyperspectral data from urban areas based on extended morphological profiles. IEEE Trans. Geosci. Remote Sens 2005, 43, 480–491. [Google Scholar]
- Bechtel, B.; Daneke, C. Classification of local climate zones based on multiple earth observation data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens 2012, 5, 1191–1202. [Google Scholar]
- Song, C.; Woodcock, C.E.; Seto, K.C.; Lenney, M.P.; Macomber, S.A. Classification and change detection using Landsat TM data: When and how to correct atmospheric effects? Remote Sens. Environ 2001, 75, 230–244. [Google Scholar]
- Bechtel, B. Robustness of annual cycle parameters to characterize the urban thermal landscapes. IEEE Geosci. Remote Sens. Lett 2012, 9, 876–880. [Google Scholar]
- SAF LSA. Land Surface Temperature (15 mins). Available online: https://landsaf.meteo.pt/algorithms.jsp?seltab=0&starttab=0 (accessed on 18 June 2012).
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens 1996, 34, 892–905. [Google Scholar]
- SAF NWC. MSG Cloud Products. Available online: http://www.nwcsaf.org/HD/MainNS.jsp (accessed on 18 June 2012).
- Trigo, I.F.; Monteiro, I.T.; Olesen, F.; Kabsch, E. An assessment of remotely sensed land surface temperature. J. Geophys. Res 2008, 113, D17108. [Google Scholar]
- Sun, D.; Pinker, R.T. Retrieval of surface temperature from the MSG-SEVIRI-observations: Part I. Methodology. Inter. J. Remote Sens 2007, 28, 5255–5272. [Google Scholar]
- Gillespie, A.; Rokugawa, S.; Matsunaga, T.; Cothern, J.S.; Hook, S.; Kahle, A.B. A temperature and emissivity separation algorithm for Advanced Spaceborne Thermal Emission and Reflection radiometer (ASTER) images. IEEE Trans. Geosci. Remote Sens 1998, 36, 1113–1126. [Google Scholar]
- Deneke, H.M.; Roebeling, R.A. Downscaling of METEOSAT SEVIRI 0.6 and 0.8 μm channel radiances utilizing the high-resolution visible channel. Atmos. Chem. Phys 2010, 10, 9761–9772. [Google Scholar]
- Peng, H.; Long, F.; Ding, C. Feature selection based on mutual information: Criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Patt. Anal. Mach. Int 2005, 27, 1226–1238. [Google Scholar]
- Chen, S.; Hong, X.; Harris, C.J.; Sharkey, P.M. Sparse Modelling Using Orthogonal Forward Regression with PRESS Statistic and Regularization. Available online: http://eprints.soton.ac.uk/259231/ (accessed on 28 June 2012).
- Noori, R.; Hoshyaripour, G.; Ashrafi, K.; Araabi, B.N. Uncertainty analysis of developed ANN and ANFIS models in prediction of carbon monoxide daily concentration. Atmos. Environ 2010, 44, 476–482. [Google Scholar]
- Keramitsoglou, I. Advanced Earth Observation Methodologies for the Study of the Thermal Environment of Cities. Proceedings of 2012 Second International Workshop on Earth Observation and Remote Sensing Applications (EORSA), Shanghai, China, 8–11 June 2012; pp. 11–15.




| Predictor Set | Calibr. | Validation (HR) | ||||
|---|---|---|---|---|---|---|
| Name | Num | R2 (LR) | MAE (K) | RMSE (K) | R2 | BIAS (K) |
| predefined sets | ||||||
| heighstat | 6 | 0.722 | 4.31 | 6.09 | 0.04 | 1.40 |
| LUCshare | 3 | 0.634 | 2.23 | 2.96 | 0.33 | 1.33 |
| NDVI | 32 | 0.825 | 6.40 | 9.15 | 0.00 | 1.46 |
| TIR | 32 | 0.867 | 3.36 | 4.46 | 0.11 | 1.42 |
| single predictors | ||||||
| bestNDVI[lres] | 1 | 0.356 | 2.51 | 3.73 | 0.03 | 1.36 |
| bestTIR[lres] | 1 | 0.628 | 2.08 | 2.63 | 0.53 | 1.32 |
| aggregated LST predictors | ||||||
| MAST | 1 | 0.468 | 1.76 | 2.17 | 0.71 | 1.29 |
| ACP | 2 | 0.593 | 1.82 | 2.21 | 0.68 | 1.31 |
| tirpca1 | 1 | 0.575 | 1.79 | 2.17 | 0.70 | 1.31 |
| tirpca3 | 3 | 0.622 | 1.89 | 2.37 | 0.63 | 1.37 |
| tirpca5 | 5 | 0.633 | 1.89 | 2.42 | 0.61 | 1.38 |
| selected by expert knowledge | ||||||
| expert1 | 7 | 0.698 | 1.86 | 2.35 | 0.63 | 1.35 |
| expert2 | 2 | 0.514 | 1.85 | 2.47 | 0.57 | 1.34 |
| expert3 | 2 | 0.591 | 1.82 | 2.31 | 0.65 | 1.33 |
| feature selection algorithms | ||||||
| MRMR2 | 2 | 0.641 | 1.98 | 2.51 | 0.54 | 1.31 |
| MRMR6 | 6 | 0.702 | 2.03 | 2.64 | 0.52 | 1.35 |
| MRMR10 | 10 | 0.717 | 2.12 | 2.91 | 0.43 | 1.35 |
| ForwSel | 5 | 0.799 | 3.07 | 4.18 | 0.19 | 1.42 |
Share and Cite
Bechtel, B.; Zakšek, K.; Hoshyaripour, G. Downscaling Land Surface Temperature in an Urban Area: A Case Study for Hamburg, Germany. Remote Sens. 2012, 4, 3184-3200. https://doi.org/10.3390/rs4103184
Bechtel B, Zakšek K, Hoshyaripour G. Downscaling Land Surface Temperature in an Urban Area: A Case Study for Hamburg, Germany. Remote Sensing. 2012; 4(10):3184-3200. https://doi.org/10.3390/rs4103184
Chicago/Turabian StyleBechtel, Benjamin, Klemen Zakšek, and Gholamali Hoshyaripour. 2012. "Downscaling Land Surface Temperature in an Urban Area: A Case Study for Hamburg, Germany" Remote Sensing 4, no. 10: 3184-3200. https://doi.org/10.3390/rs4103184