Scaling Effect of Area-Averaged NDVI: Monotonicity along the Spatial Resolution
Abstract
:1. Introduction
2. Background
3. Resolution Transform Model
3.1. Endmember Spectra and Their NDVI
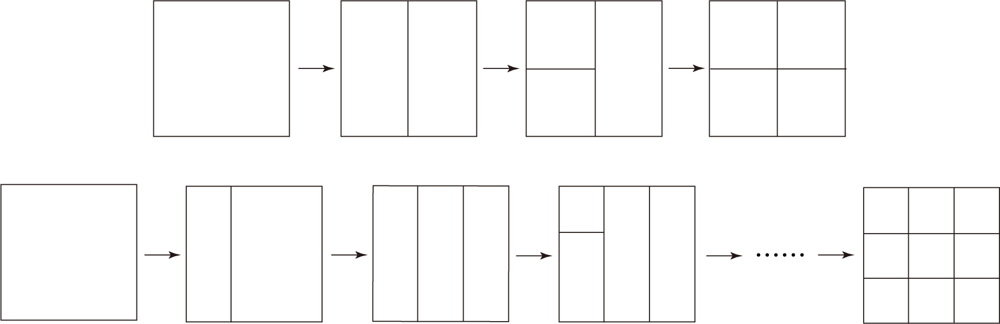
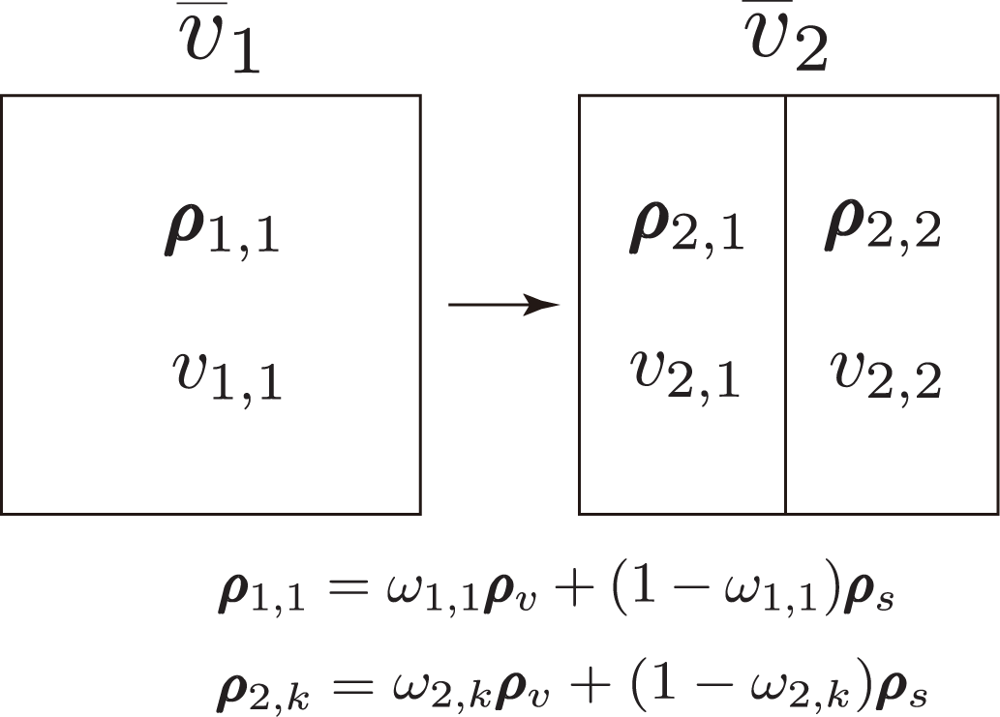
3.2. Resolution Transform Model and Area-Averaged NDVI
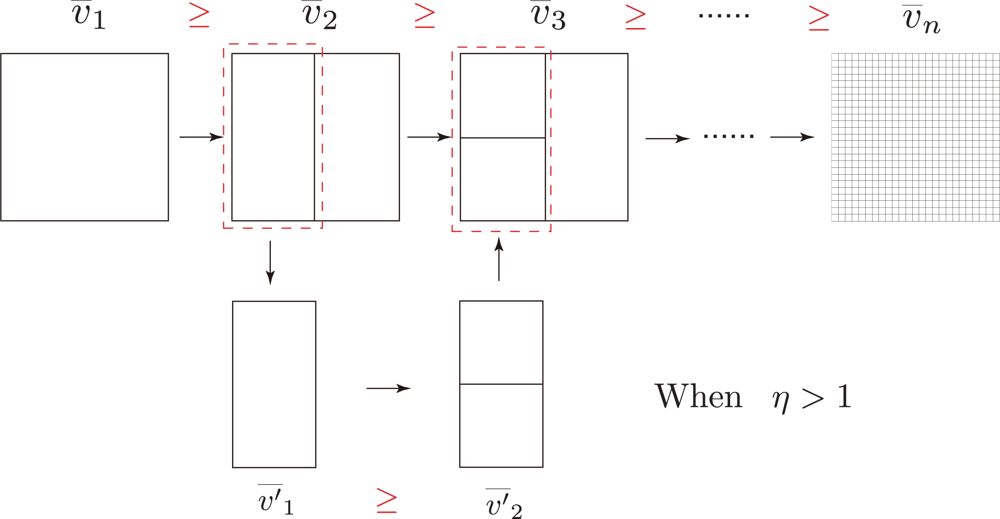
3.3. v̄j Calculated at Various Resolutions
4. Monotonicity of the Area-Averaged NDVI
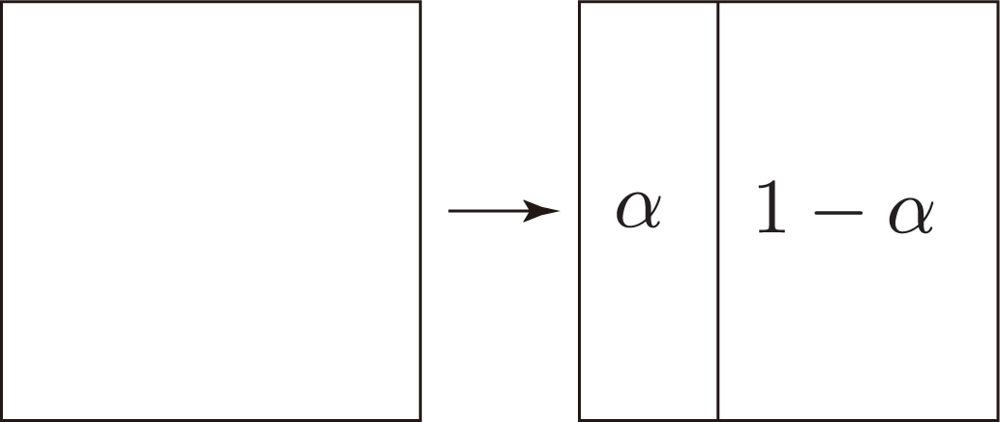
4.1. Partial Derivative of v̄2 with Respect to ω2,1
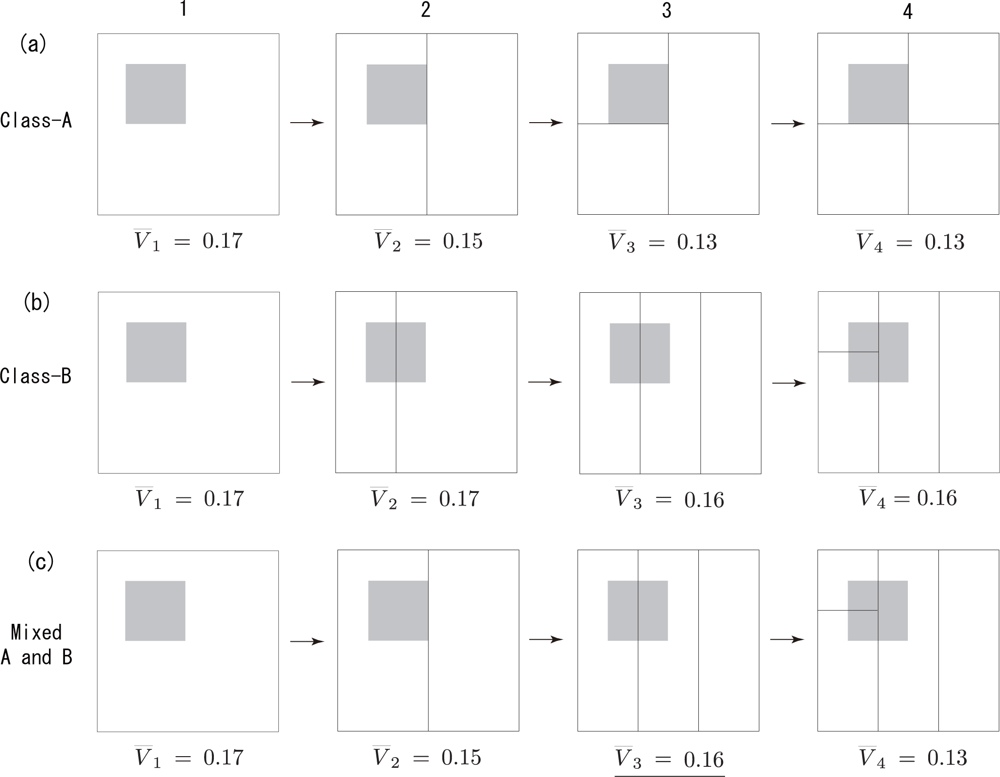
4.2. The Monotonicity of the NDVI within a Resolution Class
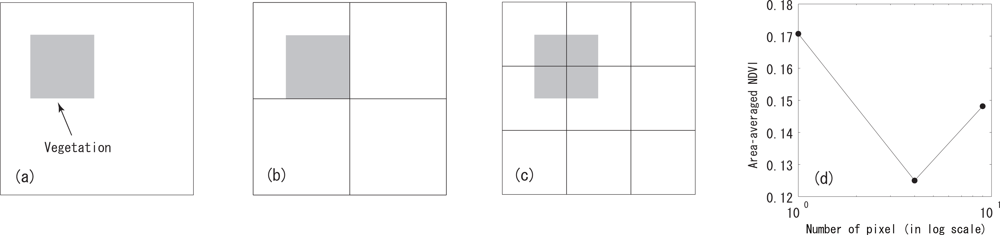
5. Numerical Simulation
6. Discussion
7. Conclusions
Acknowledgments
References
- Myneni, R.B.; Keeling, C.D.; Tucker, C.J.; Asrar, G.; Nemani, R.R. Increased plant growth in the northern high latitudes from 1981 to 1991. Nature 1997, 386, 698–702. [Google Scholar]
- Los, S.O.; Pollack, N.H.; Parris, M.T.; Collatz, G.J.; Tucker, C.J.; Sellers, P.J.; Malmstrom, C.M.; DeFries, R.S.; Bounoua, L.; Dazlich, D.A. A global 9-yr biophysical land surface dataset from NOAA AVHRR data. J. Hydrometeorol 2000, 1, 183–199. [Google Scholar]
- Sellers, P.J.; Los, S.O.; Tucker, C.J.; Justice, C.O.; Dazlich, D.A.; Collatz, G.J.; Randall, D.A. A revised land surface parameterization (SiB2) for atmospheric GCMS. Part I: Model formulation. J. Climate 1996, 9, 676–705. [Google Scholar]
- Sellers, P.J.; Randall, D.A.; Collatz, G.J.; Berry, J.A.; Field, C.B.; Dazlich, D.A.; Zhang, C.; Collelo, G.D.; Bounoua, L. A revised land surface parameterization(SiB2) for atmospheric GCMs. Part II: the generation of global fields of terrestrial biophysical parameters from satellite data. J. Climate 1996, 9, 706–737. [Google Scholar]
- Jarlan, L.; Mangiarotti, S.; Mougin, E.; Mazzega, P.; Hiernaux, P.; Dantec, V.L. Assimilation of SPOT/VEGETATION NDVI data into a sahelian vegetation dynamics model. Remote Sens. Environ 2008, 112, 1381–1394. [Google Scholar]
- Goetz, S.J. Multi-sensor analysis of NDVI, surface temperature and biophysical variables at a mixed grassland site. Int. J. Remote Sens 1997, 18, 71–94. [Google Scholar]
- Pottier, C.; Garcon, V.; Larnicol, G.; Sudre, G.; Schaeffer, P.; Traon, P.Y.L. Merging SeaWIFS and MODIS/Aqua ocean color data in North and Equatorial Atlantic using weighted averaging and objective analysis. IEEE Trans. Geosci. Remote Sens 2006, 44, 3436–3451. [Google Scholar]
- Tucker, C.J.; Pinzon, J.E.; Brown, M.E.; Slayback, D.A.; Pak, E.W.; Mahoney, R.; Vermote, E.F.; Saleous, N.E. An extended AVHRR 8-km NDVI dataset compatible with MODIS and SPOT vegetation NDVI data. Int. J. Remote Sens 2005, 26, 4485–4498. [Google Scholar]
- Pohl, C.; Van Genderen, J.L. Multisensor image fusion in remote sensing: Concepts, methods and applications. Int. J. Remote Sens 1998, 19, 823–854. [Google Scholar]
- Price, J.C. Combining multispectral data of differing spatial resolution. IEEE Trans. Geosci. Remote Sens 1999, 37, 1199–1203. [Google Scholar]
- Brown, M.; Pinzon, J.; Didan, K.; Morisette, J.; Tucker, C. Evaluation of the consistency of long-term NDVI time series derived from AVHRR,SPOT-vegetation, SeaWiFS, MODIS, and Landsat ETM+ sensors. IEEE Trans. Geosci. Remote Sens 2006, 44, 1787–1793. [Google Scholar]
- Wulder, M.A.; Butson, C.R.; White, J.C. Cross-sensor change detection over a forested landscape: Options to enable continuity of medium spatial resolution measures. Remote Sens. Environ 2008, 112, 796–809. [Google Scholar]
- Pouliot, D.; Latifovic, R.; Fernandes, R.; Olthof, I. Evaluation of compositing period and AVHRR and MERIS combination for improvement of spring phenology detection in deciduous forests. Remote Sens. Environ 2011, 115, 158–166. [Google Scholar]
- Arai, E.; Shimabukuro, Y.E.; Pereira, G.; Vijaykumar, N.L. A multi-resolution multi-temporal technique for detecting and mapping deforestation in the Brazilian Amazon rainforest. Remote Sens 2011, 3, 1943–1956. [Google Scholar]
- Stellmes, M.; Udelhoven, T.; Roder, A.; Sonnenschein, R.; Hill, J. Dryland observation at local and regional scale—Comparison of Landsat TM/ETM+ and NOAA AVHRR time series. Remote Sens. Environ 2010, 114, 2111–2125. [Google Scholar]
- Townshend, J.R.G.; Justice, C.O. Selecting the spatial resolution of satellite sensors required for global monitoring of land transformations. Int. J. Remote Sens 1988, 9, 187–236. [Google Scholar]
- van Leeuwen, W.J.; Orr, B.J.; Marsh, S.E.; Herrmann, S.M. Multi-sensor NDVI data continuity: Uncertainties and implications for vegetation monitoring applications. Remote Sens. Environ 2006, 100, 67–81. [Google Scholar]
- Ganguly, S.; Schull, M.A.; Samanta, A.; Shabanov, N.V.; Milesi, C.; Nemani, R.R.; Knyazikhin, Y.; Myneni, R.B. Generating vegetation leaf area index earth system data record from multiple sensors. Part 1: Theory. Remote Sens. Environ 2008, 112, 4333–4343. [Google Scholar]
- Zhao, T.; Bergen, K.M.; Brown, D.G.; Shugart, H.H. Scale dependence in quantification of land-cover and biomass change over Siberian boreal forest landscapes. Landscape Ecol 2009, 24, 1299–1313. [Google Scholar]
- Miura, T.; Huete, A.; Yoshioka, H. An empirical investigation of cross-sensor relationships of NDVI and red/near-infrared reflectance using EO-1 Hyperion data. Remote Sens. Environ 2006, 100, 223–236. [Google Scholar]
- Bounoua, L.; Collatz, G.J.; Los, S.O.; Sellers, P.J.; Dazlich, D.A.; Tucker, C.J.; Randall, D.A. Sensitivity of climate to changes in NDVI. J. Climate 2000, 13, 2277–2292. [Google Scholar]
- McConnell, M.; Weidman, S. Uncertainty Management in Remote Sensing of Climate Data: Summary of a Workshop; The National Academies Press: Washington, DC, USA, 2009. [Google Scholar]
- Overpeck, J.T.; Meehl, G.A.; Bony, S.; Easterling, D.R. Climate data challenges in the 21st Century. Science 2011, 331, 700–702. [Google Scholar]
- Hu, Z.; Islam, S. A frame work for analyzing and designing scale invariant remote sensing algorithms. IEEE Trans. Geosci. Remote Sens 1997, 35, 747–755. [Google Scholar]
- Jiang, Z.; Huete, A.R.; Chen, J.; Chen, Y.; Yan, G.; Zhang, X. Analysis of NDVI and scaled difference vegetation index retrievals of vegetation fraction. Remote Sens. Environ 2006, 101, 366–378. [Google Scholar]
- Wu, H.; Li, Z.L. Scale issues in remote sensing: A review on analysis, processing and modeling. Sensors 2009, 9, 1768–1793. [Google Scholar]
- Chen, J.M. Spatial scaling of a remotely sensed surface parameter by contexture. Remote Sens. Environ 1999, 69, 30–42. [Google Scholar]
- Settle, J. On the use of remotely sensed data to extimate spatially averaged geophysical variables. IEEE Trans. Geosci. Remote Sens 2004, 42, 620–631. [Google Scholar]
- Settle, J.J. On the residual term in the linear mixture model and its dependence on the point spread function. IEEE Trans. Geosci. Remote Sens 2005, 43, 398–401. [Google Scholar]
- Hall, F.G.; Huemmrich, K.F.; Goetz, S.J.; Sellers, P.J.; Nickeson, J.E. Satellite remote sensing of surface energy balance: Success, failures, and unresolved issues in FIFE. J. Geophys. Res 1992, 97, 19061–19089. [Google Scholar]
- Friedl, M.A.; Davis, F.W.; Michaelsen, J.; Moritz, M.A. Scaling and uncertainty in the relationship between the NDVI and land surface biophysical variables: An analysis using a scene simulation model and data from FIFE. Remote Sens. Environ 1995, 54, 233–246. [Google Scholar]
- Sprintsin, M.; Karnieli, A.; Berliner, P.; Rotenberg, E.; Yakir, D.; Cohen, S. The effect of spatial resolution on the accuracy of leaf area index estimation for a forest planted in the desert transition zone. Remote Sens. Environ 2007, 109, 416–428. [Google Scholar]
- Zhang, X.; Yan, G.; Li, Q.; Li, Z.L.; Wan, H.; Guo, Z. Evaluating the fraction of vegetation cover based on NDVI spatial scale correction model. Int. J. Remote Sens 2006, 27, 5359–5372. [Google Scholar]
- Garrigues, S.; Allard, D.; Baret, F.; Weiss, M. Quantifying spatial heterogeneity at the landscape scale using variogram models. Remote Sens. Environ 2006, 103, 81–96. [Google Scholar]
- Ma, L.; Li, C.; Tang, B.; Tang, L.; Bi, Y.; Zhou, B.; Li, Z.L. Impact of spatial LAI heterogeneity on estimate of directional gap fraction from SPOT-satellite data. Sensors 2008, 8, 3767–3779. [Google Scholar]
- Zheng, G.; Moskal, L.M. Retrieving Leaf Area Index(LAI) using remote sensing: Theories, method and sensors. Sensors 2009, 9, 2719–2745. [Google Scholar]
- Tao, X.; Yan, B.; Wang, K.; Wu, D.; Fan, W.; Xu, X.; Liang, S. Scale transformation of Leaf Area Index product retrieved from multiresolution remotely sensed data: Analysis and case studies. Int. J. Remote Sens 2009, 30, 5383–5395. [Google Scholar]
- Aman, A.; Randriamanantena, H.P.; Podaire, A.; Frouin, R. Upscale integration of normalized difference vegetation index: the problem of spatial heterogeneity. IEEE Trans. Geosci. Remote Sens 1992, 30, 326–338. [Google Scholar]
- Huete, A.; Kim, H.J.; Miura, T. Scaling Dependencies and Uncertainties in Vegetation Index—Biophysical Retrievals in Heterogeneous Environments. Proceedings of 2005 IEEE International Geoscience and Remote Sensing Symposium, Seoul, Korea, 25–29 July 2005; 7, pp. 5029–5032.
- Thenkabail, P.S. Inter-sensor relationships between IKONOS and Landsat-7 ETM+ NDVI data in three ecoregions of Africa. Int. J. Remote Sens 2004, 20, 389–408. [Google Scholar]
- Maselli, F.; Gilabert, M.A.; Conse, C. Integration of high and low resolution NDVI data for monitoring vegetation in Mediterranean environments. Remote Sens. Environ 1998, 63, 208–218. [Google Scholar]
- Wood, E.F.; Lakshmi, V. Scaling water and energy fluxes in climate systems: Three land-atmospheric modeling experiments. J. Climate 1993, 6, 839–857. [Google Scholar]
- Price, J.C. Using spatial context in satellite data to infer regional scale evapotranspiration. IEEE Trans. Geosci. Remote Sens 1990, 28, 940–948. [Google Scholar]
- Cola, L.D. Multiresolution covariation among Landsat and AVHRR vegetation indices. In Scale in Remote Sensing and GIS; Quattrochi, D.A., Goodchild, M.F., Eds.; Lewis: Boca Raton, FL, USA, 1997; pp. 73–91. [Google Scholar]
- Liang, S. Numerical experiments on the spatial scaling of land surface albedo and leaf area index. Int. J. Remote Sens 2000, 19, 225–242. [Google Scholar]
- Garrigues, S.; Allard, D.; Baret, F.; Weiss, M. Influence of landscape spatial heterogeneity on the non-linear estimation of leaf area index from moderate spatial resolution remote sensing data. Remote Sens. Environ 2006, 105, 286–298. [Google Scholar]
- Hu, Z.; Islam, S. Effects of subgrid-scale heterogeneity of soil wetness and temperature on grid-scale evaporation and its parameterization. Int. J. Climatol 1998, 18, 49–63. [Google Scholar]
- Bonan, G.B.; Pollard, D.; Thompson, S.L. Influence of subgrid-scale heterogeneity in leaf area index, stomatal resistance, and soil moisture on grid-scale land-atmosphere interactions. J. Climate 1993, 6, 1883–1897. [Google Scholar]
- Pielke, R.A.; Dalu, G.A.; Snook, J.S.; Lee, T.J.; Kittel, T.G. Nonlinear influence of mesoscale land use on weather and climate. J. Climate 1991, 4, 1053–1069. [Google Scholar]
- Marht, L.; Sun, J. Dependence of surface exchange coefficients on averaging scale and grid size. Q. J. Roy. Meteorol. Soc 1995, 121, 1835–1852. [Google Scholar]
- Maayar, M.E.; Chen, J.M. Spatial scaling of evapotranspiration as affected by heterogeneities in vegetation, topography, and soil texture. Remote Sens. Environ 2006, 102, 33–51. [Google Scholar]
- Chen, B.; Chen, J.M.; Mo, G.; Yuen, C.W.; Margolis, H.; Higuchi, K.; Chan, D. Modeling and scaling coupled energy, water, and carbon fluxes based on remote sensing: An application to Canada’s landmass. J. Hydrometeorol 2007, 8, 123–143. [Google Scholar]
- Simic, A.; Chen, J.M.; Liu, J.; Csillag, F. Spatial scaling of net primary productivity using subpixel information. Remote Sens. Environ 2004, 93, 246–258. [Google Scholar]
- Zheng, D.; Heath, L.S.; Ducey, M.J.; Smith, J.E. Quantifying scaling effects on satellite-derived forest area estimates for the conterminous USA. Int. J. Remote Sens 2009, 30, 3097–3114. [Google Scholar]
- Propastin, P.A. Spatial non-stationarity and scale-dependency of prediction accuracy in the remote estimation of LAI over a tropical rainforest in Sulawesi, Indonesia. Remote Sens. Environ 2009, 113, 2234–2242. [Google Scholar]
- Raffy, M. Change of scale in models of remote sensing: A general method for spatialization of models. Remote Sens. Environ 1992, 40, 101–112. [Google Scholar]
- Raffy, M. Heterogeneity and change of scale in models of remote sensing. Int. J. Remote Sens 1994, 15, 2359–2380. [Google Scholar]
- Yoshioka, H.; Wada, T.; Obata, K.; Miura, T. Monotonicity of Area Averaged NDVI as a Function of Spatial Resolution Based on a Variable Endmember Linear Mixture Model. Proceedings of 2008 IEEE International Geoscience & Remote Sensing Symposium, Boston, MA, USA, 6–11 July 2008; III, pp. 415–418.
- Horwitz, H.M.; Nalepka, R.F.; Hyde, P.D.; Morgenstern, J.P. Estimating the Proportions of Objects within a Single Resolution Element of a Multispectral Scanner. Proceedings of 7th International Symposium on Remote Sensing of Environment, Ann Arbor, MI, USA, 17–21 may 1971; pp. 1307–1320.
- Smith, M.O.; Johnson, P.E.; Adams, J.B. Quantitative determination of mineral types and abundances from reflectance spectra using principal components analysis. J. Geophys. Res 1985, 90 Suppl., C797–C804. [Google Scholar]
- Adams, J.B.; Smith, M.O.; Johnson, P.E. Spectral mixture modeling: A new analysis of rock and soil types at the Viking Lander 1 Site. J. Geophys. Res 1986, 91, 8098–8112. [Google Scholar]
- Smith, M.O.; Ustin, S.L.; Adams, J.B.; Gillespie, A.R. Vegetation in deserts: I. A regional measure of abundance from multispectral images. Remote Sens. Environ 1990, 31, 1–26. [Google Scholar]
- Settle, J.J.; Drake, N.A. Linear mixing and the estimation of ground cover proportions. Int. J. Remote Sens 1993, 14, 1159–1177. [Google Scholar]




Share and Cite
Obata, K.; Wada, T.; Miura, T.; Yoshioka, H. Scaling Effect of Area-Averaged NDVI: Monotonicity along the Spatial Resolution. Remote Sens. 2012, 4, 160-179. https://doi.org/10.3390/rs4010160
Obata K, Wada T, Miura T, Yoshioka H. Scaling Effect of Area-Averaged NDVI: Monotonicity along the Spatial Resolution. Remote Sensing. 2012; 4(1):160-179. https://doi.org/10.3390/rs4010160
Chicago/Turabian StyleObata, Kenta, Takahiro Wada, Tomoaki Miura, and Hiroki Yoshioka. 2012. "Scaling Effect of Area-Averaged NDVI: Monotonicity along the Spatial Resolution" Remote Sensing 4, no. 1: 160-179. https://doi.org/10.3390/rs4010160




