Effects of Individual Tree Detection Error Sources on Forest Management Planning Calculations
Abstract
:1. Introduction
2. Material and Methods
2.1. Study Site
2.2. Logging Machine Measurements
| Stand characteristic | Mean | Minimum | Maximum | Standard deviation |
|---|---|---|---|---|
| Stem number | 332 | 46 | 692 | 244 |
| BA, m2 | 15.5 | 4.6 | 37.5 | 11.4 |
| Vtotal, m3 | 137 | 41 | 316.5 | 94.4 |
| Dg, cm | 31.4 | 26 | 43.8 | 4.8 |
| Hg, m | 18.3 | 10.3 | 23.6 | 3.4 |
2.3. Simulation of Various Error Sources in ITD
2.3.1. Tree Detection Error
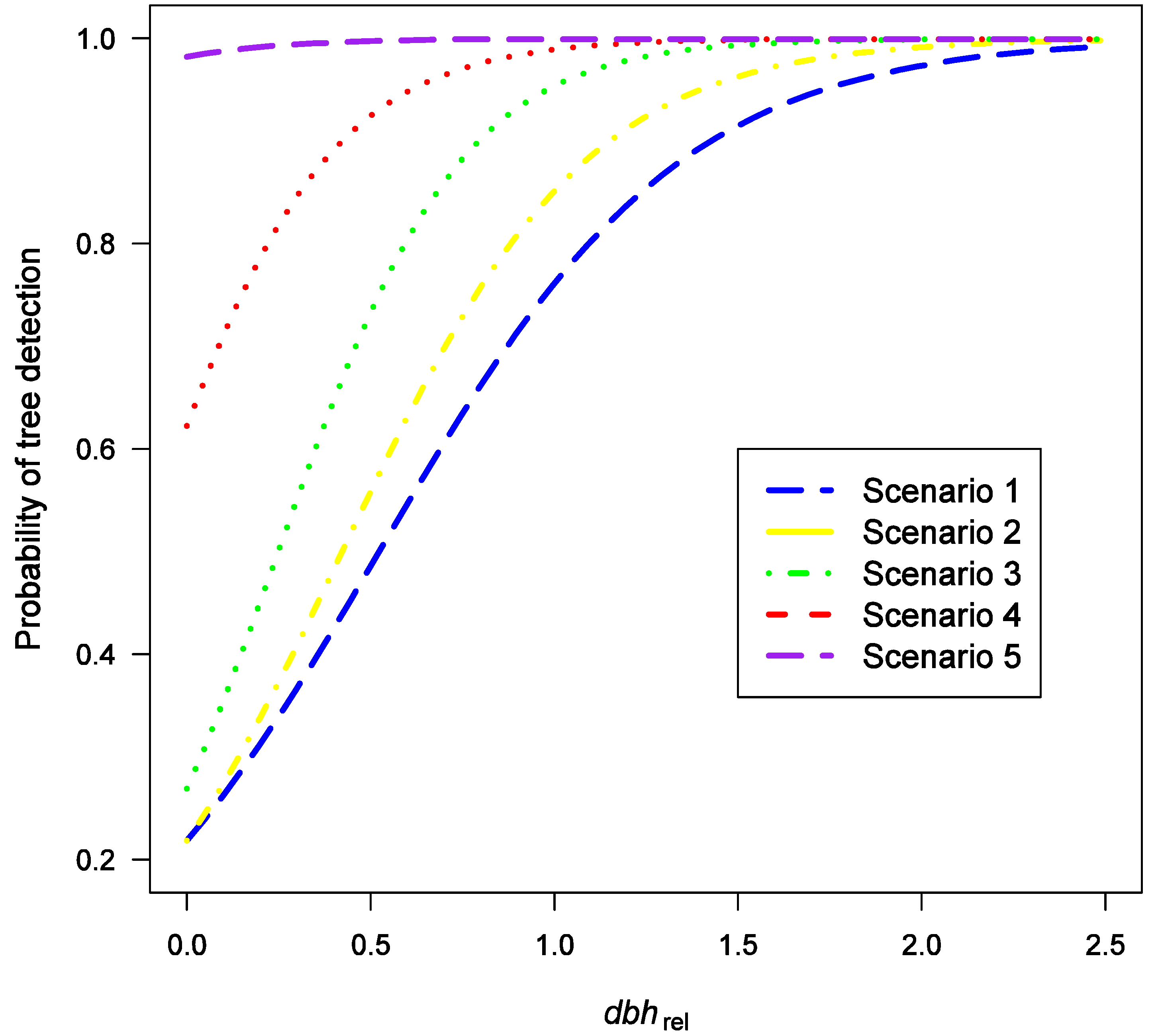
2.3.2. Tree Height and Diameter Prediction Errors
2.3.3. Monte Carlo Simulations
3. Results
3.1. Effect of Tree Detection
| Detection accuracy, % | RMSE, % | |||||||
|---|---|---|---|---|---|---|---|---|
| Scenario | Stem number | Vtotal | BA | Vtotal | Hg | Dg | Vlog | Vpulp |
| 1 | 60.2 | 75.9 | 32.4 | 29.0 | 7.8 | 5.4 | 25.1 | 37.8 |
| 2 | 65.1 | 77.4 | 29.4 | 27.0 | 6.1 | 4.5 | 24.4 | 33.3 |
| 3 | 84.9 | 94.5 | 12.0 | 10.0 | 3.9 | 2.5 | 7.5 | 14.2 |
| 4 | 95.2 | 98.6 | 4.9 | 4.1 | 1.7 | 1.1 | 3.1 | 6.1 |
| 5 | 99.8 | 100 | 0.6 | 0.5 | 0.2 | 0.1 | 0.2 | 1.0 |
3.2. Effects of Diameter Prediction and Combined Effects of Diameter Prediction and Tree Detection
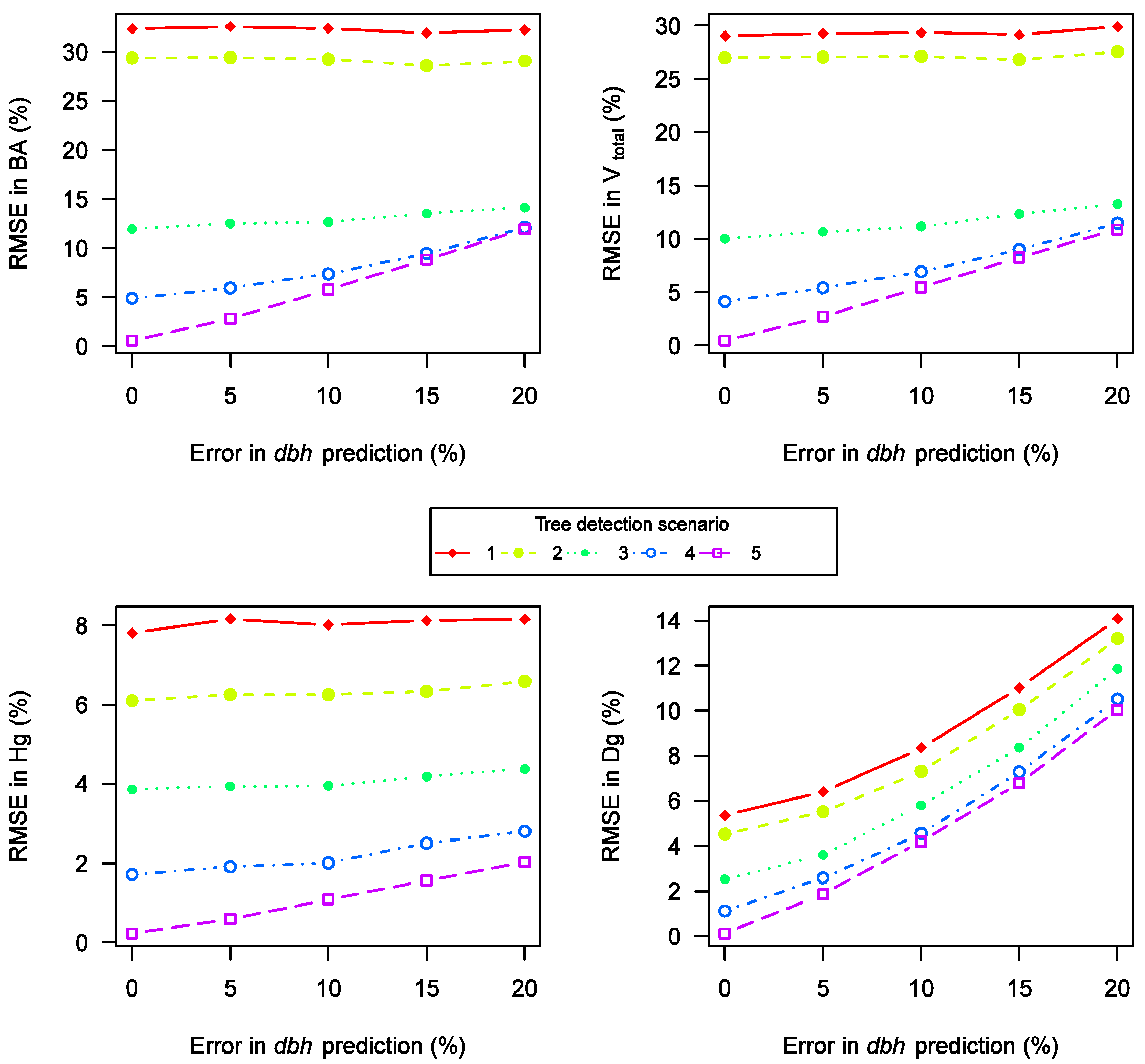
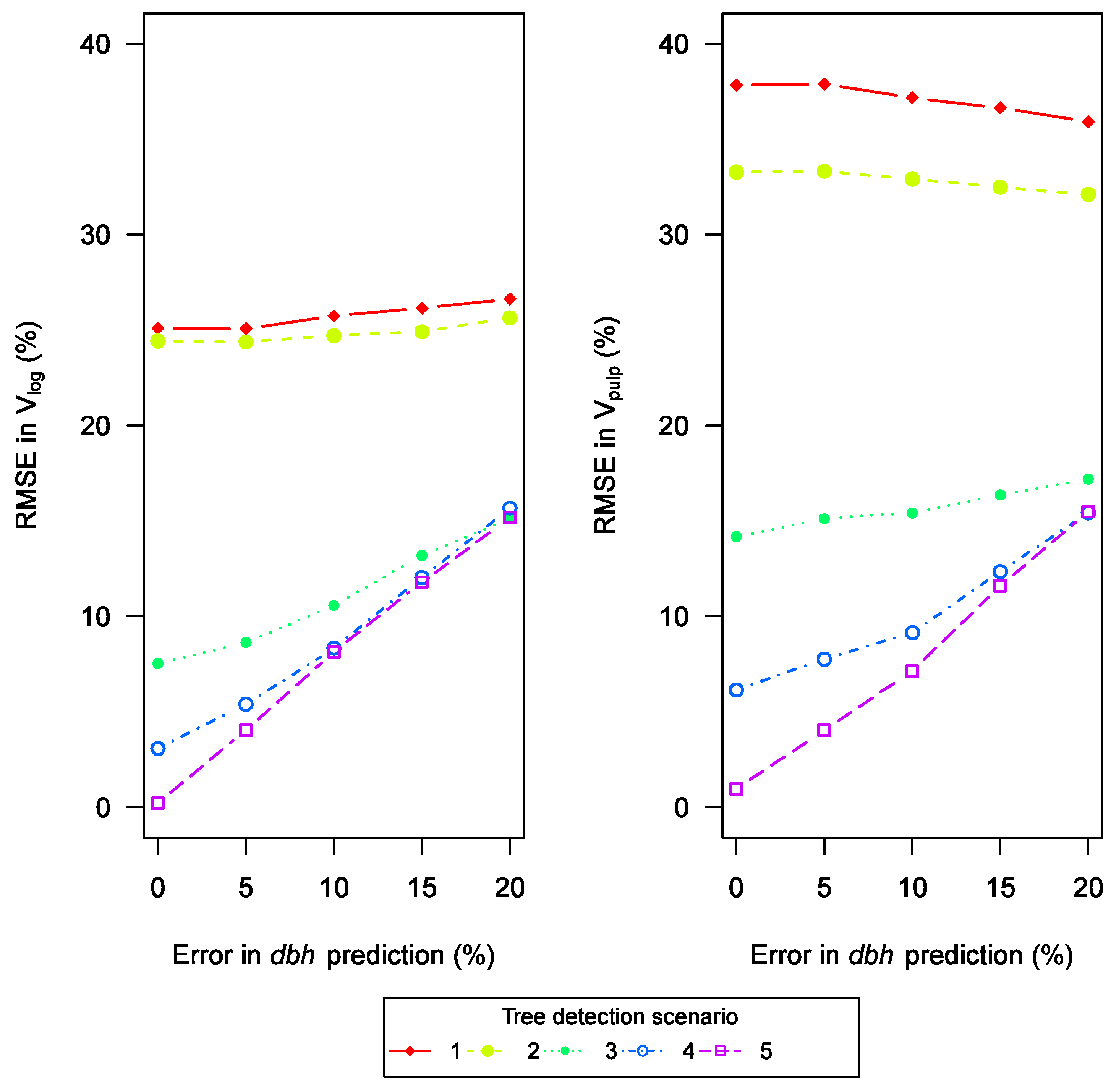
3.3. Effect of Tree Height Measurements
4. Discussion and Conclusions
References
- Næsset, E. Predicting forest stand characteristics with airborne scanning laser using a practical two-stage procedure and field data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Hyyppä, J.; Inkinen, M. Detecting and estimating attributes for single trees using laser scanner. Photogramm. J. Fin. 1999, 16, 27–42. [Google Scholar]
- Packalén, P.; Maltamo, M. The k-MSN method in the prediction of species specific stand attributes using airborne laser scanning and aerial photographs. Remote Sens. Environ. 2007, 109, 328–341. [Google Scholar] [CrossRef]
- Brandtberg, T. Automatic Individual Tree-Based Analysis of High Spatial Resolution Remotely Sensed Data. Ph.D. Thesis, Centre for Image Analysis, Swedish University of Agricultural Sciences, Uppsala, Sweden, 1999. [Google Scholar]
- Persson, Å.; Holmgren, J.; Söderman, U. Detecting and measuring individual trees using an airborne laser scanner. Photogramm. Eng. Remote Sensing 2002, 68, 925–932. [Google Scholar]
- Pitkänen, J.; Maltamo, M.; Hyyppä, J.; Yu, X. Adaptive Methods for Individual Tree Detection on Airborne Laser Based Canopy Height Model. In Proceedings of ISPRS Working Group VIII/2: Laser-Scanners for Forest and Landscape Assessment, Freiburg, Germany, 3–6 October 2004; Theis, M., Koch, B., Spiecker, H., Weinacker, H., Eds.; University of Freiburg: Freiburg, Germany, 2004; pp. 187–191. [Google Scholar]
- Yu, X.; Hyyppä, J.; Holopainen, M.; Vastaranta, M.; Viitala, R. Predicting individual tree attributes from airborne laser point clouds based on random forest technique. ISPRS J. Photogramm. Remote Sens. 2011, 66, 28–37. [Google Scholar] [CrossRef]
- Peuhkurinen, J.; Maltamo, M.; Malinen, J.; Pitkänen, J.; Packalén, P. Preharvest measurement of marked stands using airborne laser scanning. Forest Sci. 2007, 53, 653–661. [Google Scholar]
- Kaartinen, H.; Hyyppä, J. EuroSDR/ISPRS Project, Commission II “Tree Extraction”, Final Report; EuroSDR Official Publication No. 53; European Spatial Data Research: Dublin, Ireland, 2008. [Google Scholar]
- Holmgren, J.; Persson, Å. Identifying species of individual trees using airborne laser scanner. Remote Sens. Environ. 2004, 90, 415–423. [Google Scholar] [CrossRef]
- Liang, X.; Hyyppä, J.; Matikainen, L. Deciduous-Coniferous Tree Classification Using Difference Between First and Last Pulse Laser Signatures. In Proceedings of the ISPRS Workshop on Laser Scanning 2007 and SilviLaser 2007, Espoo, Finland, 12–14 September 2007.Rönnholm, P.; Hyyppä, H.; Hyyppä, J. (Eds.) IAPRS; 2007; Volume XXXVI, Part 3/W52; pp. 253–257.
- Holmgren, J.; Persson, Å.; Söderman, U. Species identification of individual trees by combining high resolution LiDAR data with multi-spectral images. Int. J. Remote Sens. 2008, 29, 1537–1552. [Google Scholar] [CrossRef]
- Vauhkonen, J.; Tokola, T.; Packalén, P.; Maltamo, M. Identification of Scandinavian commercial species of individual trees from airborne laser scanning data using alpha shape metrics. Forest Sci. 2009, 55, 37–47. [Google Scholar]
- Vauhkonen, J.; Korpela, I.; Maltamo, M.; Tokola, T. Imputation of single-tree attributes using airborne laser scanning-based height, intensity, and alpha shape metrics. Remote Sens. Environ. 2010, 114, 1263–1276. [Google Scholar] [CrossRef]
- Korpela, I.; Ørka, H.O.; Maltamo, M.; Tokola, T.; Hyyppä, J. Tree species classification using airborne LIDAR—Effects by stand and tree parameters, downsizing the training set, intensity normalization and sensor type. Silva Fenn. 2010, 44, 319–339. [Google Scholar] [CrossRef]
- Puttonen, E.; Litkey, P.; Hyyppä, J. Individual tree species classification by illuminated—Shaded area separation. Remote Sens. 2010, 2, 19–35. [Google Scholar] [CrossRef]
- Kalliovirta, J.; Tokola, T. Functions for estimating stem diameter and tree age using tree height, crown width and existing stand database information. Silva Fenn. 2005, 39, 227–248. [Google Scholar] [CrossRef]
- Maltamo, M.; Packalén, P.; Peuhkurinen, J.; Suvanto, A.; Pesonen, A.; Hyyppä, J. Experiences and Possibilities of ALS Based Forest Inventory in Finland. In Proceedings of the ISPRS Workshop on Laser Scanning 2007 and SilviLaser 2007, Espoo, Finland, 12–14 September 2007; Rönnholm, P., Hyyppä, H., Hyyppä, J., Eds.; IAPRS: Silves, Portugal, 2007; Volume XXXVI, Part 3/W52. pp. 270–279. [Google Scholar]
- Packalén, P.; Pitkänen, J.; Maltamo, M. Comparison of Individual Tree Detection and Canopy Height Distribution Approaches: A Case Study in Finland. In Proceedings of SilviLaser 2008, 8th International Conference on LiDAR Applications in Forest Assessment and Inventory, Edinburgh, UK, 17–19 September 2008; Hill, R., Rossette, J., Suárez, J., Eds.; 2008; pp. 22–29. [Google Scholar]
- Vastaranta, M.; Holopainen, M.; Haapanen, R.; Yu, X.; Melkas, T.; Hyyppä, J.; Hyyppä, H. Comparison Between an Area-Based and Individual Tree Detection Method for Low-Pulse Density ALS-Based Forest Inventory. In Proceedings of ISPRS Workshop LaserScanning 2009, Paris, France, 1–2 September 2009; Bretar, F., Pierrot-Deseilligny, M., Vosselman, G., Eds.; 2009; pp. 147–151. [Google Scholar]
- Maltamo, M.; Peuhkurinen, J.; Malinen, J.; Vauhkonen, J.; Packalén, P.; Tokola, T. Predicting tree attributes and quality characteristics of scots pine using airborne laser scanning data. Silva Fenn. 2009, 43, 507–521. [Google Scholar] [CrossRef]
- Nelson, R.; Krabill, W.; Tonelli, J. Estimating forest biomass and volume using airborne laser data. Remote Sens. Environ. 1988, 24, 247–267. [Google Scholar] [CrossRef]
- Hyyppä, J.; Hyyppä, H.; Yu, X.; Kaartinen, H.; Kukko, H.; Holopainen, M. Forest Inventory Using Small-Footprint Airborne lidar. In Topographic Laser Ranging and Scanning: Principles and Processing; Shan, J., Toth, C.K., Eds.; CRC Press: Boca Raton, FL, USA, 2009; pp. 335–370. [Google Scholar]
- Maltamo, M.; Eerikäinen, K.; Pitkänen, J.; Hyyppä, J.; Vehmas, M. Estimation of timber volume and stem density based on scanning laser altimetry and expected tree size distribution functions. Remote Sens. Environ. 2004, 90, 319–330. [Google Scholar] [CrossRef]
- Yu, X.; Hyyppä, J.; Holopainen, M.; Vastaranta, M. Comparison of area-based and individual tree-based methods for predicting plot-level forest attributes. Remote Sens. 2010, 2, 1481–1495. [Google Scholar] [CrossRef]
- StanForD: Standard for Forestry Data and Communication; SkogForsk: Uppsala, Sweden, 2009; Available online: http://www.skogforsk.se/PageFiles/60712/StanForD_MainDoc_070327.pdf (accessed on 12 April 2011).
- Varjo, J. Latvan Hukkaosan Pituusmallit Männylle, Kuuselle ja Koivulle Metsurimittausta Varten. Puutavaran Mittauksen Kehittämistutkimuksia 1989–93. In Finnish Forest Research Institute Research Papers 1995; Verkasalo, E., Ed.; 1995; Volume 558, pp. 21–23. [Google Scholar]
- Korpela, I. Individual Tree Measurements by Means of Digital Aerial Photogrammetry. Ph.D. Thesis, University of Helsinki, Helsinki, Finland, 2004. [Google Scholar]
- Falkowski, M.; Smith, A.; Gessler, P.; Hudak, A.; Vierling, L.; Evans, J. The influence of conifer forest canopy cover on the accuracy of two individual tree measurement algorithms using lidar data. Can. J. Remote Sens. 2008, 34, 338–350. [Google Scholar] [CrossRef]
- Mäkelä, A. Performance analyses of a process based stand growth model using Monte-Carlo techniques. Scan. J. Forest Res. 1988, 3, 315–331. [Google Scholar] [CrossRef]
- Kangas, A. On the prediction bias and variance in long-term growth projections. Forest Ecol. Manag. 1997, 96, 207–216. [Google Scholar] [CrossRef]
- Kangas, A. Methods for assessing uncertainty of growth and yield predictions. Can. J. Forest Res. 1999, 29, 1357–1364. [Google Scholar] [CrossRef]
- Mäkinen, A.; Holopainen, M.; Rasinmäki, J.; Kangas, A. Propagating the errors of initial forest variables through stand- and tree-level growth simulators. Eur. J. Forest Res. 2009, 129, 887–897. [Google Scholar]
- Holopainen, M.; Mäkinen, A.; Rasinmäki, J.; Hyyppä, J.; Hyyppä, H.; Kaartinen, H.; Viitala, R.; Vastaranta, M.; Kangas, A. Effect of tree level airborne laser scanning accuracy on the timing and expected value of harvest decisions. Eur. J. Forest Res. 2010, 129, 899–907. [Google Scholar] [CrossRef]
- Mäkinen, A.; Kangas, A.; Mehtätalo, L. Correlations, distributions, and trends in forest inventory errors and their effects on forest planning. Can. J. Forest Res. 2010, 40, 1386–1396. [Google Scholar] [CrossRef]
- Breidenbach, J.; Naesset, E.; Lien, V.; Gobakken, T.; Solberg, S. Prediction of species specific forest inventory attributes using a nonparametric semi-individual tree crown approach based on fused airborne laser scanning and multispectral data. Remote Sens. Environ. 2010, 114, 911–924. [Google Scholar] [CrossRef]
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Vastaranta, M.; Holopainen, M.; Yu, X.; Hyyppä, J.; Mäkinen, A.; Rasinmäki, J.; Melkas, T.; Kaartinen, H.; Hyyppä, H. Effects of Individual Tree Detection Error Sources on Forest Management Planning Calculations. Remote Sens. 2011, 3, 1614-1626. https://doi.org/10.3390/rs3081614
Vastaranta M, Holopainen M, Yu X, Hyyppä J, Mäkinen A, Rasinmäki J, Melkas T, Kaartinen H, Hyyppä H. Effects of Individual Tree Detection Error Sources on Forest Management Planning Calculations. Remote Sensing. 2011; 3(8):1614-1626. https://doi.org/10.3390/rs3081614
Chicago/Turabian StyleVastaranta, Mikko, Markus Holopainen, Xiaowei Yu, Juha Hyyppä, Antti Mäkinen, Jussi Rasinmäki, Timo Melkas, Harri Kaartinen, and Hannu Hyyppä. 2011. "Effects of Individual Tree Detection Error Sources on Forest Management Planning Calculations" Remote Sensing 3, no. 8: 1614-1626. https://doi.org/10.3390/rs3081614
APA StyleVastaranta, M., Holopainen, M., Yu, X., Hyyppä, J., Mäkinen, A., Rasinmäki, J., Melkas, T., Kaartinen, H., & Hyyppä, H. (2011). Effects of Individual Tree Detection Error Sources on Forest Management Planning Calculations. Remote Sensing, 3(8), 1614-1626. https://doi.org/10.3390/rs3081614






